Spin-Wave Channeling in Magnetization-Graded Nanostrips
Abstract
:1. Introduction
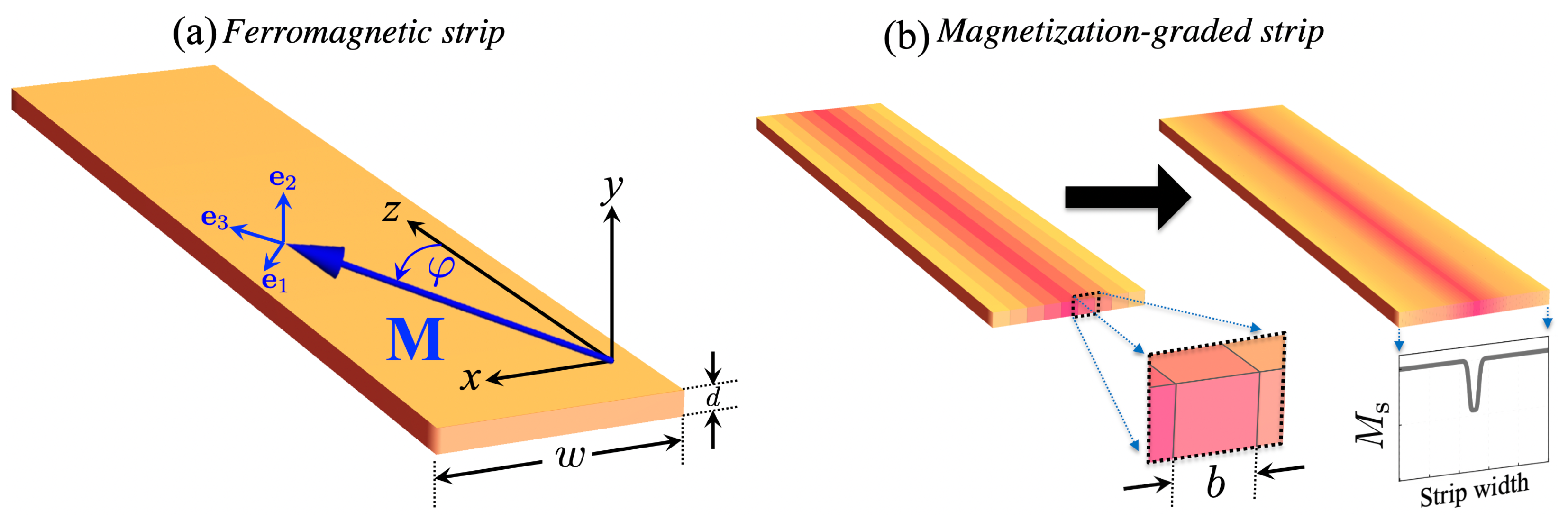
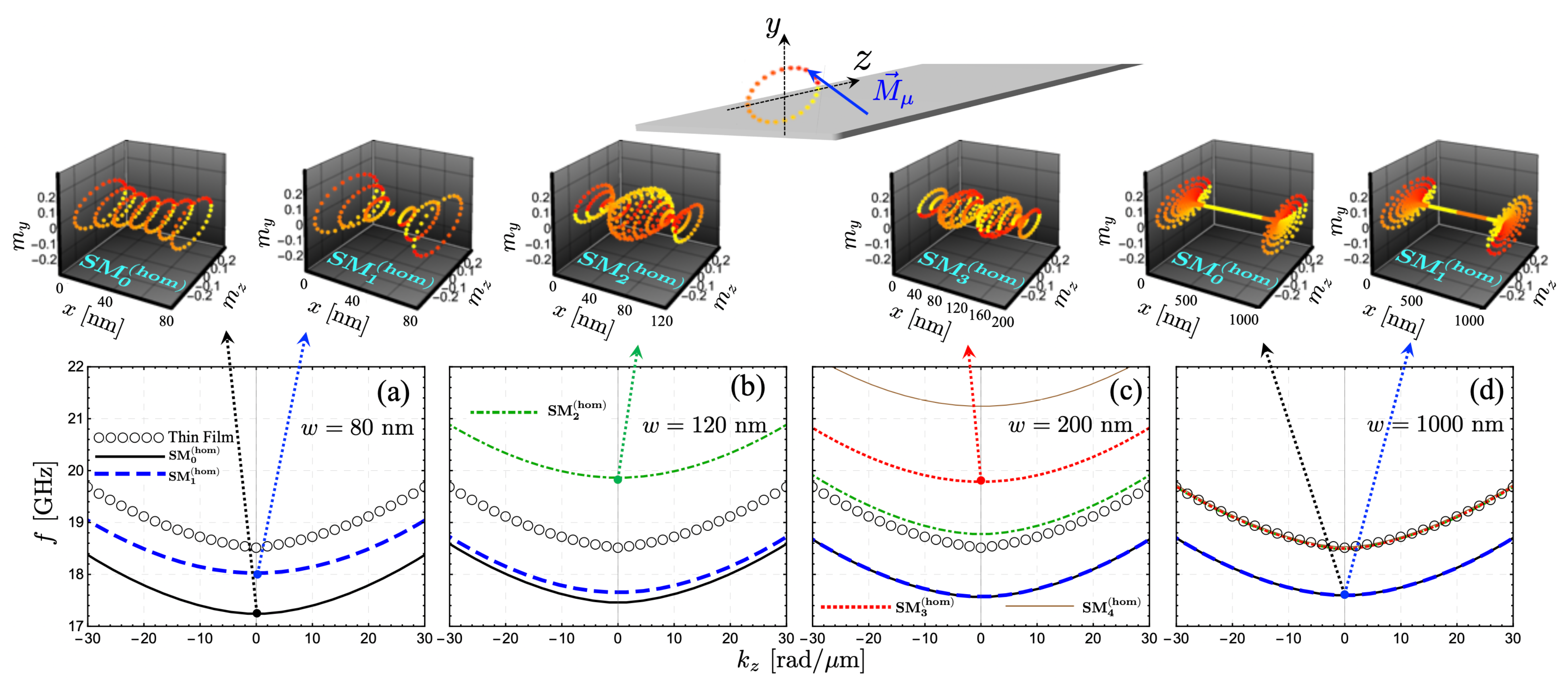
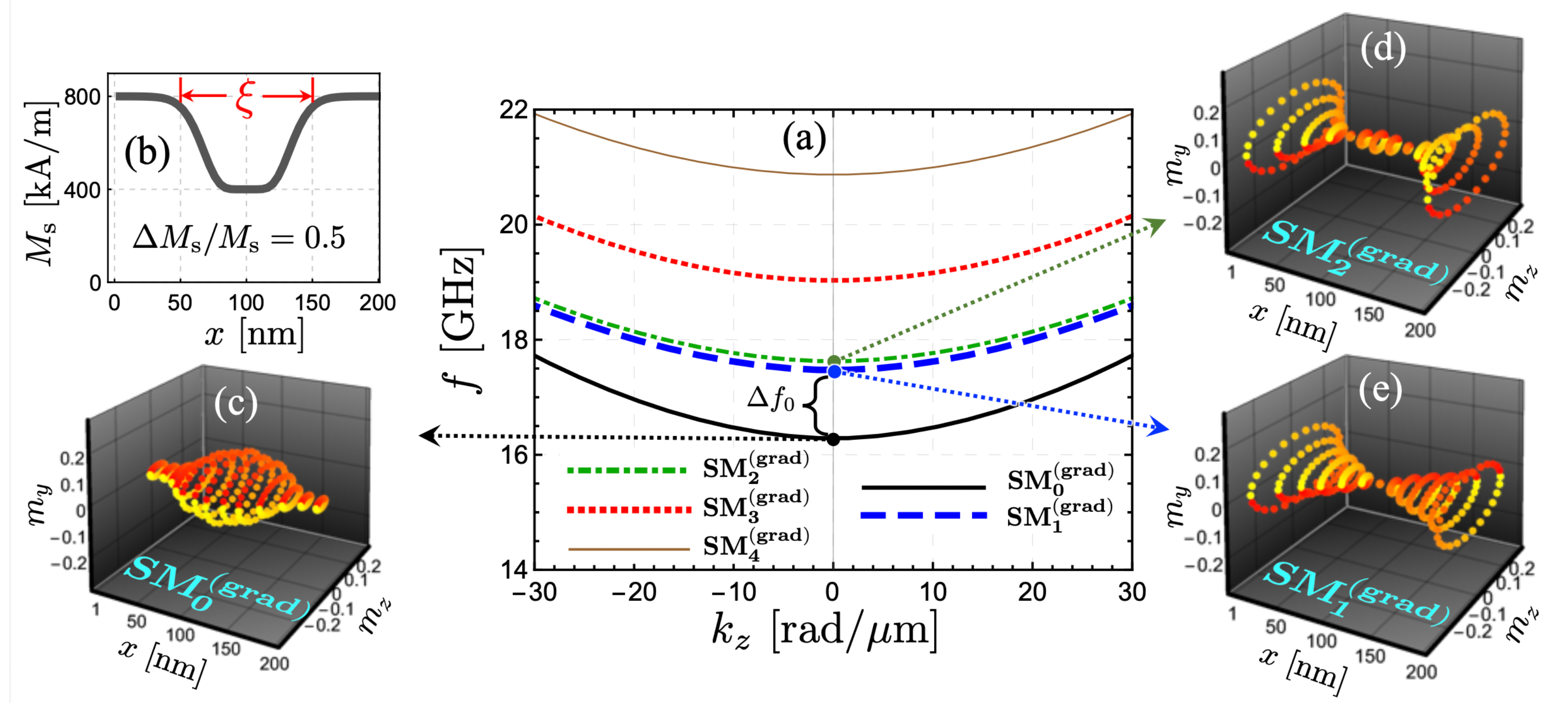
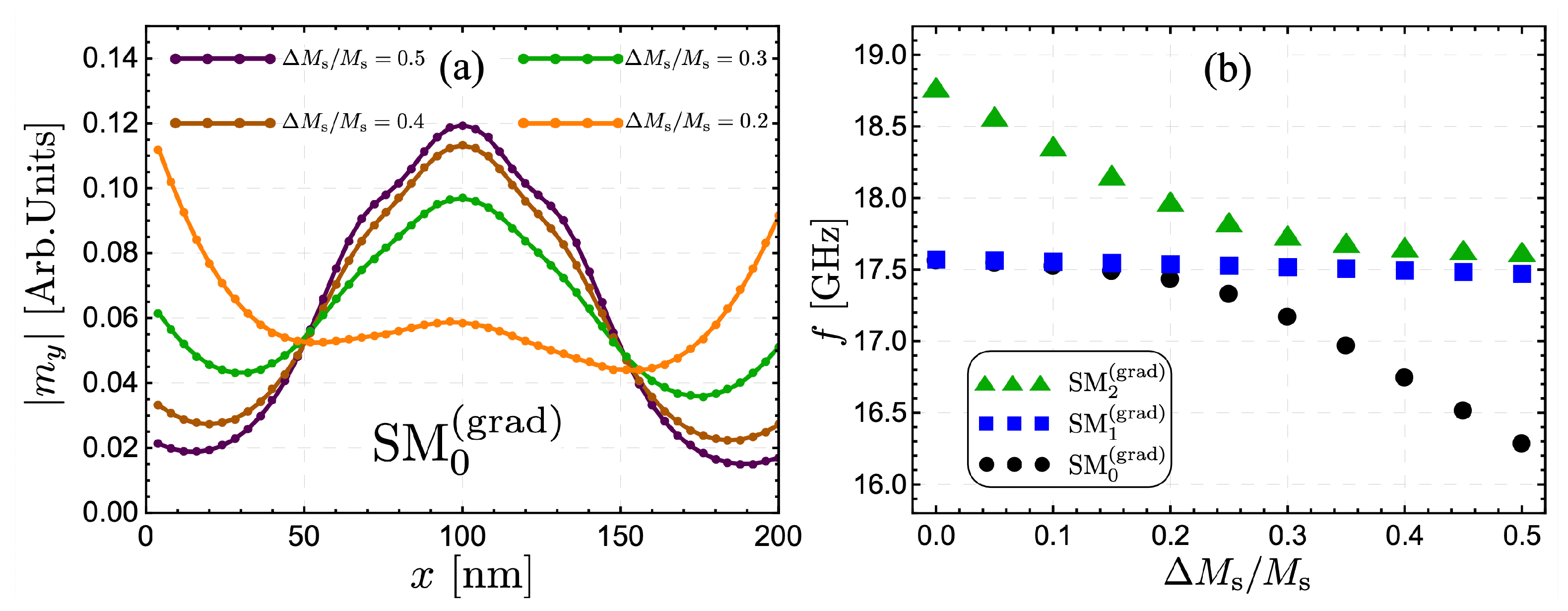
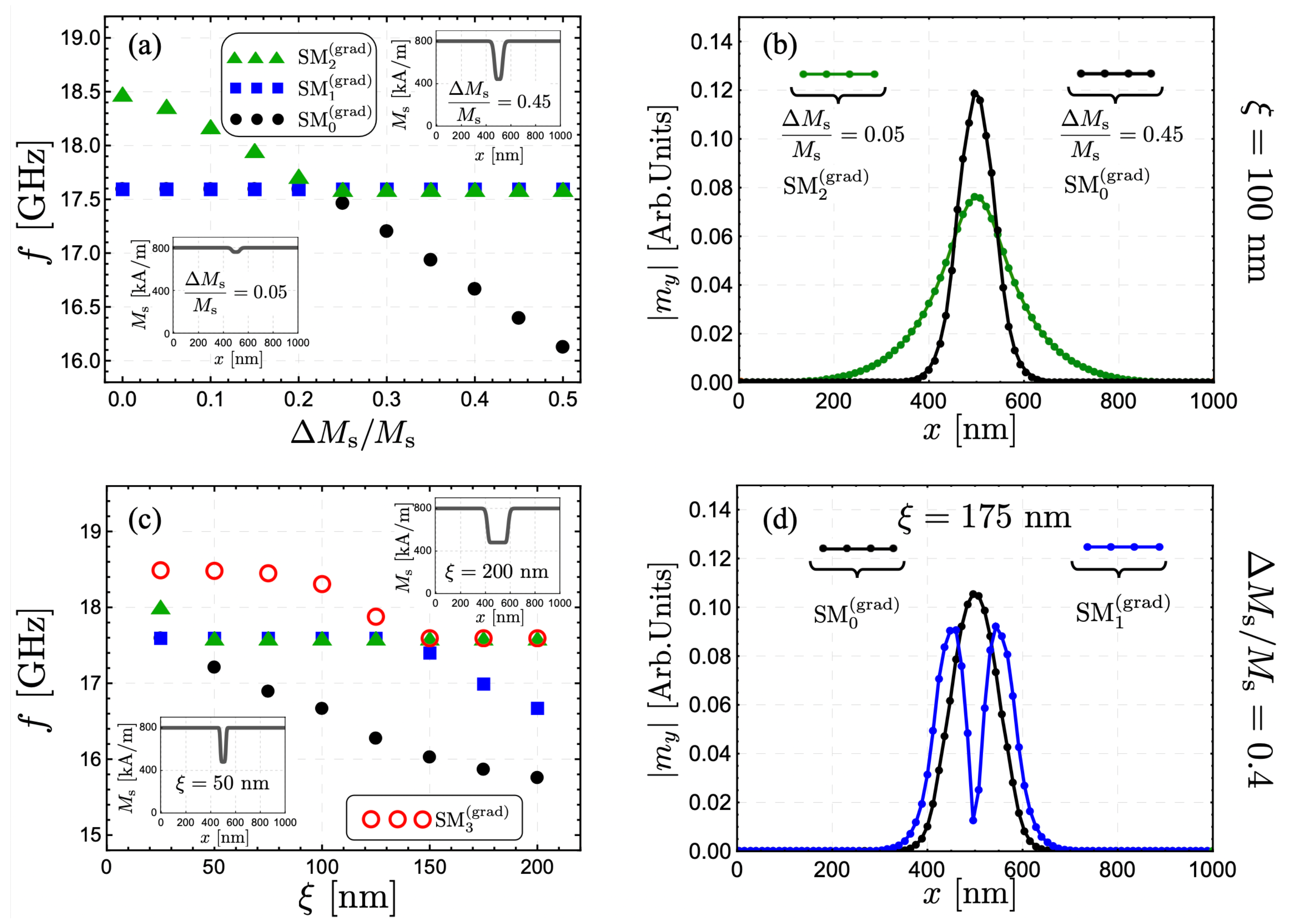
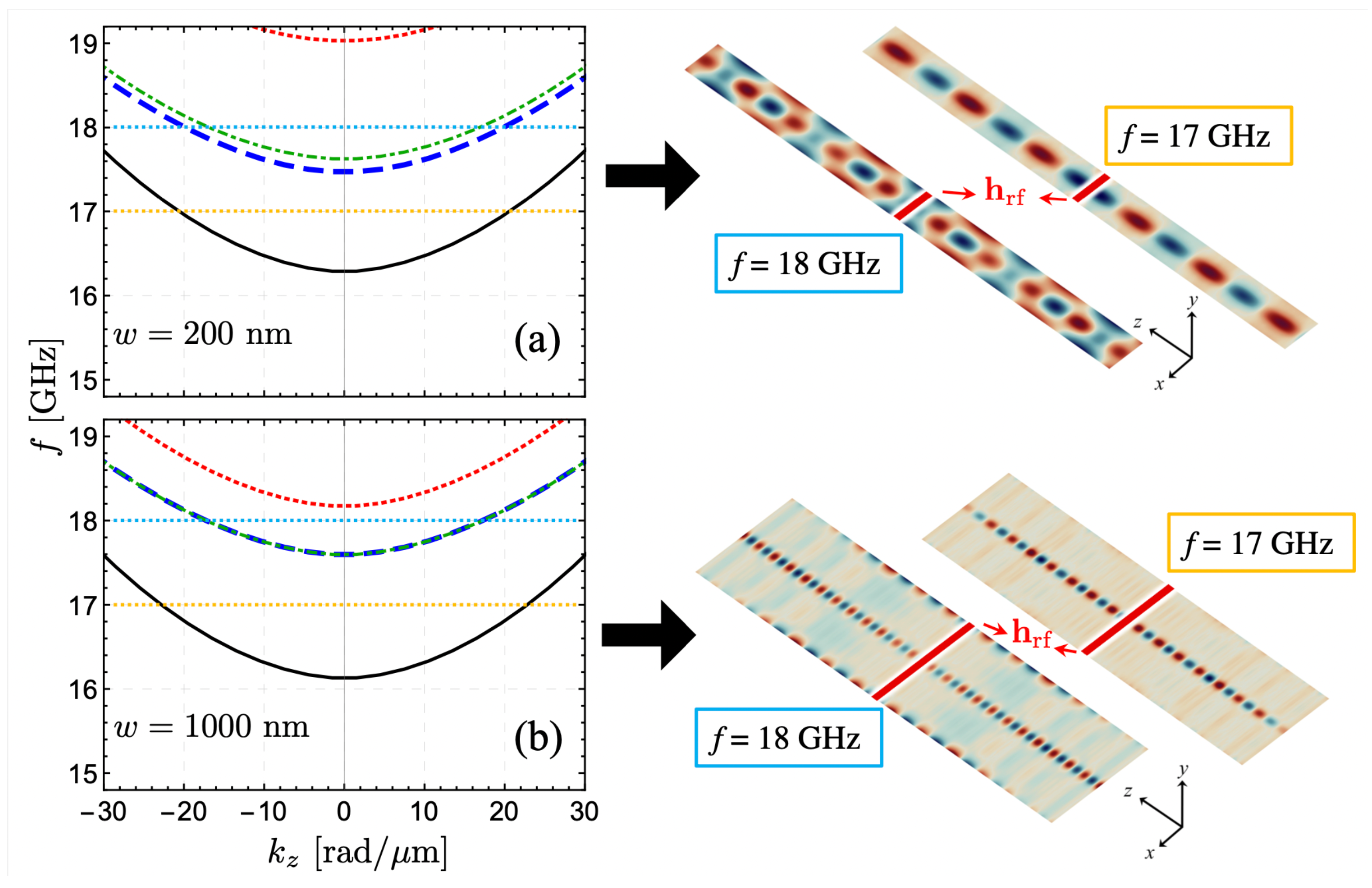
2. Results and Discussion
3. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Dynamic Matrix Method
Appendix B. Dipolar Interaction
Appendix C. Exchange Interaction
References
- Veerakumar, V.; Camley, R.E. Magnon focusing in thin ferromagnetic films. Phys. Rev. B 2006, 74, 214401. [Google Scholar] [CrossRef]
- Demidov, V.E.; Demokritov, S.O.; Birt, D.; O’Gorman, B.; Tsoi, M.; Li, X. Radiation of spin waves from the open end of a microscopic magnetic-film waveguide. Phys. Rev. B 2009, 80, 014429. [Google Scholar] [CrossRef]
- Schneider, T.; Serga, A.A.; Chumak, A.V.; Sandweg, C.W.; Trudel, S.; Wolff, S.; Kostylev, M.P.; Tiberkevich, V.S.; Slavin, A.N.; Hillebrands, B. Nondiffractive Subwavelength Wave Beams in a Medium with Externally Controlled Anisotropy. Phys. Rev. Lett. 2010, 104, 197203. [Google Scholar] [CrossRef] [PubMed]
- Mansfeld, S.; Topp, J.; Martens, K.; Toedt, J.N.; Hansen, W.; Heitmann, D.; Mendach, S. Spin Wave Diffraction and Perfect Imaging of a Grating. Phys. Rev. Lett. 2012, 108, 047204. [Google Scholar] [CrossRef]
- Sebastian, T.; Brächer, T.; Pirro, P.; Serga, A.A.; Hillebrands, B.; Kubota, T.; Naganuma, H.; Oogane, M.; Ando, Y. Nonlinear Emission of Spin-Wave Caustics from an Edge Mode of a Microstructured Co2Mn0.6Fe0.4Si Waveguide. Phys. Rev. Lett. 2013, 110, 067201. [Google Scholar] [CrossRef]
- Gieniusz, R.; Ulrichs, H.; Bessonov, V.D.; Guzowska, U.; Stognii, A.I.; Maziewski, A. Single antidot as a passive way to create caustic spin-wave beams in yttrium iron garnet films. Appl. Phys. Lett. 2013, 102, 102409. [Google Scholar] [CrossRef]
- Kim, J.V.; Stamps, R.L.; Camley, R.E. Spin Wave Power Flow and Caustics in Ultrathin Ferromagnets with the Dzyaloshinskii-Moriya Interaction. Phys. Rev. Lett. 2016, 117, 197204. [Google Scholar] [CrossRef]
- Bible, J.J.; Camley, R.E. Focusing of high-wave-vector magnons. Phys. Rev. B 2017, 95, 224412. [Google Scholar] [CrossRef]
- Krivoruchko, V.N.; Savchenko, A.S.; Kruglyak, V.V. Electric-field control of spin-wave power flow and caustics in thin magnetic films. Phys. Rev. B 2018, 98, 024427. [Google Scholar] [CrossRef]
- Gallardo, R.A.; Alvarado-Seguel, P.; Kákay, A.; Lindner, J.; Landeros, P. Spin-wave focusing induced by dipole-dipole interaction in synthetic antiferromagnets. Phys. Rev. B 2021, 104, 174417. [Google Scholar] [CrossRef]
- Winter, J.M. Bloch Wall Excitation. Application to Nuclear Resonance in a Bloch Wall. Phys. Rev. 1961, 124, 452–459. [Google Scholar] [CrossRef]
- Wagner, K.; Kákay, A.; Schultheiss, K.; Henschke, A.; Sebastian, T.; Schultheiss, H. Magnetic domain walls as reconfigurable spin-wave nanochannels. Nat. Nanotechnol. 2016, 11, 432–436. [Google Scholar] [CrossRef] [PubMed]
- Sluka, V.; Schneider, T.; Gallardo, R.A.; Kákay, A.; Weigand, M.; Warnatz, T.; Mattheis, R.; Roldán-Molina, A.; Landeros, P.; Tiberkevich, V.; et al. Emission and propagation of 1D and 2D spin waves with nanoscale wavelengths in anisotropic spin textures. Nat. Nanotechnol. 2019, 14, 328–333. [Google Scholar] [CrossRef] [PubMed]
- Kataoka, M. Spin Waves in Systems with Long Period Helical Spin Density Waves Due to the Antisymmetric and Symmetric Exchange Interactions. J. Phys. Soc. Jpn. 1987, 56, 3635–3647. [Google Scholar] [CrossRef]
- Cortés-Ortuño, D.; Landeros, P. Influence of the Dzyaloshinskii–Moriya interaction on the spin-wave spectra of thin films. J. Phys. Condens. Matter 2013, 25, 156001. [Google Scholar] [CrossRef]
- Iguchi, Y.; Uemura, S.; Ueno, K.; Onose, Y. Nonreciprocal magnon propagation in a noncentrosymmetric ferromagnet LiFe5O8. Phys. Rev. B 2015, 92, 184419. [Google Scholar] [CrossRef]
- Di, K.; Zhang, V.L.; Lim, H.S.; Ng, S.C.; Kuok, M.H.; Yu, J.; Yoon, J.; Qiu, X.; Yang, H. Direct Observation of the Dzyaloshinskii-Moriya Interaction in a Pt/Co/Ni Film. Phys. Rev. Lett. 2015, 114, 047201. [Google Scholar] [CrossRef]
- Cho, J.; Kim, N.H.; Lee, S.; Kim, J.S.; Lavrijsen, R.; Solignac, A.; Yin, Y.; Han, D.S.; van Hoof, N.J.J.; Swagten, H.J.M.; et al. Thickness dependence of the interfacial Dzyaloshinskii-Moriya interaction in inversion symmetry broken systems. Nat. Commun. 2015, 6, 7635. [Google Scholar] [CrossRef] [PubMed]
- Nembach, H.T.; Shaw, J.M.; Weiler, M.; Jue, E.; Silva, T.J. Linear relation between Heisenberg exchange and interfacial Dzyaloshinskii-Moriya interaction in metal films. Nat. Phys. 2015, 11, 825–829. [Google Scholar] [CrossRef]
- Belmeguenai, M.; Adam, J.P.; Roussigné, Y.; Eimer, S.; Devolder, T.; Kim, J.V.; Cherif, S.M.; Stashkevich, A.; Thiaville, A. Interfacial Dzyaloshinskii-Moriya interaction in perpendicularly magnetized Pt/Co/AlOx ultrathin films measured by Brillouin light spectroscopy. Phys. Rev. B 2015, 91, 180405. [Google Scholar] [CrossRef]
- Chaurasiya, A.K.; Banerjee, C.; Pan, S.; Sahoo, S.; Choudhury, S.; Sinha, J.; Barman, A. Direct Observation of Interfacial Dzyaloshinskii-Moriya Interaction from Asymmetric Spin-wave Propagation in W/CoFeB/SiO2 Heterostructures Down to Sub-nanometer CoFeB Thickness. Sci. Rep. 2016, 6, 32592. [Google Scholar] [CrossRef]
- Seki, S.; Okamura, Y.; Kondou, K.; Shibata, K.; Kubota, M.; Takagi, R.; Kagawa, F.; Kawasaki, M.; Tatara, G.; Otani, Y.; et al. Magnetochiral nonreciprocity of volume spin wave propagation in chiral-lattice ferromagnets. Phys. Rev. B 2016, 93, 235131. [Google Scholar] [CrossRef]
- Tacchi, S.; Troncoso, R.E.; Ahlberg, M.; Gubbiotti, G.; Madami, M.; Åkerman, J.; Landeros, P. Interfacial Dzyaloshinskii-Moriya Interaction in Pt/CoFeB Films: Effect of the Heavy-Metal Thickness. Phys. Rev. Lett. 2017, 118, 147201. [Google Scholar] [CrossRef] [PubMed]
- Weber, T.; Waizner, J.; Tucker, G.S.; Beddrich, L.; Skoulatos, M.; Georgii, R.; Bauer, A.; Pfleiderer, C.; Garst, M.; Böni, P. Non-reciprocal magnons in non-centrosymmetric MnSi. AIP Adv. 2018, 8, 101328. [Google Scholar] [CrossRef]
- Gallardo, R.A.; Alvarado-Seguel, P.; Schneider, T.; Gonzalez-Fuentes, C.; Roldán-Molina, A.; Lenz, K.; Lindner, J.; Landeros, P. Spin-wave non-reciprocity in magnetization-graded ferromagnetic films. New J. Phys. 2019, 21, 033026. [Google Scholar] [CrossRef]
- Gallardo, R.; Schneider, T.; Chaurasiya, A.; Oelschlägel, A.; Arekapudi, S.; Roldán-Molina, A.; Hübner, R.; Lenz, K.; Barman, A.; Fassbender, J.; et al. Reconfigurable Spin-Wave Nonreciprocity Induced by Dipolar Interaction in a Coupled Ferromagnetic Bilayer. Phys. Rev. Appl. 2019, 12, 034012. [Google Scholar] [CrossRef]
- Gallardo, R.A.; Cortés-Ortuño, D.; Troncoso, R.E.; Landeros, P. Three-Dimensional Magnonics, Layered, Micro- and Nanostructures; Jenny Stanford Publishing: Berlin/Heidelberg, Germany, 2019; pp. 121–160. [Google Scholar]
- Sheka, D.D.; Pylypovskyi, O.V.; Landeros, P.; Gaididei, Y.; Kákay, A.; Makarov, D. Nonlocal chiral symmetry breaking in curvilinear magnetic shells. Commun. Phys. 2020, 3, 128. [Google Scholar] [CrossRef]
- Albisetti, E.; Tacchi, S.; Silvani, R.; Scaramuzzi, G.; Finizio, S.; Wintz, S.; Rinaldi, C.; Cantoni, M.; Raabe, J.; Carlotti, G.; et al. Optically Inspired Nanomagnonics with Nonreciprocal Spin Waves in Synthetic Antiferromagnets. Adv. Mater. 2020, 32, 1906439. [Google Scholar] [CrossRef]
- Grassi, M.; Geilen, M.; Louis, D.; Mohseni, M.; Brächer, T.; Hehn, M.; Stoeffler, D.; Bailleul, M.; Pirro, P.; Henry, Y. Slow-Wave-Based Nanomagnonic Diode. Phys. Rev. Appl. 2020, 14, 024047. [Google Scholar] [CrossRef]
- Gallardo, R.A.; Alvarado-Seguel, P.; Landeros, P. High spin-wave asymmetry and emergence of radial standing modes in thick ferromagnetic nanotubes. Phys. Rev. B 2022, 105, 104435. [Google Scholar] [CrossRef]
- Neusser, S.; Grundler, D. Magnonics: Spin Waves on the Nanoscale. Adv. Mater. 2009, 21, 2927–2932. [Google Scholar] [CrossRef]
- Barman, A.; Gubbiotti, G.; Ladak, S.; Adeyeye, A.O.; Krawczyk, M.; Gräfe, J.; Adelmann, C.; Cotofana, S.; Naeemi, A.; Vasyuchka, V.I.; et al. The 2021 Magnonics Roadmap. J. Phys. Condens. Matter 2021, 33, 413001. [Google Scholar] [CrossRef]
- Locatelli, N.; Cros, V.; Grollier, J. Spin-torque building blocks. Nat. Mater. 2014, 13, 11–20. [Google Scholar] [CrossRef]
- Chumak, A.V.; Vasyuchka, V.I.; Serga, A.A.; Hillebrands, B. Magnon spintronics. Nat. Phys. 2015, 11, 453–461. [Google Scholar] [CrossRef]
- Bauer, G.E.W.; Saitoh, E.; van Wees, B.J. Spin caloritronics. Nat. Mater. 2012, 11, 391–399. [Google Scholar] [CrossRef]
- Khitun, A.; Bao, M.; Wang, K.L. Magnonic logic circuits. J. Phys. D Appl. Phys. 2010, 43, 264005. [Google Scholar] [CrossRef]
- Jamali, M.; Kwon, J.H.; Seo, S.M.; Lee, K.J.; Yang, H. Spin wave nonreciprocity for logic device applications. Sci. Rep. 2013, 3, 3160. [Google Scholar] [CrossRef]
- Lenk, B.; Ulrichs, H.; Garbs, F.; Münzenberg, M. The building blocks of magnonics. Phys. Rep. 2011, 507, 107–136. [Google Scholar] [CrossRef]
- Krawczyk, M.; Grundler, D. Review and prospects of magnonic crystals and devices with reprogrammable band structure. J. Phys. Condens. Matter 2014, 26, 123202. [Google Scholar] [CrossRef]
- Chumak, A.V.; Serga, A.A.; Hillebrands, B. Magnonic crystals for data processing. J. Phys. D 2017, 50, 244001. [Google Scholar] [CrossRef]
- Yu, H.; Xiao, J.; Schultheiss, H. Magnetic texture based magnonics. Phys. Rep. 2021, 905, 1–59. [Google Scholar] [CrossRef]
- Ríos-Venegas, C.; Brevis, F.; Gallardo, R.A.; Landeros, P. Dynamic origin of conical helix magnetization textures stabilized by Dzyaloshinskii-Moriya interaction. Phys. Rev. B 2022, 105, 224403. [Google Scholar] [CrossRef]
- Graczyk, P.; Kłos, J.; Krawczyk, M. Broadband magnetoelastic coupling in magnonic-phononic crystals for high-frequency nanoscale spin-wave generation. Phys. Rev. B 2017, 95, 104425. [Google Scholar] [CrossRef]
- Bozhko, D.A.; Vasyuchka, V.I.; Chumak, A.V.; Serga, A.A. Magnon-phonon interactions in magnon spintronics (Review article). Low Temp. Phys. 2020, 46, 383–399. [Google Scholar] [CrossRef]
- Gubbiotti, G. Three-Dimensional Magnonics: Layered, Micro-and Nanostructures; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Makarov, D.; Sheka, D. Curvilinear Micromagnetism: From Fundamentals to Applications; Topics in Applied Physics; Springer International Publishing: Berlin, Germany, 2022. [Google Scholar]
- Garcia-Sanchez, F.; Borys, P.; Soucaille, R.; Adam, J.P.; Stamps, R.L.; Kim, J.V. Narrow Magnonic Waveguides Based on Domain Walls. Phys. Rev. Lett. 2015, 114, 247206. [Google Scholar] [CrossRef]
- Xing, X.; Zhou, Y. Fiber optics for spin waves. NPG Asia Mater. 2016, 8, e246. [Google Scholar] [CrossRef]
- Stamps, R.L.; Kim, J.V.; Garcia-Sanchez, F.; Borys, P.; Gubbiotti, G.; Li, Y.; Camley, R.E. Spin Wave Confinement: Propagating Waves, 2nd ed.; Pan Stanford Publishing: Redwood City, CA, USA, 2017; pp. 219–260. [Google Scholar]
- Hämäläinen, S.J.; Madami, M.; Qin, H.; Gubbiotti, G.; van Dijken, S. Control of spin-wave transmission by a programmable domain wall. Nat. Commun. 2018, 9, 4853. [Google Scholar] [CrossRef]
- Henry, Y.; Stoeffler, D.; Kim, J.V.; Bailleul, M. Unidirectional spin-wave channeling along magnetic domain walls of Bloch type. Phys. Rev. B 2019, 100, 024416. [Google Scholar] [CrossRef]
- Lara, A.; Metlushko, V.; Aliev, F.G. Observation of propagating edge spin waves modes. J. Appl. Phys. 2013, 114, 213905. [Google Scholar] [CrossRef]
- Roldán-Molina, A.; Nunez, A.S.; Fernández-Rossier, J. Topological spin waves in the atomic-scale magnetic skyrmion crystal. New J. Phys. 2016, 18, 045015. [Google Scholar] [CrossRef]
- Lara, A.; Robledo Moreno, J.; Guslienko, K.Y.; Aliev, F.G. Information processing in patterned magnetic nanostructures with edge spin waves. Sci. Rep. 2017, 7, 5597. [Google Scholar] [CrossRef]
- Lan, J.; Yu, W.; Wu, R.; Xiao, J. Spin-Wave Diode. Phys. Rev. X 2015, 5, 041049. [Google Scholar] [CrossRef]
- Reiskarimian, N.; Krishnaswamy, H. Magnetic-free non-reciprocity based on staggered commutation. Nat. Commun. 2016, 7, 11217. [Google Scholar] [CrossRef]
- Sounas, D.L.; Alù, A. Non-reciprocal photonics based on time modulation. Nat. Photonics 2017, 11, 774–783. [Google Scholar] [CrossRef]
- Garst, M.; Waizner, J.; Grundler, D. Collective spin excitations of helices and magnetic skyrmions: Review and perspectives of magnonics in non-centrosymmetric magnets. J. Phys. D Appl. Phys. 2017, 50, 293002. [Google Scholar] [CrossRef]
- Heussner, F.; Serga, A.A.; Brächer, T.; Hillebrands, B.; Pirro, P. A switchable spin-wave signal splitter for magnonic networks. Appl. Phys. Lett. 2017, 111, 122401. [Google Scholar] [CrossRef]
- Heussner, F.; Talmelli, G.; Geilen, M.; Heinz, B.; Brächer, T.; Meyer, T.; Ciubotaru, F.; Adelmann, C.; Yamamoto, K.; Serga, A.A.; et al. Experimental Realization of a Passive Gigahertz Frequency-Division Demultiplexer for Magnonic Logic Networks. Phys. Status Solidi RRL 2020, 14, 1900695. [Google Scholar] [CrossRef]
- Xing, X.; Zhou, Y.; Braun, H. Magnetic Skyrmion Tubes as Nonplanar Magnonic Waveguides. Phys. Rev. Appl. 2020, 13, 034051. [Google Scholar] [CrossRef]
- Levy, U.; Abashin, M.; Ikeda, K.; Krishnamoorthy, A.; Cunningham, J.; Fainman, Y. Inhomogenous Dielectric Metamaterials with Space-Variant Polarizability. Phys. Rev. Lett. 2007, 98, 243901. [Google Scholar] [CrossRef]
- Hecht, E. Optics, 5e; Pearson Education India: Noida, India, 2002. [Google Scholar]
- Markos, C.; Travers, J.C.; Abdolvand, A.; Eggleton, B.J.; Bang, O. Hybrid photonic-crystal fiber. Rev. Mod. Phys. 2017, 89, 045003. [Google Scholar] [CrossRef]
- Boonzajer Flaes, D.E.; Stopka, J.; Turtaev, S.; de Boer, J.F.; Tyc, T.; Čižmár, T. Robustness of Light-Transport Processes to Bending Deformations in Graded-Index Multimode Waveguides. Phys. Rev. Lett. 2018, 120, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Davies, C.S.; Kruglyak, V.V. Graded-index magnonics. Low Temp. Phys. 2015, 41, 760–766. [Google Scholar] [CrossRef]
- Gruszecki, P.; Krawczyk, M. Spin-wave beam propagation in ferromagnetic thin films with graded refractive index: Mirage effect and prospective applications. Phys. Rev. B 2018, 97, 094424. [Google Scholar] [CrossRef]
- Jorzick, J.; Demokritov, S.O.; Hillebrands, B.; Bailleul, M.; Fermon, C.; Guslienko, K.Y.; Slavin, A.N.; Berkov, D.V.; Gorn, N.L. Spin Wave Wells in Nonellipsoidal Micrometer Size Magnetic Elements. Phys. Rev. Lett. 2002, 88, 047204. [Google Scholar] [CrossRef] [PubMed]
- Park, J.P.; Eames, P.; Engebretson, D.M.; Berezovsky, J.; Crowell, P.A. Spatially Resolved Dynamics of Localized Spin-Wave Modes in Ferromagnetic Wires. Phys. Rev. Lett. 2002, 89, 277201. [Google Scholar] [CrossRef] [PubMed]
- Kruglyak, V.V.; Barman, A.; Hicken, R.J.; Childress, J.R.; Katine, J.A. Picosecond magnetization dynamics in nanomagnets: Crossover to nonuniform precession. Phys. Rev. B 2005, 71, 220409. [Google Scholar] [CrossRef]
- Demidov, V.E.; Demokritov, S.O.; Rott, K.; Krzysteczko, P.; Reiss, G. Nano-optics with spin waves at microwave frequencies. Appl. Phys. Lett. 2008, 92, 232503. [Google Scholar] [CrossRef]
- Fripp, K.G.; Kruglyak, V.V. Spin-wave wells revisited: From wavelength conversion and Möbius modes to magnon valleytronics. Phys. Rev. B 2021, 103, 184403. [Google Scholar] [CrossRef]
- Mathieu, C.; Jorzick, J.; Frank, A.; Demokritov, S.O.; Slavin, A.N.; Hillebrands, B.; Bartenlian, B.; Chappert, C.; Decanini, D.; Rousseaux, F.; et al. Lateral Quantization of Spin Waves in Micron Size Magnetic Wires. Phys. Rev. Lett. 1998, 81, 3968–3971. [Google Scholar] [CrossRef]
- Jorzick, J.; Demokritov, S.O.; Mathieu, C.; Hillebrands, B.; Bartenlian, B.; Chappert, C.; Rousseaux, F.; Slavin, A.N. Brillouin light scattering from quantized spin waves in micron-size magnetic wires. Phys. Rev. B 1999, 60, 15194–15200. [Google Scholar] [CrossRef]
- Mantese, J.V.; Micheli, A.L.; Schubring, N.W.; Hayes, R.W.; Srinivasan, G.; Alpay, S.P. Magnetization-graded ferromagnets: The magnetic analogs of semiconductor junction elements. Appl. Phys. Lett. 2005, 87, 082503. [Google Scholar] [CrossRef]
- Fallarino, L.; Riego, P.; Kirby, B.J.; Miller, C.W.; Berger, A. Modulation of Magnetic Properties at the Nanometer Scale in Continuously Graded Ferromagnets. Materials 2018, 11, 251. [Google Scholar] [CrossRef] [PubMed]
- Sudakar, C.; Naik, R.; Lawes, G.; Mantese, J.V.; Micheli, A.L.; Srinivasan, G.; Alpay, S.P. Internal magnetostatic potentials of magnetization-graded ferromagnetic materials. Appl. Phys. Lett. 2007, 90, 062502. [Google Scholar] [CrossRef]
- Supper, N.; Margulies, D.; Moser, A.; Berger, A.; Do, H.; Fullerton, E. Writability enhancement using exchange spring media. IEEE Trans. Magn. 2005, 41, 3238–3240. [Google Scholar] [CrossRef]
- Berger, A.; Supper, N.; Ikeda, Y.; Lengsfield, B.; Moser, A.; Fullerton, E.E. Improved media performance in optimally coupled exchange spring layer media. Appl. Phys. Lett. 2008, 93, 122502. [Google Scholar] [CrossRef]
- Zhou, T.J.; Lim, B.C.; Liu, B. Anisotropy graded FePt–TiO2 nanocomposite thin films with small grain size. Appl. Phys. Lett. 2009, 94, 152505. [Google Scholar] [CrossRef]
- Kirby, B.J.; Davies, J.E.; Liu, K.; Watson, S.M.; Zimanyi, G.T.; Shull, R.D.; Kienzle, P.A.; Borchers, J.A. Vertically graded anisotropy in Co/Pd multilayers. Phys. Rev. B 2010, 81, 100405. [Google Scholar] [CrossRef]
- Dumas, R.K.; Fang, Y.; Kirby, B.J.; Zha, C.; Bonanni, V.; Nogués, J.; Åkerman, J. Probing vertically graded anisotropy in FePtCu films. Phys. Rev. B 2011, 84, 054434. [Google Scholar] [CrossRef]
- Kirby, B.J.; Belliveau, H.F.; Belyea, D.D.; Kienzle, P.A.; Grutter, A.J.; Riego, P.; Berger, A.; Miller, C.W. Spatial Evolution of the Ferromagnetic Phase Transition in an Exchange Graded Film. Phys. Rev. Lett. 2016, 116, 047203. [Google Scholar] [CrossRef] [PubMed]
- Fallarino, L.; Kirby, B.J.; Pancaldi, M.; Riego, P.; Balk, A.L.; Miller, C.W.; Vavassori, P.; Berger, A. Magnetic properties of epitaxial CoCr films with depth-dependent exchange-coupling profiles. Phys. Rev. B 2017, 95, 134445. [Google Scholar] [CrossRef]
- Kirby, B.J.; Fallarino, L.; Riego, P.; Maranville, B.B.; Miller, C.W.; Berger, A. Nanoscale magnetic localization in exchange strength modulated ferromagnets. Phys. Rev. B 2018, 98, 064404. [Google Scholar] [CrossRef]
- Guslienko, K.Y.; Demokritov, S.O.; Hillebrands, B.; Slavin, A.N. Effective dipolar boundary conditions for dynamic magnetization in thin magnetic stripes. Phys. Rev. B 2002, 66, 132402. [Google Scholar] [CrossRef]
- Davies, C.S.; Poimanov, V.D.; Kruglyak, V.V. Mapping the magnonic landscape in patterned magnetic structures. Phys. Rev. B 2017, 96, 094430. [Google Scholar] [CrossRef]
- Vansteenkiste, A.; Leliaert, J.; Dvornik, M.; Helsen, M.; Garcia-Sanchez, F.; Waeyenberge, B.V. The design and verification of MuMax3. AIP Adv. 2014, 4, 107133. [Google Scholar] [CrossRef]
- Fallarino, L.; Kirby, B.J.; Fullerton, E.E. Graded magnetic materials. J. Phys. D Appl. Phys. 2021, 54, 303002. [Google Scholar] [CrossRef]
- Green, M.L.; Takeuchi, I.; Hattrick-Simpers, J.R. Applications of high throughput (combinatorial) methodologies to electronic, magnetic, optical, and energy-related materials. J. Appl. Phys. 2013, 113, 231101. [Google Scholar] [CrossRef]
- Bali, R.; Wintz, S.; Meutzner, F.; Hübner, R.; Boucher, R.; Ünal, A.A.; Valencia, S.; Neudert, A.; Potzger, K.; Bauch, J.; et al. Printing Nearly-Discrete Magnetic Patterns Using Chemical Disorder Induced Ferromagnetism. Nano Lett. 2014, 14, 435–441. [Google Scholar] [CrossRef]
- Röder, F.; Hlawacek, G.; Wintz, S.; Hübner, R.; Bischoff, L.; Lichte, H.; Potzger, K.; Lindner, J.; Fassbender, J.; Bali, R. Direct Depth- and Lateral- Imaging of Nanoscale Magnets Generated by Ion Impact. Sci. Rep. 2015, 5, 16786. [Google Scholar] [CrossRef]
- Nord, M.; Semisalova, A.; Kákay, A.; Hlawacek, G.; MacLaren, I.; Liersch, V.; Volkov, O.M.; Makarov, D.; Paterson, G.W.; Potzger, K.; et al. Strain Anisotropy and Magnetic Domains in Embedded Nanomagnets. Small 2019, 15, 1904738. [Google Scholar] [CrossRef]
- Grimsditch, M.; Giovannini, L.; Montoncello, F.; Nizzoli, F.; Leaf, G.K.; Kaper, H.G. Magnetic normal modes in ferromagnetic nanoparticles: A dynamical matrix approach. Phys. Rev. B 2004, 70, 054409. [Google Scholar] [CrossRef]
- Giovannini, L.; Montoncello, F.; Nizzoli, F.; Gubbiotti, G.; Carlotti, G.; Okuno, T.; Shinjo, T.; Grimsditch, M. Spin excitations of nanometric cylindrical dots in vortex and saturated magnetic states. Phys. Rev. B 2004, 70, 172404. [Google Scholar] [CrossRef]
- Henry, Y.; Gladii, O.; Bailleul, M. Propagating spin-wave normal modes: A dynamic matrix approach using plane-wave demagnetizating tensors. arXiv 2016, arXiv:1611.06153. [Google Scholar]
- Newell, A.J.; Williams, W.; Dunlop, D.J. A generalization of the demagnetizing tensor for nonuniform magnetization. J. Geophys. Res. Solid Earth 1993, 98, 9551–9555. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gallardo, R.A.; Alvarado-Seguel, P.; Brevis, F.; Roldán-Molina, A.; Lenz, K.; Lindner, J.; Landeros, P. Spin-Wave Channeling in Magnetization-Graded Nanostrips. Nanomaterials 2022, 12, 2785. https://doi.org/10.3390/nano12162785
Gallardo RA, Alvarado-Seguel P, Brevis F, Roldán-Molina A, Lenz K, Lindner J, Landeros P. Spin-Wave Channeling in Magnetization-Graded Nanostrips. Nanomaterials. 2022; 12(16):2785. https://doi.org/10.3390/nano12162785
Chicago/Turabian StyleGallardo, Rodolfo A., Pablo Alvarado-Seguel, Felipe Brevis, Alejandro Roldán-Molina, Kilian Lenz, Jürgen Lindner, and Pedro Landeros. 2022. "Spin-Wave Channeling in Magnetization-Graded Nanostrips" Nanomaterials 12, no. 16: 2785. https://doi.org/10.3390/nano12162785
APA StyleGallardo, R. A., Alvarado-Seguel, P., Brevis, F., Roldán-Molina, A., Lenz, K., Lindner, J., & Landeros, P. (2022). Spin-Wave Channeling in Magnetization-Graded Nanostrips. Nanomaterials, 12(16), 2785. https://doi.org/10.3390/nano12162785





