Smart Systems for Material and Process Designing in Direct Nanoimprint Lithography Using Hybrid Deep Learning
Abstract
1. Introduction
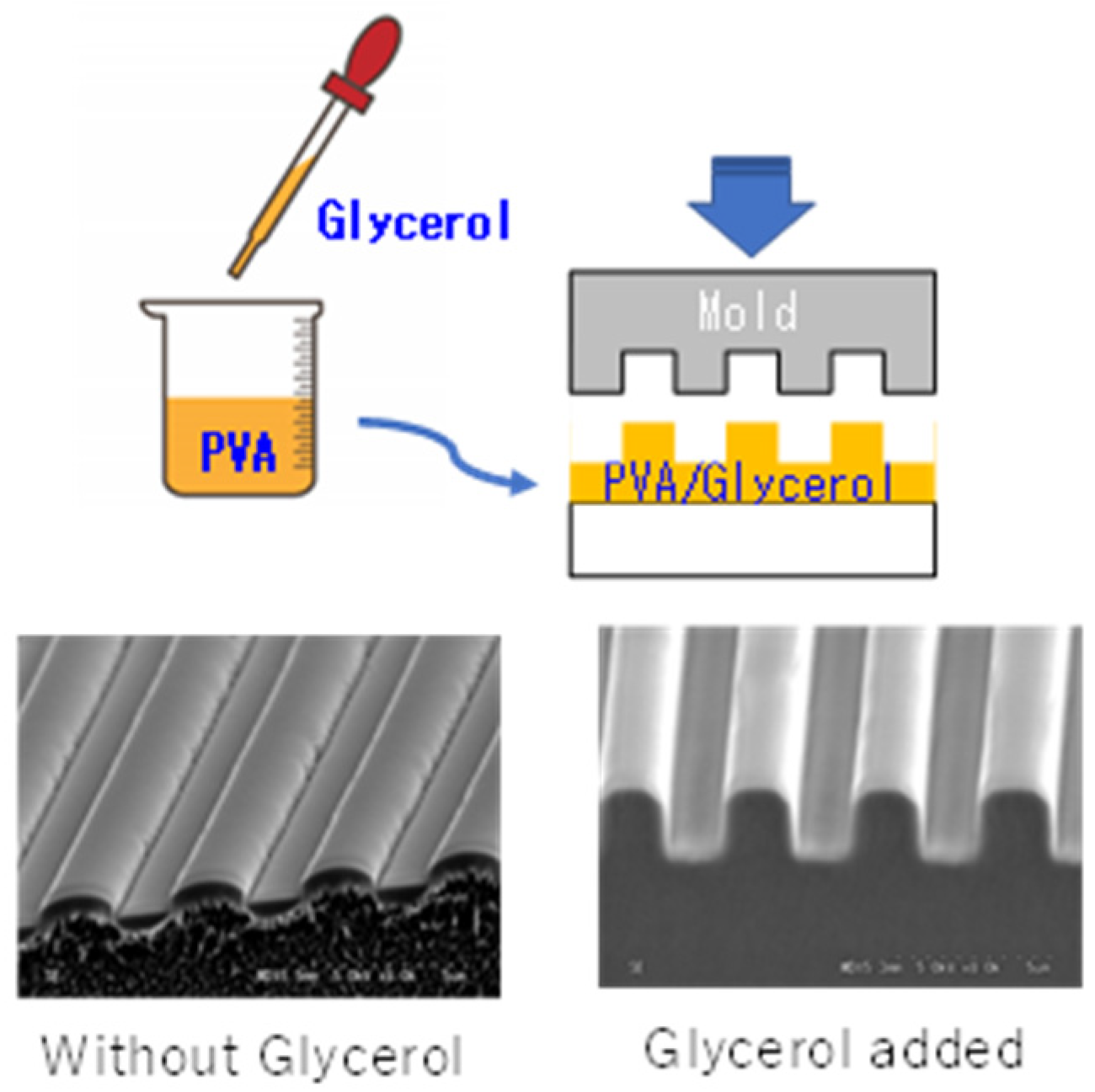
2. Low-Temperature Direct Nanoimprint for Polyvinyl Alcohol (PVA) with Glycerol Additives
3. Hybrid Deep-Learning System for Nanoimprint Material and Process
4. Results and Discussions
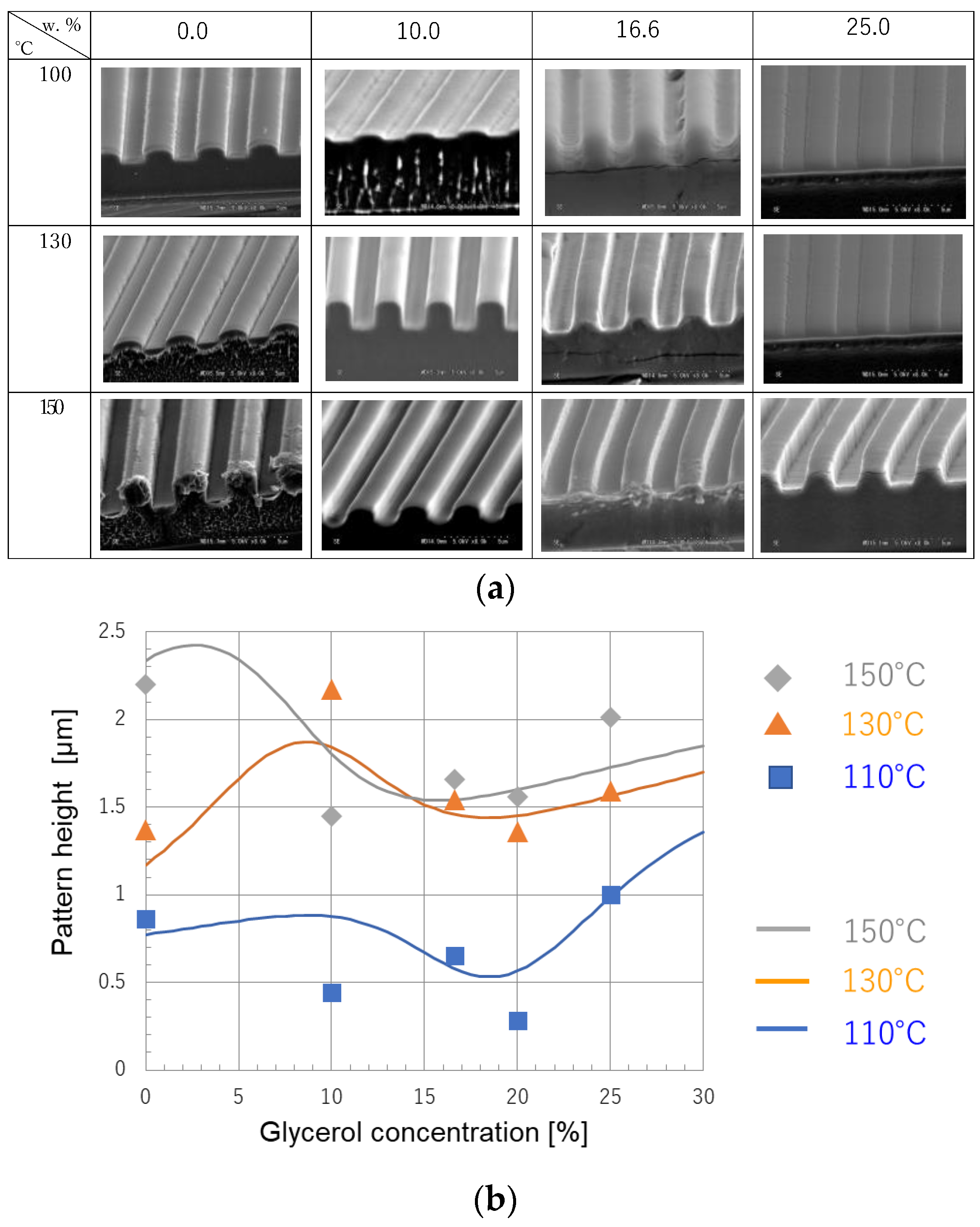
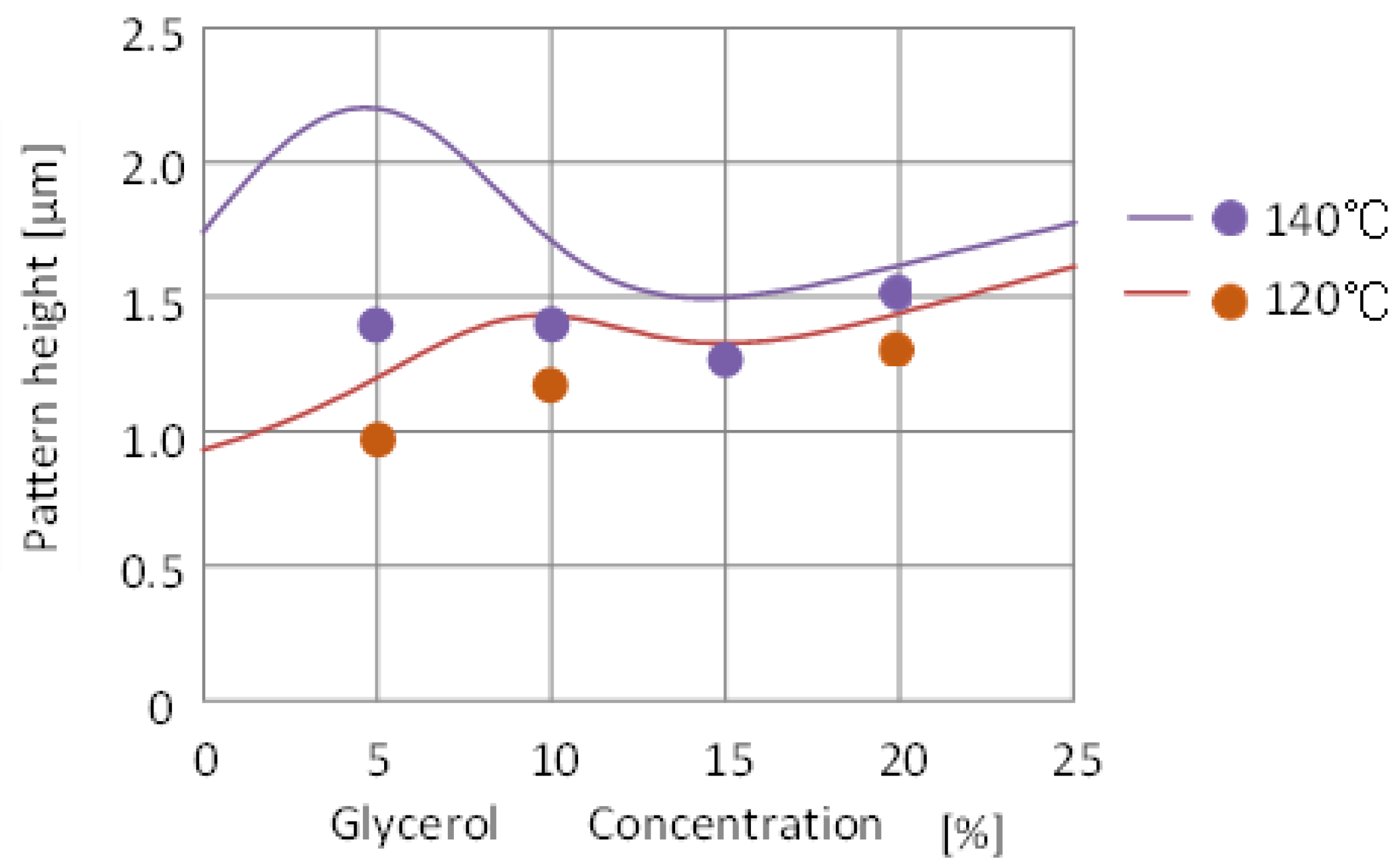
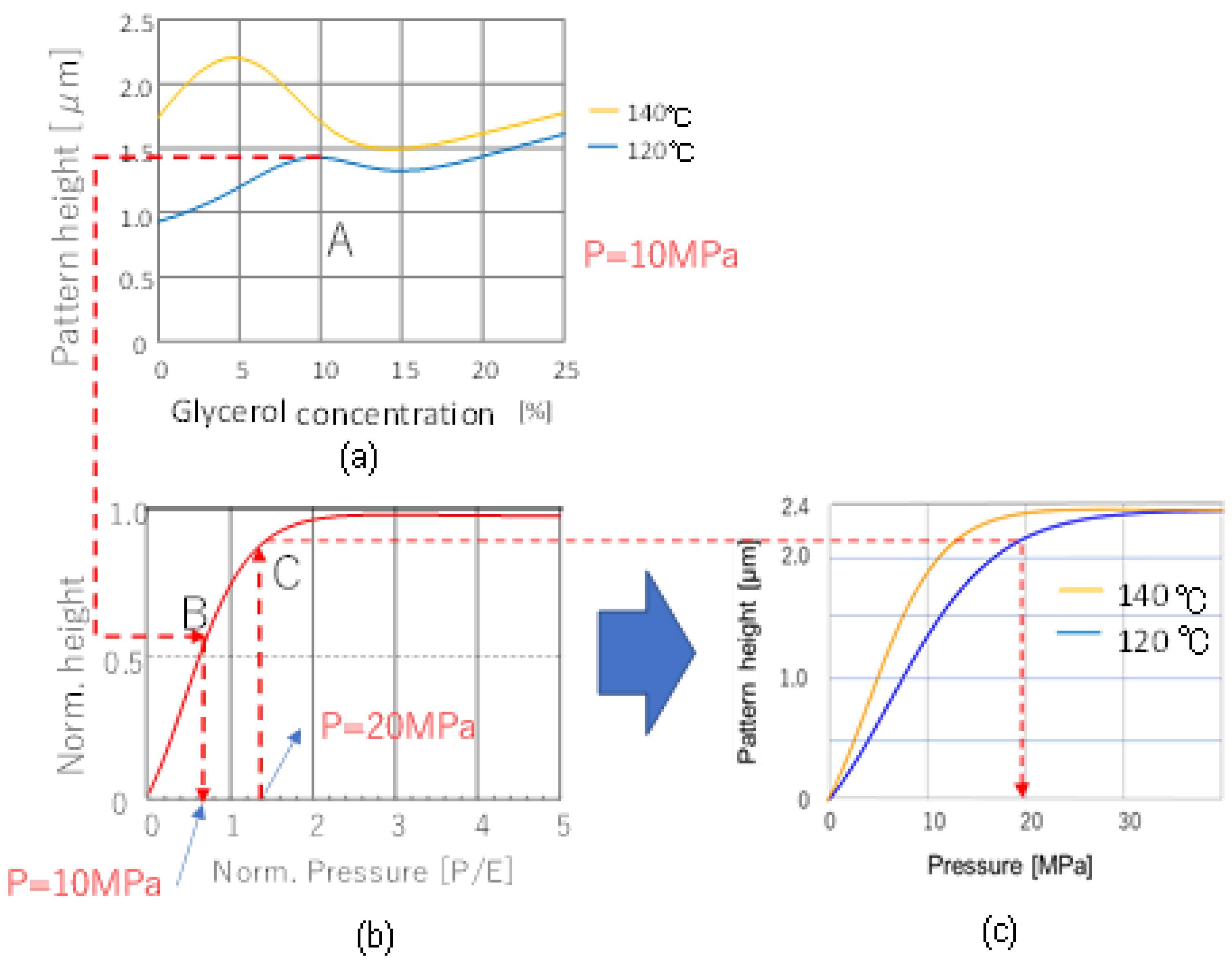
4.1. Characterization of PVA Containing Glycerol and Prediction of Pattern Formability
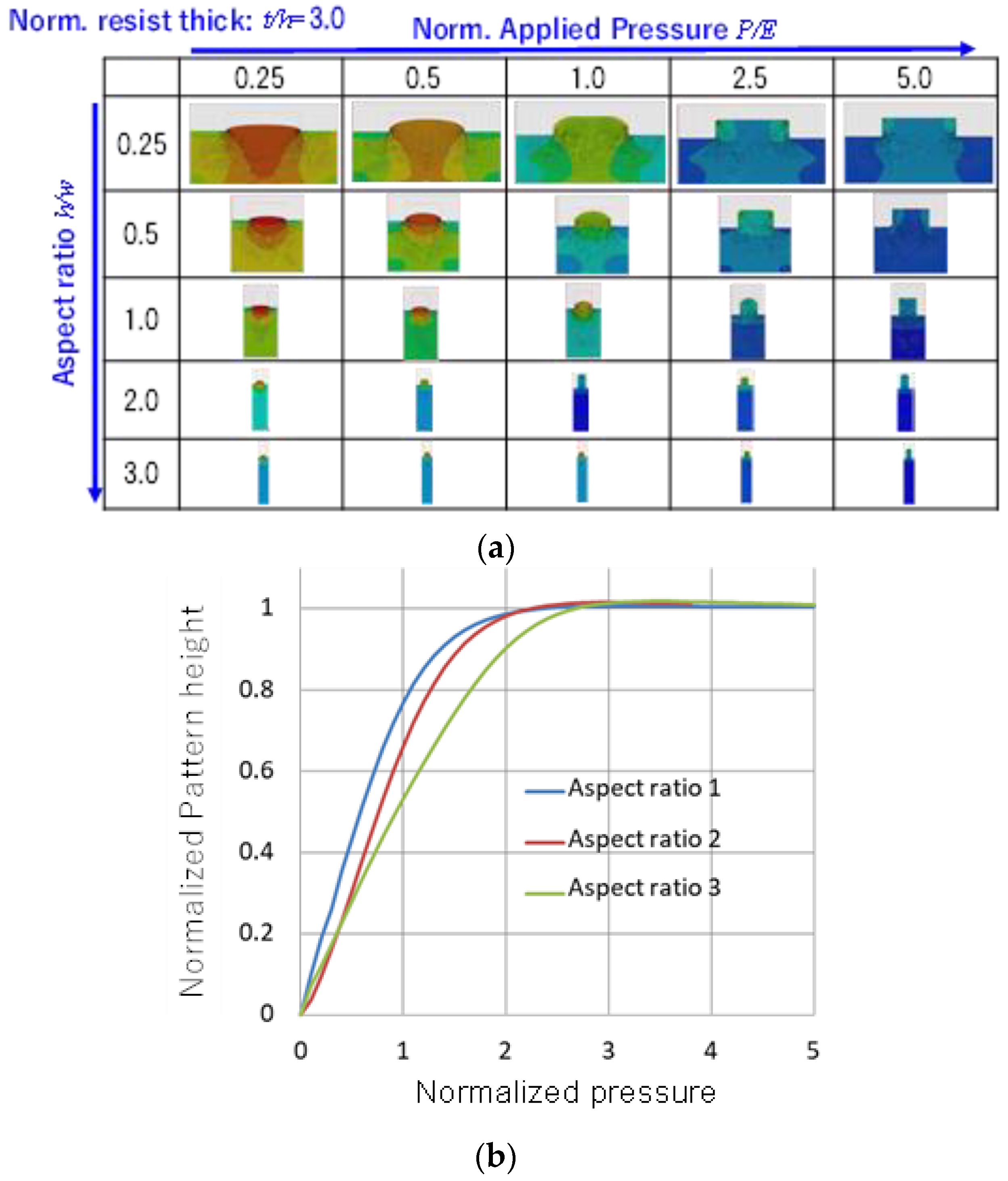
4.2. Pattern Height Prediction by Simulation-Based Learning
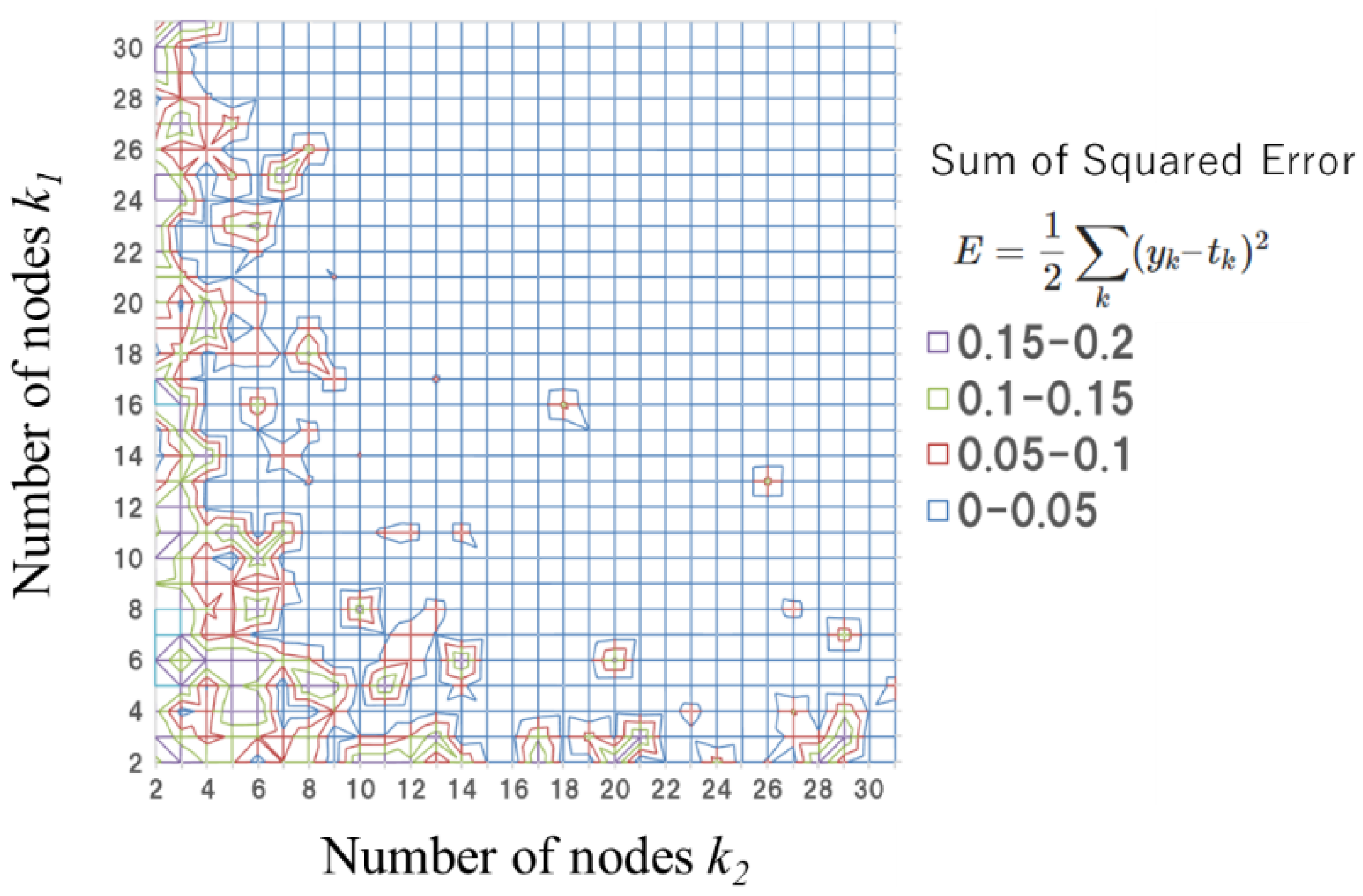
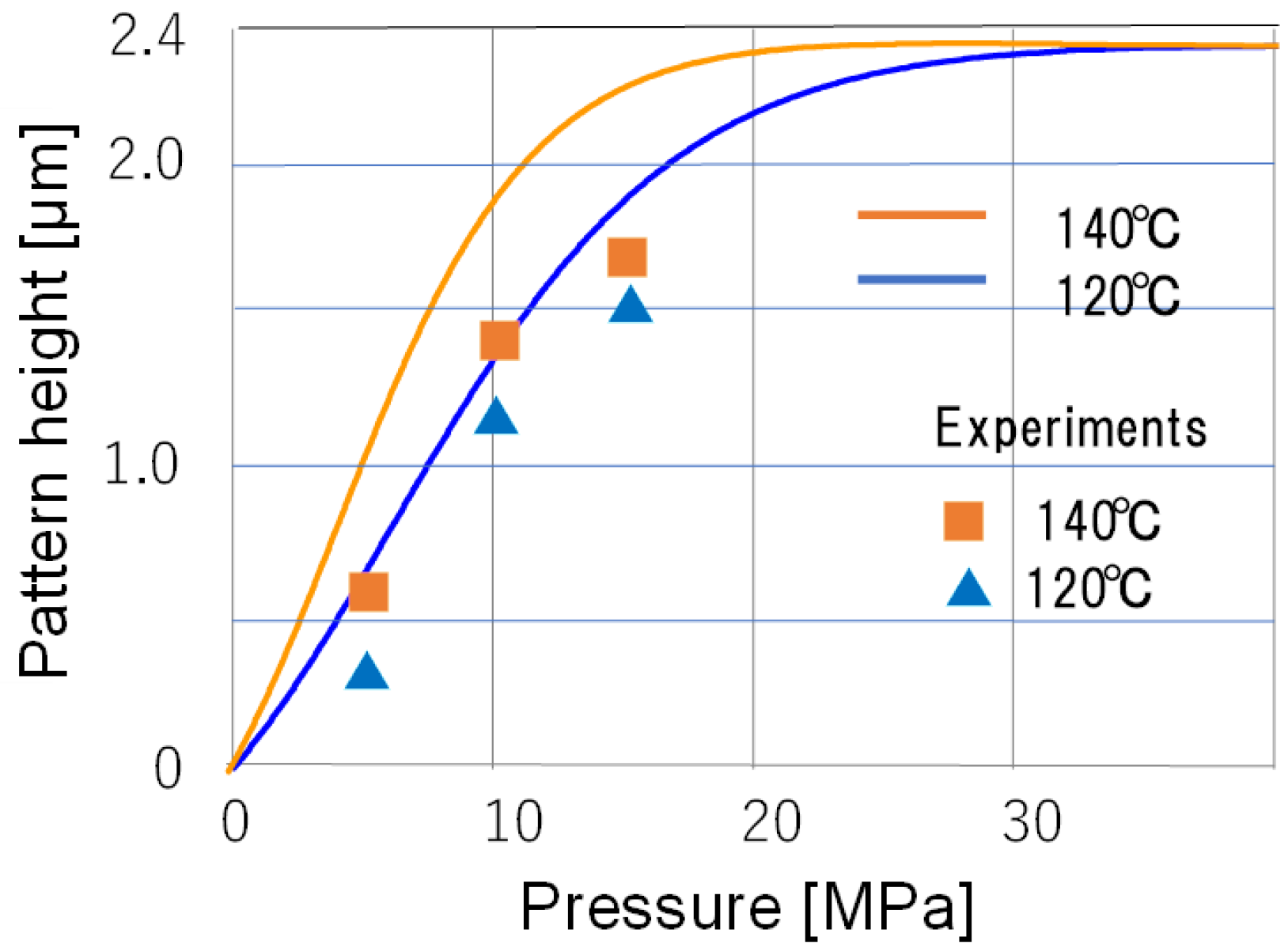
4.3. Hybrid System for Material and Process Design for Nanoimprinting
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chou, S.; Krauss, P.; Renstrom, P. Imprint of sub-25 nm vias and trenches in polymers. Appl. Phys. Lett. 1995, 67, 3114–3116. [Google Scholar] [CrossRef]
- Chou, S.; Krauss, P.; Renstrom, P. Nanoimprint lithography. J. Vac. Sci. Technol. B 1996, 14, 4129–4133. [Google Scholar] [CrossRef]
- Austin, M.; Chou, S. Fabrication of 70 nm channel length polymer organic thin-film transistors using nanoimprint lithography. Appl. Phys. Lett. 2002, 81, 4431–4433. [Google Scholar] [CrossRef]
- Leising, G.; Stadlober, B.; Haas, U.; Haase, A.; Palfinger, C.; Gold, H.; Jakopic, G. Nanoimprinted devices for integrated organic electronics. Microelectron. Eng. 2006, 83, 831–838. [Google Scholar] [CrossRef]
- Tomohiro, K.; Hoto, N.; Kawata, H.; Hirai, Y. Fine Pattern Transfer of Functional Organic Polymers by Nanoimprint. J. Photopolym. Sci. Technol. 2011, 24, 71–75. [Google Scholar] [CrossRef][Green Version]
- Li, M.; Tan, H.; Chen, L.; Wang, J.; Chou, S. Large area direct nanoimprinting of SiO2-TiO2 gel gratings for optical applications. J. Vac. Sci. Technol. B 2003, 21, 660–663. [Google Scholar] [CrossRef]
- Hirai, Y.; Kanakugi, K.; Yamaguchi, T.; Yao, K.; Kitagawa, S.; Tanaka, Y. Fine pattern fabrication on glass surface by imprint lithography. Microelectron. Eng. 2003, 67–68, 237–244. [Google Scholar] [CrossRef]
- Hirai, Y.; Tanaka, Y. Application of nano-imprint lithography. J. Photopolym. Sci. Technol. 2002, 15, 475–480. [Google Scholar] [CrossRef]
- Yang, H.; Luo, L.; Su, J.; Lin, C.; Yu, B. Imbalance aware lithography hotspot detection: A deep learning approach. J. Micro/Nanolithography MEMS MOEMS 2017, 16, 033504. [Google Scholar] [CrossRef]
- Ma, X.; Zheng, X.; Arce, G. Fast inverse lithography based on dual-channel model-driven deep learning. Opt. Express 2020, 28, 20404–20421. [Google Scholar] [CrossRef]
- Akter, T.; Desai, S. Developing a predictive model for nanoimprint lithography using artificial neural networks. Mater. Des. 2018, 160, 836–848. [Google Scholar] [CrossRef]
- Aihara, S.; Takakura, N.; Kizu, F.; Jimbo, S.; Ishibashi, K.; Seki, J.; Oguchi, Y.; Asano, T.; Matsuoka, Y.; Tamura, M.; et al. Addressing NIL integration for semiconductor device manufacturing. Proc. SPIE Novel Patterning Technol. 2021, 1161007. [Google Scholar] [CrossRef]
- Hirai, Y.; Fujiwara, M.; Okuno, T.; Tanaka, Y.; Endo, M.; Irie, S.; Nakagawa, K.; Sasago, M. Study of the resist deformation in nanoimprint lithography. J. Vac. Sci. Technol. B 2001, 19, 2811–2815. [Google Scholar] [CrossRef]
- Hirai, Y.; Yoshida, S.; Takagi, N. Defect analysis in thermal nanoimprint lithography. J. Vac. Sci. Technol. B 2003, 21, 2765–2770. [Google Scholar] [CrossRef]
- Hirai, Y.; Konishi, T.; Yoshikawa, T.; Yoshida, S. Simulation and experimental study of polymer deformation in nanoimprint lithography. J. Vac. Sci. Technol. B 2004, 22, 3288–3293. [Google Scholar] [CrossRef]
- Hirai, Y.; Onishi, Y.; Tanabe, T.; Shibata, M.; Iwasaki, T.; Irie, Y. Pressure and resist thickness dependency of resist time evolutions profiles in nanoimprint lithography. Microelectron. Eng. 2008, 85, 842–845. [Google Scholar] [CrossRef]
- Hirai, Y.; Yoshikawa, T.; Takagi, N.; Yoshida, S. Mechanical properties of poly-methyl methacrylate (PMMA) for nano imprint lithography. J. Photopolym. Sci. Technol. 2003, 16, 615–620. [Google Scholar] [CrossRef]
- Specht, D. Probabilistic neural networks. Neural Netw. 1990, 3, 109–118. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Tsukamoto, S.; Tanabe, H.; Yamamura, R.; Kameyama, K.; Kawata, H.; Yasuda, M.; Hirai, Y. Proposal of hybrid deep learning systems for process and material design in thermal nanoimprint lithography. J. Photopolym. Sci. Technol. 2021, 148, 145–148. [Google Scholar] [CrossRef]
- Moony, M. A theory of large elastic deformation. J. Appl. Phys. 1940, 11, 582–592. [Google Scholar] [CrossRef]
- Rivlin, R.S. Large elastic deformations of isotropic materials IV. Further developments of the general theory. Phil. Trans. Roy. Soc. Lond. Ser. A 1948, 241, 379–397. [Google Scholar] [CrossRef]
- The Python Software Foundation. Available online: https://www.python.org/ (accessed on 1 June 2020).
- Microsoft Corporation. Available online: https://www.microsoft.com/en-us/microsoft-365/microsoft-office/ (accessed on 1 November 2020).

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hirai, Y.; Tsukamoto, S.; Tanabe, H.; Kameyama, K.; Kawata, H.; Yasuda, M. Smart Systems for Material and Process Designing in Direct Nanoimprint Lithography Using Hybrid Deep Learning. Nanomaterials 2022, 12, 2571. https://doi.org/10.3390/nano12152571
Hirai Y, Tsukamoto S, Tanabe H, Kameyama K, Kawata H, Yasuda M. Smart Systems for Material and Process Designing in Direct Nanoimprint Lithography Using Hybrid Deep Learning. Nanomaterials. 2022; 12(15):2571. https://doi.org/10.3390/nano12152571
Chicago/Turabian StyleHirai, Yoshihiko, Sou Tsukamoto, Hidekatsu Tanabe, Kai Kameyama, Hiroaki Kawata, and Masaaki Yasuda. 2022. "Smart Systems for Material and Process Designing in Direct Nanoimprint Lithography Using Hybrid Deep Learning" Nanomaterials 12, no. 15: 2571. https://doi.org/10.3390/nano12152571
APA StyleHirai, Y., Tsukamoto, S., Tanabe, H., Kameyama, K., Kawata, H., & Yasuda, M. (2022). Smart Systems for Material and Process Designing in Direct Nanoimprint Lithography Using Hybrid Deep Learning. Nanomaterials, 12(15), 2571. https://doi.org/10.3390/nano12152571




