Molecular Dynamics Study on Behavior of Resist Molecules in UV-Nanoimprint Lithography Filling Process
Abstract
:1. Introduction
2. Simulation Models and Methods
2.1. Resist Models
| Resist | Composition 1 | η [mPa·s] |
|---|---|---|
| Resist I | 96% HDDA (1020), 4% DMPA (36) | 4 |
| Resist II 2 | 10% TMPTA (82), 57% TPGDA (448), 29% NVP (622), 4% DMPA (38) | 8 |
| Resist III | 96% TMPTA (804), 4% DMPA (34) | 95 |
| Resist IV | 96% TPGDA (816), 4% DMPA (38) | 10 |
2.2. Force Field and Common Simulation Parameters
2.3. Estimation of Resist Contact Angles
2.4. Estimation of Diffusion Coefficients
2.5. Resist Filling Simulation
2.6. Radius of Gyration and Relative Shape Anisotropy
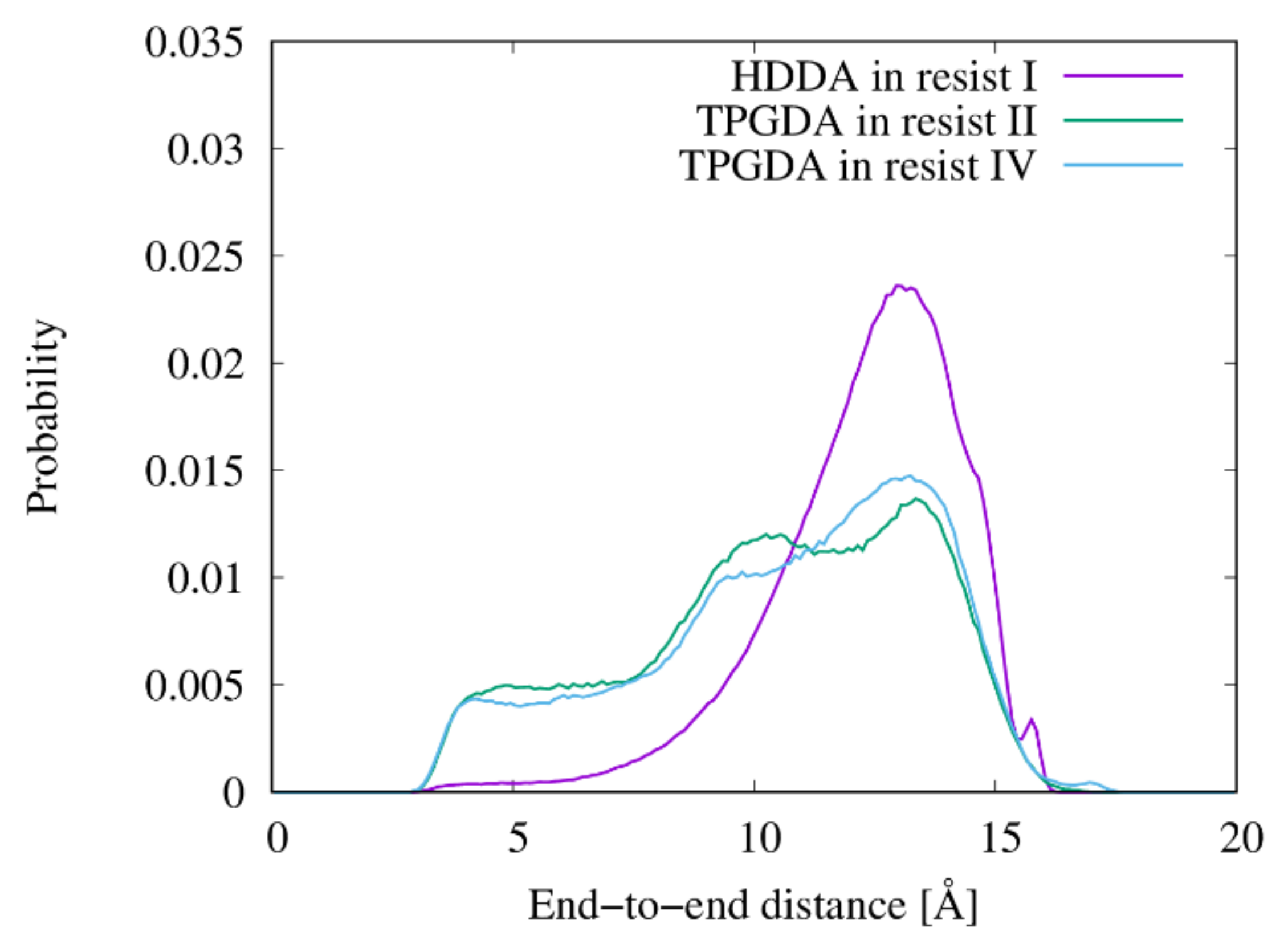
2.7. End-to-End Distance of Linear Chains
3. Results and Discussion
3.1. Resist Contact Angles
3.2. Diffusion Coefficients of DMPA in Resists
3.3. Filling Behaviors
3.4. Shapes of the Resist Molecules in the Trenches and Bulk States
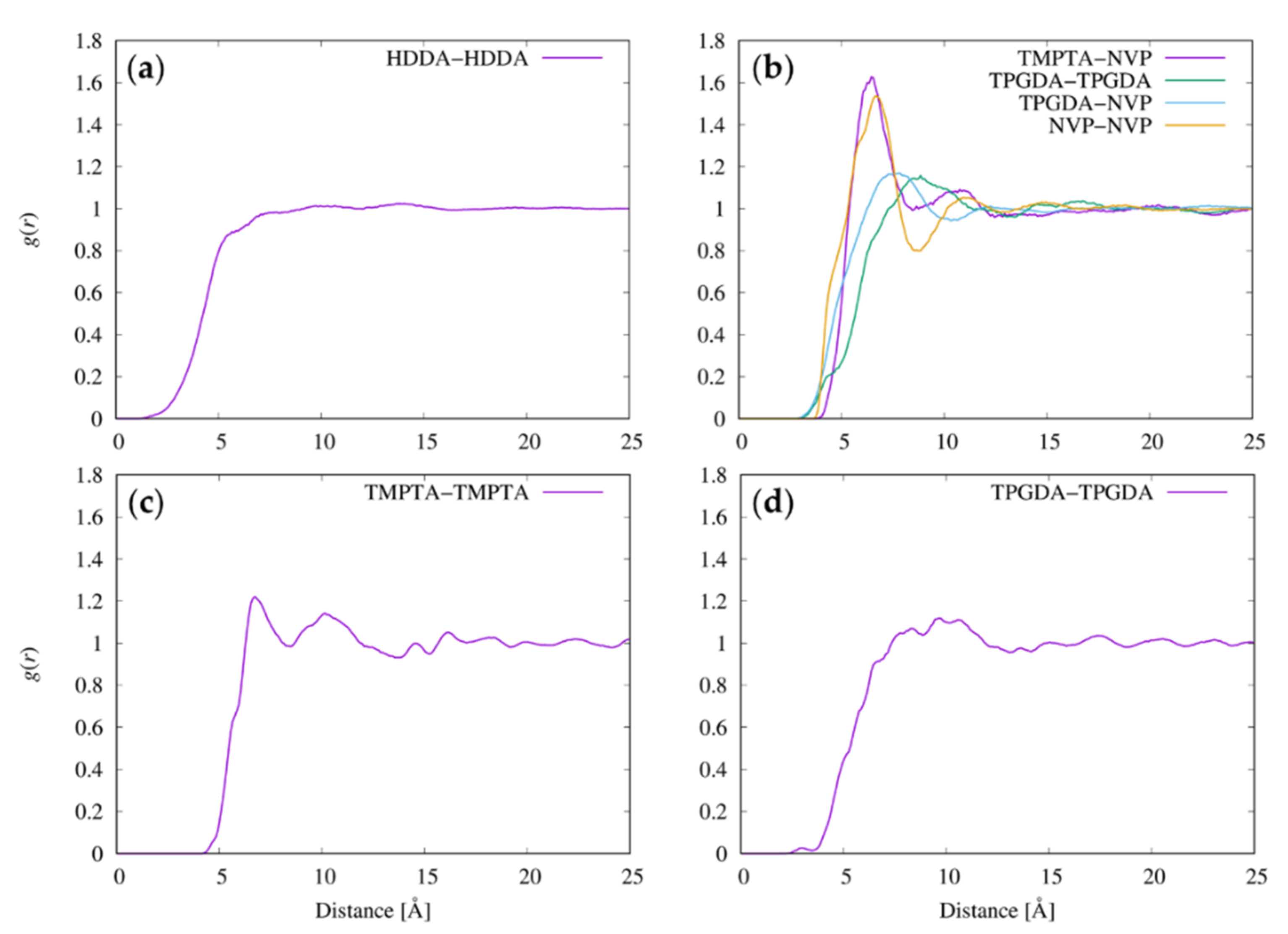
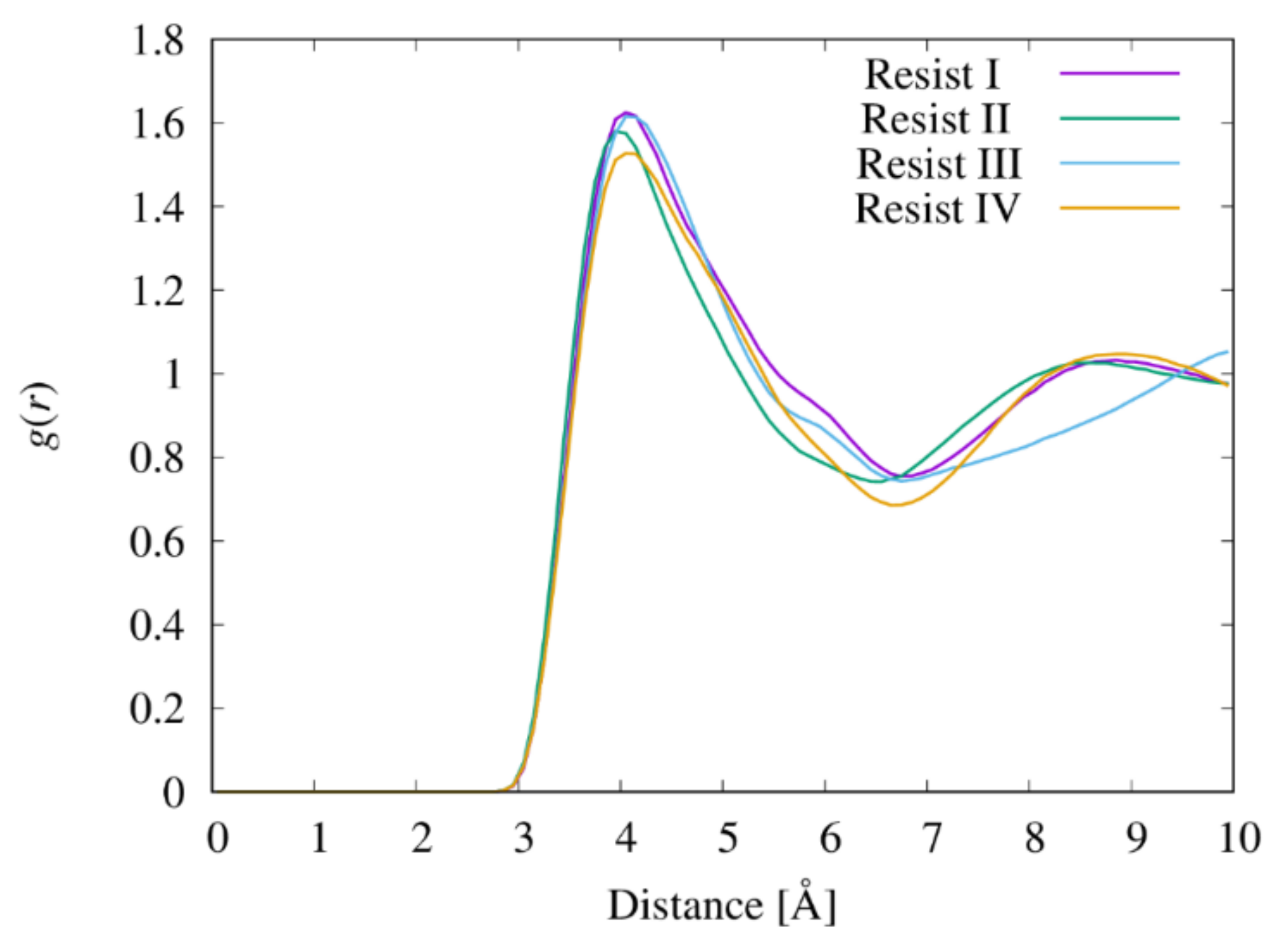
3.5. Radial Distribution Functions between Resist Molecules
3.6. Radial Distribution Functions between the Functional Groups
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chou, S.Y.; Krauss, P.R.; Renstrom, P.J. Imprint of sub-25 Nm vias and trenches in polymers. Appl. Phys. Lett. 1995, 67, 3114–3116. [Google Scholar] [CrossRef] [Green Version]
- Chou, S.Y.; Krauss, P.R.; Renstrom, P.J. Imprint lithography with 25-nanometer resolution. Science 1996, 272, 85–87. [Google Scholar] [CrossRef]
- Li, W.D.; Wu, W.; Williams, R.S. Combined helium ion beam and nanoimprint lithography attains 4 nm half-pitch dense patterns. J. Vac. Sci. Technol. B 2012, 30, 06F304. [Google Scholar] [CrossRef] [Green Version]
- Oh, D.K.; Lee, T.; Ko, B.; Badloe, T.; Ok, J.G.; Rho, J. Nanoimprint lithography for high-throughput fabrication of metasurfaces. Front. Optoelectron. 2021, 14, 229–251. [Google Scholar] [CrossRef]
- Hirai, Y.; Konishi, T.; Yoshikawa, T.; Yoshida, S. Simulation and experimental study of polymer deformation in nanoimprint lithography. J. Vac. Sci. Technol. B 2004, 22, 3288–3293. [Google Scholar] [CrossRef]
- Shibata, M.; Horiba, A.; Nagaoka, Y.; Kawata, H.; Yasuda, M.; Hirai, Y. Process-simulation system for UV-nanoimprint lithography. J. Vac. Sci. Technol. B 2010, 28, C6M108–C106M113. [Google Scholar] [CrossRef]
- Amirsadeghi, A.; Lee, J.J.; Park, S. A simulation study on the effect of cross-linking agent concentration for defect tolerant demolding in UV nanoimprint lithography. Langmuir 2012, 28, 11546–11554. [Google Scholar] [CrossRef]
- Taga, A.; Yasuda, M.; Kawata, H.; Hirai, Y. Impact of molecular size on resist filling process in nanoimprint lithography: Molecular dynamics study. J. Vac. Sci. Technol. B 2010, 28, C6m68–C66m71. [Google Scholar] [CrossRef]
- Yasuda, M.; Araki, K.; Taga, A.; Horiba, A.; Kawata, H.; Hirai, Y. Computational study on polymer filling process in nanoimprint lithography. Microelectron. Eng. 2011, 88, 2188–2191. [Google Scholar] [CrossRef]
- Kim, S.; Lee, D.E.; Lee, W.I. Molecular dynamic simulation on the effect of polymer molecular size in thermal nanoimprint lithographic (T-NIL) process. Tribol. Lett. 2013, 49, 421–430. [Google Scholar] [CrossRef]
- Woo, Y.S.; Lee, D.E.; Lee, W.I. Molecular dynamic studies on deformation of polymer resist during thermal nano imprint lithographic process. Tribol. Lett. 2009, 36, 209–222. [Google Scholar] [CrossRef]
- Odujole, J.; Desai, S. Atomistic investigation of material deformation behavior of polystyrene in nanoimprint lithography. Surfaces 2020, 3, 649–663. [Google Scholar] [CrossRef]
- Odujole, J.I.; Desai, S. Molecular dynamics investigation of material deformation behavior of PMMA in nanoimprint lithography. AIP Adv. 2020, 10, 095102. [Google Scholar] [CrossRef]
- Kang, J.H.; Kim, K.S.; Kim, K.W. Molecular dynamics study on the effects of stamp shape, adhesive energy, and temperature on the nanoimprint lithography process. Appl. Surf. Sci. 2010, 257, 1562–1572. [Google Scholar] [CrossRef]
- Kwon, S.; Lee, Y.; Park, J.; Im, S. Molecular simulation study on adhesions and deformations for polymethyl methacrylate (PMMA) resist in nanoimprint lithography. J. Mech. Sci. Technol. 2011, 25, 2311–2322. [Google Scholar] [CrossRef]
- Yang, S.; Yu, S.; Cho, M. Influence of mold and substrate material combinations on nanoimprint lithography process: MD simulation approach. Appl. Surf. Sci. 2014, 301, 189–198. [Google Scholar] [CrossRef]
- Uchida, H.; Imoto, R.; Ando, T.; Okabe, T.; Taniguchi, J. Molecular dynamics simulation of the resist filling process in UV-nanoimprint lithography. J. Photopolym. Sci. Technol. 2021, 34, 139–144. [Google Scholar] [CrossRef]
- Kloosterboer, J.G. Network formation by chain crosslinking photopolymerization and its applications in electronics. In Electronic Applications; Advances in Polymer Science; Springer: Berlin/Heidelberg, Germany, 1988; Volume 84, pp. 1–61. [Google Scholar]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. Model. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and testing of a general amber force field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef]
- Jakalian, A.; Bush, B.L.; Jack, D.B.; Bayly, C.I. Fast, efficient generation of high-quality atomic Charges. AM1-BCC model: I. Method. J. Comput. Chem. 2000, 21, 132–146. [Google Scholar] [CrossRef]
- Jakalian, A.; Jack, D.B.; Bayly, C.I. Fast, efficient generation of high-quality atomic charges. AM1-BCC model: II. Parameterization and validation. J. Comput. Chem. 2002, 23, 1623–1641. [Google Scholar] [CrossRef]
- Rappe, A.K.; Casewit, C.J.; Colwell, K.S.; Goddard, W.A.; Skiff, W.M. UFF, a full periodic-table force-field for molecular mechanics and molecular-dynamics simulations. J. Am. Chem. Soc. 1992, 114, 10024–10035. [Google Scholar] [CrossRef]
- Lithoxoos, G.P.; Samios, J.; Carissan, Y. Investigation of silicon model nanotubes as potential candidate nanomaterials for efficient hydrogen storage: A combined ab initio/grand canonical Monte Carlo simulation study. J. Phys. Chem. C 2008, 112, 16725–16728. [Google Scholar] [CrossRef]
- Lorentz, H.A. Ueber die Anwendung des Satzes vom Virial in der kinetischen Theorie der Gase. Ann. Phys. 1881, 248, 127–136. [Google Scholar] [CrossRef] [Green Version]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N·log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef] [Green Version]
- Ryckaert, J.-P.; Ciccotti, G.; Berendsen, H.J.C. Numerical integration of the cartesian equations of motion of a system with constraints: Molecular dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327–341. [Google Scholar] [CrossRef] [Green Version]
- Loncharich, R.J.; Brooks, B.R.; Pastor, R.W. Langevin dynamics of peptides: The frictional dependence of isomerization rates of N-acetylalanyl-N’-methylamide. Biopolymers 1992, 32, 523–535. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Postma, J.P.M.; Vangunsteren, W.F.; Dinola, A.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef] [Green Version]
- Jiang, H.; Patel, A.J. Recent advances in estimating contact angles using molecular simulations and enhanced sampling methods. Curr. Opin. Chem. Eng. 2019, 23, 130–137. [Google Scholar] [CrossRef]
- Shi, B.; Dhir, V.K. Molecular dynamics simulation of the contact angle of liquids on solid surfaces. J. Chem. Phys. 2009, 130, 034705. [Google Scholar] [CrossRef] [Green Version]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids, 2nd ed.; Oxford University Press: Oxford, UK, 2017; p. 640. [Google Scholar]
- Basconi, J.E.; Shirts, M.R. Effects of temperature control algorithms on transport properties and kinetics in molecular dynamics simulations. J. Chem. Theory Comput. 2013, 9, 2887–2899. [Google Scholar] [CrossRef] [PubMed]
- Theodorou, D.N.; Suter, U.W. Shape of unperturbed linear-polymers: Polypropylene. Macromolecules 1985, 18, 1206–1214. [Google Scholar] [CrossRef]
- Maginn, E.J.; Messerly, R.A.; Carlson, D.J.; Roe, D.R.; Elliot, J.R. Best practices for computing transport properties 1. Self-diffusivity and viscosity from equilibrium molecular dynamics [Article v1.0]. Living J. Comput. Mol. Sci. 2018, 1, 6324. [Google Scholar] [CrossRef] [Green Version]
- Carey, F.; Sundberg, R. Advanced Organic Chemistry: Part A: Structure and Mechanisms; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Hossain, M.A.; Hasan, T.; Khan, M.A.; Idriss Ali, K.M. Characterization of UV-cured film of urethane acrylate. Polym. Plast. Technol. Eng. 1994, 33, 1–11. [Google Scholar] [CrossRef]
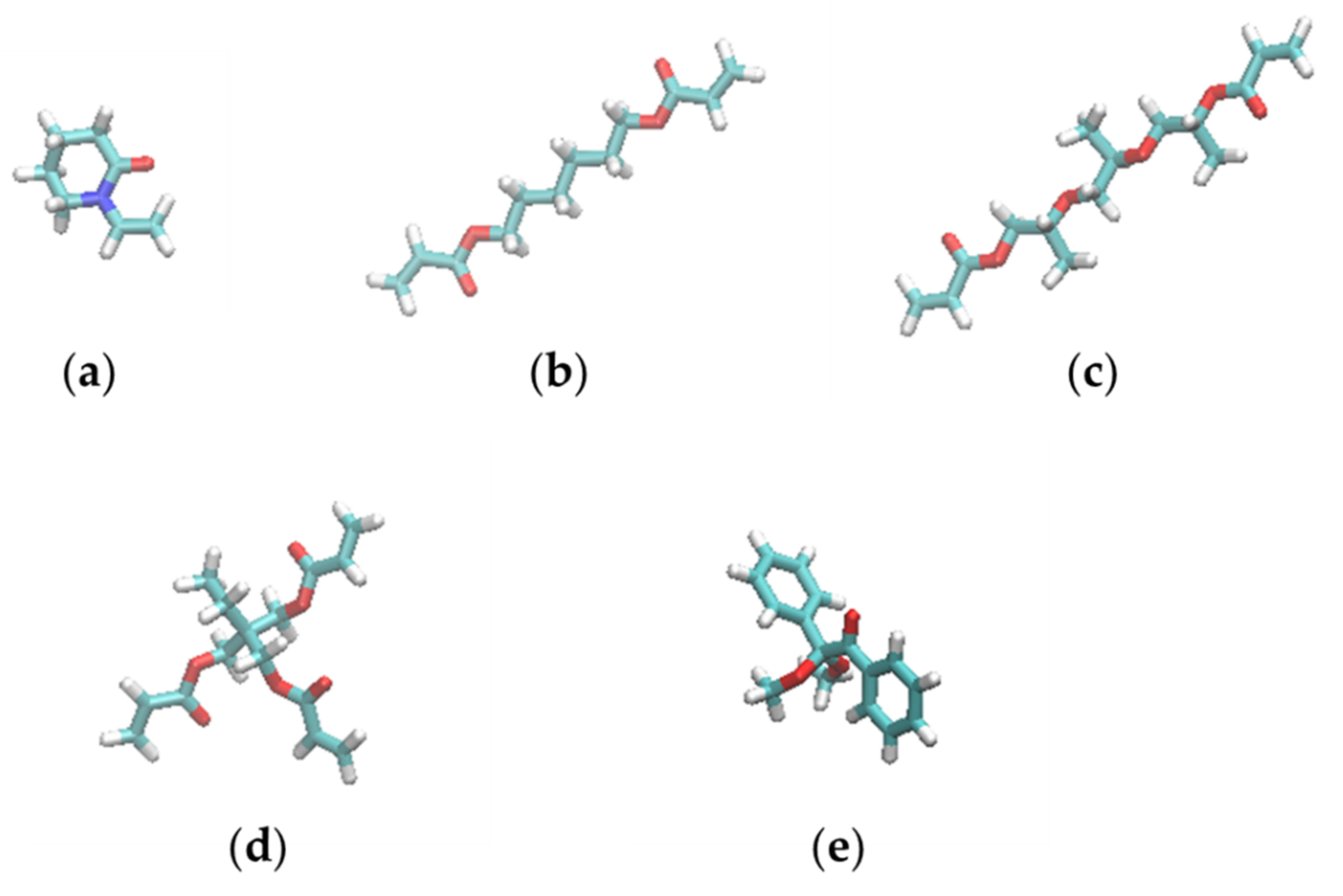
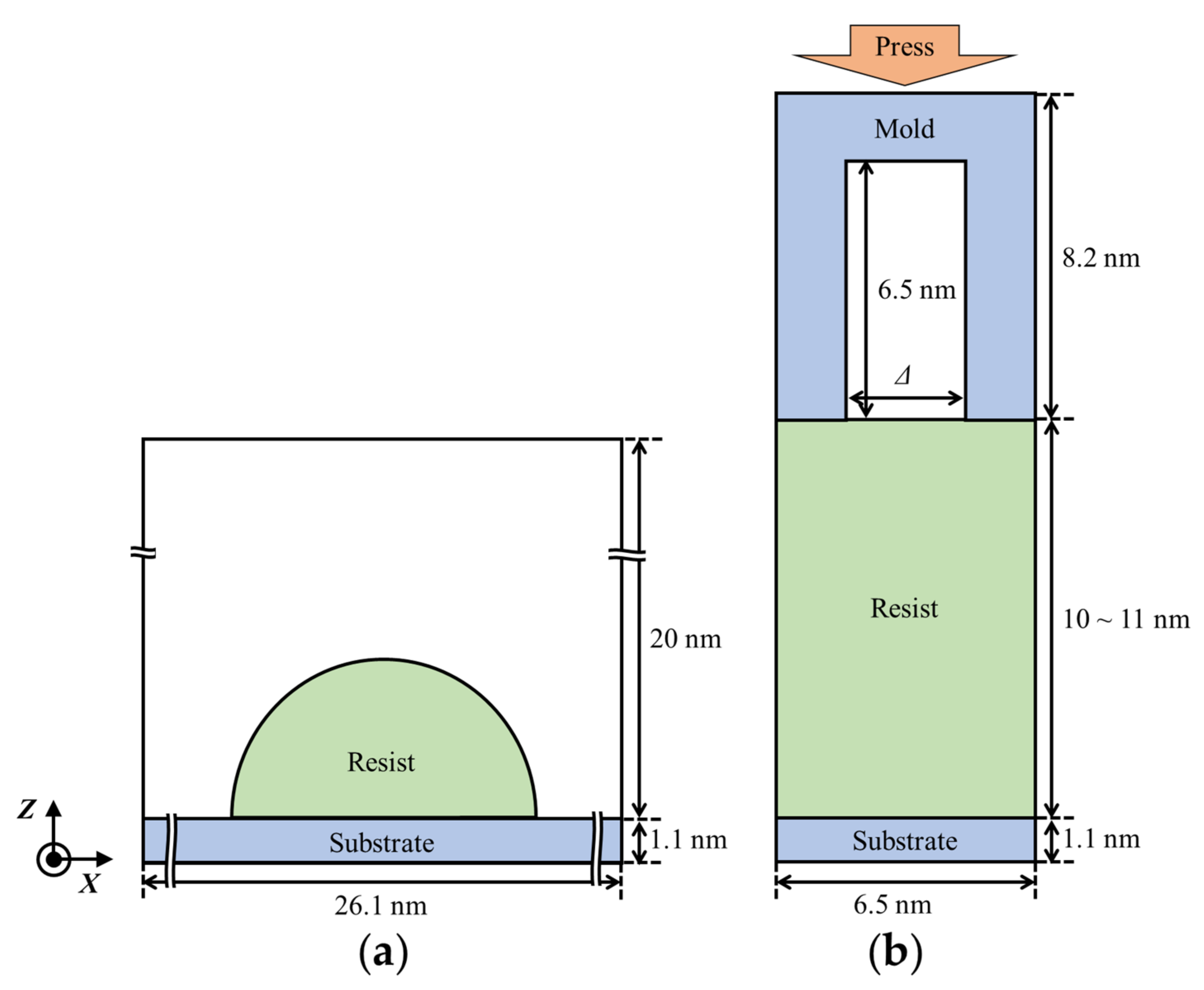
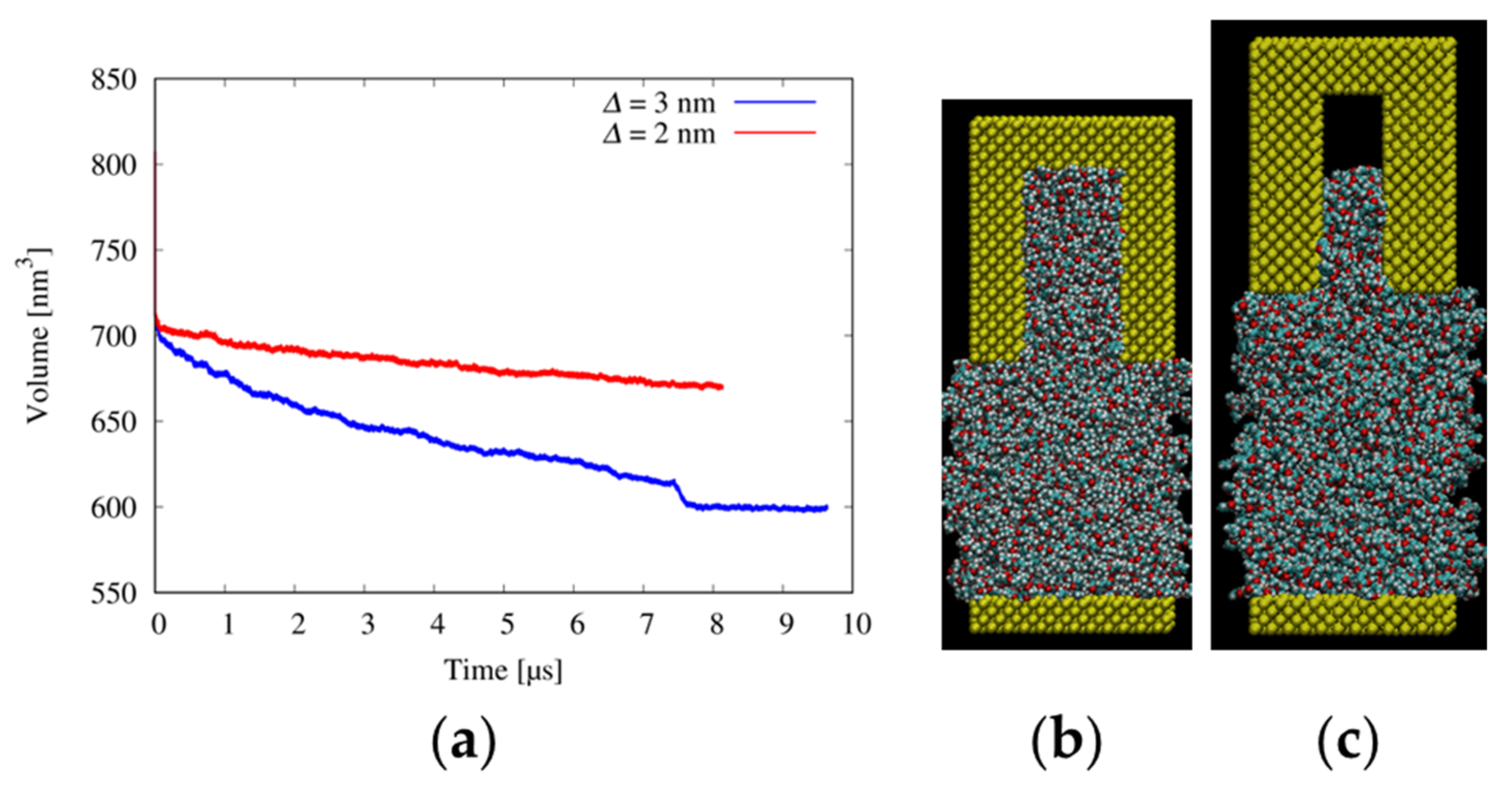
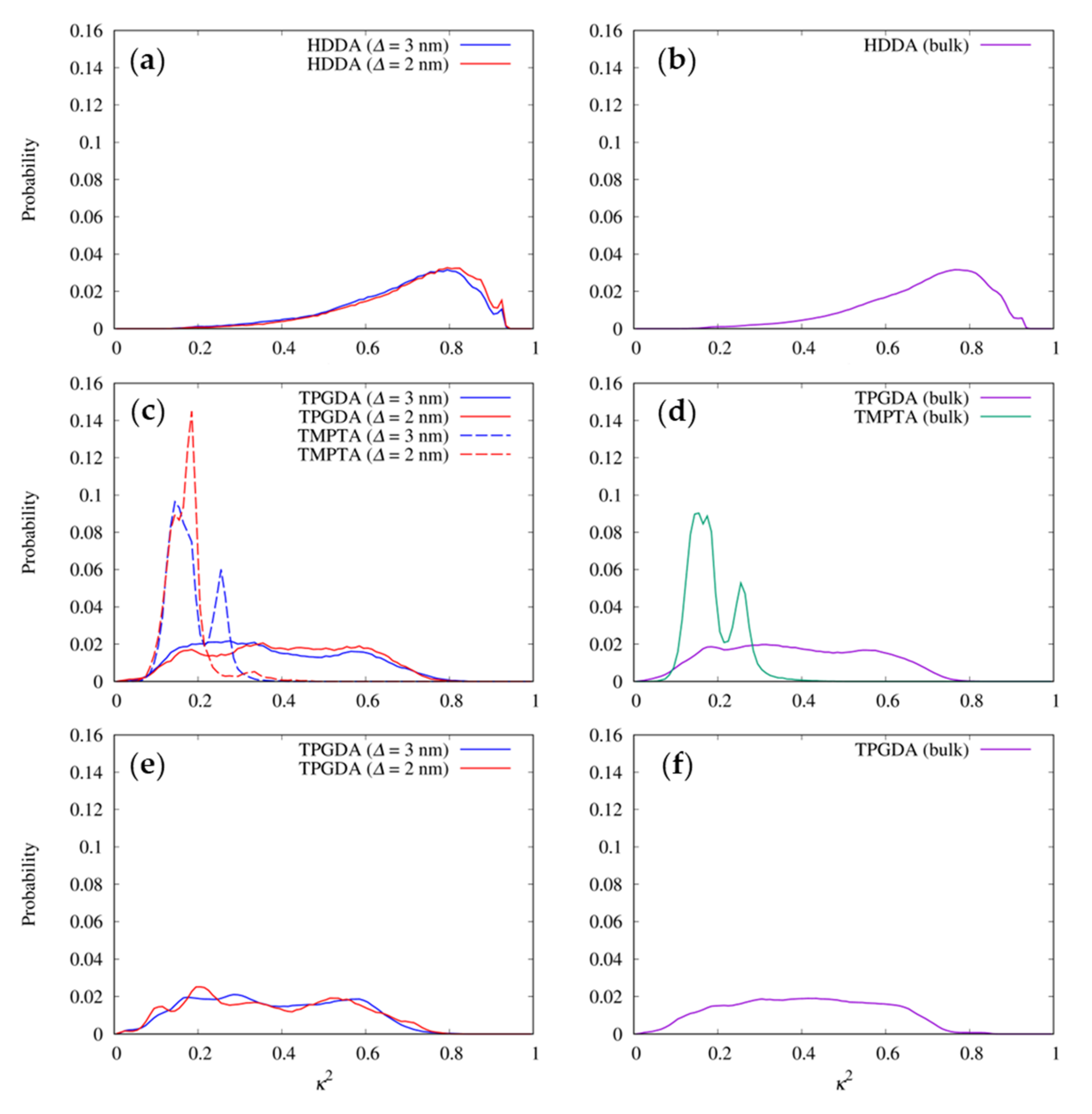
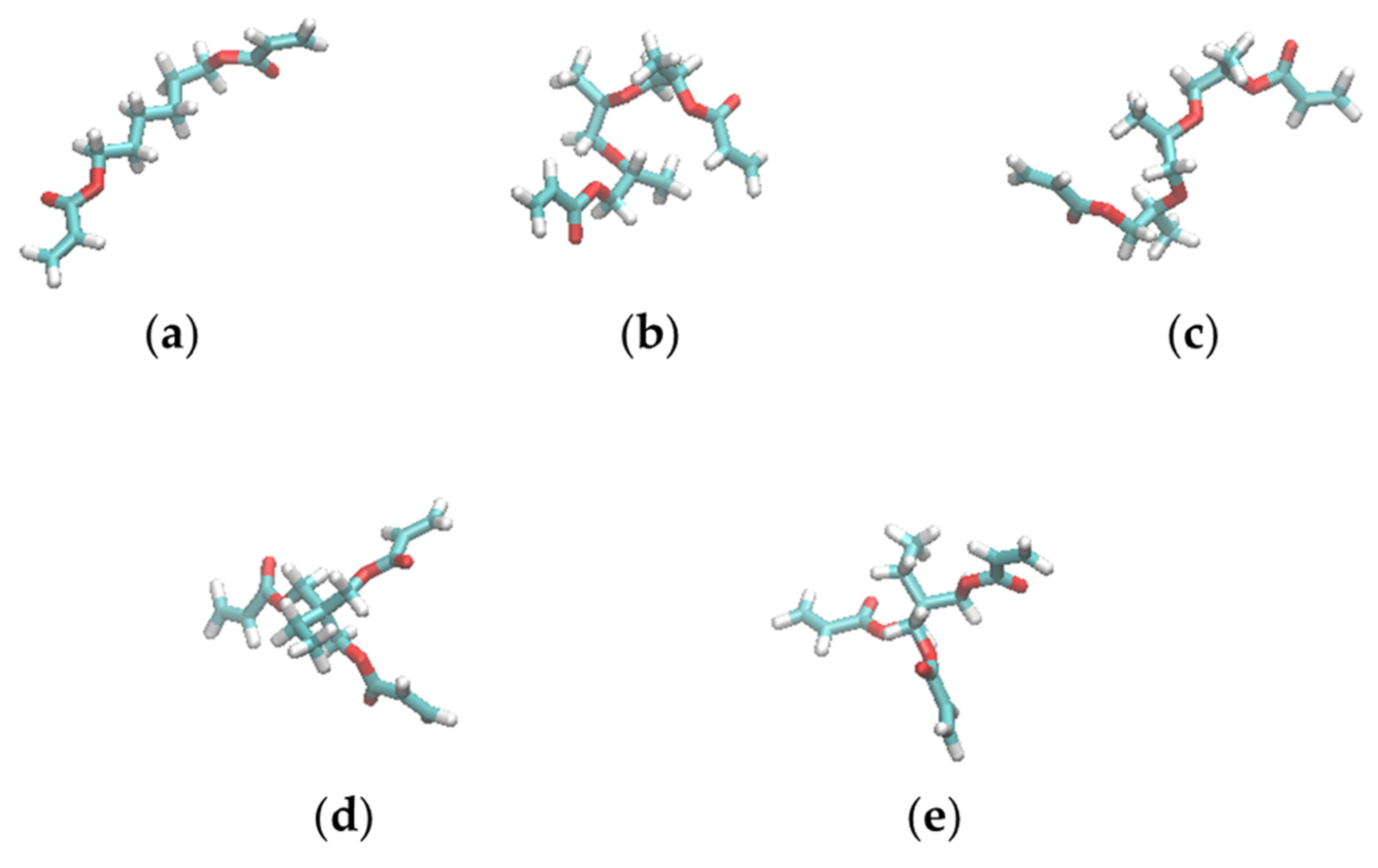
| Resist | Contact Angle [°] | D [10−12 m2/s] | Dresist I/D | η/ηresist I |
|---|---|---|---|---|
| Resist I | 111 ± 1.8 | 4.79 ± 0.26 | 1.0 | 1.0 |
| Resist II | 104 ± 3.3 | 3.32 ± 0.31 | 1.4 | 2.0 |
| Resist III | 126 ± 2.1 | 0.13 ± 0.01 | 36 | 24 |
| Resist IV | 111 ± 0.3 | 0.22 ± 0.03 | 21 | 2.5 |
| Resist | ∆ = 3 nm | ∆ = 2 nm | ||
|---|---|---|---|---|
| Time [μs] | Ratio to Resist I | Time [μs] | Ratio to Resist I | |
| Resist I | 0.15 | 1.0 | 0.25 | 1.0 |
| Resist II | 0.35 | 2.3 | 0.95 | 3.8 |
| Resist IV | 7.8 | 52 | - | - |
| Resist | Molecule | Radii of Gyration [Å] | |||
|---|---|---|---|---|---|
| ∆ = 3 nm 1 | ∆ = 2 nm 1 | Bulk 1 | Extended Conformation 2 | ||
| Resist I | HDDA | 4.34 | 4.34 | 4.32 | 5.03 |
| Resist II | TMPTA | 3.76 | 3.75 | 3.75 | 3.67 |
| TPGDA | 3.97 | 3.98 | 4.01 | 5.40 | |
| NVP | 2.07 | 2.07 | 2.07 | 2.01 | |
| Resist III | TMPTA | - | - | 3.74 | 3.67 |
| Resist IV | TPGDA | 4.04 | 3.96 | 4.03 | 5.40 |
| Resist | Pair of Molecules | r* [Å] | σRg [Å] | δ [Å] |
|---|---|---|---|---|
| Resist I | HDDA–HDDA | - 1 | 8.6 | - |
| Resist II | TMPTA–TMPTA | - 1 | 7.5 | - |
| TMPTA–TPGDA | 8.4 | 7.8 | 0.6 | |
| TMPTA–NVP | 6.5 | 5.7 | 0.8 | |
| TPGDA–TPGDA | 8.8 | 8.0 | 0.8 | |
| TPGDA–NVP | 7.9 | 6.1 | 1.8 | |
| NVP–NVP | 6.7 | 4.1 | 2.6 | |
| Resist III | TMPTA–TMPTA | 6.9 | 7.5 | −0.6 |
| Resist IV | TPGDA–TPGDA | 9.6 | 8.0 | 1.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iwata, J.; Ando, T. Molecular Dynamics Study on Behavior of Resist Molecules in UV-Nanoimprint Lithography Filling Process. Nanomaterials 2022, 12, 2554. https://doi.org/10.3390/nano12152554
Iwata J, Ando T. Molecular Dynamics Study on Behavior of Resist Molecules in UV-Nanoimprint Lithography Filling Process. Nanomaterials. 2022; 12(15):2554. https://doi.org/10.3390/nano12152554
Chicago/Turabian StyleIwata, Jun, and Tadashi Ando. 2022. "Molecular Dynamics Study on Behavior of Resist Molecules in UV-Nanoimprint Lithography Filling Process" Nanomaterials 12, no. 15: 2554. https://doi.org/10.3390/nano12152554
APA StyleIwata, J., & Ando, T. (2022). Molecular Dynamics Study on Behavior of Resist Molecules in UV-Nanoimprint Lithography Filling Process. Nanomaterials, 12(15), 2554. https://doi.org/10.3390/nano12152554





