Disordered Rock-Salt Type Li2TiS3 as Novel Cathode for LIBs: A Computational Point of View
Abstract
1. Introduction
2. Computational Details
3. Results
3.1. Sulfide Compounds Properties
| Set A | Set B | Experimental | |
|---|---|---|---|
| Li2S—Fm—3m | |||
| Cell Parameter a (A) | 5.81 | 5.81 | 5.72 |
| Li-S distance (A) | 2.51 | 2.51 | 2.47 |
| Band Gap (eV) | 5.32 | 5.41 | 3.8–4.0 [31] |
| TiS2—P—3m1 | |||
| Cell Parameter a,b (A) | 3.46 | 3.46 | 3.41 |
| Cell Parameter c (A) | 5.89 | 6.00 | 5.70 |
| Band Gap (eV) | 1.51 | 0.98 | 0.5–1.0 [32,33] |
| TiS3—P 21/m | |||
| Cell Parameter a (A) | 5.19 | 5.19 | 4.95 |
| Cell Parameter b (A) | 3.46 | 3.45 | 3.40 |
| Cell Parameter c (A) | 12.80 | 12.93 | 8.77 |
| β (°) | 94.81 | 96.33 | 97.32 |
| Band Gap (eV) | 1.85 | 1.47 | 1.0–1.2 [34,35] |
| LiTiS2—P—3m1 | |||
| Cell Parameter a, b (A) | 3.48 | 3.49 | 3.45 |
| Cell Parameter c (A) | 6.23 | 6.32 | 6.18 [36] |
| Band Gap (eV) | conductor | conductor | conductor |
| Li2TiS3—C2/m | |||
| Cell Parameter a (A) | 6.28 | 6.26 | 6.15 |
| Cell Parameter b (A) | 10.88 | 10.84 | 10.67 |
| Cell Parameter c (A) | 6.45 | 6.43 | 6.32 |
| β (°) | 109.2 | 109.2 | 109.0 [1] |
| Band Gap (eV) | 2.40 | 2.06 | - |
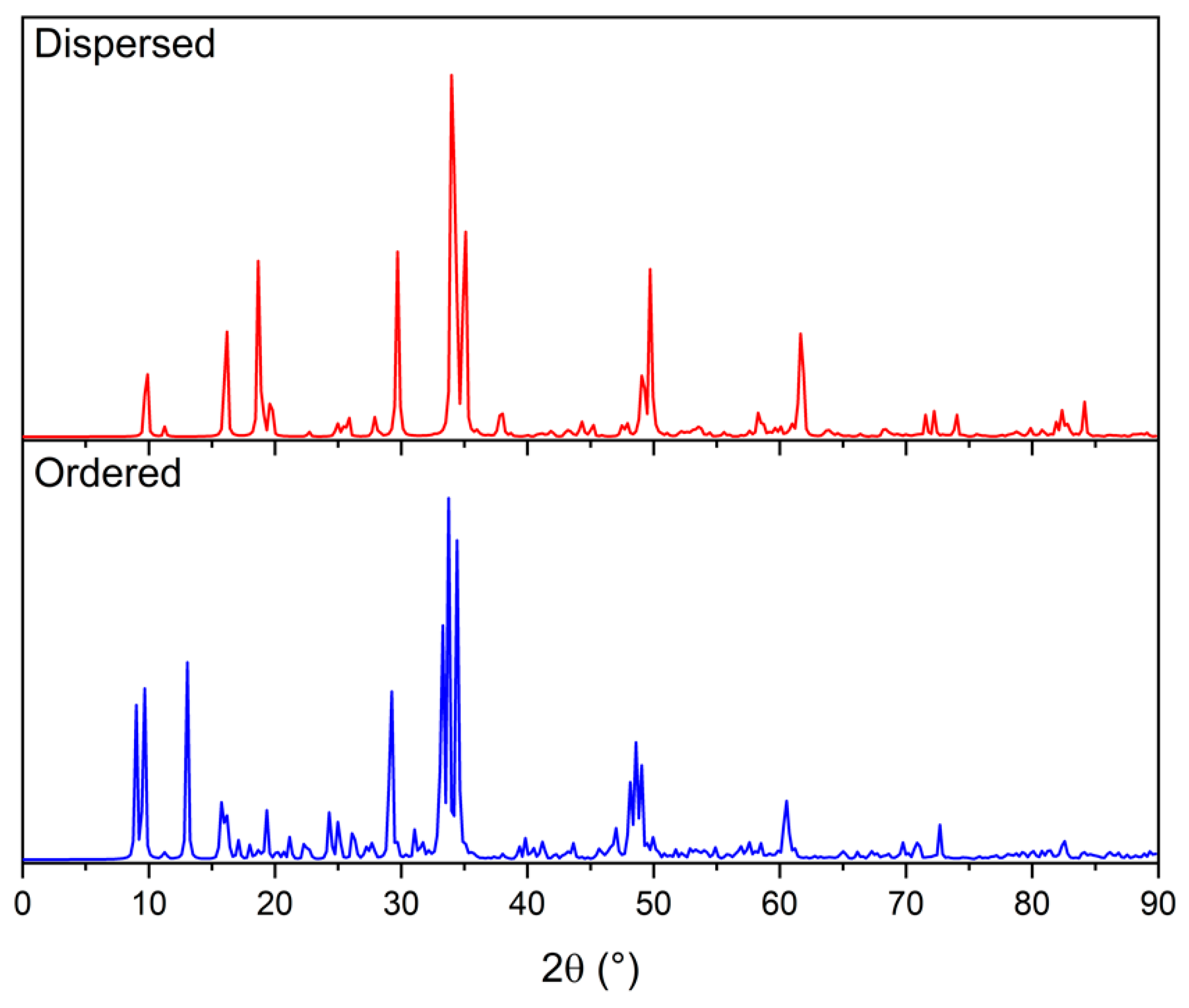
3.2. Disordered Cubic Li2TiS3
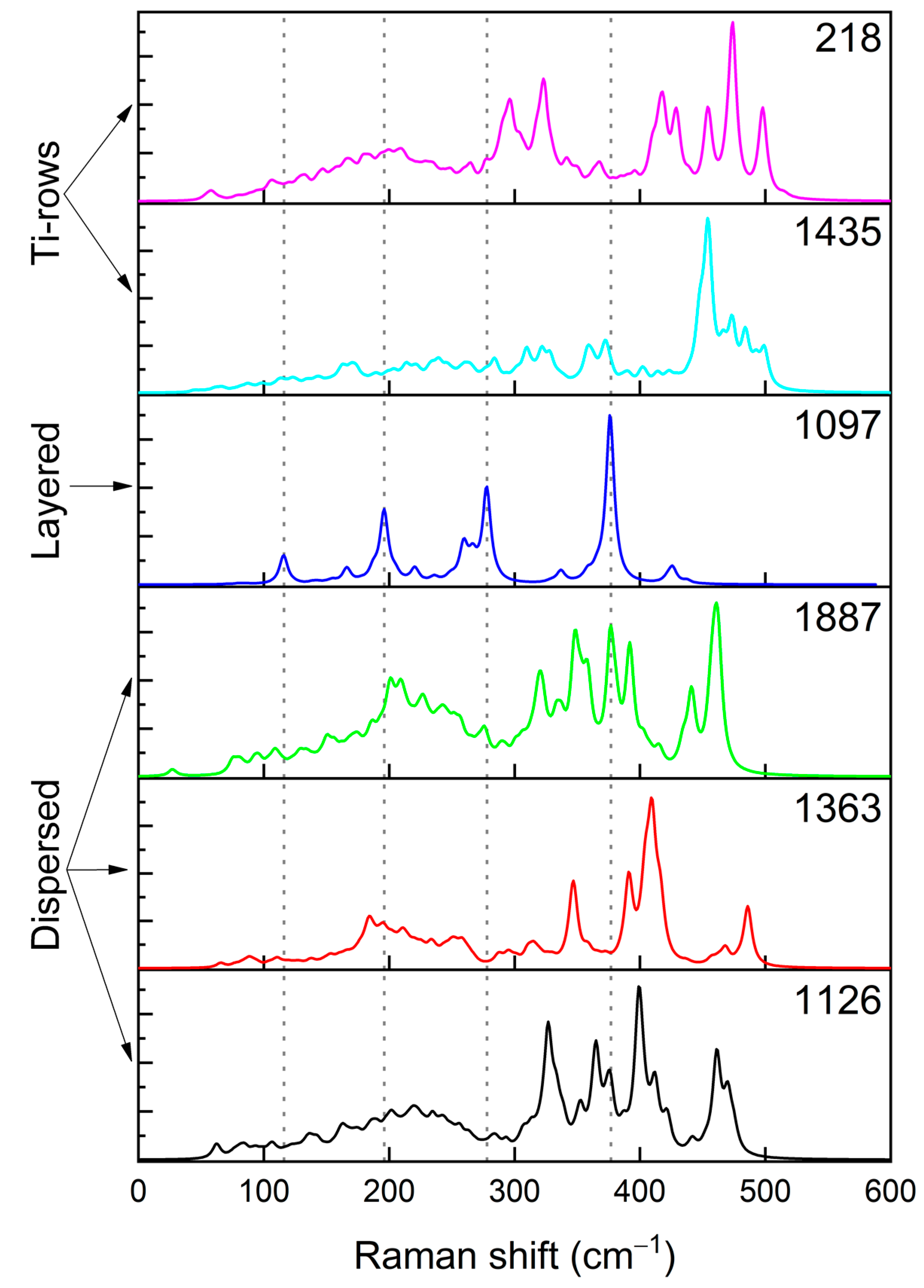
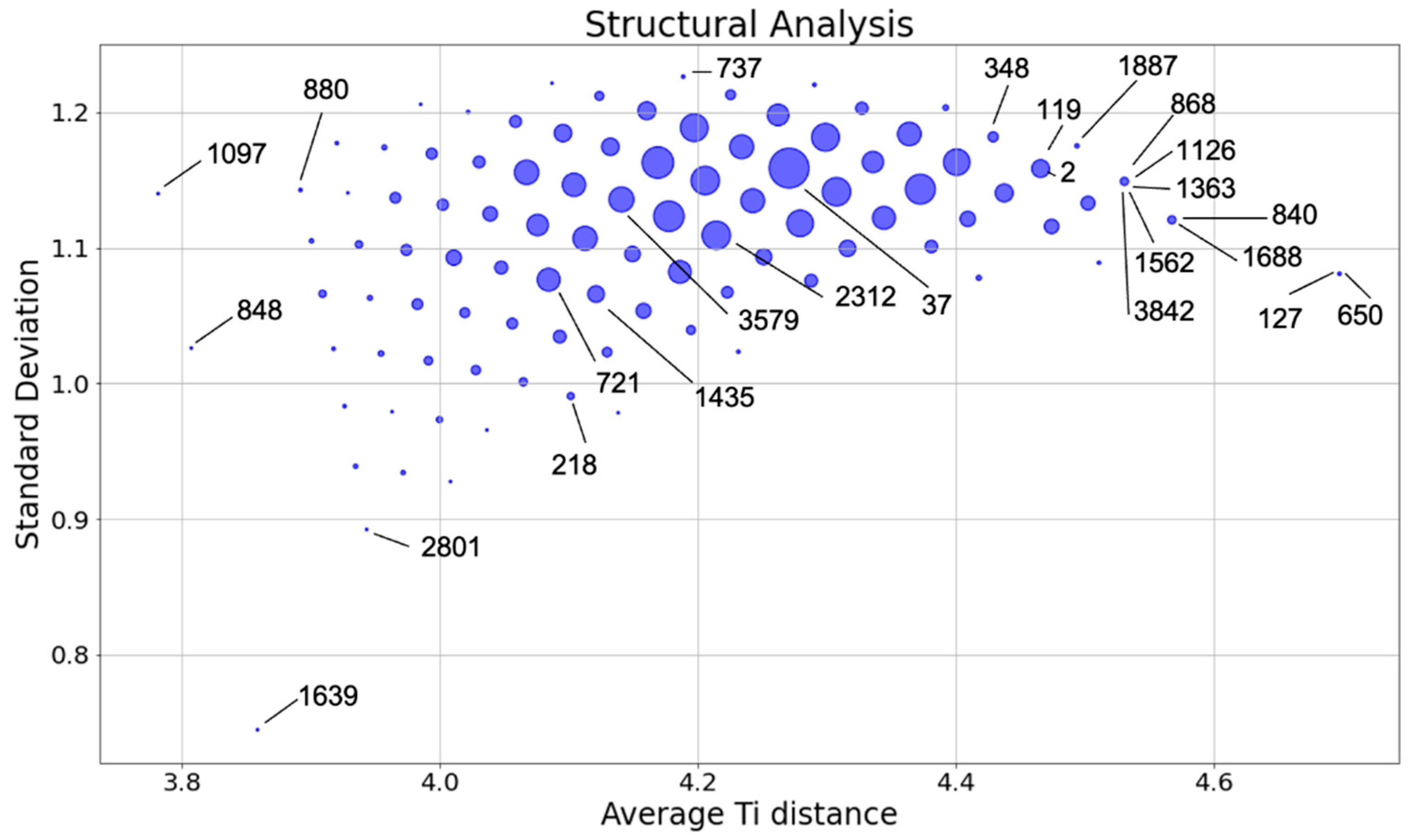
- structures 1639, 848, 1097, 127, and 650 were chosen as they are the outlier points
- structures 2801, 880, 737, 218, and 840 represent the borders of the main distribution
- structures 37, 3579, and 2312 were chosen as they sample the center of the main distribution
- structures 868, 1126, 1363, 1526, and 3842 were deliberately chosen to have the same values of and in order to study how the electronic properties vary within the same group
- structures 127 and 650 are of particular interest since, despite belonging to the same group, the structure 650 is largely dispersed, whereas the structure 127 has some level of nanostructuring. This nanostructuring can be described as a spiral structure where each Ti atom has two Ti atoms in its second coordination shell.
- all structures are less stable than the monoclinic one by 0.1–0.7 eV per Formula Unit (FU);
- dispersed structures (top of Table S3) result, overall, to be more stable than the structures displaying some level of ordering/nanostructuring (bottom of Table S3). The energy of the dispersed systems varies in a range of 0.1 eV/FU range (from 0.15 eV for structure 1887 to 0.24 eV for structure 840); the energy of the nanostructured systems varies in a range of 0.5 eV/FU (from 0.45 eV for structure 2312 to 0.70 eV for structure 880). The only exception in this trend (among the structures selected for this study) is structure 2, whose energy falls into the dispersed energy ones, despite the presence of a Ti row. However, by looking at its structure, it can be observed that aside from the single Ti row, the other Ti atoms appear to be evenly dispersed. This is also confirmed by the fact that structure 2 can be found at the top right corner of Figure 3 and it can, therefore, be considered to be at the border between the dispersed and nanostructured structures as it is also suggested by its energy and band gap;
- the band gap follows a similar trend as for relative stability, as it decreases regularly with the increasing level of Ti nanostructuring, from 2.5 eV (dispersed structures) to 1.71 eV (structures with multiple Ti rows or plane). As highlighted before, the hybrid B3LYP method generally overestimate the band gap values, we expect that a similar behavior occurs in these systems;
- the structure is pseudo-cubic with small deviations from the ideal cubic one; structures showing some ordering tend to have larger volumes that can be seen as an indication of the distortion that nanostructuring imposes to the lattice. In order to further study such distortion, the maximum and minimum Li-S, Li-Ti, and Li-Ti distances are reported in Table S3. The ordered structures have the largest variability among these values. The effect of this distortion on the electronic structure of the material is discussed below.
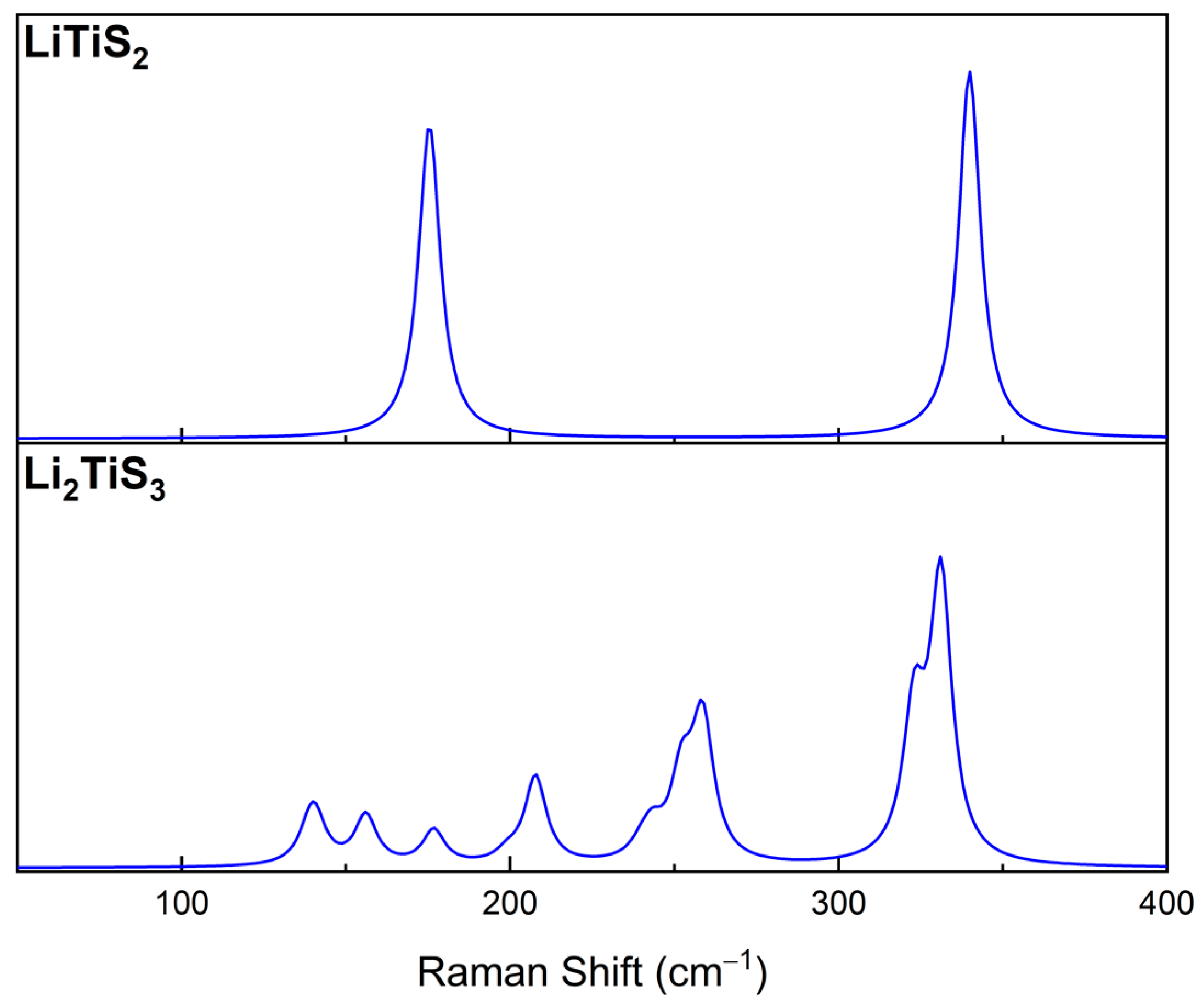
- the asymmetric stretching of Ti-S and Li-S bonds are shifted to 400 cm−1 by ~30 cm−1;
- the symmetric stretching of Li-S bonds is shifted to ~350 cm−1, with a Δν of ~50 cm−1;
- the symmetric stretching of Ti-S and Li-S bonds falls in the region close to 450 cm−1.
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Flamary-Mespoulie, F.; Boulineau, A.; Martinez, H.; Suchomel, M.R.; Delmas, C.; Pecquenard, B.; Le Cras, F. Lithium-rich layered titanium sulfides: Cobalt- and Nickel-free high capacity cathode materials for lithium-ion batteries. Energy Storage Mater. 2020, 26, 213–222. [Google Scholar] [CrossRef]
- Leube, B.T.; Robert, C.; Foix, D.; Porcheron, B.; Dedryvère, R.; Rousse, G.; Salager, E.; Cabelguen, P.-E.; Abakumov, A.M.; Vezin, H.; et al. Activation of anionic redox in d0 transition metal chalcogenides by anion doping. Nat. Commun. 2021, 12, 5485. [Google Scholar] [CrossRef] [PubMed]
- Celasun, Y.; Colin, J.-F.; Martinet, S.; Benayad, A.; Peralta, D. Lithium-Rich Rock Salt Type Sulfides-Selenides (Li2TiSexS3−x): High Energy Cathode Materials for Lithium-Ion Batteries. Materials 2022, 15, 3037. [Google Scholar] [CrossRef] [PubMed]
- Sakuda, A.; Takeuchi, T.; Shikano, M.; Ohara, K.; Fukuda, K.; Uchimoto, Y.; Ogumi, Z.; Kobayashi, H.; Sakaebe, H. Development of Li2TiS3–Li3NbS4 by a mechanochemical process. J. Ceram. Soc. Jpn. 2017, 125, 268–271. [Google Scholar] [CrossRef][Green Version]
- Grimaud, A.; Hong, W.T.; Shao-Horn, Y.; Tarascon, J.-M. Anionic redox processes for electrochemical devices. Nat. Mater. 2016, 15, 121–126. [Google Scholar] [CrossRef]
- Sakuda, A.; Ohara, K.; Kawaguchi, T.; Fukuda, K.; Nakanishi, K.; Arai, H.; Uchimoto, Y.; Ohta, T.; Matsubara, E.; Ogumi, Z.; et al. A Reversible Rocksalt to Amorphous Phase Transition Involving Anion Redox. Sci. Rep. 2018, 8, 15086. [Google Scholar] [CrossRef]
- Sakuda, A.; Takeuchi, T.; Okamura, K.; Kobayashi, H.; Sakaebe, H.; Tatsumi, K.; Ogumi, Z. Rock-salt-type lithium metal sulphides as novel positive-electrode materials. Sci. Rep. 2015, 4, 4883. [Google Scholar] [CrossRef]
- D’Amore, M.; Takasao, G.; Chikuma, H.; Wada, T.; Taniike, T.; Pascale, F.; Ferrari, A.M. Spectroscopic Fingerprints of MgCl2/TiCl4 Nanoclusters Determined by Machine Learning and DFT. J. Phys. Chem. C 2021, 125, 20048–20058. [Google Scholar] [CrossRef]
- D’Amore, M.; Taniike, T.; Terano, M.; Ferrari, A.M. Effect of Internal Donors on Raman and IR Spectroscopic Fingerprints of MgCl2/TiCl4 Nanoclusters Determined by Machine Learning and DFT. Materials 2022, 15, 909. [Google Scholar] [CrossRef]
- Dresselhaus, M.S.; Dresselhaus, G.; Saito, R.; Jorio, A. Raman spectroscopy of carbon nanotubes. Phys. Rep. 2005, 409, 47–99. [Google Scholar] [CrossRef]
- Piovano, A.; D’Amore, M.; Wada, T.; Cleto Bruzzese, P.; Takasao, G.; Thakur, A.; Chammingkwan, P.; Terano, M.; Civalleri, B.; Bordiga, S.; et al. Revisiting the identity of δ-MgCl2: Part II. Morphology and exposed surfaces studied by vibrational spectroscopies and DFT calculation. J. Catal. 2020, 387, 1–11. [Google Scholar] [CrossRef]
- Platonenko, A.; Gentile, F.S.; Pascale, F.; Ferrari, A.M.; D’Amore, M.; Dovesi, R. Nitrogen substitutional defects in silicon. A quantum mechanical investigation of the structural, electronic and vibrational properties. Phys. Chem. Chem. Phys. 2019, 21, 20939–20950. [Google Scholar] [CrossRef] [PubMed]
- Dovesi, R.; Erba, A.; Orlando, R.; Zicovich-Wilson, C.M.; Civalleri, B.; Maschio, L.; Rérat, M.; Casassa, S.; Baima, J.; Salustro, S.; et al. Quantum-mechanical condensed matter simulations with CRYSTAL. WIREs Comput. Mol. Sci. 2018, 8. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
- Vilela Oliveira, D.; Laun, J.; Peintinger, M.F.; Bredow, T. BSSE-correction scheme for consistent gaussian basis sets of double- and triple-zeta valence with polarization quality for solid-state calculations. J. Comput. Chem. 2019, 40, 2364–2376. [Google Scholar] [CrossRef]
- Piskunov, S.; Heifets, E.; Eglitis, R.I.; Borstel, G. Bulk properties and electronic structure of SrTiO3, BaTiO3, PbTiO3 perovskites: An ab initio HF/DFT study. Comput. Mater. Sci. 2004, 29, 165–178. [Google Scholar] [CrossRef]
- Schäfer, A.; Huber, C.; Ahlrichs, R. Fully optimized contracted Gaussian basis sets of triple zeta valence quality for atoms Li to Kr. J. Chem. Phys. 1994, 100, 5829–5835. [Google Scholar] [CrossRef]
- Dovesi, R.; Ermondi, C.; Ferrero, E.; Pisani, C.; Roetti, C. Hartree-Fock study of lithium hydride with the use of a polarizable basis set. Phys. Rev. B 1984, 29, 3591–3600. [Google Scholar] [CrossRef]
- Tasci, E.S.; de la Flor, G.; Orobengoa, D.; Capillas, C.; Perez-Mato, J.M.; Aroyo, M.I. An introduction to the tools hosted in the Bilbao Crystallographic Server. EPJ Web Conf. 2012, 22, 00009. [Google Scholar] [CrossRef]
- McColm, G. Prospects for mathematical crystallography. Acta Crystallogr. Sect. Found. Adv. 2014, 70, 95–105. [Google Scholar] [CrossRef] [PubMed]
- Setyawan, W.; Curtarolo, S. High-throughput electronic band structure calculations: Challenges and tools. Comput. Mater. Sci. 2010, 49, 299–312. [Google Scholar] [CrossRef]
- Celasun, Y. Synthesis and Characterization of New Positive Electrode Materials for Li-Ion High Energy Applications. Ph.D. Thesis. Available online: https://tel.archives-ouvertes.fr/tel-03080208 (accessed on 16 January 2021).
- Mustapha, S.; D’Arco, P.; Ferrabone, M.; Dovesi, R. On the use of symmetry in the configurational analysis for the simulation of disordered solids. J. Phys. Condens. Matter 2013, 25, 105401. [Google Scholar] [CrossRef] [PubMed]
- Solid-Solutions. Computational Materials Science Group ICL: 2022. Available online: https://github.com/cmsg-icl/solid-solutions/blob/4ac473507adcf3badc3077df2f101c55f448354c/Li2TiS.ipynb (accessed on 25 April 2022).
- Crystal-Code-Tools Crystal_Functions. Available online: https://github.com/crystal-code-tools/crystal_functions (accessed on 25 April 2022).
- Allen, F.H.; Shields, G.P. Crystallographic Databases and Knowledge Bases in Materials Design. In Implications of Molecular and Materials Structure for New Technologies; Howard, J.A.K., Allen, F.H., Shields, G.P., Eds.; Springer: Dordrecht, The Netherlands, 1999; pp. 291–302. ISBN 978-0-7923-5817-6. [Google Scholar]
- Garza, A.J.; Scuseria, G.E. Predicting Band Gaps with Hybrid Density Functionals. J. Phys. Chem. Lett. 2016, 7, 4165–4170. [Google Scholar] [CrossRef] [PubMed]
- Xiao, H.; Tahir-Kheli, J.; Goddard, W.A. Accurate Band Gaps for Semiconductors from Density Functional Theory. J. Phys. Chem. Lett. 2011, 2, 212–217. [Google Scholar] [CrossRef]
- Pan, Y.; Guan, W.; Mao, P. Insulator-to-metal transition of lithium–sulfur battery. RSC Adv. 2017, 7, 44326–44332. [Google Scholar] [CrossRef]
- Ohno, Y. Optical properties and the optical joint density of states of the misfit-layer compounds (MS)1+x TS2. J. Phys. Condens. Matter 1994, 6, 8655–8668. [Google Scholar] [CrossRef]
- Liu, B.; Yang, J.; Han, Y.; Hu, T.; Ren, W.; Liu, C.; Ma, Y.; Gao, C. Electronic structure of TiS2 and its electric transport properties under high pressure. J. Appl. Phys. 2011, 109, 053717. [Google Scholar] [CrossRef]
- Jin, Y.; Li, X.; Yang, J. Single layer of MX3 (M = Ti, Zr; X = S, Se, Te): A new platform for nano-electronics and optics. Phys. Chem. Chem. Phys. 2015, 17, 18665–18669. [Google Scholar] [CrossRef]
- Island, J.O.; Molina-Mendoza, A.J.; Barawi, M.; Biele, R.; Flores, E.; Clamagirand, J.M.; Ares, J.R.; Sánchez, C.; van der Zant, H.S.J.; D’Agosta, R.; et al. Electronics and optoelectronics of quasi-1D layered transition metal trichalcogenides. 2D Mater. 2017, 4, 022003. [Google Scholar] [CrossRef]
- Patel, S.N.; Balchin, A.A. Observation of intermediate phases during the lithium intercalation of TiX2 (X = S, Se). Z. Für Krist.-Cryst. Mater. 1983, 164, 273–278. [Google Scholar] [CrossRef]
- Mishra, K.K.; Ravindran, T.R.; Island, J.O.; Flores, E.; Ares, J.R.; Sanchez, C.; Ferrer, I.J.; van der Zant, H.S.J.; Pawbake, A.; Kanawade, R.; et al. Raman Fingerprint of Pressure-Induced Phase Transitions in TiS3 Nanoribbons: Implications for Thermal Measurements under Extreme Stress Conditions. ACS Appl. Nano Mater. 2020, 3, 8794–8802. [Google Scholar] [CrossRef]
- Bertheville, B.; Bill, H.; Hagemann, H. Experimental Raman scattering investigation of phonon anharmonicity effects in Li2S. J. Phys. Condens. Matter 1998, 10, 2155. [Google Scholar] [CrossRef]
- Sherrell, P.C.; Sharda, K.; Grotta, C.; Ranalli, J.; Sokolikova, M.S.; Pesci, F.M.; Palczynski, P.; Bemmer, V.L.; Mattevi, C. Thickness-Dependent Characterization of Chemically Exfoliated TiS2 Nanosheets. ACS Omega 2018, 3, 8655–8662. [Google Scholar] [CrossRef]
- Talib, M.; Tabassum, R.; Islam, S.S.; Mishra, P. Influence of growth temperature on titanium sulphide nanostructures: From trisulphide nanosheets and nanoribbons to disulphide nanodiscs. RSC Adv. 2019, 9, 645–657. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA: A three-dimensional visualization system for electronic and structural analysis. J. Appl. Crystallogr. 2008, 41, 653–658. [Google Scholar] [CrossRef]


| Set A | Set B | Experimental | |
|---|---|---|---|
| Li2S | |||
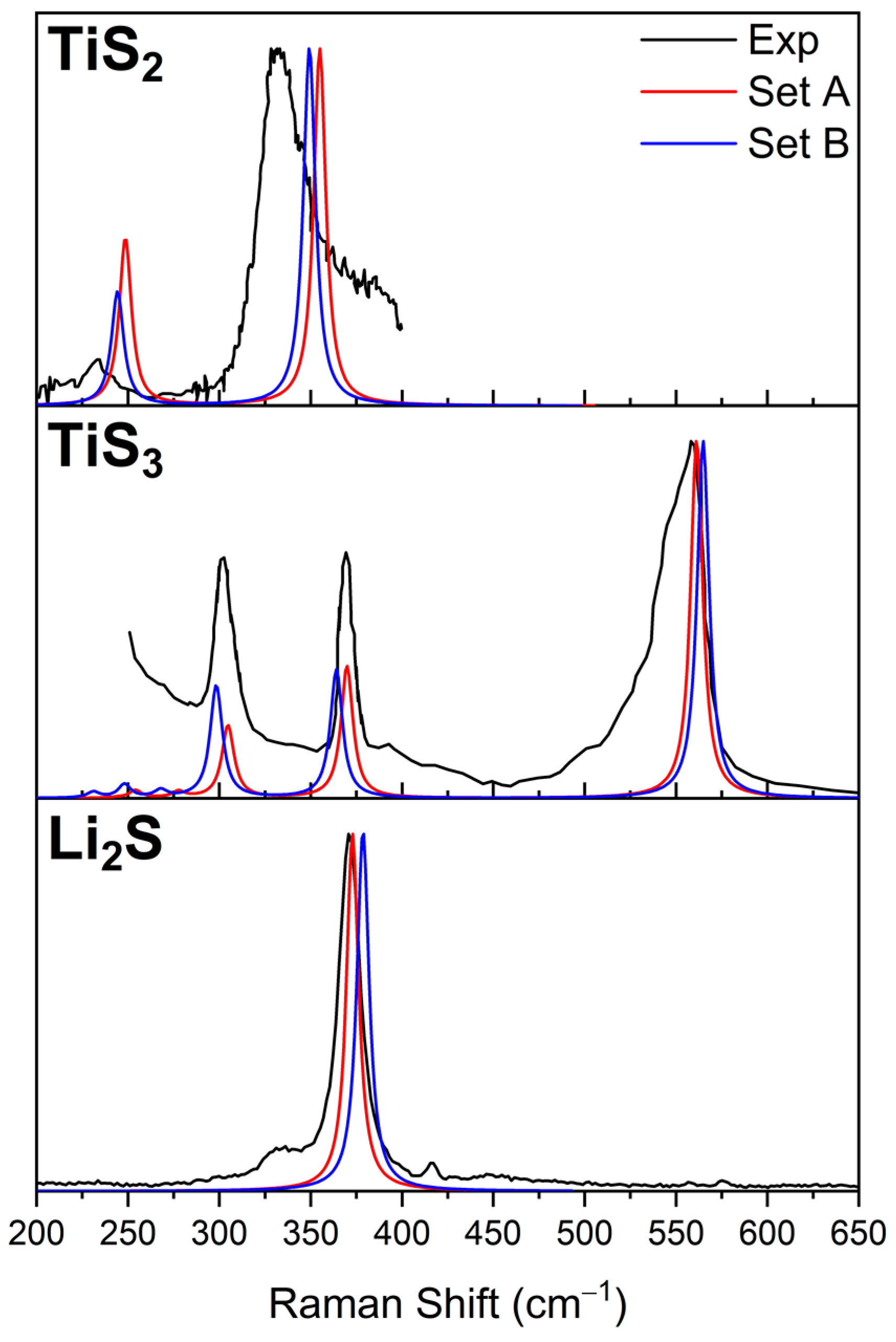
| Raman Peak | 372 cm−1 | 375 cm−1 | 370 cm−1 [38] |
| TiS2 | |||
| Raman Peak 1 | 248 cm−1 | 244 cm−1 | 250 cm−1 |
| Raman Peak 2 | 359 cm−1 | 349 cm−1 | 334 cm−1 [39] |
| TiS3 | |||
| Raman Peak 1 | 304 cm−1 | 298 cm−1 | 299 cm−1 |
| Raman Peak 2 | 370 cm−1 | 364 cm−1 | 365 cm−1 |
| Raman Peak 3 | 561 cm−1 | 565 cm−1 | 560 cm−1 [37,40] |
| Large | Nanostructuring (Ti planes) | Disordered structures (no Ti nanostructuring) |
| Small | Ordered structures (Ti clusters, vicinal rows) | Disordered structures (local Ti nanostructuring) |
| Structure ID | ΔE (eV) | Band Gap (eV) | V1 (Å3) | q (Ti) | q (Li) | q (S) | Description |
|---|---|---|---|---|---|---|---|
| 1887 | 0.146 | 2.465 | 948.99 | 0.64 | 0.85 | −0.78 | Dispersed |
| 1363 | 0.148 | 2.531 | 950.81 | 0.63 | 0.85 | −0.78 | Dispersed |
| 1126 | 0.164 | 2.509 | 953.42 | 0.64 | 0.85 | −0.78 | Dispersed |
| 218 | 0.589 | 1.854 | 1002.55 | 0.57 | 0.85 | −0.76 | Ti rows |
| 1097 | 0.695 | 1.795 | 1046.59 | 0.57 | 0.85 | −0.76 | Ti Planes (1 0 0) |
| 1435 | 0.699 | 1.706 | 1030.19 | 0.56 | 0.85 | −0.75 | Ti rows |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rocca, R.; Sgroi, M.F.; Camino, B.; D’Amore, M.; Ferrari, A.M. Disordered Rock-Salt Type Li2TiS3 as Novel Cathode for LIBs: A Computational Point of View. Nanomaterials 2022, 12, 1832. https://doi.org/10.3390/nano12111832
Rocca R, Sgroi MF, Camino B, D’Amore M, Ferrari AM. Disordered Rock-Salt Type Li2TiS3 as Novel Cathode for LIBs: A Computational Point of View. Nanomaterials. 2022; 12(11):1832. https://doi.org/10.3390/nano12111832
Chicago/Turabian StyleRocca, Riccardo, Mauro Francesco Sgroi, Bruno Camino, Maddalena D’Amore, and Anna Maria Ferrari. 2022. "Disordered Rock-Salt Type Li2TiS3 as Novel Cathode for LIBs: A Computational Point of View" Nanomaterials 12, no. 11: 1832. https://doi.org/10.3390/nano12111832
APA StyleRocca, R., Sgroi, M. F., Camino, B., D’Amore, M., & Ferrari, A. M. (2022). Disordered Rock-Salt Type Li2TiS3 as Novel Cathode for LIBs: A Computational Point of View. Nanomaterials, 12(11), 1832. https://doi.org/10.3390/nano12111832