Abstract
High-performance modeling of neurophysiological processes is an urgent task that requires new approaches to information processing. In this context, two- and three-junction superconducting quantum interferometers with Josephson weak links based on gold nanowires are fabricated and investigated experimentally. The studied cells are proposed for the implementation of bio-inspired neurons—high-performance, energy-efficient, and compact elements of neuromorphic processor. The operation modes of an advanced artificial neuron capable of generating the burst firing activation patterns are explored theoretically. A comparison with the Izhikevich mathematical model of biological neurons is carried out.
1. Introduction
Modeling the processes in the brain of living beings is a complex and urgent task [1,2,3,4,5,6,7,8,9]. One of the main problems in this area is an insufficient number of neurons and synapses in modern Complementary-Metal-Oxide-Semiconductor (CMOS) neuromorphic processors. Their complexity is closely tightened by large power consumption and heat dissipation of the circuits. The best CMOS neuromorphic systems simulate the networks consisting of about 1 million neurons and a quarter of a billion synapses [10,11,12]. However, the most ambitious biological projects state the goals of neurons and synapses [13]. The demand for such a high complexity makes important the consideration of novel physical principles for signal transmission and processing.
There are many approaches addressing this issue. Among others, the emerging nonvolatile memory devices [14] are pushing the limits beyond CMOS technology. In particular, ferroelectric memory devices with fast write/read times (of an order of 1 ns) have been recognized as promising neuromorphic elements [15]. They are compatible with CMOS circuits operating at the same voltage level, while consuming several orders of magnitude less energy (of an order of fJ) than CMOS neuron composed of dozens of transistors [16].
The application of superconducting materials [17,18,19] also allows for competing CMOS in the implementation of artificial neurons. Josephson junction switching provides the generation of picosecond-width quantized voltage spike of ∼mV amplitude accompanied by sub-aJ energy dissipation [20,21]. The shape of this spike can be quite close to the one produced in neurophysiological processes [22]. It was shown that an artificial neuron can be implemented using only two Josephson junctions [22,23] (see illustration in Figure 1). This is an order of magnitude less than the number of transistors in CMOS counterparts [16]. At the same time, it is possible to implement the synaptic memory using just single junction with ferromagnetic material [24,25,26,27,28,29,30]. The superconductivity enables ballistic signal transfer along the wires. The voltage spikes can be transmitted with a speed approaching the speed of light over long distances with low crosstalk [31]. Note that the Josephson junctions can be fabricated in any layer of multilayer superconducting circuit [32]. These features are favor for the implementation of complex and energy-efficient 3D neural networks closely mimic biological nerve tissue.
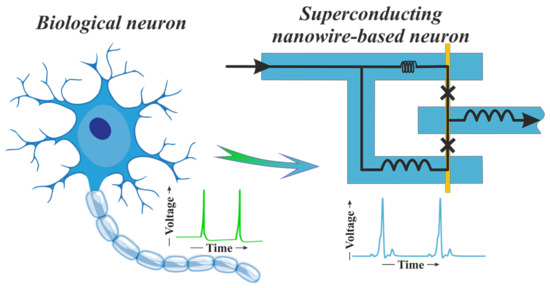
Figure 1.
Sketch of a biological neuron and its artificial counterpart made of a superconducting material with a normal metal nanowire.
While the superconducting neural networks of various kinds are rapidly developed currently [22,23,24,28,33,34,35,36,37,38,39,40], their complexity is severely limited by the low integration density of superconducting circuits [41,42]. One of the main reasons for this is a comparatively large area (an order of a micron to few tenths of a micron squared) of commonly used superconductor-insulator-superconductor tunnel Josephson junction [32]. Elaboration of nanoscale junctions are highly important for many applications [20,43,44,45,46,47,48,49,50,51,52]. In this work, we develop the nanowire-based Josephson structures for the implementation of superconducting bio-inspired neurons. We further elaborate the superconducting artificial neuron schematic enabling operation modes corresponding to important biological activity missed in previously proposed devices.
2. Results and Discussion
2.1. Preparation of Samples and Experimental Results
The fabricated samples are based on gold nanowires, 60 nm in diameter. The nanowires were grown by metal electrodeposition into porous templates of anodic alumina from cyanide-free Ecomet 04-ZG electrolyte solution at a constant deposition potential of −1.0 V versus Ag/AgCl reference electrode. Different types of superconducting quantum interferometers (SQUIDs) were fabricated using e-beam lithography and magnetron sputtering of superconducting niobium (see Supplementary Materials and Ref. [53] for more details).
We have implemented two types of SQUID cells. The first one is a device with two Josephson weak links, sample A, shown in Figure 2a with a quantization loop area of 5.1 m. The other one is a SQUID cell with three Josephson junctions, sample B (Figure 2b), with two loops having quantization areas of 11.3 and 13.8 m. We have also implemented a more exotic variant of a two-junction SQUID composed of closely spaced nanowires placed between bulk superconducting electrodes—Sample C (Figure 2c). Here the working area between two wires is about 0.5 m.
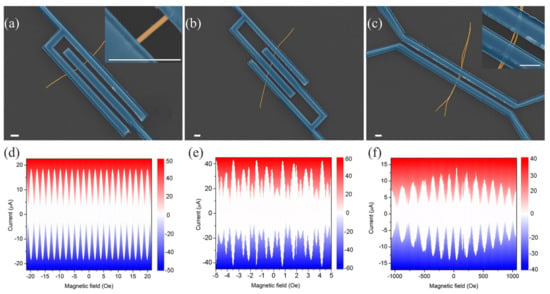
Figure 2.
Scanning electron microscope images of (a) sample A (insert—Zoom of the Josephson junction), (b) sample B, and (c) sample C with zoom of the central part of the sample C. The scale bar is 1 m. The corresponding sets of current-voltage characteristics in various magnetic fields for these samples are shown in panels (d–f); voltage scale is in V (displayed in color).
The sample A serves as a reference device demonstrating operation of conventional SQUID fabricated using the proposed technology. At the same time, the SQUID is a basic cell for previously proposed superconducting bio-inspired neuron [22]. The sample B is a prototype cell of an improved artificial neuron capable of burst firing (or bursting) corresponding to specific activation patterns of biological neurons in the central nervous system and spinal cord, see below. Finally, with the sample C we test an approach for a possible miniaturization of SQUIDs. The area of this device is so small that we see the characteristic Fraunhofer pattern in just a dozen periods of typical oscillations of critical current-magnetic field dependencies.
The current–voltage characteristics of the samples were measured in a dilution refrigerator. They exhibit some asymmetry in their critical current which can be attributed to a frozen magnetic flux (see Supplementary Materials). The shape of the I–V curves becomes hysteretic below 1 K temperature that is likely due to thermal effects caused by the difference between the physical and electronic temperatures [54,55,56]. The critical current of Josephson junctions decreases by about an order with the temperature increase from 20 mK to 2.4 K, see Supplementary Materials.
The sets of I-V curves presented in Figure 2d–f were measured at mK in various perpendicular magnetic fields. The sample A with a maximum critical current, , of 18.5 A, shows regular oscillations of critical current-magnetic field dependence with a period of about Oe (Figure 2d). The symmetry of curve shape indicates that the critical currents of the SQUID Josephson junctions are close in values. The depth of the critical current modulation can be used for the estimation of the SQUID circuit inductance to be less than , where is the flux quantum (h is Planck’s constant and e is the electron charge). Similar oscillations of for the sample B is irregular due to more complex geometry of the cell (the maximum critical current is A, see Figure 2e). For the sample C, the period of the oscillations is much longer and is approximately 140 Oe. The maximum critical current, A, decays twice in a field of 1000 Oe (Figure 2f).
On the one hand, the experimental data show that the fabricated Josephson junctions possess ∼A critical current and normal state resistance of several Ohms exhibiting no overheating above 1 K temperature. The critical current can be further improved by shrinking the gap between superconducting electrodes. On the other hand, these junctions can be connected in SQUID cells such that even the cell with closely located nanowires provides the typical magnetic flux-voltage characteristics. These results have motivated us to investigate the bio-inspired neurons which can be implemented utilizing nanowire–Josephson–junction SQUID-based cells.
2.2. Bio-Inspired Neuron
A conventional SQUID cell such as sample A can be naturally used for the implementation of the SQUID-based neuron proposed in [22]. However, more useful circuit may be developed using three-Josephson-junction cell corresponding to the sample B, see Figure 3 and Supplementary Materials. This circuit can be analyzed using the resistively shunted junction model with capacitance of Josephson junctions [20,21], while the experimentally studied junctions have vanishing self capacitance, here we include it into consideration to capture all possible operation regimes of the considered neuron circuit. We assume that the critical currents of the junctions and (Figure 3) are equal to and fixed, whereas the critical current of , , can be varied. Kirchhoff’s equations augmented by the phase-based circuit Equations [57] lead to the following system (see Supplementary Materials):
where input current, , and bias current, , are normalized to the reference current , whereas is the ratio of to . , , inductances, l, , are normalized to . are Josephson phases of the junctions, dots indicate derivatives (the number of dots means the derivative order) with respect to time, t, normalized to the inverse plasma frequency, , , where C is the junction capacitance. is the Stewart–McCumber parameter, R is the junction resistance in the normal state, and is the characteristic frequency.
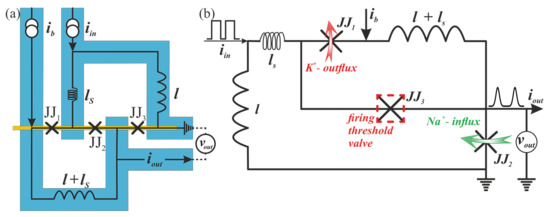
Figure 3.
(a) Sketch of the proposed superconducting bio-inspired neuron with nanowire-based Josephson junctions. (b) Schematic of the proposed bio-inspired neuron.
The circuit dynamics are governed mainly by two parameters at fixed bias current value. They are the normalized critical current of the third junction, , determining the neuron firing threshold, and the normalized capacitance of the junctions, , responsible for the refractory period.
The first and second Josephson junctions play the role of sodium () and potassium () ion channels in the neuron membrane [1,58], respectively. The voltage across the cell, (see Figure 3b), reflects the following processes during the neuron firing, see the circled numbers on a spike shown in Figure 4a: 1—the neuron is stimulated above the firing threshold, channels are opened so that begins to enter the cell; 2— channels are opened, begins to leave the cell; 3— channels become refractory, no more enters the cell; 4— leaves the cell and rapidly repolarizes the membrane; 5— channels are closed and channels reset; 6—extra outside diffuses away.
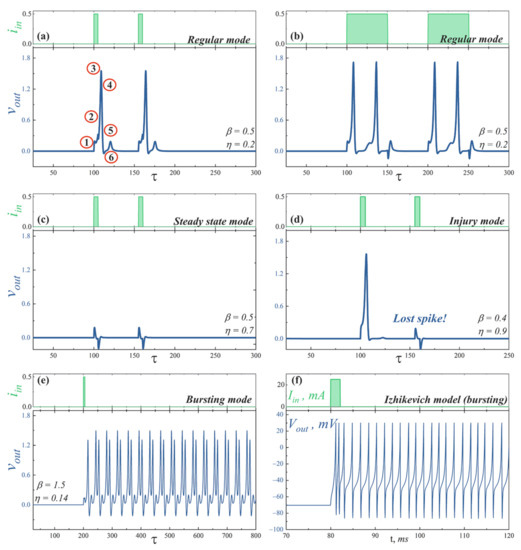
Figure 4.
Simulations of the superconducting bio-inspired neuron dynamics in the various operation modes: (a,b) regular mode (, ), (c) steady state mode (, ), (d) injury mode (, ), and (e) bursting mode (, ). The figures show the output voltage across the second Josephson junction of the cell stimulated by the input current pulse. The circuit parameters are , , . (f) Bursting dynamics obtained in the framework of the Izhikevich model, see Figure S3d of Supplementary Materials and its description therein.
The proposed neuron is capable of mimic the biological activity corresponding to the modes presented in Figure 4 (see Supplementary Materials for comparison with simulations performed within the framework of the Izhikevich mathematical model of biological neurons):
- Regular mode shows the typical response of a neuron to external stimulation. A short input current pulse of a sufficient amplitude causes single spike, whereafter the system returns to a stable state, see Figure 4a. A long pulse leads to repeated overcoming of the firing threshold. Thus, a series of spikes is observed, Figure 4b. The interspike interval is determined by a neuron refractory period, which, in consequence, is related to the recovery of channels.
- Steady state mode (Figure 4c) is characterized by the weak damped output pulses. This is analog of the maintenance of constant internal concentrations of ions in the cell in response to an under threshold stimulation.
- Injury mode (Figure 4d) is characterized by the losses of spikes, or vice versa, the generation of “extra” spikes. This mimics the biophysical abnormality caused by different nervous diseases and neuron injuries.
- Bursting mode (Figure 4e) demonstrates the generation of a series of spikes in response to singe stimulating current pulse. Such behavior may be the result of the complex neuron interaction in the network. However, this can also be a consequence of internal processes in a neuron. In the last case, the reason is the after-depolarization (ADP), a membrane depolarisation at the last stages of repolarisation (circled “4” on the spike shown in Figure 4a) [59,60]. A slow sodium current appears at membrane voltage ∼−50…−70 mV and overcomes outward current, causing a membrane voltage to rise again. Such current is resistant to inactivation and may last for long times. The bursting pattern parameters—the spike sequence frequency and its length—are determined by the concentration of ion channels of different kinds, properties of these channels, and ionic concentrations in extracellular space. Though only relatively small cohort of neurons in vivo exhibits a bursting behavior [61,62,63], it plays an important role in synaptic plasticity [64,65], synchronization of big neuron groups [66], detection of frequency features of input stimuli [67], information encoding [68,69], and reliability of synaptic transmission [64,70], which may be crucial for processing of important stimuli [71].
- Figure 4f illustrates the bursting dynamics of biological neuron simulated in the frame of the fractional-order Izhikevich model [72,73] for comparison, see also Supplementary Materials.
The map of the proposed neuron operation modes on the plane of parameters (, ) is shown in Figure 5. The parameters used for simulations presented in Figure 4 are marked by stars.
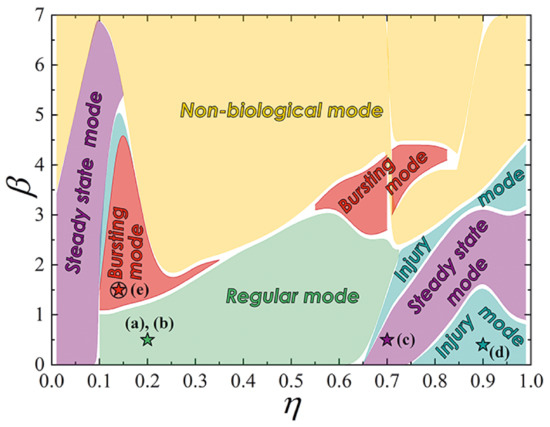
Figure 5.
Map of the proposed bio-inspired neuron operating modes on the plane of parameters (, ). White boundaries represent the areas where transient processes complicating identification of a particular mode take place. Stars mark parameters taken for simulations presented in Figure 4. The regular, steady state, and injury modes can be obtained in the overdamped circuits () such as the studied experimental samples. Implementation of the bursting mode requires underdamped system.
The non-biological dynamics, which are not observed in vivo under any conditions, take place at small damping in the system (large ). In the overdamped circuits () such as the studied experimental samples, the steady state, regular, and injury modes can be obtained. Small critical current of the third Josephson junction () effectively blocks the inflow of the input current into the output junction, , redirecting it to the inductance, l, connected to the ground, see Figure 3b. This results in the steady state mode where no spike is produced. An increase in value opens access to the output junction, such that the input current pulse triggers successive switching of the junctions , , . This mimics ions inflow succeeded by outflow corresponding to the regular mode. At larger values the neuron circuit becomes bistable with one enabling and one inhibiting intracellular current configuration for the output junction switching. In this case, the steady state and injury modes are determined by the initial current configuration in the circuit: inhibiting or enabling (switched to inhibiting after the first spike), respectively.
Unfortunately, the bursting mode clearly requires finite capacitance to maintain periodic switching of the Josephson junctions. This indicates the necessity for complication of the studied cell circuit, e.g., an introduction of the shunting capacitor.
While the regular and steady state mode can be reproduced in the previously proposed bio-inspired neuron [22], the injury and bursting modes appear only in the presented advanced neuron cell.
3. Conclusions
The distinctive features of the superconducting technology are the high frequency operation and high energy efficiency. The possibility of processing of up to spikes/s by an artificial neuron (versus maximum spikes/s in the human brain [74] or 100–200 spikes/s widely spread [75,76]) and power consumption of about 0.1 MW [28] for human brain model pave the way for high performance neurophysiological simulations. We have addressed the low integration density issue of superconducting circuits by the development of technology intended for fabrication of compact SQUIDs utilizing nanowire-based nanobridge Josephson junctions. We have experimentally demonstrated two types of SQUIDs suitable for the implementation of bio-inspired neurons. Numerical simulations show that the proposed three-junction cell is capable of mimic specific biological neuron activity missed in previously presented superconducting artificial neurons. In this mode of operation, regular and irregular spike sequences are generated as activation patterns occurring in vivo in many cases including stereotypical motor programs, neural coding, and neuropathologies. An introduction of capacitance in the cell designs and studying options for signal transfer between the artificial neurons are urgent tasks in the considered research direction.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/nano12101671/s1. Figure S1: I-V characteristics of samples A (a), B (b), and C (c) measured at different temperatures at zero magnetic field. Figure S2: Sketch with superimposed schematic of the sample B (a) and a bio-inspired neuron cell based on it (b). (c) The lumped element circuit of the neuron cell. Figure S3: Numerical simulations of biological neurons in the framework of the the fractional-order Izhikevich model. The model parameters are as follows. (a), (b) regular mode: a = 0:02, b = 0:2, c = −65, d = 8, a = 1, (c) injury mode: a = 2 · 10, b = 0:2, c = −65, d = 8, a = 1, (d) bursting mode: a = 0:02, b = 0:2, c = −65, d = 8, a = 0:63, (e) bursting with early termination: a = 0:1, b = 0:2, c = −65, d = 2, a = 0:65, (f) regular mode (bursting is not observed): a = 0:1, b = 0:2, c = −65, d = 2, a = 0:7. References [73,74,77,78,79,80,81,82] are cited in the supplementary materials.
Author Contributions
Conceptualization, A.E.S., N.V.K., I.I.S. and V.S.S.; Data curation, N.V.K.; Formal analysis, N.V.K.; Funding acquisition, V.S.S., I.I.S.; Investigation, O.V.S., A.G.S., S.V.S. and K.S.N.; Methodology, O.V.S., A.E.S. and V.S.S.; Software, A.E.S., S.V.B., I.A.N. and I.I.S.; Supervision, M.Y.K. and V.S.S.; Validation, N.V.K., I.I.S. and M.Y.K.; Visualization, O.V.S. and V.S.S.; Writing—original draft, O.V.S., A.E.S. and N.V.K.; Writing—review and editing, S.V.B. and I.I.S. with contribution from the coauthors. All authors have read and agreed to the published version of the manuscript.
Funding
The conceptualisation, nanowire sintezation, niobium films deposition, and measurements of experimental samples were supported by the Russian Science Foundation grant No. 18-72-10118. The development of the artificial neuron numerical model and the neuron simulations were performed under the support of the Russian Science Foundation grant No. 20-69-47013. M.K. and N.K. are grateful to the Interdisciplinary Scientific–Educational School of the Moscow State University “Photonic and Quantum Technologies. Digital Medicine” for access to the necessary scientific and technical information. A.G.S. is grateful for support the e-beam litography realisation by the Ministry of Science and Higher Education of the Russian Federation (No. FSMG-2021-0005).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hodgkin, A.L.; Huxley, A.F. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 1952, 117, 500. [Google Scholar] [CrossRef] [PubMed]
- Forrest, M.D. Simulation of alcohol action upon a detailed Purkinje neuron model and a simpler surrogate model that runs >400 times faster. BMC Neurosci. 2015, 16, 27. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Deng, Y.; Liu, H.; Uhlmann, G. On an inverse boundary problem arising in brain imaging. J. Differ. Equ. 2019, 267, 2471–2502. [Google Scholar] [CrossRef] [Green Version]
- Sætra, M.J.; Einevoll, G.T.; Halnes, G. An electrodiffusive, ion conserving Pinsky-Rinzel model with homeostatic mechanisms. PLoS Comput. Biol. 2020, 16, e1007661. [Google Scholar] [CrossRef] [PubMed]
- Sætra, M.J.; Einevoll, G.T.; Halnes, G. An electrodiffusive neuron-extracellular-glia model for exploring the genesis of slow potentials in the brain. PLoS Comput. Biol. 2021, 17, e1008143. [Google Scholar] [CrossRef]
- Chance, F. Lessons from a Dragon Fly’s Brain: Evolution Built a Small, Fast, Efficient Neural Network in a Dragonfly. Why Not Copy It for Missile Defense? IEEE Spectr. 2021, 58, 28–33. [Google Scholar] [CrossRef]
- Jürgensen, A.M.; Khalili, A.; Chicca, E.; Indiveri, G.; Nawrot, M.P. A neuromorphic model of olfactory processing and sparse coding in the Drosophila larva brain. Neuromorphic Comput. Eng. 2021, 1, 024008. [Google Scholar] [CrossRef]
- Ham, D.; Park, H.; Hwang, S.; Kim, K. Neuromorphic electronics based on copying and pasting the brain. Nat. Electron. 2021, 4, 635–644. [Google Scholar] [CrossRef]
- Toomey, E.; Segall, K.; Castellani, M.; Colangelo, M.; Lynch, N.; Berggren, K.K. Superconducting nanowire spiking element for neural networks. Nano Lett. 2020, 20, 8059–8066. [Google Scholar] [CrossRef]
- Markram, H.; Muller, E.; Ramaswamy, S.; Reimann, M.W.; Abdellah, M.; Sanchez, C.A.; Ailamaki, A.; Alonso-Nanclares, L.; Antille, N.; Arsever, S.; et al. Reconstruction and simulation of neocortical microcircuitry. Cell 2015, 163, 456–492. [Google Scholar] [CrossRef]
- Furber, S. Large-scale neuromorphic computing systems. J. Neural Eng. 2016, 13, 051001. [Google Scholar] [CrossRef] [PubMed]
- Sourikopoulos, I.; Hedayat, S.; Loyez, C.; Danneville, F.; Hoel, V.; Mercier, E.; Cappy, A. A 4-fJ/spike artificial neuron in 65 nm CMOS technology. Front. Neurosci. 2017, 11, 123. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Azevedo, F.A.; Carvalho, L.R.; Grinberg, L.T.; Farfel, J.M.; Ferretti, R.E.; Leite, R.E.; Filho, W.J.; Lent, R.; Herculano-Houzel, S. Equal numbers of neuronal and nonneuronal cells make the human brain an isometrically scaled-up primate brain. J. Comp. Neurol. 2009, 513, 532–541. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, W. Challenges and Applications of Emerging Nonvolatile Memory Devices. Electronics 2020, 9, 1029. [Google Scholar] [CrossRef]
- Chen, L.; Pam, M.E.; Li, S.; Ang, K.W. Ferroelectric memory based on two-dimensional materials for neuromorphic computing. Comput. Eng. 2022, 2, 022001. [Google Scholar] [CrossRef]
- Qiao, N.; Mostafa, H.; Corradi, F.; Osswald, M.; Stefanini, F.; Sumislawska, D.; Indiveri, G. A reconfigurable on-line learning spiking neuromorphic processor comprising 256 neurons and 128 K synapses. Front. Neurosci. 2015, 9, 141. [Google Scholar] [CrossRef] [Green Version]
- Holmes, D.S.; Ripple, A.L.; Manheimer, M.A. Energy-efficient superconducting computing—Power budgets and requirements. IEEE Trans. Appl. Supercond. 2013, 23, 1701610. [Google Scholar] [CrossRef]
- Tolpygo, S.K. Superconductor digital electronics: Scalability and energy efficiency issues. Low Temp. Phys. 2016, 42, 361–379. [Google Scholar] [CrossRef] [Green Version]
- Soloviev, I.I.; Klenov, N.V.; Bakurskiy, S.V.; Kupriyanov, M.Y.; Gudkov, A.L.; Sidorenko, A.S. Beyond Moore’s technologies: Operation principles of a superconductor alternative. Beilstein J. Nanotechnol. 2017, 8, 2689–2710. [Google Scholar] [CrossRef] [Green Version]
- Likharev, K.K. Dynamics of Josephson Junctions and Circuits; Routledge: London, UK, 2022. [Google Scholar]
- Barone, A.; Paterno, G. Physics and Applications of the Josephson Effect; Wiley Online Library: Hoboken, NJ, USA, 1982; Volume 1. [Google Scholar]
- Crotty, P.; Schult, D.; Segall, K. Josephson junction simulation of neurons. Phys. Rev. E 2010, 82, 011914. [Google Scholar] [CrossRef] [Green Version]
- Primavera, B.A.; Shainline, J.M. An active dendritic tree can mitigate fan-in limitations in superconducting neurons. Appl. Phys. Lett. 2021, 119, 242601. [Google Scholar] [CrossRef]
- Schneider, M.; Segall, K. Fan-out and fan-in properties of superconducting neuromorphic circuits. J. Appl. Phys. 2020, 128, 214903. [Google Scholar] [CrossRef]
- Soloviev, I.; Klenov, N.; Bakurskiy, S.; Bol’ginov, V.; Ryazanov, V.; Kupriyanov, M.Y.; Golubov, A.A. Josephson magnetic rotary valve. Appl. Phys. Lett. 2014, 105, 242601. [Google Scholar] [CrossRef] [Green Version]
- Bakurskiy, S.; Klenov, N.; Soloviev, I.; Kupriyanov, M.Y.; Golubov, A.A. Superconducting phase domains for memory applications. Appl. Phys. Lett. 2016, 108, 042602. [Google Scholar] [CrossRef] [Green Version]
- Bakurskiy, S.; Klenov, N.; Soloviev, I.; Pugach, N.; Kupriyanov, M.Y.; Golubov, A. Protected 0-π states in SIsFS junctions for Josephson memory and logic. Appl. Phys. Lett. 2018, 113, 082602. [Google Scholar] [CrossRef] [Green Version]
- Schneider, M.L.; Donnelly, C.A.; Russek, S.E.; Baek, B.; Pufall, M.R.; Hopkins, P.F.; Dresselhaus, P.D.; Benz, S.P.; Rippard, W.H. Ultralow power artificial synapses using nanotextured magnetic Josephson junctions. Sci. Adv. 2018, 4, e1701329. [Google Scholar] [CrossRef] [Green Version]
- Shafraniuk, S.E.; Nevirkovets, I.P.; Mukhanov, O.A. Modeling computer memory based on ferromagnetic/superconductor multilayers. Phys. Rev. Appl. 2019, 11, 064018. [Google Scholar] [CrossRef]
- Klenov, N.; Khaydukov, Y.; Bakurskiy, S.; Morari, R.; Soloviev, I.; Boian, V.; Keller, T.; Kupriyanov, M.; Sidorenko, A.; Keimer, B. Periodic Co/Nb pseudo spin valve for cryogenic memory. Beilstein J. Nanotechnol. 2019, 10, 833–839. [Google Scholar] [CrossRef]
- Likharev, K.K.; Semenov, V.K. RSFQ logic/memory family: A new Josephson-junction technology for sub-terahertz-clock-frequency digital systems. IEEE Trans. Appl. Supercond. 1991, 1, 3–28. [Google Scholar] [CrossRef]
- Tolpygo, S.K.; Bolkhovsky, V.; Rastogi, R.; Zarr, S.; Day, A.L.; Golden, E.; Weir, T.J.; Wynn, A.; Johnson, L.M. Advanced fabrication processes for superconductor electronics: Current status and new developments. IEEE Trans. Appl. Supercond. 2019, 29, 1–13. [Google Scholar] [CrossRef]
- Schegolev, A.E.; Klenov, N.V.; Soloviev, I.I.; Tereshonok, M.V. Adiabatic superconducting cells for ultra-low-power artificial neural networks. Beilstein J. Nanotechnol. 2016, 7, 1397–1403. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Segall, K.; LeGro, M.; Kaplan, S.; Svitelskiy, O.; Khadka, S.; Crotty, P.; Schult, D. Synchronization dynamics on the picosecond time scale in coupled Josephson junction neurons. Phys. Rev. E 2017, 95, 032220. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Soloviev, I.I.; Schegolev, A.E.; Klenov, N.V.; Bakurskiy, S.V.; Kupriyanov, M.Y.; Tereshonok, M.V.; Shadrin, A.V.; Stolyarov, V.S.; Golubov, A.A. Adiabatic superconducting artificial neural network: Basic cells. J. Appl. Phys. 2018, 124, 152113. [Google Scholar] [CrossRef] [Green Version]
- Schegolev, A.; Klenov, N.; Soloviev, I.; Tereshonok, M. Learning cell for superconducting neural networks. Supercond. Sci. Technol. 2020, 34, 015006. [Google Scholar] [CrossRef]
- Goteti, U.S.; Dynes, R.C. Superconducting neural networks with disordered Josephson junction array synaptic networks and leaky integrate-and-fire loop neurons. J. Appl. Phys. 2021, 129, 073901. [Google Scholar] [CrossRef]
- Ishida, K.; Byun, I.; Nagaoka, I.; Fukumitsu, K.; Tanaka, M.; Kawakami, S.; Tanimoto, T.; Ono, T.; Kim, J.; Inoue, K. Superconductor Computing for Neural Networks. IEEE Micro 2021, 41, 19–26. [Google Scholar] [CrossRef]
- Feldhoff, F.; Toepfer, H. Niobium Neuron: RSFQ Based Bio-Inspired Circuit. IEEE Trans. Appl. Supercond. 2021, 31, 1–5. [Google Scholar] [CrossRef]
- Semenov, V.K.; Golden, E.B.; Tolpygo, S.K. A new family of bioSFQ logic/memory cells. IEEE Trans. Appl. Supercond. 2021, 32, 1–5. [Google Scholar] [CrossRef]
- Soloviev, I.; Bakurskiy, S.; Ruzhickiy, V.; Klenov, N.; Kupriyanov, M.Y.; Golubov, A.; Skryabina, O.; Stolyarov, V. Miniaturization of Josephson Junctions for Digital Superconducting Circuits. Phys. Rev. Appl. 2021, 16, 044060. [Google Scholar] [CrossRef]
- Soloviev, I.; Ruzhickiy, V.; Bakurskiy, S.; Klenov, N.; Kupriyanov, M.Y.; Golubov, A.; Skryabina, O.; Stolyarov, V. Superconducting circuits without inductors based on bistable Josephson junctions. Phys. Rev. Appl. 2021, 16, 014052. [Google Scholar] [CrossRef]
- Faivre, T.; Golubev, D.; Pekola, J.P. Josephson junction based thermometer and its application in bolometry. J. Appl. Phys. 2014, 116, 094302. [Google Scholar] [CrossRef] [Green Version]
- Kirtley, J.R.; Paulius, L.; Rosenberg, A.J.; Palmstrom, J.C.; Holland, C.M.; Spanton, E.M.; Schiessl, D.; Jermain, C.L.; Gibbons, J.; Fung, Y.K.K.; et al. Scanning SQUID susceptometers with sub-micron spatial resolution. Rev. Sci. Instrum. 2016, 87, 093702. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Finkler, A.; Segev, Y.; Myasoedov, Y.; Rappaport, M.L.; Ne’eman, L.; Vasyukov, D.; Zeldov, E.; Huber, M.E.; Martin, J.; Yacoby, A. Self-aligned nanoscale SQUID on a tip. Nano Lett. 2010, 10, 1046–1049. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Biswas, S.; Winkelmann, C.B.; Courtois, H.; Gupta, A.K. Josephson coupling in the dissipative state of a thermally hysteretic μ-SQUID. Phys. Rev. B 2018, 98, 174514. [Google Scholar] [CrossRef] [Green Version]
- Dimov, B.; Balashov, D.; Khabipov, M.; Ortlepp, T.; Buchholz, F.I.; Zorin, A.; Niemeyer, J.; Uhlmann, F. Implementation of superconductive passive phase shifters in high-speed integrated RSFQ digital circuits. Supercond. Sci. Technol. 2008, 21, 045007. [Google Scholar] [CrossRef]
- Wiedenmann, J.; Bocquillon, E.; Deacon, R.S.; Hartinger, S.; Herrmann, O.; Klapwijk, T.M.; Maier, L.; Ames, C.; Brüne, C.; Gould, C.; et al. 4π-periodic Josephson supercurrent in HgTe-based topological Josephson junctions. Nat. Commun. 2016, 7, 10303. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dominguez, F.; Hassler, F.; Platero, G. Dynamical detection of Majorana fermions in current-biased nanowires. Phys. Rev. B 2012, 86, 140503. [Google Scholar] [CrossRef] [Green Version]
- Kalenyuk, A.A.; Pagliero, A.; Borodianskyi, E.A.; Kordyuk, A.; Krasnov, V.M. Phase-Sensitive Evidence for the Sign-Reversal s ± Symmetry of the Order Parameter in an Iron-Pnictide Superconductor Using Nb/Ba1−x Nax Fe2 As2 Josephson Junctions. Phys. Rev. Lett. 2018, 120, 067001. [Google Scholar] [CrossRef] [Green Version]
- Zheng, G.H. Mathematical analysis of plasmonic resonance for 2-D photonic crystal. J. Differ. Equ. 2019, 266, 5095–5117. [Google Scholar] [CrossRef] [Green Version]
- Deng, Y.; Liu, H.; Zheng, G.H. Mathematical analysis of plasmon resonances for curved nanorods. J. Math. Pures Appl. 2019, 153, 248–280. [Google Scholar] [CrossRef]
- Skryabina, O.; Egorov, S.; Goncharova, A.; Klimenko, A.; Kozlov, S.; Ryazanov, V.; Bakurskiy, S.; Kupriyanov, M.Y.; Golubov, A.; Napolskii, K.; et al. Josephson coupling across a long single-crystalline Cu nanowire. Appl. Phys. Lett. 2017, 110, 222605. [Google Scholar] [CrossRef]
- Dubos, P.; Courtois, H.; Pannetier, B.; Wilhelm, F.; Zaikin, A.; Schön, G. Josephson critical current in a long mesoscopic SNS junction. Phys. Rev. B 2001, 63, 064502. [Google Scholar] [CrossRef] [Green Version]
- Courtois, H.; Meschke, M.; Peltonen, J.; Pekola, J.P. Origin of hysteresis in a proximity Josephson junction. Phys. Rev. Lett. 2008, 101, 067002. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Skryabina, O.; Bakurskiy, S.; Shishkin, A.; Klimenko, A.; Napolskii, K.; Klenov, N.; Soloviev, I.; Ryazanov, V.; Golubov, A.; Roditchev, D.; et al. Environment-induced overheating phenomena in Au-nanowire based Josephson junctions. Sci. Rep. 2021, 11, 15274. [Google Scholar] [CrossRef] [PubMed]
- Schindler, L.; Fourie, C.J. Application of Phase-Based Circuit Theory to RSFQ Logic Design. IEEE Trans. Appl. Supercond. 2022, 32, 1300512. [Google Scholar] [CrossRef]
- Hodgkin, A.L.; Katz, B. The effect of sodium ions on the electrical activity of the giant axon of the squid. J. Physiol. 1949, 108, 37. [Google Scholar] [CrossRef]
- Azouz, R.; Jensen, M.S.; Yaari, Y. Ionic basis of spike after-depolarization and burst generation in adult rat hippocampal CA1 pyramidal cells. J. Physiol. 1996, 492, 211–223. [Google Scholar] [CrossRef] [Green Version]
- Yue, C.; Remy, S.; Su, H.; Beck, H.; Yaari, Y. Proximal persistent Na+ channels drive spike afterdepolarizations and associated bursting in adult CA1 pyramidal cells. J. Neurosci. 2005, 25, 9704–9720. [Google Scholar] [CrossRef] [Green Version]
- Schwartzkroin, P.A. Characteristics of CA1 neurons recorded intracellularly in the hippocampalin vitro slice preparation. Brain Res. 1975, 85, 423–436. [Google Scholar] [CrossRef]
- Jensen, M.S.; Azouz, R.; Yaari, Y. Variant firing patterns in rat hippocampal pyramidal cells modulated by extracellular potassium. J. Neurophysiol. 1994, 71, 831–839. [Google Scholar] [CrossRef]
- Jensen, M.S.; Azouz, R.; Yaari, Y. Spike after-depolarization and burst generation in adult rat hippocampal CA1 pyramidal cells. J. Physiol. 1996, 492, 199–210. [Google Scholar] [CrossRef] [PubMed]
- Lisman, J.E. Bursts as a unit of neural information: Making unreliable synapses reliable. Trends Neurosci. 1997, 20, 38–43. [Google Scholar] [CrossRef]
- Selig, D.K.; Nicoll, R.A.; Malenka, R.C. Hippocampal long-term potentiation preserves the fidelity of postsynaptic responses to presynaptic bursts. J. Neurosci. 1999, 19, 1236–1246. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gray, C.M.; McCormick, D.A. Chattering cells: Superficial pyramidal neurons contributing to the generation of synchronous oscillations in the visual cortex. Science 1996, 274, 109–113. [Google Scholar] [CrossRef] [PubMed]
- Izhikevich, E.M.; Desai, N.S.; Walcott, E.C.; Hoppensteadt, F.C. Bursts as a unit of neural information: Selective communication via resonance. Trends Neurosci. 2003, 26, 161–167. [Google Scholar] [CrossRef]
- Cattaneo, A.; Maffei, L.; Morrone, C. Patterns in the discharge of simple and complex visual cortical cells. Proc. R. Soc. Lond. Ser. B Biol. Sci. 1981, 212, 279–297. [Google Scholar]
- Otto, T.; Eichenbaum, H.; Wible, C.G.; Wiener, S.I. Learning-related patterns of CA1 spike trains parallel stimulation parameters optimal for inducing hippocampal long-term potentiation. Hippocampus 1991, 1, 181–192. [Google Scholar] [CrossRef]
- Williams, S.R.; Stuart, G.J. Mechanisms and consequences of action potential burst firing in rat neocortical pyramidal neurons. J. Physiol. 1999, 521, 467. [Google Scholar] [CrossRef]
- Fabian, J.M.; Wiederman, S.D. Spike bursting in a dragonfly target-detecting neuron. Sci. Rep. 2021, 11, 4005. [Google Scholar] [CrossRef]
- Izhikevich, E.M. Simple model of spiking neurons. IEEE Trans. Neural Netw. 2003, 14, 1569–1572. [Google Scholar] [CrossRef] [Green Version]
- Teka, W.W.; Upadhyay, R.K.; Mondal, A. Spiking and bursting patterns of fractional-order Izhikevich model. Commun. Nonlinear Sci. Numer. Simul. 2018, 56, 161–176. [Google Scholar] [CrossRef]
- Wang, B.; Ke, W.; Guang, J.; Chen, G.; Yin, L.; Deng, S.; He, Q.; Liu, Y.; He, T.; Zheng, R.; et al. Firing frequency maxima of fast-spiking neurons in human, monkey, and mouse neocortex. Front. Cell. Neurosci. 2016, 10, 239. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ray, S.; Maunsell, J.H. Different origins of gamma rhythm and high-gamma activity in macaque visual cortex. PLoS Biol. 2011, 9, e1000610. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alekseichuk, I.; Turi, Z.; De Lara, G.A.; Antal, A.; Paulus, W. Spatial working memory in humans depends on theta and high gamma synchronization in the prefrontal cortex. Curr. Biol. 2016, 26, 1513–1521. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Connors, B.W.; Gutnick, M.J. Intrinsic firing patterns of diverse neocortical neurons. Trends Neurosci. 1990, 13, 99–104. [Google Scholar] [CrossRef]
- Gruß, M.; Henrich, M.; König, P.; Hempelmann, G.; Vogel, W.; Scholz, A. Ethanol reduces excitability in a subgroup of primary sensory neurons by activation of BKCa channels. Eur. J. Neurosci. 2001, 14, 1246–1256. [Google Scholar] [CrossRef]
- Grafe, P.; Bostock, H.; Schneider, U. The effects of hyperglycaemic hypoxia on rectification in rat dorsal root axons. J. Physiol. 1994, 480, 297–307. [Google Scholar] [CrossRef]
- Oldham, K.; Spanier, J. The Fractional Calculus Theory and Applications of Differentiation and Integration to Arbitrary Order; Elsevier: Amsterdam, The Netherlands, 1974. [Google Scholar]
- Ionescu, C.; Lopes, A.; Copot, D.; Machado, J.T.; Bates, J.H. The role of fractional calculus in modeling biological phenomena: A review. Commun. Nonlinear Sci. Numer. Simul. 2017, 51, 141–159. [Google Scholar] [CrossRef]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent—II. Geophys. J. Int. 1967, 13, 529–539. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).