Spectroscopy of Filled Single-Walled Carbon Nanotubes
Abstract
:1. Introduction
2. Methods of the Investigation of the Electronic Properties of Filled SWCNTs
2.1. Optical Absorption Spectroscopy
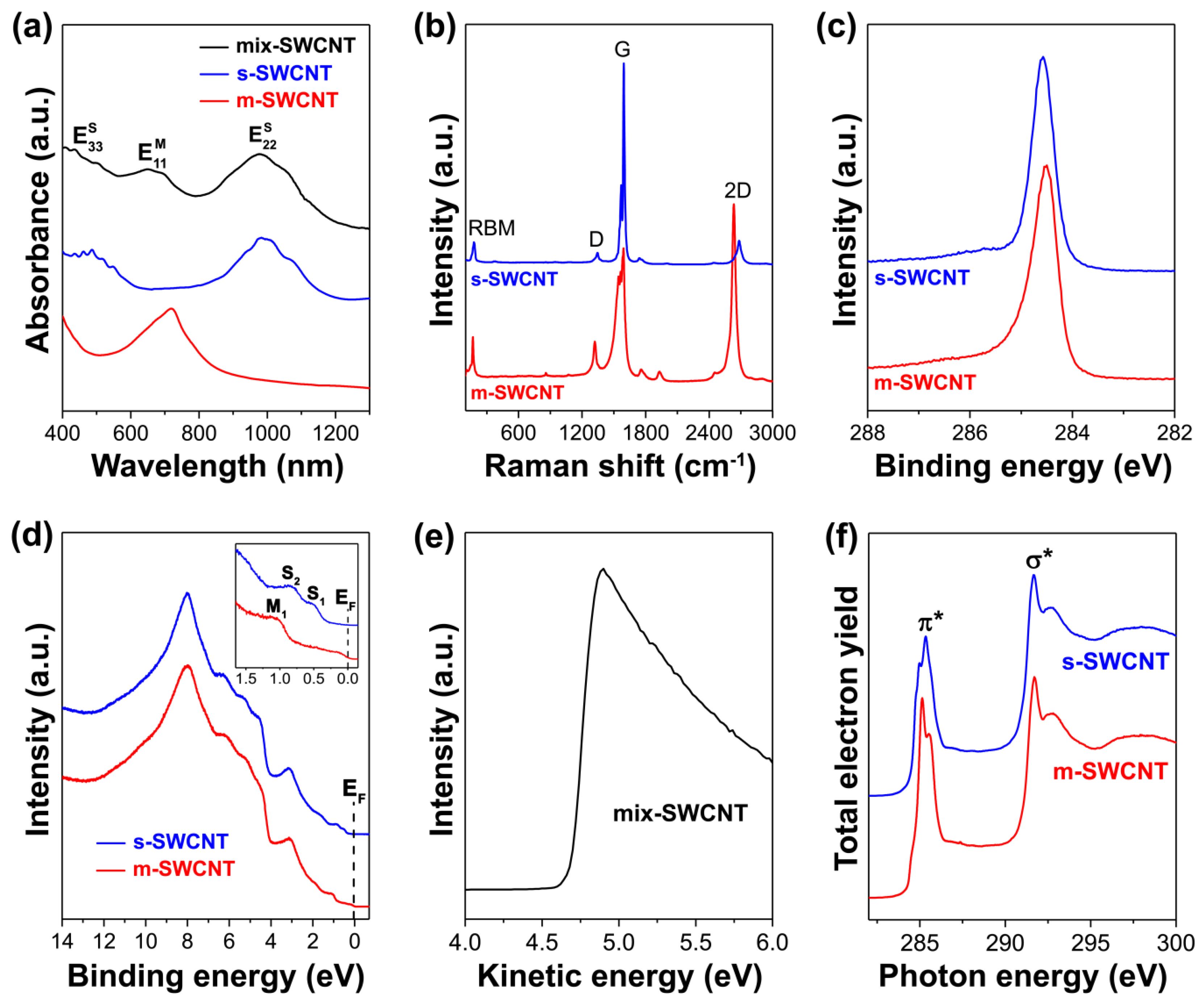
2.1.1. Basic Principle and Main Features of the OAS Spectra of SWCNTs
2.1.2. Signatures of Doping-Induced Modifications of the OAS Spectra of SWCNTs
2.1.3. Further Developments of the OAS Spectroscopy of Carbon Nanotubes
2.2. Raman Spectroscopy
2.2.1. Basic Principle and Main Features of the Raman Spectra of SWCNTs
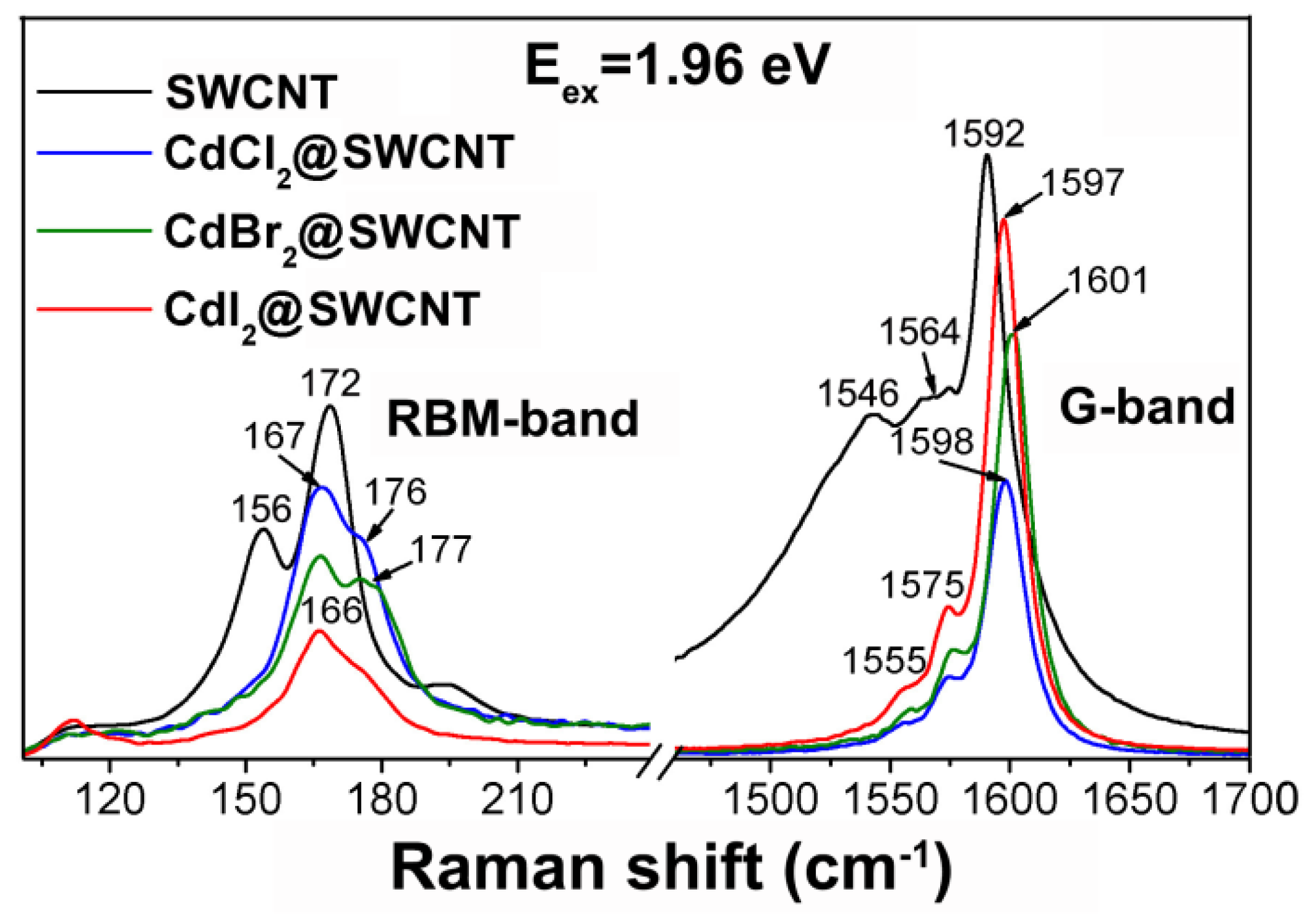
2.2.2. Signatures of Doping-Induced Modifications of the Raman Spectra of SWCNTs
2.2.3. Further Developments of Raman Spectroscopy of Carbon Nanotubes
2.3. Photoemission Spectroscopy
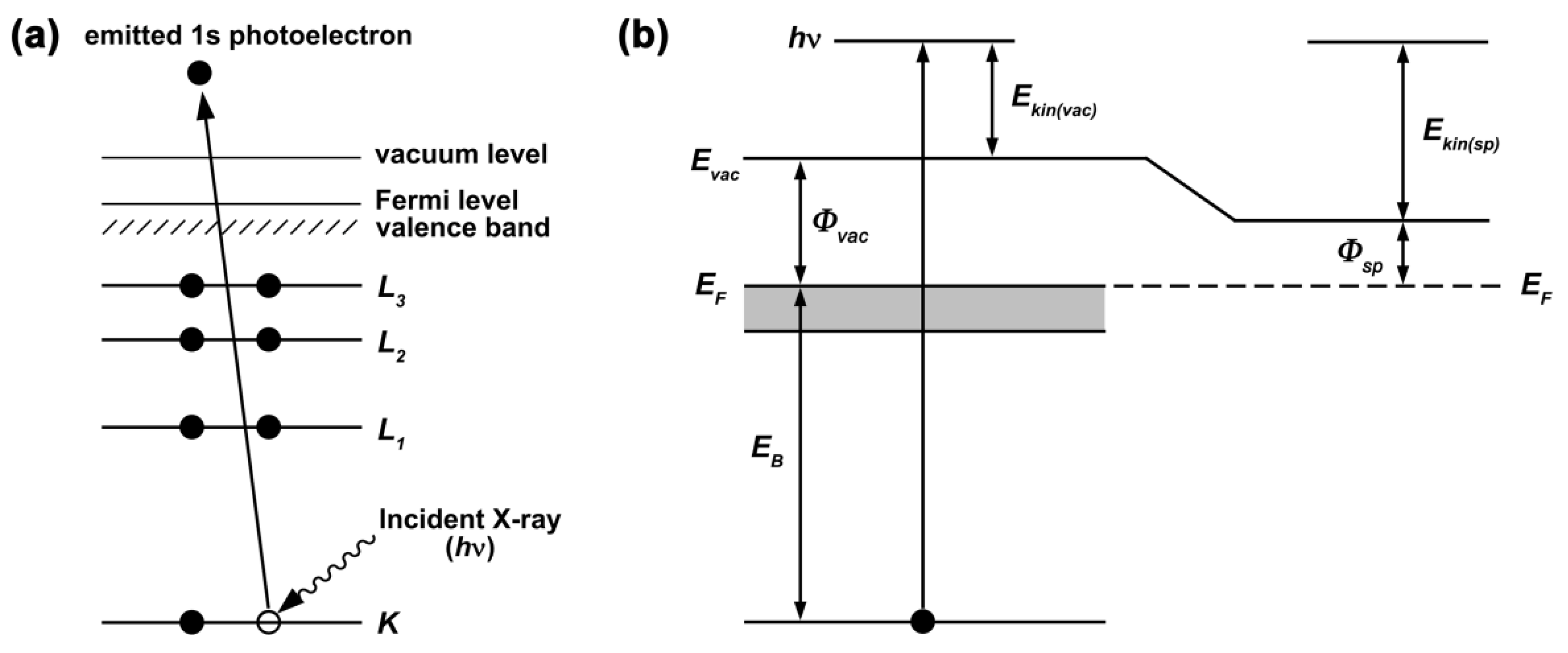
2.3.1. Basic Principle and Main Features of the PES Spectra of SWCNTs
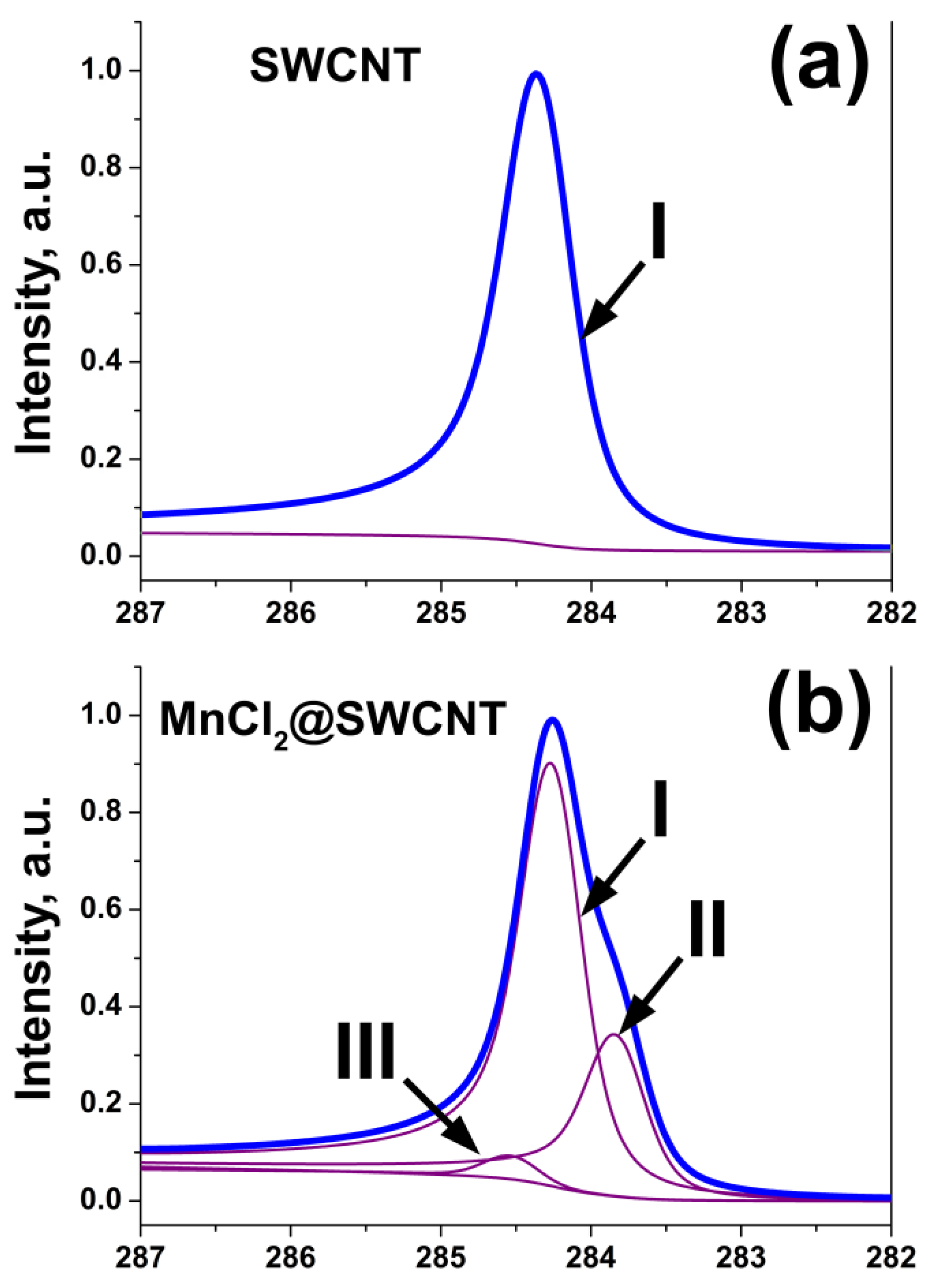
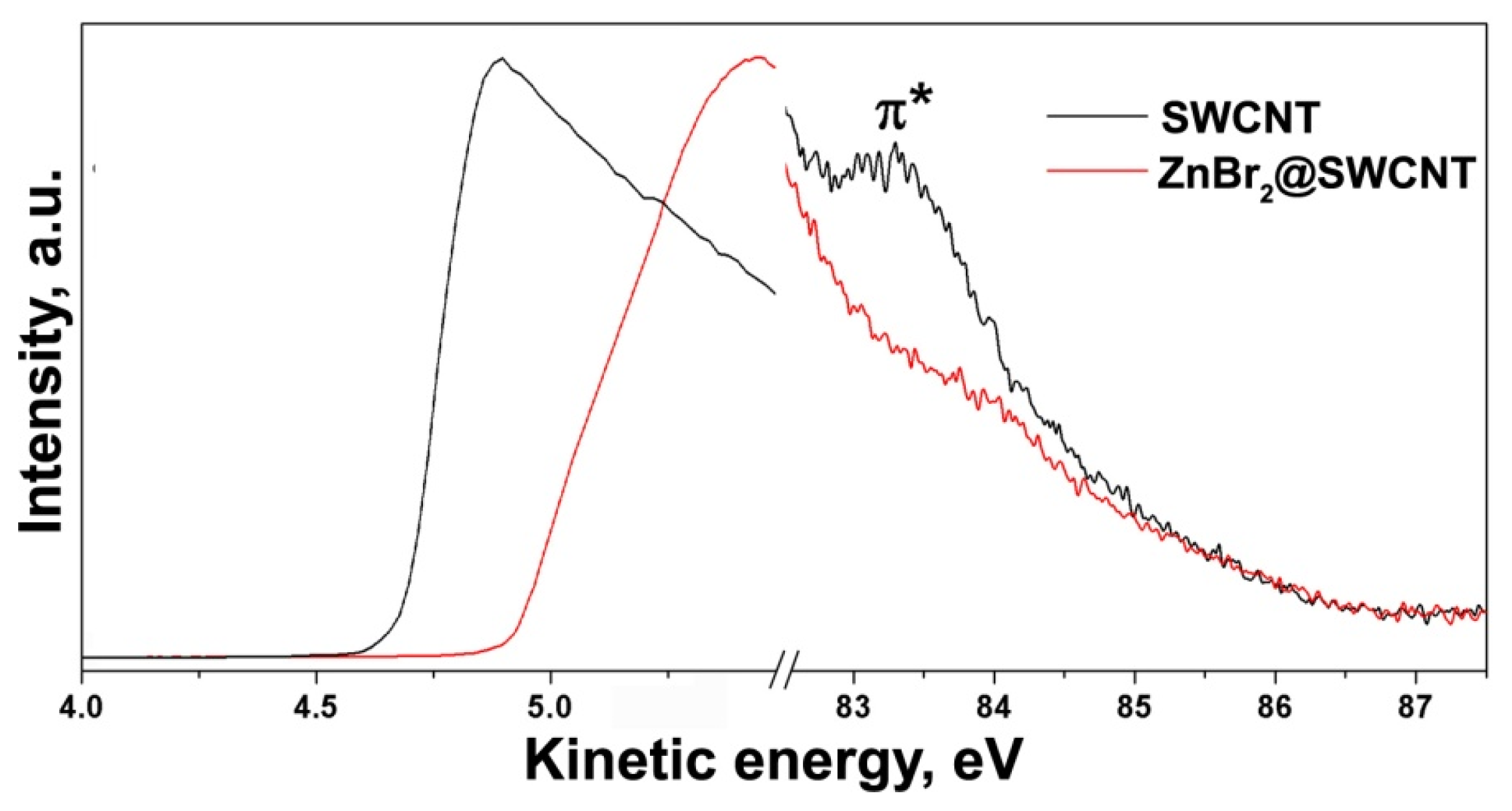
2.3.2. Signatures of Doping-Induced Modifications of the PES Spectra of SWCNTs
2.3.3. Further Developments of XPS Spectroscopy of Carbon Nanotubes
2.4. X-ray Absorption Spectroscopy
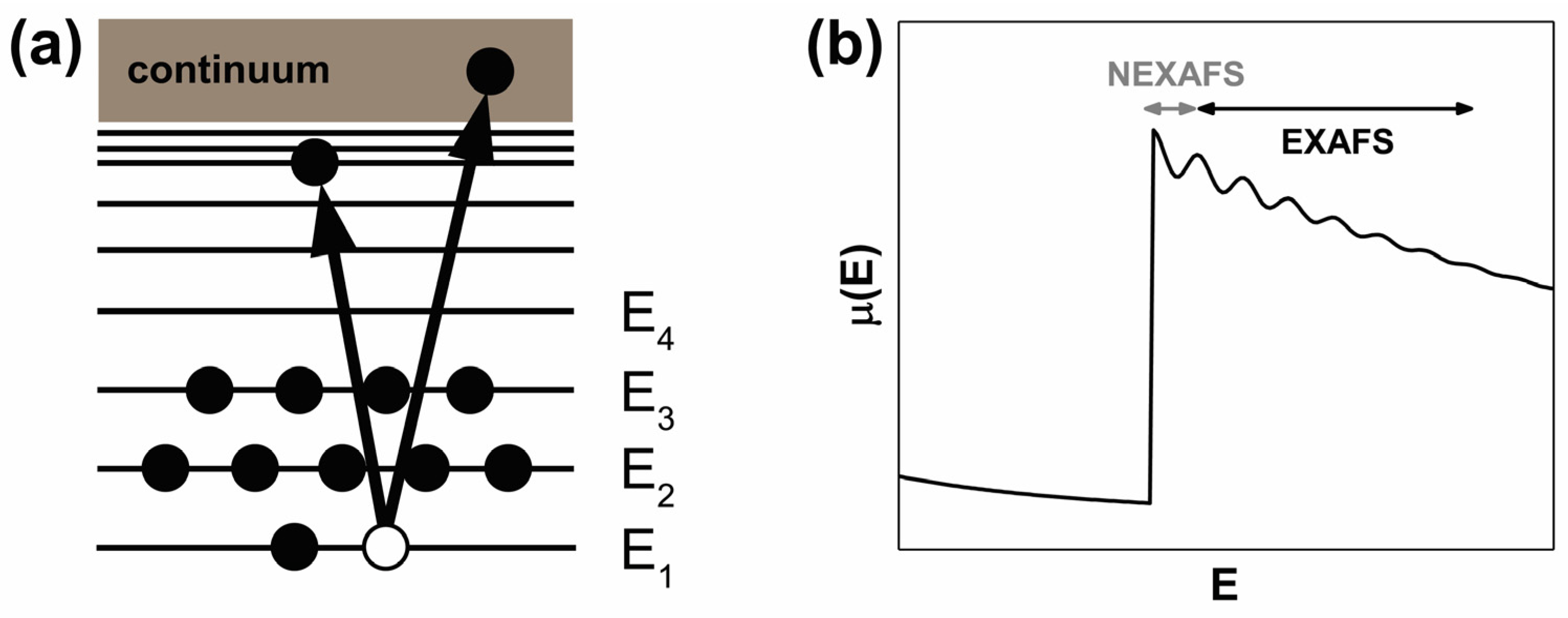
2.4.1. Basic Principle and Main Features of the XAS Spectra of SWCNTs
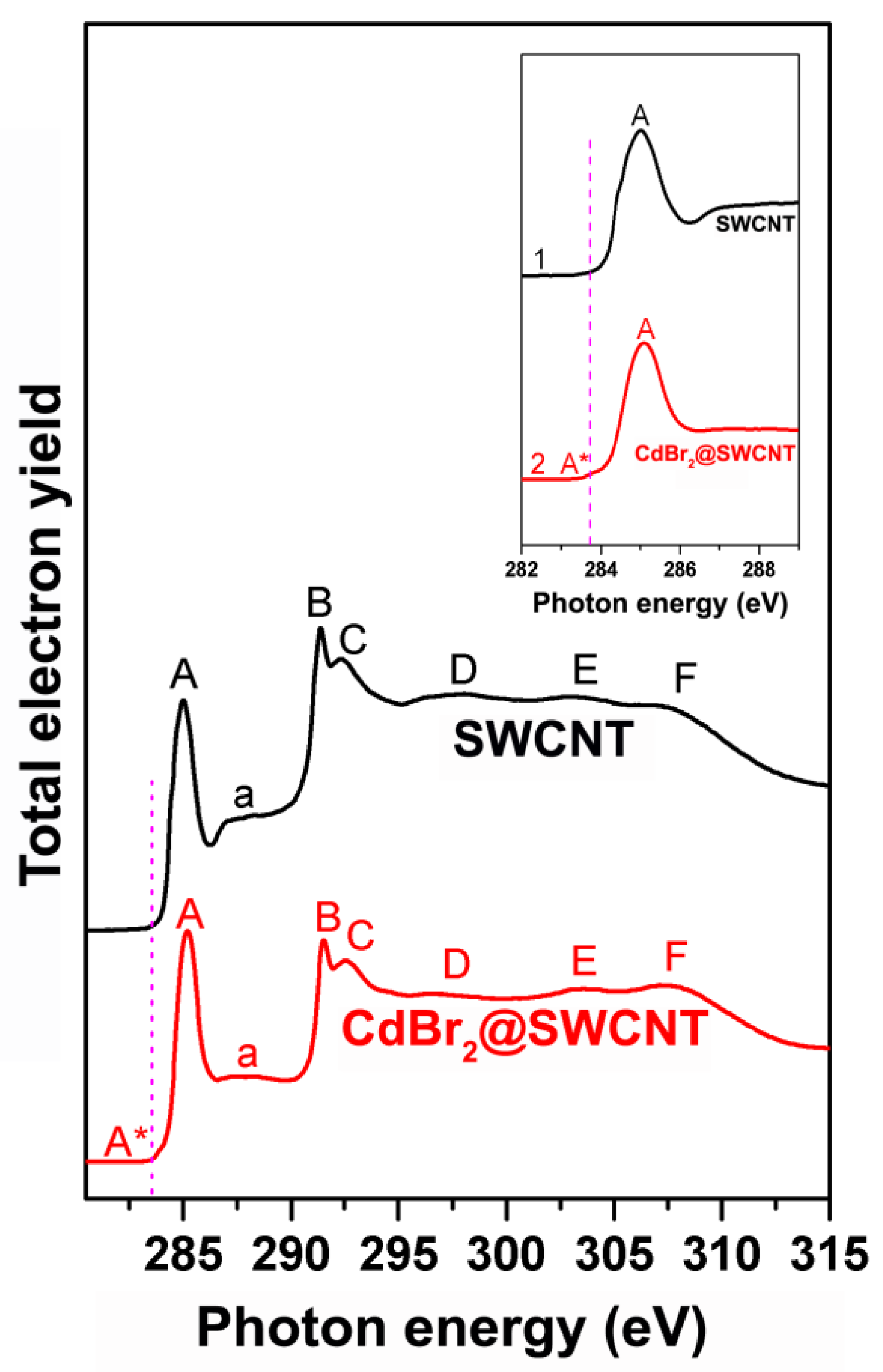
2.4.2. Signatures of Doping-Induced Modifications of the XAS Spectra of SWCNTs
2.4.3. Further Developments of the XAS Spectroscopy of Carbon Nanotubes
3. Conclusions
4. Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jeon, I.; Xiang, R.; Shawky, A.; Matsuo, Y.; Maruyama, S. Single-Walled Carbon Nanotubes in Emerging Solar Cells: Synthesis and Electrode Applications. Adv. Energy Mater. 2019, 9, 1801312. [Google Scholar] [CrossRef]
- Ferguson, V.; Silva, S.R.P.; Zhang, W. Carbon Materials in Perovskite Solar Cells: Prospects and Future Challenges. Energy Environ. Mater. 2019, 2, 107–118. [Google Scholar] [CrossRef] [Green Version]
- Fukumaru, T.; Fujigaya, T.; Nakashima, N. Development of n-type cobaltocene-encapsulated carbon nanotubes with remarkable thermoelectric property. Sci. Rep. 2015, 5, 7951. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, J.W.; Jeon, I.; Lin, H.S.; Seo, S.; Han, T.H.; Anisimov, A.; Kauppinen, E.I.; Matsuo, Y.; Maruyama, S.; Yang, Y. Vapor-Assisted Ex-Situ Doping of Carbon Nanotube toward Efficient and Stable Perovskite Solar Cells. Nano Lett. 2019, 19, 2223–2230. [Google Scholar] [CrossRef] [PubMed]
- Jordan, J.W.; Lowe, G.A.; McSweeney, R.L.; Stoppiello, C.T.; Lodge, R.W.; Skowron, S.T.; Biskupek, J.; Rance, G.A.; Kaiser, U.; Walsh, D.A.; et al. Host-Guest Hybrid Redox Materials Self-Assembled from Polyoxometalates and Single-Walled Carbon Nanotubes. Adv. Mater. 2019, 31, 1904182. [Google Scholar] [CrossRef]
- Martincic, M.; Tobias, G. Filled carbon nanotubes in biomedical imaging and drug delivery. Expert Opin. Drug Deliv. 2015, 12, 563–581. [Google Scholar] [CrossRef]
- Liu, B.L.; Wu, F.Q.; Gui, H.; Zheng, M.; Zhou, C.W. Chirality-Controlled Synthesis and Applications of Single-Wall Carbon Nanotubes. Acs Nano 2017, 11, 31–53. [Google Scholar] [CrossRef]
- Bati, A.S.R.; Yu, L.P.; Batmunkh, M.; Shapter, J.G. Recent Advances in Applications of Sorted Single-Walled Carbon Nanotubes. Adv. Funct. Mater. 2019, 29, 1902273. [Google Scholar] [CrossRef]
- Moore, K.E.; Tune, D.D.; Flavel, B.S. Double-Walled Carbon Nanotube Processing. Adv. Mater. 2015, 27, 3105–3137. [Google Scholar] [CrossRef] [PubMed]
- Kharlamova, M.V. Advances in tailoring the electronic properties of single-walled carbon nanotubes. Prog. Mater. Sci. 2016, 77, 125–211. [Google Scholar] [CrossRef]
- Tkachenko, N.V. Optical Spectroscopy: Methods and Instrumentations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Kharlamova, M.V.; Brzhezinskaya, M.; Vinogradov, A.; Suzdalev, I.; Maksimov, Y.V.; Imshennik, V.; Novichikhin, S.V.; Krestinin, A.V.; Yashina, L.V.; Lukashin, A.V.; et al. The forming and properties of one-dimensional FeHaI2 (HaI = Cl, Br, I) nanocrystals in channels of single-walled carbon nanotubes. Russ. Nanotechnol. 2009, 4, 8777–8787. [Google Scholar] [CrossRef]
- Kharlamova, M.V.; Eliseev, A.A.; Yashina, L.V.; Petukhov, D.I.; Liu, C.P.; Wang, C.Y.; Semenenko, D.A.; Belogorokhov, A.I. Study of the electronic structure of single-walled carbon nanotubes filled with cobalt bromide. JETP Lett. 2010, 91, 196–200. [Google Scholar] [CrossRef]
- Kharlamova, M.V.; Yashina, L.V.; Volykhov, A.A.; Niu, J.J.; Neudachina, V.S.; Brzhezinskaya, M.M.; Zyubina, T.S.; Belogorokhov, A.I.; Eliseev, A.A. Acceptor doping of single-walled carbon nanotubes by encapsulation of zinc halogenides. Eur. Phys. J. B 2012, 85, 34. [Google Scholar] [CrossRef]
- Eliseev, A.A.; Yashina, L.V.; Brzhezinskaya, M.M.; Chernysheva, M.V.; Kharlamova, M.V.; Verbitsky, N.I.; Lukashin, A.V.; Kiselev, N.A.; Kumskov, A.S.; Zakalyuhin, R.M.; et al. Structure and electronic properties of AgX (X = Cl, Br, I)-intercalated single-walled carbon nanotubes. Carbon 2010, 48, 2708–2721. [Google Scholar] [CrossRef]
- Kharlamova, M.V.; Yashina, L.V.; Lukashin, A.V. Charge transfer in single-walled carbon nanotubes filled with cadmium halogenides. J. Mater. Sci. 2013, 48, 8412–8419. [Google Scholar] [CrossRef]
- Fedotov, P.V.; Tonkikh, A.A.; Obraztsova, E.A.; Nasibulin, A.G.; Kauppinen, E.I.; Chuvilin, A.L.; Obraztsova, E.D. Optical properties of single-walled carbon nanotubes filled with CuCl by gas-phase technique. Phys. Status Solidi B-Basic Solid State Phys. 2014, 251, 2466–2470. [Google Scholar] [CrossRef]
- Eliseev, A.A.; Yashina, L.V.; Verbitskiy, N.I.; Brzhezinskaya, M.M.; Kharlamova, M.V.; Chernysheva, M.V.; Lukashin, A.V.; Kiselev, N.A.; Kumskov, A.S.; Freitag, B.; et al. Interaction between single walled carbon nanotube and 1D crystal in CuX@SWCNT (X = Cl, Br, I) nanostructures. Carbon 2012, 50, 4021–4039. [Google Scholar] [CrossRef]
- Kharlamova, M.V.; Volykhov, A.A.; Yashina, L.V.; Egorov, A.V.; Lukashin, A.V. Experimental and theoretical studies on the electronic properties of praseodymium chloride-filled single-walled carbon nanotubes. J. Mater. Sci. 2015, 50, 5419–5430. [Google Scholar] [CrossRef]
- Kharlamova, M.V. Comparison of influence of incorporated 3d-, 4d-and 4f-metal chlorides on electronic properties of single-walled carbon nanotubes. Appl. Phys. A 2013, 111, 725–731. [Google Scholar] [CrossRef]
- Kharlamova, M.V. Novel approach to tailoring the electronic properties of single-walled carbon nanotubes by the encapsulation of high-melting gallium selenide using a single-step process. JETP Lett. 2013, 98, 272–277. [Google Scholar] [CrossRef]
- Kharlamova, M.V. Comparative analysis of electronic properties of tin, gallium, and bismuth chalcogenide-filled single-walled carbon nanotubes. J. Mater. Sci. 2014, 49, 8402–8411. [Google Scholar] [CrossRef]
- Yashina, L.V.; Eliseev, A.A.; Kharlamova, M.V.; Volykhov, A.A.; Egorov, A.V.; Savilov, S.V.; Lukashin, A.V.; Puttner, R.; Belogorokhov, A.I. Growth and Characterization of One-Dimensional SnTe Crystals within the Single-Walled Carbon Nanotube Channels. J. Phys. Chem. C 2011, 115, 3578–3586. [Google Scholar] [CrossRef]
- Kharlamova, M.V.; Yashina, L.V.; Lukashin, A.V. Comparison of modification of electronic properties of single-walled carbon nanotubes filled with metal halogenide, chalcogenide, and pure metal. Appl. Phys. A 2013, 112, 297–304. [Google Scholar] [CrossRef]
- Kharlamova, M.V.; Kramberger, C.; Sauer, M.; Yanagi, K.; Pichler, T. Comprehensive spectroscopic characterization of high purity metallicity-sorted single-walled carbon nanotubes. Phys. Status Solidi B-Basic Solid State Phys. 2015, 252, 2512–2518. [Google Scholar] [CrossRef]
- Ayala, P.; Miyata, Y.; De Blauwe, K.; Shiozawa, H.; Feng, Y.; Yanagi, K.; Kramberger, C.; Silva, S.R.P.; Follath, R.; Kataura, H.; et al. Disentanglement of the electronic properties of metallicity-selected single-walled carbon nanotubes. Phys. Rev. B 2009, 80, 205427. [Google Scholar] [CrossRef]
- Kuzmany, H. Solid-State Spectroscopy: An Introduction, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Atalla, R.H.; Agarwal, U.P.; Bond, J.L. Raman Spectroscopy. Springer Series in Wood Science. Methods in Lignin Chemistry; Springer: Berlin/Heidelberg, Germany, 1992; pp. 162–176. [Google Scholar]
- Smekal, A. The quantum theory of dispersion. Naturwissenschaften 1923, 11, 873–875. [Google Scholar] [CrossRef]
- Raman, C.V.; Krishnan, K.S. The optical analog of the Compton eect. Nature 1928, 121, 711. [Google Scholar] [CrossRef]
- Lamdsberg, G.; Mandelstam, L. A novel effect of light scattering in crystals. Naturwissenschaften 1928, 16, 557. [Google Scholar]
- Maiman, T.H. Stimulated optical radiation in ruby. Nature 1960, 187, 493–494. [Google Scholar] [CrossRef]
- Porto, S.P.S.; Wood, D.L. Ruby optical maser as a raman source. J. Opt. Soc. Am. 1962, 52, 251–252. [Google Scholar] [CrossRef]
- Smith, E.; Dent, G. Modern Raman Spectroscopy: A Practical Approach; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2005. [Google Scholar]
- Kharlamova, M.V.; Eliseev, A.A.; Yashina, L.V.; Lukashin, A.V.; Tretyakov, Y.D. Synthesis of Nanocomposites on Basis of Single-Walled Carbon Nanotubes Intercalated by Manganese Halogenides; IOP Publishing, Ltd.: Bristol, UK, 2012. [Google Scholar]
- Kharlamova, M.V. Electronic properties of single-walled carbon nanotubes filled with manganese halogenides. Appl. Phys. A 2016, 122, 791. [Google Scholar] [CrossRef]
- Kharlamova, M.V.; Yashina, L.V.; Eliseev, A.A.; Volykhov, A.A.; Neudachina, V.S.; Brzhezinskaya, M.M.; Zyubina, T.S.; Lukashin, A.V.; Tretyakov, Y.D. Single-walled carbon nanotubes filled with nickel halogenides: Atomic structure and doping effect. Phys. Status Solidi B-Basic Solid State Phys. 2012, 249, 2328–2332. [Google Scholar] [CrossRef]
- Kharlamova, M.V.; Kramberger, C.; Mittelberger, A.; Yanagi, K.; Pichler, T.; Eder, D. Silver Chloride Encapsulation-Induced Modifications of Raman Modes of Metallicity-Sorted Semiconducting Single-Walled Carbon Nanotubes. J. Spectrosc. 2018, 2018, 5987428. [Google Scholar] [CrossRef]
- Kharlamova, M.V.; Kramberger, C.; Domanov, O.; Mittelberger, A.; Yanagi, K.; Pichler, T.; Eder, D. Fermi level engineering of metallicity-sorted metallic single-walled carbon nanotubes by encapsulation of few-atom-thick crystals of silver chloride. J. Mater. Sci. 2018, 53, 13018–13029. [Google Scholar] [CrossRef]
- Chernysheva, M.V.; Eliseev, A.A.; Lukashin, A.V.; Tretyakov, Y.D.; Savilov, S.V.; Kiselev, N.A.; Zhigalina, O.M.; Kumskov, A.S.; Krestinin, A.V.; Hutchison, J.L. Filling of single-walled carbon nanotubes by Cul nanocrystals via capillary technique. Phys. E 2007, 37, 62–65. [Google Scholar] [CrossRef]
- Kumskov, A.S.; Zhigalina, V.G.; Chuvilin, A.L.; Verbitskiy, N.I.; Ryabenko, A.G.; Zaytsev, D.D.; Eliseev, A.A.; Kiselev, N.A. The structure of 1D and 3D CuI nanocrystals grown within 1.5–2.5 nm single wall carbon nanotubes obtained by catalyzed chemical vapor deposition. Carbon 2012, 50, 4696–4704. [Google Scholar] [CrossRef]
- Kharlamova, M.V.; Kramberger, C.; Pichler, T. Semiconducting response in single-walled carbon nanotubes filled with cadmium chloride. Phys. Status Solidi B-Basic Solid State Phys. 2016, 253, 2433–2439. [Google Scholar] [CrossRef]
- Kharlamova, M.V.; Kramberger, C.; Rudatis, P.; Pichler, T.; Eder, D. Revealing the doping effect of encapsulated lead halogenides on single-walled carbon nanotubes. Appl. Phys. A 2019, 125, 320. [Google Scholar] [CrossRef]
- Zakalyukin, R.M.; Mavrin, B.N.; Dem’yanets, L.N.; Kiselev, N.A. Synthesis and characterization of single-walled carbon nanotubes filled with the superionic material SnF2. Carbon 2008, 46, 1574–1578. [Google Scholar] [CrossRef]
- Kharlamova, M.V.; Kramberger, C.; Rudatis, P.; Yanagi, K.; Eder, D. Characterization of the Electronic Properties of Single-Walled Carbon Nanotubes Filled with an Electron Donor-Rubidium Iodide: Multifrequency Raman and X-ray Photoelectron Spectroscopy Studies. Phys. Status Solidi B-Basic Solid State Phys. 2019, 256, 1900209. [Google Scholar] [CrossRef]
- Falaleev, N.S.; Kumskov, A.S.; Zhigalina, V.G.; Verbitskiy, I.I.; Vasiliev, A.L.; Makarova, A.A.; Vyalikh, D.V.; Kiselev, N.A.; Eliseev, A.A. Capsulate structure effect on SWNTs doping in RbxAg1-xI@SWNT composites. Crystengcomm 2017, 19, 3063–3070. [Google Scholar] [CrossRef] [Green Version]
- Kharlamova, M.V. Rare-earth metal halogenide encapsulation-induced modifications in Raman spectra of single-walled carbon nanotubes. Appl. Phys. A 2015, 118, 27–35. [Google Scholar] [CrossRef]
- Kharlamova, M.V.; Kramberger, C.; Mittelberger, A. Raman spectroscopy study of the doping effect of the encapsulated terbium halogenides on single-walled carbon nanotubes. Appl. Phys. A 2017, 123, 239. [Google Scholar] [CrossRef]
- Santidrian, A.; Kierkowicz, M.; Pach, E.; Darvasiova, D.; Ballesteros, B.; Tobias, G.; Kalbac, M. Charge transfer in steam purified arc discharge single walled carbon nanotubes filled with lutetium halides. Phys. Chem. Chem. Phys. 2020, 22, 10063–10075. [Google Scholar] [CrossRef]
- Fedoseeva, Y.V.; Orekhov, A.S.; Chekhova, G.N.; Koroteev, V.O.; Kanygin, M.A.; Senkovskiy, B.V.; Chuvilin, A.; Pontiroli, D.; Ricco, M.; Bulusheva, L.G.; et al. Single-Walled Carbon Nanotube Reactor for Redox Transformation of Mercury Dichloride. ACS Nano 2017, 11, 8643–8649. [Google Scholar] [CrossRef]
- Kharlamova, M.V.; Niu, J.J. Donor doping of single-walled carbon nanotubes by filling of channels with silver. J. Exp. Theor. Phys. 2012, 115, 485–491. [Google Scholar] [CrossRef]
- Corio, P.; Santos, A.P.; Santos, P.S.; Temperini, M.L.A.; Brar, V.W.; Pimenta, M.A.; Dresselhaus, M.S. Characterization of single wall carbon nanotubes filled with silver and with chromium compounds. Chem. Phys. Lett. 2004, 383, 475–480. [Google Scholar] [CrossRef]
- Kharlamova, M.V.; Niu, J.J. Comparison of metallic silver and copper doping effects on single-walled carbon nanotubes. Appl. Phys. A 2012, 109, 25–29. [Google Scholar] [CrossRef]
- Kharlamova, M.V.; Niu, J.J. New method of the directional modification of the electronic structure of single-walled carbon nanotubes by filling channels with metallic copper from a liquid phase. JETP Lett. 2012, 95, 314–319. [Google Scholar] [CrossRef]
- Briones, A.; Liu, X.J.; Kramberger, C.; Saito, T.; Pichler, T. Nanochemical reactions by laser annealing of ferrocene filled single-walled carbon nanotubes. Phys. Status Solidi B-Basic Solid State Phys. 2011, 248, 2488–2491. [Google Scholar] [CrossRef]
- Kharlamova, M.V.; Sauer, M.; Saito, T.; Krause, S.; Liu, X.; Yanagi, K.; Pichler, T.; Shiozawa, H. Inner tube growth properties and electronic structure of ferrocene-filled large diameter single-walled carbon nanotubes. Phys. Status Solidi B-Basic Solid State Phys. 2013, 250, 2575–2580. [Google Scholar] [CrossRef]
- Liu, X.J.; Kuzmany, H.; Saito, T.; Pichler, T. Temperature dependence of inner tube growth from ferrocene-filled single-walled carbon nanotubes. Phys. Status Solidi B-Basic Solid State Phys. 2011, 248, 2492–2495. [Google Scholar] [CrossRef]
- Kharlamova, M.V.; Kramberger, C.; Saito, T.; Shiozawa, H.; Pichler, T. In situ Raman spectroscopy studies on time-dependent inner tube growth in ferrocene-filled large diameter single-walled carbon nanotubes. Phys. Status Solidi B-Basic Solid State Phys. 2014, 251, 2394–2400. [Google Scholar] [CrossRef]
- Kharlamova, M.V.; Kramberger, C.; Saito, T.; Shiozawa, H.; Pichler, T. Growth dynamics of inner tubes inside cobaltocene-filled single-walled carbon nanotubes. Appl. Phys. A 2016, 122, 749. [Google Scholar] [CrossRef]
- Kharlamova, M.V.; Kramberger, C.; Sato, Y.; Saito, T.; Suenaga, K.; Pichler, T.; Shiozawa, H. Chiral vector and metal catalyst-dependent growth kinetics of single-wall carbon nanotubes. Carbon 2018, 133, 283–292. [Google Scholar] [CrossRef]
- Kharlamova, M.V.; Sauer, M.; Saito, T.; Sato, Y.; Suenaga, K.; Pichler, T.; Shiozawa, H. Doping of single-walled carbon nanotubes controlled via chemical transformation of encapsulated nickelocene. Nanoscale 2015, 7, 1383–1391. [Google Scholar] [CrossRef] [Green Version]
- Kharlamova, M.V.; Sauer, M.; Egorov, A.; Kramberger, C.; Saito, T.; Pichler, T.; Shiozawa, H. Temperature-dependent inner tube growth and electronic structure of nickelocene-filled single-walled carbon nanotubes. Phys. Status Solidi B-Basic Solid State Phys. 2015, 252, 2485–2490. [Google Scholar] [CrossRef]
- Kharlamova, M.V.; Kramberger, C.; Saito, T.; Sato, Y.; Suenaga, K.; Pichler, T.; Shiozawa, H. Chirality-dependent growth of single-wall carbon nanotubes as revealed inside nano-test tubes. Nanoscale 2017, 9, 7998–8006. [Google Scholar] [CrossRef] [Green Version]
- Dresselhaus, M.S.; Dresselhaus, G.; Jorio, A.; Souza, A.G.; Saito, R. Raman spectroscopy on isolated single wall carbon nanotubes. Carbon 2002, 40, 2043–2061. [Google Scholar] [CrossRef]
- Araujo, P.T.; Maciel, I.O.; Pesce, P.B.C.; Pimenta, M.A.; Doorn, S.K.; Qian, H.; Hartschuh, A.; Steiner, M.; Grigorian, L.; Hata, K.; et al. Nature of the constant factor in the relation between radial breathing mode frequency and tube diameter for single-wall carbon nanotubes. Phys. Rev. B 2008, 77, 241403. [Google Scholar] [CrossRef] [Green Version]
- Fouquet, M.; Telg, H.; Maultzsch, J.; Wu, Y.; Chandra, B.; Hone, J.; Heinz, T.F.; Thomsen, C. Longitudinal Optical Phonons in Metallic and Semiconducting Carbon Nanotubes. Phys. Rev. Lett. 2009, 102, 75501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brown, S.D.M.; Corio, P.; Marucci, A.; Dresselhaus, M.S.; Pimenta, M.A.; Kneipp, K. Anti-Stokes Raman spectra of single-walled carbon nanotubes. Phys. Rev. B 2000, 61, R5137–R5140. [Google Scholar] [CrossRef]
- Das, A.; Sood, A.K. Renormalization of the phonon spectrum in semiconducting single-walled carbon nanotubes studied by Raman spectroscopy. Phys. Rev. B 2009, 79, 235429. [Google Scholar] [CrossRef]
- Grimm, S.; Schiessl, S.P.; Zakharko, Y.; Rother, M.; Brohmann, M.; Zaumseil, J. Doping-dependent G-mode shifts of small diameter semiconducting single-walled carbon nanotubes. Carbon 2017, 118, 261–267. [Google Scholar] [CrossRef]
- Tsang, J.C.; Freitag, M.; Perebeinos, V.; Liu, J.; Avouris, P. Doping and phonon renormalization in carbon nanotubes. Nat. Nanotechnol. 2007, 2, 725–730. [Google Scholar] [CrossRef]
- Das, A.; Sood, A.K.; Govindaraj, A.; Saitta, A.M.; Lazzeri, M.; Mauri, F.; Rao, C.N.R. Doping in carbon nanotubes probed by Raman and transport measurements. Phys. Rev. Lett. 2007, 99, 136803. [Google Scholar] [CrossRef] [Green Version]
- Kalbac, M.; Farhat, H.; Kavan, L.; Kong, J.; Dresselhaus, M.S. Competition between the Spring Force Constant and the Phonon Energy Renormalization in Electrochemically Doped Semiconducting Single-Walled Carbon Nanotubes. Nano Lett. 2008, 8, 3532–3537. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Liao, V.; Yu, Z.H. Raman spectroelectrochemistry of a single-wall carbon nanotube bundle. Carbon 2010, 48, 2582–2589. [Google Scholar] [CrossRef]
- Piscanec, S.; Lazzeri, M.; Robertson, J.; Ferrari, A.C.; Mauri, F. Optical phonons in carbon nanotubes: Kohn anomalies, Peierls distortions, and dynamic effects. Phys. Rev. B 2007, 75, 35427. [Google Scholar] [CrossRef] [Green Version]
- Lazzeri, M.; Piscanec, S.; Mauri, F.; Ferrari, A.C.; Robertson, J. Phonon linewidths and electron-phonon coupling in graphite and nanotubes. Phys. Rev. B 2006, 73, 155426. [Google Scholar] [CrossRef] [Green Version]
- Caudal, N.; Saitta, A.M.; Lazzeri, M.; Mauri, F. Kohn anomalies and nonadiabaticity in doped carbon nanotubes. Phys. Rev. B 2007, 75, 115423. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, K.T.; Gaur, A.; Shim, M. Fano lineshape and phonon softening in single isolated metallic carbon nanotubes. Phys. Rev. Lett. 2007, 98, 145504. [Google Scholar] [CrossRef]
- Farhat, H.; Son, H.; Samsonidze, G.G.; Reich, S.; Dresselhaus, M.S.; Kong, J. Phonon softening in individual metallic carbon nanotubes due to the Kohn anomaly. Phys. Rev. Lett. 2007, 99, 145506. [Google Scholar] [CrossRef] [Green Version]
- Watts, J.F.; Wolstenholme, J. An Introduction to Surface Analysis by XPS and AES; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2003. [Google Scholar]
- Leckrey, R. Ultraviolet Photoelectron Spectroscopy of Solids. Surface Analysis Methods in Materials Science; Springer Series in Surface Sciences; O’Connor, D.J., Sexton, B.A., Smart, R.S.C., Eds.; Springer: Berlin/Heidelberg, Germany, 1992; Volume 23. [Google Scholar]
- Hertz, H. Uber einen einuss des ultravioletten lichtes auf die electrische entladung. Ann. Phys. 1887, 267, 983–1000. [Google Scholar] [CrossRef] [Green Version]
- Einstein, A. Uber einen die erzeugung und verwandlung des lichtes betreenden heuristischen gesichtspunkt. Ann. Phys. 1905, 322, 132–148. [Google Scholar] [CrossRef]
- Innes, P.D. On the velocity of the cathode particles emitted by various metals under the inuence of Rontgen rays, and its bearing on the theory of atomic disintegration. Proc. R. Soc. Lond. Ser. A 1907, 79, 442–462. [Google Scholar]
- Briggs, D.; Grant, G.T. Perspectives on XPS and AES. Surface Analysis by Auger and X-ray Photoelectron Spectroscopy; IM Publications and Surface Spectra Limited: Chichester, UK, 2003; pp. 1–30. [Google Scholar]
- Steinhardt, R.G.; Serfass, E.J. Surface analysis with X-ray photoelectron spectrometer. Anal. Chem. 1953, 25, 697–700. [Google Scholar] [CrossRef]
- Nordling, C.; Sokolowski, E.; Siegbahn, K. Precision method for obtaining absolute values of atomic binding energies. Rhys. Rev. 1957, 105, 1676–1677. [Google Scholar] [CrossRef]
- Siegbahn, K.; Nordling, C.; Fahlman, A.; Nordberg, L.; Hamrin, K.; Hedman, J.; Johansson, J.; Bergmark, T.; Karlsson, S.E.; Lindgren, I.; et al. Electron Spectroscopy for Chemical Analysis. Atomic, Molecular and Solid State Structure Studies by Means of Electron Spectroscopy; Almquist and Wiksells: Stockholm, Sweden, 1967. [Google Scholar]
- Briggs, D. XPS: Basic Principles, Spectral Features and Qualitative Analysis. Surface Analysis by Auger and X-ray Photoelectron Spectroscopy; IM Publications and SurfaceSpectra Limited: Chichester, UK, 2003; pp. 31–56. [Google Scholar]
- Vilesov, F.I.; Kurbatov, B.L.; Terenin, A.N. Electron Distribution over Energies in Photoionization of Aromatic Amines in Gaseous Phase. Sov. Phys. Dokl. 1961, 6, 490. [Google Scholar]
- Spicer, W.E.; Beglund, C.N. d-Band of copper. Phys. Rev. Lett. 1964, 12, 9–11. [Google Scholar] [CrossRef]
- Berglund, C.N.; Spicer, W.E. Photoemission studies of copper and silver. Phys. Rev. 1964, 136, 1030. [Google Scholar] [CrossRef]
- Turner, D.W.; Baker, C.; Baker, A.D.; Brundle, C.R. Molecular Photoelectron Spectroscopy; Wiley-Interscience: Hoboken, NJ, USA, 1970. [Google Scholar]
- Turner, D.W.; Al-Joboury, M.I. Determination of ionization potentials by photoelectron energy measurement. J. Chem. Phys. 1962, 37, 3007–3008. [Google Scholar] [CrossRef]
- Heber, M.; Grunert, W. Application of ultraviolet photoelectron spectroscopy (UPS) in the surface characterisation of polycrystalline oxide catalysts. I. Methodics and analytical potential. Top. Catal. 2001, 15, 3–11. [Google Scholar] [CrossRef]
- Park, Y.; Choong, V.; Gao, Y. Work function of indium tin oxide transparent conductor measured by photoelectron spectroscopy. Appl. Phys. Lett. 2021, 68, 2699–2701. [Google Scholar] [CrossRef]
- Kramberger, C.; Rauf, H.; Shiozawa, H.; Knupfer, M.; Buchner, B.; Pichler, T.; Batchelor, D.; Kataura, H. Unraveling van Hove singularities in X-ray absorption response of single-wall carbon nanotubes. Phys. Rev. B 2007, 75, 235437. [Google Scholar] [CrossRef]
- Su, W.S.; Leung, T.C.; Chan, C.T. Work function of single-walled and multiwalled carbon nanotubes: First-principles study. Phys. Rev. B 2007, 76, 235413. [Google Scholar] [CrossRef] [Green Version]
- Doniach, S.; Sunjic, M. Many-Electron Singularity in X-ray Photoemission and X-ray Line Spectra from Metals. J. Phys. Part C Solid State Phys. 1970, 3, 285. [Google Scholar] [CrossRef]
- Ishii, H.; Kataura, H.; Shiozawa, H.; Yoshioka, H.; Otsubo, H.; Takayama, Y.; Miyahara, T.; Suzuki, S.; Achiba, Y.; Nakatake, M.; et al. Direct observation of Tomonaga-Luttinger-liquid state in carbon nanotubes at low temperatures. Nature 2003, 426, 540–544. [Google Scholar] [CrossRef] [PubMed]
- Rauf, H.; Pichler, T.; Knupfer, M.; Fink, J.; Kataura, H. Transition from a Tomonaga-Luttinger liquid to a Fermi liquid in potassium-intercalated bundles of single-wall carbon nanotubes. Phys. Rev. Lett. 2004, 93, 96805. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schnohr, C.S.; Ridgway, M. (Eds.) X-ray Absorption Spectroscopy of Semiconductors; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Stohr, J. NEXAFS Spectroscopy; Springer Series in Surface Sciences; Springer: Berlin/Heidelberg, Germany, 1992; Volume 25. [Google Scholar]
- Wang, M.Y.; Arnadottir, L.; Xu, Z.C.J.; Feng, Z.X. In Situ X-ray Absorption Spectroscopy Studies of Nanoscale Electrocatalysts. Nano-Micro Lett. 2019, 11, 47. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bianconi, A. Surface X-ray Absorption-Spectroscopy—Surface Exafs and Surface Xanes. Appl. Surf. Sci. 1980, 6, 392–418. [Google Scholar] [CrossRef]
- de Broglie, M. Sur une nouveau procédé permettant d’obtenir la photographie des spectres de raies des rayons Rontgen. C R. Acad. Sci. 1913, 157, 924–926. [Google Scholar]
- Fricke, H. The K-Characteristic Absorption Frequencies for the Chemical Elements Magnesium to Chromium. Phys. Rev. 1920, 16, 202–215. [Google Scholar] [CrossRef]
- Hertz, G. Uber die Absorptionsgrenzen in der L-Serie. Z. Phys. 1920, 3, 19–25. [Google Scholar] [CrossRef] [Green Version]
- Hanawalt, J.D. The Dependence of X-ray Absorption Spectra upon Chemical and Physical State. Phys. Rev. 1931, 37, 715–726. [Google Scholar] [CrossRef]
- Kronig, R.d.L. Zur Theorie der Feinstruktur in den Rontgenabsorptionsspektren. Z. Phys. 1931, 70, 317–323. [Google Scholar] [CrossRef]
- Kronig, R.d.L. Zur Theorie der Feinstruktur in den Rontgenabsorptionsspektren. II. Z. Phys. 1932, 75, 191–210. [Google Scholar] [CrossRef]
- Kronig, R.d.L. Zur Theorie der Feinstruktur in den Rontgenabsorptionsspektren. III. Z. Phys. 1932, 75, 468–475. [Google Scholar] [CrossRef]
- Petersen, H. Zur Theorie der Rontgenabsorption molekularer Gase. Z. Phys. 1932, 76, 768–776. [Google Scholar] [CrossRef]
- Petersen, H. Zur Theorie der Rontgenabsorption molekularer Gase. II. Z. Phys. 1933, 80, 258–266. [Google Scholar] [CrossRef]
- Petersen, H. Zur Theorie der Rontgenabsorption molekularer Gase. III. Z. Phys. 1936, 98, 569–575. [Google Scholar] [CrossRef]
- Cauchois, Y.; Mott, N.F. The Interpretation of X-ray Absorption Spectra of Solids. Philos. Mag. 1949, 40, 1260–1269. [Google Scholar] [CrossRef]
- Lytle, F.W. X-ray Absorption Fine-Structure Investigations at Cryogenic Temperatures. In Developments in Applied Spectroscopy; Ferraro, J.R., Ziomek, J., Plenum, S., Eds.; Springer: Boston, MA, USA, 1963; Volume 2, pp. 285–296. [Google Scholar]
- Sawada, M.; Tsutsumi, K.; Shiraiwa, T.; Obashi, M. On the Fine Structures of X-ray Absorption Spectra of Amorphous Substances: The Amorphous State of the Binary System of Nickel-Sulfur. II. J. Phys. Soc. Jpn. 1955, 10, 464–468. [Google Scholar] [CrossRef]
- Shiraiwa, T. The Theory of the Fine Structure of the X-ray Absorption Spectrum, II. J. Phys. Soc. Jpn. 1960, 15, 240–250. [Google Scholar] [CrossRef]
- Snyder, T.M.; Shaw, C.H. The Fine Structure of the X-ray Absorption Limits of Bromine and Chlorine. Phys. Rev. 1940, 57, 881–886. [Google Scholar] [CrossRef]
- Lytle, F. Determination of Interatomic Distances from X-ray Absorption Fine Structure. Adv. X-ray Anal. 1966, 9, 398–409. [Google Scholar]
- Van Nordstand, R.A. The Use of X-ray K-Absorption Edges in the Study of Catalytically Active Solids. Adv. Catal. 1960, 12, 149–187. [Google Scholar]
- Van Nordstrand, R. Handbook of X-rays; Kaelble, E., Ed.; McGraw-Hill: New York, NY, USA, 1967; pp. 41–48. [Google Scholar]
- Sayers, D.E.; Stern, E.A.; Lytle, F.W. New Technique for Investigating Noncrystalline Structures: Fourier Analysis of the Extended X-ray Absorption Fine Structure. Phys. Rev. Lett. 1971, 27, 1204–1207. [Google Scholar] [CrossRef]
- Lytle, F.W.; Sayers, D.E.; Stern, E.A. Extended X-ray-Absorption Fine-Structure Technique. II. Experimental Practice and Selected Results. Phys. Rev. B 1975, 11, 4825–4835. [Google Scholar] [CrossRef]
- Rehr, J.J.; Stern, E.A.; Martin, E.L.; Davidson, E.R. Extended X-ray-Absorption Fine-Structure Amplitudes, Wave-Function Relaxation and Chemical Effects. Phys. Rev. B 1978, 17, 560–565. [Google Scholar] [CrossRef]
- Sandstrom, D.R.; Lytle, F.W. Developments in Extended X-ray Absorption Fine Structure Applied to Chemical Systems. Ann. Rev. Phys. Chem. 1979, 30, 215–238. [Google Scholar] [CrossRef]
- Stern, E.A. Theory of the Extended X-ray-Absorption Fine Structure. Phys. Rev. B 1974, 10, 3027–3037. [Google Scholar] [CrossRef]
- Stern, E.A.; Sayers, D.E.; Lytle, F.W. Extended X-ray-Absorption Fine-Structure Technique. III. Determination of Physical Parameters. Phys. Rev. B 1975, 11, 4836–4846. [Google Scholar] [CrossRef]
- Ashley, C.A.; Doniach, S. Theory of Extended X-ray Absorption Edge Fine Structure (EXAFS) in Crystalline Solids. Phys. Rev. B 1975, 11, 1279–1288. [Google Scholar] [CrossRef]
- Beni, G.; Platzman, P.L. Temperature and Polarization Dependence of Extended X-ray Absorption Fine-Structure Spectra. Phys. Rev. B 1976, 14, 1514–1518. [Google Scholar] [CrossRef]
- Lee, P.A.; Pendry, J.B. Theory of the Extended X-ray Absorption Fine Structure. Phys. Rev. B 1975, 11, 2795–2811. [Google Scholar] [CrossRef]
- Schaich, W.L. Comment on the Theory of Extended X-ray-Absorption Fine Structure. Phys. Rev. B 1973, 8, 4028–4032. [Google Scholar] [CrossRef]
- Sevillano, G.; Meuth, H.; Rehr, J. Extended X-ray Absorption Fine Structure Debye-Waller Factors. I. Monatomic Crystals. Phys. Rev. B 1979, 20, 4908–4911. [Google Scholar] [CrossRef]
- Lamberti, C.; van Bockhoven, J.A. Introduction: Historical Perspective on XAS. X-ray Absorption and X-ray Emission Spectroscopy: Theory and Applications, 1st ed.; van Bockhoven, J.A., Lamberti, C., Eds.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2016. [Google Scholar]
- Yano, J.; Yachandra, V.K. X-ray absorption spectroscopy. Photosynth. Res. 2009, 102, 241–254. [Google Scholar] [CrossRef] [Green Version]


| Filled Substance | Observed Modification of the OAS Spectrum | Reference |
|---|---|---|
| FeCl2, FeBr2, FeI2 | peak | [12] |
| CoBr2 | peak | [13] |
| ZnCl2, ZnBr2, ZnI2 | peak | [14] |
| AgCl, AgBr, AgI | peak | [15] |
| CdCl2, CdBr2, CdI2 | peak | [16] |
| CuCl | peak | [17] |
| CuCl, CuBr, CuI | peak | [18] |
| PrCl3 | peak | [19] |
| TbCl3 | peak | [20] |
| GaSe, GaTe | peak | [21,22] |
| SnS, SnTe | No modifications | [22,23] |
| Bi2Se3 | No modifications | [22] |
| Bi2Te3 | No modifications | [24] |
| Filled Substance | Observed Modification of the Raman Spectrum | Reference |
|---|---|---|
| MnCl2, MnBr2 | Shifts and changes in relative intensities of peaks in the RBM and G-bands | [35,36] |
| FeCl2, FeBr2, FeI2 | Shifts and changes in relative intensities of peaks in the RBM and G-bands | [12] |
| CoBr2 | Shifts and changes in relative intensities of peaks in the RBM and G-bands | [13] |
| NiCl2, NiBr2 | Shifts and changes in relative intensities of peaks in the RBM and G-bands | [37] |
| ZnCl2 | Shifts and changes in relative intensities of peaks in the RBM and G-bands | [20] |
| ZnCl2, ZnBr2, ZnI2 | Shifts and changes in relative intensities of peaks in the RBM and G-bands | [14] |
| AgCl, AgBr, AgI | Shifts and changes in relative intensities of peaks in the RBM and G-bands | [15] |
| AgCl | Shifts and changes in relative intensities of peaks in the RBM and G-bands | [38,39] |
| CuCl | Shifts and changes in relative intensities of peaks in the RBM and G-bands | [17] |
| CuI | Shifts and changes in relative intensities of peaks in the RBM and G-bands | [40,41] |
| CuCl, CuBr, CuI | Shifts and changes in relative intensities of peaks in the RBM and G-bands | [18] |
| CdCl2 | Shifts and changes in relative intensities of peaks in the RBM and G-bands | [20,42] |
| CdCl2, CdBr2, CdI2 | Shifts and changes in relative intensities of peaks in the RBM and G-bands | [16] |
| PbCl2, PbBr2, PbI2 | Shifts and changes in relative intensities of peaks in the RBM and G-bands | [43] |
| SnF2 | No modifications | [44] |
| RbI | Shifts and changes in relative intensities of peaks in the RBM and G-bands | [45] |
| RbAg4I5 | Shifts and changes in relative intensities of peaks in the RBM and G-bands | [46] |
| TbCl3 | Shifts and changes in relative intensities of peaks in the RBM and G-bands | [20,47,48] |
| TbBr3, TbI3 | Shifts and changes in relative intensities of peaks in the RBM and G-bands | [48] |
| TmCl3 | Shifts and changes in relative intensities of peaks in the RBM and G-bands | [24,47] |
| PrCl3 | Shifts and changes in relative intensities of peaks in the RBM and G-bands | [19,47] |
| LuCl3, LuBr3, LuI3 | Shifts and changes in relative intensities of peaks in the RBM and G-bands | [49] |
| HgCl2 | Shifts and changes in relative intensities of peaks in the RBM and G-bands | [50] |
| GaSe, GaTe | Shifts and changes in relative intensities of peaks in the RBM and G-bands | [21,22] |
| SnS, SnTe | No modifications | [22,23] |
| Bi2Se3 | Slight modifications | [22] |
| Bi2Te3 | Slight modifications | [24] |
| Ag | Shifts and changes in relative intensities of peaks in the RBM and G-bands | [24,51,52,53] |
| Cu | Shifts and changes in relative intensities of peaks in the RBM and G-bands | [53,54] |
| Ferrocene | No modifications | [55,56,57,58] |
| Cobaltocene | No modifications | [59,60] |
| Nickelocene | No modifications | [61,62,63] |
| Filled Substance | Observed Modification of the C 1s XPS Spectrum | Reference |
|---|---|---|
| MnCl2, MnBr2 | Appearance of new downshifted components and broadening | [35,36] |
| FeCl2, FeBr2, FeI2 | Appearance of new downshifted components and broadening | [12] |
| CoBr2 | Appearance of new downshifted components and broadening | [13] |
| NiCl2, NiBr2 | Appearance of new downshifted components and broadening | [37] |
| ZnCl2, ZnBr2, ZnI2 | Appearance of new downshifted components and broadening | [14] |
| AgCl | Downshift, broadening and increase in asymmetry | [39] |
| AgCl, AgBr, AgI | Appearance of new downshifted components and broadening | [15] |
| PbCl2, PbBr2, PbI2 | Downshift, broadening and increase in asymmetry | [43] |
| CdCl2, CdBr2, CdI2 | Appearance of new downshifted components and broadening | [16] |
| ZnCl2, CdCl2, TbCl3 | Appearance of new downshifted components and broadening | [20] |
| CuCl, CuBr, CuI | Appearance of new downshifted components and broadening | [18] |
| RbI | Upshift, broadening and increase in asymmetry | [45] |
| RbAg4I5 | Appearance of new downshifted components and broadening | [46] |
| TmCl3 | Appearance of new downshifted components and broadening | [24] |
| PrCl3 | Appearance of new downshifted components and broadening | [19] |
| HgCl2 | Downshift, broadening and increase in asymmetry | [50] |
| GaSe, GaTe | Appearance of new downshifted components and broadening | [21,22] |
| SnS, SnTe | Broadening | [22,23] |
| Bi2Se3 | Broadening | [22] |
| Bi2Te3 | Broadening | [24] |
| Ag | Appearance of new upshifted components and broadening | [24,51,53] |
| Cu | Appearance of new upshifted components and broadening | [53,54] |
| Ferrocene | Upshift, broadening and increase in asymmetry | [56] |
| Nickelocene | Uphift, broadening and increase in asymmetry | [61,62] |
| Filled Substance | Observed Modification of the C 1s NEXAFS Spectrum | Reference |
|---|---|---|
| FeCl2, FeBr2, FeI2 | Appearance of additional component below π-resonance | [12] |
| NiCl2, NiBr2 | Appearance of additional component below π-resonance | [37] |
| ZnCl2, ZnBr2, ZnI2 | Appearance of additional component below π-resonance | [14] |
| CdCl2, CdBr2, CdI2 | Appearance of additional component below π-resonance | [16] |
| AgCl, AgBr, AgI | Appearance of additional component below π-resonance | [15] |
| CuCl, CuBr, CuI | Appearance of additional component below π-resonance | [18] |
| HgCl2 | Appearance of additional component below π-resonance | [50] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kharlamova, M.V.; Kramberger, C. Spectroscopy of Filled Single-Walled Carbon Nanotubes. Nanomaterials 2022, 12, 42. https://doi.org/10.3390/nano12010042
Kharlamova MV, Kramberger C. Spectroscopy of Filled Single-Walled Carbon Nanotubes. Nanomaterials. 2022; 12(1):42. https://doi.org/10.3390/nano12010042
Chicago/Turabian StyleKharlamova, Marianna V., and Christian Kramberger. 2022. "Spectroscopy of Filled Single-Walled Carbon Nanotubes" Nanomaterials 12, no. 1: 42. https://doi.org/10.3390/nano12010042
APA StyleKharlamova, M. V., & Kramberger, C. (2022). Spectroscopy of Filled Single-Walled Carbon Nanotubes. Nanomaterials, 12(1), 42. https://doi.org/10.3390/nano12010042







