Magnetic Structure and Origin of Insulating Behavior in the Ba₂CuOsO₆ System, and the Role of A-Site Ionic Size in Its Bandgap Opening: Density Functional Theory Approaches

Abstract

The magnetic structure and the origin of band gap opening for Ba₂CuOsO₆ were investigated by exploring the spin exchange interactions and employing the spin–orbit coupling effect. It revealed that the double-perovskite Ba₂CuOsO₆, composed of the 3d (Cu²⁺) and 5d (Os⁶⁺) transition metal magnetic ions is magnetic insulator. The magnetic susceptibilities of Ba₂CuOsO₆ obey the Curie–Weiss law, with an estimated Weiss temperature of −13.3 K, indicating AFM ordering. From the density functional theory approach, it is demonstrated that the spin exchange interaction between Cu ions plays a major role in exhibiting an antiferromagnetic behavior in the Ba₂CuOsO₆ system. An important factor to understand regarding the insulating behavior on Ba₂CuOsO₆ is the structural distortion shape of OsO₆ octahedron, which should be closely connected with the ionic size of the A-site ion. Since the d-block of Os⁶⁺ (d²) ions of Ba₂CuOsO₆ is split into four states (xy < xz, yz < x²–y² < z²), the crucial key is separation of doubly degenerated xz and yz levels to describe the magnetic insulating states of Ba₂CuOsO₆. By orbital symmetry breaking, caused by the spin–orbit coupling, the t_2g level of Os⁶⁺ (d²) ions is separated into three sublevels. Two electrons of Os⁶⁺ (d²) ions occupy two levels of the three spin–orbit-coupled levels. Since Ba₂CuOsO₆ is a strongly correlated system, and the Os atom belongs to the heavy element group, one speculates that it is necessary to take into account both electron correlation and the spin–orbit coupling effect in describing the magnetic insulating states of Ba₂CuOsO₆.

1. Introduction

Various osmium oxide compounds exhibit attractive magnetic and electronic phenomena developed from their electron correlation effects, such as the ferromagnetic gapped state in Ba₂NiOsO₆ [1], the singlet ground-state excitonic magnetism in Y₂OsO₇ [2,3,4], the spin-driven metal to insulator transition in Pb₂CaOsO₆ [5], and the unusual superconductivity in AOsO₆ (A = Cs, Rb, and K) [6].

The solid-state osmium oxides are noteworthy for the following two reasons. One lies in understanding the origin of the band gap inducing of the metal to insulator transition. So far, various mechanisms for explaining the band gap opening for solid-state osmium oxide compounds have been extensively considered, such as the Mott-type mechanism, the d-level splitting pattern caused by the electron correlation effect, the Slater-type mechanism, and the orbital symmetry breaking mechanism, driven by the spin–orbit coupling (SOC) effect. As an example, the band gap opening for Cd₂Os₂O₇ and NaOsO₃ is explained by Slater-type insulators, which are associated with magnetic ordering [7,8,9].

For Ba₂NaOsO₆, there has been a debate on whether it is a Mott-type insulator or a SOC effect-driven insulator. In a study by Erickson et al., the nature of the insulating phase for Ba₂NaOsO₆ is represented as a Mott-type insulator [10,11]. Xiang et al. suggest that the insulating behavior of Ba₂NaOsO₆ should be developed by the simultaneous effects of electron correlation and SOC [12]. Although it is well known that the 5d-block element has considerably extended valence orbitals, resulting in weak on-site Coulomb repulsion, the magnetic insulating features of Sr₂MOsO₆ (M = Cu and Ni) are reproduced with a significantly large on-site repulsion at the Os atom site [13]. Thus, it is of great importance to explore the origin of the band gap opening in solid-state osmium oxide compounds.

The other issue on solid-state osmium oxide is related to the various oxidation states of the Os ion. Osmium forms compounds with oxidation states, ranging from −2 to +8. As an example, the oxidation states of the Os ion in Na₂[Os(CO)], Na₂[Os₄(CO)₁₃], Os₃(CO)₁₂, OsI, OsI₂, OsBr₃, OsO₂, OsF₅, OsF₆, OsOF₅, and OsO₄ are −2, −1, 0, +1, +2, +3, +4, +5, +6, +7, and +8, respectively. A large spatial extension of Os at the 5d level is a main reason for the wide spectrum of oxidation states of the Os atom in osmium compounds. In general, the nd orbital of metal in the zero-oxidation state shows a spatial extension that increases in the order 3d < 4d < 5d, so that the widths of the d-block bands should increase in the order 3d < 4d < 5d. For this reason, 5d oxides show various valence states with the wide band widths of d-blocks. The electron correlation effects for 4d and 5d systems are weak while the effects of SOC are strong [14].

Recently, a new double perovskite osmium oxide Ba₂CuOsO₆ was synthesized under somewhat extreme conditions (~6 GPa and ~1800 K). The crystal structure and magnetic properties of Ba₂CuOsO₆ were characterized with synchrotron X-ray diffraction, thermo-gravimetric analysis, magnetic susceptibility, isothermal magnetization, and specific heat measurements [15]. The temperature dependence of the specific heat showed an electrically insulating behavior at all measured temperatures [15]. They also found that the Ba₂CuOsO₆ obeys the Curie–Weiss law with the estimated Weiss temperature −13.3 K [15]. Interestingly, a magnetic susceptibility measurement shows two T_max at ~55 K and ~70 K. This would be associated with two different magnetic ions in Ba₂CuOsO₆, which lead to more than two types of magnetic sublattice.

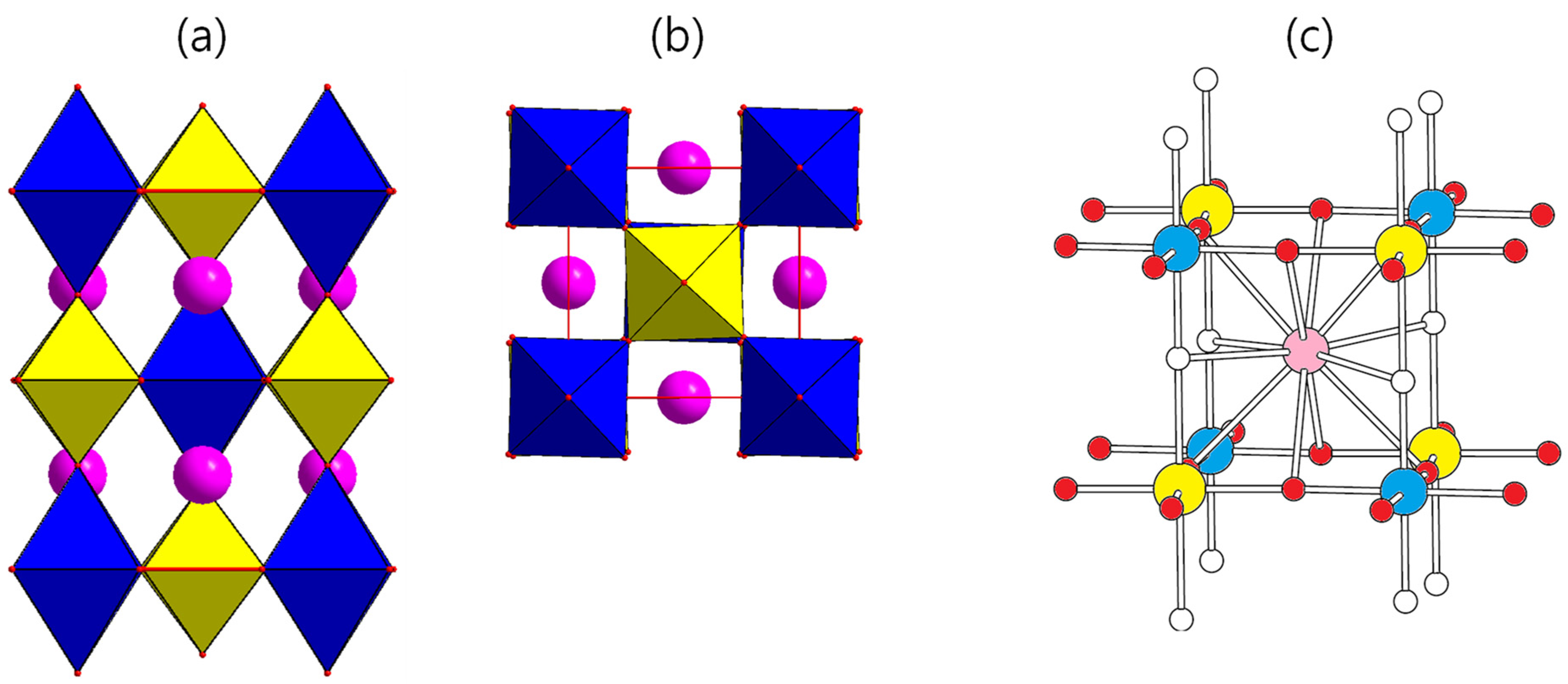
The Ba₂CuOsO₆ crystallizes in a tetragonal space group, I4/m, in which the valence states of the Os and Cu atoms are Os⁶⁺ (d², S = 1) and Cu²⁺ (d⁹, S = 1/2), respectively. The Cu²⁺ and Os⁶⁺ ions are located on the perovskite B-site, and they form the CuO₆ and OsO₆ octahedrons, respectively. They share their corners in all crystallographic directions, such that alternating CuO₆ and OsO₆ run in all three crystallographic directions, as shown in Figure 1. The Ba²⁺ ion is located on the center of the Cu₄Os₄ cube (see Figure 1). With the structural distortion of CuO₆ and OsO₆ octahedrons from the ideal MO₆ octahedron, the Cu-O-Os bridges in the ab plane are bent, whereas those along the c direction are linear, which should be closely related with the orbital splitting and the orbital occupancy.

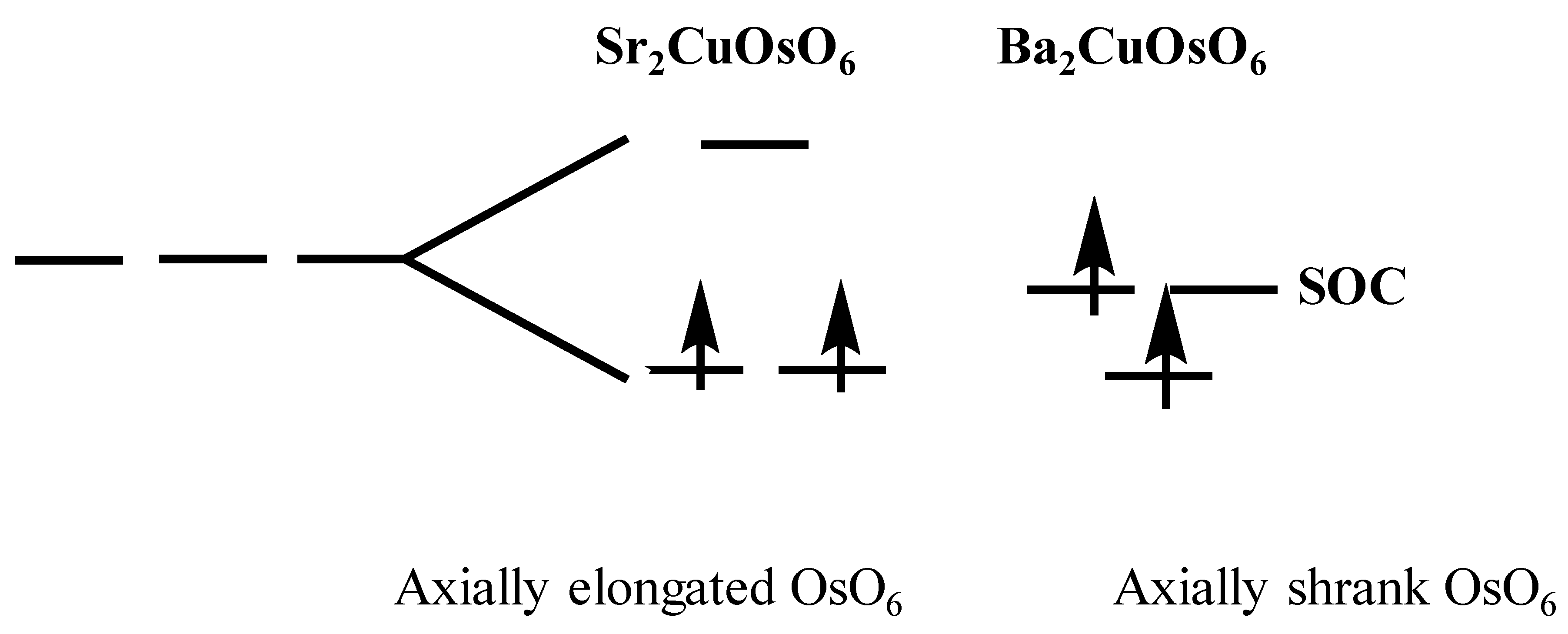
One can easily predict that the axial Cu-O bond is elongated by a strong Jahn–Teller distortion, associated with the electron configuration of the Cu²⁺ (d⁹) ion in each CuO₆ octahedron, with two long Cu-O_ax bonds along the z² orbital direction (crystallographic c direction) and four short equatorial Cu-O bonds in the x²–y² orbital locating plane (the crystallographic ab plane). Besides, in each OsO₆ octahedron, the (t_2g)² electron configuration of the Os⁶⁺ ion exhibits a weak Jahn–Teller distortion, associated with spatial extension of 5d orbital (see Scheme 1). As a consequence, unlike CuO₆ octahedrons, each OsO₆ octahedron is weakly compressed in the axial direction with two short Os-O_ax bonds along the c direction and four elongated Os-O_eq bonds in the ab plane.

Here, we examined the causes of several interesting and seemingly puzzling phenomena, such as the magnetic structures and the origin of the insulating phase in Ba₂CuOsO₆, by performing the DFT, the DFT + U, and the DFT + U + SOC electronic band structure calculations. Then, we studied the spin exchange interactions of Ba₂CuOsO₆ by a relative energy-mapping analysis. The magnetic properties of Ba₂CuOsO₆ were explained by the aspect of their orbital interactions and their spin exchange interactions. The double antiferromagnetic (AFM) anomaly at ~55 K and ~70 K of the susceptibility curve was investigated by analyzing its spin exchange interaction. Finally, we examined the reason for the insulating phase on the basis of the DFT studies and a perturbation theory analysis using ${\widehat{H}}_{soc}$ as perturbation.

2. Computational Details

In our DFT calculations, we employed the frozen-core, projector-augmented wave method [16,17], encoded in the Vienna ab initio simulation package (VASP) [18], and the generalized-gradient approximation of Perdew, Burke, and Ernzerhof [19], for the exchange correlation functional, with the plane-wave cut-off energy of 450 eV and a set of 48 k-points for the irreducible Brillouin zone.

In general, the orbitals of the 5d element are much more diffuse than 3d orbitals, so the U_Os value is expected to be smaller than the U value of Cu. However, in Ba₂CuOsO₆, the oxidation state of Os ion is +6, so that 5d state of Os⁶⁺ ion is strongly contracted. Note that the ionic size of six coordinated Cu²⁺ ions (0.870 Å) is larger than that of six coordinated Os⁶⁺ ions (0.685 Å) [20]. Moreover, the electronegativity of six coordinated Os⁶⁺ and Cu²⁺ ions are 2.362 and 1.372, respectively [21]. Thus, we use the larger U values on the Os⁶⁺ ion than on the Cu²⁺ ion. In our DFT calculation, we employed U value sets of U_Cu = 2, U_Os = 3 eV and U_Cu = 4, U_Os = 5 eV, respectively [22].

The measured electrical resistivity (ρ) vs. temperature of Ba₂CuOsO₆, given in the previous study [15], shows an insulating behavior for all temperature ranges, which means that the insulating behavior of Ba₂CuOsO₆ is an intrinsic nature, not a phenomenon coupled with magnetic ordering. Additionally, Khaliullin et al. suggest that the band gap is developed from excitonic transition from singlet to triplet in the Y₂Os₂O₇ system [4]. The Y₂Os₂O₇ (Os⁴⁺, d⁴) belongs to the van Vleck-type Mott system, showing non-magnetic ground state, due to SOC and weak temperature dependence, such as uniform magnetic susceptibility above Neel temperature. However, magnetic susceptibility curve in Ba₂CuOsO₆ showed Curie–Weiss behavior over a broad temperature range [15], implying that it is not a case of suppressed effective magnetic moment by SOC. Thus, we considered the ferromagnetic (FM) state of Ba₂CuOsO₆ in our DFT + U + SOC calculation, even though this system undergoes the antiferromagnetic ordering. In order to find proper U value set for reproducing the insulating state of Ba₂CuOsO₆, we perform systematic DFT + U + SOC calculations with various U value sets. However, all U sets failed to reproduce the insulating state of Ba₂CuOsO₆ except U value set of U_Cu = 4 and U_Os = 5 eV (see Table S1 and Figure S1). Thereby, we carried out the DFT + U + SOC calculation with the U value set of U_Os = 5 and U_Cu = 4 eV for understanding the origin of the insulating behavior on Ba₂CuOsO₆.

3. Spin Exchange Interaction and Spin Lattice

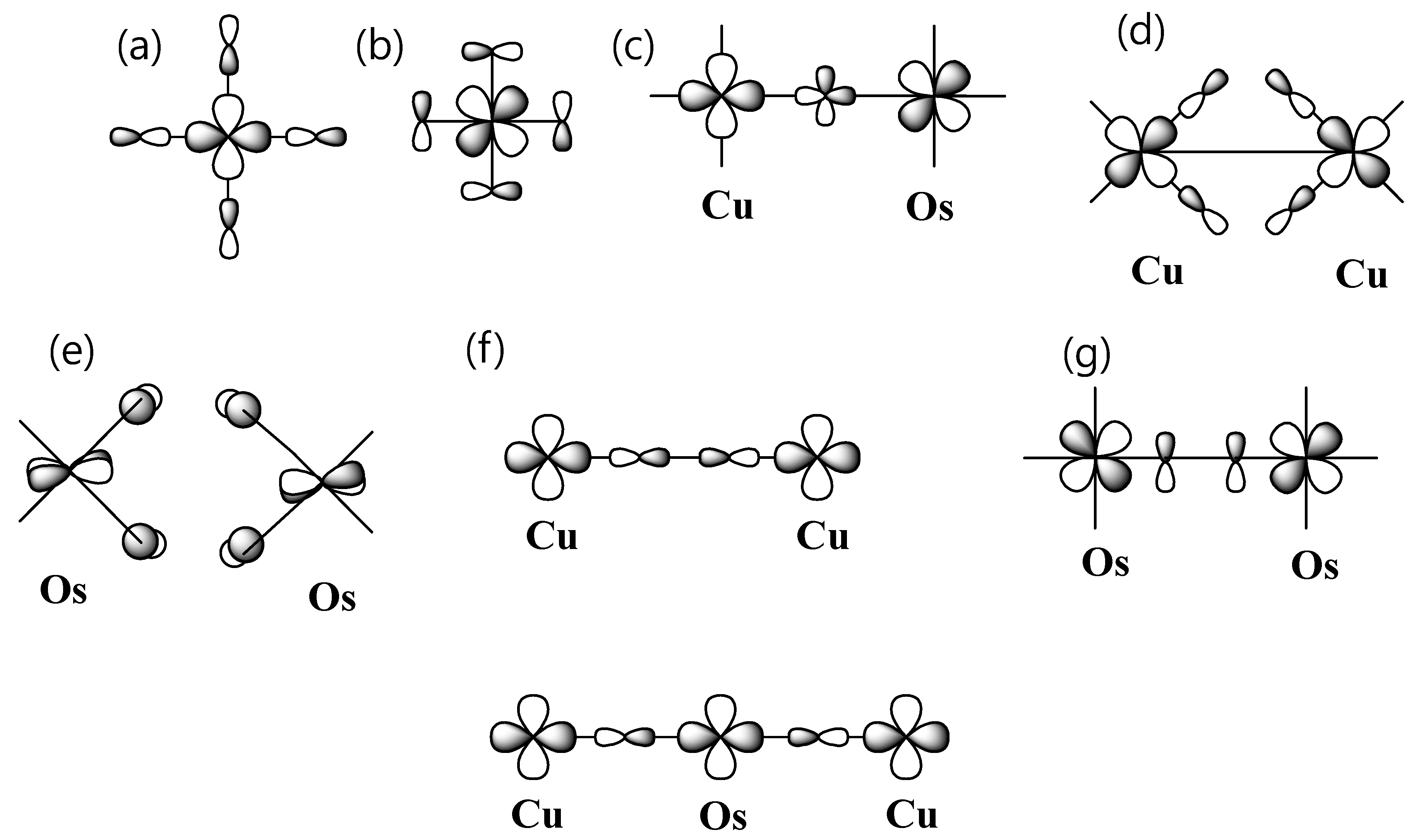
In understanding the magnetic structure of Ba₂CuOsO₆, it is important to inspect its local structure and its following spin exchange paths. Figure 2 shows eight possible spin exchange paths of Ba₂CuOsO₆. There are three spin exchanges between Cu ions, three spin exchanges between Os ions, and two Cu-Os spin exchanges. The J₁ and J₂ are the superexchange (SE) type, involving the Cu-O-Os path, while the J₃–J₈ are super-superexchange (SSE), involving M-O···M-O exchange path (M = Cu or Os). The J₁, J₃, J₄ J₇, and J₈ exchanges are ab plane interactions and the J₂, J₅, and J₆ exchanges are interactions between ab planes. The geometrical parameters associated with these paths are listed in

Table 1. Geometrical parameters associated with the exchange paths J₁–J₈ in Ba₂CuOsO₆; distance (Å); angle (°).

			M-M	Cu-O	Os-O	O-O	∠Cu-O-Os	∠M-O-O-M
J1	Cu-Os	ab plane	3.937	1.986	1.960		172.6
J2	Cu-Os	c-axis	4.256	2.31	1.946		180
J3	Cu-Cu	ab plane	5.568	1.986 (×2)		2.771 (×2)		127.6142.4
J4	Os-Os	ab plane	5.568		1.960	2.808		127.6142.4
J5	Cu-Cu	ac	5.798	1.986 2.310		2.762 (×2)		134.7134.8
J6	Os-Os	ac	5.798			3.047 (×2)
J7	Cu-Cu	ab plane	7.874
J8	Os-Os	ab plane	7.874

.

Let us examine the relationship between the spin exchange interactions J₁–J₈ and the structural parameters associated with their exchange pathways and the spin exchange interactions in a viewpoint of orbital interaction. As mentioned, the CuO₆ and OsO₆ octahedrons are distorted from regular MO₆ octahedrons. The nature of distortion should be explained by the crystal field effect, the Jahn–Teller instability, and the different magnitude of interaction between the Ba²⁺ ion and the MO₆ (M = Os, and Cu) octahedron. The distortion of the CuO₆ and OsO₆ octahedrons plays an important role in the nature and the strength of the spin exchanges. The CuO₆ octahedron is axially elongated and the OsO₆ octahedron is axially shrunk by the Jahn–Teller instability. Thus, the d-orbital sequence of Cu²⁺ ion is xz, yz < xy < z² < x²–y² and the d-orbital splitting of Os⁶⁺ ion is xy < xz,yz < x²–y² < z². As depicted in Figure 3a,b, the magnetic orbitals of Cu²⁺ ion and Os⁶⁺ are singly occupied x²–y² orbital and two orbitals of three t_2g orbitals, respectively. The structural parameters are listed in Table 1. The ∠Cu-O-Os angle in J₁ path is close to 180° (172.6°), so the J₁ exchange should be strong FM, because of orthogonality between Cu x²–y² and Os t_2g orbitals, according to Goodenough’s role [23]. In the J₂ exchange, the Cu-O and Os-O bonds of the Cu-O-Os linkage does not contain magnetic orbitals and the ∠Cu-O-Os angle is 180°. Thus, the Cu²⁺ ion and the Os⁶⁺ ion in the J₂ exchange do not interact. The J₂ exchange interaction should be a very weak interaction. The J₃ exchange is unsymmetrical and the ∠Cu-O···O-Cu angles are 127.6 and 142.4°, which contain magnetic orbitals, indicating possible good orbital overlap between Cu²⁺ ions (see Figure 3d). Thus, we expect that J₃ should be AFM. The geometrical structure of J₄ exchange is almost identical to that of the J₃ exchange. However, the J₄ exchange contains two magnetic orbitals, indicating multiple channel spin exchange interactions, suggesting a presence of a strong orbital overlap via the Os-O···O-Os linkage (Figure 2a). The J₄ spin exchange should have strong AFM because the two magnetic orbitals of the t_2g orbitals can overlap across their O···O contacts, as shown in Figure 3e. The J₅ and J₆ exchanges are the interactions between the adjacent ab layers, and the O···O contact distances of the SSE path J₅ and J₆ are 4.264 Å. The M-O bonds of the M-O···O-M linkage are not located in the magnetic orbital plane. One can predict that the magnetic interaction of J₅ and J₆ exchange path is negligibly weak.

The ∠M-O···O-M angles of the SE paths J₇ and J₈ are close to 180° (172.6°) and the M-O bond of M-O···M-O linkage contains a magnetic orbital. Thus, the spin exchange interaction J₇ and J₈ should have strong AFM. However, the magnitude of the J₇ spin exchange is much stronger than that of J₈. It is due to the fact that the orbital interaction in the J₇ exchange is a π-type orbital interaction, while the orbital interaction in J₈ is a σ-type orbital interaction, as shown in Figure 3f,g.

We extracted the spin exchange interactions using the DFT + U + SOC calculation to elucidate our analysis of the spin exchange interactions in terms of the local geometrical structure and the orbital interaction analysis. To extract the values for the J₁–J₈ exchanges, we carried out a total energy calculation of the nine ordered spin configurations of Ba₂CuOsO₆, shown in Figure 4. To obtain the values of J₁–J₈, we determined the relative energies of the abovementioned cases obtained from the DFT + U + SOC calculations with U_Cu = 2, U_Os = 3 eV and U_Cu = 4, U_Os = 5 eV. The relative energies of various AFM cases obtained are summarized in Figure 4. In terms of the spin Hamiltonian $\widehat{\mathrm{H}}=-{\displaystyle {\sum }_{i<j}}{\mathrm{J}}_{\mathrm{ij}}{\widehat{\mathrm{S}}}_{\mathrm{i}}\cdot {\widehat{\mathrm{S}}}_{\mathrm{j}}$, where J_ij = J₁–J₈, the total spin exchange energies of these states per formula units (FUs) are expressed as follows:

E_spin = (n₁J₁)(MN/4) + n₂J₂(MN/4) + n₃J₃(M²/4) + n₄J₄(N²/4) + n₅J₅(M²/4) + n₆J₆(N²/4) + n₇J₇(M²/4) + n₈J₈(N²/4)

(1)

by using the energy expressions obtained for spin dimers with M and N unpaired spins per spin site (here, M(Cu²⁺) = 1 and N(Os⁶⁺) = 2) [24]. The values of n₁−n₈ for the eight ordered spin states, FM, and AF1–AF8, are described in Table S2.

Thus, by mapping the relative energies of the nine spin arrangements presented in Figure 2 onto corresponding energies expected from Equation (1), we obtain J₁–J₈, as summarized in

Table 2. Values of the spin exchanges J₁–J₈ (in k_BK) of Ba₂CuOsO₆ obtained from the DFT + U + SOC calculations with U_Cu = 2, U_Os = 3 eV and U_Cu = 4, U_Os = 5 eV.

			M-M (Å)	UCu = 2, UOs = 3	UCu = 4, UOs = 5
J1	Cu-Os	ab plane	3.937	92.1	112.0
J2	Cu-Os	c-axis	4.256	−20.0	1.4
J3	Cu-Cu	ab plane	5.568	−81.0	−79.4
J4	Os-Os	ab plane	5.568	−120.9	−247.5
J5	Cu-Cu	ac	5.798	3.3	−4.2
J6	Os-Os	ac	5.798	18.7	7.4
J7	Cu-Cu	ab plane	7.874	−190.8	−291.2
J8	Os-Os	ab plane	7.874	−24.4	−98.7

.

The determined spin exchange interactions, based on the DFT + U + SOC calculation (U = 4 and 5 eV for Cu and Os), show that the relative strength of the spin exchange interactions associated with their strongest interaction, J₇, are |J₁| ≈ 0.385 |J₇|, |J₂| ≈ 0.005 |J₇|, |J₃| ≈ 0.283 |J₇|, |J₄| ≈ 0.850 |J₇|, |J₅| ≈ 0.015 |J₇|, |J₆| ≈ 0.025 |J₇|, and |J₈| ≈ 0.339|J₇|, respectively. This suggests that the magnetic property of Ba₂CuOsO₆ is mainly governed by J₁, J₃, J₄, J₇, and J₈ exchanges, in which all of them are AFM except J₁. The J₁ exchange is an FM interaction, as expected in the previous section. The J₄ and J₇ spin exchanges are much stronger than others. As a consequence, the magnetic property of the Ba₂CuOsO₆ system mainly comes from the J₄ and J₇ spin exchange interactions, which would deduce the existence of magnetic sublattice. In addition, the observed phenomena of two T_max at ~55 K and ~70 K in susceptibility measurement would support such a possibility of magnetic sublattice [15]. The presence of two different magnetic ions in Ba₂CuOsO₆ system should be related with the double AFM-like anomaly at ~55 K and ~70 K. We roughly obtained Neel temperature T_N using a mean field approximation with the extracted spin exchange interactions, based on the DFT + U + SOC calculation (U_Cu = 4 and U_Os = 5 eV). The calculated Neel temperatures for the Cu²⁺ ion and Os⁶⁺ ion sublattices are 256 K and 297 K, respectively. The expected T_N for the Cu and Os sublattices is largely overestimated. The overestimation of the calculated T_N is comprehensible because it is well known that the DFT calculations generally overestimate the magnitude of spin exchange interactions by a factor of, approximately, up to four [25,26,27,28].

Although there is a possibility of spin frustration occurred by (J₁,J₁,J₇), (J₁,J₁,J₈), (J₁,J₁,J₃), (J₁,J₁,J₄), (J₃,J₃,J₇), and (J₄,J₄,J₈) triangles, it does not occur due to the fact that the strong J₄ and J₇ exchanges are forced to avoid spin frustration. This is in good agreement with the experimental result, in which the spin frustration factor (f = |θ|/|T_N|) is just ~0.24, and there is no divergence between the zero-field and field susceptibility curves in Ba₂CuOsO₆ indicating the absence of spin frustration [15]. For a spin frustrated magnetic system, it is generally expected that the ratio, f = |θ|/|T_N|, is greater than 6 [29,30,31]. The spin frustration factor f-value for Ba₂CuOsO₆ system is much lower than this critical value. Thus, the low f-value suggests that the spin frustration is very weak or does not occur in Ba₂CuOsO₆, despite its similar system (Sr₂CuOsO₆, Sr₂CuIrO₆) [32,33] showing strong spin frustration.

In summary, the overall magnetic property of the Ba₂CuOsO₆ system should be explained by AFM, and it does not show spin frustration.

4. Describing the Magnetic Insulating Behavior of Ba₂CuOsO₆

As mentioned in the introduction section, the Ba₂CuOsO₆ system is a magnetic insulator. Feng et al. [15] measured the temperature dependence of resistivity ρ of polycrystalline Ba₂CuOsO₆, in which it showed an insulating behavior at all measured temperature ranges. This reveals that the insulating behavior of Ba₂CuOsO₆ is an intrinsic nature, not a phenomenon coupled with magnetic ordering.

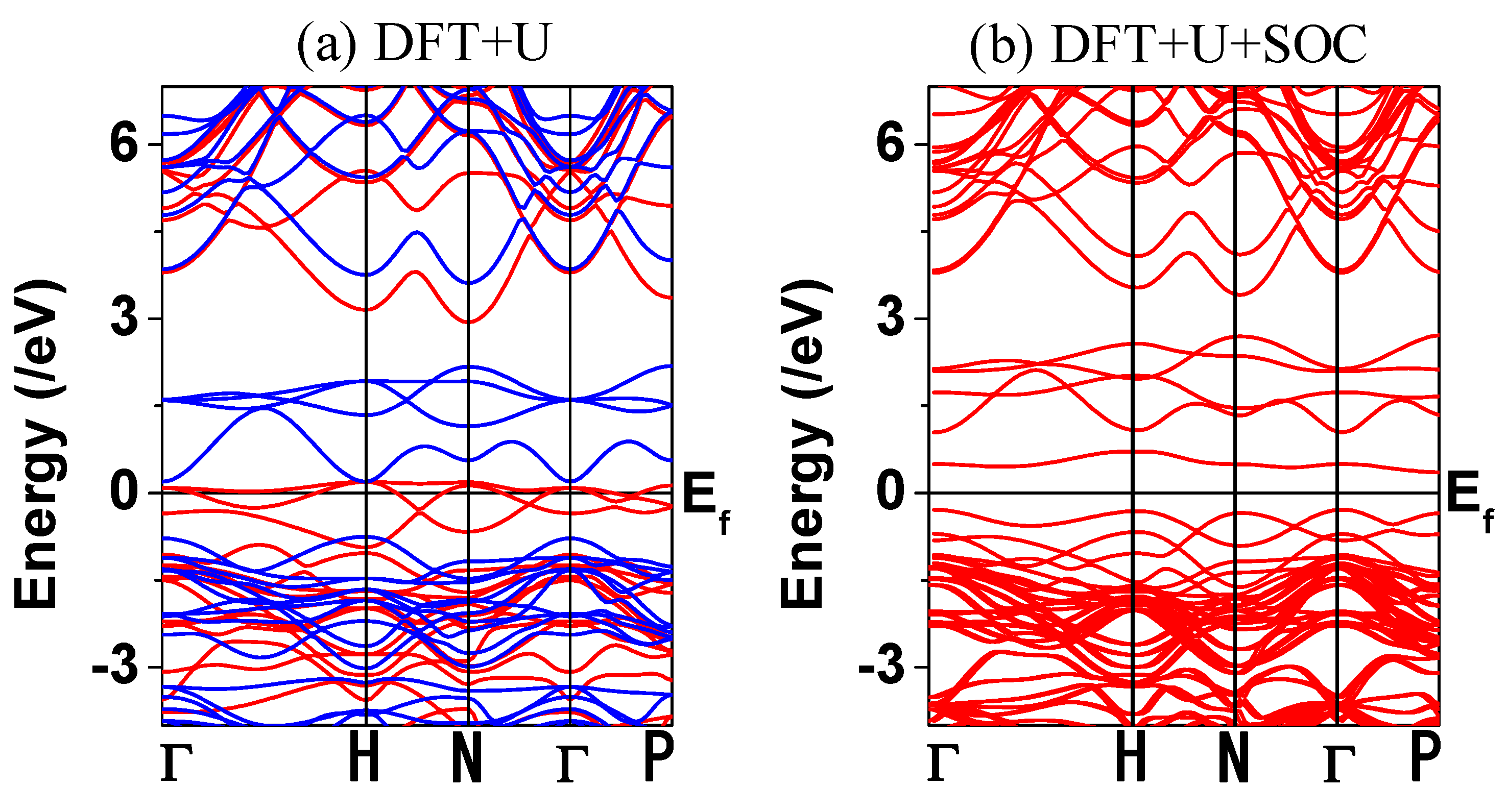
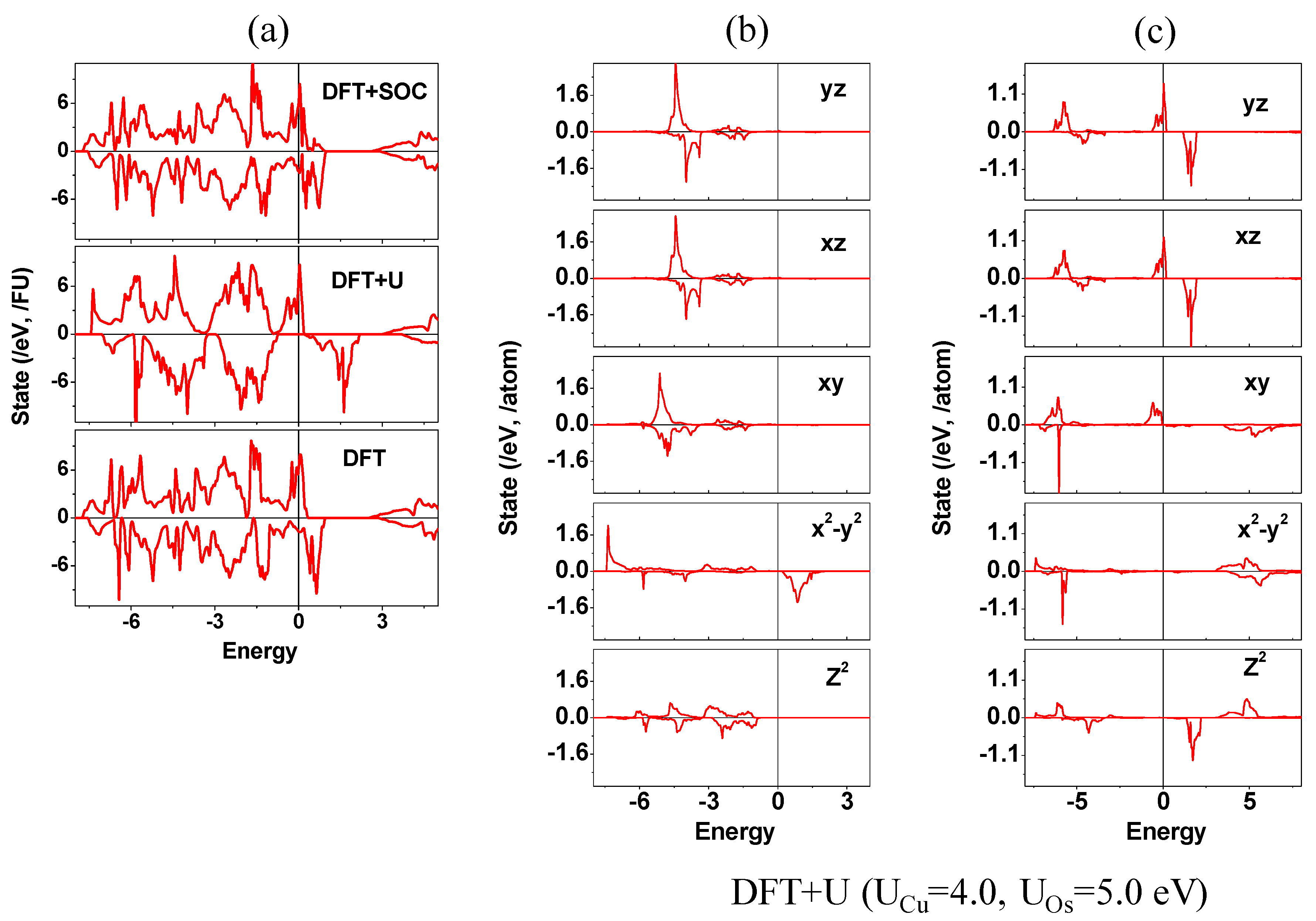
Although they mentioned the origin of the band gap in terms of a theoretical approach, they did not show evidence as well as a discussion for opening the band gap. Here, we discuss the origin of the insulating state of Ba₂CuOsO₆. The calculated electronic structures for Ba₂CuOsO₆ are presented in Figure 5 and Figure 6. The main distribution near the Fermi level comes from the Os⁶⁺ ion rather than the Cu²⁺ ion, which connotes that the Os⁶⁺ 5d states are mainly concerned with the insulating behavior of Ba₂CuOsO₆ (see Figure 5b,c).

For Sr₂CuOsO₆, it should be required to use larger Hubbard value on the Os atom than usual in realizing the magnetic insulating state [13]. Each OsO₆ octahedron with axially elongated OsO₆ octahedron (i.e., Os-O_ax = 1.928 (×2) Å, Os-O_eq = 1.888 (×4) Å) appears slightly distorted, compared with the CuO₆ octahedron, caused by a weak Jahn–Teller instability. Therefore, the Os 5d state of axially elongated OsO₆ octahedron is split into four states (xz,yz < xy < z² < x²–y²) by the Jahn–Teller distortion. Two t_2g electrons in the Os⁶⁺ ion are now occupied to the degeneracy-lifted xz and yz states (see Scheme 1). The band gap is then created by the energy difference between occupied (xz, yz) and unoccupied states (xy). The large Hubbard U value, which enhances the electron correlation effect, is enough to describe the insulating behavior of Sr₂CuOsO₆. On the other hand, each OsO₆ of Ba₂CuOsO₆ has an axially shrunk octahedron, indicating the different types of Os 5d state splitting with Sr₂CuOsO₆. The Os 5d state of Ba₂CuOsO₆ is split into four states (xy < xz,yz < x²–y² < z²). However, the Os 5d state splitting of Ba₂CuOsO₆ is very weak compared to that of Sr₂CuOsO₆, as shown in the Scheme 1 and Figure 5c. Split Os 5d state of Ba₂CuOsO₆ is presented in Figure 5c, in terms of the projected DOS, which shows that the t_2g level of the Os 5d state is very weakly separated into the two states. In the (t_2g)² electron of the Os⁶⁺, one electron is occupied in the lowest xy state, and the remaining electron is occupied in doubly degenerated xz and yz states, as depicted in Scheme 1. Thus, one can predict that the simple DFT and DFT + U approaches are insufficient to describe the magnetic insulating behavior of Ba₂CuOsO₆. The crucial key to describing the insulating behavior of Ba₂CuOsO₆ is in splitting the degenerate xz and yz states of the Os⁶⁺ ion. The SOC effect splits the t_2g state into three substates by the orbital symmetry breaking. Thus, one can speculate that the SOC effect should play an important role in describing the insulating behavior of Ba₂CuOsO₆, thereby it is necessary to consider the SOC effect.

Moreover, since the Os atom belongs to a heavy element group, the SOC effect should be expected to have a dramatically strong effect on the electronic structure of Ba₂CuOsO₆.

The spin–orbital part of the Hamiltonian in the Os sphere is then given by the following:

$${\widehat{H}}_{SOC}=\lambda \widehat{S}\cdot \widehat{L}$$

(2)

where the SOC constant λ > 0 for the Os⁶⁺ (d²) ion, with less than half-filled t_2g levels. With θ and φ as the azimuthal and polar angles of the magnetization in the rectangular crystal coordinate system, respectively, the $\widehat{L}$ and $\widehat{S}$ terms are rewritten [34,35] as follows:

$$\begin{gathered} {\widehat{H}}_{soc}=\lambda {\widehat{S}}_{z^{\prime }}\left({\widehat{L}}_z\cos \theta +\frac{1}{2}{\widehat{L}}_{+}{e}^{-i\varphi }\sin \theta +\frac{1}{2}{\widehat{L}}_{-}{e}^{i\varphi }\sin \theta \right) \\ +\frac{\lambda }{2}{\widehat{S}}_{{+}^{\prime }}\left(-{\widehat{L}}_z\sin \theta -{\widehat{L}}_{+}{e}^{-i\varphi }{\sin }^2\frac{\theta }{2}+{\widehat{L}}_{-}{e}^{i\varphi }{\cos }^2\frac{\theta }{2}\right) \\ +\frac{\lambda }{2}{\widehat{S}}_{{-}^{\prime }}\left(-{\widehat{L}}_z\sin \theta +{\widehat{L}}_{+}{e}^{-i\varphi }{\cos }^2\frac{\theta }{2}-{\widehat{L}}_{-}{e}^{i\varphi }{\sin }^2\frac{\theta }{2}\right) \end{gathered}$$

(3)

Since the spin-up and spin-down t_2g states are separated by the exchange splitting in the first order approximation, there is no need to consider interactions between different spin-up and -down states in SOC. Thus, one simply needs to consider only spin-up parts of t_2g states in using the degenerate perturbation theory, which requires calculation of the matrix elements $i\left|{\widehat{H}}_{so}\right|j$ (i, j = xy, yz, xz) [6]_. For that reason, only the S_z operator term, as in the first line of Equation (3), brings about non-zero matrix elements. In evaluating these matrix elements, it is convenient to rewrite the angular parts of the xy, yz, and xz orbitals in terms of the spherical harmonics [12], as follows:

$$\begin{gathered} d_{xy}=\frac{-i}{\sqrt{2}}\left(Y_2^2-Y_2^2\right) \\ {d}_{yz}=\frac{i}{\sqrt{2}}\left(Y_2^1+Y_2^{-1}\right) \\ {d}_{xz}=\frac{-1}{\sqrt{2}}\left(Y_2^1-Y_2^{-1}\right) \end{gathered}$$

(4)

Using these functions, the matrix representation elements $i\left|{\widehat{H}}_{so}\right|j$ (i, j = xy, yz, xz) are found as follows:

$$\raisebox{1ex}{$i\hslash \lambda $}\!\left/ \!\raisebox{-1ex}{$2$}\right.\left(\begin{array}{ccc}0& sin\theta sin\varphi & -sin\theta sin\varphi \\ -sin\theta sin\varphi & 0& cos\theta \\ sin\theta cos\varphi & -cos\theta & 0\end{array}\right)$$

(5)

By the diagonalization of Equation (5), we obtain eigenvalues of the three spin–orbit coupled states, $E_1=-\hslash \lambda /2$, $E_2=0$, and $E_3=\hslash \lambda /2$. The associated eigenfunctions ${\psi }_1$,${\psi }_2$, and${\psi }_3$ are given [12,34,35] by the following:

$$\begin{array}{l}{\psi }_1=\frac{\sqrt{2}}{2}[sin\theta d_{xy}+\left(isin\varphi -cos\theta cos\varphi \right)d_{yz}-\left(icos\varphi +cos\theta sin\varphi \right)d_{xz}]\\ {\psi }_2=\frac{\sqrt{2}}{2}[sin\theta d_{xy}-\left(isin\varphi +cos\theta cos\varphi \right)d_{yz}+\left(icos\varphi -cos\theta sin\varphi \right)d_{xz}]\\ {\psi }_3=cos\theta d_{xy}+sin\theta cos\varphi d_{yz}+sin\theta sin\varphi d_{xz}\end{array}$$

(6)

The above analysis indicates that the SOC effect splits the t_2g states into three substates by orbital symmetry breaking. For the Os⁶⁺ (d²) ion, two electrons of t_2g state should occupy ${\psi }_1$and${\psi }_2$. Therefore, the band gap around the Fermi level should be developed in between the occupied ${\psi }_2$ and the unoccupied ${\psi }_3$ state.

To elucidate the above discussion, we carried out calculations to reproduce the insulating state of Ba₂CuOsO₆ by employing different theoretical methods, namely, simple DFT, DFT + U (U_Cu = 4, U_Os = 5 eV), and DFT + SOC methods, but all of them failed to reproduce the insulating behavior for Ba₂CuOsO₆ (see Figure 5a). Metallic electronic structures obtained from the DFT and the DFT + U calculations are already expected because the exchange splitting is not enough condition to open the band gap in Ba₂CuOsO₆. However, the electronic structure obtained from the DFT + SOC still failed to reproduce the insulating behavior for Ba₂CuOsO₆ (See Figure 5a). Presented in Figure 3a, the spin-up and spin-down bands are overlapped, which leads to a metallic state for Ba₂CuOsO₆. This means that not only the breaking of orbital symmetry by adapting the SOC effect, but also the separation of energy between the filled level (spin-up) and the empty level (spin-down) by increasing exchange splitting, should be required to describe the insulating state of Ba₂CuOsO₆. On-site repulsion, which properly describes the electron correlation effect, gives help to enhance the exchange splitting; thereby, the energy separation between the filled and the unfilled states within each spin channel is increased. Thus, the on-site repulsion should be also a crucial key to be considered in explaining the insulating state of Ba₂CuOsO₆.

To gain insight into this analysis, we carried out the band structure calculation, considering the electron correlation and the SOC effect simultaneously. The band structure calculated for the FM state of Ba₂CuOsO₆ using the DFT + U + SOC (U_eff = 4 and 5 eV on Cu and Os) is shown in Figure 6b. Indeed, the calculated electronic structure clearly shows an insulating band gap. In consequence, the interplay between the electron correlation and the SOC effect plays an essential role in opening a band gap for Ba₂CuOsO₆.

Meanwhile, there remains one question about the origin of the band gap opening in Ba₂CuOsO₆. The insulating behavior of Ba₂CuOsO₆ is intimately linked with the structural distortion of the OsO₆ octahedron. We remind that the OsO₆ octahedron for Ba₂CuOsO₆ is an axially compressed octahedral shape, while the OsO₆ octahedron of Sr₂CuOsO₆ is an axially elongated octahedral shape. This implies that they undergo different types of structural distortion by the Jahn–Teller instability, which leads to different orbital splitting at the Os⁶⁺ t_2g level. Thus, they show different chemical and physical properties, especially in explaining the mechanism of band gap opening. The only difference between Sr₂CuOsO₆ and Ba₂CuOsO₆ is an ionic size of the A-site ion, namely, the ionic size of the Ba²⁺ ion is larger than that of the Sr²⁺ ion. In A₂CuOsO₆ (A = Sr and Ba), the A-site ion is located in the center of Cu₄Os₄ distorted cubes and distorted (O_ax)₄ squares, presented in Figure 1c. It is connected with 8 O_eq and 4 O_ax atoms to form a 12-coordinate AO₁₂ (see Figure 1c). In A₂CuOsO₆, a change in the A-O_eq distance affects a, b, and c lattice parameters symmetrically; whereas, a change of A-O_ax distance affects the lattice parameter a (=b). Assuming that the increase of the A-O_ax distance leads to structural distortion forming axially shrunk type-OsO₆ octahedrons, by increasing the Os-O_eq distance in the ab plane, while the decrease of the A-O_ax distance causes structural distortion to have axially elongated OsO₆ octahedrons by decreasing the Os-O_eq distance. The A-O_ax distance should be mainly dominated by the ionic size of the A-site ion. Since the ionic size of the Ba²⁺ ion is larger than that of the Sr²⁺ ion, the Ba-O_ax distance is longer than the Sr-O_ax distance, which gives rise to a much longer Os-O_eq distance on Ba₂CuOsO₆, associated with the expansion of its lattice parameter a (=b). On the other hand, the effect of ionic size of the A-site on the change of the Os-O_ax distance is relatively insignificant. Indeed, the Os-O_eq distances in Ba₂CuOsO₆ and Sr₂CuOsO₆ are 1.960 and 1.888 Å, respectively, while the Os-O_ax distances in Ba₂CuOsO₆ and Sr₂CuOsO₆ are 1.928 Å and 1.946 Å, respectively [15,33]. Hence, the ionic size of the A-site ion should play an important role in determining the shape of the OsO₆ octahedron in A₂CuOsO₆.

To verify the importance of the ionic size effect, we examine the aforementioned questions with the DFT + U + SOC (U_Cu = 4, U_Os = 5 eV) calculation for Ba₂CuOsO₆. We imagine the hypothetical compounds of A₂CuOsO₆ (A = Sr, Ca) by replacing the Ba atoms of Ba₂CuOsO₆ with other alkali earth atoms—Sr and Ca. A₂CuOsO₆ (A = Ba, Sr, and Ca) are fully optimized with the DFT + U + SOC (U_Cu = 4, U_Os = 5 eV) calculation. The optimized atomic positions and cell parameters are presented in the Supplementary Materials, Table S3. Results show that the lattice parameters decrease gradually with the decreasing ionic size of the A-site ion, but the decreasing of the a lattice parameter is greater than that of the c lattice parameter, which means that each Os-O_eq distance is increased as the A-site ionic size increases. Therefore, the cooperative effect of the A-site ionic size and the Jahn–Teller distortion, is responsible not only for the axially compressed OsO₆ octahedrons in Ba₂CuOsO₆ but also for the axial elongation of OsO₆ octahedrons in Sr₂CuOsO₆; this is closely related to the description of the insulating behavior of A₂CuOsO₆ (A = Ba, Sr, and Ca).

5. Concluding Remarks

The magnetic structure and the origin of the band gap opening for Ba₂CuOsO₆ are investigated by exploring the spin exchange interactions and analyzing the spin–orbit coupling effect. The magnetic property of Ba₂CuOsO₆ is explained by AFM, and it does not show spin frustration caused by the strong AFM interactions of J₄ and J₇. The structural distortion shape of the OsO₆ octahedron, which should be closely connected with the ionic size of the A-site ion, is an important factor in understanding the insulating behavior of Ba₂CuOsO₆. Each OsO₆ octahedron of Sr₂CuOsO₆ displays an axially elongated octahedral shape, while each OsO₆ octahedron of Ba₂CuOsO₆ exhibits an axially compressed octahedral shape, which is caused by an ionic size effect of the A-site ion. Therefore, the t_2g level splitting of the Os⁶⁺ ions of Ba₂CuOsO₆ and Sr₂CuOsO₆ by the Jahn–Teller instability is differently depicted in Scheme 1. Consequently, to explain the magnetic insulating states of Sr₂CuOsO₆, which are isostructural and isoelectronic in Ba₂CuOsO₆, it is necessary to properly employ an electron correlation effect. On the other hand, a cooperative effect of electron correlation and spin–orbit coupling is essential in describing the insulating behavior of Ba₂CuOsO₆, which is highly related with the t_2g orbital splitting of the Os⁶⁺ ion.