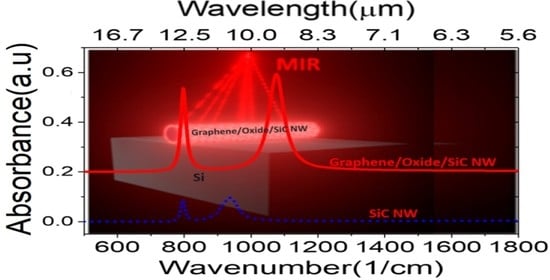
Enhanced Absorption with Graphene-Coated Silicon Carbide Nanowires for Mid-Infrared Nanophotonics
Abstract
:1. Introduction
2. Materials and Methods
2.1. Numerical Simulations
2.2. Graphene Growth and Experimental Characterization
3. Results
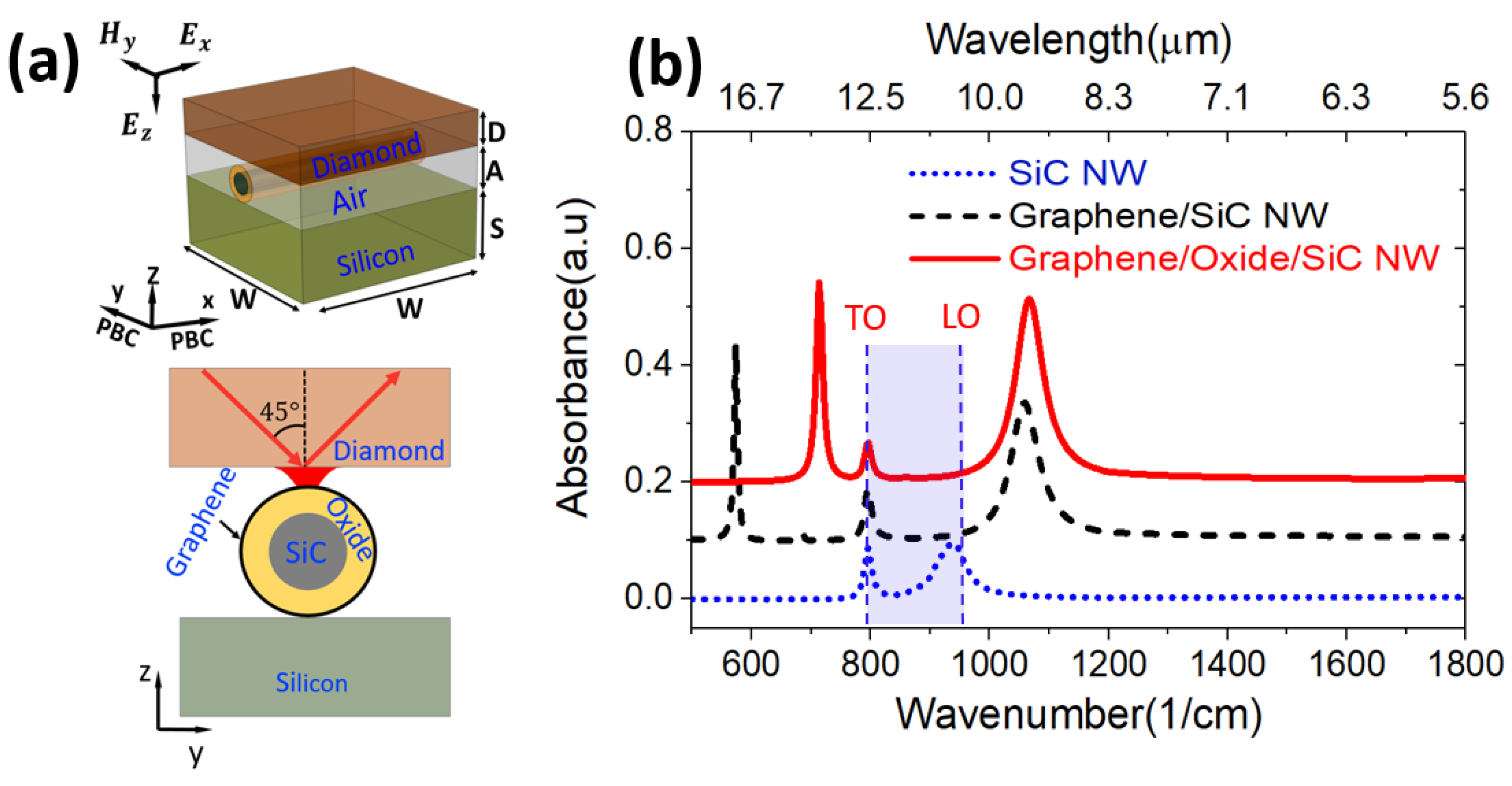
3.1. Simulation Results
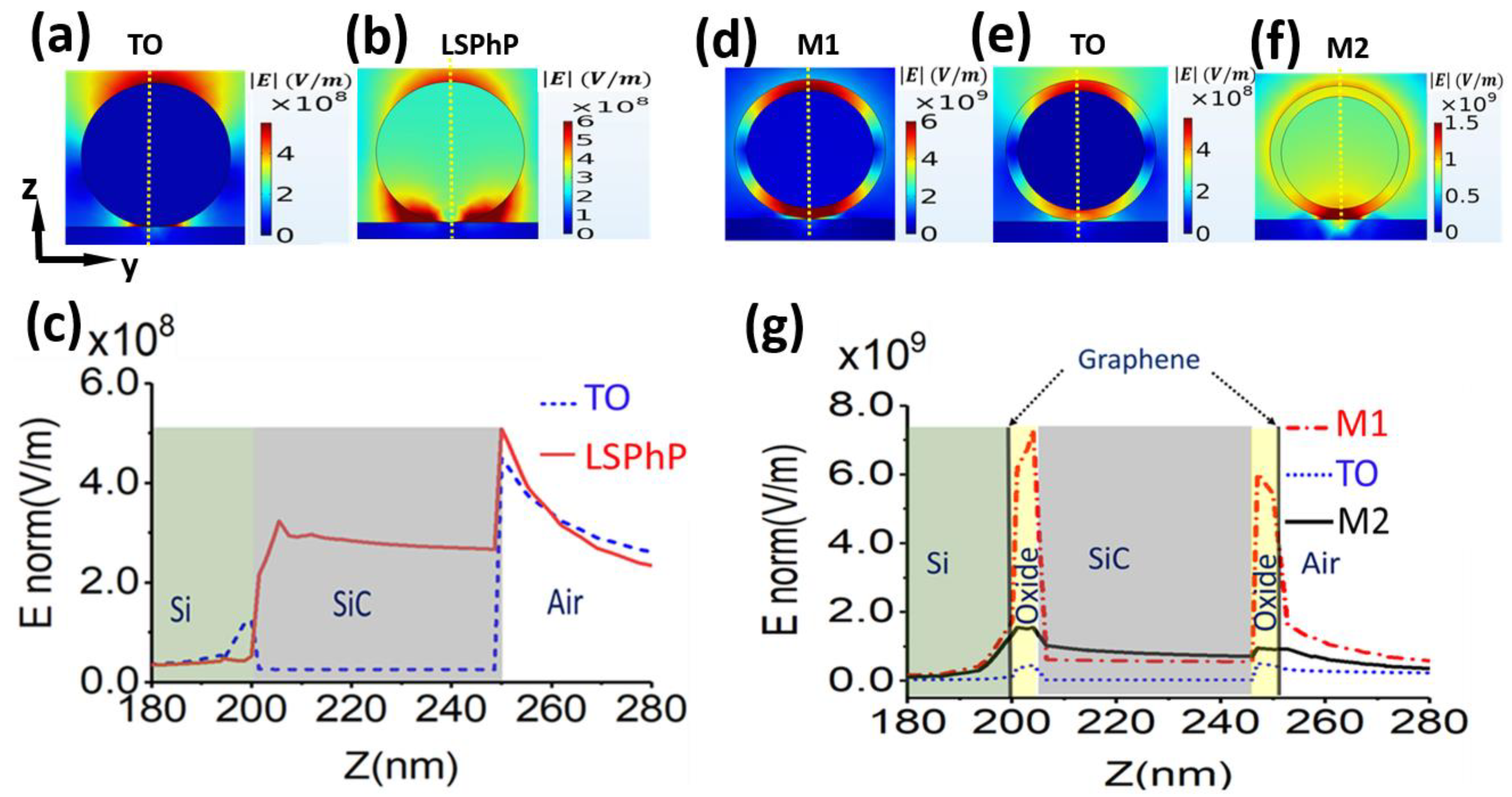
3.1.1. Modes and Electric Fields Analysis
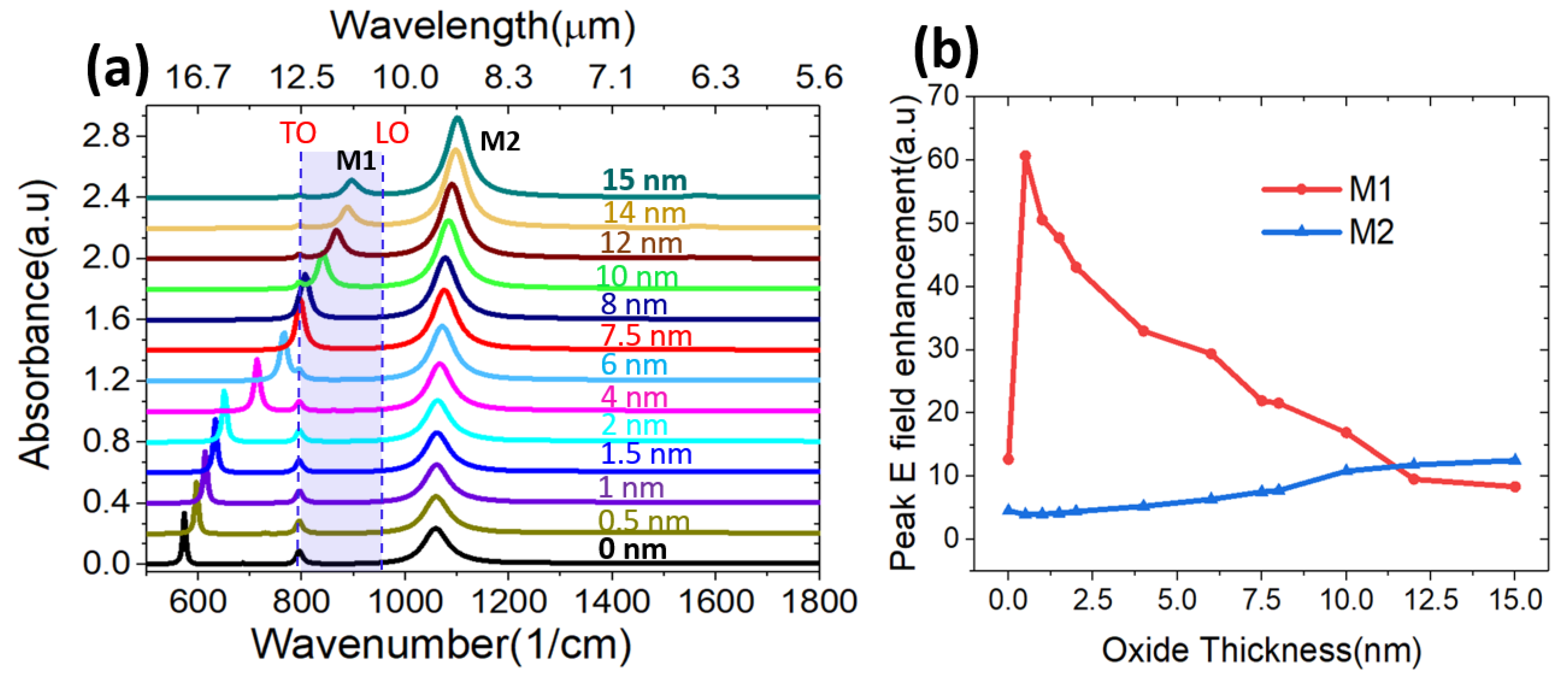
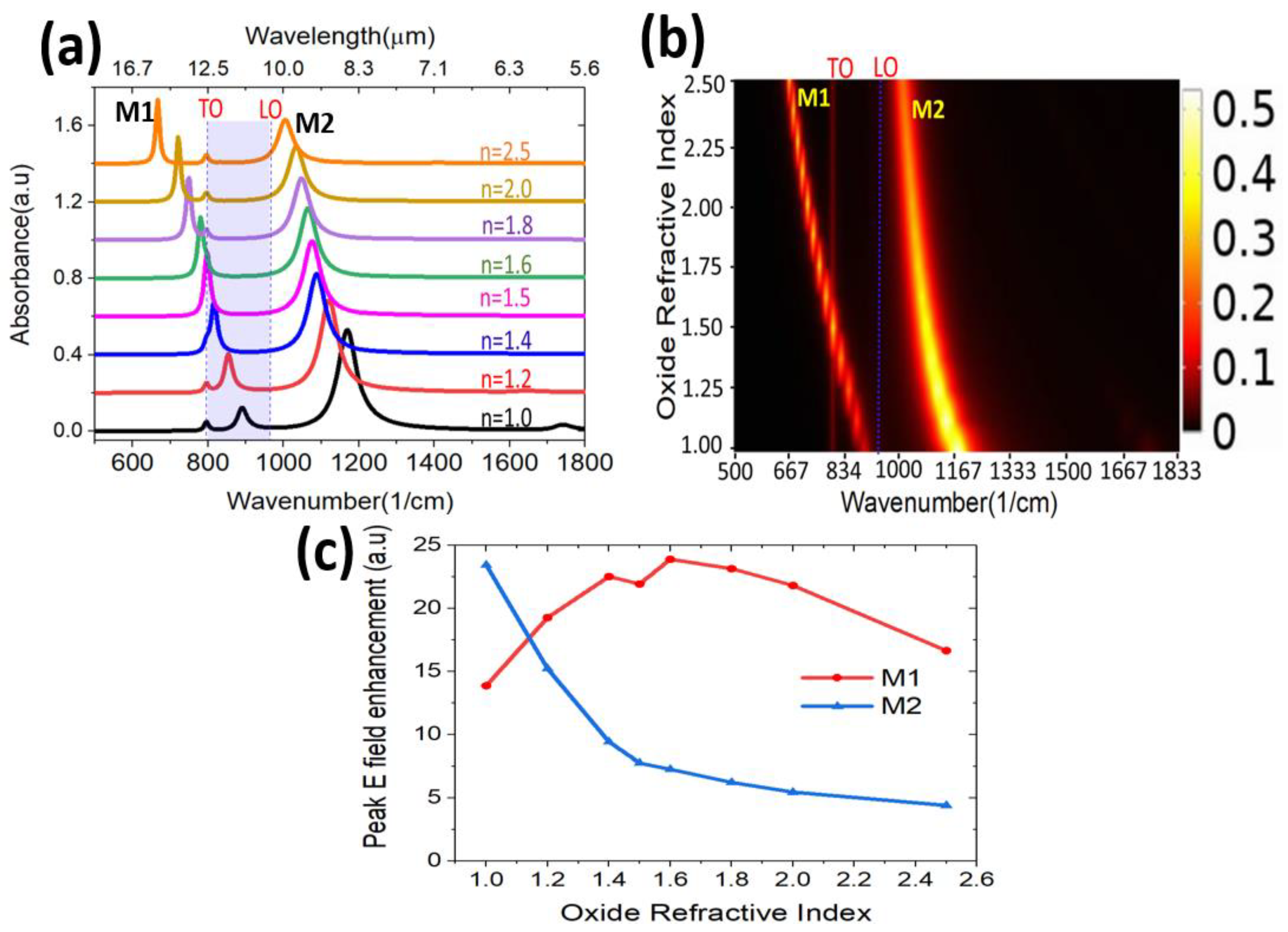
3.1.2. The Roles of the Oxide Shell Thickness and Refractive Index on the MIR Response of the System
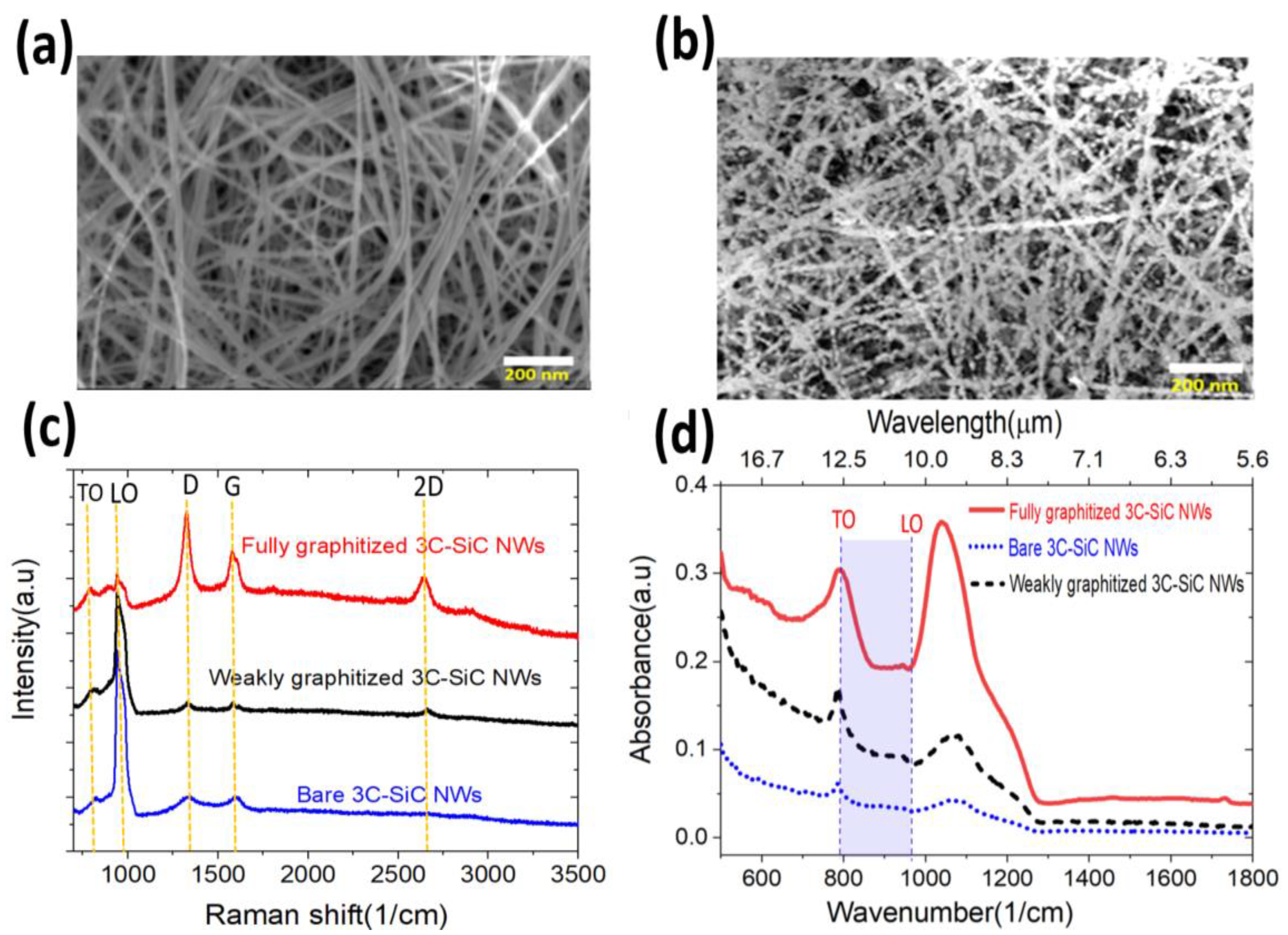
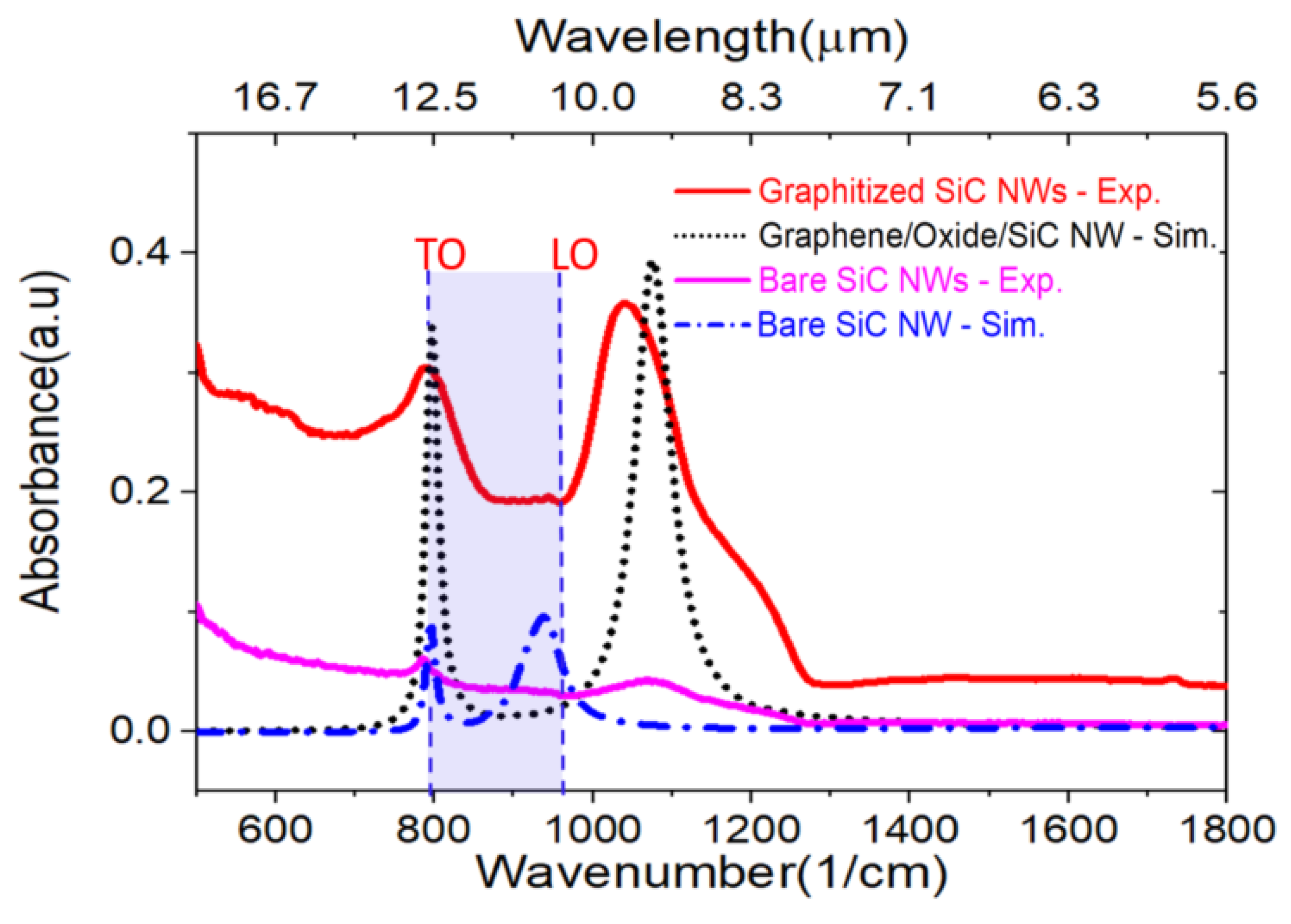
3.2. Experimental Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huth, F.; Govyadinov, A.; Amarie, S.; Nuansing, W.; Keilmann, F.; Hillenbrand, R. Nano-FTIR absorption spectroscopy of molecular fingerprints at 20 nm spatial resolution. Nano Lett. 2012, 12, 3973–3978. [Google Scholar] [CrossRef] [PubMed]
- Petersen, C.R.; Møller, U.; Kubat, I.; Zhou, B.; Dupont, S.; Ramsay, J.; Benson, T.; Sujecki, S.; Abdel-Moneim, N.; Tang, Z. Mid-infrared supercontinuum covering the 1.4–13.3 μm molecular fingerprint region using ultra-high NA chalcogenide step-index fibre. Nat. Photonics 2014, 8, 830–834. [Google Scholar] [CrossRef]
- Jackson, S.D. Towards high-power mid-infrared emission from a fibre laser. Nat. Photonics 2012, 6, 423–431. [Google Scholar] [CrossRef]
- Huang, L.; Dong, B.; Guo, X.; Chang, Y.; Chen, N.; Huang, X.; Liao, W.; Zhu, C.; Wang, H.; Lee, C. Waveguide-integrated black phosphorus photodetector for mid-infrared applications. ACS Nano 2018, 13, 913–921. [Google Scholar] [CrossRef]
- Selvaraj, R.; Vasa, N.J.; Nagendra, S.; Mizaikoff, B. Advances in Mid-Infrared Spectroscopy-Based Sensing Techniques for Exhaled Breath Diagnostics. Molecules 2020, 25, 2227. [Google Scholar] [CrossRef]
- Thämer, M.; De Marco, L.; Ramasesha, K.; Mandal, A.; Tokmakoff, A. Ultrafast 2D IR spectroscopy of the excess proton in liquid water. Science 2015, 350, 78–82. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fernandez, D.C.; Bhargava, R.; Hewitt, S.M.; Levin, I.W. Infrared spectroscopic imaging for histopathologic recognition. Nat. Biotechnol. 2005, 23, 469–474. [Google Scholar] [CrossRef]
- Bareza, N.J.; Gopalan, K.K.; Alani, R.; Paulillo, B.; Pruneri, V. Mid-infrared Gas. Sensing Using Graphene Plasmons Tuned by Reversible Chemical Doping. ACS Photonics 2020, 7, 879–884. [Google Scholar] [CrossRef] [Green Version]
- Low, T.; Avouris, P. Graphene plasmonics for terahertz to mid-infrared applications. ACS Nano 2014, 8, 1086–1101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bao, Q.; Loh, K.P. Graphene photonics, plasmonics, and broadband optoelectronic devices. ACS Nano 2012, 6, 3677–3694. [Google Scholar] [CrossRef]
- Garcia de Abajo, F.J. Graphene plasmonics: Challenges and opportunities. Acs Photonics 2014, 1, 135–152. [Google Scholar] [CrossRef] [Green Version]
- Grigorenko, A.N.; Polini, M.; Novoselov, K.S. Graphene plasmonics. Nat. Photonics 2012, 6, 749. [Google Scholar] [CrossRef]
- Liu, M.; Yin, X.; Zhang, X. Double-layer graphene optical modulator. Nano Lett. 2012, 12, 1482–1485. [Google Scholar] [CrossRef] [PubMed]
- Xia, F.; Mueller, T.; Lin, Y.-m.; Valdes-Garcia, A.; Avouris, P. Ultrafast graphene photodetector. Nat. Nanotechnol. 2009, 4, 839. [Google Scholar] [CrossRef] [Green Version]
- Mueller, T.; Xia, F.; Avouris, P. Graphene photodetectors for high-speed optical communications. Nat. Photonics 2010, 4, 297. [Google Scholar] [CrossRef] [Green Version]
- Ni, G.; Wang, L.; Goldflam, M.; Wagner, M.; Fei, Z.; McLeod, A.; Liu, M.; Keilmann, F.; Özyilmaz, B.; Neto, A.C. Ultrafast optical switching of infrared plasmon polaritons in high-mobility graphene. Nat. Photonics 2016, 10, 244–247. [Google Scholar] [CrossRef] [Green Version]
- Fang, Z.; Liu, Z.; Wang, Y.; Ajayan, P.M.; Nordlander, P.; Halas, N.J. Graphene-antenna sandwich photodetector. Nano Lett. 2012, 12, 3808–3813. [Google Scholar] [CrossRef]
- Ono, M.; Hata, M.; Tsunekawa, M.; Nozaki, K.; Sumikura, H.; Chiba, H.; Notomi, M. Ultrafast and energy-efficient all-optical switching with graphene-loaded deep-subwavelength plasmonic waveguides. Nat. Photonics 2020, 14, 37–43. [Google Scholar] [CrossRef] [Green Version]
- Rodrigo, D.; Limaj, O.; Janner, D.; Etezadi, D.; De Abajo, F.J.G.; Pruneri, V.; Altug, H. Mid-infrared plasmonic biosensing with graphene. Science 2015, 349, 165–168. [Google Scholar] [CrossRef] [Green Version]
- Bao, Q.; Zhang, H.; Wang, B.; Ni, Z.; Lim, C.H.Y.X.; Wang, Y.; Tang, D.Y.; Loh, K.P. Broadband graphene polarizer. Nat. Photonics 2011, 5, 411–415. [Google Scholar] [CrossRef]
- Caldwell, J.D.; Lindsay, L.; Giannini, V.; Vurgaftman, I.; Reinecke, T.L.; Maier, S.A.; Glembocki, O.J. Low-loss, infrared and terahertz nanophotonics using surface phonon polaritons. Nanophotonics 2015, 4, 44–68. [Google Scholar] [CrossRef] [Green Version]
- Gan, X.; Shiue, R.-J.; Gao, Y.; Meric, I.; Heinz, T.F.; Shepard, K.; Hone, J.; Assefa, S.; Englund, D. Chip-integrated ultrafast graphene photodetector with high responsivity. Nat. Photonics 2013, 7, 883. [Google Scholar] [CrossRef]
- Qiang, B.; Dubrovkin, A.M.; Krishnamoorthy, H.N.; Wang, Q.; Zheludev, N.I.; Wang, Q.J. Germanium-on-Carborundum Surface Phonon-Polariton Infrared Metamaterial. Adv. Opt. Mater. 2020, 9, 2001652. [Google Scholar] [CrossRef]
- Echtermeyer, T.; Britnell, L.; Jasnos, P.; Lombardo, A.; Gorbachev, R.; Grigorenko, A.; Geim, A.; Ferrari, A.C.; Novoselov, K. Strong plasmonic enhancement of photovoltage in graphene. Nat. Commun. 2011, 2, 458. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, Y.; Willis, R.F. Plasmon-phonon strongly coupled mode in epitaxial graphene. Phys. Rev. B 2010, 81, 081406. [Google Scholar] [CrossRef] [Green Version]
- Dai, S.; Ma, Q.; Liu, M.; Andersen, T.; Fei, Z.; Goldflam, M.; Wagner, M.; Watanabe, K.; Taniguchi, T.; Thiemens, M. Graphene on hexagonal boron nitride as a tunable hyperbolic metamaterial. Nat. Nanotechnol. 2015, 10, 682. [Google Scholar] [CrossRef]
- Mishra, N.; Boeckl, J.; Motta, N.; Iacopi, F. Graphene growth on silicon carbide: A review. Phys. Status Solidi A 2016, 213, 2277–2289. [Google Scholar] [CrossRef]
- Berger, C.; Song, Z.; Li, T.; Li, X.; Ogbazghi, A.Y.; Feng, R.; Dai, Z.; Marchenkov, A.N.; Conrad, E.H.; First, P.N. Ultrathin epitaxial graphite: 2D electron gas properties and a route toward graphene-based nanoelectronics. J. Phys. Chem. B 2004, 108, 19912–19916. [Google Scholar] [CrossRef] [Green Version]
- Hwang, E.; Sensarma, R.; Sarma, S.D. Plasmon-phonon coupling in graphene. Phys. Rev. B 2010, 82, 195406. [Google Scholar] [CrossRef] [Green Version]
- Li, K.; Fitzgerald, J.M.; Xiao, X.; Caldwell, J.D.; Zhang, C.; Maier, S.A.; Li, X.; Giannini, V. Graphene Plasmon Cavities Made with Silicon Carbide. ACS Omega 2017, 2, 3640–3646. [Google Scholar] [CrossRef]
- Xiao, X.; Li, X.; Caldwell, J.D.; Maier, S.A.; Giannini, V. Theoretical analysis of graphene plasmon cavities. Appl. Mater. Today 2018, 12, 283–293. [Google Scholar] [CrossRef]
- Rufangura, P.; Folland, T.G.; Agrawal, A.; Caldwell, J.D.; Iacopi, F. Towards low-loss on-chip nanophotonics with coupled graphene and silicon carbide: A review. J. Phys. Mater. 2020, 3, 032005. [Google Scholar] [CrossRef]
- Iacopi, F.; Mishra, N.; Cunning, B.V.; Goding, D.; Dimitrijev, S.; Brock, R.; Dauskardt, R.H.; Wood, B.; Boeckl, J. A catalytic alloy approach for graphene on epitaxial SiC on silicon wafers. J. Mater. Res. 2015, 30, 609–616. [Google Scholar] [CrossRef] [Green Version]
- Pradeepkumar, A.; Amjadipour, M.; Mishra, N.; Liu, C.; Fuhrer, M.S.; Bendavid, A.; Isa, F.; Zielinski, M.; Sirikumara, H.I.; Jayasekara, T.; et al. p-Type Epitaxial Graphene on Cubic Silicon Carbide on Silicon for Integrated Silicon Technologies. ACS Appl. Nano Mater. 2019, 3, 830–841. [Google Scholar] [CrossRef] [Green Version]
- Coleman, D.; Mangolini, L. Plasmonic Core–Shell Silicon Carbide–Graphene Nanoparticles. ACS Omega 2019, 4, 10089–10093. [Google Scholar] [CrossRef]
- Mishra, N.; Bosi, M.; Rossi, F.; Salviati, G.; Boeckl, J.; Iacopi, F. Growth of graphitic carbon layers around silicon carbide nanowires. J. Appl. Phys. 2019, 126, 065304. [Google Scholar] [CrossRef]
- Larin, A.; Sun, Y.; Zuev, D. Numerical design of Au/Si core-shell nanoparticles. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2018. [Google Scholar]
- Lv, W.; Phelan, P.E.; Swaminathan, R.; Otanicar, T.P.; Taylor, R.A. Multifunctional core-shell nanoparticle suspensions for efficient absorption. J. Sol. Energy Eng. 2013, 135, 021004. [Google Scholar] [CrossRef]
- Xu, H. Multilayered metal core-shell nanostructures for inducing a large and tunable local optical field. Phys. Rev. B 2005, 72, 073405. [Google Scholar] [CrossRef] [Green Version]
- Paria, D.; Zhang, C.; Barman, I. Towards rational design and optimization of near-field enhancement and spectral tunability of hybrid core-shell plasmonic nanoprobes. Sci. Rep. 2019, 9, 16071. [Google Scholar] [CrossRef] [Green Version]
- Wu, W.; Wan, M.; Gu, P.; Chen, Z.; Wang, Z. Strong coupling between few molecular excitons and Fano-like cavity plasmon in two-layered dielectric-metal core-shell resonators. Opt. Express 2017, 25, 1495–1504. [Google Scholar] [CrossRef]
- Khlebtsov, N.G.; Lin, L.; Khlebtsov, B.N.; Ye, J. Gap-enhanced Raman tags: Fabrication, optical properties, and theranostic applications. Theranostics 2020, 10, 2067. [Google Scholar] [CrossRef] [PubMed]
- N’Diaye, J.; Hmam, O.; Zidi, M.; Tavares, A.C.; Izquierdo, R.; Szkopek, T.; Siaj, M. One-Step In-Situ Growth of Core–Shell SiC@ Graphene Nanoparticles/Graphene Hybrids by Chemical Vapor Deposition. Adv. Mater. Interfaces 2016, 3, 1500806. [Google Scholar] [CrossRef]
- Chen, Z.; Zhou, M.; Cao, Y.; Ai, X.; Yang, H.; Liu, J. In situ generation of few-layer graphene coatings on SnO2-SiC core-shell nanoparticles for high-performance lithium-ion storage. Adv. Energy Mater. 2012, 2, 95–102. [Google Scholar] [CrossRef]
- Bhardwaj, S.; Uma, R.; Sharma, R. A study of metal@ graphene core–shell spherical nano-geometry to enhance the SPR tunability: Influence of graphene monolayer shell thickness. Plasmonics 2017, 12, 961–969. [Google Scholar] [CrossRef]
- Li, Y.; He, X.; Wan, M.; Wu, W.; Chen, Z. Unconventional Fano effect based spectrally selective absorption enhancement in graphene using plasmonic core-shell nanostructures. Appl. Phys. Lett. 2016, 109, 031909. [Google Scholar] [CrossRef] [Green Version]
- Christensen, T.; Jauho, A.-P.; Wubs, M.; Mortensen, N.A. Localized plasmons in graphene-coated nanospheres. Phys. Rev. B 2015, 91, 125414. [Google Scholar] [CrossRef] [Green Version]
- Song, J.; Cheng, Q.; Luo, Z.; Zhou, X.; Zhang, Z. Modulation and splitting of three-body radiative heat flux via graphene/SiC core-shell nanoparticles. Int. J. Heat Mass Transf. 2019, 140, 80–87. [Google Scholar] [CrossRef]
- Multiphysics, C. User’s Guide; release 5.2 A; COMSOL Inc.: Burlington, MA, USA, 2016. [Google Scholar]
- Memon, F.A.; Morichetti, F.; Melloni, A. Silicon Oxycarbide Waveguides for Photonic Applications. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2018. [Google Scholar]
- Temple, P.A.; Hathaway, C. Multiphonon Raman spectrum of silicon. Phys. Rev. B 1973, 7, 3685. [Google Scholar] [CrossRef]
- Mishra, N.; Boeckl, J.J.; Tadich, A.; Jones, R.T.; Pigram, P.J.; Edmonds, M.; Fuhrer, M.S.; Nichols, B.M.; Iacopi, F. Solid source growth of graphene with Ni–Cu catalysts: Towards high quality in situ graphene on silicon. J. Phys. D Appl. Phys. 2017, 50, 095302. [Google Scholar] [CrossRef] [Green Version]
- Negri, M.; Dhanabalan, S.; Attolini, G.; Lagonegro, P.; Campanini, M.; Bosi, M.; Fabbri, F.; Salviati, G. Tuning the radial structure of core—Shell silicon carbide nanowires. CrystEngComm 2015, 17, 1258–1263. [Google Scholar] [CrossRef]
- Tzarouchis, D.; Sihvola, A. Light scattering by a dielectric sphere: Perspectives on the Mie resonances. Appl. Sci. 2018, 8, 184. [Google Scholar] [CrossRef] [Green Version]
- Raad, S.H.; Atlasbaf, Z. Equivalent RLC ladder circuit for scattering by graphene-coated nanospheres. IEEE Trans. Nanotechnol. 2019, 18, 212–219. [Google Scholar] [CrossRef]
- Barchiesi, D.; Otto, A. Excitations of surface plasmon polaritons by attenuated total reflection, revisited. Riv. Nuovo Cim. 2013, 36, 173–209. [Google Scholar]
- Lee, I.-H.; Yoo, D.; Avouris, P.; Low, T.; Oh, S.-H. Graphene acoustic plasmon resonator for ultrasensitive infrared spectroscopy. Nat. Nanotechnol. 2019, 14, 313. [Google Scholar] [CrossRef] [PubMed]
- Lin, H.; Sturmberg, B.C.; Lin, K.-T.; Yang, Y.; Zheng, X.; Chong, T.K.; de Sterke, C.M.; Jia, B. A 90-nm-thick graphene metamaterial for strong and extremely broadband absorption of unpolarized light. Nat. Photonics 2019, 13, 270–276. [Google Scholar] [CrossRef]
- Aksyanov, I.; Kompan, M.; Kul’kova, I. Raman scattering in mosaic silicon carbide films. Phys. Solid State 2010, 52, 1850–1854. [Google Scholar] [CrossRef]
- Pan, Q.; Tong, N.; He, N.; Liu, Y.; Shim, E.; Pourdeyhimi, B.; Gao, W. Electrospun mat of poly (vinyl alcohol)/graphene oxide for superior electrolyte performance. ACS Appl. Mater. Interfaces 2018, 10, 7927–7934. [Google Scholar] [CrossRef] [PubMed]
- Sarkar, S.; Raul, K.; Pradhan, S.; Basu, S.; Nayak, A. Magnetic properties of graphite oxide and reduced graphene oxide. Phys. E Low-Dimens. Syst. Nanostruct. 2014, 64, 78–82. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rufangura, P.; Khodasevych, I.; Agrawal, A.; Bosi, M.; Folland, T.G.; Caldwell, J.D.; Iacopi, F. Enhanced Absorption with Graphene-Coated Silicon Carbide Nanowires for Mid-Infrared Nanophotonics. Nanomaterials 2021, 11, 2339. https://doi.org/10.3390/nano11092339
Rufangura P, Khodasevych I, Agrawal A, Bosi M, Folland TG, Caldwell JD, Iacopi F. Enhanced Absorption with Graphene-Coated Silicon Carbide Nanowires for Mid-Infrared Nanophotonics. Nanomaterials. 2021; 11(9):2339. https://doi.org/10.3390/nano11092339
Chicago/Turabian StyleRufangura, Patrick, Iryna Khodasevych, Arti Agrawal, Matteo Bosi, Thomas G. Folland, Joshua D. Caldwell, and Francesca Iacopi. 2021. "Enhanced Absorption with Graphene-Coated Silicon Carbide Nanowires for Mid-Infrared Nanophotonics" Nanomaterials 11, no. 9: 2339. https://doi.org/10.3390/nano11092339
APA StyleRufangura, P., Khodasevych, I., Agrawal, A., Bosi, M., Folland, T. G., Caldwell, J. D., & Iacopi, F. (2021). Enhanced Absorption with Graphene-Coated Silicon Carbide Nanowires for Mid-Infrared Nanophotonics. Nanomaterials, 11(9), 2339. https://doi.org/10.3390/nano11092339