Numerical Modelling of the Optical Properties of Plasmonic and Latex Nanoparticles to Improve the Detection Limit of Immuno-Turbidimetric Assays
Abstract
1. Introduction
2. Materials and Methods
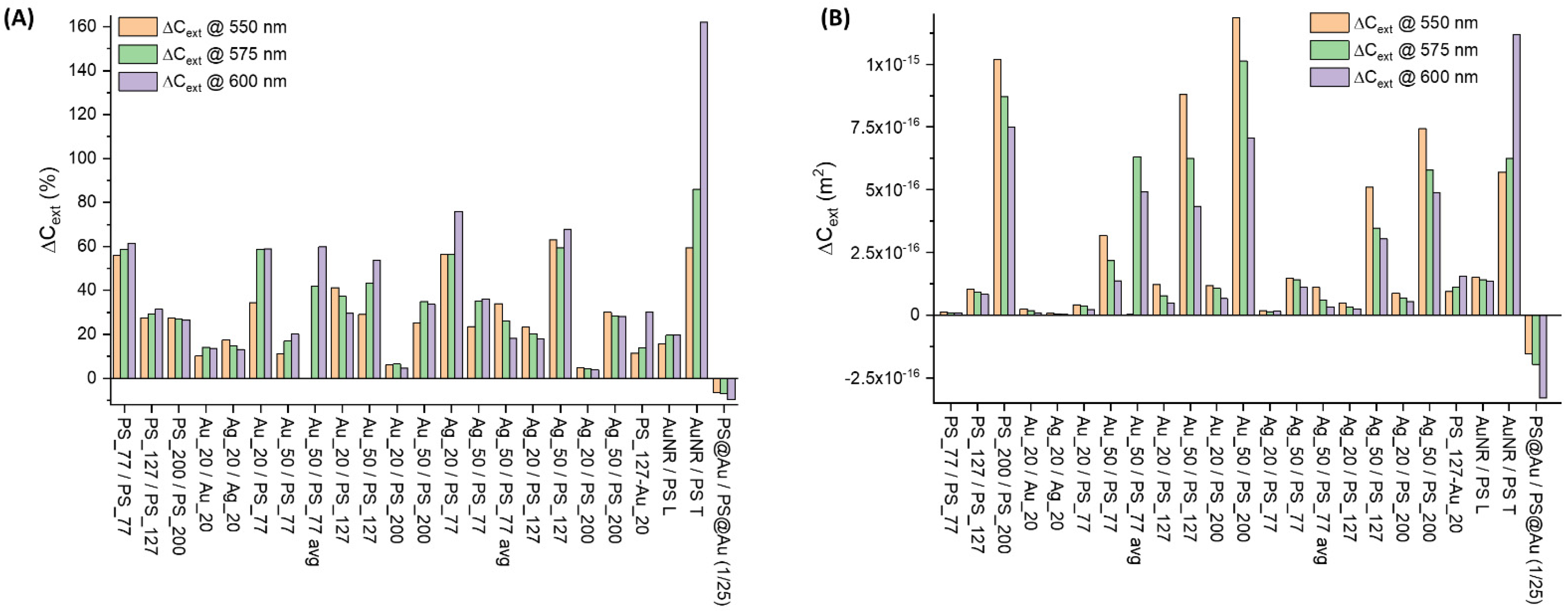
3. Results
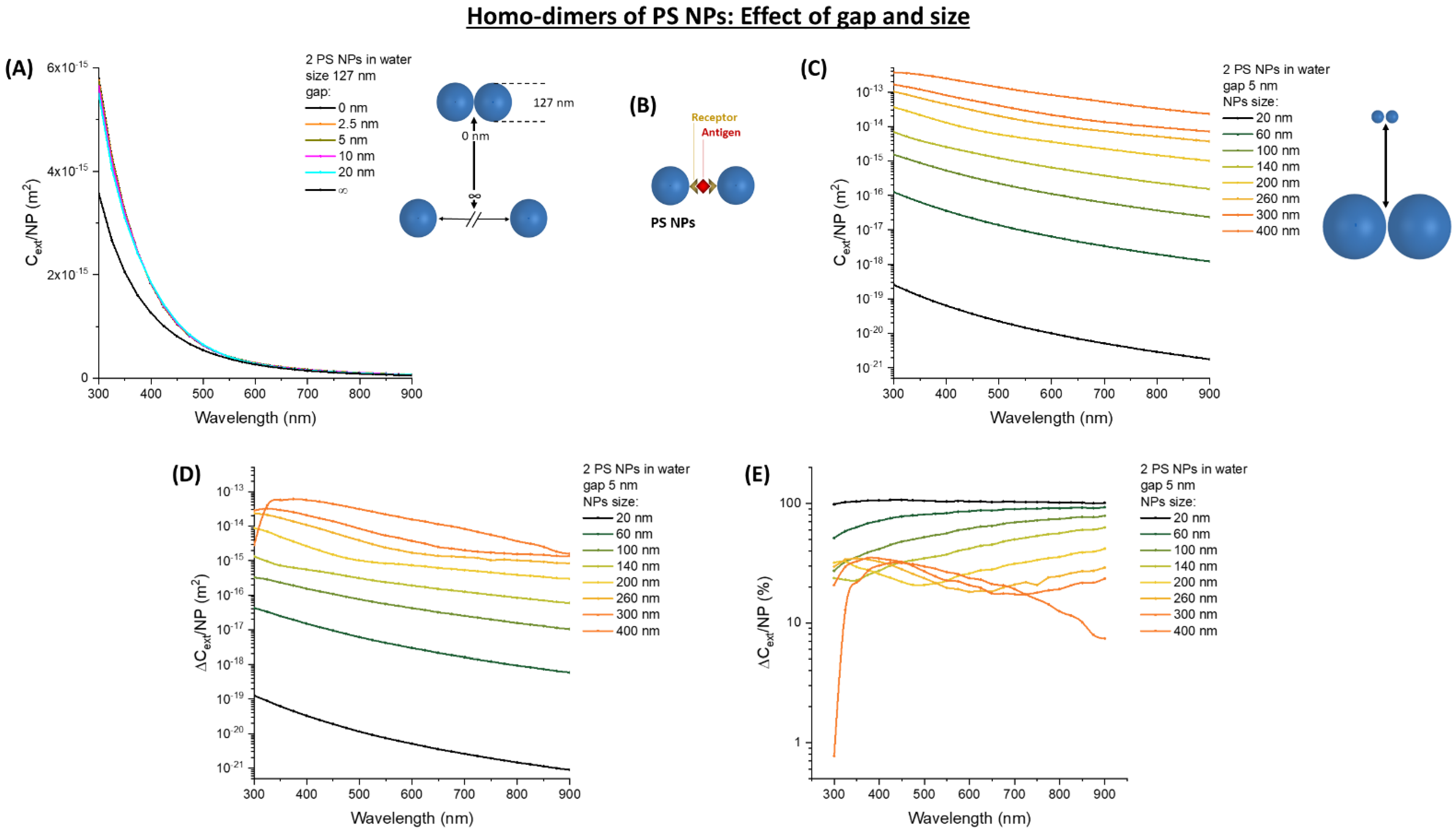
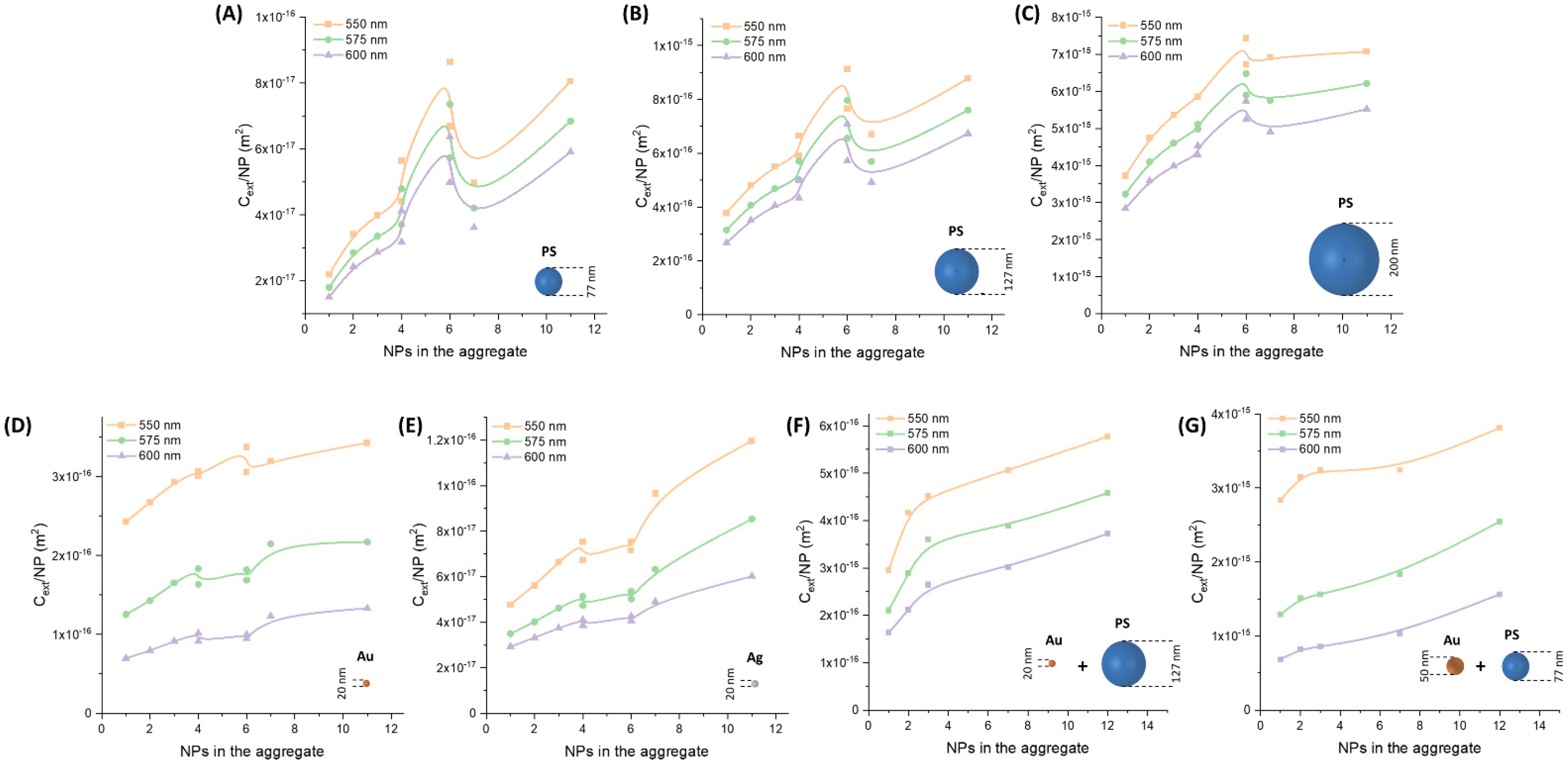
3.1. Homo-Aggregates of Latex Nanospheres
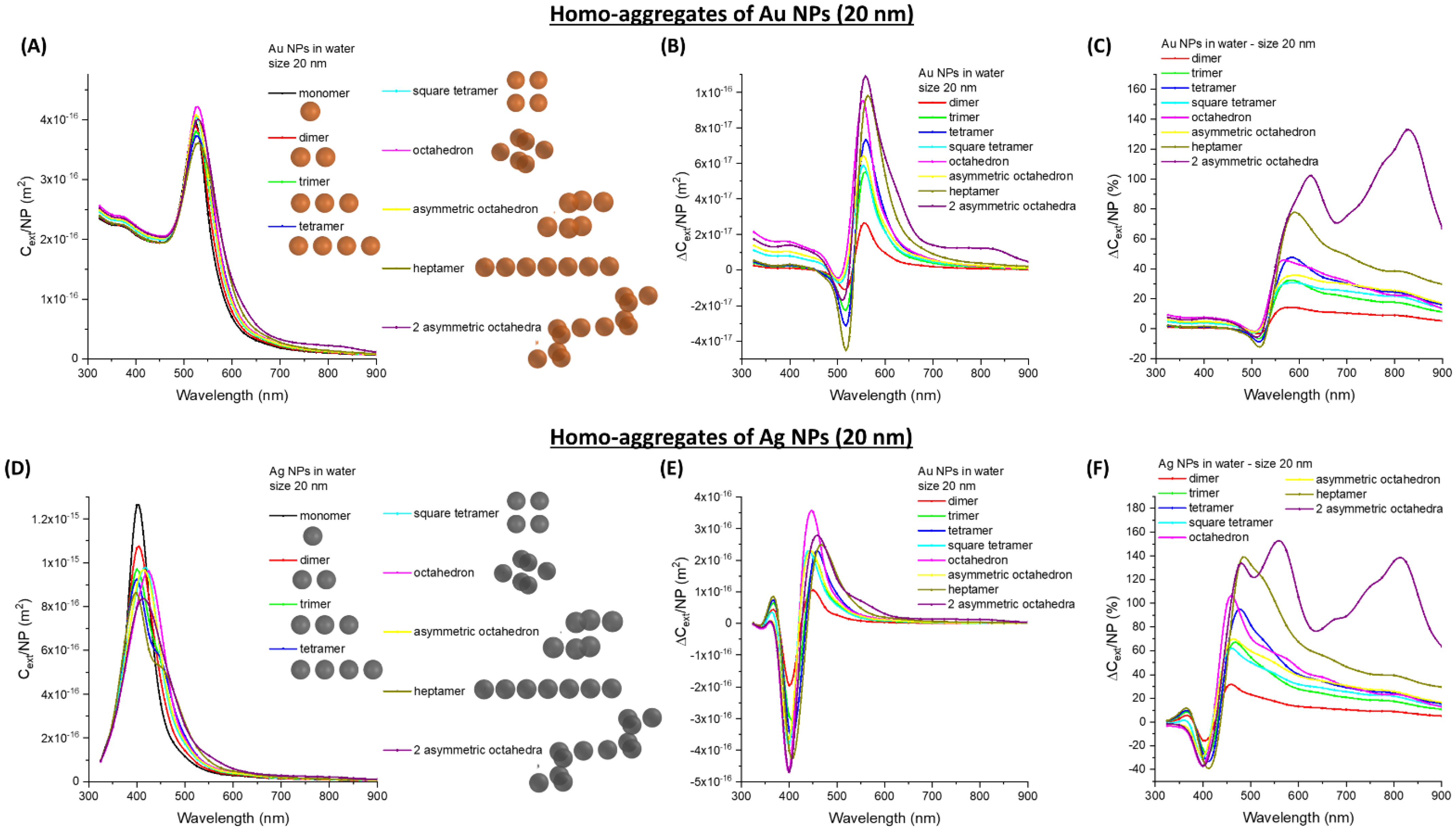
3.2. Homo-Aggregates of Au or Ag Nanospheres
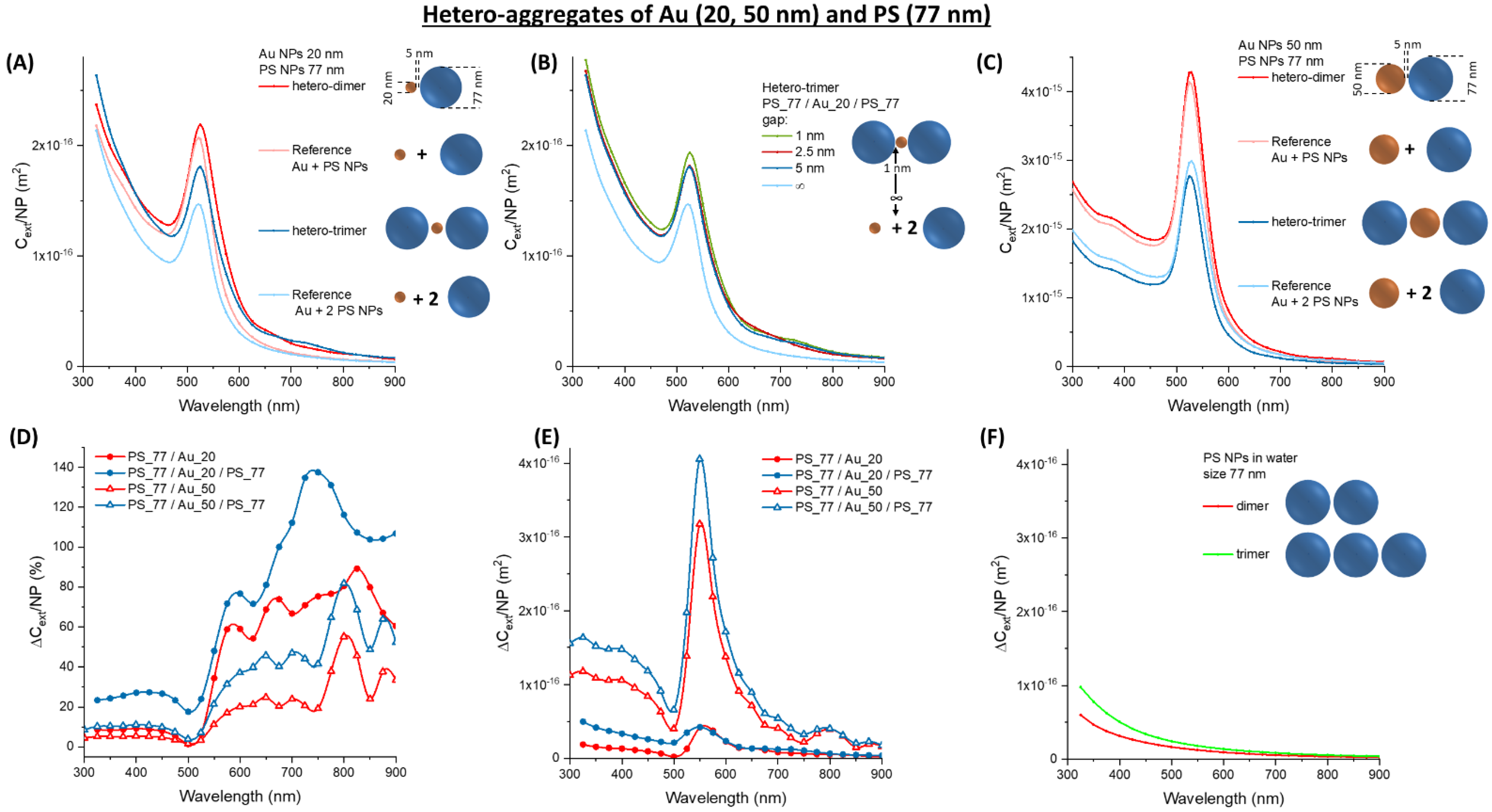
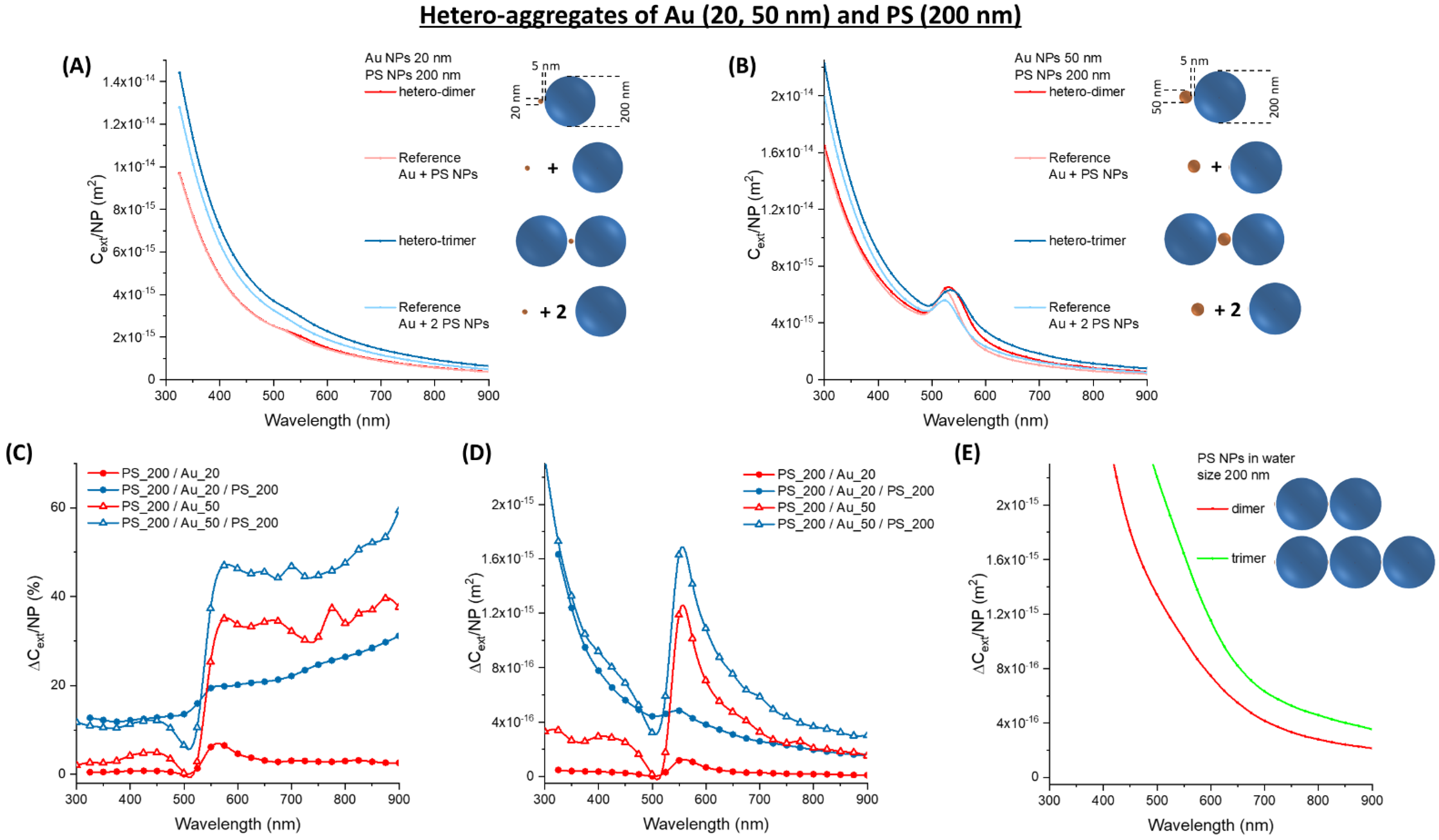
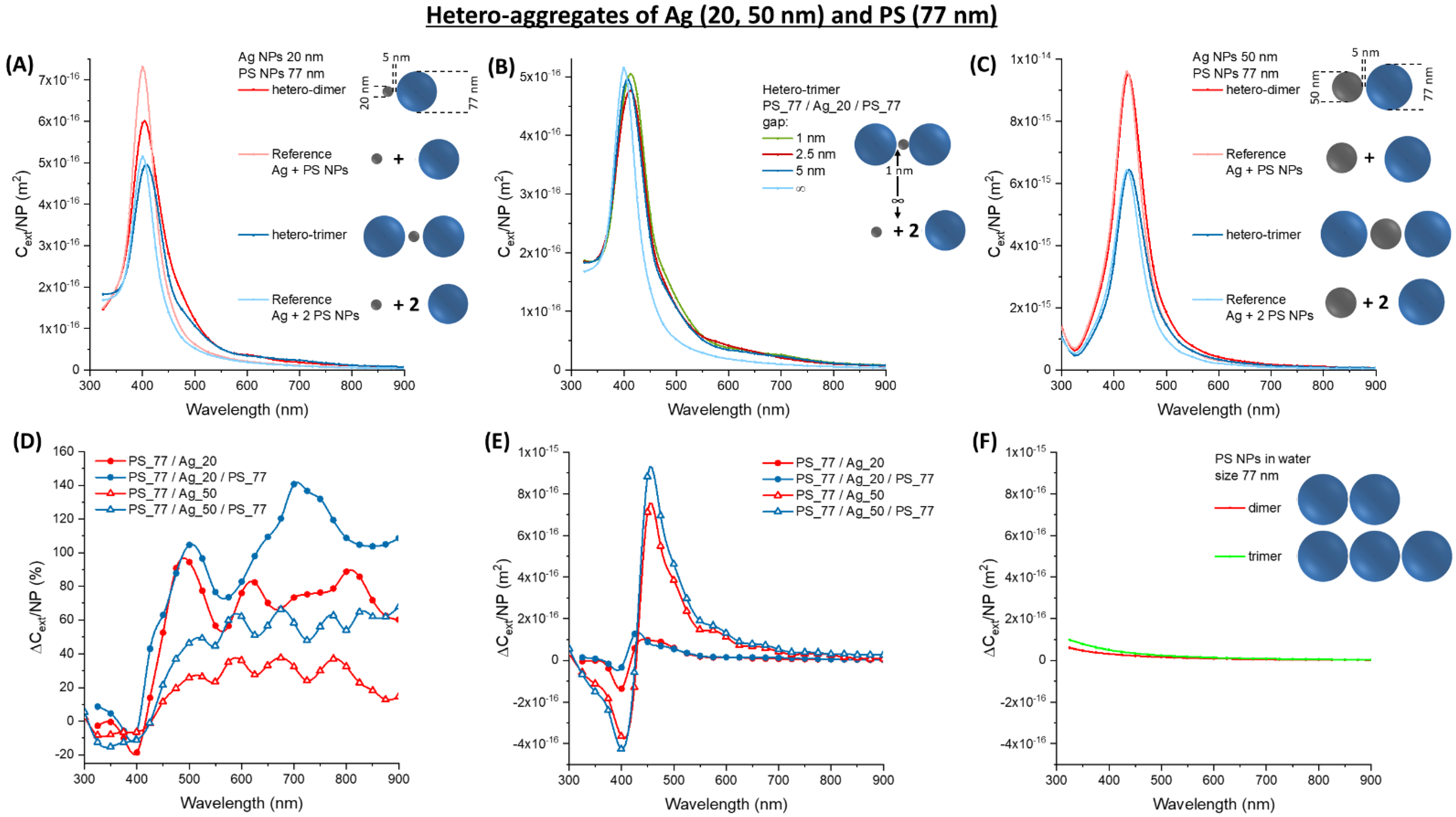
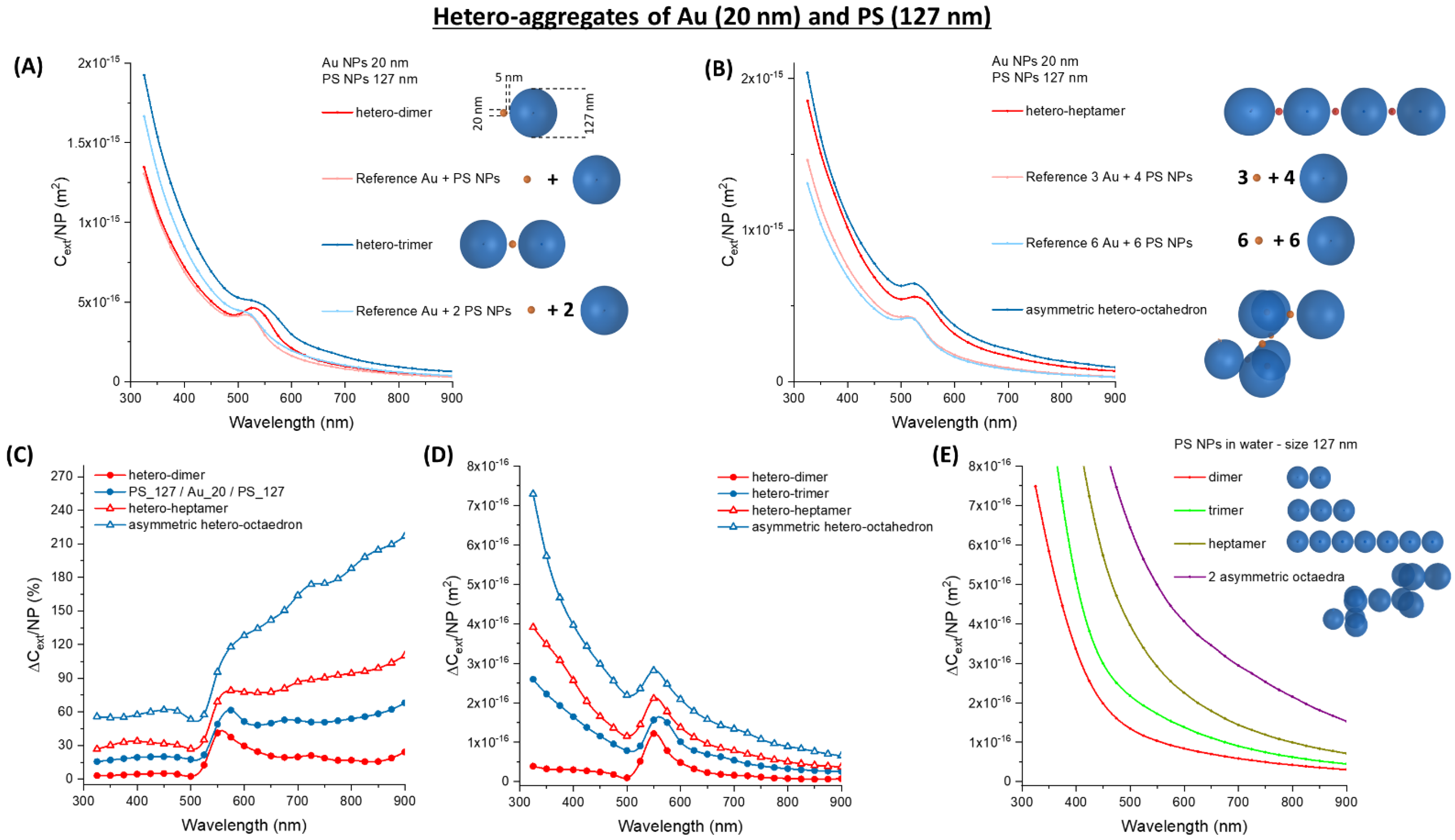
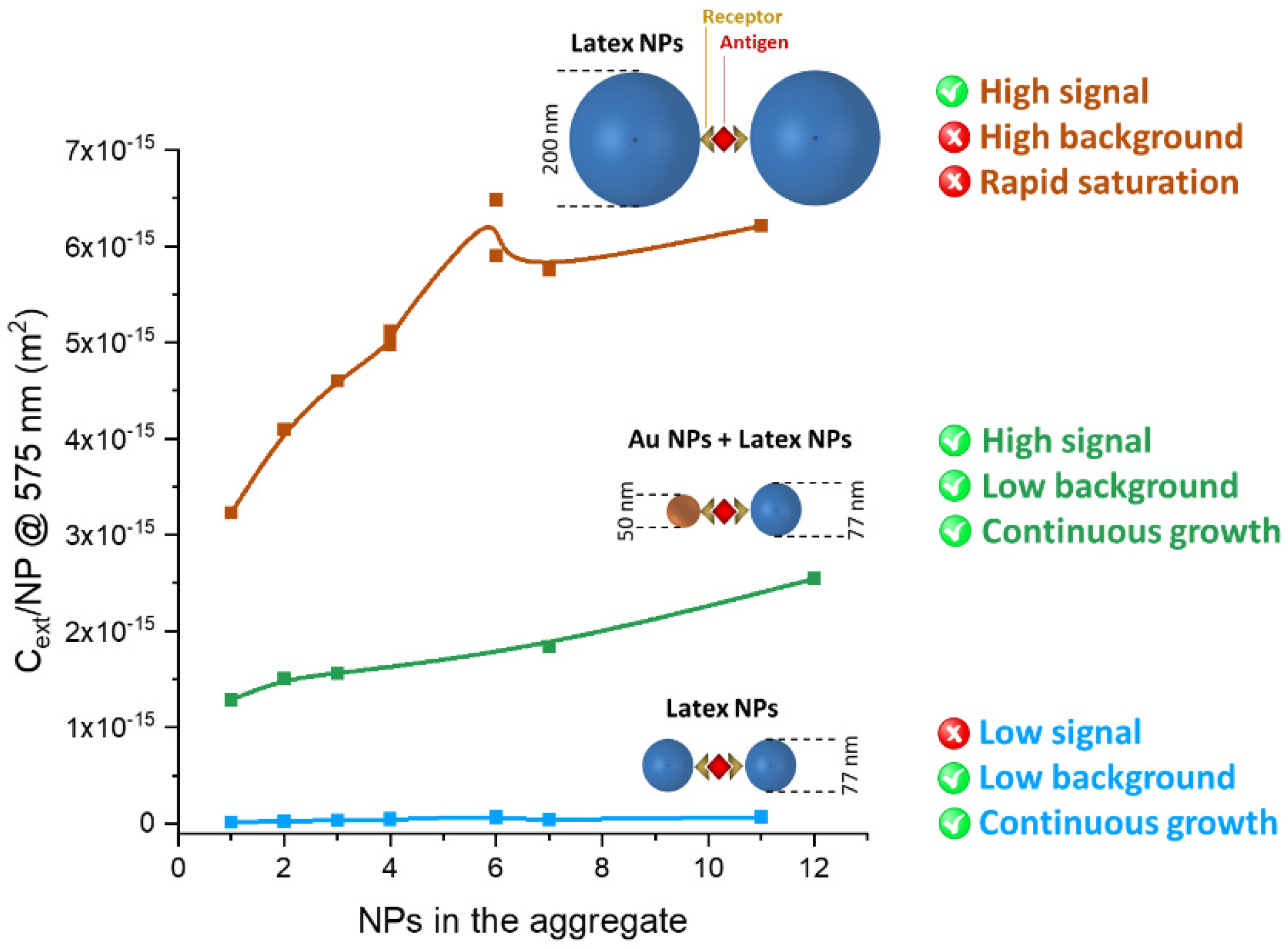
3.3. Hetero-Aggregates of Metal and Latex NPs
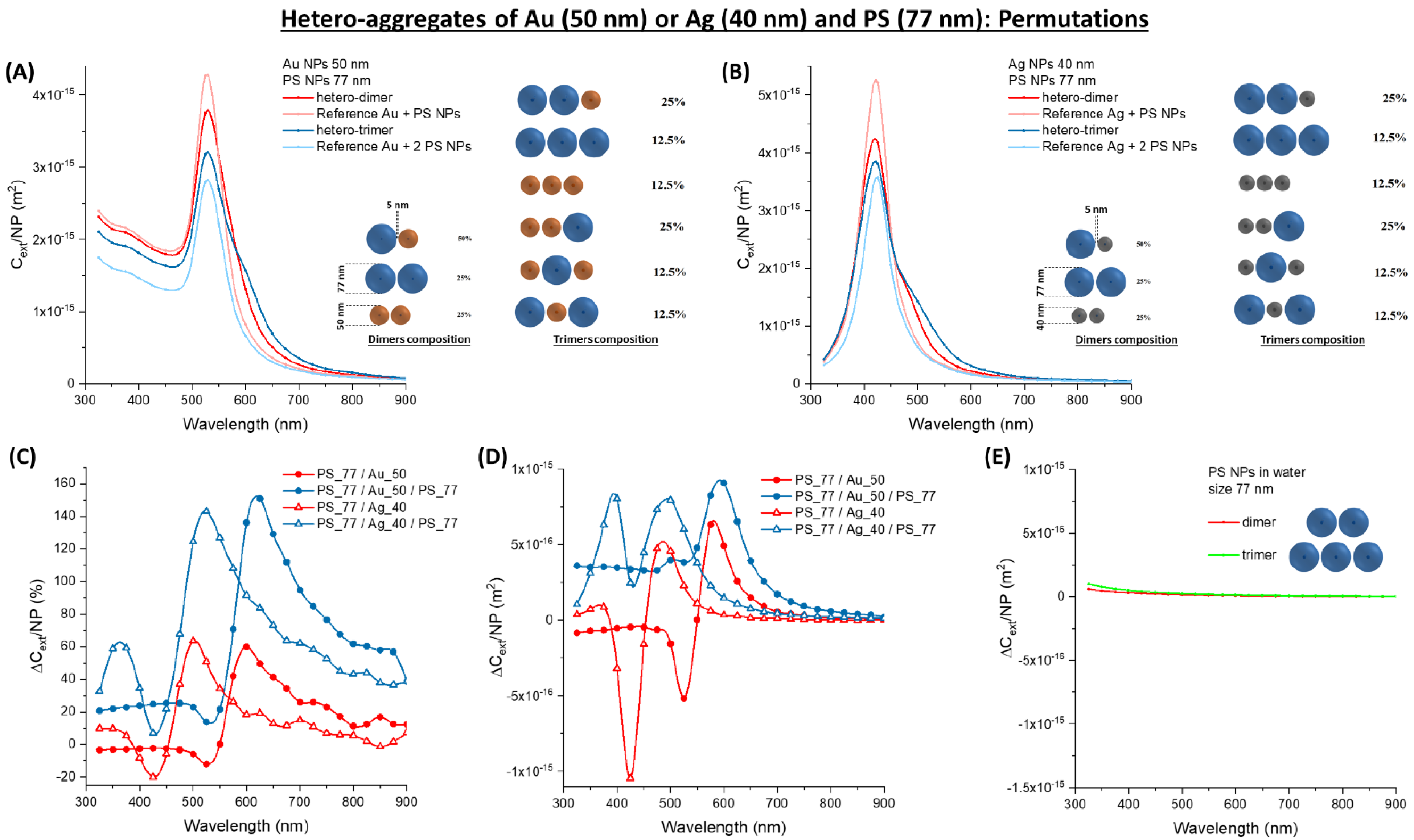
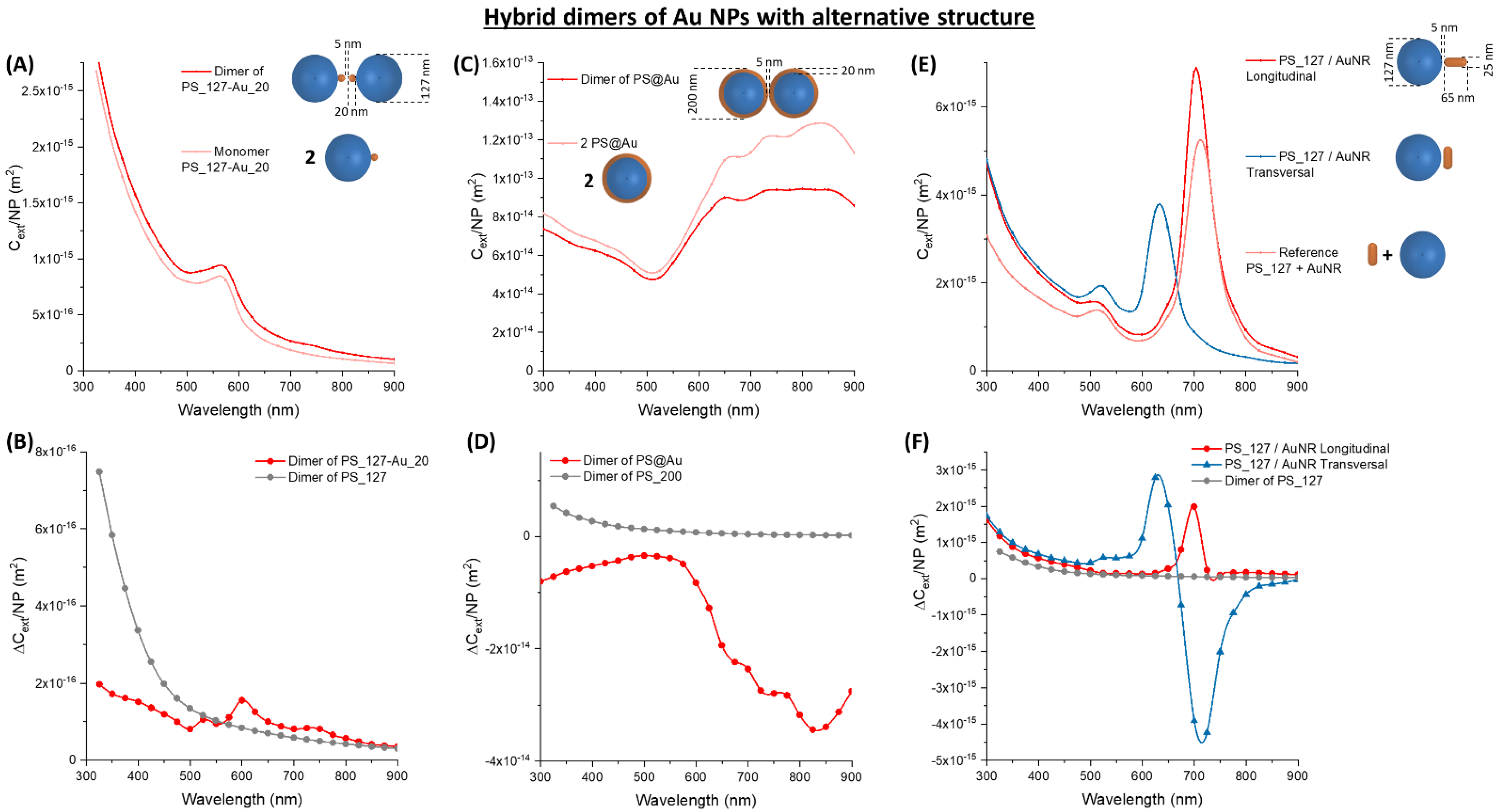
3.4. Optimising Hetero-Aggregates of Metal and Latex NPs
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cölfen, H.; Völkel, A.; Eda, S.; Kobold, U.; Kaufmann, J.; Puhlmann, A.; Göltner, C.; Wachernig, H. Mechanism of Nanoparticle-Enhanced Turbidimetric Assays Applying Nanoparticles of Different Size and Immunoreactivity. Langmuir 2002, 18, 7623–7628. [Google Scholar] [CrossRef]
- Eda, S.; Kaufmann, J.; Roos, W.; Pohl, S. Development of a New Microparticle-Enhanced Turbidimetric Assay for C- Reactive Protein with Superior Features in Analytical Sensitivity and Dynamic Range. J. Clin. Lab. Anal. 1998, 12, 137–144. [Google Scholar] [CrossRef]
- Uehara, N.; Numanami, Y.; Oba, T.; Onishi, N.; Xie, X. Thermal-Induced Immuno-Nephelometry Using Gold Nanoparticles Conjugated with a Thermoresponsive Polymer for the Detection of Avidin. Anal. Sci. 2015, 31, 495–501. [Google Scholar] [CrossRef] [PubMed]
- Newman, D.J.; Henneberry, H.; Price, C.P. Particle Enhanced Light Scattering Immunoassay. Ann. Clin. Biochem. 1992, 22–42. [Google Scholar] [CrossRef] [PubMed]
- Dzantiev, B.B.; Urusov, A.E.; Zherdev, A.V. Modern Techniques of Immunochemical Analysis: Integration of Sensitivity and Rapidity. Biotechnol. Acta 2013, 6, 94–104. [Google Scholar] [CrossRef][Green Version]
- Ortega-Vinuesa, J.L.; Bastos-González, D. A Review of Factors Affecting the Performances of Latex Agglutination Tests. J. Biomater. Sci. Polym. Ed. 2001, 12, 379–408. [Google Scholar] [CrossRef] [PubMed]
- Goryacheva, I.Y. Contemporary Trends in the Development of Immunochemical Methods for Medical Analysis. J. Anal. Chem. 2015, 70, 903–914. [Google Scholar] [CrossRef]
- Bogatyrev, V.A.; Dykman, L.A.; Khlebtsov, B.N.; Khlebtsov, N.G. Measurement of Mean Size and Evaluation of Polydispersity of Gold Nanoparticles from Spectra of Optical Absorption and Scattering. Opt. Spectrosc. 2004, 96, 128–135. [Google Scholar] [CrossRef]
- Quesada, M.; Puig, J.; Delgado, J.M.; Hidalgo-Álvarez, R. Modelling the Kinetics of Antigen-Antibody Reactions at Particle Enhanced Optical Immunoassays. J. Biomater. Sci. Polym. Ed. 1998, 9, 961–971. [Google Scholar] [CrossRef]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; Wiley-Interscience: New York, NY, USA, 1983. [Google Scholar]
- Saija, R.; Iatì, M.A.; Borghese, F.; Denti, P.; Aiello, S.; Cecchi-Pestellini, C. Beyond Mie Theory: The Transition Matrix Approach in Interstellar Dust Modeling. Astrophys. J. 2001, 559, 993. [Google Scholar] [CrossRef]
- Kato, H.; Nakamura, A.; Kinugasa, S. Effects of Angular Dependency of Particulate Light Scattering Intensity on Determination of Samples with Bimodal Size Distributions Using Dynamic Light Scattering Methods. Nanomaterials 2018, 8, 708. [Google Scholar] [CrossRef]
- Kato, H.; Nakamura, A.; Takahashi, K.; Kinugasa, S. Accurate Size and Size-Distribution Determination of Polystyrene Latex Nanoparticles in Aqueous Medium Using Dynamic Light Scattering and Asymmetrical Flow Field Flow Fractionation with Multi-Angle Light Scattering. Nanomaterials 2012, 2, 15–30. [Google Scholar] [CrossRef]
- Kim Thanh, N.T.; Rosenzweig, Z. Development of an Aggregation-Based Immunoassay for Anti-Protein A Using Gold Nanoparticles. Anal. Chem. 2002, 74, 1624–1628. [Google Scholar] [CrossRef]
- António, M.; Nogueira, J.; Vitorino, R.; Daniel-da-Silva, A.L. Functionalized Gold Nanoparticles for the Detection of C-Reactive Protein. Nanomaterials 2018, 8, 200. [Google Scholar] [CrossRef]
- Amendola, V.; Bakr, O.M.M.; Stellacci, F. A Study of the Surface Plasmon Resonance of Silver Nanoparticles by the Discrete Dipole Approximation Method: Effect of Shape, Size, Structure, and Assembly. Plasmonics 2010, 5, 85–97. [Google Scholar] [CrossRef]
- Amendola, V.; Pilot, R.; Frasconi, M.; Maragò, O.M.; Iatì, M.A. Surface Plasmon Resonance in Gold Nanoparticles: A Review. J. Phys. Condens. Matter 2017, 29, 203002. [Google Scholar] [CrossRef]
- Byun, J.-Y.; Shin, Y.-B.; Kim, D.-M.; Kim, M.-G. A Colorimetric Homogeneous Immunoassay System for the C-Reactive Protein. Analyst 2013, 138, 1538–1543. [Google Scholar] [CrossRef] [PubMed]
- António, M.; Ferreira, R.; Vitorino, R.; Daniel-da-Silva, A.L. A Simple Aptamer-Based Colorimetric Assay for Rapid Detection of C-Reactive Protein Using Gold Nanoparticles. Talanta 2020, 214, 120868. [Google Scholar] [CrossRef] [PubMed]
- Venditti, I. Nanostructured Materials Based on Noble Metals for Advanced Biological Applications. Nanomaterials 2019, 9, 1593. [Google Scholar] [CrossRef] [PubMed]
- Sreekanth, K.V.; Alapan, Y.; Elkabbash, M.; Ilker, E.; Hinczewski, M.; Gurkan, U.A.; De Luca, A.; Strangi, G. Extreme Sensitivity Biosensing Platform Based on Hyperbolic Metamaterials. Nat. Mater. 2016, 15, 621–627. [Google Scholar] [CrossRef]
- Ahmadivand, A.; Gerislioglu, B.; Ahuja, R.; Kumar Mishra, Y. Terahertz Plasmonics: The Rise of Toroidal Metadevices towards Immunobiosensings. Mater. Today 2020, 32, 108–130. [Google Scholar] [CrossRef]
- Gerislioglu, B.; Dong, L.; Ahmadivand, A.; Hu, H.; Nordlander, P.; Halas, N.J. Monolithic Metal Dimer-on-Film Structure: New Plasmonic Properties Introduced by the Underlying Metal. Nano Lett. 2020, 20, 2087–2093. [Google Scholar] [CrossRef] [PubMed]
- Bravin, C.; Amendola, V. Wide Range Detection of C-Reactive Protein with a Homogeneous Immunofluorimetric Assay Based on Cooperative Fluorescence Quenching Assisted by Gold Nanoparticles. Biosens. Bioelectron. 2020, 169, 112591. [Google Scholar] [CrossRef]
- Kolanowski, J.L.; Liu, F.; New, E.J. Fluorescent Probes for the Simultaneous Detection of Multiple Analytes in Biology. Chem. Soc. Rev. 2018, 47, 195–208. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Yu, C. Detection of Chemical Pollutants in Water Using Gold Nanoparticles as Sensors: A Review. Rev. Anal. Chem. 2013, 32, 1–14. [Google Scholar] [CrossRef]
- Peceros, K.E.; Xu, X.; Bulcock, S.R.; Cortie, M.B. Dipole—Dipole Plasmon Interactions in Gold-on-Polystyrene Composites. J. Phys. Chem. B 2005, 109, 21516–21520. [Google Scholar] [CrossRef] [PubMed]
- Iatì, M.A.; Lidorikis, E.; Saija, R. Modeling of Enhanced Electromagnetic Fields in Plasmonic Nanostructures. In Handbook of Enhanced Spectroscopies; Pan Stanford Publishing: New York, NY, USA, 2016. [Google Scholar]
- Zhao, W.; Brook, M.A.; Li, Y. Design of Gold Nanoparticle-based Colorimetric Biosensing Assays. ChemBioChem 2008, 9, 2363–2371. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Rothberg, L. Colorimetric Detection of DNA Sequences Based on Electrostatic Interactions with Unmodified Gold Nanoparticles. Proc. Natl. Acad. Sci. USA 2004, 101, 14036–14039. [Google Scholar] [CrossRef] [PubMed]
- Rahmani, M.; Luk’yanchuk, B.; Hong, M. Fano Resonance in Novel Plasmonic Nanostructures. Laser Photon. Rev. 2013, 7, 329–349. [Google Scholar] [CrossRef]
- Morandi, V.; Marabelli, F.; Amendola, V.; Meneghetti, M.; Comoretto, D. Light Localization Effect on the Optical Properties of Opals Doped with Gold Nanoparticles. J. Phys. Chem. C 2008, 112, 6293–6298. [Google Scholar] [CrossRef]
- Fuller, K.A.; Gonzalez, R.J.; Kochar, M.S. Light Scattering from Dimers: Latex-Latex and Gold-Latex. In Advances in Optical Biophysics; Lakowicz, J.R., Ross, J.B.A., Eds.; SPIE: San Jose, CA, SUA, 1998; Volume 3256, p. 186. [Google Scholar] [CrossRef]
- Draine, B.T.; Flatau, P.J. Discrete-Dipole Approximation for Scattering Calculations. J. Opt. Soc. Am. A 1994, 11, 1491–1499. [Google Scholar] [CrossRef]
- Gonzalez, A.L.; Noguez, C.; Ortiz, G.P.; Rodriguez-Gattorno, G. Optical Absorbance of Colloidal Suspensions of Silver Polyhedral Nanoparticles. J. Phys. Chem. B 2005, 109, 17512–17517. [Google Scholar] [CrossRef] [PubMed]
- Goodman, J.J.; Draine, B.T.; Flatau, P.J. Application of Fast-Fourier-Transform Techniques to the Discrete-Dipole Approximation. Opt. Lett. 1991, 16, 1198–1200. [Google Scholar] [CrossRef]
- Khlebtsov, N.G. An Approximate Method for Calculating Scattering and Absorption of Light by Fractal Aggregates. Opt. Spectrosc. 2000, 88, 594–601. [Google Scholar] [CrossRef]
- Lv, R.; Feng, M.; Parak, W. Up-Conversion Luminescence Properties of Lanthanide-Gold Hybrid Nanoparticles as Analyzed with Discrete Dipole Approximation. Nanomaterials 2018, 8, 989. [Google Scholar] [CrossRef]
- Draine, B.T.; Flatau, P.J. User Guide for the Discrete Dipole Approximation Code DDSCAT 7.3. arXiv 2013, arXiv:1305.6497. [Google Scholar]
- Amendola, V. Surface Plasmon Resonance of Silver and Gold Nanoparticles in the Proximity of Graphene Studied Using the Discrete Dipole Approximation Method. Phys. Chem. Chem. Phys. 2016, 18, 2230–2241. [Google Scholar] [CrossRef]
- Olmon, R.L.; Slovick, B.; Johnson, T.W.; Shelton, D.; Oh, S.-H.; Boreman, G.D.; Raschke, M.B. Optical Dielectric Function of Gold. Phys. Rev. B 2012, 86, 235147. [Google Scholar] [CrossRef]
- Johnson, P.B.; Christy, R.W. Optical Constants of the Noble Metals. Phys. Rev. B 1972, 6, 4370–4379. [Google Scholar] [CrossRef]
- Sultanova, N.; Kasarova, S.; Nikolov, I. Dispersion Properties of Optical Polymers. Acta Phys. Pol. A 2009, 116, 585–587. [Google Scholar] [CrossRef]
- Hale, G.M.; Querry, M.R. Optical Constants of Water in the 200-Nm to 200-Μm Wavelength Region. Appl. Opt. 1973, 12, 555. [Google Scholar] [CrossRef]
- Kreibig, U.; Vollmer, M. Optical Properties of Metal Clusters; Springer: Berlin, Germany, 1995. [Google Scholar]
- Poletti, A.; Fracasso, G.; Conti, G.; Pilot, R.; Amendola, V. Laser Generated Gold Nanocorals with Broadband Plasmon Absorption for Photothermal Applications. Nanoscale 2015, 7, 13702–13714. [Google Scholar] [CrossRef]
- Mendoza-Herrera, L.J.; Schinca, D.C.; Scaffardi, L.B.; Grumel, E.E.; Trivi, M. Measurement of Latex Microparticle Size by Dynamic Speckle Technique. Opt. Lasers Eng. 2021, 140, 106528. [Google Scholar] [CrossRef]
- Kubitschko, S.; Spinke, J.; Brückner, T.; Pohl, S.; Oranth, N. Sensitivity Enhancement of Optical Immunosensors with Nanoparticles. Anal. Biochem. 1997, 253, 112–122. [Google Scholar] [CrossRef] [PubMed]
- Greenfield, E.A. Antibodies: A Laboratory Manual, 2nd ed.; CSH Press: Woodbury, NY, SUA, 2014. [Google Scholar]
- Lambert, S.; Thill, A.; Ginestet, P.; Audic, J.M.; Bottero, J.Y. Structural Interpretations of Static Light Scattering Patterns of Fractal Aggregates: I. Introduction of a Mean Optical Index: Numerical Simulations. J. Colloid Interface Sci. 2000, 228, 379–385. [Google Scholar] [CrossRef] [PubMed]
- Serra, T.; Casamitjana, X. Structure of the Aggregates during the Process of Aggregation and Breakup under a Shear Flow. J. Colloid Interface Sci. 1998, 206, 505–511. [Google Scholar] [CrossRef]
- Tang, S.; McFarlane, C.M.; Paul, G.C.; Thomas, C.R. Characterising Latex Particles and Fractal Aggregates Using Image Analysis. Colloid Polym. Sci. 1999, 277, 325–333. [Google Scholar] [CrossRef]
- Khlebtsov, N.G.; Dykman, L.A.; Krasnov, Y.M.; Mel’nikov, A.G. Light Absorption by the Clusters of Colloidal Gold and Silver Particles Formed during Slow and Fast Aggregation. Colloid J. 2000, 62, 765–779. [Google Scholar] [CrossRef]
- Mao, S.-Y. Conjugation of Fluorochromes to Antibodies BT—Immunocytochemical Methods and Protocols; Javois, L.C., Ed.; Humana Press: Totowa, NJ, USA, 1999; pp. 35–38. [Google Scholar] [CrossRef]
- Lou, S.; Ye, J.Y.; Li, K.Q.; Wu, A. A Gold Nanoparticle-Based Immunochromatographic Assay: The Influence of Nanoparticulate Size. Analyst 2012, 137, 1174–1181. [Google Scholar] [CrossRef] [PubMed]
- Reynolds, R.A.; Mirkin, C.A.; Letsinger, R.L. A Gold Nanoparticle/Latex Microsphere-Based Colorimetric Oligonucleotide Detection Method. Pure Appl. Chem. 2000, 72, 229–235. [Google Scholar] [CrossRef]
- Haick, H. Chemical Sensors Based on Molecularly Modified Metallic Nanoparticles. J. Phys. D. Appl. Phys. 2007, 40, 7173–7186. [Google Scholar] [CrossRef]
- Cacciola, A.; Iatì, M.A.; Saija, R.; Borghese, F.; Denti, P.; Maragò, O.M.; Gucciardi, P.G. Spectral Shift between the Near-Field and Far-Field Optoplasmonic Response in Gold Nanospheres, Nanoshells, Homo- and Hetero-Dimers. J. Quant. Spectrosc. Radiat. Transf. 2017, 195, 97–106. [Google Scholar] [CrossRef]
- Yong, K.T.; Sahoo, Y.; Swihart, M.T.; Prasad, P.N. Synthesis and Plasmonic Properties of Silver and Gold Nanoshells on Polystyrene Cores of Different Size and of Gold-Silver Core-Shell Nanostructures. Colloids Surf. A Physicochem. Eng. Asp. 2006, 290, 89–105. [Google Scholar] [CrossRef]
- Gold, Nanorods 25 nm Diameter, Absorption, 650 nm, Dispersion in H2O, Citrate Capped|Au Nanorods|Sigma-Aldrich. Available online: https://www.sigmaaldrich.com/catalog/product/aldrich/900367?lang=it®ion=IT (accessed on 31 March 2021).
- Alekseeva, A.V.; Bogatyrev, V.A.; Dykman, L.A.; Khlebtsov, B.N.; Trachuk, L.A.; Melnikov, A.G.; Khlebtsov, N.G. Preparation and Optical Scattering Characterization of Gold Nanorods and Their Application to a Dot-Immunogold Assay. Appl. Opt. 2005, 44, 6285–6295. [Google Scholar] [CrossRef]
- Dey, P.; Baumann, V.; Rodríguez-Fernández, J. Gold Nanorod Assemblies: The Roles of Hot-Spot Positioning and Anisotropy in Plasmon Coupling and SERS. Nanomaterials 2020, 10, 942. [Google Scholar] [CrossRef] [PubMed]
- Arce, V.B.; Santillán, J.M.J.; Muñetón Arboleda, D.; Muraca, D.; Scaffardi, L.B.; Schinca, D.C. Characterization and Stability of Silver Nanoparticles in Starch Solution Obtained by Femtosecond Laser Ablation and Salt Reduction. J. Phys. Chem. C 2017, 121, 10501–10513. [Google Scholar] [CrossRef]
- Kassavetis, S.; Kaziannis, S.; Pliatsikas, N.; Avgeropoulos, A.; Karantzalis, A.E.; Kosmidis, C.; Lidorikis, E.; Patsalas, P. Formation of Plasmonic Colloidal Silver for Flexible and Printed Electronics Using Laser Ablation. Appl. Surface Sci. 2015, 336, 262–266. [Google Scholar] [CrossRef]
- Li, H.; Sun, Z.; Zhong, W.; Hao, N.; Xu, D.; Chen, H.Y. Ultrasensitive Electrochemical Detection for DNA Arrays Based on Silver Nanoparticle Aggregates. Anal. Chem. 2010, 82, 5477–5483. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Coletta, G.; Amendola, V. Numerical Modelling of the Optical Properties of Plasmonic and Latex Nanoparticles to Improve the Detection Limit of Immuno-Turbidimetric Assays. Nanomaterials 2021, 11, 1147. https://doi.org/10.3390/nano11051147
Coletta G, Amendola V. Numerical Modelling of the Optical Properties of Plasmonic and Latex Nanoparticles to Improve the Detection Limit of Immuno-Turbidimetric Assays. Nanomaterials. 2021; 11(5):1147. https://doi.org/10.3390/nano11051147
Chicago/Turabian StyleColetta, Giuliano, and Vincenzo Amendola. 2021. "Numerical Modelling of the Optical Properties of Plasmonic and Latex Nanoparticles to Improve the Detection Limit of Immuno-Turbidimetric Assays" Nanomaterials 11, no. 5: 1147. https://doi.org/10.3390/nano11051147
APA StyleColetta, G., & Amendola, V. (2021). Numerical Modelling of the Optical Properties of Plasmonic and Latex Nanoparticles to Improve the Detection Limit of Immuno-Turbidimetric Assays. Nanomaterials, 11(5), 1147. https://doi.org/10.3390/nano11051147





