Nanoantennas Inversely Designed to Couple Free Space and a Metal–Insulator–Metal Waveguide
Abstract
:1. Introduction
2. Topology Optimization Method
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. The Direct Coupling of the Free Space and MIM Waveguide
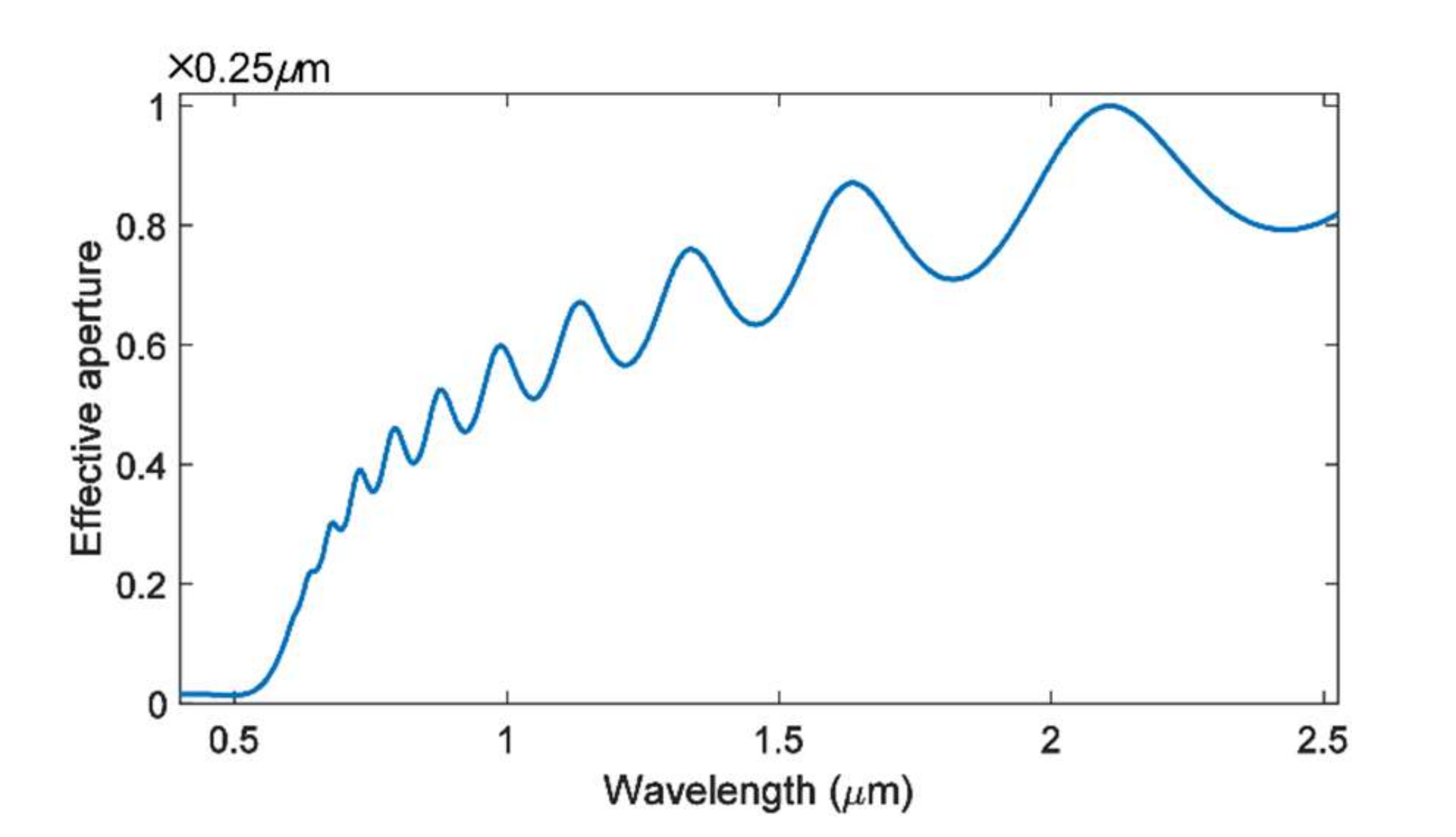
Appendix B. The Simulation Result
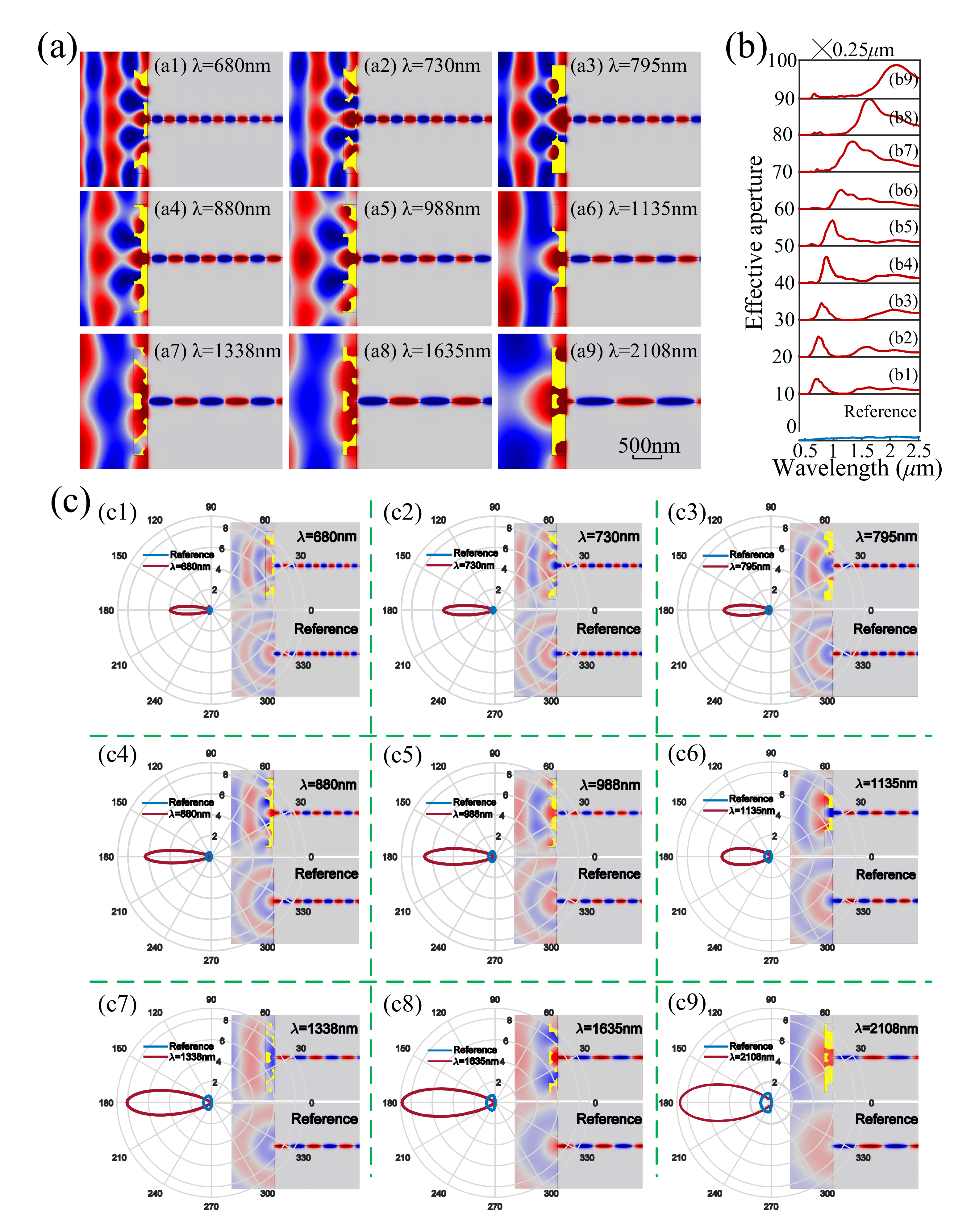



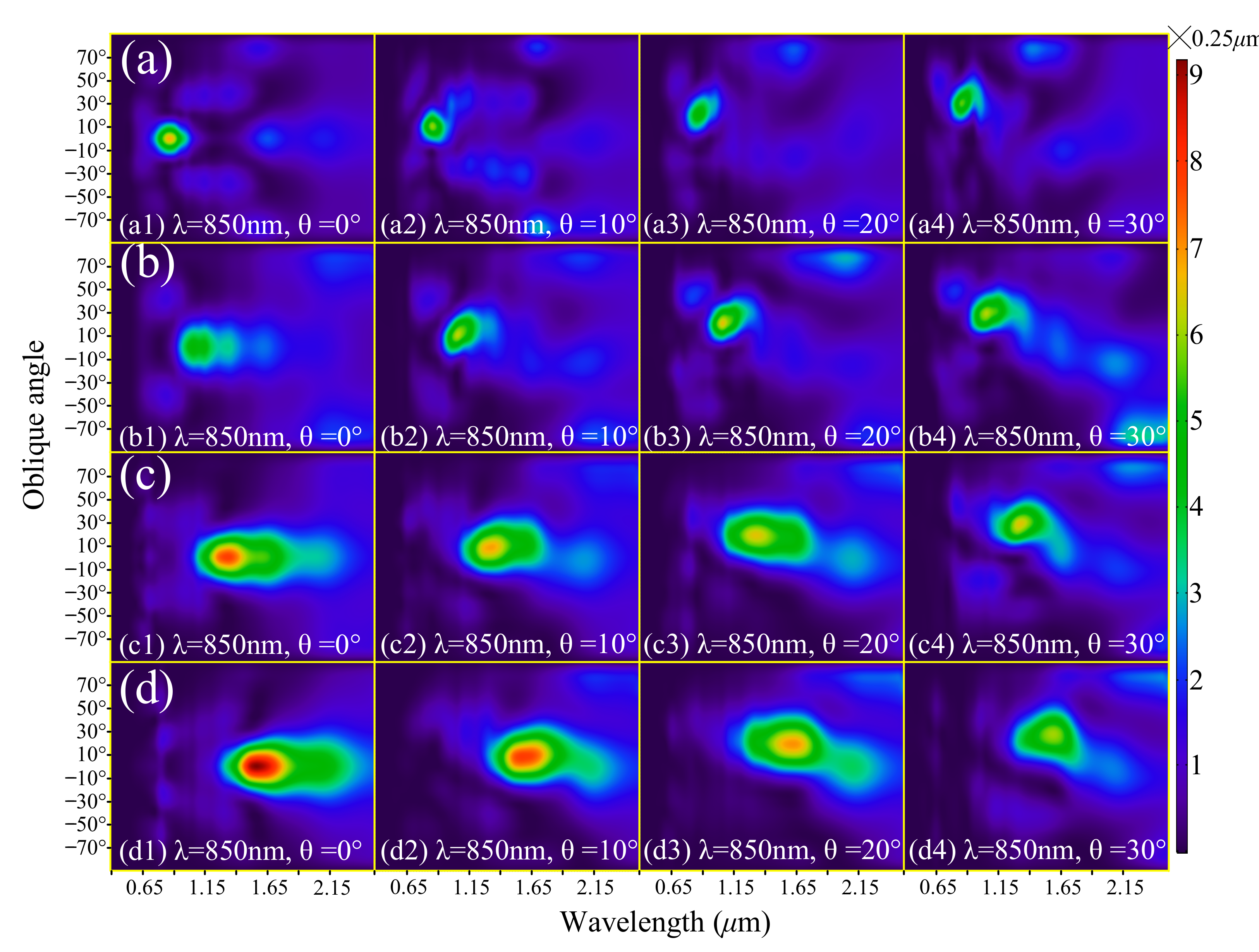
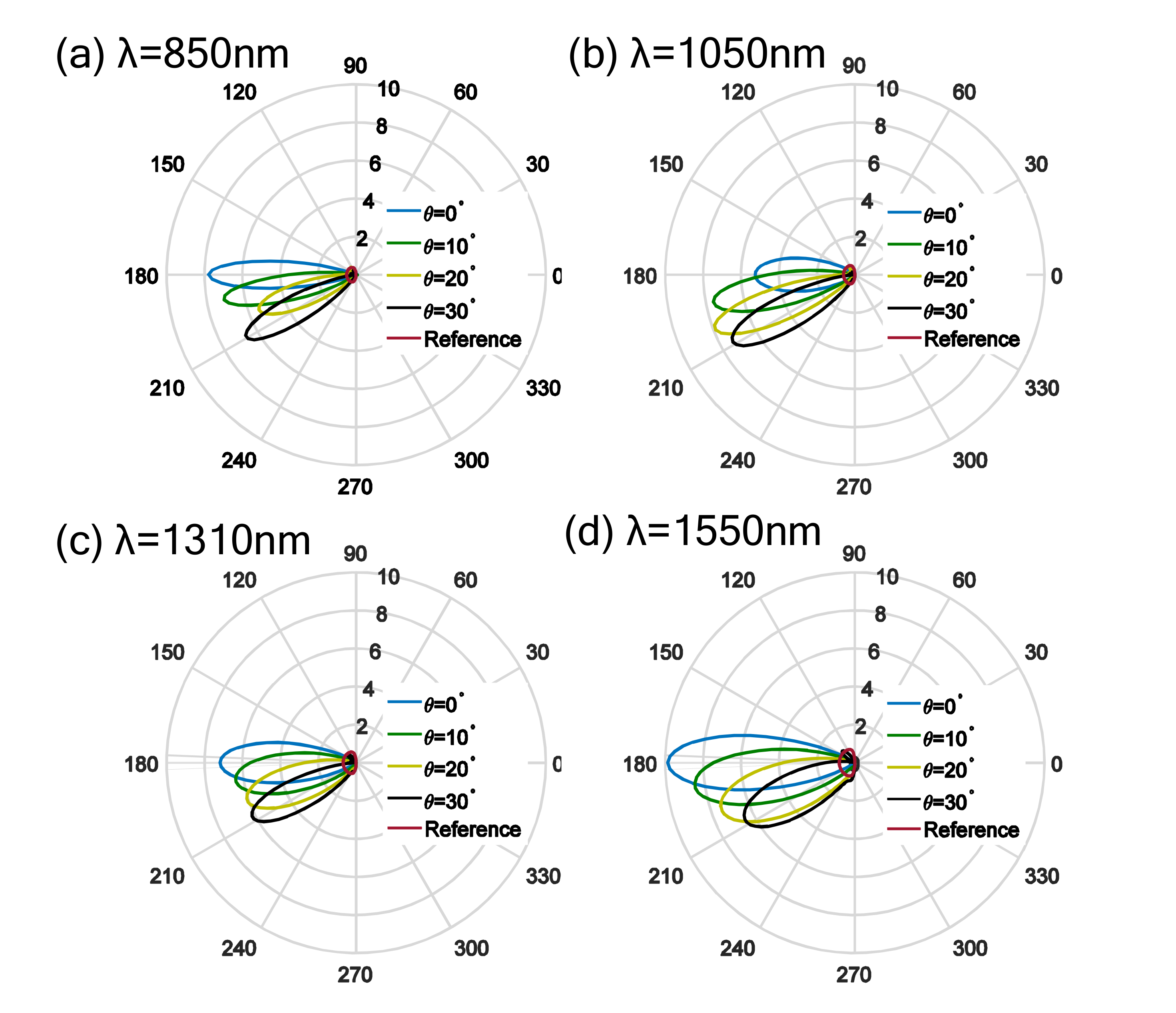
Appendix C. Sketch of the Experimental Setup

References
- Genet, C.; Ebbesen, T.W. Light in tiny holes. Nature 2007, 445, 39–46. [Google Scholar] [CrossRef]
- Chou Chau, Y.F.; Ming, T.Y.; Chou Chao, C.T.; Thotagamuge, R.; Kooh, M.R.R.; Huang, H.J.; Lim, C.M.; Chiang, H.P. Significantly enhanced coupling effect and gap plasmon resonance in a MIM-cavity based sensing structure. Sci. Rep. 2021, 11, 18515. [Google Scholar] [CrossRef]
- Andam, N.; Refki, S.; Hayashi, S.; Sekkat, Z. Plasmonic mode coupling and thin film sensing in metal-insulator-metal structures. Sci. Rep. 2021, 11, 15093. [Google Scholar] [CrossRef]
- Kazanskiy, N.L.; Khonina, S.N.; Butt, M.A.; Kazmierczak, A.; Piramidowicz, R. A Numerical Investigation of a Plasmonic Sensor Based on a Metal-Insulator-Metal Waveguide for Simultaneous Detection of Biological Analytes and Ambient Temperature. Nanomaterials 2021, 11, 2551. [Google Scholar] [CrossRef]
- Takahara, J.; Yamagishi, S.; Taki, H.; Morimoto, A.; Kobayashi, T. Guiding of a one-dimensional optical beam with nanometer diameter. Opt. Lett. 1997, 22, 475–477. [Google Scholar] [CrossRef] [PubMed]
- Weeber, J.C.; De Reux, A.; Girard, C.; Krenn, J.R.; Goudonnet, J.P. Plasmon polaritons of metallic nanowires for controlling submicron propagation of light. Phys. Rev. B 1999, 60, 9061–9068. [Google Scholar] [CrossRef]
- Krenn, J.R.; Lamprecht, B.; Ditlbacher, H.; Schider, G.; Aussenegg, F.R. Non–diffraction-limited light transport by gold nanowires. EPL 2002, 607945, 663–669. [Google Scholar] [CrossRef]
- Brongersma, M.L.; Hartman, J.W.; Atwater, H.A. Electromagnetic energy transfer and switching in nanoparticle chain arrays below the diffraction limit. Mrs Proc. 1999, 582, 16356–16359. [Google Scholar] [CrossRef]
- Maier, S.A.; Kik, P.G.; Atwater, H.A.; Meltzer, S.; Harel, E.; Koel, B.E.; Requicha, A. Local detection of electromagnetic energy transport below the diffraction limit in metal nanoparticle plasmon waveguides. Nat. Mater. 2003, 2, 229–232. [Google Scholar] [CrossRef] [PubMed]
- Bozhevolnyi, S.I.; Volkov, V.S.; Devaux, E.; Ebbesen, T.W. Channel Plasmon-Polariton Guiding by Subwavelength Metal Grooves. Phys. Rev. Lett. 2005, 95, 046802. [Google Scholar] [CrossRef] [Green Version]
- Economou, E.N. Surface Plasmons in Thin Films. Phys. Rev. 1969, 182, 539. [Google Scholar] [CrossRef]
- Zia, R.; Selker, M.; Catrysse, P.B.; Brongersma, M.L. Geometries and materials for subwavelength surface plasmon modes. J. Opt. Soc. Am. A 2004, 21, 2442–2446. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Veronis, G.; Fan, S. Bends and splitters in metal-dielectric-metal subwavelength plasmonic waveguides. Appl. Phys. Lett. 2005, 87, 131102–131103. [Google Scholar] [CrossRef]
- Sparks, P.; Sjodin, T.; Reed, B.; Stege, J. Light emission from the slow mode of tunnel junctions on short period diffraction gratings. Phys. Rev. Lett. 1992, 68, 2668. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Miyazaki, H.T.; Kurokawa, Y. Squeezing Visible Light Waves into a 3-nm-Thick and 55-nm-Long Plasmon Cavity. Phys. Rev. Lett. 2006, 96, 097401. [Google Scholar] [CrossRef]
- Lezec, H.J.; Dionne, J.A.; Atwater, H.A. Negative Refraction at Visible Frequencies. Science 2007, 316, 430–432. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dionne, J.A.; Sweatlock, L.A.; Atwater, H.A.; Polman, A. Plasmon slot waveguides: Towards chip-scale propagation with subwavelength-scale localization. Phys. Rev. B Condens. Matter Mater. Phys. 2006, 73, 035401–035407. [Google Scholar] [CrossRef] [Green Version]
- Kurokawa, Y.; Miyazaki, H.T. Metal-insulator-metal plasmon nanocavities: Analysis of optical properties. Phys. Rev. B 2007, 75, 035411. [Google Scholar] [CrossRef]
- Veronis, G.; Fan, S. Theoretical investigation of compact couplers between dielectric slab waveguides and two-dimensional metal-dielectric-metal plasmonic waveguides. Opt. Express 2007, 15, 1211–1221. [Google Scholar] [CrossRef] [Green Version]
- Preiner, M.J.; Shimizu, K.T.; White, J.S.; Melosh, N.A. Efficient optical coupling into metal-insulator-metal plasmon modes with subwavelength diffraction gratings. Appl. Phys. Lett. 2008, 92, 39. [Google Scholar] [CrossRef]
- Novotny, L.; Hulst, N.V. Antennas for light. Nat. Photonics 2011, 5, 83–90. [Google Scholar] [CrossRef]
- Piatkowski, L.; Accanto, N.; Van Hulst, N.F. Ultrafast Meets Ultrasmall: Controlling Nanoantennas and Molecules. Acs Photonics 2016, 3, 1401–1414. [Google Scholar] [CrossRef] [Green Version]
- Ma, W.; Liu, Z.; Kudyshev, Z.A.; Boltasseva, A.; Cai, W.; Liu, Y. Deep learning for the design of photonic structures. Nat. Photonics 2021, 15, 77–90. [Google Scholar] [CrossRef]
- Campbell, S.D.; Whiting, E.B.; Werner, P.L.; Werner, D.H.; Zhu, D.Z. Three-dimensional Nanoantenna Inverse-design. In Proceedings of the 2019 IEEE International Symposium on Antennas and Propagation and USNC-URSI Radio Science Meeting, Atlanta, GA, USA, 7–12 July 2019. [Google Scholar]
- Liu, Y.; Li, K.; Cao, S.; Xiong, G.; Zhu, L. Optimization Design of a Multi-slot Nanoantenna Based on Genetic Algorithm for Energy Harvesting. Plasmonics 2019, 14, 1577–1586. [Google Scholar] [CrossRef]
- Chen, Y.; Hu, Y.; Zhao, J.; Deng, Y.; Wang, Z.; Cheng, X.; Lei, D.; Deng, Y.; Duan, H. Topology Optimization-Based Inverse Design of Plasmonic Nanodimer with Maximum Near-Field Enhancement. Adv. Funct. Mater. 2020, 30, 2000642. [Google Scholar] [CrossRef]
- Chen, Y.; Shu, Z.; Zhang, S.; Zeng, P.; Liang, H.; Zheng, M.; Duan, H. Sub-10 nm fabrication: Methods and applications. Int. J. Extrem. Manuf. 2021, 3, 032002. [Google Scholar] [CrossRef]
- Yoon, G.H.; Kim, Y.Y.; Bendse, M.P.; Sigmund, O. Hinge-free topology optimization with embedded translation-invariant differentiate wavelet shrinkage. Struct. Multidiscip. Optim. 2004, 27, 139–150. [Google Scholar] [CrossRef]
- Bendsøe, M.; Kikuchi, N. Generating optimal topologies in structural design using a homogenization method. Comput. Methods Appl. Mech. Eng. 1988, 71, 197–224. [Google Scholar] [CrossRef]
- Sigmund, O. Design of multiphysics actuators using topology optimization–Part I: One-material structures. Comput. Methods Appl. Mech. Eng. 2001, 190, 6605–6627. [Google Scholar] [CrossRef]
- Dühring, M.; Jensen, J.S.; Sigmund, O. Acoustic design by topology optimization. J. Sound Vib. 2008, 317, 557–575. [Google Scholar] [CrossRef]
- S Rensen, R.; Lund, E. Thickness filters for gradient based multi-material and thickness optimization of laminated composite structures. Struct. Multidiscip. Optim. 2015, 52, 227–250. [Google Scholar] [CrossRef]
- Christiansen, R.E.; Sigmund, O. Experimental validation of systematically designed acoustic hyperbolic meta material slab exhibiting negative refraction. Appl. Phys. Lett. 2016, 109, 469–482. [Google Scholar] [CrossRef] [Green Version]
- Jensen, J.S.; Sigmund, O. Topology optimization for nano-photonics. Laser Photonics Rev. 2011, 5, 308–321. [Google Scholar] [CrossRef]
- Andkjær, J.; Nishiwaki, S.; Nomura, T.; Sigmund, O. Topology optimization of grating couplers for the efficient excitation of surface plasmons. J. Opt. Soc. Am. B 2010, 27, 1828–1832. [Google Scholar] [CrossRef] [Green Version]
- Duhring, M.B. Plasmonic versus dielectric enhancement in thin-film solar cells. Appl. Phys. Lett. 2012, 100, 667–669. [Google Scholar] [CrossRef] [Green Version]
- Deng, Y.; Liu, Z.; Chao, S.; Peng, H.; Wu, Y.; Liu, Y.; Korvink, J.G. Topology optimization of metal nanostructures for localized surface plasmon resonances. Struct. Multidiscip. Optim. 2016, 53, 967–972. [Google Scholar] [CrossRef]
- Jin, J.-M. The Finite Element Method in Electromagnetics; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Johnson, P.B.; Christy, R.W. Optical Constants of the Noble Metals. Phys. Rev. B 1972, 6, 4370–4379. [Google Scholar] [CrossRef]
- Gric, T.; Cada, M. Analytic solution to field distribution in one-dimensional inhomogeneous media. Opt. Commun. 2014, 322, 183–187. [Google Scholar] [CrossRef]
- Gric, T.; Eldlio, M.; Cada, M.; Pistora, J. Analytic solution to field distribution in two-dimensional inhomogeneous waveguides. J. Electromagn. Waves Appl. 2015, 29, 1068–1081. [Google Scholar] [CrossRef]
- Berenger, J.P. A perfectly matched layer for the absorption of electromagnetic waves. Phys. Plasmas 2015, 114, 185–200. [Google Scholar] [CrossRef]
- Fan, S.S. Choice of the perfectly matched layer boundary condition for frequency-domain Maxwell’s equations solvers. J. Comput. Phys. 2012, 231, 3406–3431. [Google Scholar]
- Deng, Y.; Korvink, J.G. Topology optimization for three-dimensional electromagnetic waves using an edge element-based finite-element method. Proc. R. Soc. Lond. 2016, 472, 20150835. [Google Scholar] [CrossRef]
- Guest, J.K.; Prévost, J.; Belytschko, T. Achieving minimum length scale in topology optimization using nodal design variables and projection functions. Int. J. Numer. Methods Eng. 2004, 61, 238–254. [Google Scholar] [CrossRef]
- Wang, F.; Lazarov, B.S.; Sigmund, O. On projection methods, convergence and robust formulations in topology optimization. Struct. Multidiscip. Optim. 2011, 43, 767–784. [Google Scholar] [CrossRef]
- Sigmund, O. Morphology-based black and white filters for topology optimization. Struct. Multidiscip. Optim. 2007, 33, 401–424. [Google Scholar] [CrossRef] [Green Version]
- Hinze; Pinnau, M.; Ulbrich, R.; Ulbri, M. Optimization with PDE Constraints; Springer: Berlin, Germany, 2009. [Google Scholar]
- Svanberg, K. The method of moving asymptotes—A new method for structural optimization. Int. J. Numer. Methods Eng. 1987, 24, 359–373. [Google Scholar] [CrossRef]
- Deng, Y.; Korvink, J.G. Self-consistent adjoint analysis for topology optimization of electromagnetic waves. J. Comput. Phys. 2018, 361, 353–376. [Google Scholar] [CrossRef]
- Weise, W. Image formation of confocal microscopes using Lorentz's reciprocity theorem. Opt. Commun. 2002, 202, 21–28. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Y.; Lin, Y.; Ma, W.; Korvink, J.G.; Duan, H.; Deng, Y. Nanoantennas Inversely Designed to Couple Free Space and a Metal–Insulator–Metal Waveguide. Nanomaterials 2021, 11, 3219. https://doi.org/10.3390/nano11123219
Han Y, Lin Y, Ma W, Korvink JG, Duan H, Deng Y. Nanoantennas Inversely Designed to Couple Free Space and a Metal–Insulator–Metal Waveguide. Nanomaterials. 2021; 11(12):3219. https://doi.org/10.3390/nano11123219
Chicago/Turabian StyleHan, Yeming, Yu Lin, Wei Ma, Jan G. Korvink, Huigao Duan, and Yongbo Deng. 2021. "Nanoantennas Inversely Designed to Couple Free Space and a Metal–Insulator–Metal Waveguide" Nanomaterials 11, no. 12: 3219. https://doi.org/10.3390/nano11123219
APA StyleHan, Y., Lin, Y., Ma, W., Korvink, J. G., Duan, H., & Deng, Y. (2021). Nanoantennas Inversely Designed to Couple Free Space and a Metal–Insulator–Metal Waveguide. Nanomaterials, 11(12), 3219. https://doi.org/10.3390/nano11123219






