Microscopic and Macroscopic Fragmentation Characteristics under Hypervelocity Impact Based on MD and SPH Method
Abstract
:1. Introduction
2. Numerical Simulation Method
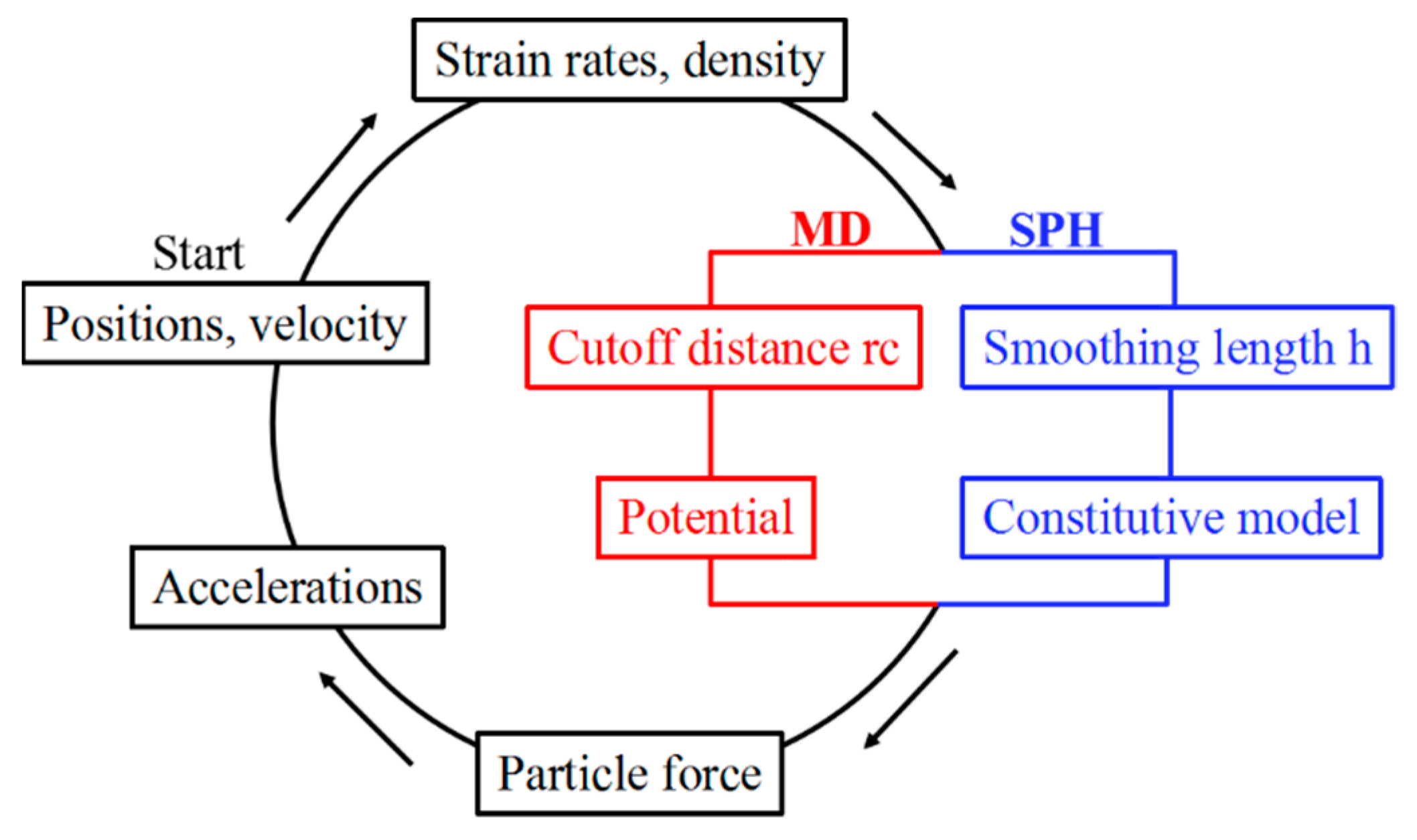
2.1. Molecular Dynamics
2.2. Smoothed Particle Hydrodynamics
3. Simulation Details
3.1. MD Computational Details
3.2. SPH Computational Details
4. Results and Discussion
4.1. Analysis of Debris Formation Process
4.2. Comparison of Debris Cloud Characteristics
5. Conclusions
- (1)
- Compared with the typical microscopic debris cloud, the microscopic results show distinct differences. Under low shock intensity, the impacted area of the target gradually dents inward, and eventually protrudes on the back of target, showing good penetration resistance. Under high shock intensity, the width of the ejecta veil and external bubble of the debris cloud are narrower. More interestingly, the number of voids formed in the internal structure region is smaller, but the size is larger. In addition, the velocity decay rate and temperature rise rate of the bullet are much faster than those under the macro-scale.
- (2)
- The propagation law of shock wave is very similar for the microscopic and macroscopic results. However, after the loading and unloading, the residual velocity of bullet, crater diameter and expansion angle of the debris cloud at the micro-scale are all smaller than those at the macro-scale, especially for low-velocity conditions. These characteristics indicate that the degree of conversion of kinetic energy to internal energy at the microscopic scale is much higher (by about one) than that of the macroscopic results.
- (3)
- The MD simulation method can further provide more details of the physical characteristics at the micro-scale. Both the dislocation under low shock intensity and local melting under high shock intensity are shown. Furthermore, the number of disordered atoms increases rapidly from 0, and then gradually stabilizes due to the end of the penetration process. The fraction of disordered atoms then increases exponentially with the increasing incident kinetic energy.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Verma, P.N.; Dhote, K.D. Characterising primary fragment in debris cloud formed by hypervelocity impact of spherical stainless steel projectile on thin steel plate. Int. J. Impact Eng. 2018, 120, 118–125. [Google Scholar] [CrossRef]
- Piekutowski, A.J. Debris clouds generated by hypervelocity impact of cylindrical projectiles with thin aluminum plates. Int. J. Impact Eng. 1987, 5, 509–518. [Google Scholar] [CrossRef]
- Piekutowski, A.J. A simple dynamic model for the formation of debris clouds. Int. J. Impact Eng. 1990, 10, 453–471. [Google Scholar] [CrossRef]
- Piekutowski, A.J. Characteristics of debris clouds produced by hypervelocity impact of aluminum spheres with thin aluminum plates. Int. J. Impact Eng. 1993, 14, 573–586. [Google Scholar] [CrossRef]
- Kipp, M.E.; Grady, D.E.; Swegle, J.W. Numerical and experimental studies of high-velocity impact fragmentation. Int. J. Impact Eng. 1993, 14, 427–438. [Google Scholar] [CrossRef]
- Piekutowski, A.J. Fragmentation-initiation threshold for spheres impacting at hypervelocity. Int. J. Impact Eng. 2003, 29, 563–574. [Google Scholar] [CrossRef]
- Myers, B.A.; Schonberg, W.P.; Williamsen, J.E. Temperature effects on bumper hole diameters for impact velocities from 2 to 7 km/s. Int. J. Impact Eng. 2003, 29, 487–495. [Google Scholar] [CrossRef]
- Alme, M.L.; Rhoades, C.E. A computational study of projectile melt in impact with typical whipple shields. Int. J. Impact Eng. 1995, 17, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Reimerdes, H.G.; Nolke, D.; Schafer, F. Modified Cour-Palais/Christiansen damage equations for double-wall structures. Int. J. Impact Eng. 2006, 33, 645–654. [Google Scholar] [CrossRef]
- Hill, S.A. Determination of an empirical model for the prediction of penetration hole diameter in thin plates from hypervelocity impact. Int. J. Impact Eng. 2004, 30, 303–321. [Google Scholar] [CrossRef]
- Huang, J.; Ma, Z.X.; Ren, L.S.; Li, Y.; Zhou, Z.-X.; Liu, S. A new engineering model of debris cloud produced by hypervelocity impact. Int. J. Impact Eng. 2013, 56, 32–39. [Google Scholar] [CrossRef]
- Kawai, N.; Zama, S.; Takemoto, W.; Moriguchi, K.; Arai, K.; Hasegawa, S.; Sato, E. Stress wave and damage propagation in transparent materials subjected to hypervelocity impact. Procedia Eng. 2015, 103, 287–293. [Google Scholar] [CrossRef]
- Song, W.J.; Chen, X.W.; Chen, P. A simplified approximate model of compressible hypervelocity penetration. Acta Mech. Sinica-Prc. 2018, 34, 910–924. [Google Scholar] [CrossRef]
- Barbosa, H.J.C.; Hughes, T.J.R. The finite element method with Lagrange multipliers on the boundary: Circumventing the Babuška-Brezzi condition. Comput. Method Appl. Mech. Eng. 1991, 85, 109–128. [Google Scholar] [CrossRef]
- Pai, P.F.; Anderson, T.J.; Wheater, E.A. Large-deformation tests and total-Lagrangian finite-element analyses of flexible beams. Int. J. Solids Struct. 2000, 37, 2951–2980. [Google Scholar] [CrossRef]
- Chen, X.; Guo, H.Y.; Zhao, P.; Peng, X.; Wang, S.Z. Numerical modeling of large deformation and nonlinear frictional contact of excavation boundary of deep soft rock tunnel. J. Rock Mech. Geotech. 2011, 3, 421–428. [Google Scholar] [CrossRef]
- Hu, Y.J.; Zhou, H.T.; Zhu, W.D.; Jiang, C. Large deformation analysis of composite spatial curved beams with arbitrary undeformed configurations described by Euler angles with discontinuities and singularities. Comp. Struct. 2018, 210, 122–134. [Google Scholar] [CrossRef]
- Liu, J.C.; Li, S.H.; Wang, L.; Feng, C.; Qian, F.; Wang, J.; Zhu, X. A numerical method for the solid mechanics with Euler variables. J. Phys. Conf. Ser. 2021, 1980, 012018. [Google Scholar] [CrossRef]
- Liu, M.B.; Liu, G.R. Smoothed particle hydrodynamics (SPH): An overview and recent developments. Arch. Comp. Methods Eng. 2010, 17, 25–76. [Google Scholar] [CrossRef] [Green Version]
- Fahrenthold, E.P. Oblique hypervelocity impact simulation for Whipple shield-protected structures. Int. J. Impact Eng. 1995, 17, 291–302. [Google Scholar] [CrossRef]
- Silnikov, M.V.; Guk, I.V.; Nechunaev, A.F.; Smirnov, N. Numerical simulation of hypervelocity impact problem for spacecraft shielding elements. Acta Astronaut. 2018, 150, 56–62. [Google Scholar] [CrossRef]
- He, Q.G.; Chen, X.W.; Chen, J.F. Finite element-smoothed particle hydrodynamics adaptive method in simulating debris cloud. Acta Astronaut. 2020, 175, 99–117. [Google Scholar] [CrossRef]
- Zhang, C.B.; Di, D.N.; Chen, X.W.; Wen, K. Characteristics structure analysis on debris cloud in the hypervelocity impact of disk projectile on thin plate. Def. Technol. 2020, 16, 299–307. [Google Scholar] [CrossRef]
- Madruga, S.; Curbelo, J. Dynamic of plumes and scaling during the melting of a Phase Change Material heated from below. Int. J. Heat Mass Tran. 2018, 126, 206–220. [Google Scholar] [CrossRef] [Green Version]
- Li, B.; Perotti, L.; Adams, M.; Mihály, J.; Rosakis, A.; Stalzer, M.; Ortiz, M. Large scale optimal transportation meshfree (OTM) simulations of hypervelocity impact. Procedia Eng. 2013, 58, 320–327. [Google Scholar] [CrossRef] [Green Version]
- Johnson, G.; Beissel, S.; Gerlach, C. A combined particle-element method for high-velocity impact computations. Procedia Eng. 2013, 58, 269–278. [Google Scholar] [CrossRef] [Green Version]
- Baluch, A.H.; Park, Y.; Kim, C.G. High velocity impact characterization of Al alloys for oblique impacts. Acta Astronaut. 2014, 105, 128–135. [Google Scholar] [CrossRef]
- Silnikov, M.; Guk, I.; Mikhaylin, A.; Nechunaev, A. Efficiency of needle structure at hypervelocity impact. Acta Astronaut. 2018, 150, 73–80. [Google Scholar] [CrossRef]
- Zhang, X.; Sze, K.; Mam, S. An explicit material point finite element method for hyper-velocity impact. Int. J. Numer. Methods Eng. 2006, 66, 689–706. [Google Scholar] [CrossRef]
- Wang, H.Y.; Li, X.S.; Zhu, W.J.; Deng, X.-L.; Song, Z.-F.; Chen, X.-R. Atomistic modelling of the plastic deformation of helium bubbles and voids in aluminum under shock compression. Radiat. Eff. Defects Solids 2014, 169, 109. [Google Scholar] [CrossRef]
- Shao, J.L.; Wang, P.; He, A.M. Compression-induced stacking fault tetrahedra around He bubbles in Al. J. Appl. Phys. 2014, 116, 163516. [Google Scholar] [CrossRef]
- Zhou, T.T.; He, A.M.; Wang, P.; Shao, J.-L. Spall damage in single crystal Al with helium bubbles under decaying shock loading via molecular dynamics study. Comp. Mater. Sci. 2019, 162, 255–267. [Google Scholar] [CrossRef]
- Shao, J.L.; Wang, P.; He, A.M.; Duan, S.-Q.; Qin, C.-S. Influence of voids or He bubbles on the spall damage in single crystal Al. Model. Simul. Mater. Sci. Eng. 2014, 22, 025012. [Google Scholar] [CrossRef]
- Li, B.; Wang, L.; Eisenstein, J.C.; Ma, H.H.; Luo, S.N. Shock response of He bubbles in single crystal Cu. J. Appl. Phys. 2014, 116, 213506. [Google Scholar] [CrossRef]
- Holian, B.L. Hypervelocity-impact phenomena via molecular dynamics. Phys. Rev. A 1987, 36, 3943–3947. [Google Scholar] [CrossRef]
- Steinhauser, M.O. Particle-based modeling of hypervelocity impact and fragmentation in materials. First Int. Orbital Debris Conf. 2019, 2109, 6200. [Google Scholar]
- Bažant, Z.P. Size effect on structural strength: A review. Arch. Appl. Mech. 1999, 69, 703–725. [Google Scholar] [CrossRef]
- Zhakhovskii, V.V.; Inogamov, N.A.; Petrov, Y.V.; Ashitkov, S.; Nishihara, K. Molecular dynamics simulation of femtosecond ablation and spallation with different interatomic potentials. Appl. Surf. Sci. 2009, 255, 9592–9596. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comp. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO: The open visualization tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Liu, W.D.; Liu, K.X.; Chen, Q.Y.; Wang, J.; Yan, H.; Li, X. Metallic glass coating on metals plate by adjusted explosive welding technique. Appl. Surf. Sci. 2009, 255, 9343–9347. [Google Scholar] [CrossRef]
- Messerschmidt, U.; Bartsch, M. Generation of dislocations during plastic deformation. Mater. Chem. Phys. 2003, 81, 518–523. [Google Scholar] [CrossRef]
- Zaccone, A.; Scossa-Romano, E. Approximate analytical description of the nonaffine response of amorphous solids. Phys. Rev. B 2011, 83, 184205. [Google Scholar] [CrossRef] [Green Version]
- Milkus, R.; Zaccone, A. Local inversion-symmetry breaking controls the boson peak in glasses and crystals. Phys. Rev. B 2016, 93, 094204. [Google Scholar] [CrossRef]
- Sprakel, J.; Zaccone, A.; Spaepen, F.; Schall, P.; Weitz, D.A. Direct Observation of Entropic Stabilization of bcc Crystals Near Melting. Phys. Rev. Lett. 2017, 118, 088003. [Google Scholar] [CrossRef] [Green Version]
- Depczuk, D.; Schonberg, W.P. Characterizing debris clouds created in oblique orbital debris particle impact. J. Aerospace Eng. 2003, 16, 177–190. [Google Scholar] [CrossRef]








| ρ (g/cm3) | A (MPa) | B (MPa) | Heat Capacity (J/(kg·°C)) | Thermal Conductivity (w/(m·°C)) |
|---|---|---|---|---|
| 2.77 | 265 | 426 | 880 | 237 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, W.-D.; Liu, J.-M.; Xie, W.; Xing, Y.; Shao, J.-L. Microscopic and Macroscopic Fragmentation Characteristics under Hypervelocity Impact Based on MD and SPH Method. Nanomaterials 2021, 11, 2953. https://doi.org/10.3390/nano11112953
Wu W-D, Liu J-M, Xie W, Xing Y, Shao J-L. Microscopic and Macroscopic Fragmentation Characteristics under Hypervelocity Impact Based on MD and SPH Method. Nanomaterials. 2021; 11(11):2953. https://doi.org/10.3390/nano11112953
Chicago/Turabian StyleWu, Wei-Dong, Jin-Ming Liu, Wei Xie, Yan Xing, and Jian-Li Shao. 2021. "Microscopic and Macroscopic Fragmentation Characteristics under Hypervelocity Impact Based on MD and SPH Method" Nanomaterials 11, no. 11: 2953. https://doi.org/10.3390/nano11112953
APA StyleWu, W.-D., Liu, J.-M., Xie, W., Xing, Y., & Shao, J.-L. (2021). Microscopic and Macroscopic Fragmentation Characteristics under Hypervelocity Impact Based on MD and SPH Method. Nanomaterials, 11(11), 2953. https://doi.org/10.3390/nano11112953






