Simulating the Self-Assembly and Hysteresis Loops of Ferromagnetic Nanoparticles with Sticking of Ligands
Abstract
1. Introduction
2. Materials and Methods
2.1. Simulations
2.2. Estimate of the Sticking Parameter
3. Results
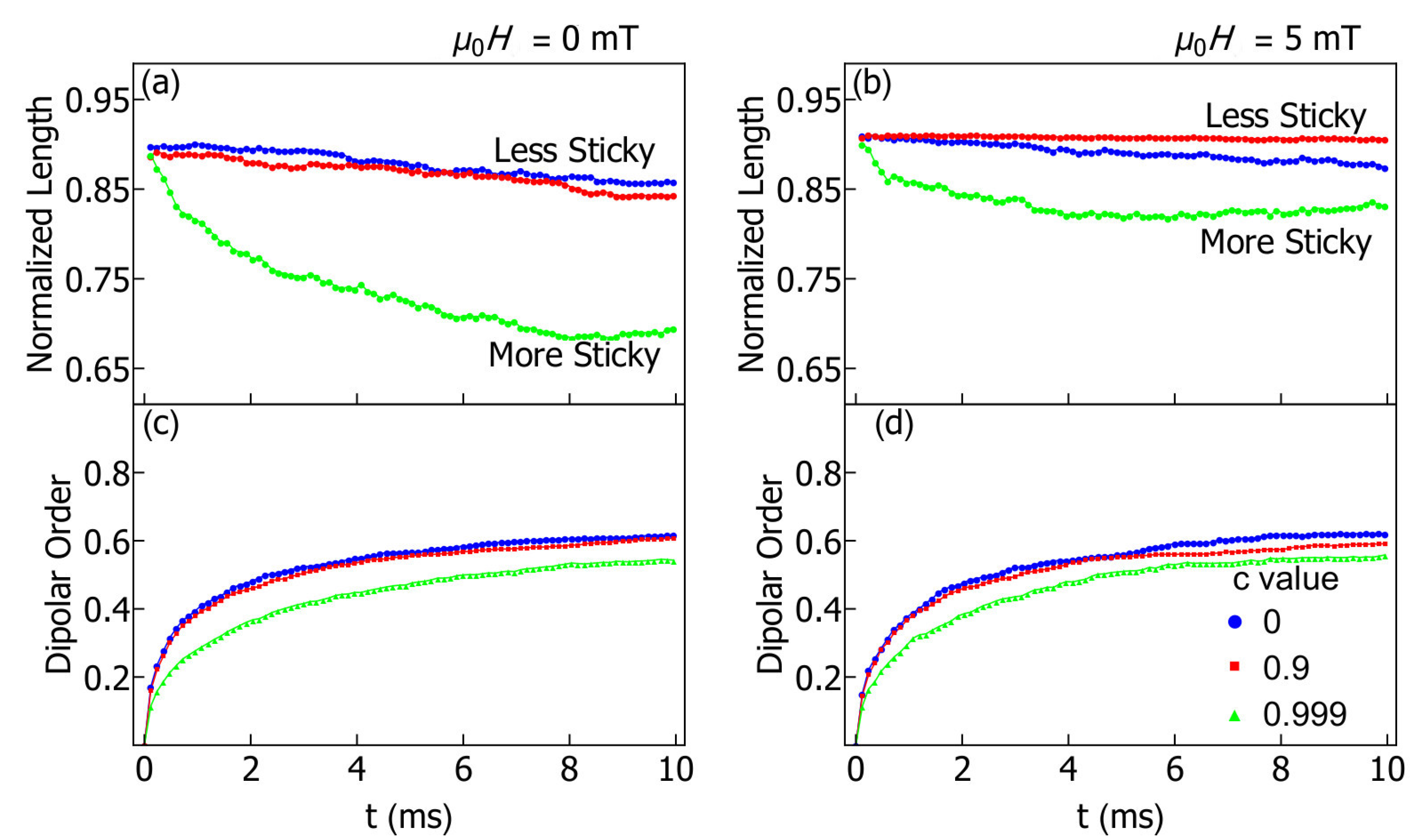
3.1. Assembly in a Uniform, Constant Field
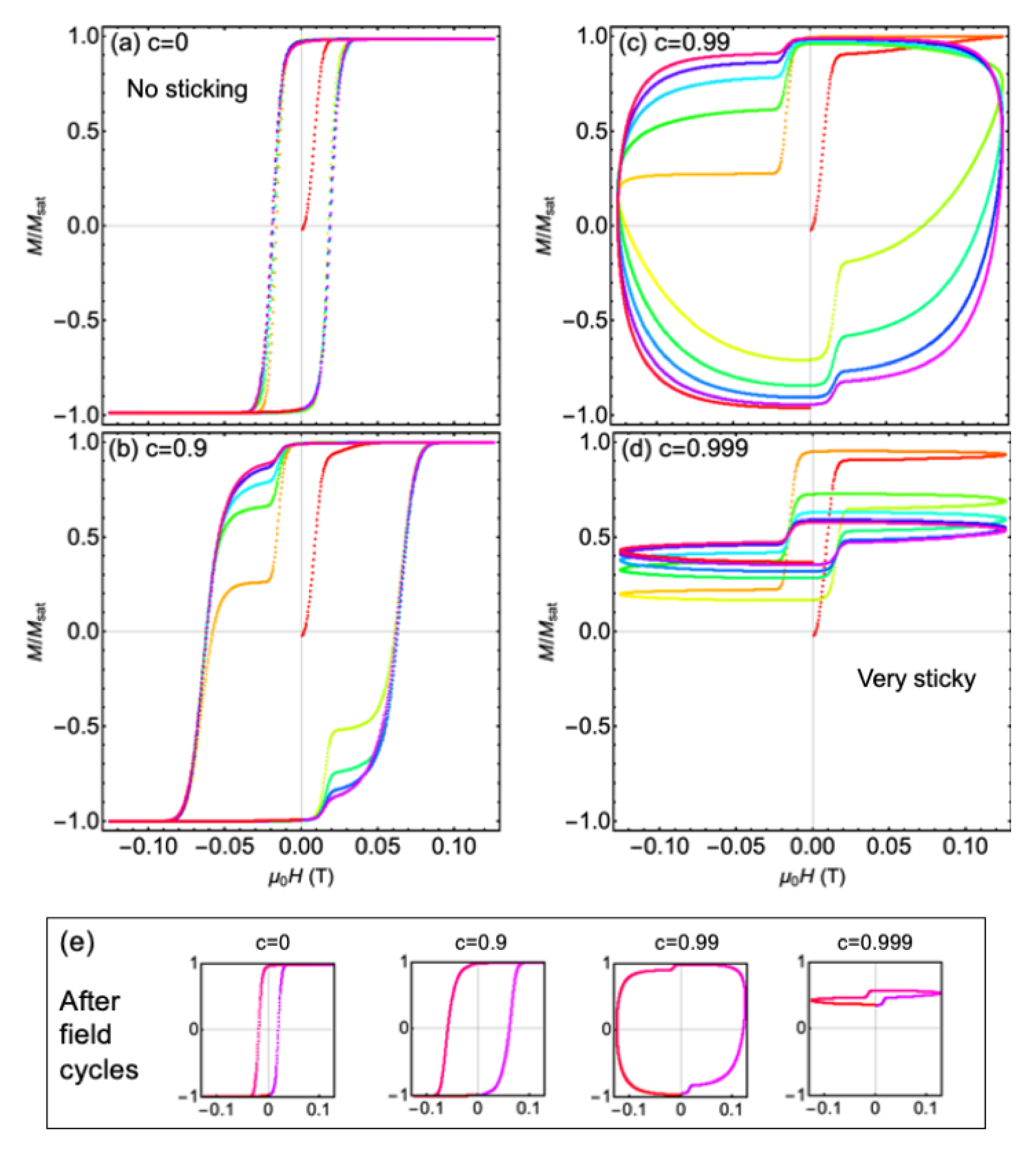
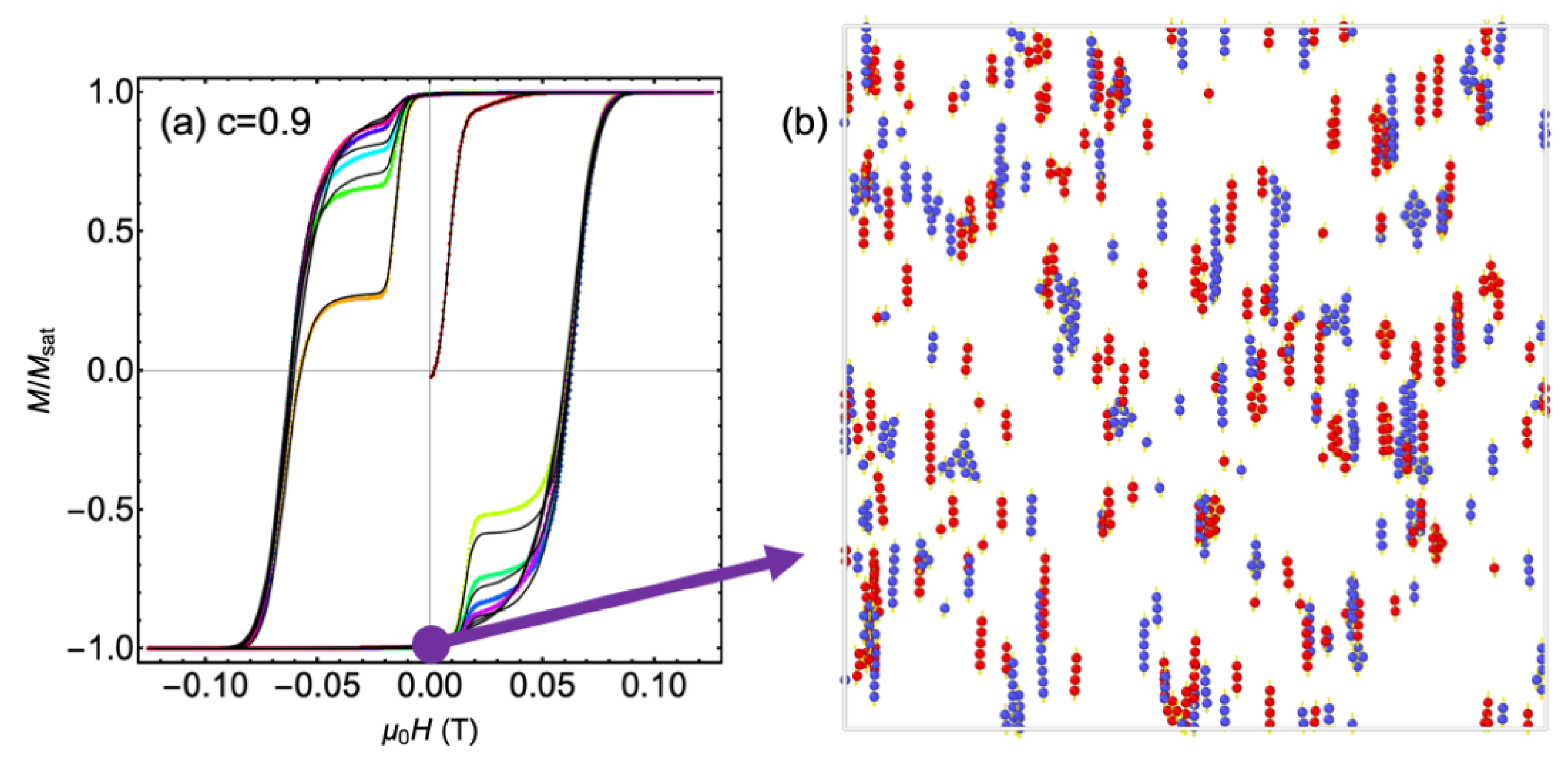
3.2. Hysteresis Loops
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Particle Interactions
References
- Badia, A.; Singh, S.; Demers, L.; Cuccia, L.; Brown, G.R.; Lennox, R.B. Self-Assembled Monolayers on Gold Nanoparticles. Chem.–Eur. J. 1996, 2, 359–363. [Google Scholar] [CrossRef]
- Sahoo, Y.; Pizem, H.; Fried, T.; Golodnitsky, D.; Burstein, L.; Sukenik, C.N.; Markovich, G. Alkyl phosphonate/phosphate coating on magnetite nanoparticles: A comparison with fatty acids. Langmuir 2001, 17, 7907–7911. [Google Scholar] [CrossRef]
- Wang, J.C.; Neogi, P.; Forciniti, D. On one-dimensional self-assembly of surfactant-coated nanoparticles. J. Chem. Phys. 2006, 125, 194717. [Google Scholar] [CrossRef] [PubMed]
- Nakata, K.; Hu, Y.; Uzun, O.; Bakr, O.; Stellacci, F. Chains of superparamagnetic nanoparticles. Adv. Mater. 2008, 20, 4294–4299. [Google Scholar] [CrossRef]
- Zhou, S.; Sakamoto, T.; Wang, J.; Sugawara-Narutaki, A.; Shimojima, A.; Okubo, T. One-dimensional assembly of silica nanospheres: Effects of nonionic block copolymers. Langmuir 2012, 28, 13181–13188. [Google Scholar] [CrossRef] [PubMed]
- Etheridge, M.L.; Hurley, K.R.; Zhang, J.; Jeon, S.; Ring, H.L.; Hogan, C.; Haynes, C.L.; Garwood, M.; Bischof, J.C. Accounting for biological aggregation in heating and imaging of magnetic nanoparticles. Technology 2014, 2, 214–228. [Google Scholar] [CrossRef] [PubMed]
- Kahmei, R.R.; Borah, J. Clustering of MnFe2O4 nanoparticles and the effect of field intensity in the generation of heat for hyperthermia application. Nanotechnology 2018, 30, 035706. [Google Scholar] [CrossRef]
- Walkey, C.D.; Chan, W.C. Understanding and controlling the interaction of nanomaterials with proteins in a physiological environment. Chem. Soc. Rev. 2012, 41, 2780–2799. [Google Scholar] [CrossRef]
- Pankhurst, Q.; Connolly, J.; Jones, S.; Dobson, J. Applications of magnetic nanoparticles in biomedicine. J. Phys. D Appl. Phys. 2003, 36, R167–R181. [Google Scholar] [CrossRef]
- Johannsen, M.; Gneveckow, U.; Taymoorian, K.; Thiesen, B.; Waldöfner, N.; Scholz, R.; Jung, K.; Jordan, A.; Wust, P.; Loening, S. Morbidity and quality of life during thermotherapy using magnetic nanoparticles in locally recurrent prostate cancer: Results of a prospective phase I trial. Int. J. Hyperth. 2007, 23, 315–323. [Google Scholar] [CrossRef]
- Dobson, J. Magnetic nanoparticles for drug delivery. Drug Dev. Res. 2006, 67, 55–60. [Google Scholar] [CrossRef]
- Nam, J.M.; Thaxton, C.S.; Mirkin, C.A. Nanoparticle-based bio-bar codes for the ultrasensitive detection of proteins. Science 2003, 301, 1884–1886. [Google Scholar] [CrossRef]
- Zabow, G.; Dodd, S.; Moreland, J.; Koretsky, A. Micro-engineered local field control for high-sensitivity multispectral MRI. Nature 2008, 453, 1058–1063. [Google Scholar] [CrossRef]
- Maldonado-Camargo, L.; Unni, M.; Rinaldi, C. Magnetic Characterization of Iron Oxide Nanoparticles for Biomedical Applications. In Biomedical Nanotechnology: Methods and Protocols; Hurst Petrosko, S., Day, E., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; pp. 47–71. [Google Scholar]
- Saville, S.L.; Qi, B.; Baker, J.; Stone, R.; Camley, R.E.; Livesey, K.L.; Ye, L.; Crawford, T.M.; Mefford, O.T. The formation of linear aggregates in magnetic hyperthermia: Implications on specific absorption rate and magnetic anisotropy. J. Colloid Interf. Sci. 2014, 424, 141–151. [Google Scholar] [CrossRef]
- Serantes, D.; Simeonidis, K.; Angelakeris, M.; Chubykalo-Fesenko, O.; Marciello, M.; del Puerto Morales, M.; Baldomir, D.; Martinez-Boubeta, C. Multiplying Magnetic Hyperthermia Response by Nanoparticle Assembling. J. Phys. Chem. C 2014, 118, 5927–5934. [Google Scholar] [CrossRef]
- Tan, R.; Carrey, J.; Respaud, M. Magnetic hyperthermia properties of nanoparticles inside lysosomes using kinetic Monte Carlo simulations: Influence of key parameters and dipolar interactions, and evidence for strong spatial variation of heating power. Phys. Rev. B 2014, 90, 214421. [Google Scholar] [CrossRef]
- Varón, M.; Beleggia, M.; Kasama, T.; Harrison, R.; Dunin-Borkowski, R.; Puntes, V.; Frandsen, C. Dipolar magnetism in ordered and disordered low-dimensional nanoparticle assemblies. Sci. Rep. 2013, 3, 1234. [Google Scholar] [CrossRef] [PubMed]
- Faraudo, J.; Andreu, J.S.; Calero, C.; Camacho, J. Predicting the Self-Assembly of Superparamagnetic Colloids under Magnetic Fields. Adv. Funct. Mater. 2016, 26, 3837–3858. [Google Scholar] [CrossRef]
- Satoh, A.; Chantrell, R.W.; Kamiyama, S.I.; Coverdale, G.N. Two-dimensional Monte Carlo simulations to capture thick chainlike clusters of ferromagnetic particles in colloidal dispersions. J. Colloid Interf. Sci. 1996, 178, 620–627. [Google Scholar] [CrossRef]
- Satoh, A.; Chantrell, R.W.; Kamiyama, S.I.; Coverdale, G.N. Three dimensional Monte Carlo simulations of thick chainlike clusters composed of ferromagnetic fine particles. J. Colloid Interf. Sci. 1996, 181, 422–428. [Google Scholar] [CrossRef]
- Lemons, D.S.; Gythiel, A. Paul Langevin’s 1908 paper “On the theory of Brownian motion” [“Sur la théorie du mouvement Brownien,” CR Acad. Sci.(Paris) 146, 530–533 (1908)]. Am. J. Phys. 1997, 65, 1079–1081. [Google Scholar] [CrossRef]
- Ermak, D.L.; McCammon, J. Brownian dynamics with hydrodynamic interactions. J. Chem. Phys. 1978, 69, 1352–1360. [Google Scholar] [CrossRef]
- Durlofsky, L.; Brady, J.F.; Bossis, G. Dynamic simulation of hydrodynamically interacting particles. J. Fluid Mech. 1987, 180, 21–49. [Google Scholar] [CrossRef]
- Andreu, J.; Calero, C.; Camacho, J.; Faraudo, J. On-the-fly coarse-graining methodology for the simulation of chain formation of superparamagnetic colloids in strong magnetic fields. Phys. Rev. E 2012, 85, 036709. [Google Scholar] [CrossRef]
- Dong, M.; Sahin, O. A nanomechanical interface to rapid single-molecule interactions. Nat. Commun. 2011, 2, 247. [Google Scholar] [CrossRef] [PubMed]
- Xue, Y.; Li, X.; Li, H.; Zhang, W. Quantifying thiol-gold interactions towards the efficient strength control. Nat. Commun. 2014, 5, 4348. [Google Scholar] [CrossRef]
- Wang, Z.; Holm, C.; Müller, H.W. Molecular dynamics study on the equilibrium magnetization properties and structure of ferrofluids. Phys. Rev. E 2002, 66, 021405. [Google Scholar] [CrossRef]
- Liu, T.; Gong, X.; Xu, Y.; Xuan, S. Magneto-induced stress enhancing effect in a colloidal suspension of paramagnetic and superparamagnetic particles dispersed in a ferrofluid medium. Soft Matter 2014, 10, 813–818. [Google Scholar] [CrossRef] [PubMed]
- Israelachvili, J.N. Intermolecular and Surface Forces; Academic Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Weddemann, A.; Ennen, I.; Regtmeier, A.; Albon, C.; Wolff, A.; Eckstädt, K.; Mill, N.; Peter, M.K.H.; Mattay, J.; Plattner, C.; et al. Review and outlook: From single nanoparticles to self-assembled monolayers and granular GMR sensors. Beilstein J. Nanotechnol. 2010, 1, 75–93. [Google Scholar] [CrossRef] [PubMed]
- Berkov, D.V.; Gorn, N.L.; Schmitz, R.; Stock, D. Langevin dynamic simulations of fast remagnetization processes in ferrofluids with internal magnetic degrees of freedom. J. Phys.-Cond. Mat. 2006, 18, S2595. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Oxford University Press: Oxford, UK, 1989. [Google Scholar]
- Wang, Z.; Holm, Z. Estimate of the curoff errors in the Ewald summation for dipolar systems. J. Chem. Phys. 2001, 115, 6351–6359. [Google Scholar] [CrossRef]
- Van Gunsteren, W.; Berendsen, H. Algorithms for Brownian dynamics. Mol. Phys. 1982, 45, 637–647. [Google Scholar] [CrossRef]
- Faure, B.; Salazar-Alvarez, G.; Bergstrom, L. Hamaker Constants of Iron Oxide Nanoparticles. Langmuir 2011, 27, 8659–8664. [Google Scholar] [CrossRef]
- Balakrishnan, P.B.; Silvestri, N.; Fernandez-Cabada, T.; Marinaro, F.; Fernandes, S.; Fiorito, S.; Miscuglio, M.; Serantes, D.; Ruta, S.; Livesey, K.; et al. Exploiting Unique Alignment of Cobalt Ferrite Nanoparticles, Mild Hyperthermia, and Controlled Intrinsic Cobalt Toxicity for Cancer Therapy. Adv. Mater. 2020, 32, 2003712. [Google Scholar] [CrossRef]
- Lamb, H. Hydrodynamics; Dover: New York, NY, USA, 1945. [Google Scholar]
- Pathria, R.K.; Beale, P.D. Statistical Mechanics, 3rd ed.; Elsevier: Oxford, UK, 2011. [Google Scholar]
- Wozniak, M.; Onofri, F.; Barbosa, S.; Yon, J.; Mroczka, J. Comparison of methods to derive morphological parameters of multi-fractal samples of particle aggregates from TEM images. J. Aerosol Sci. 2012, 47, 12–26. [Google Scholar] [CrossRef]
- Hovorka, O. Thermal activation in statistical clusters of magnetic nanoparticles. J. Phys. D Appl. Phys. 2017, 50, 044004. [Google Scholar] [CrossRef][Green Version]
- Holthoff, H.; Egelhaaf, S.U.; Borkovec, M.; Schurtenberger, P.; Sticher, H. Coagulation rate measurements of colloidal particles by simultaneous static and dynamic light scattering. Langmuir 1996, 12, 5541–5549. [Google Scholar] [CrossRef]
- Di Marco, M.; Guilbert, I.; Port, M.; Robic, C.; Couvreur, P.; Dubernet, C. Colloidal stability of ultrasmall superparamagnetic iron oxide (USPIO) particles with different coatings. Int. J. Pharm. 2007, 331, 197–203. [Google Scholar] [CrossRef]
- Hergt, R.; Dutz, S.; Müller, R.; Zeisberger, M. Magnetic particle hyperthermia: Nanoparticle magnetism and materials development for cancer therapy. J. Phys. Condens. Matter 2006, 18, S2919. [Google Scholar] [CrossRef]
- Muñoz Menendez, C.; Serantes, D.; Chubykalo-Fesenko, O.; Ruta, S.; Hovorka, O.; Nieves, P.; Livesey, K.L.; Baldomir, D.; Chantrell, R. Disentangling local heat contributions in interacting magnetic nanoparticles. Phys. Rev. B 2020, 102, 214412. [Google Scholar] [CrossRef]
- Lee, W.K.; Ilavsky, J. Particle size distribution in ferrofluid macro-clusters. J. Magn. Magn. Mater. 2013, 330, 31–36. [Google Scholar] [CrossRef]
- Aoshima, M.; Satoh, A. Two-dimensional Monte Carlo simulations of a colloidal dispersion composed of polydisperse ferromagnetic particles in an applied magnetic field. J. Colloid Interf. Sci. 2005, 288, 475–488. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Zhang, J.; Zhang, H.; Zhou, Z. Magnetic moment and volume fraction controlling chain-like structures of magnetic nanoparticles in uniform magnetic fields. J. Nanopartic. Res. 2021, 23, 1–9. [Google Scholar] [CrossRef]
- Morales, I.; Costo, R.; Mille, N.; Carrey, J.; Hernando, A.; de la Presa, P. Time-dependent AC magnetometry and chain formation in magnetite: The influence of particle size, initial temperature and the shortening of the relaxation time by the applied field. Nanoscale Adv. 2021, 3, 5801–5812. [Google Scholar] [CrossRef]
- Tay, Z.W.; Savliwala, S.; Hensley, D.W.; Fung, K.B.; Colson, C.; Fellows, B.D.; Zhou, X.; Huynh, Q.; Lu, Y.; Zheng, B.; et al. Superferromagnetic Nanoparticles Enable Order-of-Magnitude Resolution & Sensitivity Gain in Magnetic Particle Imaging. Small Methods 2021, 2021, 2100796. [Google Scholar] [CrossRef]
- Mohebi, M.; Jamasbi, N.; Liu, J. Simulation of the formation of nonequilibrium structures in magnetorheological fluids subject to an external magnetic field. Phys. Rev. E 1996, 54, 5407. [Google Scholar] [CrossRef] [PubMed]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anderson, N.R.; Davidson, J.; Louie, D.R.; Serantes, D.; Livesey, K.L. Simulating the Self-Assembly and Hysteresis Loops of Ferromagnetic Nanoparticles with Sticking of Ligands. Nanomaterials 2021, 11, 2870. https://doi.org/10.3390/nano11112870
Anderson NR, Davidson J, Louie DR, Serantes D, Livesey KL. Simulating the Self-Assembly and Hysteresis Loops of Ferromagnetic Nanoparticles with Sticking of Ligands. Nanomaterials. 2021; 11(11):2870. https://doi.org/10.3390/nano11112870
Chicago/Turabian StyleAnderson, Nicholas R., Jonathon Davidson, Dana R. Louie, David Serantes, and Karen L. Livesey. 2021. "Simulating the Self-Assembly and Hysteresis Loops of Ferromagnetic Nanoparticles with Sticking of Ligands" Nanomaterials 11, no. 11: 2870. https://doi.org/10.3390/nano11112870
APA StyleAnderson, N. R., Davidson, J., Louie, D. R., Serantes, D., & Livesey, K. L. (2021). Simulating the Self-Assembly and Hysteresis Loops of Ferromagnetic Nanoparticles with Sticking of Ligands. Nanomaterials, 11(11), 2870. https://doi.org/10.3390/nano11112870






