Impedance Spectroscopy Analysis of PbSe Nanostructures Deposited by Aerosol Assisted Chemical Vapor Deposition Approach
Abstract
:1. Introduction
2. Materials Used
2.1. Preparation of Lead (II) Diphenyldiselenophosphinate
2.2. AACVD System
2.3. Dielectric and Impedance Studies
2.4. Instrumentation
3. Results and Discussion
3.1. Analysis of Lead (II) Diphenyldiselenophosphinate Complex
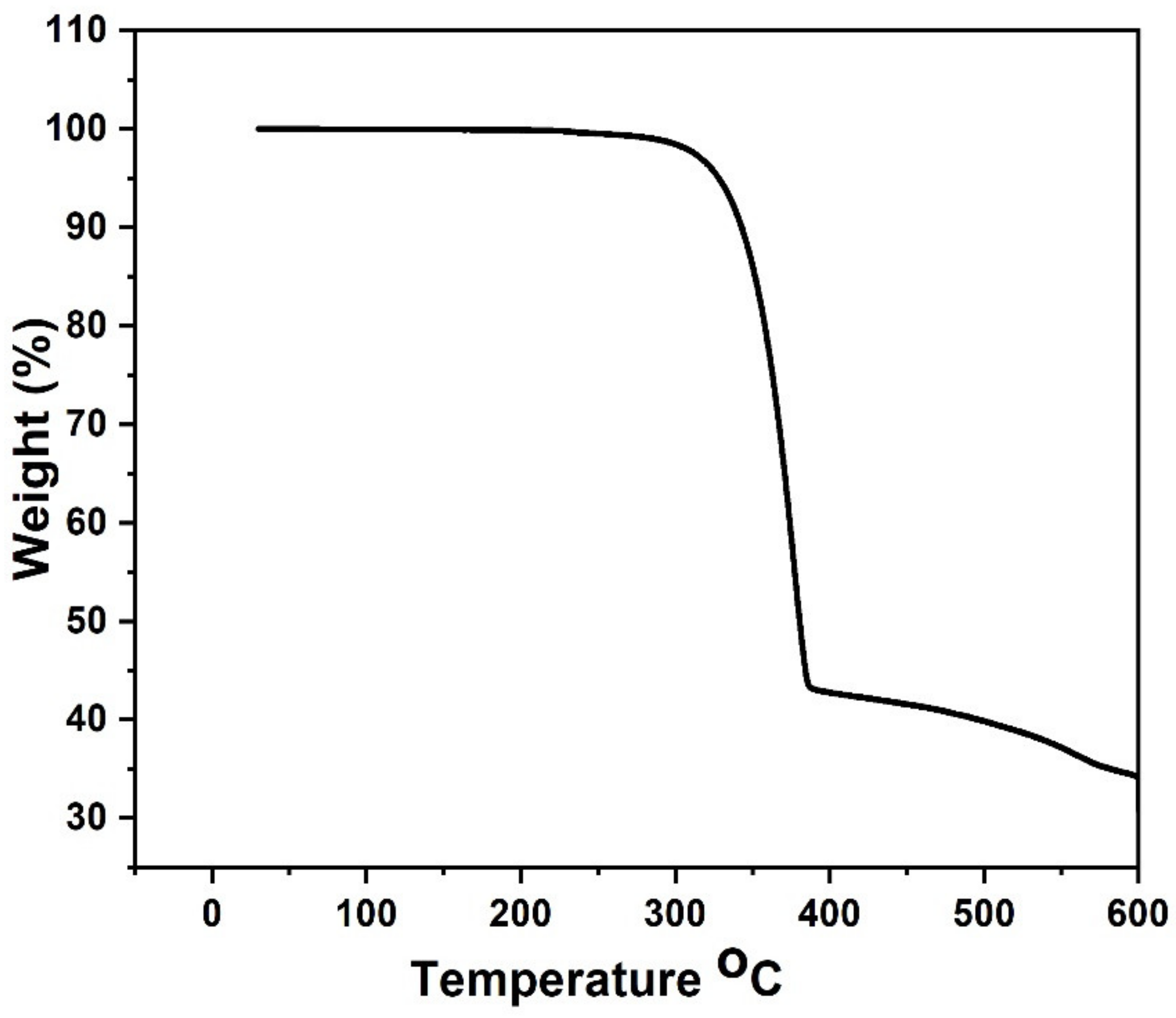
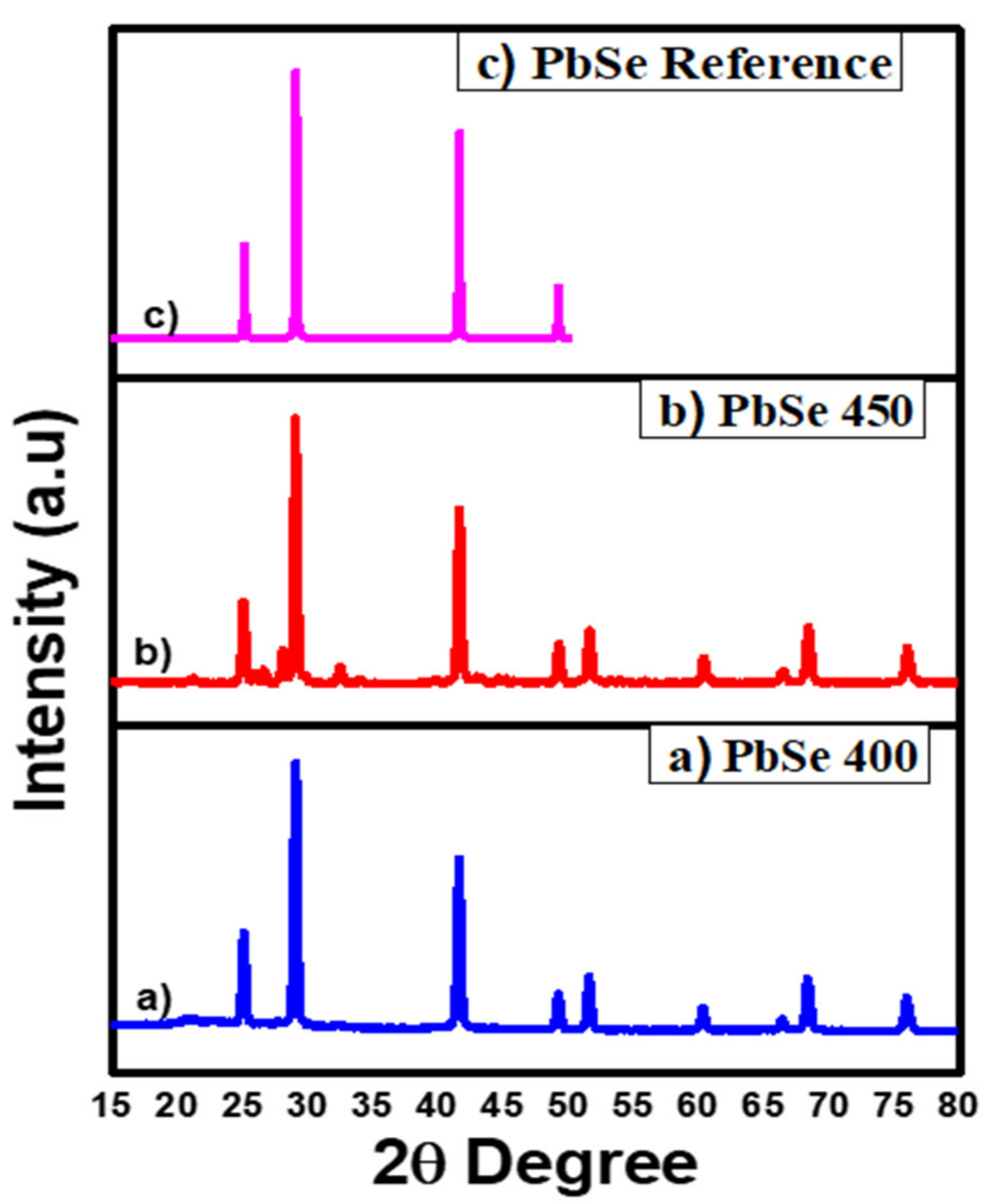
3.2. Structural and Gravimetric Profile
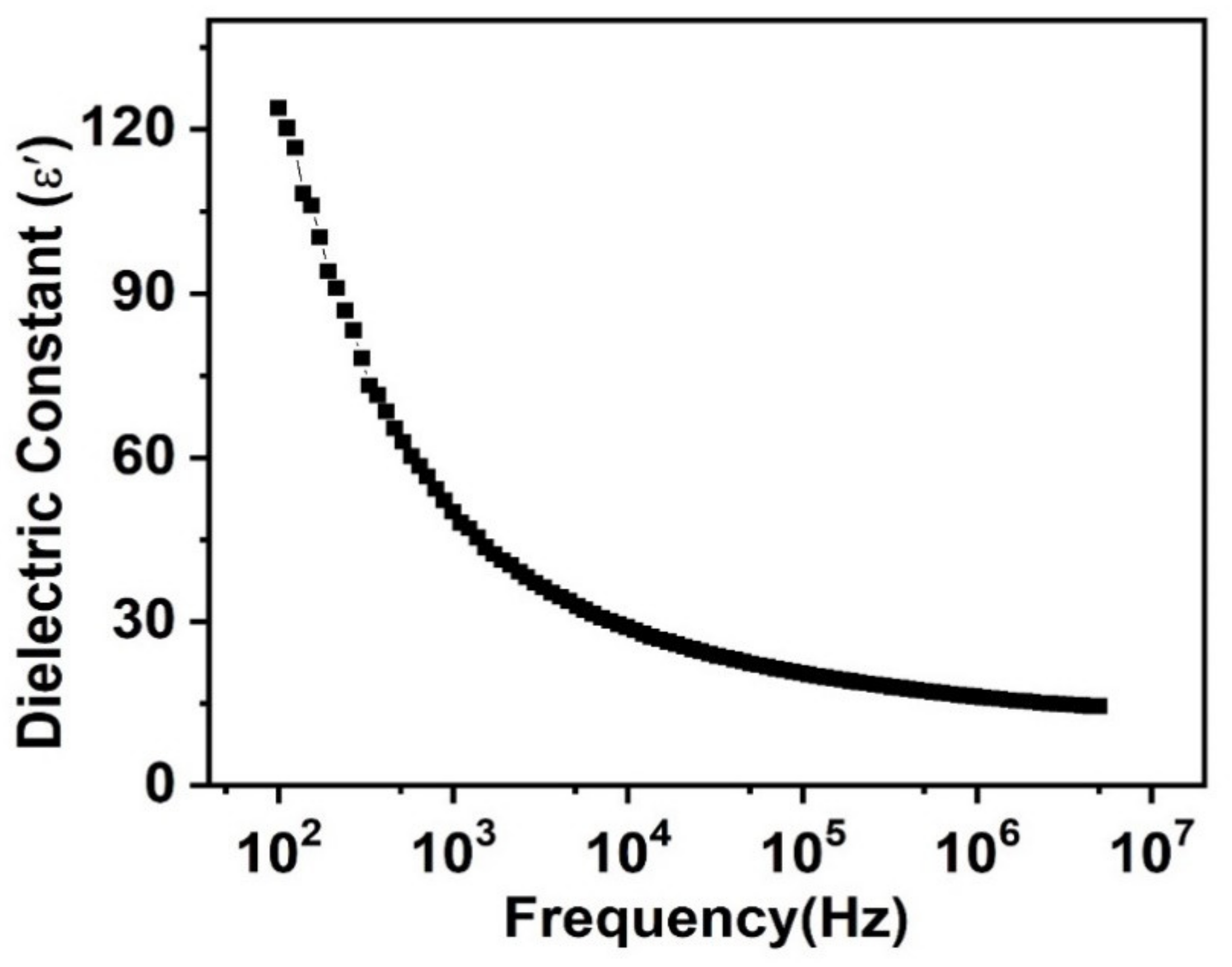
3.3. Dielectric Constant Behavior
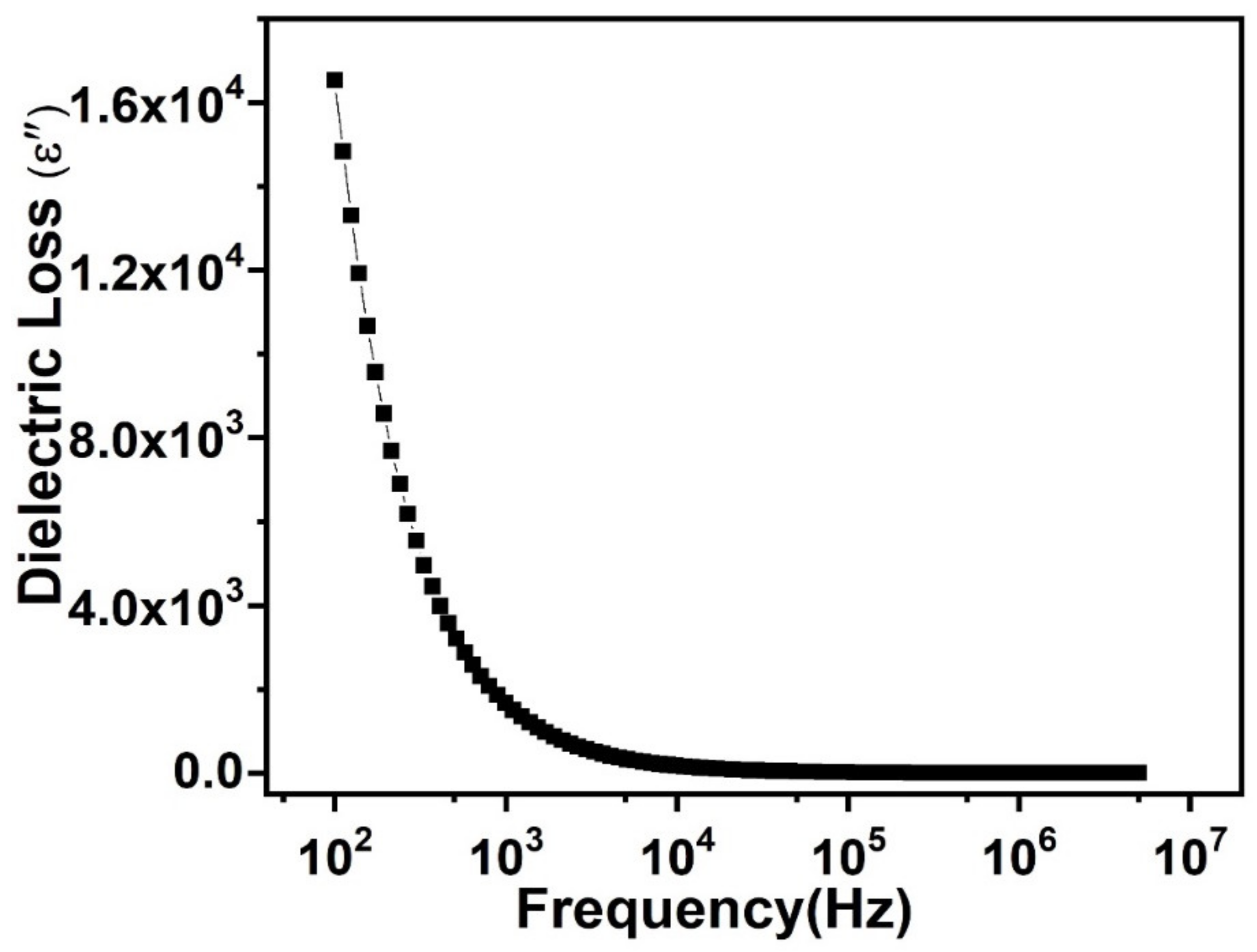
3.4. Dielectric Loss Behavior
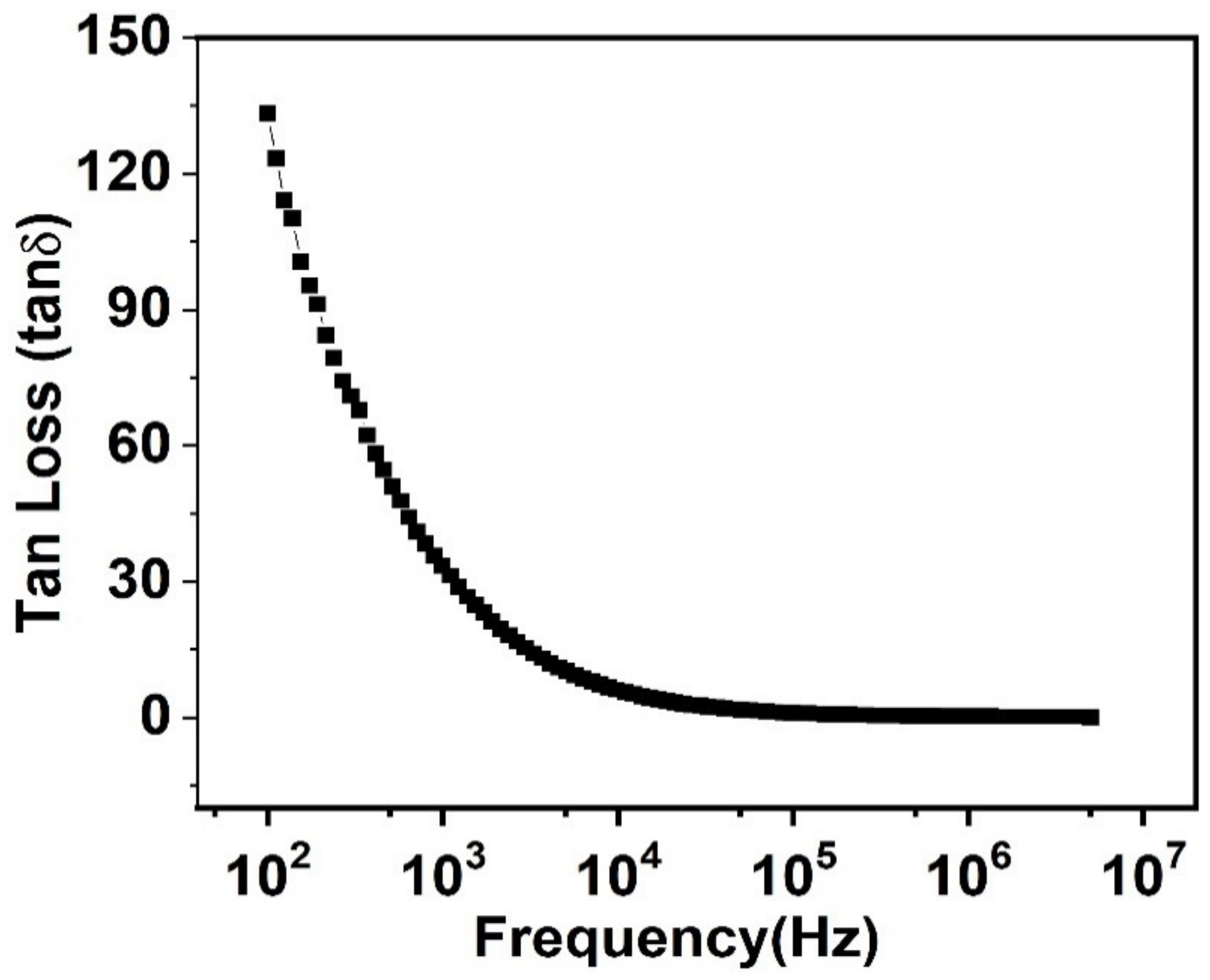
3.5. Behavior of Tangent Loss
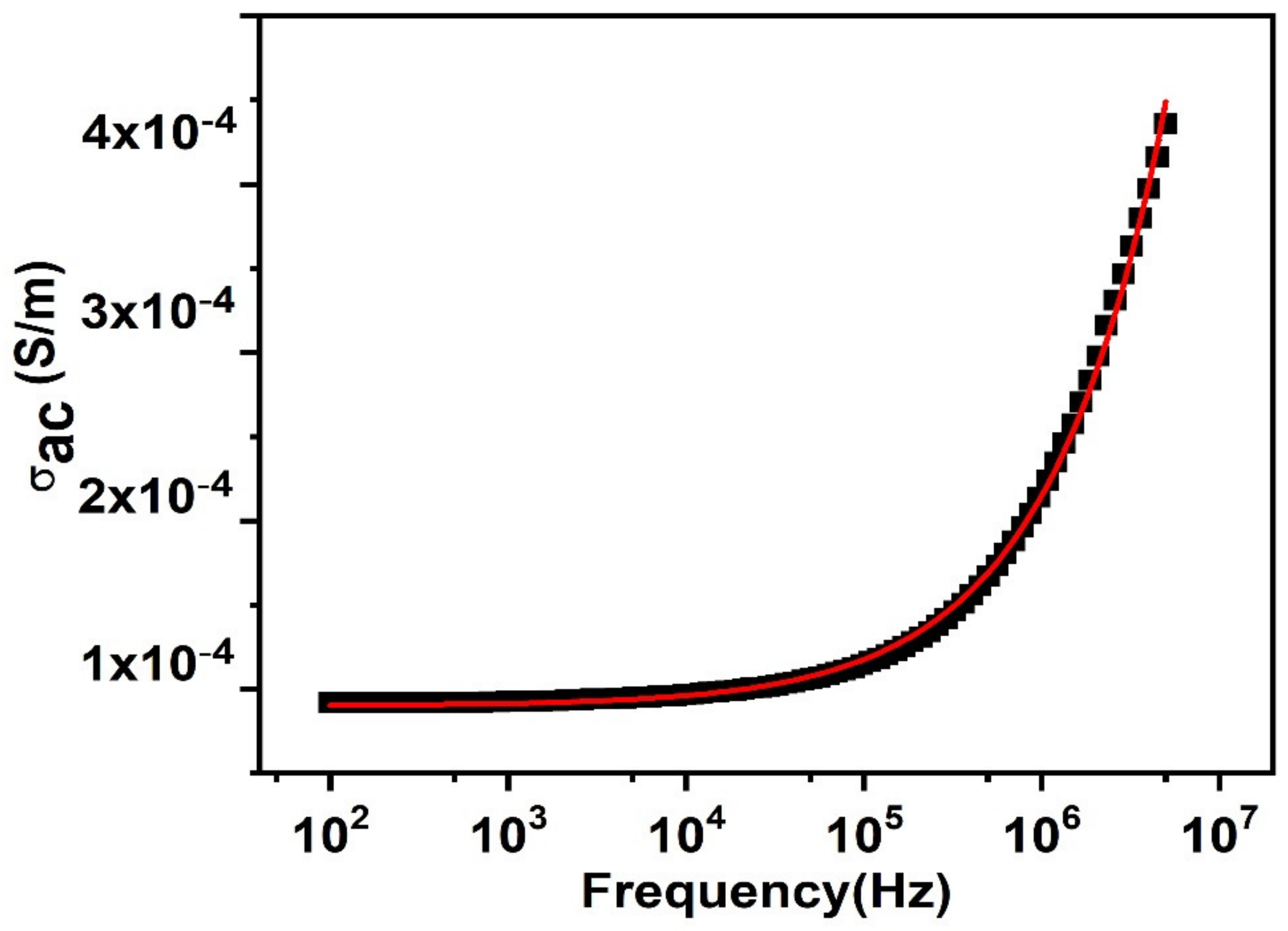
3.6. The ac Conductivity (σac)
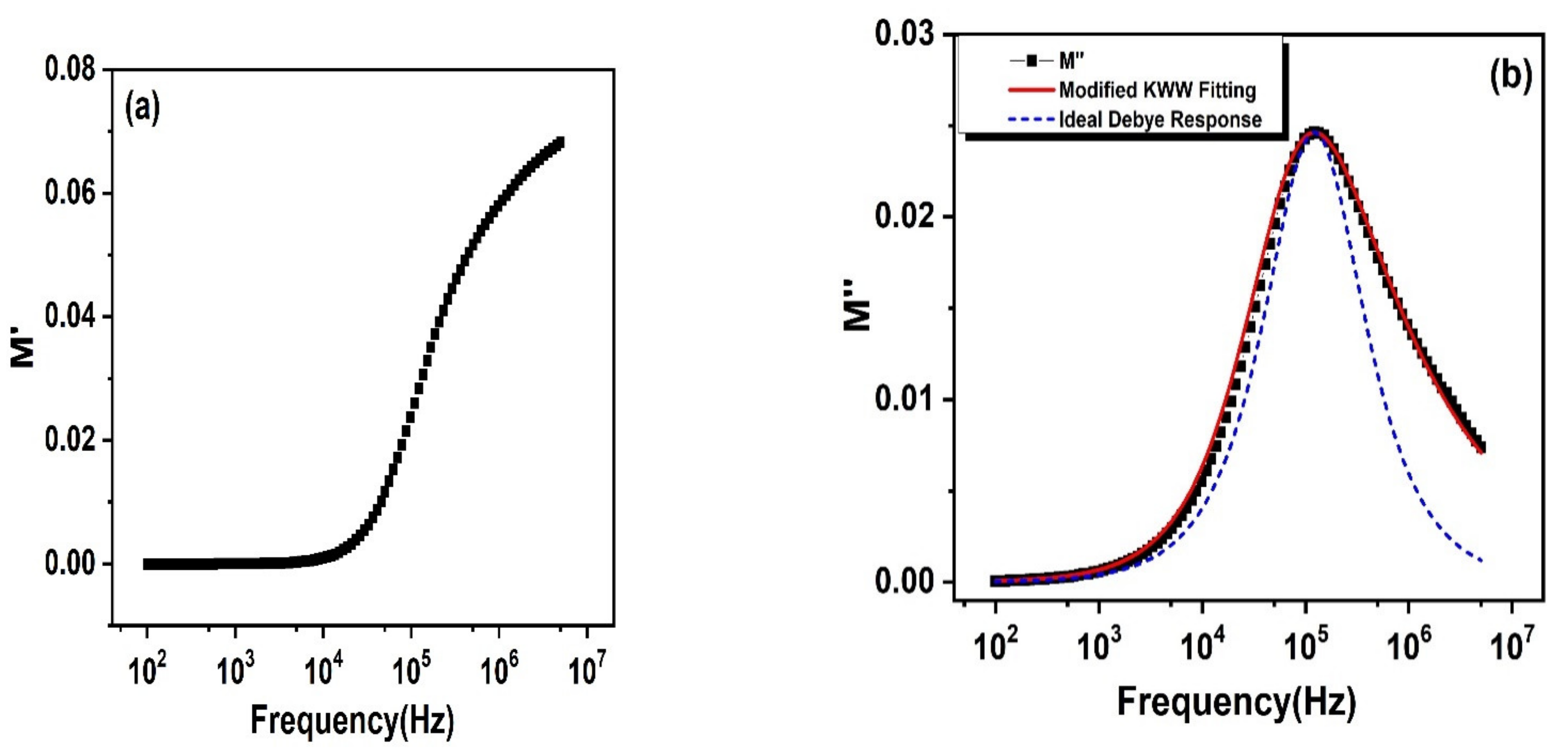
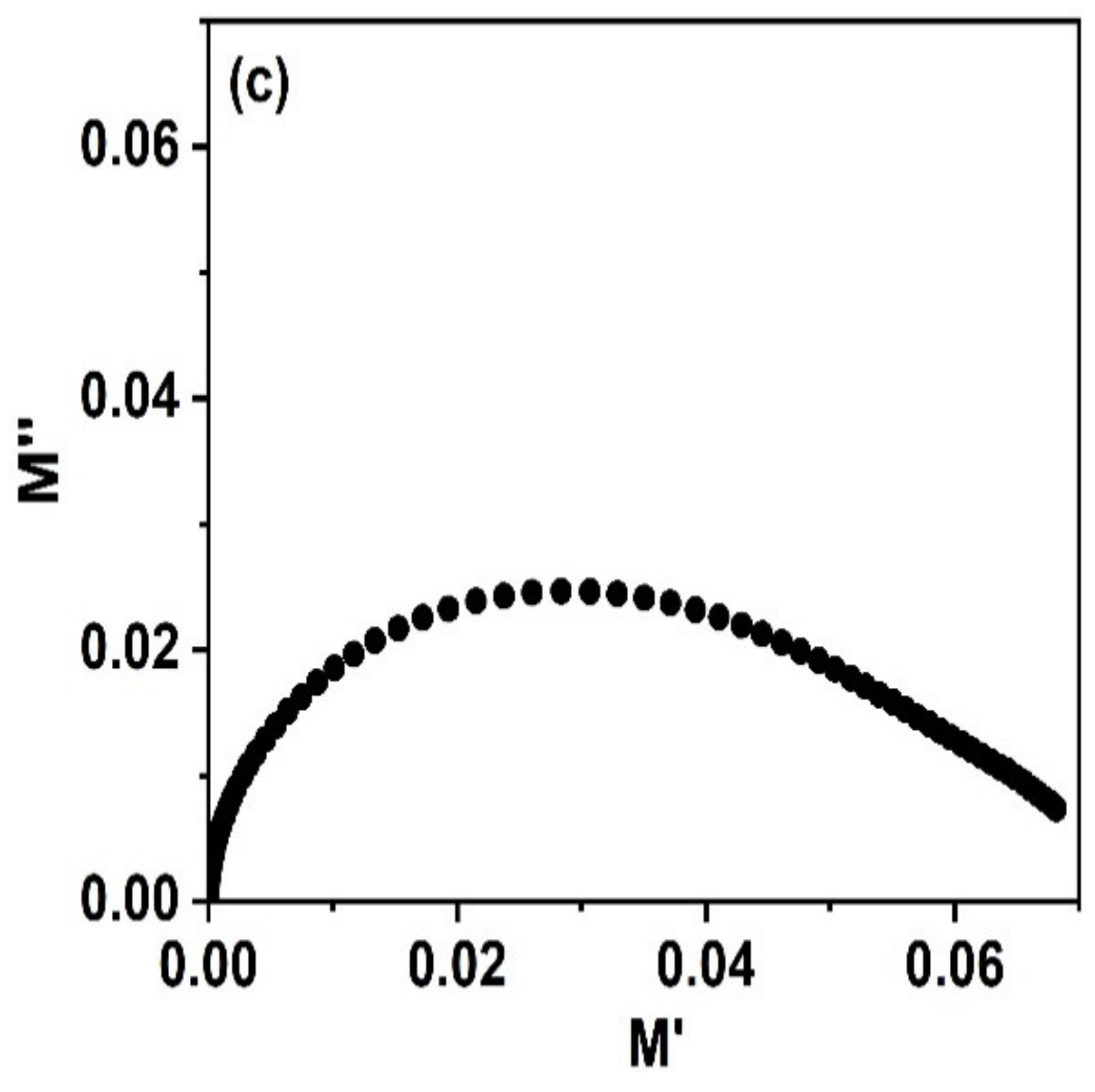
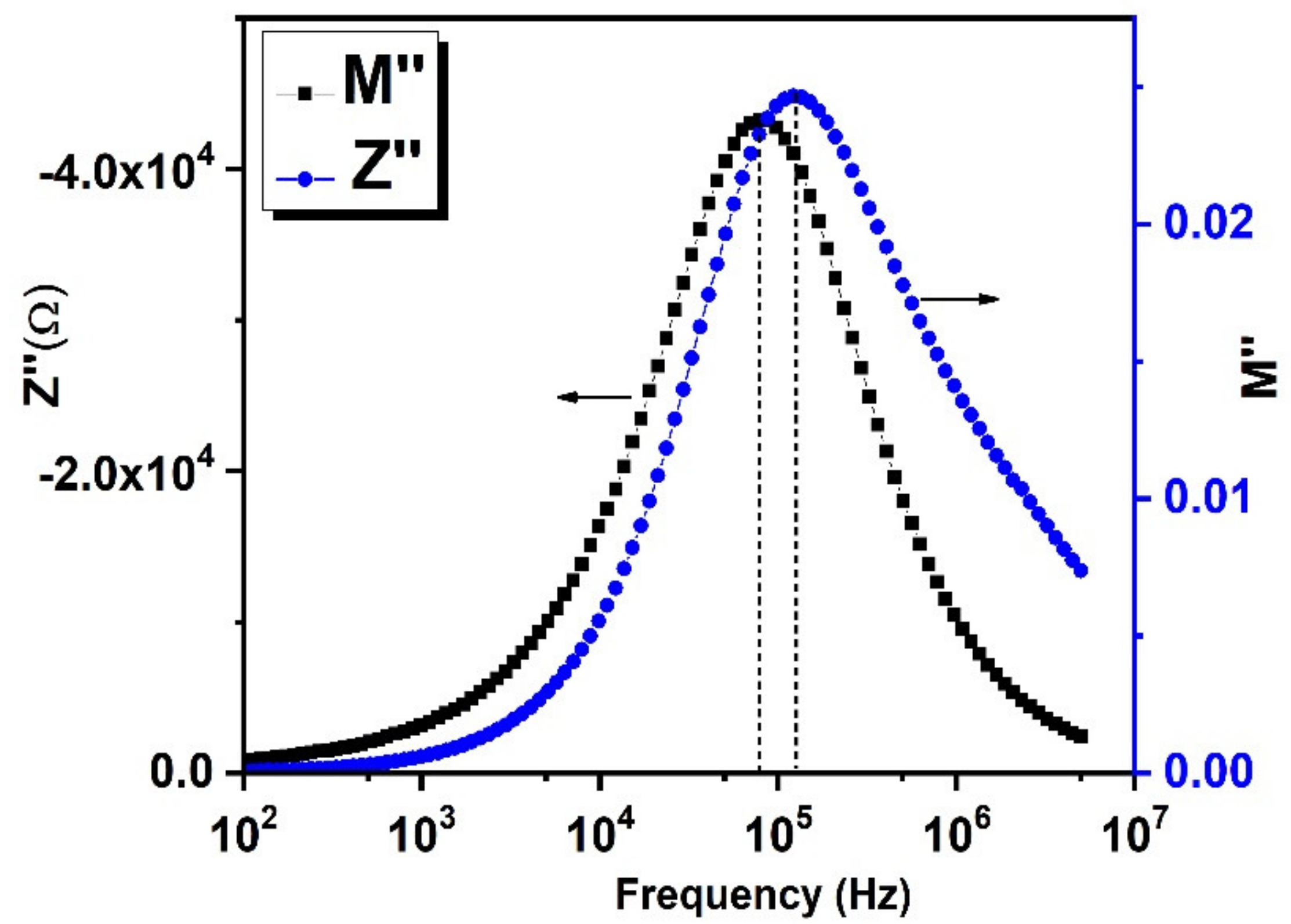
3.7. Complex Electric Modulus
3.8. Impedance Spectroscopy
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zogg, H.; Arnold, M. Narrow spectral band monolithic lead-chalcogenide-on-Si mid-IR photodetectors. Infrared Phys. Technol. 2007, 49, 183–186. [Google Scholar] [CrossRef]
- Maulu, A.; Navarro-Arenas, J.; Rodríguez-Cantó, P.J.; Sánchez-Royo, J.K.; Abargues, R.; Suárez, I. Charge transport in trap-sensitized infrared PbS quantum-dot-based photoconductors: Pros and cons. Nanomaterials 2018, 8, 677. [Google Scholar] [CrossRef] [Green Version]
- Besson, J.M.; Paul, W.; Calawa, A.R. Tuning of PbSe Lasers by Hydrostatic Pressure from 8 to 22 μ. Phys. Review. 1968, 173, 699–713. [Google Scholar] [CrossRef]
- Qiu, J.; Weng, B.; McDowell, L.L.; Shi, Z. Low-cost uncooled MWIR PbSe quantum dots photodiodes. RSC Adv. 2019, 9, 42516–42523. [Google Scholar] [CrossRef] [Green Version]
- Zhang, N.; Liu, X.; Wei, Z.; Liu, H.; Peng, J.; Zhou, L. Cell imaging using two-photon excited CdS fluorescent quantum dots working within the biological window. Nanomaterials 2019, 9, 369. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Eibelhuber, M.; Schwarzl, T.; Pichler, S.; Heiss, W.; Springholz, W. Growth and characterization of mid-infrared micro disk lasers operating in continuous-wave mode up to 2 °C. J. Cryst. Growth 2011, 323, 460–462. [Google Scholar] [CrossRef]
- Park, M.; Roh, J.; Lim, J.; Lee, H.; Lee, D.J.N. Double Metal Oxide Electron Transport Layers for Colloidal Quantum Dot Light-Emitting Diodes. Nanomaterials 2020, 10, 726. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Woolf, D.N.; Kadlec, E.A.; Bethke, D.; Grine, A.D.; Nogan, J.J.; Cederberg, J.G. High-efficiency thermo photovoltaic energy conversion enabled by a metamaterial selective emitter. Optica 2018, 5, 213–218. [Google Scholar] [CrossRef]
- Yang, H.; Li, X.; Wang, G.; Zheng, J. Lead Selenide Polycrystalline Coatings Sensitized Using Diffusion and Ion Beam Methods for Uncooled Mid-Infrared Photodetection. Coatings 2018, 8, 444. [Google Scholar] [CrossRef] [Green Version]
- Weng, B.; Qiu, J.; Zhao, L.; Yuan, Z.; Chang, C.; Shi, Z. Recent development on the uncooled mid-infrared PbSe detectors with high detectivity. In Quantum Sensing and Nanophotonic Devices XI.; International Society for Optics and Photonics; Proceedings of SPIE—The International Society for Optical Engineering At: San Fancisco, CA, USA, 2014; International Society for Optics and Photonics; Proceedings of SPIE—The International Society for Optical Engineering At: San Fancisco, CA, USA, 2014; Volume 8993, p. 8993. [Google Scholar]
- Fu, T. Research on gas-sensing properties of lead sulfide-based sensor for detection of NO2 and NH3 at room temperature. Sens. Actuators B Chem. 2009, 140, 116–121. [Google Scholar] [CrossRef]
- Zeng, Y.; Lin, S.; Gu, D.; Li, X.J.N. Two-dimensional nanomaterials for gas sensing applications: The role of theoretical calculations. Nanomaterials 2018, 8, 851. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Diko, C.S.; Qu, Y.; Henglin, Z.; Li, Z.; Nahyoon, N.A.; Fan, S. Biosynthesis and characterization of lead selenide semiconductor nanoparticles (PbSe NPs) and its antioxidant and photocatalytic activity. Arab. J. Chem. 2020, 13, 8411–8423. [Google Scholar] [CrossRef]
- Elafandi, S.; Ahmadi, Z.; Azam, N.; Mahjouri, M.J.N. Gas-Phase Formation of Highly Luminescent 2D GaSe Nanoparticle Ensembles in a Nonequilibrium Laser Ablation Process. Nanomaterials 2020, 10, 908. [Google Scholar] [CrossRef] [PubMed]
- Sakai, E. Present status of room temperature semiconductor detectors. Nucl. Instrum. Methods Phys. Res. 1982, 196, 121–130. [Google Scholar] [CrossRef]
- Sierra, C.; Torquemada, M.C.; Vergara, G.; Rodrigo, M.T.; Gutiérrez, C.; Pérez, G. Multicolour PbSe sensors for analytical applications. Sens. Actuators B Chem. 2014, 190, 464–471. [Google Scholar] [CrossRef]
- Hummer, K.; Grüneis, A.; Kresse, G. Structural and electronic properties of lead chalcogenides from first principles. Phys. Rev. B 2007, 75, 195211. [Google Scholar] [CrossRef]
- Zhu, J.; Liao, X.; Wang, J.; Chen, H.Y. Photochemical synthesis and characterization of PbSe nanoparticles. Mater. Res. Bull. 2001, 36, 1169–1176. [Google Scholar] [CrossRef]
- Hosseinpour-Mashkani, S.M.; Ramezani, M.; Vatanparast, M. Synthesis and characterization of lead selenide nanostructure through simple sonochemical method in the presence of novel precursor. Mater. Sci. Semicond. Process. 2014, 26, 112–118. [Google Scholar] [CrossRef]
- Compton, S.; Cox, U.; Happek, R.; Vaidyanathan, R.; Stickney, J. Electrochemical Atomic Layer Epitaxy: Deposition of PbSe, PbTe, and PbSe/PbTe-superlattice thin films. In APS Southeastern Section Meeting Abstracts; The 69th Annual Meeting of the Southeastern; American Physical Society: University Park City, MD, USA, 2002; Volume 69. [Google Scholar]
- Rumianowski, R.; Dygdala, R.; Jung, W.; Bala, W. Growth of PbSe thin films on Si substrates by pulsed laser deposition method. J. Cryst. Growth 2003, 252, 230–235. [Google Scholar] [CrossRef]
- Min, H.; Kassim, A.; Nagalingam, S. Preparation of lead selenide thin films by chemical bath deposition method in the presence of complexing agent (tartaric acid). Turk. J. Sci. Technol. 2011, 6, 17–23. [Google Scholar]
- Oli, V.A.; Parvathi, M.M.; Rajesh, S. Impact of thickness on vacuum deposited PbSe thin films. Vacuum 2011, 86, 1092–1096. [Google Scholar] [CrossRef]
- Anicai, L.; Sin, I.; Brincoveanu, O.; Costovici, S.; Cotarta, A.; Cojocaru, A. Electrodeposition of lead selenide films from ionic liquids based on choline chloride. Appl. Surf. Sci. 2019, 475, 803–812. [Google Scholar] [CrossRef]
- Zhu, J.; Aruna, S.T.; Koltypin, Y.; Gedanken, A. A Novel Method for the Preparation of Lead Selenide: Pulse Sonoelectrochemical Synthesis of Lead Selenide Nanoparticles. Chem. Mater. 2000, 12, 143–147. [Google Scholar] [CrossRef]
- Bhat, T.S.; Vanalakar, S.A.; Devan, R.S.; Mali, S.S.; Pawar, S.A.; Ma, Y.R. Compact nanoarchitectures of lead selenide via successive ionic layer adsorption and reaction towards optoelectronic devices. J. Mater. Sci. Mater. Electron. 2016, 27, 4996–5005. [Google Scholar] [CrossRef]
- Boadi, N.O.; Mcnaughter, P.D.; Helliwell, M.; Malik, M.A.; Awudza, J.A.M.; O’Brien, P. The deposition of PbS and PbSe thin films from lead dichalcogenoimidophosphinates by AACVD. Inorg. Chim. Acta 2016, 453, 439–442. [Google Scholar] [CrossRef]
- Udofia, K.; Ikhioya, I. Electrical Properties of Electrodeposited Lead Selenide (PbSe) Thin Films. Asian J. Phys. Chem. Sci. 2018, 5, 1–7. [Google Scholar] [CrossRef]
- Prabahar, S.; Suriyanarayanan, N.; Srikanth, S.; Mills, G. Dielectric properties of lead selenide thin films. Chalcogenide Lett. 2009, 6, 399–402. [Google Scholar]
- Yang, H.; Li, X.; Wang, G.; Zheng, J. The electrical properties of carrier transport between lead selenide polycrystallites manipulated by iodine concentration. AIP Adv. 2018, 8, 085316. [Google Scholar] [CrossRef] [Green Version]
- Oluyamo, S.; Ojo, A. Characterization of nanostructured lead selenide (PbSe) thin films for solar device application. IOSR J. Eng. 2018, 8, 89–93. [Google Scholar]
- Feng, W.; Song, J.; Ren, Y.; Yi, L.; Hu, J.; Zhu, R. Structural, morphological, electrical and optical properties of PbSe thin films sputtered at various pressures. Phys. E Low-Dimens. Syst. Nanostructures 2018, 102, 153–159. [Google Scholar] [CrossRef]
- Lewis, E.; Haigh, S.; O’Brien, P. The synthesis of metallic and semiconducting nanoparticles from reactive melts of precursors. J. Mater. Chem. A 2014, 2, 570–580. [Google Scholar] [CrossRef] [Green Version]
- Baodi, N.O.; Malik, M.A.; O’Brien, P.; Awudza, J.A.M. Single source molecular precursor routes to lead chalcogenides. Dalton Trans. 2012, 41, 10497–10506. [Google Scholar] [CrossRef] [PubMed]
- Malik, M.A.; Afzaal, M.; O’Brien, P. Precursor Chemistry for Main Group Elements in Semiconducting Materials. Chem. Rev. 2010, 110, 4417–4446. [Google Scholar] [CrossRef]
- Afzaal, M.; Ellwood, K.; Pickett, N.L.; O’Brien, P.; Raftery, J.; Waters, J. Growth of lead chalcogenide thin films using single-source precursors. J. Mater. Chem. 2004, 14, 1310–1315. [Google Scholar] [CrossRef]
- Trindade, T.; O’Brien, P.; Zhang, X.; Motevalli, M. Synthesis of PbS nanocrystallites using a novel single molecule precursors approach: X-ray single-crystal structure of Pb(S2CNEtPri)2. J. Mater. Chem. 1997, 7, 1011–1016. [Google Scholar] [CrossRef] [Green Version]
- Pradhan, N.; Efrima, S. Single-Precursor, One-Pot Versatile Synthesis under near Ambient Conditions of Tunable, Single and Dual Band Fluorescing Metal Sulfide Nanoparticles. J. Am. Chem. Soc. 2003, 125, 2050–2051. [Google Scholar] [CrossRef] [PubMed]
- Saah, S.A.; Boadi, N.O.; Wilkins, C. Deposition of PbS Thin Films from Lead Hexadecyl and Octadecyl Xanthate Complexes Using the Spin Coating Method. MRS Adv. 2019, 4, 733–742. [Google Scholar] [CrossRef]
- Nguyen, C.Q.; Adeogun, A.; Afzaal, M.; Malik, M.A.; O’Brien, P. Metal complexes of selenophosphinates from reactions with (R2PSe)2Se: [M(R2PSe2)n] (M = ZnII, CdII, PbII, InIII, GaIII, CuI, BiIII, NiII.; R = iPr, Ph) and [MoV2O2Se2(Se2PiPr2)2]. Chem. Commun. 2006, 20, 2182–2184. [Google Scholar] [CrossRef]
- Boadi, N.O.; Saah, S.A.; Awudza, J.A.M. Synthesis of a Novel Single-Source Precursor for the Production of Lead Chalcogenide Thin Films. J. Chem. 2020, 2020, 8349549. [Google Scholar] [CrossRef]
- Akhtar, J.; Akhtar, M.; Malik, M.A.; O’Brien, P.; Raftery, J. A Single-Source Precursor Route to Unusual PbSe Nanostructures by a Solution–Liquid–Solid Method. J. Am. Chem. Soc. 2012, 134, 2485–2487. [Google Scholar] [CrossRef]
- Iram, S.; Mahmood, A.; Sitara, E.; Bukhari, S.A.B.; Fatima, A.; Shaheen, R.; Malik, A.M. Nanostructured Lead Sulphide Depositions by AACVD Technique Using Bis(Isobutyldithiophosphinato)Lead(II) Complex as Single Source Precursor and Its Impedance Study. Nanomaterials 2020, 10, 1438. [Google Scholar] [CrossRef] [PubMed]
- Iram, S.; Mahmood, A.; Ehsan, M.F.; Mumtaz, A.; Sohail, M.; Sitara, E.; Fatima, A.; Shaheen, R.; Malik, A.M.; Malik, S.N. Impedance Spectroscopic Study of Nickel Sulfide Nanostructures Deposited by Aerosol Assisted Chemical Vapor Deposition Technique. Nanomaterials 2021, 11, 1105. [Google Scholar] [CrossRef]
- Kuchen, W.; Judat, A.; Metten, J. Metallkomplexe der Dialkyldithiophosphinsäuren, II. Synthese und Dipolmomente einiger Diäthyldithiophosphinato-Komplexe. Chem. Ber. 1965, 98, 3981–3987. [Google Scholar] [CrossRef]
- Atuchin, V.V.; Aleksandrovsky, A.; Chimitova, O.; Gavrilova, T.; Krylov, A.; Molokeev, M. Synthesis and Spectroscopic Properties of Monoclinic α-Eu2(MoO4)3. J. Phys. Chem. C 2014, 118, 15404–15411. [Google Scholar] [CrossRef]
- Chattopadhyay, T.; Schnering, H.G.; Grosshans, W.A.; Holzapfel, W.B. High pressure X-ray diffraction study on the structural phase transitions in PbS, PbSe and PbTe with synchrotron radiation. Phys. B+ C 1986, 139, 356–360. [Google Scholar] [CrossRef]
- Traiphop, S.; Thongbai, P.; Kamwanna, T. Effect of synthesis method on magnetic and dielectric properties of CuBO2 delafossite oxide. J. Aust. Ceram. Soc. 2020, 56, 499–505. [Google Scholar] [CrossRef]
- Norouzzadeh, P.; Mabhouti, K.; Golzan, M.M.; Naderali, R. Comparative study on dielectric and structural properties of undoped, Mn-doped, and Ni-doped ZnO nanoparticles by impedance spectroscopy analysis. J. Mater. Sci. Mater. Electron. 2020, 31, 7335–7347. [Google Scholar] [CrossRef]
- Gijp, S.V.; Ten Elshof, A.; Steigelmann, O.; Verweij, H. Influence of Stress and Chemical Homogeneity on Dielectric Properties of BaTi0.9Zr0.1O3. J. Am. Ceram. Soc. 2004, 83, 2610–2612. [Google Scholar] [CrossRef]
- Atif, M.; Rafique, T.; UrRehman, A.; Wahab, H.; Khalid, W.; Ali, Z. Effect of cation distribution on the structural and dielectric properties of Ni(0.5-x)Co(x)Zn(0.5)Fe2O4 (0.0 ≤ x ≤ 0.5) ferrites. J. Mater. Sci. Mater. Electron. 2020, 31, 10970–10980. [Google Scholar] [CrossRef]
- Sahoo, S.; Mahapatra, P.K.; Choudhary, R.N.P. Effect of sintering temperature on dielectric, electrical and magneto-electric characteristics of chemico-thermally synthesized (Ba0.9Gd0.1)(Ti0.9Fe0.1)O3. Ceram. Int. 2016, 42, 15955–15967. [Google Scholar] [CrossRef]
- Heilmann, A.; Dartora, C. The relation between dielectric breakdown and transported power density in high-voltage transmission lines. Rev. Bras. Ensino Física 2014, 36, 4. [Google Scholar] [CrossRef] [Green Version]
- Praveenkumar, B.; Kumar, H.; Kharat, D. Effect of Porosity on Dielectric Properties and Microstructure of Porous PZT Ceramics. Mater. Sci. Eng. B-Adv. Funct. Solid-State Mater. 2006, 127, 130–133. [Google Scholar]
- Hasan, B. AC Conduction and Dielectric Characterization of Vacuum Evaporated PbSe thin Films. Int. J. Thin Fil. Sci. Tech. 2014, 3, 71–76. [Google Scholar] [CrossRef]
- Halder, S.; Dey, A.; Sil, S.; Ray, P. Study of AC conductivity and dielectric behaviour of hydrothermally synthesised molybdenum disulphide. J. Mater. Sci. Mater. Electron. 2021, 32, 168–181. [Google Scholar] [CrossRef]
- Fatima, S.A.; Khan, M.N.; Shaheen, R.; Shahzad, K.; Iqbal, M. Temperature dependent AC-Conduction and relaxation mechanism of spinel MgCo2O4 system by impedance spectroscopy. Phys. B Condens. Matter 2021, 600, 412581. [Google Scholar] [CrossRef]
- Thakur, V.; Singh, A.; Awasthi, A.M.; Singh, L. Temperature dependent electrical transport characteristics of BaTiO3 modified lithium borate glasses. AIP Adv. 2015, 5, 087110. [Google Scholar] [CrossRef]
- Rana, D.K.; Singh, S.K.; Kundu, S.K.; Roy, S.; Angappane, S.; Basu, S. Electrical and room temperature multiferroic properties of polyvinylidene fluoride nanocomposites doped with nickel ferrite nanoparticles. New J. Chem. 2019, 43, 3128–3138. [Google Scholar] [CrossRef]
- Bashir, J.; Shaheen, R. Structural and complex AC impedance spectroscopic studies of A2CoNbO6 (A = Sr, Ba) ordered double perovskites. Solid State Sci. 2011, 13, 993–999. [Google Scholar] [CrossRef]
- Halder, S.; Parida, K.; Das, S.N.; Pradhan, S.K.; Bhuyan, S.; Choudhary, R.N.P. Dielectric and impedance properties of Bi(Zn2/3V1/3)O3 electronic material. Phys. Lett. A 2018, 382, 716–722. [Google Scholar] [CrossRef]



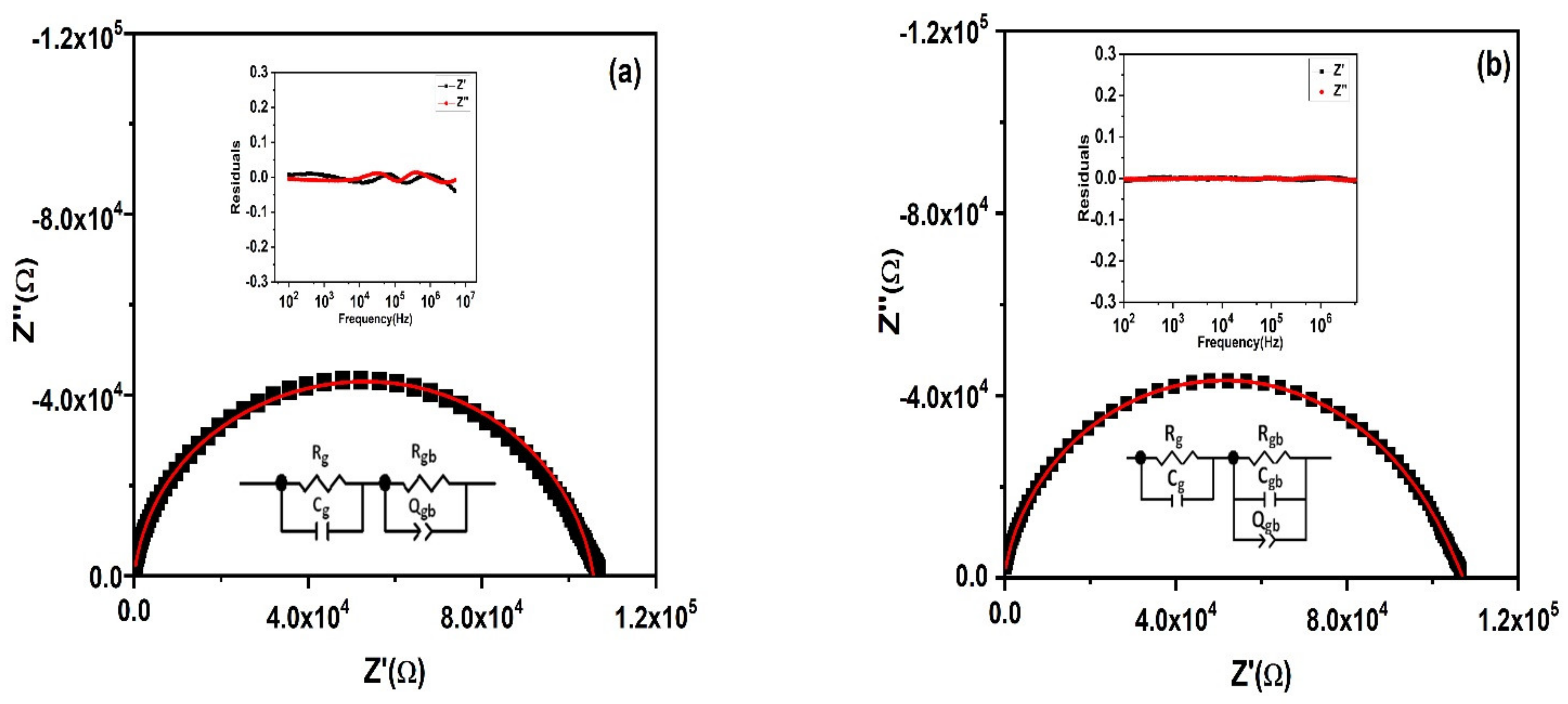
| σdc (S/m) | A | s |
|---|---|---|
| 9.0148 × 10−5 | 1.4195 × 10−8 | 0.657 |
| Rg (Ω) | Cg (F) | Rgb (Ω) | Cgb (F) | Qgb | ngb |
|---|---|---|---|---|---|
| 26,642 | 1.295 × 10−11 | 80,562 | 7.422 × 10−11 | 1.361 × 10−9 | 0.654 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iram, S.; Mahmood, A.; Ehsan, M.F.; Mumtaz, A.; Sohail, M.; Sitara, E.; Mushtaq, S.; Malik, M.A.; Fatima, S.A.; Shaheen, R.; et al. Impedance Spectroscopy Analysis of PbSe Nanostructures Deposited by Aerosol Assisted Chemical Vapor Deposition Approach. Nanomaterials 2021, 11, 2817. https://doi.org/10.3390/nano11112817
Iram S, Mahmood A, Ehsan MF, Mumtaz A, Sohail M, Sitara E, Mushtaq S, Malik MA, Fatima SA, Shaheen R, et al. Impedance Spectroscopy Analysis of PbSe Nanostructures Deposited by Aerosol Assisted Chemical Vapor Deposition Approach. Nanomaterials. 2021; 11(11):2817. https://doi.org/10.3390/nano11112817
Chicago/Turabian StyleIram, Sadia, Azhar Mahmood, Muhammad Fahad Ehsan, Asad Mumtaz, Manzar Sohail, Effat Sitara, Shehla Mushtaq, Mohammad Azad Malik, Syeda Arooj Fatima, Rubina Shaheen, and et al. 2021. "Impedance Spectroscopy Analysis of PbSe Nanostructures Deposited by Aerosol Assisted Chemical Vapor Deposition Approach" Nanomaterials 11, no. 11: 2817. https://doi.org/10.3390/nano11112817
APA StyleIram, S., Mahmood, A., Ehsan, M. F., Mumtaz, A., Sohail, M., Sitara, E., Mushtaq, S., Malik, M. A., Fatima, S. A., Shaheen, R., Ahmad, N. M., & Malik, S. N. (2021). Impedance Spectroscopy Analysis of PbSe Nanostructures Deposited by Aerosol Assisted Chemical Vapor Deposition Approach. Nanomaterials, 11(11), 2817. https://doi.org/10.3390/nano11112817







