Studies on Aggregated Nanoparticles Steering during Deep Brain Membrane Crossing
Abstract
:1. Introduction
2. Results and Discussion
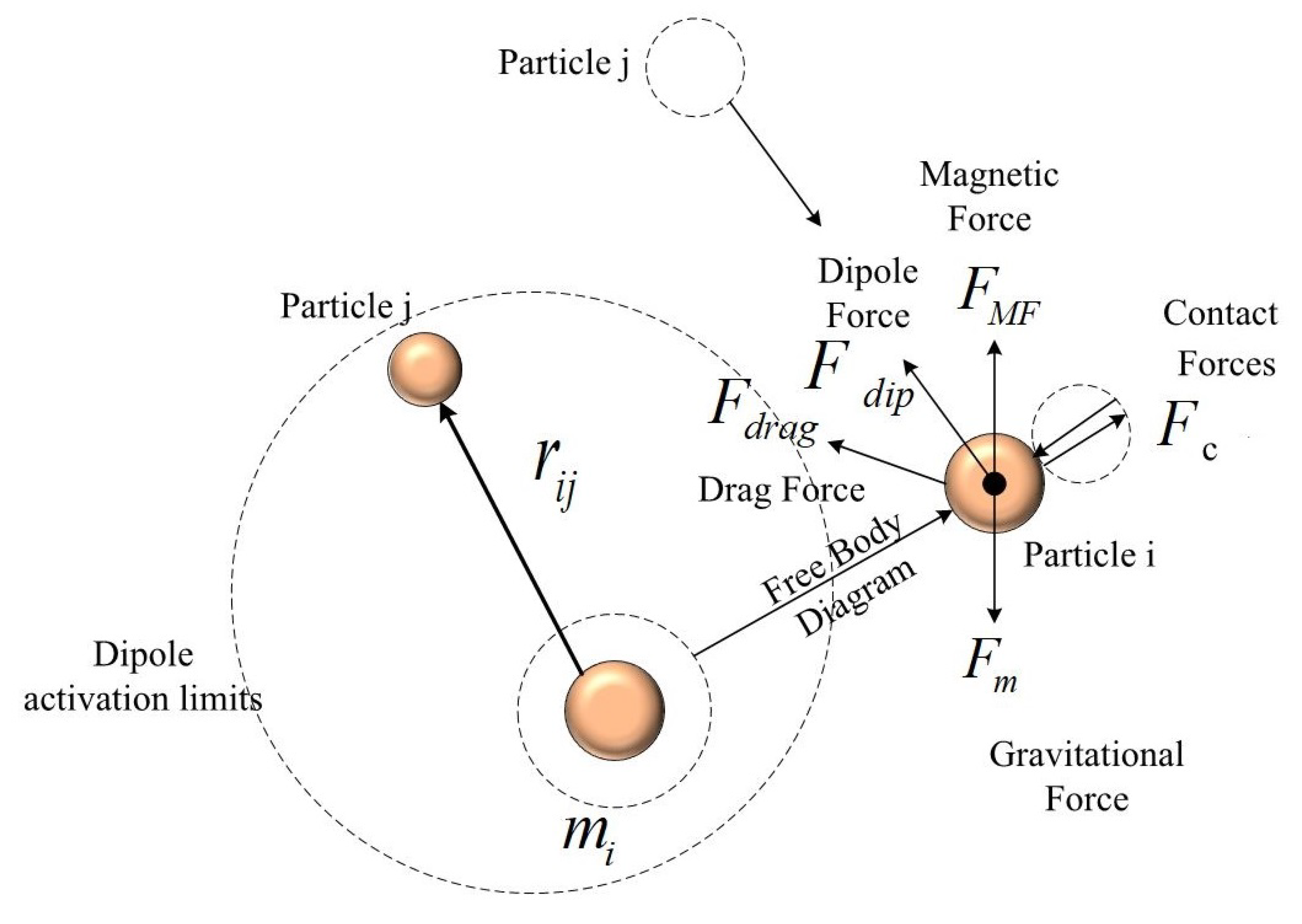
2.1. Forces Governing Aggregation
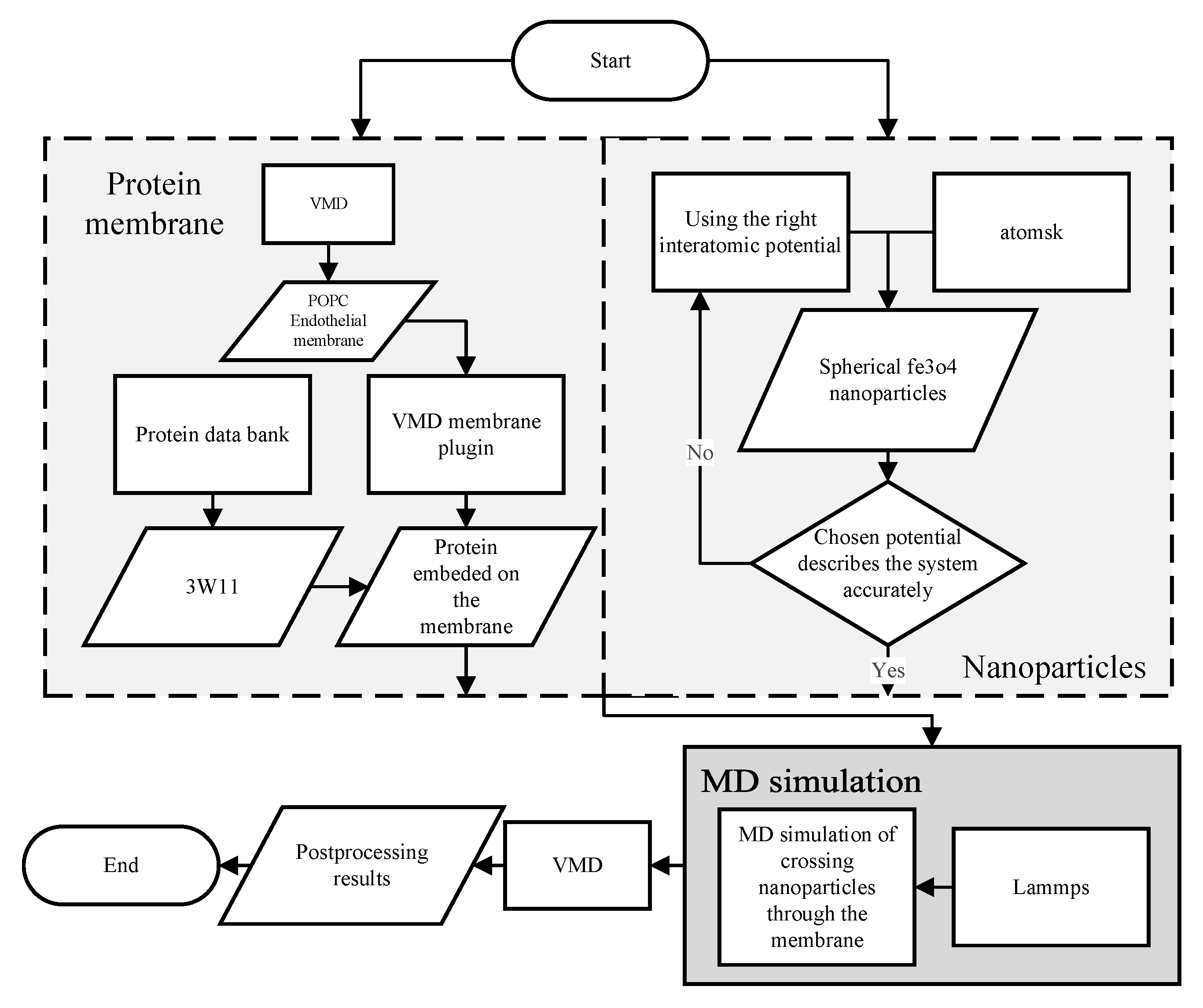
2.2. Molecular Dynamics Modeling and Simulation for the Blood–Brain Barrier (BBB) Crossing
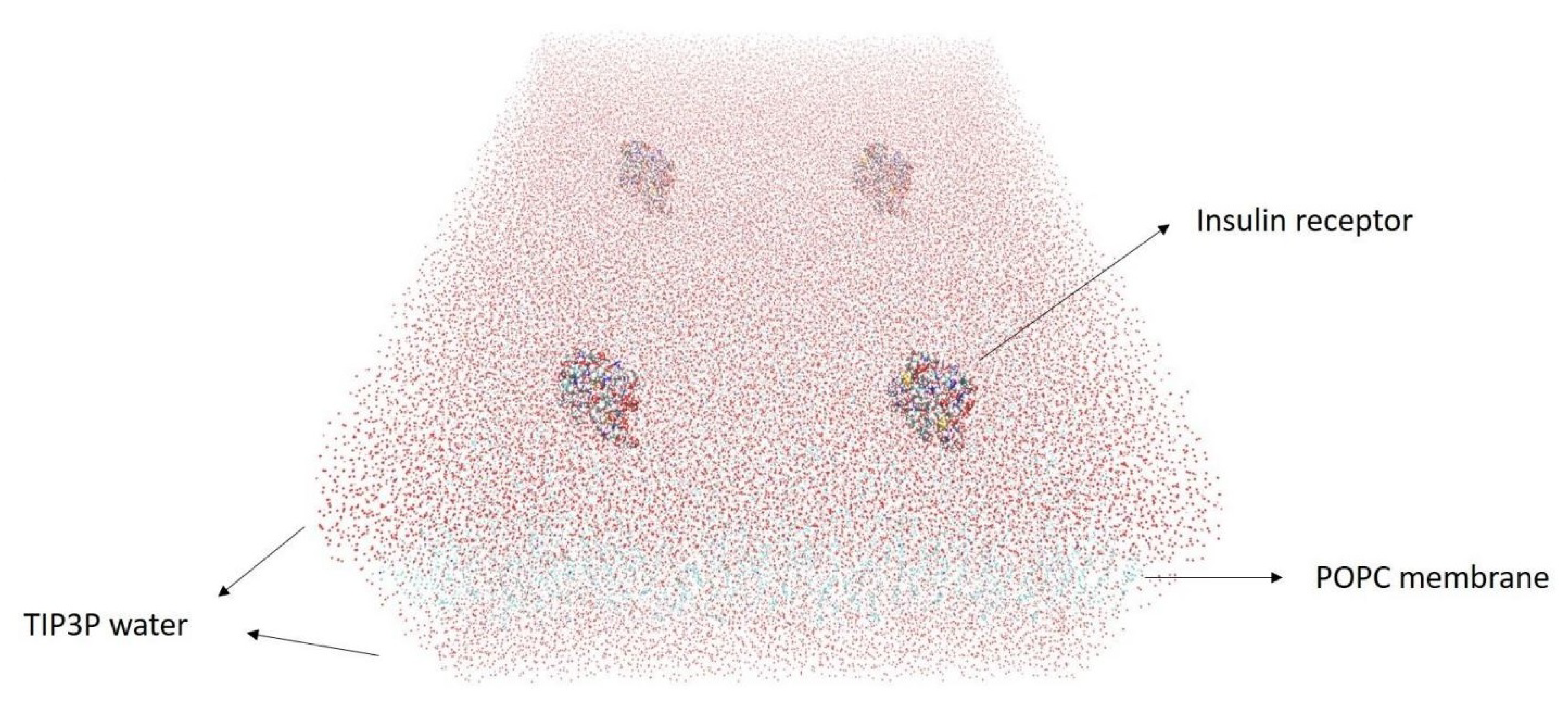
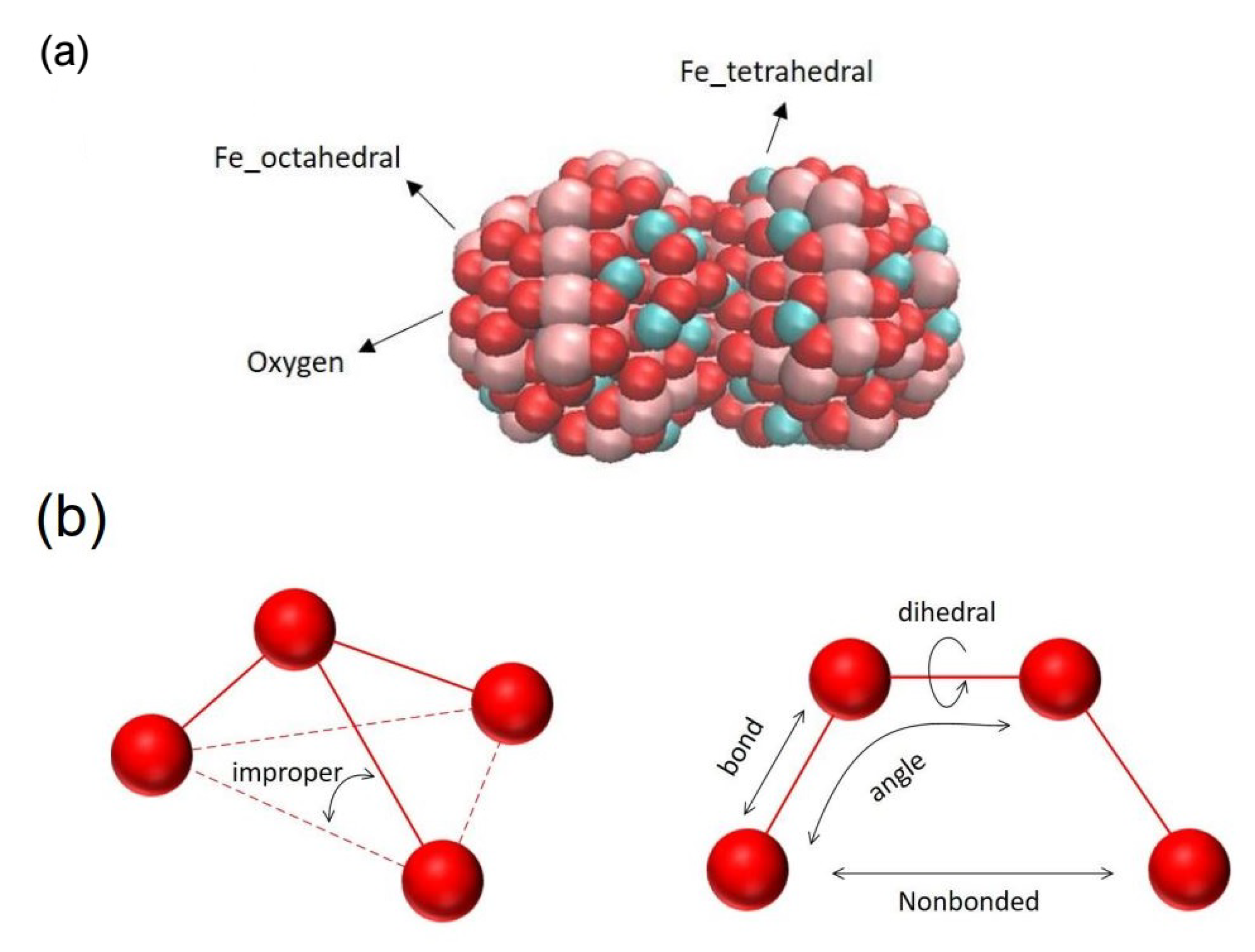
2.2.1. Blood–Brain Barrier (BBB) Modeling
2.2.2. Nanoparticles Modeling
2.2.3. Force Analysis
2.2.4. Molecular Dynamics Conditions
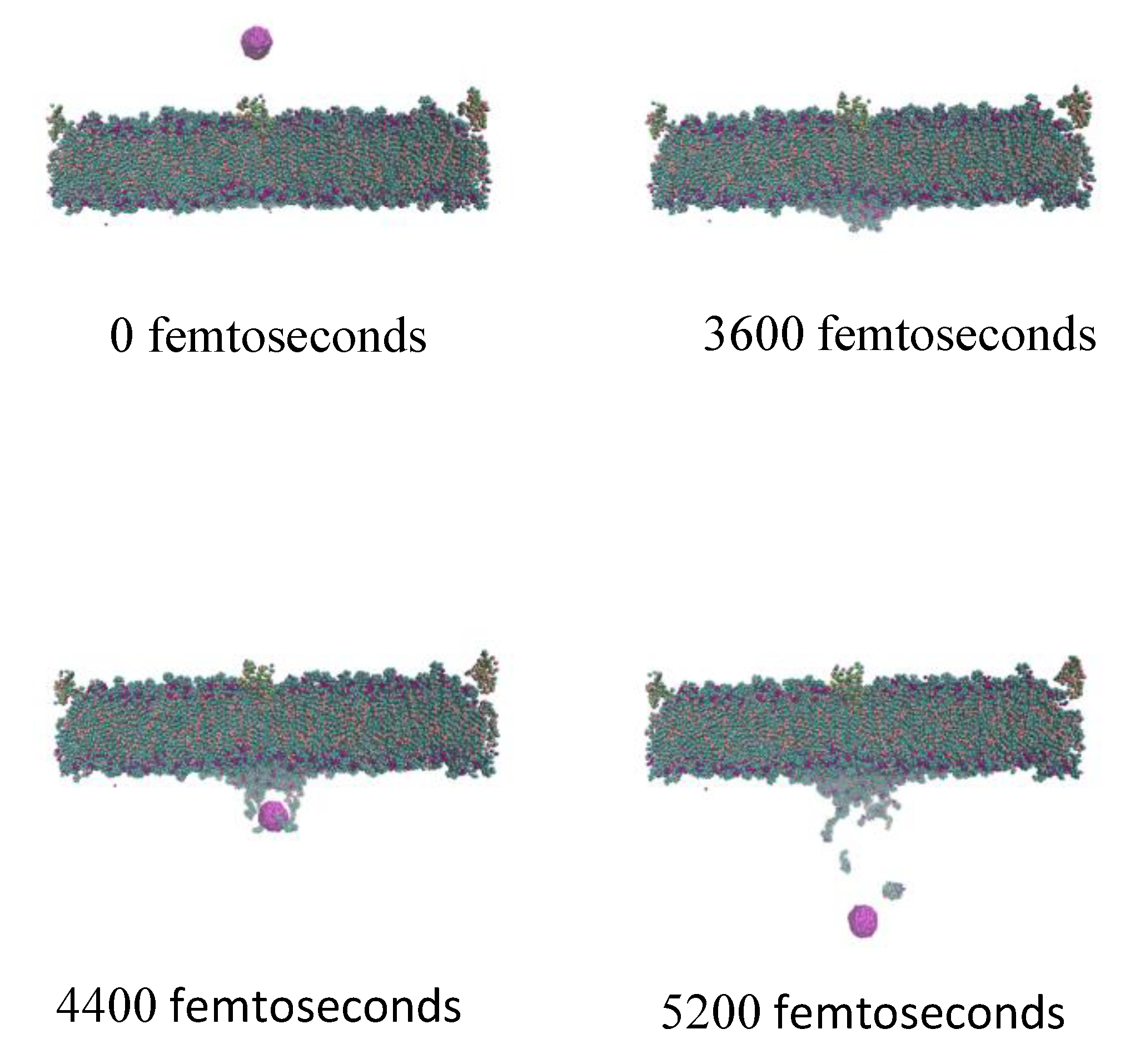
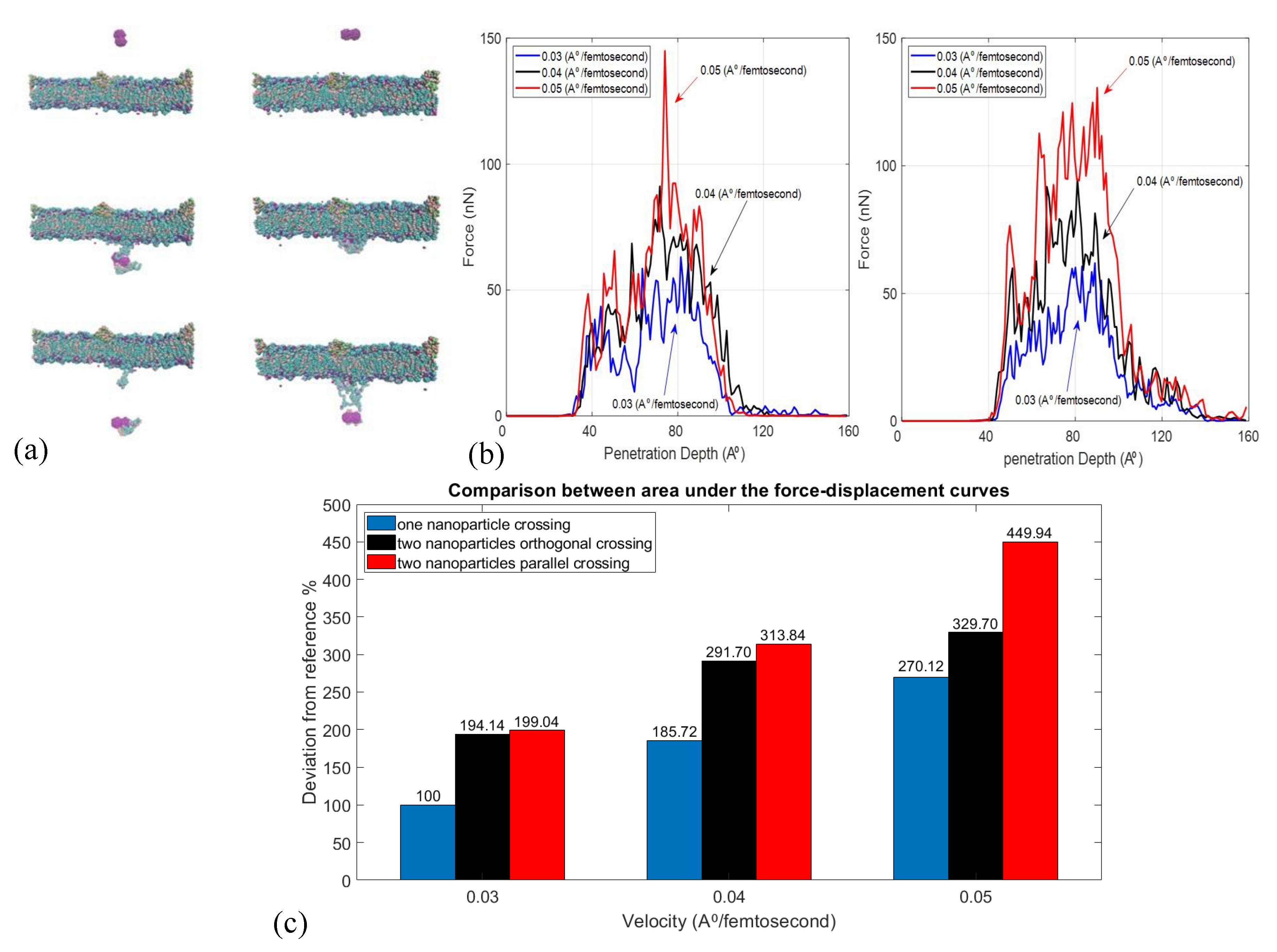
2.3. Effect of Velocity and Particle Aggregation on BBB Crossing
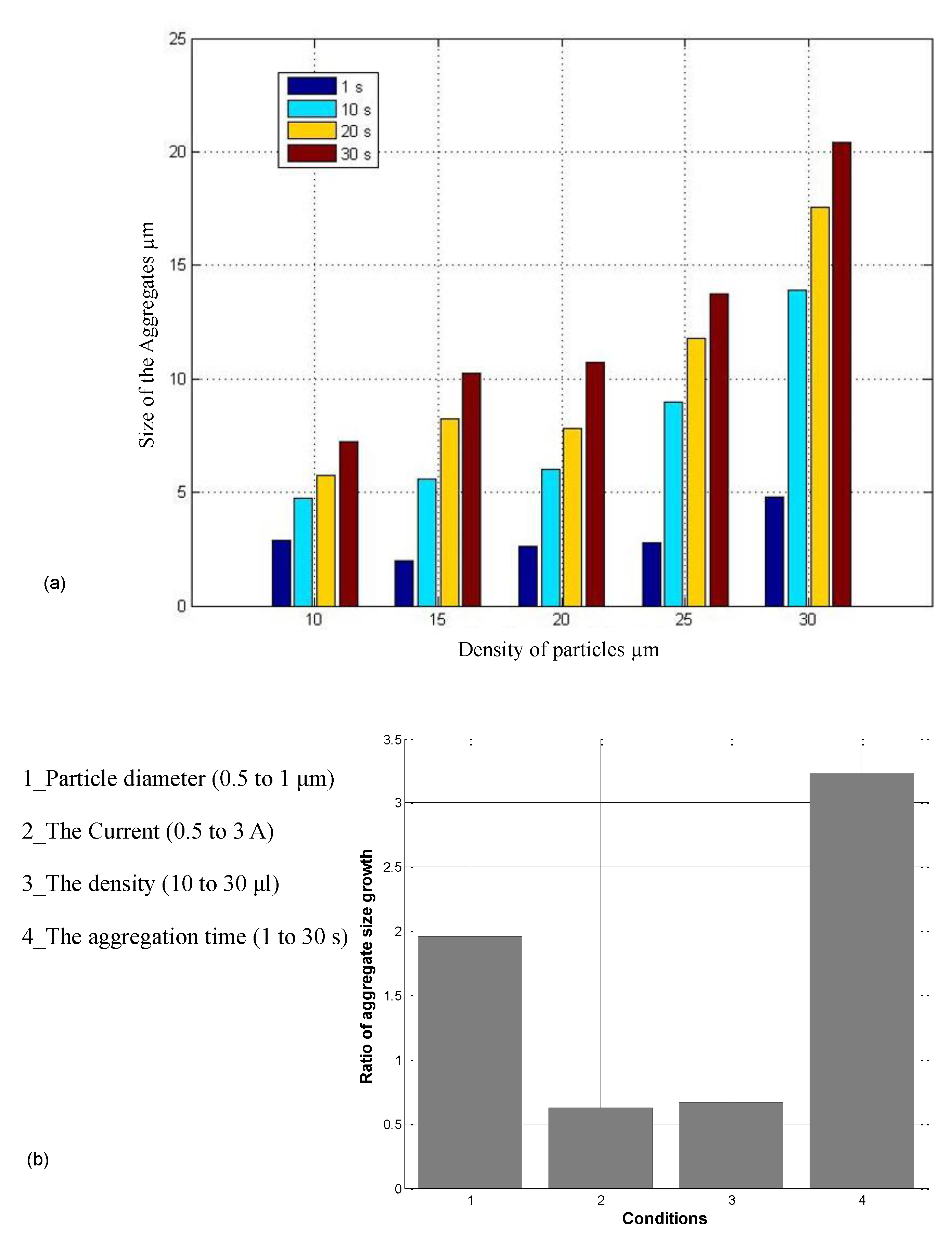
2.4. Parameters Affecting Aggregation
2.5. Discussion
3. Experimental Section
3.1. Materials
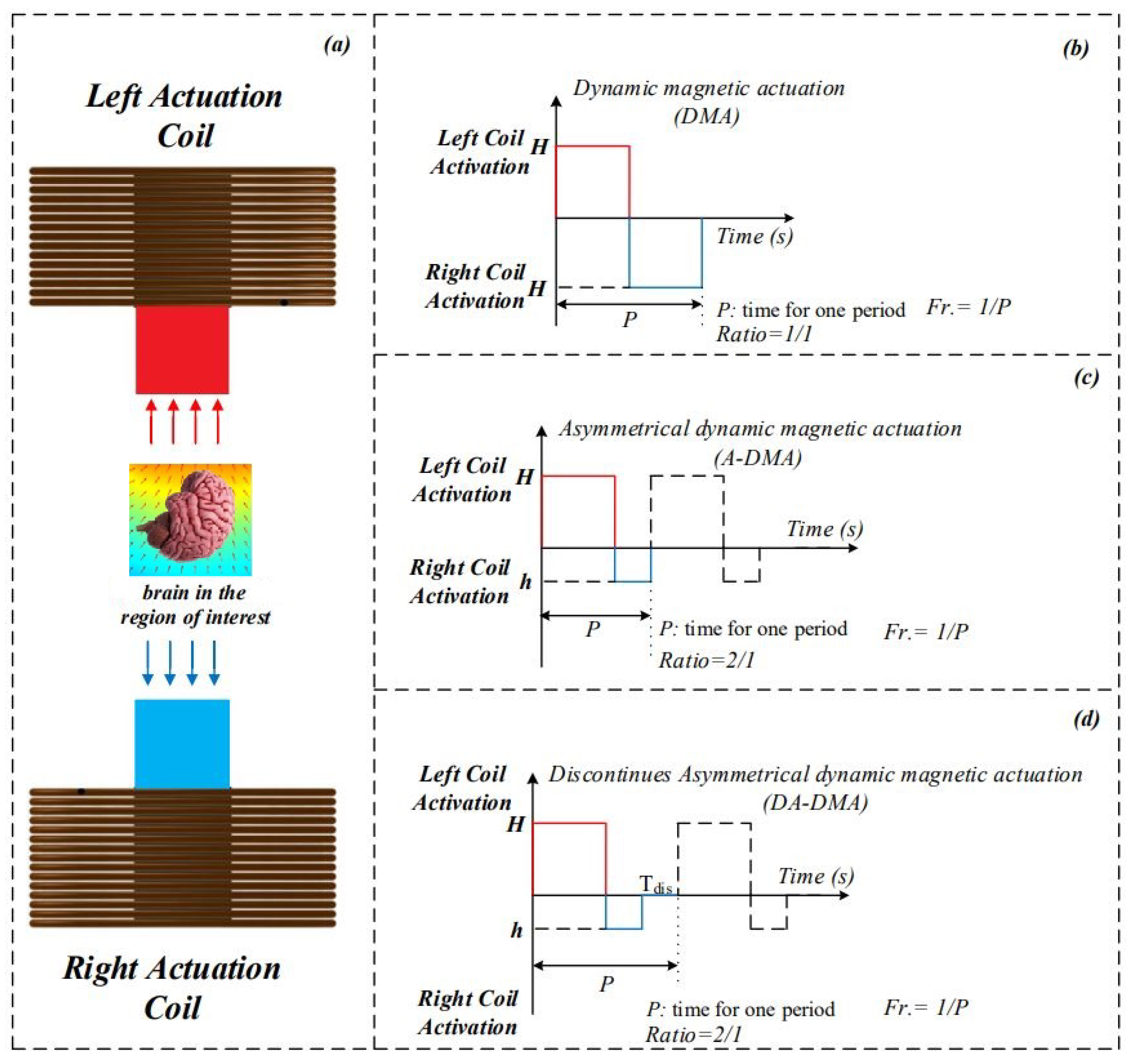
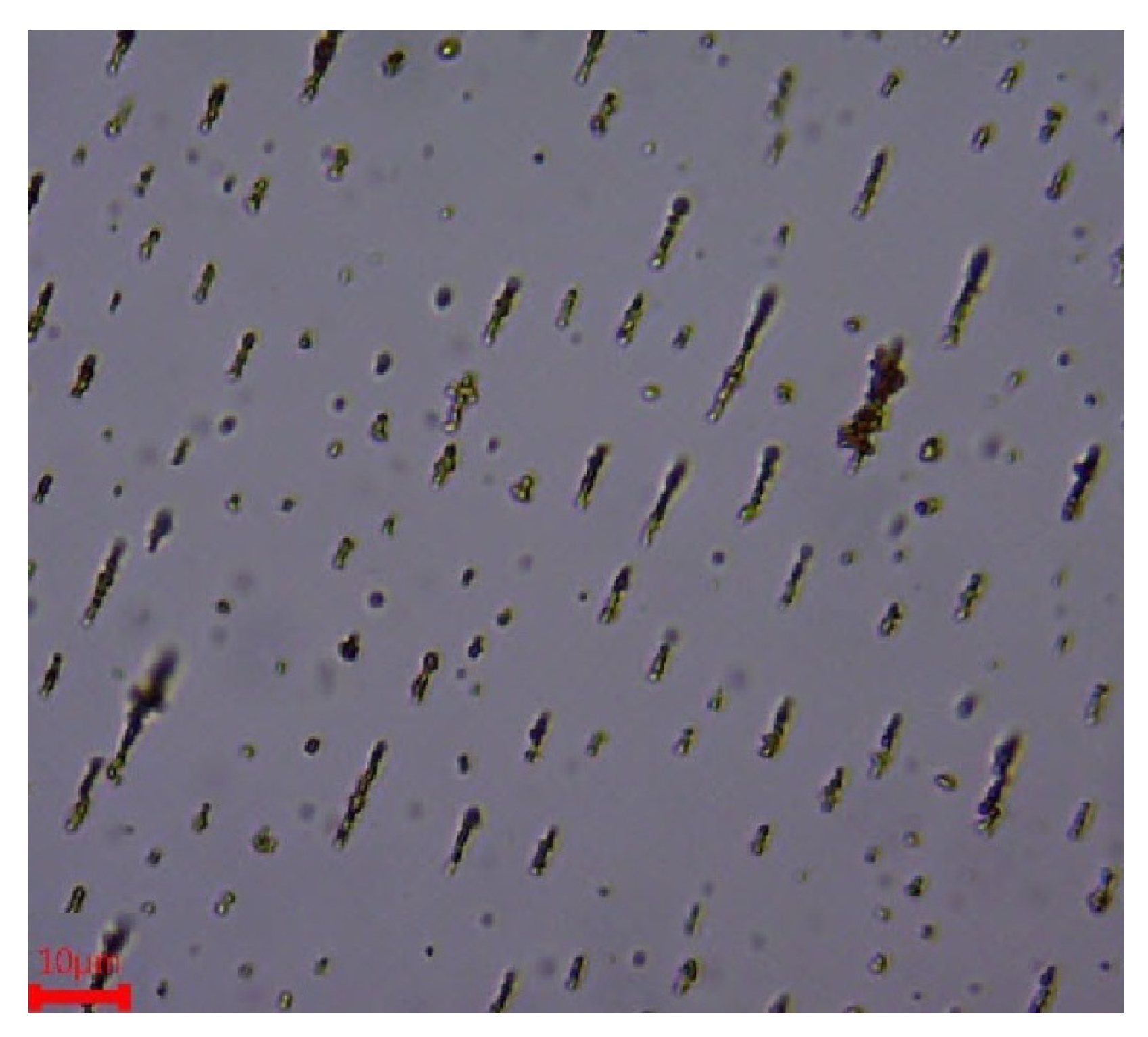
3.2. Experimental Setup to Study Effective Parameters on Magnetic Nanoparticles Aggregation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- International, A.D. World Alzheimer Report 2010: The Global Economic Impact of Dementia; Alzheimer’s Disease International: London, UK, 2010. [Google Scholar]
- Alzheimer’s Association; Thies, W.; Bleiler, L. 2013 Alzheimer’s disease facts and figures. Alzheimer’s Dement. 2013, 9, 208–245. [Google Scholar]
- Hardy, J.; Selkoe, D.J. The Amyloid Hypothesis of Alzheimer’s Disease: Progress and Problems on the Road to Therapeutics. Science 2002, 297, 353–356. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lyketsos, C.G.; Szekely, C.A.; Mielke, M.M.; Rosenberg, P.B.; Zandi, P.P. Developing new treatments for Alzheimer’s disease: The who, what, when, and how of biomarker-guided therapies. Int. Psychogeriatr. 2008, 20, 871–889. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shityakov, S.; Roewer, N.; Broscheit, J.A.; Förster, C. In silico models for nanotoxicity evaluation and prediction at the blood-brain barrier level: A mini-review. Comput. Toxicol. 2017, 2, 20–27. [Google Scholar] [CrossRef]
- Arruebo, M.; Fernández-Pacheco, R.; Ibarra, M.R.; Santamaría, J. Magnetic nanoparticles for drug delivery. Nano Today 2007, 2, 22–32. [Google Scholar] [CrossRef]
- Pankhurst, Q.A.; Thanh, N.T.K.; Jones, S.K.; Dobson, J. Progress in applications of magnetic nanoparticles in biomedicine. J. Phys. D Appl. Phys. 2009, 42, 224001. [Google Scholar] [CrossRef] [Green Version]
- Béduneau, A.; Saulnier, P.; Benoit, J.P. Active targeting of brain tumors using nanocarriers. Biomaterials 2007, 28, 4947–4967. [Google Scholar] [CrossRef]
- Masserini, M. Nanoparticles for Brain Drug Delivery. ISRN Biochem. 2013, 2013, 23842. [Google Scholar] [CrossRef] [Green Version]
- Dilnawaz, F.; Sahoo, S.K. Therapeutic approaches of magnetic nanoparticles for the central nervous system. Drug Discov. Today 2015, 20, 1256–1264. [Google Scholar] [CrossRef]
- Merino, S.; Martín, C.; Kostarelos, K.; Prato, M.; Vázquez, E. Nanocomposite Hydrogels: 3D Polymer–Nanoparticle Synergies for On-Demand Drug Delivery. ACS Nano 2015, 9, 4686–4697. [Google Scholar] [CrossRef] [Green Version]
- Larimi, M.; Ramiar, A.; Ranjbar, A. Numerical simulation of magnetic nanoparticles targeting in a bifurcation vessel. J. Magn. Magn. Mater. 2014, 362, 58–71. [Google Scholar] [CrossRef]
- Hamdi, M.; Ferreira, A. Computational study of superparamagnetic nanocapsules crossing the blood-brain barrier: A robotics approach. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura-Algarve, Portugal, 7–12 October 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 2313–2318. [Google Scholar]
- Pedram, M.Z.; Shamloo, A.; Ghafar-Zadeh, E.; Alasty, A. Dynamic analysis of magnetic nanoparticles crossing cell membrane. J. Magn. Magn. Mater. 2017, 429, 372–378. [Google Scholar] [CrossRef]
- Wang, W.; Yang, R.; Zhang, F.; Yuan, B.; Yang, K.; Ma, Y.Q. Partner-facilitating transmembrane penetration of nanoparticles: A biological test in silico. Nanoscale 2018, 10, 11670–11678. [Google Scholar] [CrossRef]
- Yang, K.; Ma, Y.Q. Computer simulation of the translocation of nanoparticles with different shapes across a lipid bilayer. Nat. Nanotechnol. 2010, 5, 579–583. [Google Scholar] [CrossRef] [PubMed]
- Gupta, R.; Rai, B. Molecular dynamics simulation study of translocation of fullerene C60 through skin bilayer: Effect of concentration on barrier properties. Nanoscale 2017, 9, 4114–4127. [Google Scholar] [CrossRef] [PubMed]
- Campbell, S.D.; Regina, K.J.; Kharasch, E.D. Significance of Lipid Composition in a Blood-Brain Barrier–Mimetic PAMPA Assay. J. Biomol. Screen. 2014, 19, 437–444. [Google Scholar] [CrossRef] [Green Version]
- Kong, S.D.; Lee, J.; Ramachandran, S.; Eliceiri, B.P.; Shubayev, V.I.; Lal, R.; Jin, S. Magnetic targeting of nanoparticles across the intact blood–brain barrier. J. Control. Release 2012, 164, 49–57. [Google Scholar] [CrossRef] [Green Version]
- Tehrani, M.D.; Yoon, J.H.; Kim, M.O.; Yoon, J. A Novel Scheme for Nanoparticle Steering in Blood Vessels Using a Functionalized Magnetic Field. IEEE Trans. Biomed. Eng. 2015, 62, 303–313. [Google Scholar] [CrossRef]
- Soheilian, R.; Choi, Y.S.; David, A.E.; Abdi, H.; Maloney, C.E.; Erb, R.M. Toward Accumulation of Magnetic Nanoparticles into Tissues of Small Porosity. Langmuir 2015, 31, 8267–8274. [Google Scholar] [CrossRef]
- Min, K.A.; Shin, M.C.; Yu, F.; Yang, M.; David, A.E.; Yang, V.C.; Rosania, G.R. Pulsed Magnetic Field Improves the Transport of Iron Oxide Nanoparticles through Cell Barriers. ACS Nano 2013, 7, 2161–2171. [Google Scholar] [CrossRef] [Green Version]
- Amin, F.U.; Hoshiar, A.K.; Do, T.D.; Noh, Y.; Shah, S.A.; Khan, M.S.; Yoon, J.; Kim, M.O. Osmotin-loaded magnetic nanoparticles with electromagnetic guidance for the treatment of Alzheimer’s disease. Nanoscale 2017, 9, 10619–10632. [Google Scholar] [CrossRef] [Green Version]
- Hoshiar, A.K.; Le, T.A.; Amin, F.U.; Kim, M.O.; Yoon, J. A novel magnetic actuation scheme to disaggregate nanoparticles and enhance passage across the blood–brain barrier. Nanomaterials 2018, 8, 3. [Google Scholar] [CrossRef] [Green Version]
- Hoshiar, A.K.; Le, T.A.; Valdastri, P.; Yoon, J. Swarm of magnetic nanoparticles steering in multi-bifurcation vessels under fluid flow. J. Micro-Bio Robot. 2020, 16, 137–145. [Google Scholar] [CrossRef]
- Limpabandhu, C.; Hoshiar, A.K. A Novel Haptic Based Guidance Scheme for Swarm of Magnetic Nanoparticles Steering. In Proceedings of the 2021 7th International Conference on Automation, Robotics and Applications (ICARA), Prague, Czech Republic, 4–6 February 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 216–220. [Google Scholar]
- Abolfathi, K.; Yazdi, M.R.H.; Hoshiar, A.K. Studies of Different Swarm Modes for the MNPs Under the Rotating Magnetic Field. IEEE Trans. Nanotechnol. 2020, 19, 849–855. [Google Scholar] [CrossRef]
- Hoshiar, A.K.; Le, T.A.; Amin, F.U.; Kim, M.O.; Yoon, J. Functionalized electromagnetic actuation method for aggregated nanoparticles steering. In Proceedings of the 2017 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Jeju, Korea, 11–15 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 885–888. [Google Scholar]
- Li, S.; Marshall, J.S.; Liu, G.; Yao, Q. Adhesive particulate flow: The discrete-element method and its application in energy and environmental engineering. Prog. Energy Combust. Sci. 2011, 37, 633–668. [Google Scholar] [CrossRef]
- Vartholomeos, P.; Mavroidis, C. In silico studies of magnetic microparticle aggregations in fluid environments for MRI-guided drug delivery. IEEE Trans. Biomed. Eng. 2012, 59, 3028–3038. [Google Scholar] [CrossRef] [PubMed]
- Pedram, M.Z.; Shamloo, A.; Alasty, A.; Ghafar-Zadeh, E. Optimal magnetic field for crossing super-para-magnetic nanoparticles through the brain blood barrier: A computational approach. Biosensors 2016, 6, 25. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bera, S.; Kar, R.K.; Mondal, S.; Pahan, K.; Bhunia, A. Structural Elucidation of the Cell-Penetrating Penetratin Peptide in Model Membranes at the Atomic Level: Probing Hydrophobic Interactions in the Blood–Brain Barrier. Biochemistry 2016, 55, 4982–4996. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Ward, C.W.; Lawrence, M.C. Ligand-induced activation of the insulin receptor: A multi-step process involving structural changes in both the ligand and the receptor. Bioessays 2009, 31, 422–434. [Google Scholar] [CrossRef]
- Haavik, C.; Stølen, S.; Fjellvag, H.; Hanfland, M.; Hausermann, D. Equation of state of magnetite and its high-pressure modification: Thermodynamics of the Fe-O system at high pressure. Am. Mineral. 2000, 85, 514–523. [Google Scholar] [CrossRef]
- Hirel, P. Atomsk: A tool for manipulating and converting atomic data files. Comput. Phys. Commun. 2015, 197, 212–219. [Google Scholar] [CrossRef]
- Vanommeslaeghe, K.; Hatcher, E.; Acharya, C.; Kundu, S.; Zhong, S.; Shim, J.; Darian, E.; Guvench, O.; Lopes, P.; Vorobyov, I.; et al. CHARMM general force field: A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields. J. Comput. Chem. 2010, 31, 671–690. [Google Scholar] [CrossRef] [Green Version]
- Klauda, J.B.; Venable, R.M.; Freites, J.A.; O’Connor, J.W.; Tobias, D.J.; Mondragon-Ramirez, C.; Vorobyov, I.; MacKerell, A.D., Jr.; Pastor, R.W. Update of the CHARMM all-atom additive force field for lipids: Validation on six lipid types. J. Phys. Chem. B 2010, 114, 7830–7843. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rappé, A.K.; Casewit, C.J.; Colwell, K.; Goddard, W.A., III; Skiff, W.M. UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations. J. Am. Chem. Soc. 1992, 114, 10024–10035. [Google Scholar] [CrossRef]
- Noh, J.; Abdelkarim, O.; Aziz, S.; Winget, P.; Brédas, J.L. A density functional theory investigation of the electronic structure and spin moments of magnetite. Sci. Technol. Adv. Mater. 2014, 15, 044202. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Gupta, A.K.; Gupta, M. Synthesis and surface engineering of iron oxide nanoparticles for biomedical applications. Biomaterials 2005, 26, 3995–4021. [Google Scholar] [CrossRef]
- Krishnan, K.M. Biomedical Nanomagnetics: A Spin Through Possibilities in Imaging, Diagnostics, and Therapy. IEEE Trans. Magn. 2010, 46, 2523–2558. [Google Scholar] [CrossRef] [Green Version]
- Pankhurst, Q.A.; Connolly, J.; Jones, S.K.; Dobson, J. Applications of magnetic nanoparticles in biomedicine. J. Phys. D Appl. Phys. 2003, 36, R167. [Google Scholar] [CrossRef] [Green Version]
- Tartaj, P.; del Puerto Morales, M.; Veintemillas-Verdaguer, S.; González-Carreño, T.; Serna, C.J. The preparation of magnetic nanoparticles for applications in biomedicine. J. Phys. D Appl. Phys. 2003, 36, R182. [Google Scholar] [CrossRef]
- Trahms, L. Biomedical Applications of Magnetic Nanoparticles. In Colloidal Magnetic Fluids: Basics, Development and Application of Ferrofluids; Odenbach, S., Ed.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–32. [Google Scholar]
- Mykhaylyk, O.; Zelphati, O.; Hammerschmid, E.; Anton, M.; Rosenecker, J.; Plank, C. Recent Advances in Magnetofection and Its Potential to Deliver siRNAs In Vitro. In siRNA and miRNA Gene Silencing: From Bench to Bedside; Sioud, M., Ed.; Humana Press: Totowa, NJ, USA, 2009; pp. 1–36. [Google Scholar]
- Plank, C.; Schillinger, U.; Scherer, F.; Bergemann, C.; Rémy, J.S.; Krötz, F.; Anton, M.; Lausier, J.; Rosenecker, J. The magnetofection method: Using magnetic force to enhance gene delivery. Biol. Chem. 2003, 384, 737–747. [Google Scholar] [CrossRef] [PubMed]
- Clement, J.; Schwalbe, M.; Buske, N.; Wagner, K.; Schnabelrauch, M.; Görnert, P.; Kliche, K.; Pachmann, K.; Weitschies, W.; Höffken, K. Differential interaction of magnetic nanoparticles with tumor cells and peripheral blood cells. J. Cancer Res. Clin. Oncol. 2006, 132, 287–292. [Google Scholar] [CrossRef] [PubMed]
- Alexiou, C.; Jurgons, R.; Seliger, C.; Brunke, O.; Iro, H.; Odenbach, S. Delivery of superparamagnetic nanoparticles for local chemotherapy after intraarterial infusion and magnetic drug targeting. Anticancer Res. 2007, 27, 2019–2022. [Google Scholar]
- Polyak, B.; Friedman, G. Magnetic targeting for site-specific drug delivery: Applications and clinical potential. Expert Opin. Drug Deliv. 2009, 6, 53–70. [Google Scholar] [CrossRef] [PubMed]
- Khandhar, A.P.; Ferguson, R.M.; Simon, J.A.; Krishnan, K.M. Tailored magnetic nanoparticles for optimizing magnetic fluid hyperthermia. J. Biomed. Mater. Res. Part A 2012, 100, 728–737. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hilger, I.; Hergt, R.; Kaiser, W.A. Effects of magnetic thermoablation in muscle tissue using iron oxide particles: An in vitro study. Investig. Radiol. 2000, 35, 170–179. [Google Scholar] [CrossRef]
- Neumaier, C.E.; Baio, G.; Ferrini, S.; Corte, G.; Daga, A. MR and iron magnetic nanoparticles. Imaging opportunities in preclinical and translational research. Tumori 2008, 94, 226. [Google Scholar] [CrossRef]
- Le, T.A.; Zhang, X.; Hoshiar, A.K.; Yoon, J. An electromagnetic navigation system with real-time 2D magnetic particle imaging for targeted drug delivery. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1895–1900. [Google Scholar]
- Le, T.A.; Zhang, X.; Hoshiar, A.K.; Yoon, J. Real-time two-dimensional magnetic particle imaging for electromagnetic navigation in targeted drug delivery. Sensors 2017, 17, 2050. [Google Scholar] [CrossRef] [Green Version]
- Liang, S.; Wang, Y.; Yu, J.; Zhang, C.; Xia, J.; Yin, D. Surface modified superparamagnetic iron oxide nanoparticles: As a new carrier for bio-magnetically targeted therapy. J. Mater. Sci. Mater. Med. 2007, 18, 2297–2302. [Google Scholar] [CrossRef] [PubMed]
- Maxwell, D.J.; Bonde, J.; Hess, D.A.; Hohm, S.A.; Lahey, R.; Zhou, P.; Creer, M.H.; Piwnica-Worms, D.; Nolta, J.A. Fluorophore-Conjugated Iron Oxide Nanoparticle Labeling and Analysis of Engrafting Human Hematopoietic Stem Cells. Stem Cells 2008, 26, 517–524. [Google Scholar] [CrossRef] [PubMed] [Green Version]

| Atom | q (|e|) |
|---|---|
| +1.68 | |
| +1.60 | |
| O | −1.22 |
| Parameter | Value/Name |
|---|---|
| Membrane type | POPC with two 15 nm layers of water |
| Membrane number of atoms (without waters) | 152,874 |
| Membrane number of atoms (with waters) | 382,098 |
| Nanoparticle type | FeO |
| Temperature | 310 K |
| Relaxation time | 100,000 femtoseconds |
| Simulation box size | 200 A × 200 A × 370 A |
| Distance | |||||
|---|---|---|---|---|---|
| Current | 1 mm | 2.5 mm | 5 mm | 7.5 mm | 10 mm |
| 1 Amp. | 17 | 8 | 4.5 | 2.3 | 1.6 |
| 2 Amp. | 28 | 13 | 10 | 5.5 | 3.5 |
| 3 Amp. | 43 | 25.5 | 13 | 7 | 4.5 |
| 4 Amp. | 53 | 25 | 12.5 | 7.8 | 5.1 |
| 5 Amp. | 58 | 34.5 | 16 | 11 | 7.2 |
| Current (Amp) | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 |
| Aggregates size (m) | 3.8 | 4.4 | 4.5 | 4.8 | 5.4 | 6.2 |
| Diameter (m) | Time (s) | Current (A) | Density (L) | |
|---|---|---|---|---|
| Nominal | 0.5 | 1 | 3 | 30 |
| Range | 0.5 to 1 | 1 to 30 | 0.5 to 3 | 10 to 30 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kafash Hoshiar, A.; Dadras Javan, S.; Le, T.-A.; Hairi Yazdi, M.R.; Yoon, J. Studies on Aggregated Nanoparticles Steering during Deep Brain Membrane Crossing. Nanomaterials 2021, 11, 2754. https://doi.org/10.3390/nano11102754
Kafash Hoshiar A, Dadras Javan S, Le T-A, Hairi Yazdi MR, Yoon J. Studies on Aggregated Nanoparticles Steering during Deep Brain Membrane Crossing. Nanomaterials. 2021; 11(10):2754. https://doi.org/10.3390/nano11102754
Chicago/Turabian StyleKafash Hoshiar, Ali, Shahriar Dadras Javan, Tuan-Anh Le, Mohammad Reza Hairi Yazdi, and Jungwon Yoon. 2021. "Studies on Aggregated Nanoparticles Steering during Deep Brain Membrane Crossing" Nanomaterials 11, no. 10: 2754. https://doi.org/10.3390/nano11102754
APA StyleKafash Hoshiar, A., Dadras Javan, S., Le, T.-A., Hairi Yazdi, M. R., & Yoon, J. (2021). Studies on Aggregated Nanoparticles Steering during Deep Brain Membrane Crossing. Nanomaterials, 11(10), 2754. https://doi.org/10.3390/nano11102754








