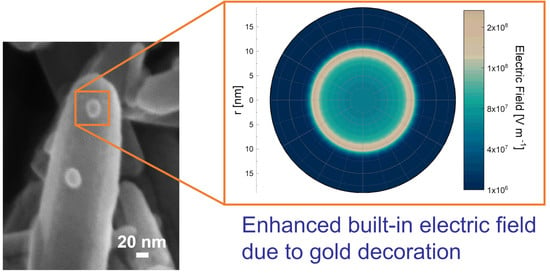
Localized Energy Band Bending in ZnO Nanorods Decorated with Au Nanoparticles
Abstract
:1. Introduction
2. Materials and Methods
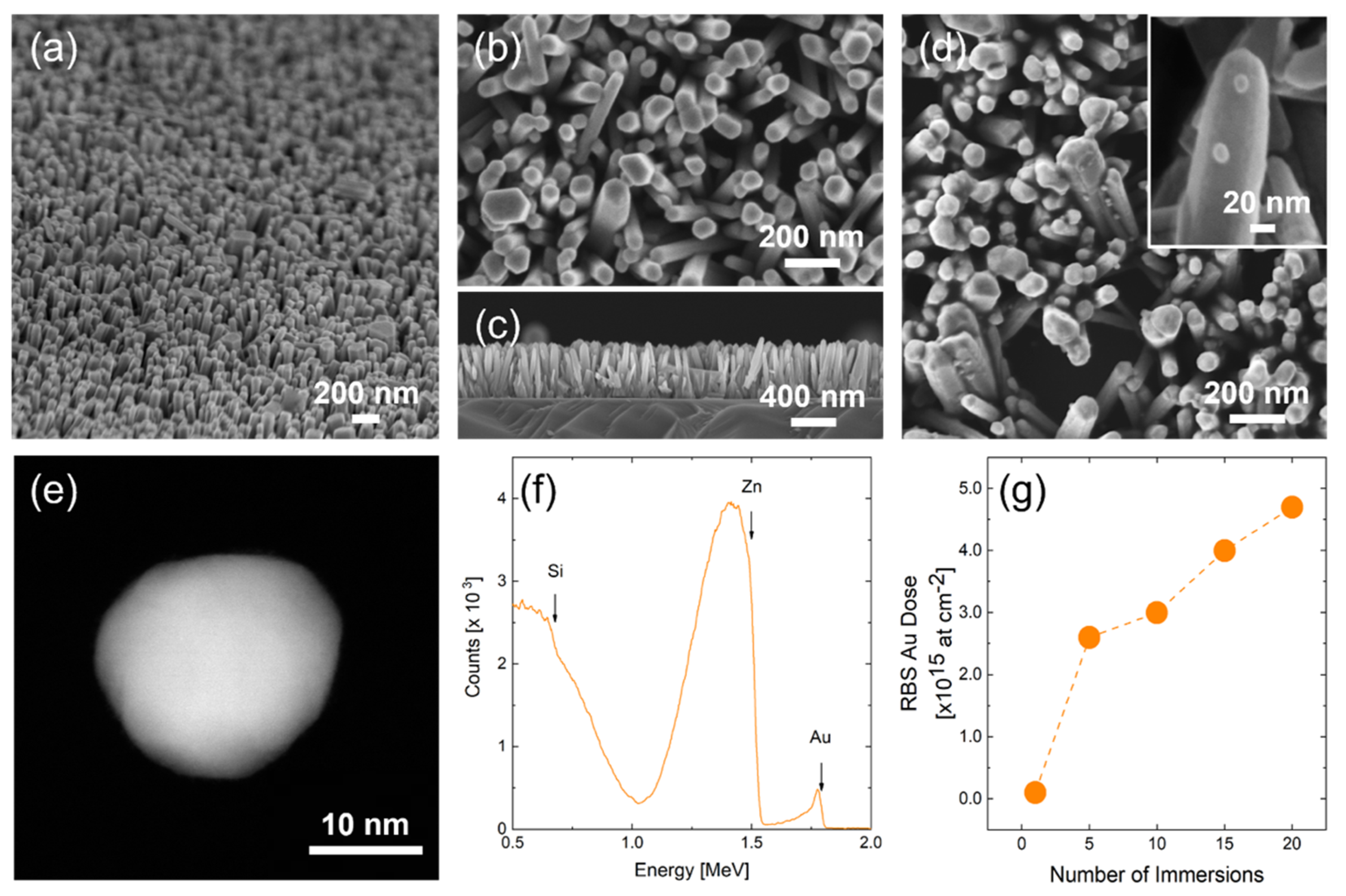
2.1. Synthesis and Decoration of ZnO Nanorods
2.2. Characterization
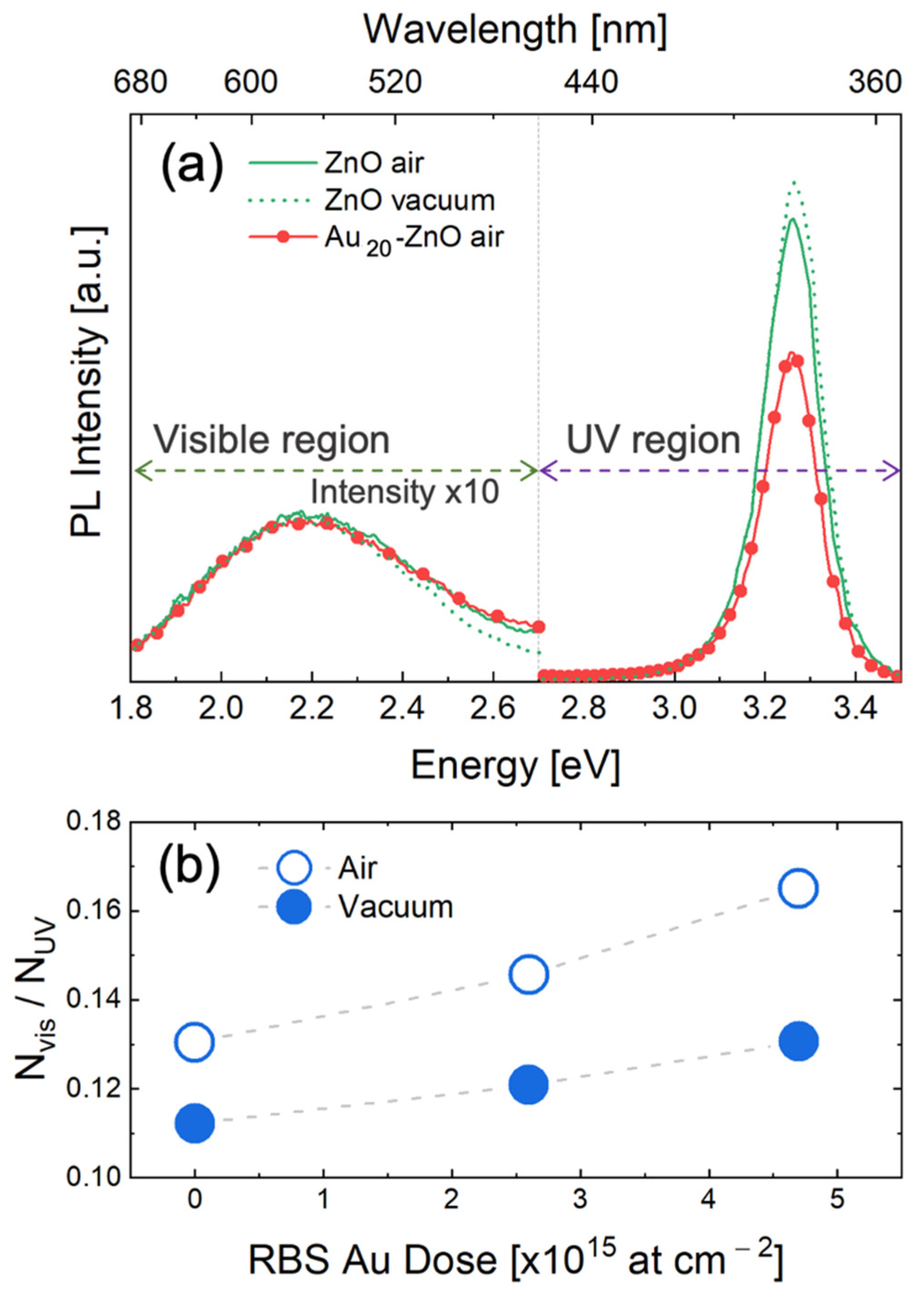
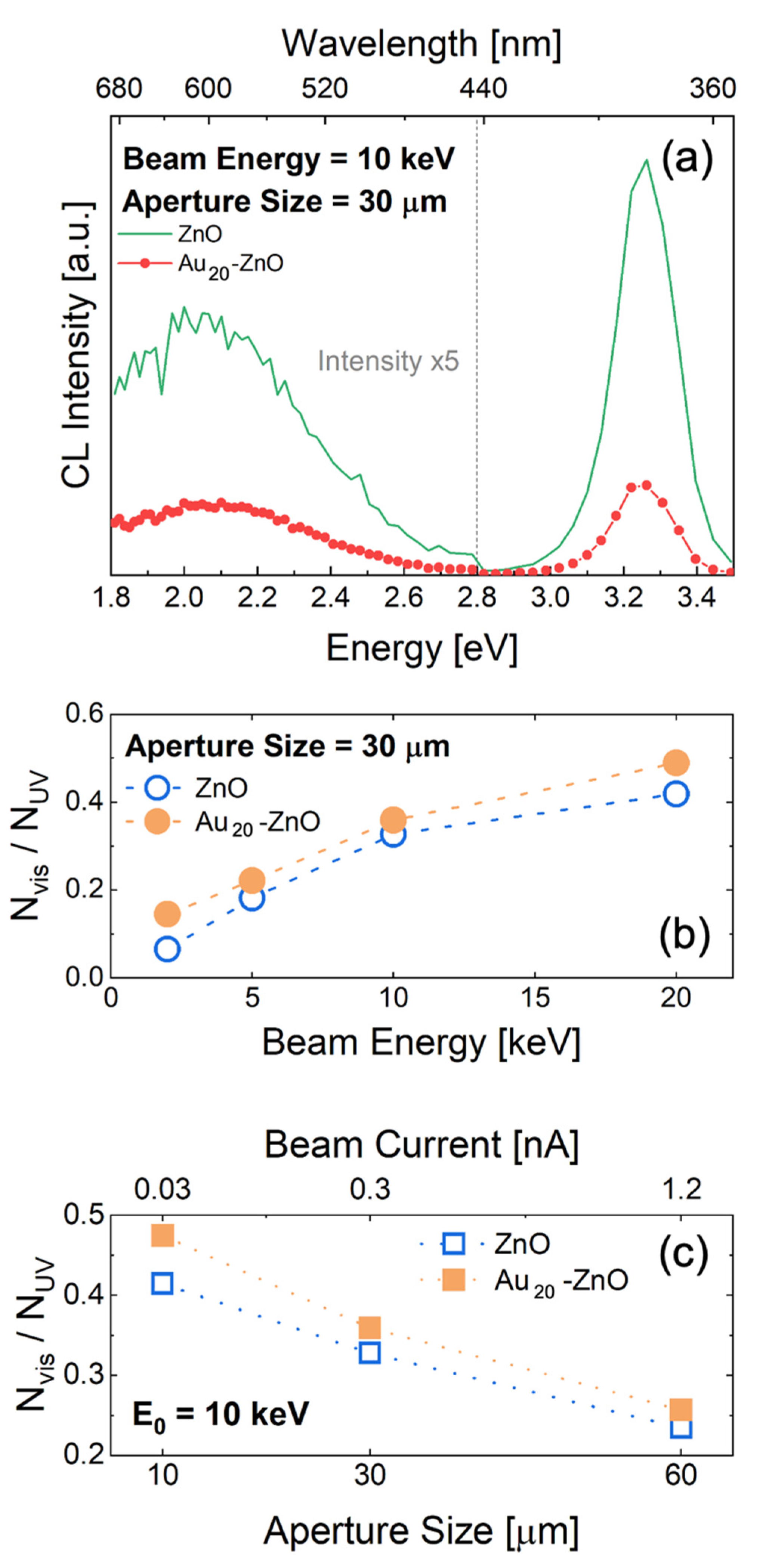
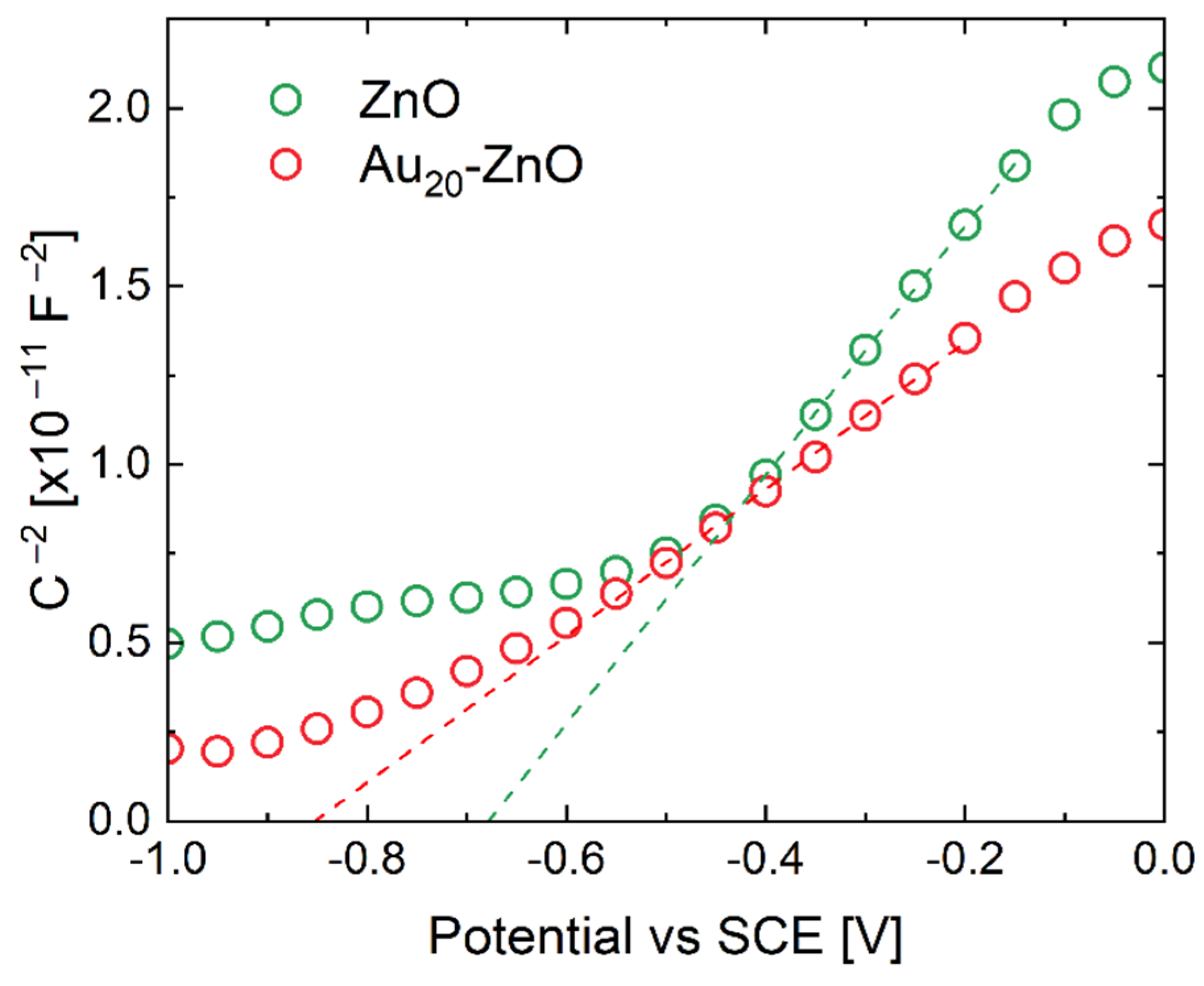
3. Results and Discussion
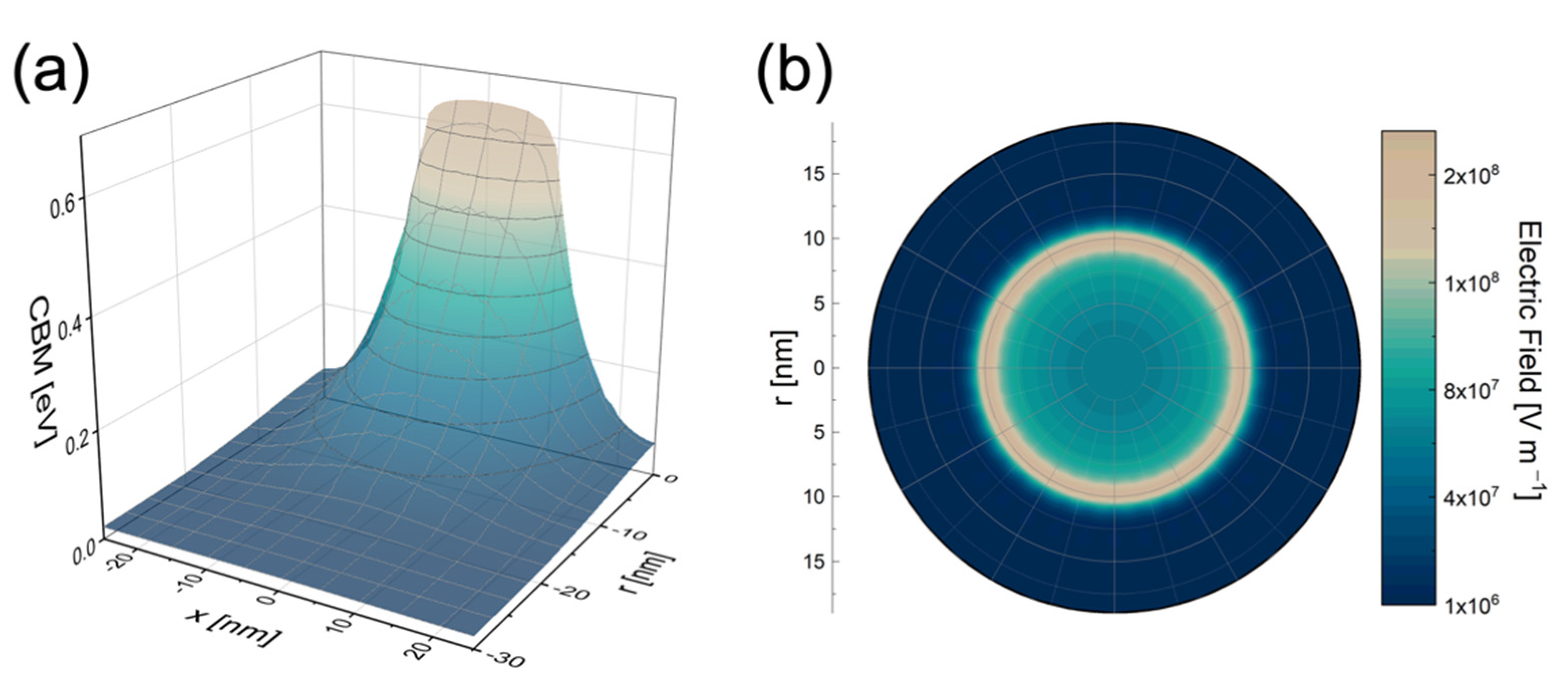
4. Modeling the Au NP Decoration Effect
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Djurišić, A.B.; Leung, Y.H. Optical Properties of ZnO Nanostructures. Small 2006, 2, 944–961. [Google Scholar] [CrossRef]
- Wang, Z.L. Nanostructures of zinc oxide. Mater. Today 2004, 7, 26–33. [Google Scholar] [CrossRef]
- Battaglia, C.; Escarré, J.; Söderström, K.; Charrière, M.; Despeisse, M.; Haug, F.-J.; Ballif, C. Nanomoulding of transparent zinc oxide electrodes for efficient light trapping in solar cells. Nat. Photon 2011, 5, 535–538. [Google Scholar] [CrossRef] [Green Version]
- Hu, L.; Yan, J.; Liao, M.; Xiang, H.; Gong, X.; Zhang, L.; Fang, X. An Optimized Ultraviolet-A Light Photodetector with Wide-Range Photoresponse Based on ZnS/ZnO Biaxial Nanobelt. Adv. Mater. 2012, 24, 2305–2309. [Google Scholar] [CrossRef] [PubMed]
- Sergent, S.; Takiguchi, M.; Tsuchizawa, T.; Yokoo, A.; Taniyama, H.; Kuramochi, E.; Notomi, M. Nanomanipulating and Tuning Ultraviolet ZnO-Nanowire-Induced Photonic Crystal Nanocavities. ACS Photon 2017, 4, 1040–1047. [Google Scholar] [CrossRef]
- Sergent, S.; Takiguchi, M.; Tsuchizawa, T.; Taniyama, H.; Notomi, M. ZnO-Nanowire-Induced Nanocavities in Photonic Crystal Disks. ACS Photon 2019, 6, 1132–1138. [Google Scholar] [CrossRef]
- Akermi, M.; Jaballah, N.; Alarifi, I.M.; Rahimi-Gorji, M.; Ben Chaabane, R.; Ben Ouada, H.; Majdoub, M. Synthesis and characterization of a novel hydride polymer P-DSBT/ZnO nano-composite for optoelectronic applications. J. Mol. Liq. 2019, 287, 110963. [Google Scholar] [CrossRef]
- Zhou, J.; Nomenyo, K.; Cesar, C.C.; Lusson, A.; Schwartzberg, A.; Yen, C.-C.; Woon, W.-Y.; Lerondel, G. Giant defect emission enhancement from ZnO nanowires through desulfurization process. Sci. Rep. 2020, 10, 4237. [Google Scholar] [CrossRef]
- Ramya, M.; Nideep, T.K.; Nampoori, V.P.N.; Kailasnath, M. Solvent assisted evolution and growth mechanism of zero to three dimensional ZnO nanostructures for dye sensitized solar cell applications. Sci. Rep. 2021, 11, 1–14. [Google Scholar] [CrossRef]
- Mehmood, M.; Ali, S.M.; Ramay, S.M.; Alkhuraiji, T.S. Au/ZnO hybrid nanocomposites and their optical and photocatalytic properties. Appl. Phys. A 2020, 126, 1–14. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Do, T.A.T.; Giang, H.T.; Ho, T.G.; Pham, Q.N.; Man, M.T. Effect of metal-support couplings on the photocatalytic performance of Au-decorated ZnO nanorods. J. Mater. Sci. Mater. Electron. 2020, 31, 14946–14952. [Google Scholar] [CrossRef]
- Ponnuvelu, D.V.; Dhakshinamoorthy, J.; Prasad, A.K.; Dhara, S.K.; Kamruddin, M.; Pullithadathil, B. Geometrically Controlled Au-Decorated ZnO Heterojunction Nanostructures for NO2 Detection. ACS Appl. Nano Mater. 2020, 3, 5898–5909. [Google Scholar] [CrossRef]
- Wang, J.; Fan, S.; Xia, Y.; Yang, C.; Komarneni, S. Room-temperature gas sensors based on ZnO nanorod/Au hybrids: Visible-light-modulated dual selectivity to NO2 and NH3. J. Hazard. Mater. 2020, 381, 120919. [Google Scholar] [CrossRef]
- Laskowski, F.; Oener, S.Z.; Nellist, M.R.; Gordon, A.M.; Bain, D.C.; Fehrs, J.L.; Boettcher, S.W. Nanoscale semiconductor/catalyst interfaces in photoelectrochemistry. Nat. Mater. 2019, 19, 69–76. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Xing, G.Z.; Zhang, Z.; Chen, H.Y.; Wu, T. Tailoring the photoluminescence of ZnO nanowires using Au nanoparticles. Nanotechnology 2008, 19, 435711. [Google Scholar] [CrossRef] [PubMed]
- Bora, T.; Myint, M.T.Z.; Al-Harthi, S.H.; Dutta, J. Role of surface defects on visible light enabled plasmonic photocatalysis in Au–ZnO nanocatalysts. RSC Adv. 2015, 5, 96670–96680. [Google Scholar] [CrossRef] [Green Version]
- Raji, R.; Gopchandran, K. Plasmonic photocatalytic activity of ZnO:Au nanostructures: Tailoring the plasmon absorption and interfacial charge transfer mechanism. J. Hazard. Mater. 2019, 368, 345–357. [Google Scholar] [CrossRef]
- Shahine, I.; Jradi, S.; Beydoun, N.; Gaumet, J.-J.; Akil, S. Plasmon-Enhanced Photoluminescence and Photocatalysis Reactions in Metal-Semiconductor Nanomaterials: UV-Generated Hot Electron in Gold-Zinc Oxide. ChemPhotoChem 2019, 4, 181–194. [Google Scholar] [CrossRef]
- Bahariqushchi, R.; Cosentino, S.; Scuderi, M.; Dumons, E.; Tran-Huu-Hue, L.P.; Strano, V.; Grandjean, D.; Lievens, P.; Poulin-Vittrant, G.; Spinella, C.; et al. Free carrier enhanced depletion in ZnO nanorods decorated with bimetallic AuPt nanoclusters. Nanoscale 2020, 12, 19213–19222. [Google Scholar] [CrossRef] [PubMed]
- Hsu, N.E.; Hung, W.K.; Chen, Y.F. Origin of defect emission identified by polarized luminescence from aligned ZnO nanorods. J. Appl. Phys. 2004, 96, 4671. [Google Scholar] [CrossRef]
- Shan, W.; Walukiewicz, W.; Ager, J.; Yu, K.M.; Yuan, H.B.; Xin, H.P.; Cantwell, G.; Song, J.J. Nature of room-temperature photoluminescence in ZnO. Appl. Phys. Lett. 2005, 86, 191911. [Google Scholar] [CrossRef]
- Djurišić, A.B.; Leung, Y.H.; Tam, K.H.; Ding, L.; Ge, W.K.; Chen, H.Y.; Gwo, S. Green, yellow, and orange defect emission from ZnO nanostructures: Influence of excitation wavelength. Appl. Phys. Lett. 2006, 88, 103107. [Google Scholar] [CrossRef] [Green Version]
- Tam, K.H.; Cheung, C.K.; Leung, Y.H.; Djurišić, A.B.; Ling, C.C.; Beling, C.D.; Fung, S.; Kwok, W.M.; Chan, W.K.; Phillips, D.L.; et al. Defects in ZnO Nanorods Prepared by a Hydrothermal Method. J. Phys. Chem. B 2006, 110, 20865–20871. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Reynolds, N. Photoluminescence of Zinc Oxide Nanowires: The Effect of Surface Band Bending. ISRN Condens. Matter Phys. 2012, 2012, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Fabbri, F.; Villani, M.; Catellani, A.; Calzolari, A.; Cicero, G.; Calestani, G.; Zappettini, A.; Dierre, B.; Sekiguchi, T.; Salviati, G. Zn vacancy induced green luminescence on non-polar surfaces in ZnO nanostructures. Sci. Rep. 2015, 4, 5158. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kumar, V.; Ntwaeaborwa, O.M.; Soga, T.; Dutta, V.; Swart, H.C. Rare Earth Doped Zinc Oxide Nanophosphor Powder: A Future Material for Solid State Lighting and Solar Cells. ACS Photon 2017, 4, 2613–2637. [Google Scholar] [CrossRef]
- Fiedler, S.; Lem, L.O.L.C.; Ton-That, C.; Phillips, M.R. The role of surface depletion layer effects on the enhancement of the UV emission in ZnO induced by a nanostructured Al surface coating. Appl. Surf. Sci. 2019, 504, 144409. [Google Scholar] [CrossRef] [Green Version]
- Peralta, M.D.L.R.; Pal, U.; Zeferino, R.S. Photoluminescence (PL) Quenching and Enhanced Photocatalytic Activity of Au-Decorated ZnO Nanorods Fabricated through Microwave-Assisted Chemical Synthesis. ACS Appl. Mater. Interfaces 2012, 4, 4807–4816. [Google Scholar] [CrossRef]
- Park, S.; Mun, Y.; An, S.; Lee, W.I.; Lee, C. Enhanced photoluminescence of Au-functionalized ZnO nanorods annealed in a hydrogen atmosphere. J. Lumin 2014, 147, 5–8. [Google Scholar] [CrossRef]
- Udawatte, N.; Lee, M.; Kim, J.; Lee, D. Well-Defined Au/ZnO Nanoparticle Composites Exhibiting Enhanced Photocatalytic Activities. ACS Appl. Mater. Interfaces 2011, 3, 4531–4538. [Google Scholar] [CrossRef]
- Rai, P.; Kim, Y.-S.; Song, H.-M.; Song, M.-K.; Yu, Y.-T. The role of gold catalyst on the sensing behavior of ZnO nanorods for CO and NO2 gases. Sens. Actuators B Chem. 2012, 165, 133–142. [Google Scholar] [CrossRef]
- Strano, V.; Urso, R.G.; Scuderi, M.; Iwu, K.O.; Simone, F.; Ciliberto, E.; Spinella, C.; Mirabella, S. Double Role of HMTA in ZnO Nanorods Grown by Chemical Bath Deposition. J. Phys. Chem. C 2014, 118, 28189–28195. [Google Scholar] [CrossRef]
- Turkevich, J.; Stevenson, P.C.; Hillier, J. A study of the nucleation and growth processes in the synthesis of colloidal gold. Discuss. Faraday Soc. 1951, 11, 55–75. [Google Scholar] [CrossRef]
- Frens, G. Controlled Nucleation for the Regulation of the Particle Size in Monodisperse Gold Suspensions. Nat. Phys. Sci. 1973, 241, 20–22. [Google Scholar] [CrossRef]
- Tyagi, H.; Kushwaha, A.K.; Kumar, A.; Aslam, M. A Facile pH Controlled Citrate-Based Reduction Method for Gold Nanoparticle Synthesis at Room Temperature. Nanoscale Res. Lett. 2016, 11, 1–11. [Google Scholar] [CrossRef] [Green Version]
- ImageJ. Available online: www.imagej.nih.gov (accessed on 1 February 2021).
- Thompson, M. Xrump. Available online: www.genplot.com (accessed on 1 February 2021).
- Mooney, J.; Kambhampati, P. Get the basics right: Jacobian conversion of wavelength and energy scales for quantitative analysis of emission spectra. J. Phys. Chem. Lett. 2013, 4, 3316–3318. [Google Scholar] [CrossRef]
- Drouin, D.; Couture, A.R.; Joly, D.; Tastet, X.; Aimez, V.; Gauvin, R. CASINO V2.42—A Fast and Easy-to-use Modeling Tool for Scanning Electron Microscopy and Microanalysis Users. Scanning 2007, 29, 92–101. [Google Scholar] [CrossRef] [PubMed]
- COMSOL Multiphysics® v. 5.3. COMSOL AB, Stockholm, Sweden. Available online: http://www.comsol.com (accessed on 1 February 2021).
- Feldman, L.C.; Mayer, J.W.; Grasserbauer, M. Fundamentals of surface and thin film analysis. Anal. Chim. Acta 1987, 199, 288. [Google Scholar] [CrossRef]
- Studenikin, S.A.; Cocivera, M. Time-resolved luminescence and photoconductivity of polycrystalline ZnO films. J. Appl. Phys. 2002, 91, 5060–5065. [Google Scholar] [CrossRef]
- Hong, S.; Joo, T.; Park, W.I.; Jun, Y.H.; Yi, G.-C. Time-resolved photoluminescence of the size-controlled ZnO nanorods. Appl. Phys. Lett. 2003, 83, 4157. [Google Scholar] [CrossRef] [Green Version]
- Kwok, W.-M.; Djurišić, A.B.; Leung, Y.H.; Chan, W.K.; Phillips, D.L. Time-resolved photoluminescence from ZnO nanostructures. Appl. Phys. Lett. 2005, 87, 223111. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.H.; Chua, S.J.; Yong, A.M.; Yang, H.Y.; Lau, S.P.; Yu, S.F.; Sun, X.W.; Miao, L.; Tanemura, M.; Tanemura, S. Exciton radiative lifetime in ZnO nanorods fabricated by vapor phase transport method. Appl. Phys. Lett. 2007, 90, 013107. [Google Scholar] [CrossRef]
- Zhao, Q.; Yang, L.L.; Willander, M.; Sernelius, B.; Holtz, P.-O. Surface recombination in ZnO nanorods grown by chemical bath deposition. J. Appl. Phys. 2008, 104, 073526. [Google Scholar] [CrossRef]
- Klason, P.; Børseth, T.M.; Zhao, Q.X.; Svensson, B.G.; Kuznetsov, A.Y.; Bergman, P.J.; Willander, M. Temperature dependence and decay times of zinc and oxygen vacancy related photoluminescence bands in zinc oxide. Solid State Commun. 2008, 145, 321–326. [Google Scholar] [CrossRef]
- Layek, A.; Manna, B.; Chowdhury, A. Carrier recombination dynamics through defect states of ZnO nanocrystals: From nanoparticles to nanorods. Chem. Phys. Lett. 2012, 539–540, 133–138. [Google Scholar] [CrossRef]
- Biroju, R.K.; Giri, P.K. Strong visible and near infrared photoluminescence from ZnO nanorods/nanowires grown on single layer graphene studied using sub-band gap excitation. J. Appl. Phys. 2017, 122, 044302. [Google Scholar] [CrossRef] [Green Version]
- Barbagiovanni, E.G.; Reitano, R.; Franzò, G.; Strano, V.; Terrasi, A.; Mirabella, S. Radiative mechanism and surface modification of four visible deep level defect states in ZnO nanorods. Nanoscale 2016, 8, 995–1006. [Google Scholar] [CrossRef]
- Barbagiovanni, E.G.; Strano, V.; Franzò, G.; Crupi, I.; Mirabella, S. Photoluminescence transient study of surface defects in ZnO nanorods grown by chemical bath deposition. Appl. Phys. Lett. 2015, 106, 093108. [Google Scholar] [CrossRef] [Green Version]
- Brillson, L.; Mosbacker, H.; Hetzer, M.; Strzhemechny, Y.; Look, D.; Cantwell, G.; Zhang, J.; Song, J. Surface and near-surface passivation, chemical reaction, and Schottky barrier formation at ZnO surfaces and interfaces. Appl. Surf. Sci. 2008, 254, 8000–8004. [Google Scholar] [CrossRef]
- Barbagiovanni, E.G.; Strano, V.; Franzò, G.; Reitano, R.; Dahiya, A.S.; Poulin-Vittrant, G.; Alquier, D.; Mirabella, S. Universal model for defect-related visible luminescence in ZnO nanorods. RSC Adv. 2016, 6, 73170–73175. [Google Scholar] [CrossRef]
- Brillson, L.J. Applications of depth-resolved cathodoluminescence spectroscopy. J. Phys. D Appl. Phys. 2012, 45, 183001. [Google Scholar] [CrossRef] [Green Version]
- Ye, J.D.; Zhao, H.; Liu, W.; Gu, S.L.; Zhang, R.; Zheng, Y.D.; Tan, S.T.; Sun, X.W.; Lo, G.Q.; Teo, K.L. Theoretical and experimental depth-resolved cathodoluminescence microanalysis of excitonic emission from ZnO epilayers. Appl. Phys. Lett. 2008, 92, 131914. [Google Scholar] [CrossRef]
- Toth, M.; Phillips, M.R. Monte Carlo modeling of cathodoluminescence generation using electron energy loss curves. Scanning 1998, 20, 425–432. [Google Scholar] [CrossRef]
- Bott, A.W. Electrochemistry of Semiconductors. Curr. Sep. 1998, 17, 3, ISSN 0891-0006. [Google Scholar]
- Beranek, R. (Photo)electrochemical Methods for the Determination of the Band Edge Positions of TiO2-Based Nanomaterials. Adv. Phys. Chem. 2011, 2011, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Fabregat-Santiago, F.; Garcia-Belmonte, G.; Bisquert, J.; Bogdanoff, P.; Zaban, A. Mott-Schottky Analysis of Nanoporous Semiconductor Electrodes in Dielectric State Deposited on SnO2(F) Conducting Substrates. J. Electrochem. Soc. 2003, 150, E293–E298. [Google Scholar] [CrossRef]
- Hankin, A.; Bedoya-Lora, F.E.; Alexander, J.C.; Regoutz, A.; Kelsall, G.H. Flat band potential determination: Avoiding the pitfalls. J. Mater. Chem. A 2019, 7, 26162–26176. [Google Scholar] [CrossRef] [Green Version]
- Memming, R. Semiconductor Electrochemistry; Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Scholz, F. Electroanalytical Methods: Guide to Experiments and Applications; Springer: Berlin/Heidelberg, Germany, 2010; ISBN 9783642029141. [Google Scholar]
- Xu, P.; Milstein, T.J.; Mallouk, T.E. Flat-Band Potentials of Molecularly Thin Metal Oxide Nanosheets. ACS Appl. Mater. Interfaces 2016, 8, 11539–11547. [Google Scholar] [CrossRef]
- Gelderman, K.; Lee, L.; Donne, S. Flat-Band Potential of a Semiconductor: Using the Mott–Schottky Equation. J. Chem. Educ. 2007, 84, 685. [Google Scholar] [CrossRef]
- Darowicki, K.; Krakowiak, S.; Ślepski, P. Selection of measurement frequency in Mott–Schottky analysis of passive layer on nickel. Electrochim. Acta 2006, 51, 2204–2208. [Google Scholar] [CrossRef]
- Henry, M.; Fanet, H. Physique des Semiconducteurs et des Composants Électroniques; Dunod: Malakoff, France, 2019. [Google Scholar]
- Gutmann, S.; Conrad, M.; Wolak, M.A.; Beerbom, M.M.; Schlaf, R. Work function measurements on nano-crystalline zinc oxide surfaces. J. Appl. Phys. 2012, 111, 123710. [Google Scholar] [CrossRef]
- Ahn, C.H.; Kim, Y.Y.; Kim, D.C.; Mohanta, S.K.; Cho, H.K. A comparative analysis of deep level emission in ZnO layers deposited by various methods. J. Appl. Phys. 2009, 105, 013502. [Google Scholar] [CrossRef]
- Janotti, A.; Van de Walle, C.G. Native point defects in ZnO. Phys. Rev. B 2007, 76, 165202. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bruno, L.; Strano, V.; Scuderi, M.; Franzò, G.; Priolo, F.; Mirabella, S. Localized Energy Band Bending in ZnO Nanorods Decorated with Au Nanoparticles. Nanomaterials 2021, 11, 2718. https://doi.org/10.3390/nano11102718
Bruno L, Strano V, Scuderi M, Franzò G, Priolo F, Mirabella S. Localized Energy Band Bending in ZnO Nanorods Decorated with Au Nanoparticles. Nanomaterials. 2021; 11(10):2718. https://doi.org/10.3390/nano11102718
Chicago/Turabian StyleBruno, Luca, Vincenzina Strano, Mario Scuderi, Giorgia Franzò, Francesco Priolo, and Salvo Mirabella. 2021. "Localized Energy Band Bending in ZnO Nanorods Decorated with Au Nanoparticles" Nanomaterials 11, no. 10: 2718. https://doi.org/10.3390/nano11102718
APA StyleBruno, L., Strano, V., Scuderi, M., Franzò, G., Priolo, F., & Mirabella, S. (2021). Localized Energy Band Bending in ZnO Nanorods Decorated with Au Nanoparticles. Nanomaterials, 11(10), 2718. https://doi.org/10.3390/nano11102718