Towards Poly(vinylidene fluoride-trifluoroethylene-chlorotrifluoroethylene)-Based Soft Actuators: Films and Electrospun Aligned Nanofiber Mats
Abstract
1. Introduction
2. Materials
2.1. P(VDF-TrFE-CTFE)
2.1.1. P(VDF-TrFE-CTFE) Films
2.1.2. P(VDF-TrFE-CTFE) Electrospun Nanofibers Mats
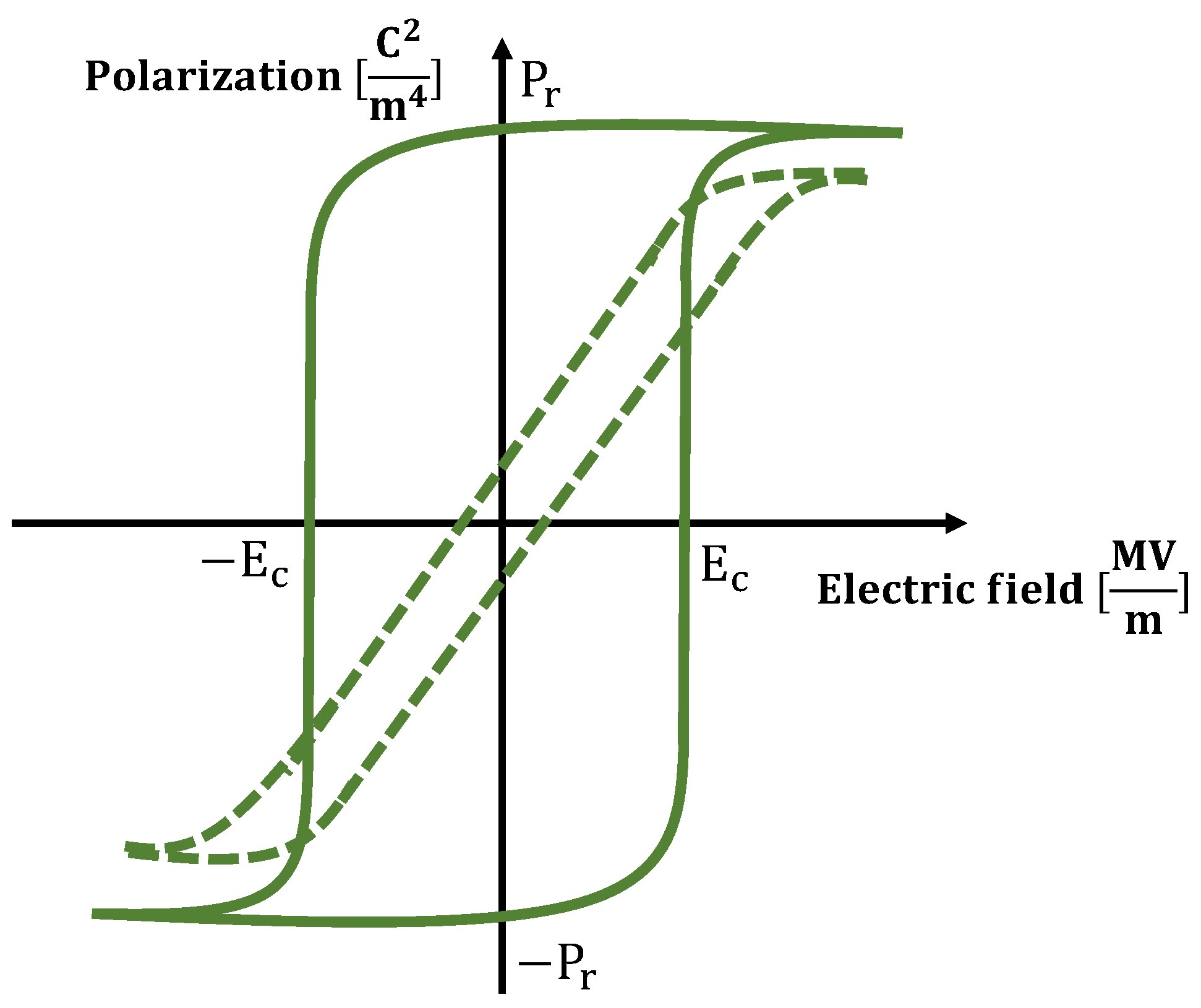
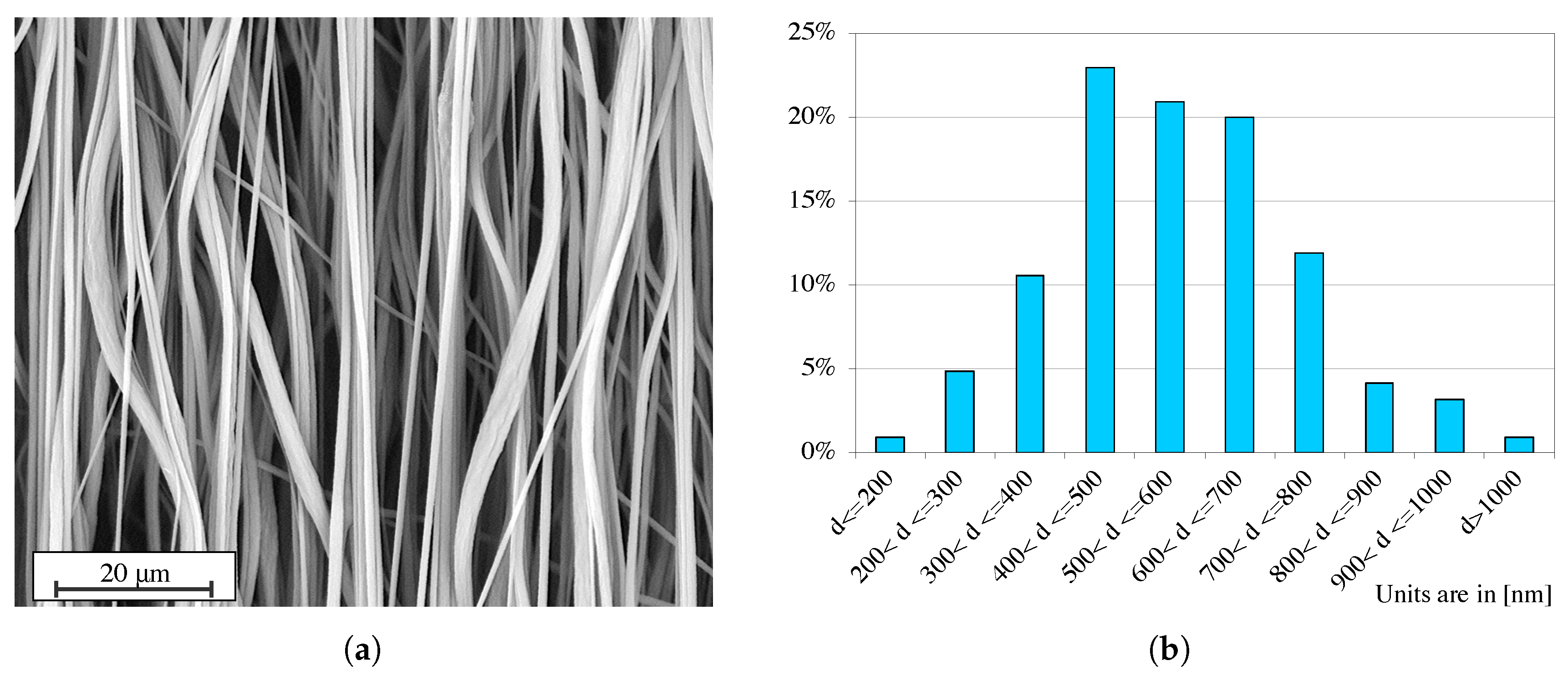
2.1.3. SEM Analysis
2.2. PFA
PFA Films
3. Method
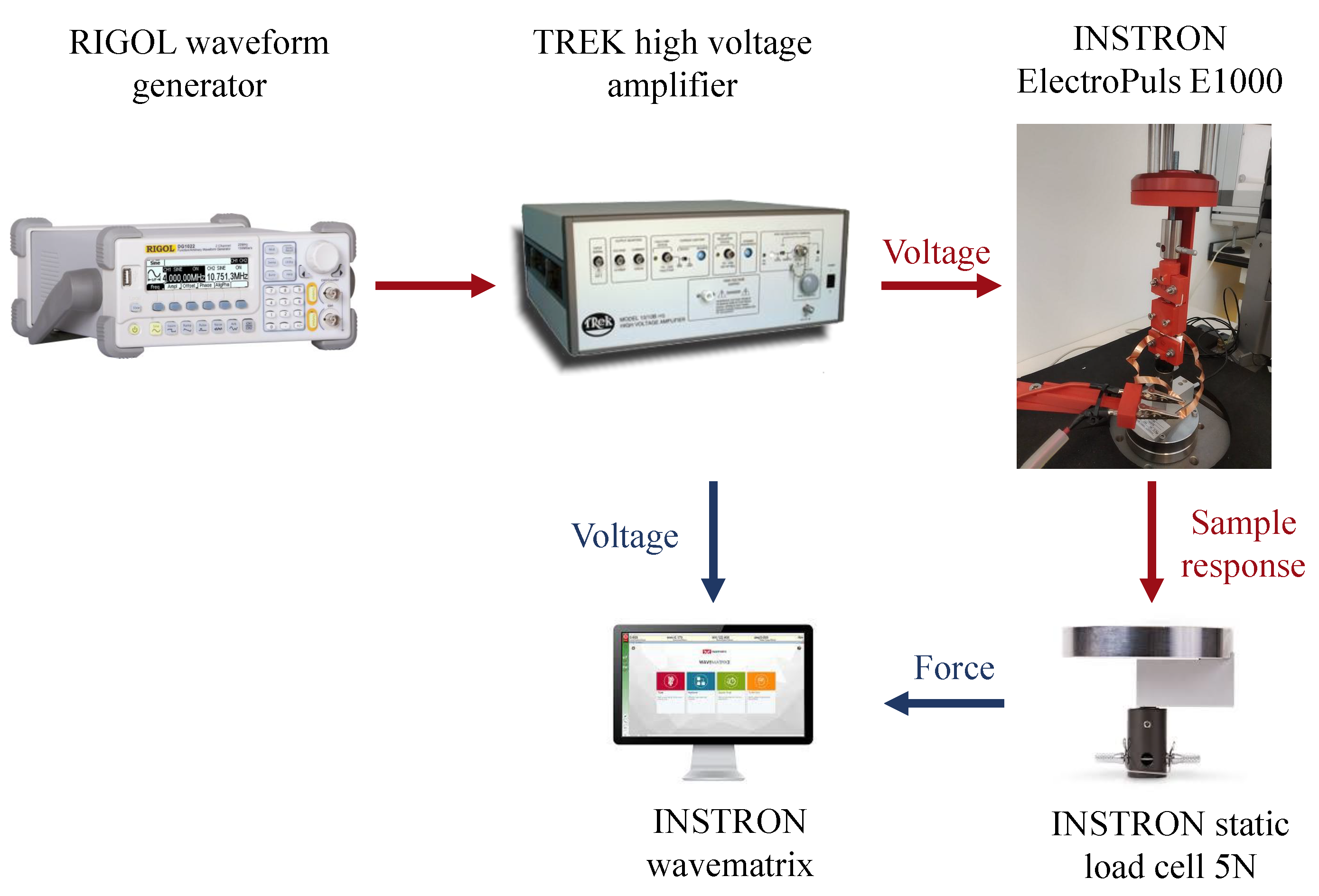
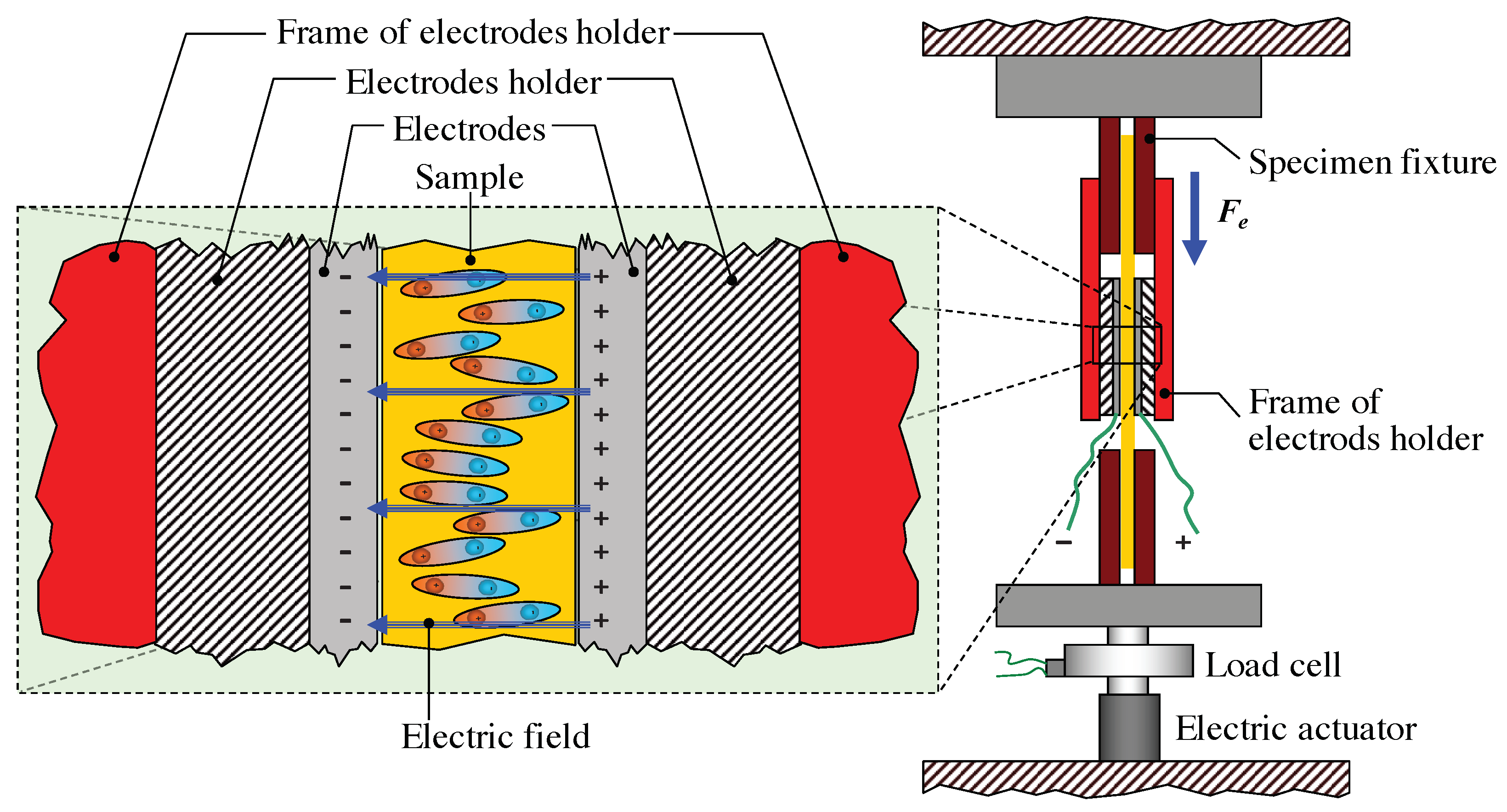
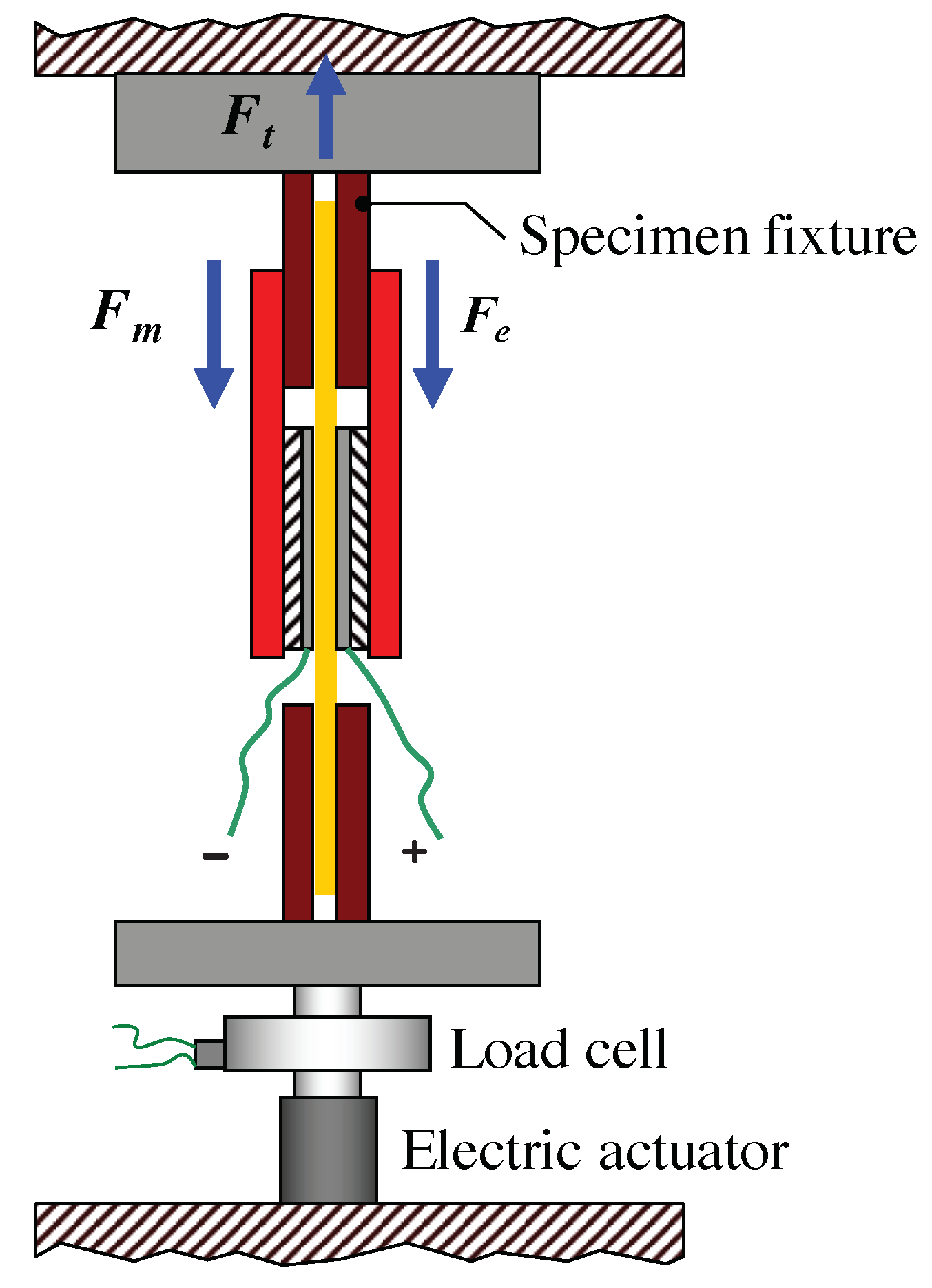
3.1. Experimental Test Set-Up
3.2. Experiment 1: Uniaxial Load Test
3.3. Experiment 2: Uniaxial Tensile Load Test
- The displacement between the fixtures is kept constant for 10 s and the desired electric field is applied.
- The displacement between the fixtures is changed by applying an ascending ramp of 0.6 mm with a rate of 0.01 mm/s.
- The displacement between the fixtures is changed by applying a descending ramp of 0.6 mm with a rate of 0.01 mm/s.
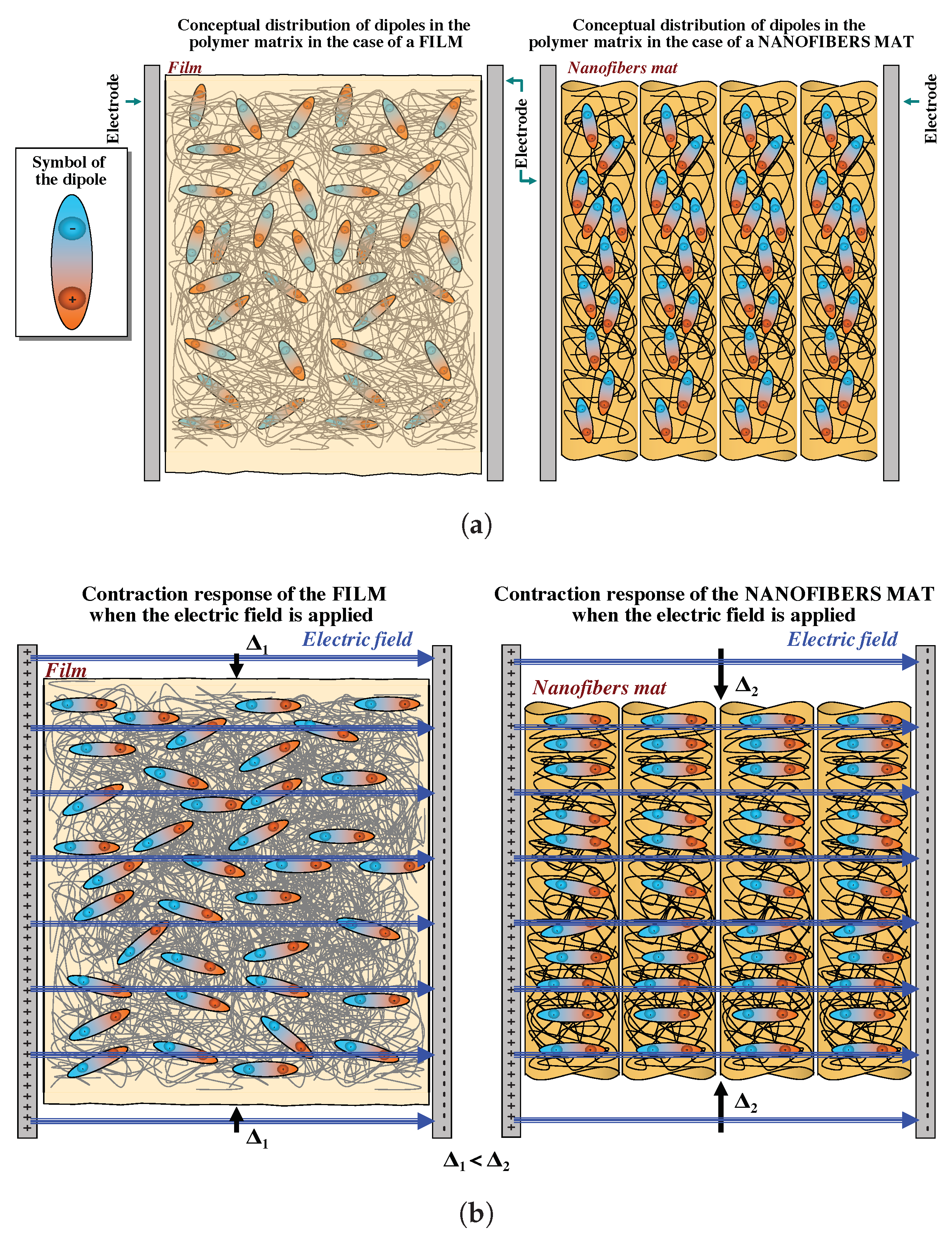
4. Results and Discussion
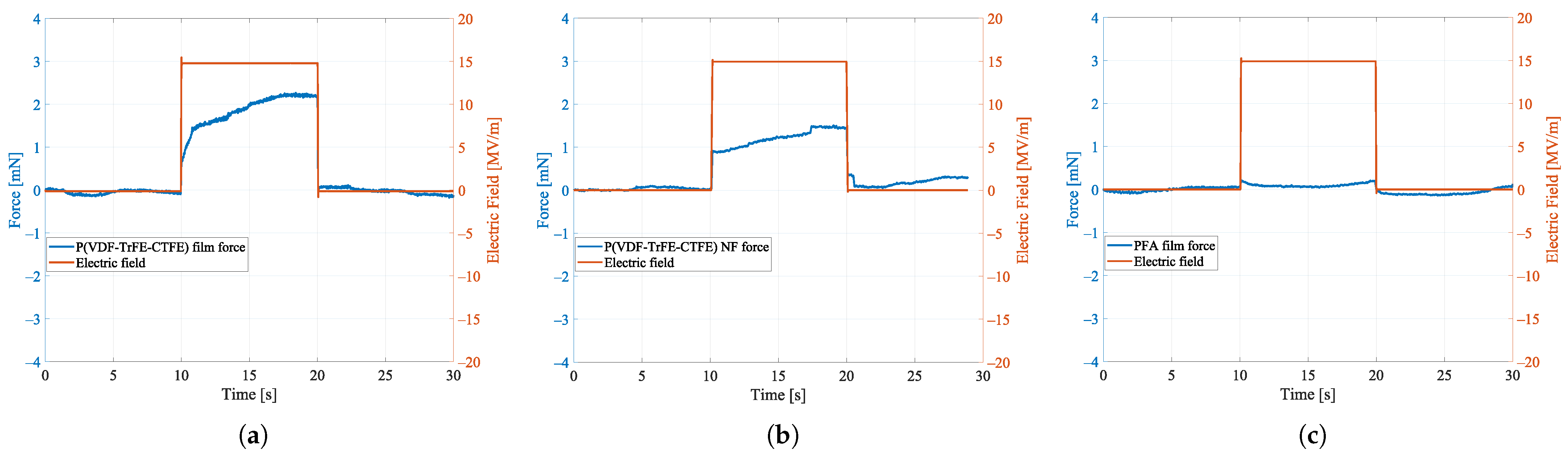
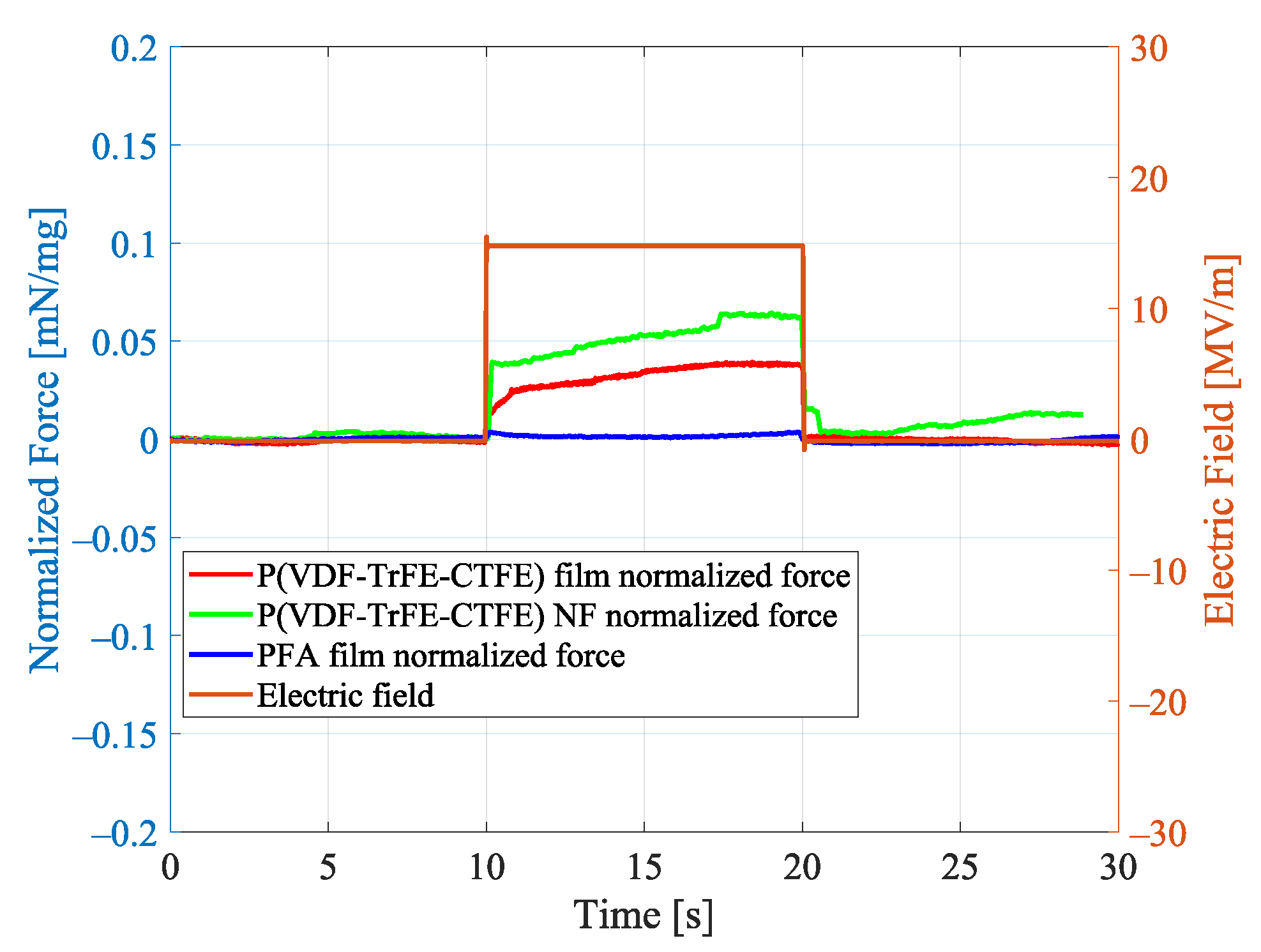
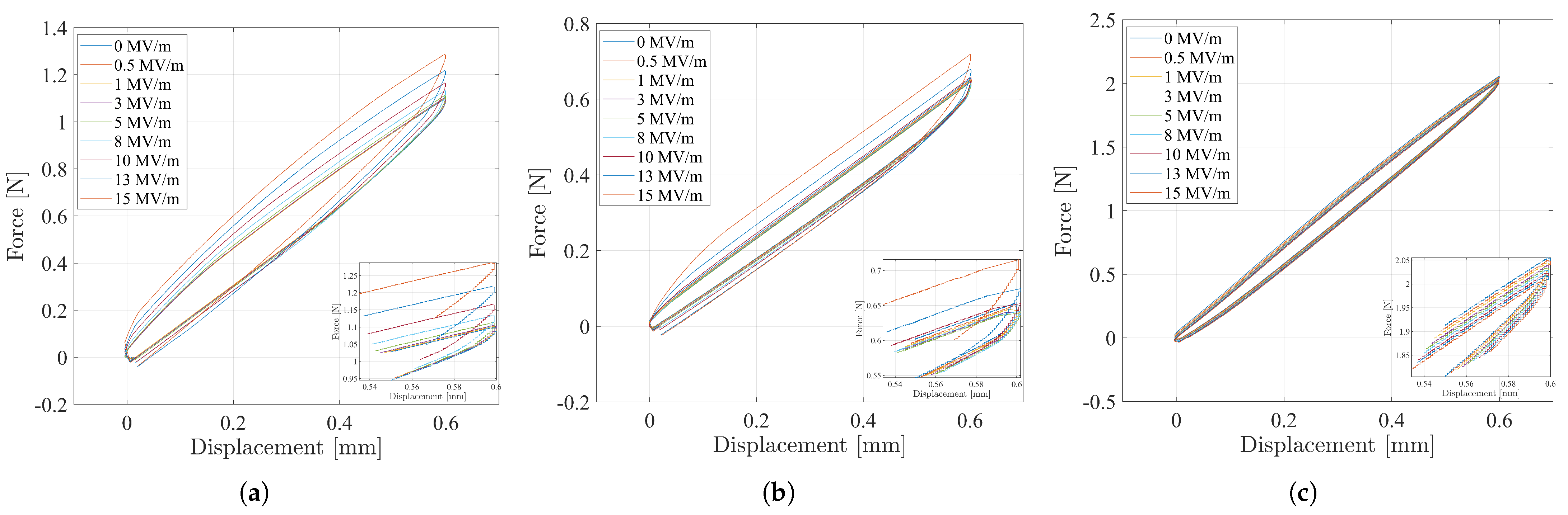
4.1. Results Experiment 1: Uniaxial Load Test
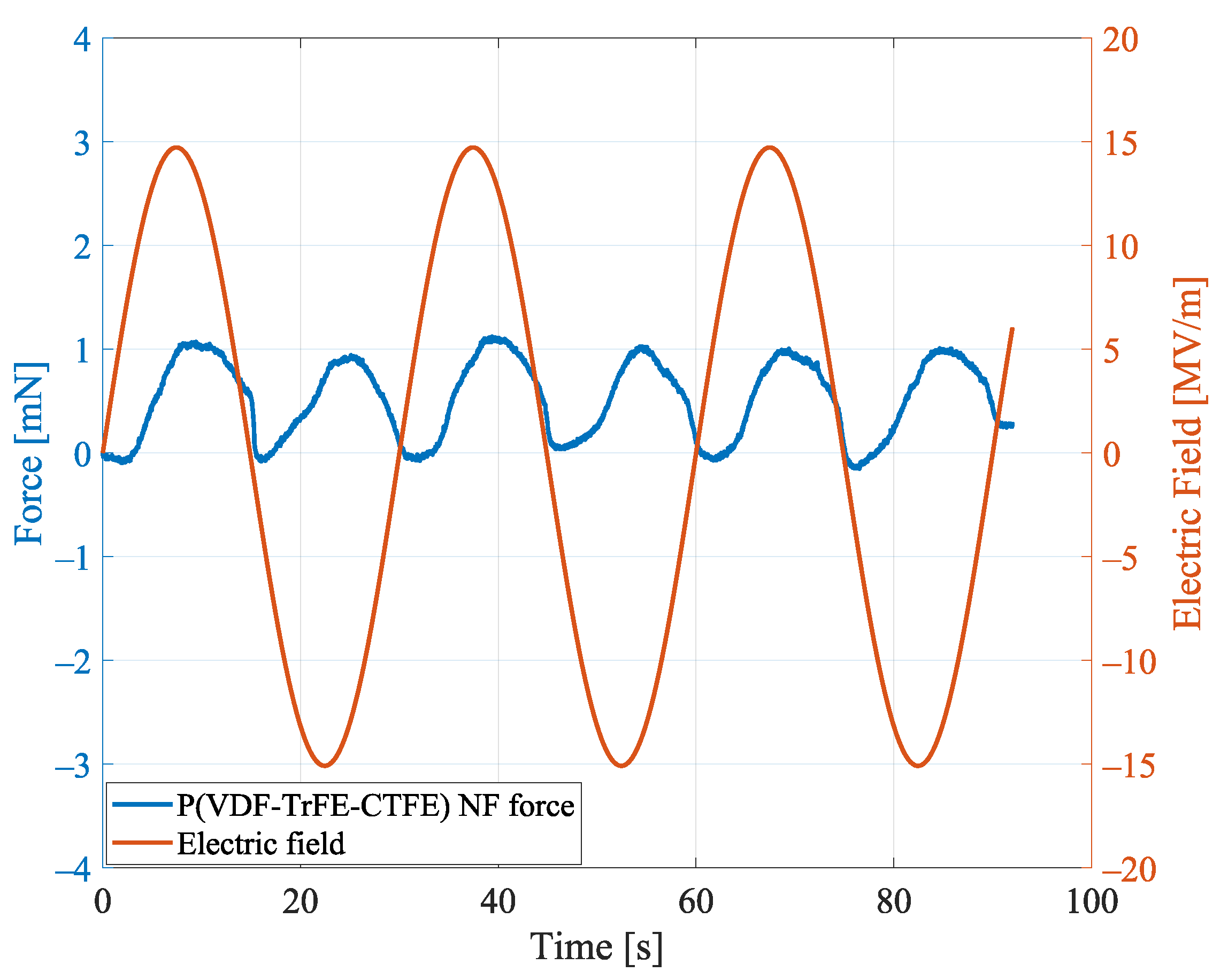
Aligned Nanofibers Mat: Repeatability
4.2. Results Experiment 2: Uniaxial Tensile Load Test
4.3. Future Outlook: P(VDF-TrFE-CTFE)-Based Soft Actuators
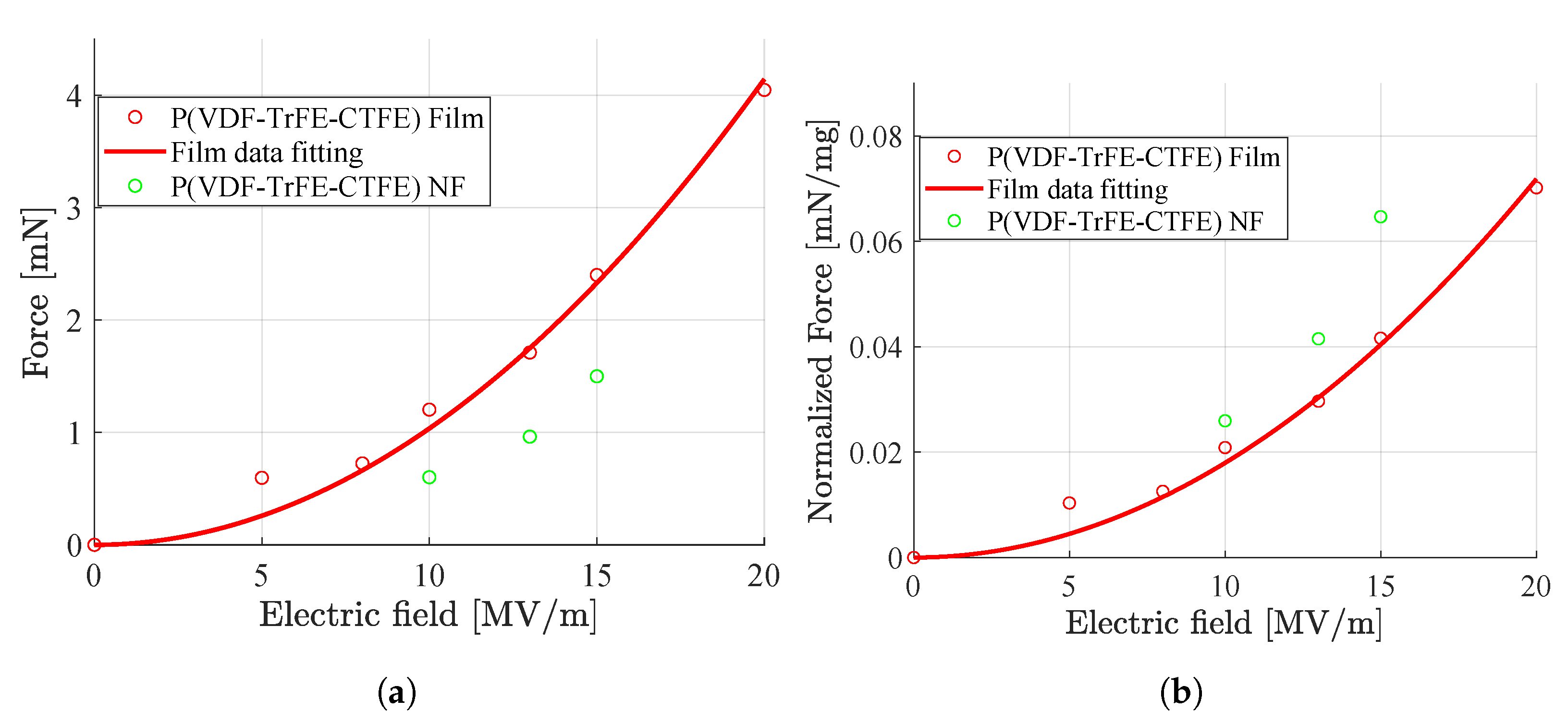
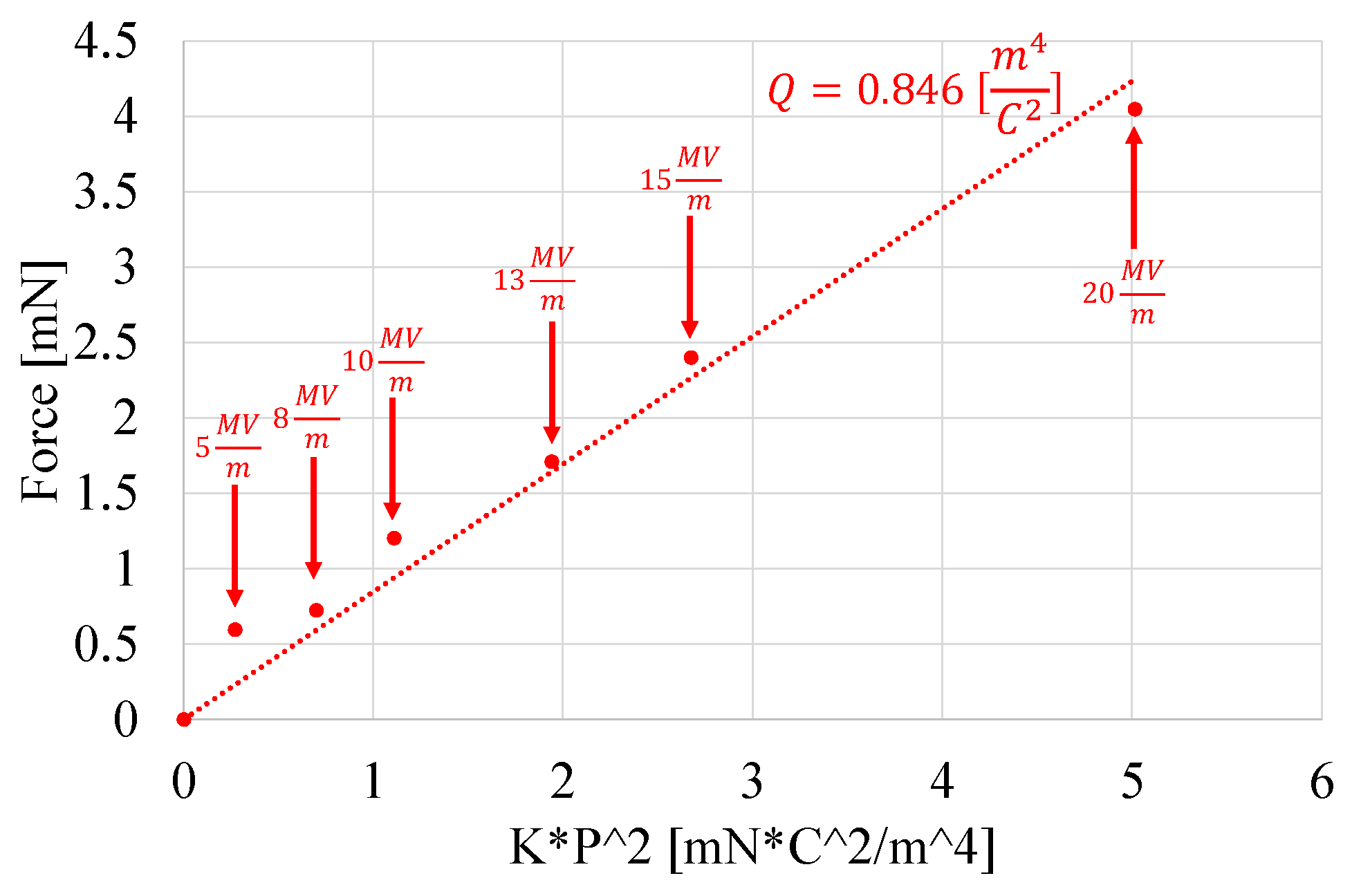
4.3.1. Force-to-Weight Ratio
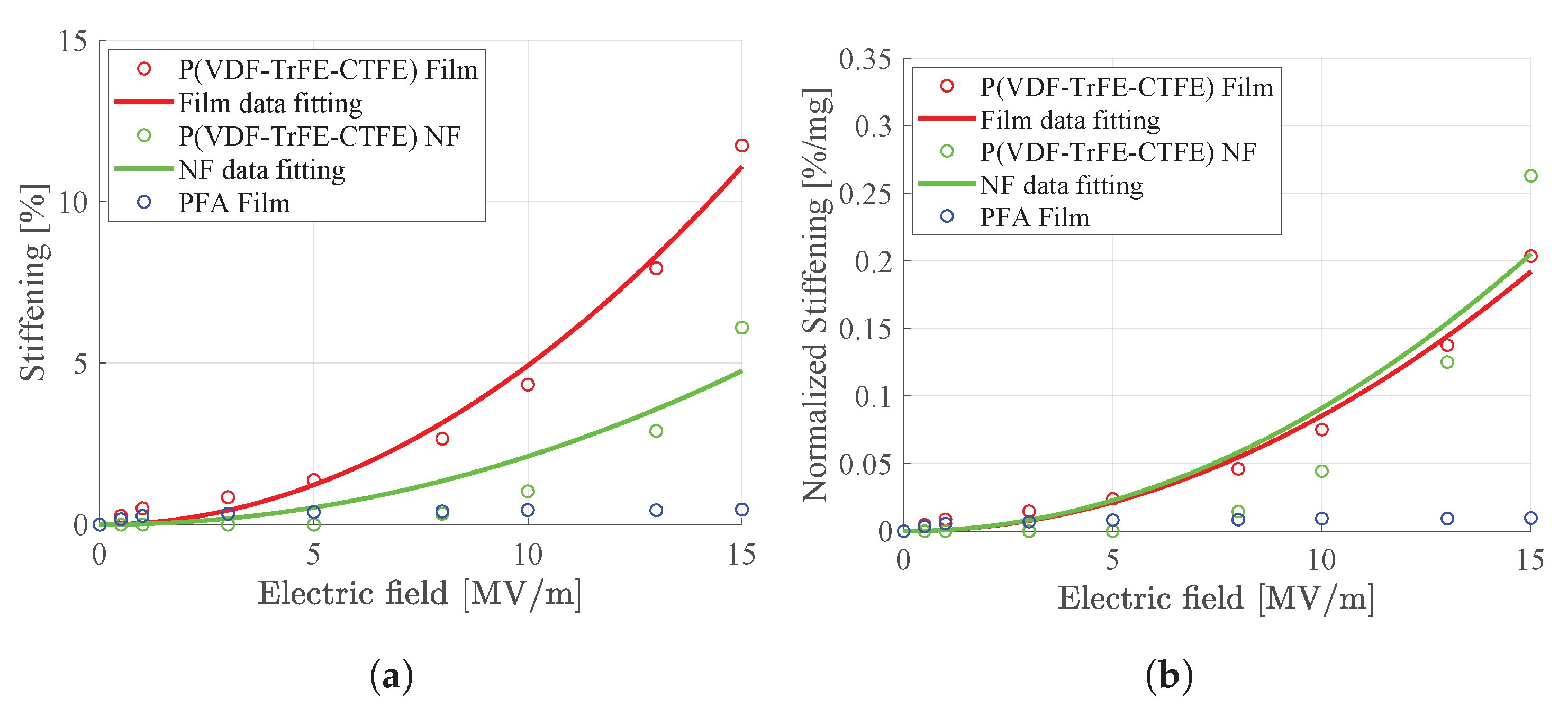
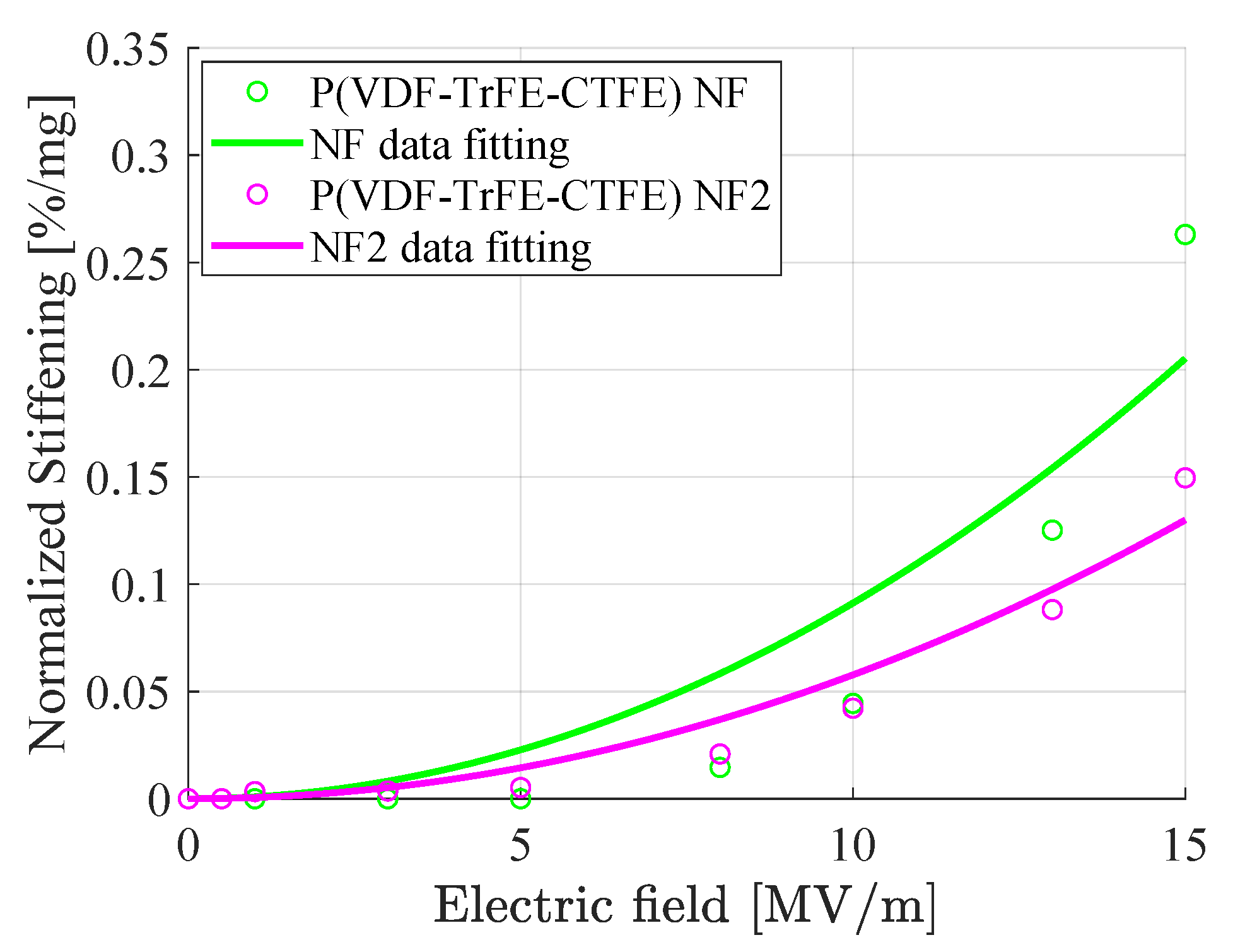
4.3.2. Stiffening
4.3.3. Scalability
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bar-Cohen, Y. Artificial Muscles Using Electroactive Polymers (EAP): Capabilities, Challenges and Potential; JPL Technical Report Server; Jet Propulsion Laboratory, National Aeronautics and Space Administration: Pasadena, CA, USA, 2005. [Google Scholar]
- Xu, H.; Cheng, Z.; Olson, D.; Mai, T.; Zhang, Q.M. Ferroelectric and electromechanical properties of poly(vinylidene-fluoride-trifluoroethylene-chlorotrifluoroethylene) terpolymer. Appl. Phys. Lett. 2001, 78, 2360–2362. [Google Scholar] [CrossRef]
- Yu, Z.; Ang, C.; Cross, L.E.; Petchsuk, A.; Chung, T.C. Dielectric and electroactive strain properties of poly(vinylidene-fluoride-trifluoroethylene-chlorotrifluoroethylene) terpolymers. Appl. Phys. Lett. 2004, 84, 1737–1739. [Google Scholar] [CrossRef]
- Wan, C.; Bowen, C.R. Multiscale-structuring of polyvinylidene fluoride for energy harvesting: The impact of molecular-micro-and macro-structure. J. Mater. Chem. A 2017, 5, 3091–3128. [Google Scholar] [CrossRef]
- Soulestin, T.; Ladmiral, V.; Santos, F.D.D.; Ameduri, B. Vinylidene fluoride- and trifluoroethylene-containing fluorinated electroactive copolymers. How does chemistry impact properties? Prog. Polym. Sci. 2017, 72, 16–60. [Google Scholar] [CrossRef]
- Cho, Y.; Ahn, D.; Park, J.B.; Pak, S.; Lee, S.; Jun, B.O.; Hong, J.; Lee, S.Y.; Jang, J.E.; Hong, J.; et al. Enhanced ferroelectric property of P(VDF-TrFE-CTFE) film using room-temperature crystallization for high-performance ferroelectric device applications. Adv. Electron. Mater. 2016, 2, 1600225. [Google Scholar] [CrossRef]
- Klein, R.J.; Runt, J.; Zhang, Q.M. Influence of crystallization conditions on the microstructure and electromechanical properties of poly(vinylidene-fluoride-trifluoroethylene-chlorofluoroethylene) terpolymers. Macromolecules 2003, 36, 7220–7226. [Google Scholar] [CrossRef]
- Chung, T.C.; Petchsuk, A. Synthesis and properties of ferroelectric fluoroterpolymers with Curie transitions at ambient temperature. Macromolecules 2002, 35, 7678–7684. [Google Scholar] [CrossRef]
- Gotti, C.; Sensini, A.; Zucchelli, A.; Carloni, R.; Focarete, M.L. Hierarchical fibrous structures for muscle-inspired soft-actuators: A review. Appl. Mater. Today 2020, 20, 100772. [Google Scholar] [CrossRef]
- Mokhtari, F.; Shamshirsaz, M.; Latifi, M.; Foroughi, J. Nanofibers-based piezoelectric energy harvester for self-powered wearable technologies. Polymers 2020, 12, 2697. [Google Scholar] [CrossRef]
- Ding, Y.; Li, W.; Wang, F.; Li, H.; Yang, S.; Wang, L.; Wang, Z.; Tebyetekerwa, M.; Tang, B.Z. Which is a better fluorescent sensor: Aggregation-induced emission-based nanofibers or thin-coating films? Mater. Adv. 2020, 1, 574–578. [Google Scholar] [CrossRef]
- Ghosal, K.; Chandra, A.; Praveen, G.; Snigdha, S.; Roy, S.; Agatemor, C.; Thomas, S.; Provaznik, I. Electrospinning over Solvent Casting: Tuning of Mechanical Properties of Membranes. Sci. Rep. 2018, 8, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Robinson, A.; Kumar, J. Comparing Conjugated Polymer Thin Film and Electrospun Nanofiber Sensing Elements for Detection of Explosives. J. Nanosci. Nanotechnol. 2014, 14, 6781–6785. [Google Scholar] [CrossRef] [PubMed]
- Carloni, R.; Lapp, V.I.; Cremonese, A.; Belcari, J.; Zucchelli, A. A variable stiffness joint with electrospun P(VDF-TrFE-CTFE) variable stiffness springs. IEEE Robot. Autom. Lett. 2018, 3, 973–978. [Google Scholar] [CrossRef]
- Imamura, H.; Kadookab, K.; Taya, M. A variable stiffness dielectric elastomer actuator based on electrostatic chucking. Soft Matter 2017, 13, 3440–3448. [Google Scholar] [CrossRef]
- Della Schiava, N.; Thetpraphi, K.; Le, M.Q.; Lermusiaux, P.; Millon, A.; Capsal, J.F.; Cottinet, P.J. Enhanced figures of merit for a high-performing actuator in electrostrictive materials. Polymers 2018, 10, 263. [Google Scholar] [CrossRef]
- Qiao, B.; Wang, X.; Tan, S.; Zhu, W.; Zhang, Z. Synergistic effects of Maxwell stress and electrostriction in electromechanical properties of poly(vinylidene fluoride)-based ferroelectric polymers. Macromolecules 2019, 52, 9000–9011. [Google Scholar] [CrossRef]
- Yamwong, T.; Voice, A.M.; Davies, G.R. Electrostrictive response of an ideal polar rubber. J. Appl. Phys. 2002, 91, 1472–1476. [Google Scholar] [CrossRef]
- Li, F.; Jin, L.; Xu, Z.; Zhang, S. Electrostrictive effect in ferroelectrics: An alternative approach to improve piezoelectricity. Appl. Phys. Rev. 2014, 1, 011103. [Google Scholar] [CrossRef]
- Li, F.; Jin, L.; Xu, Z.; Wang, D.; Zhang, S. Electrostrictive effect in Pb(Mg1/3Nb2/3)O3-xPbTiO3 crystals. Appl. Phys. Lett. 2013, 102, 152910. [Google Scholar] [CrossRef]
- Viola, G.; Saunders, T.; Wei, X.; Chong, K.; Luo, H.; Recce, M.; Yan, H. Contribution of piezoelectric effect, electrostriction and ferroelectric/ferroelastic switching to strain-electric field response of dielectrics. J. Adv. Dielectr. 2013, 3, 1350007. [Google Scholar] [CrossRef]
- Newnham, R.; Sundar, V.; Yimnirun, R.; Su, J.; Zhang, Q. Electrostriction: Nonlinear electromechanical coupling in solid dielectrics. J. Phys. Chem. B 1997, 101, 10141–10150. [Google Scholar] [CrossRef]
- ANSI/IEEE Standard No. 176-1987. IEEE Standard on Piezoelectricity; IEEE: Piscataway, NJ, USA, 1988. [Google Scholar]
- Zhao, J.; Glazounov, A.; Zhang, Q.; Toby, B. Neutron diffraction study of electrostrictive coefficients of prototype cubic phase of relaxor ferroelectric Pb(Mg1/3Nb2/3)O3. Appl. Phys. Lett. 1998, 72, 1048–1050. [Google Scholar] [CrossRef]
- Craciun, F. Strong variation of electrostrictive coupling near an intermedi- ate temperature of relaxor ferroelectrics. Phys. Rev. B 2010, 81, 184111. [Google Scholar] [CrossRef]
- Wang, S.; Li, Q. Design, synthesis and processing of PVDF-based dielectric polymers. IET Nanodielectr. 2018, 1, 80–91. [Google Scholar] [CrossRef]
- O’Connor, R.; McGuinness, G. Electrospun nanofibre bundles and yarns for tissue engineering applications: A review. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2016, 230, 987–998. [Google Scholar] [CrossRef]
- Tarus, B.; Fadel, N.; Al-Oufy, A.; El-Messiry, M. Effect of polymer concentration on the morphology and mechanical characteristics of electrospun cellulose acetate and poly (vinyl chloride) nanofiber mats. Alex. Eng. J. 2016, 55, 2975–2984. [Google Scholar] [CrossRef]
- Maccaferri, E.; Mazzocchetti, L.; Benelli, T.; Zucchelli, A.; Giorgini, L. Morphology, thermal, mechanical properties and ageing of nylon 6,6/ graphene nanofibers as Nano2 materials. Compos. Part B Eng. 2019, 166, 120–129. [Google Scholar] [CrossRef]
- Ask, A.; Menzel, A.; Ristinma, M. Electrostriction in electro-viscoelastic polymers. Mech. Mater. 2012, 50, 9–21. [Google Scholar] [CrossRef]
- Shkel, Y.M. Electrostriction: Material parameters and stress/strain constitutive relations. Philos. Mag. 2007, 87, 1743–1767. [Google Scholar] [CrossRef]
- Wongtimnoi, K.; Guiffard, B.; Bogner-Van de Moortéle, A.L.; Seveyrat, C.G.; Cavaillé, J.Y. Improvement of electrostrictive properties of a polyether-based polyurethane elastomer filled with conductive carbon black. Compos. Sci. Technol. 2011, 71, 885–892. [Google Scholar] [CrossRef]
- Tohluebaji, N.; Putson, C.; Muensit, N. High electromechanical deformation based on structural beta-phase content and electrostrictive properties of electrospun poly(vinylidene fluoride-hexafluoropropylene) nanofibers. Polymers 2019, 11, 1817. [Google Scholar] [CrossRef] [PubMed]
- Nawaka, K.; Putson, C. Enhanced electric field induced strain in electrostrictive polyurethane composites fibers with polyaniline (emeraldine salt) spider-web network. Compos. Sci. Technol. 2020, 198, 108293. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, J.; Cheng, Y.; Chen, S.; Yang, M.; Huang, J.; Wang, H.; Wu, G.; Wu, H. Alignment of boron nitride nanofibers in epoxy composite films for thermal conductivity and dielectric breakdown strength improvement. Nanomaterials 2018, 8, 242. [Google Scholar] [CrossRef] [PubMed]
- Fabiani, D.; Grolli, F.; Speranza, M.; Suraci, S.V.; Brugo, T.M.; Zucchelli, A.; Maccaferri, E. Piezoelectric nanofibers for integration in multifunctional materials. In Proceedings of the 2018 IEEE Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Cancun, Mexico, 21–24 October 2018; pp. 14–17. [Google Scholar]
- Kao, K.C. Dielectric Phenomena in Solids: With Emphasis on Physical Concepts of Electronic Processes; Elsevier Academic Press: San Diego, CA, USA, 2004; pp. 49–50. [Google Scholar]
- Zhang, Q.M.; Bharti, V.; Zhao, X. Giant electrostriction and relaxor ferroelectric behavior in electron-irradiated poly(vinylidene fluoride-trifluoroethylene) copolymer. J. Phys. Chem. B 1998, 280, 2101–2104. [Google Scholar] [CrossRef] [PubMed]
- Kuang, Y.; Chen, C.; Cheng, J.; Pastel, G.; Li, T.; Song, J.; Jiang, F.; Li, Y.; Zhang, Y.; Jang, S.H.; et al. Selectively aligned cellulose nanofibers towards high-performance soft actuators. Extrem. Mech. Lett. 2019, 29, 100463. [Google Scholar] [CrossRef]
- Liu, L.; Jiang, S.; Sun, Y.; Agarwal, S. Giving direction to motion and surface with ultra-fast speed using oriented hydrogel fibers. Adv. Funct. Mater. 2016, 26, 1021–1027. [Google Scholar] [CrossRef]
- Manti, M.; Cacucciolo, V.; Cianchetti, M. Stiffening in soft robotics: A review of the state of the art. IEEE Robot. Autom. Mag. 2016, 23, 93–106. [Google Scholar] [CrossRef]
- Shintake, J.; Schubert, B.; Rosset, S.; Shea, H.; Floreano, D. Variable stiffness actuator for soft robotics using dielectric elastomer and low-melting-point alloy. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Hamburg, Germany, 28 September–2 October 2015; pp. 1097–1102. [Google Scholar]
- Chen, Y.; Sun, J.; Liu, Y.; Leng, J. Variable stiffness property study on shape memory polymer composite tube. Smart Mater. Struct. 2012, 21, 094021. [Google Scholar] [CrossRef]
- Mutlu, R.; Alici, G. Artificial muscles with adjustable stiffness. Smart Mater. Struct. 2010, 19, 045004. [Google Scholar] [CrossRef]
- Karsten, R.; Schlaak, H.F. Adaptive absorber based on dielectric elastomer stack actuator with variable stiffness. Electroact. Polym. Actuators Devices (EAPAD) 2012, 8340, 486–493. [Google Scholar]
- Gu, B.K.; Ismail, Y.A.; Spinks, G.M.; Kim, S.I.; So, I.; Kim, S.J. A linear actuation of polymeric nanofibrous bundle for artificial muscles. Chem. Mater. 2009, 21, 511–515. [Google Scholar] [CrossRef]
- Severt, S.Y.; Maxwell, S.L.; Bontrager, J.S.; Leger, J.M.; Murphy, A.R. Mimicking muscle fiber structure and function through electromechanical actuation of electrospun silk fiber bundles. J. Mater. Chem. B 2017, 5, 8105–8114. [Google Scholar] [CrossRef] [PubMed]


| Material | l [mm] | b [mm] | t [μm] | w [mg] |
|---|---|---|---|---|
| P(VDF-TrFE-CTFE) film | 55 | 9 | ∼60 | 57.7 |
| P(VDF-TrFE-CTFE) NF | 55 | 9 | ∼80 | 23.2 |
| P(VDF-TrFE-CTFE) NF2 | 55 | 9 | ∼60 | 16.6 |
| PFA film | 55 | 9 | ∼55 | 48.1 |
| Flow rate [mL/h] | 0.8 |
| Electric potential [kV] | 26 |
| Drum rotation speed [rpm] | 2430 |
| Distance needles-drum [cm] | 14 |
| Relative humidity [%] | 52 |
| Temperature [°C] | 20 |
| Electric Field [MV/m] | Film Stiffness [N/mm] | Mat (NF) Stiffness [N/mm] |
|---|---|---|
| 0 | ||
| 0.5 | ||
| 1 | ||
| 3 | ||
| 5 | ||
| 8 | ||
| 10 | ||
| 13 | ||
| 15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
D’Anniballe, R.; Zucchelli, A.; Carloni, R. Towards Poly(vinylidene fluoride-trifluoroethylene-chlorotrifluoroethylene)-Based Soft Actuators: Films and Electrospun Aligned Nanofiber Mats. Nanomaterials 2021, 11, 172. https://doi.org/10.3390/nano11010172
D’Anniballe R, Zucchelli A, Carloni R. Towards Poly(vinylidene fluoride-trifluoroethylene-chlorotrifluoroethylene)-Based Soft Actuators: Films and Electrospun Aligned Nanofiber Mats. Nanomaterials. 2021; 11(1):172. https://doi.org/10.3390/nano11010172
Chicago/Turabian StyleD’Anniballe, Riccardo, Andrea Zucchelli, and Raffaella Carloni. 2021. "Towards Poly(vinylidene fluoride-trifluoroethylene-chlorotrifluoroethylene)-Based Soft Actuators: Films and Electrospun Aligned Nanofiber Mats" Nanomaterials 11, no. 1: 172. https://doi.org/10.3390/nano11010172
APA StyleD’Anniballe, R., Zucchelli, A., & Carloni, R. (2021). Towards Poly(vinylidene fluoride-trifluoroethylene-chlorotrifluoroethylene)-Based Soft Actuators: Films and Electrospun Aligned Nanofiber Mats. Nanomaterials, 11(1), 172. https://doi.org/10.3390/nano11010172







