Mechanical Properties of Electrospun, Blended Fibrinogen: PCL Nanofibers
Abstract
1. Introduction
2. Materials and Methods
2.1. Preparation of 50:50 Fibrinogen:PCL Solution
2.2. Preparation of Striated Substrate
2.3. Electrospinning of 50:50 Fibrinogen:PCL Fibers
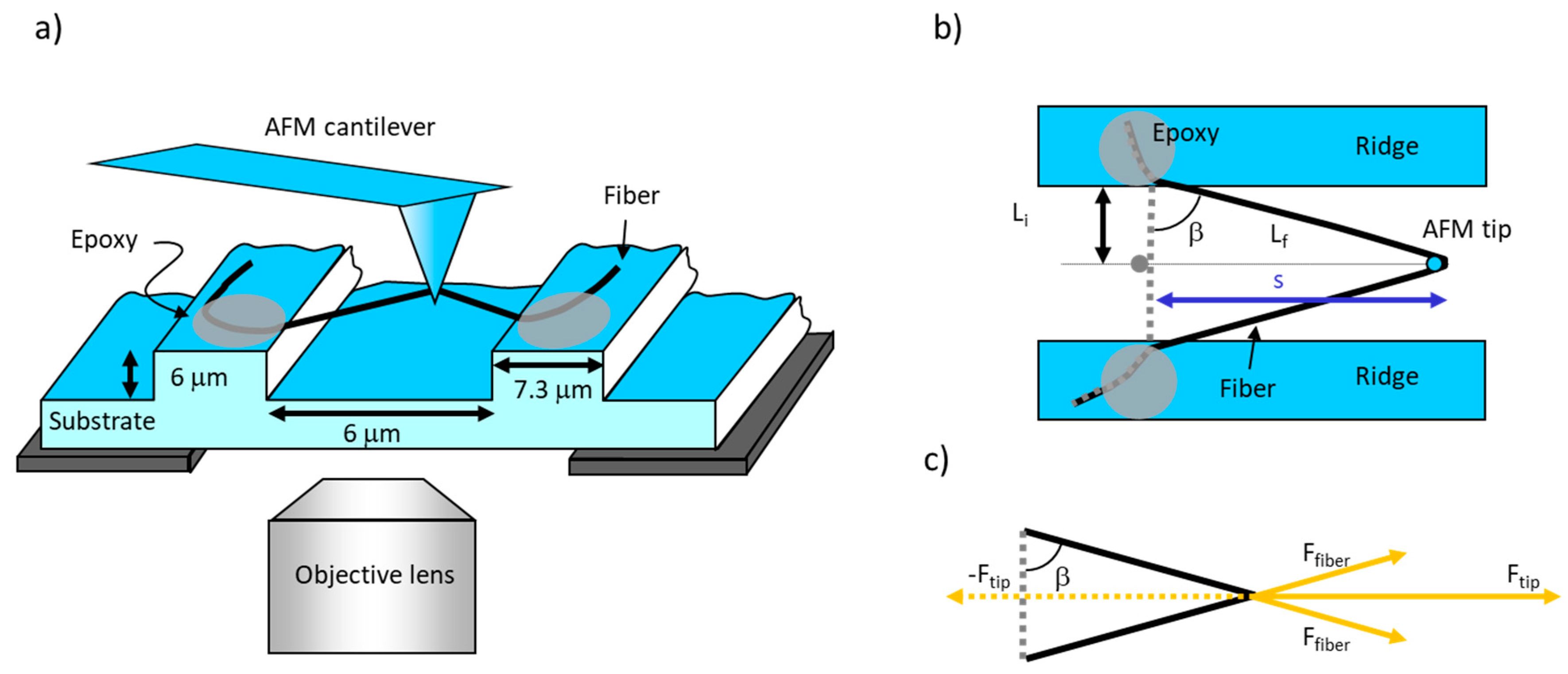
2.4. Anchoring of Fibers to Ridges
2.5. Combined AFM/Optical Microscopy
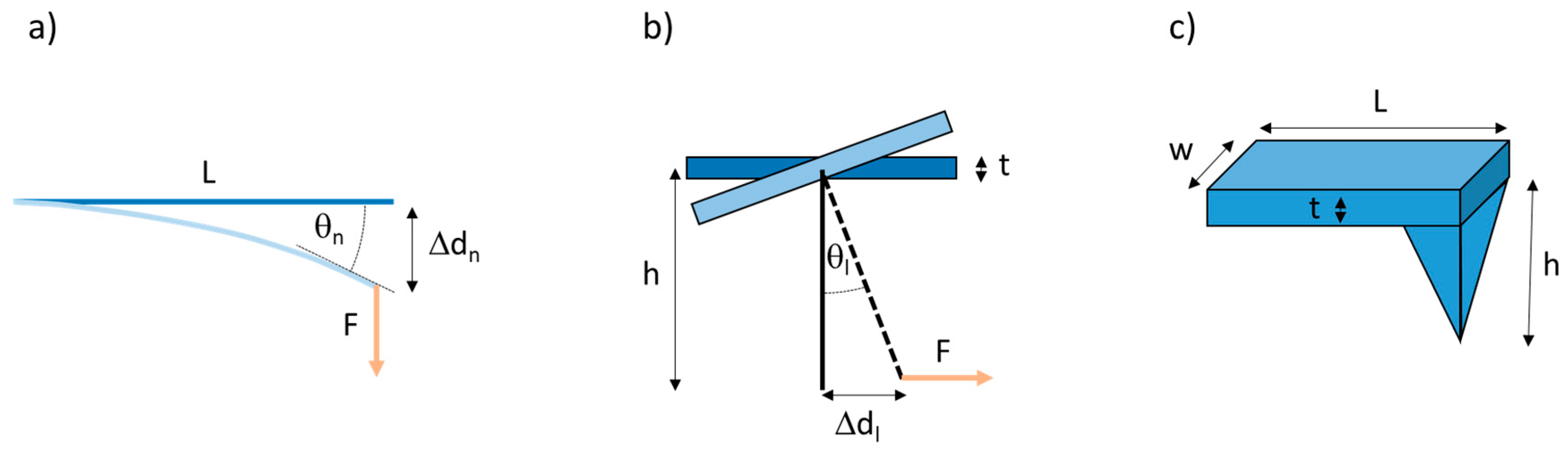
2.6. AFM Force Measurements
2.7. Fiber Stress–Strain Curves
2.8. Incremental Stress–Strain Curves
3. Results
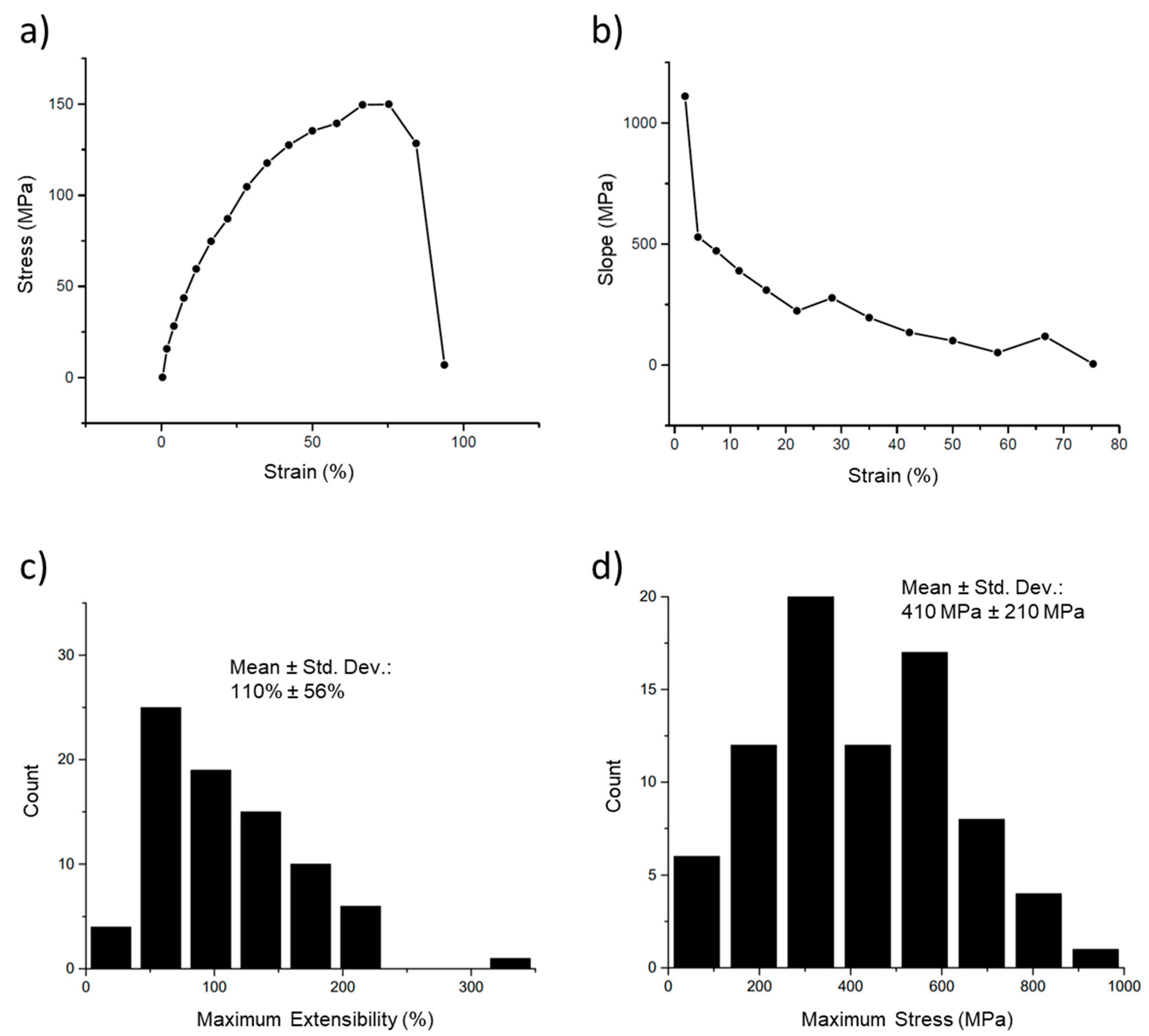
3.1. Simple Stress–Strain Curves
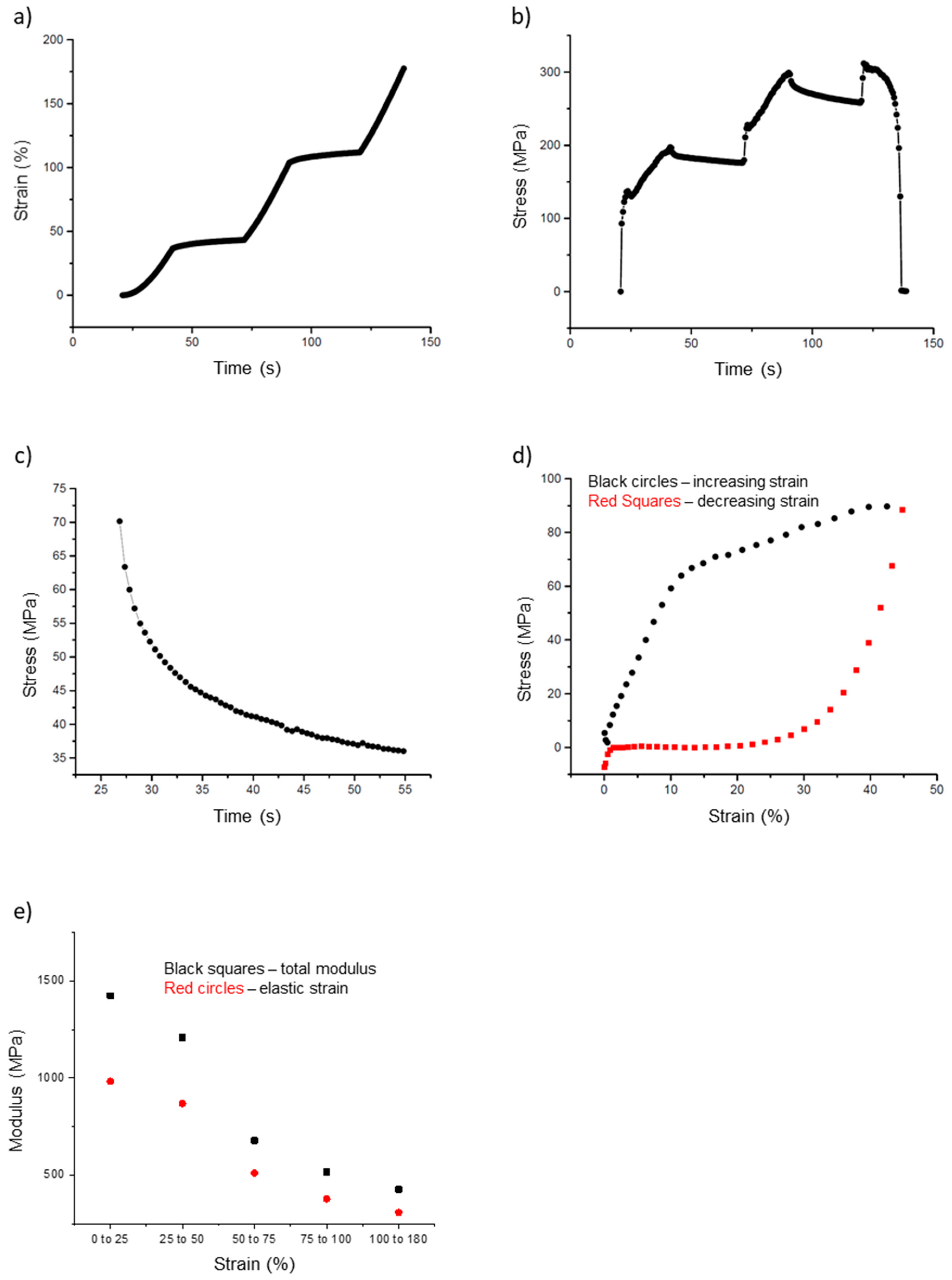
3.2. Incremental Stress–Strain Curves
3.3. Energy Loss and Elastic Limit
4. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Xue, J.J.; Wu, T.; Dai, Y.Q.; Xia, Y.N. Electrospinning and electrospun nanofibers: Methods, materials, and applications. Chem. Rev. 2019, 119, 5298–5415. [Google Scholar] [CrossRef]
- Cooley, J.F. Apparatus for Electrically Dispersing Fluids. U.S. Patent 692,631, 4 February 1902. [Google Scholar]
- Morton, W.J. Method of Dispersing Fluid. U.S. Patent 705,691, 29 July 1902. [Google Scholar]
- Formhals, A. Process and Apparatus for Preparing ArtificialThreads. U.S. Patent 1,975,504, 2 October 1934. [Google Scholar]
- Taylor, G. Electrically driven jets. Proc. R. Soc. A Math. Phys. Sci. 1969, 313, 453–475. [Google Scholar] [CrossRef]
- Braghirolli, D.I.; Steffens, D.; Pranke, P. Electrospinning for regenerative medicine: A review of the main topics. Drug Discov. Today 2014, 19, 743–753. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Jia, X.; Han, F.; Zhao, J.; Zhao, Y.; Fan, Y.; Yuan, X. Dual-delivery of VEGF and PDGF by double-layered electrospun membranes for blood vessel regeneration. Biomaterials 2013, 34, 2202–2212. [Google Scholar] [CrossRef] [PubMed]
- Han, F.; Jia, X.; Dai, D.; Yang, X.; Zhao, J.; Zhao, Y.; Fan, Y.; Yuan, X. Performance of a multilayered small-diameter vascular scaffold dual-loaded with VEGF and PDGF. Biomaterials 2013, 34, 7302–7313. [Google Scholar] [CrossRef] [PubMed]
- Xie, J.W.; MacEwan, M.R.; Ray, W.Z.; Liu, W.Y.; Siewe, D.Y.; Xia, Y.N. Radially aligned, electrospun nanofibers as dural substitutes for wound closure and tissue regeneration applications. ACS Nano 2010, 4, 5027–5036. [Google Scholar] [CrossRef] [PubMed]
- Qiu, X.; Lee, B.L.-P.; Ning, X.; Murthy, N.; Dong, N.; Li, S. End-point immobilization of heparin on plasma-treated surface of electrospun polycarbonate-urethane vascular graft. Acta Biomater. 2017, 51, 138–147. [Google Scholar] [CrossRef]
- Zhao, X.; Yuan, Z.; Yildirimer, L.; Zhao, J.; Lin, Z.Y.; Cao, Z.; Pan, G.; Cui, W. Tumor-triggered controlled drug release from electrospun fibers using inorganic caps for inhibiting cancer relapse. Small 2015, 11, 4284–4291. [Google Scholar] [CrossRef]
- Ren, X.; Han, Y.; Wang, J.; Jiang, Y.; Yi, Z.; Xu, H.; Ke, Q. An aligned porous electrospun fibrous membrane with controlled drug delivery-an efficient strategy to accelerate diabetic wound healing with improved angiogenesis. Acta Biomater. 2018, 70, 140–153. [Google Scholar] [CrossRef]
- Li, X.R.; Li, M.Y.; Sun, J.; Zhuang, Y.; Shi, J.J.; Guan, D.W.; Chen, Y.Y.; Dai, J.W. Radially aligned electrospun fibers with continuous gradient of SDF1 alpha for the guidance of neural stem cells. Small 2016, 12, 5009–5018. [Google Scholar] [CrossRef]
- Xu, H.; Li, H.; Ke, Q.; Chang, J. An anisotropically and heterogeneously aligned patterned electrospun scaffold with tailored mechanical property and improved bioactivity for vascular tissue engineering. ACS Appl. Mater. Interfaces 2015, 7, 8706–8718. [Google Scholar] [CrossRef] [PubMed]
- Sundararaghavan, H.G.; Saunders, R.L.; Hammer, D.A.; Burdick, J.A. Fiber alignment directs cell motility over chemotactic gradients. Biotechnol. Bioeng. 2013, 110, 1249–1254. [Google Scholar] [CrossRef]
- Qu, J.; Zhou, D.; Xu, X.; Zhang, F.; He, L.; Ye, R.; Zhu, Z.; Zuo, B.; Zhang, H. Optimization of electrospun TSF nanofiber alignment and diameter to promote growth and migration of mesenchymal stem cells. Appl. Surf. Sci. 2012, 261, 320–326. [Google Scholar] [CrossRef]
- Rao, S.S.; Nelson, M.T.; Xue, R.; DeJesus, M.S.; Viapiano, J.K.; Lannutti, J.J.; Sarkar, A.; Winter, J.O. Mimicking white matter tract topography using core-shell electrospun nanofibers to examine migration of malignant brain tumors. Biomaterials 2013, 34, 5181–5190. [Google Scholar] [CrossRef]
- Wu, S.; Wang, Y.; Streubel, P.N.; Duan, B. Living nanofiber yarn-based woven biotextiles for tendon tissue engineering using cell tri-culture and mechanical stimulation. Acta Biomater. 2017, 62, 102–115. [Google Scholar] [CrossRef] [PubMed]
- Kennedy, K.M.; Bhaw-Luximon, A.; Jhurry, D. Cell-matrix mechanical interaction in electrospun polymeric scaffolds for tissue engineering: Implications for scaffold design and performance. Acta Biomater. 2017, 50, 41–55. [Google Scholar] [CrossRef]
- Vatankhah, E.; Prabhakaran, M.P.; Semnani, D.; Razavi, S.; Zamani, M.; Ramakrishna, S. Phenotypic modulation of smooth muscle cells by chemical and mechanical cues of electrospun tecophilic/gelatin nanofibers. ACS Appl. Mater. Interfaces 2014, 6, 4089–4101. [Google Scholar] [CrossRef]
- Wang, X.F.; Ding, B.; Li, B.Y. Biomimetic electrospun nanofibrous structures for tissue engineering. Mater. Today 2013, 16, 229–241. [Google Scholar] [CrossRef] [PubMed]
- Wise, S.G.; Byrom, M.J.; Waterhouse, A.; Bannon, P.G.; Ng, M.K.C.; Weiss, A.S. A multilayered synthetic human elastin/polycaprolactone hybrid vascular graft with tailored mechanical properties. Acta Biomater. 2011, 7, 295–303. [Google Scholar] [CrossRef] [PubMed]
- Wu, T.; Zhang, J.; Wang, Y.; Li, D.; Sun, B.; El-Hamshary, H.; Yin, M.; Mo, X. Fabrication and preliminary study of a biomimetic tri-layer tubular graft based on fibers and fiber yarns for vascular tissue engineering. Mater. Sci. Eng. C Mater. Biol. Appl. 2018, 82, 121–129. [Google Scholar] [CrossRef] [PubMed]
- Hasan, A.; Memic, A.; Annabi, N.; Hossain, M.; Paul, A.; Dokmeci, M.R.; Dehghani, F.; Khademhosseini, A. Electrospun scaffolds for tissue engineering of vascular grafts. Acta Biomater. 2014, 10, 11–25. [Google Scholar] [CrossRef]
- Sundaramurthi, D.; Krishnan, U.M.; Sethuraman, S. Electrospun nanofibers as scaffolds for skin tissue engineering. Polym. Rev. 2014, 54, 348–376. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, L.; Guo, B.; Ma, P.X. Interwoven aligned conductive nanofiber yarn/hydrogel composite scaffolds for engineered 3D cardiac anisotropy. ACS Nano 2017, 11, 5646–5659. [Google Scholar] [CrossRef] [PubMed]
- Zhao, G.; Zhang, X.; Lu, T.J.; Xu, F. Recent advances in electrospun nanofibrous scaffolds for cardiac tissue engineering. Adv. Funct. Mater. 2015, 25, 5726–5738. [Google Scholar] [CrossRef]
- Asadnia, M.; Kottapalli, A.G.P.; Karavitaki, K.D.; Warkiani, M.E.; Miao, J.; Corey, D.P.; Triantafyllou, M. From biological cilia to artificial flow sensors: Biomimetic soft polymer nanosensors with high sensing performance. Sci. Rep. 2016, 6, 32955. [Google Scholar] [CrossRef] [PubMed]
- Khan, H.; Razmjou, A.; Majid Ebrahimi, W.; Kottapalli, A.; Asadnia, M. Sensitive and flexible polymeric strain sensor for accurate human motion monitoring. Sensors 2018, 18, 418. [Google Scholar] [CrossRef]
- Engler, A.J.; Sen, S.; Sweeney, H.L.; Discher, D.E. Matrix elasticity directs stem cell lineage specification. Cell 2006, 126, 677–689. [Google Scholar] [CrossRef]
- Baker, S.R.; Banerjee, S.; Bonin, K.; Guthold, M. Determining the mechanical properties of electrospun poly-epsilon-caprolactone (PCL) nanofibers using AFM and a novel fiber anchoring technique. Mater. Sci. Eng. C Mater. Biol. Appl. 2016, 59, 203–212. [Google Scholar] [CrossRef]
- Baker, S.; Sigley, J.; Helms, C.C.; Stitzel, J.; Berry, J.; Bonin, K.; Guthold, M. The mechanical properties of dry, electrospun fibrinogen fibers. Mater. Sci. Eng. C Mater. Biol. Appl. 2012, 32, 215–221. [Google Scholar] [CrossRef]
- Carlisle, C.R.; Coulais, C.; Guthold, M. The mechanical stress-strain properties of single electrospun collagen type I nanofibers. Acta Biomater. 2010, 6, 2997–3003. [Google Scholar] [CrossRef]
- Carlisle, C.R.; Coulais, C.; Namboothiry, M.; Carroll, D.L.; Hantgan, R.R.; Guthold, M. The mechanical properties of individual, electrospun fibrinogen fibers. Biomaterials 2009, 30, 1205–1213. [Google Scholar] [CrossRef]
- Xia, Y.N.; Whitesides, G.M. Soft lithography. Angew. Chem. Int. 1998, 37, 551–575. [Google Scholar] [CrossRef]
- Dippold, D.; Cai, A.J.; Hardt, M.; Boccaccini, A.R.; Horch, R.; Beier, J.P.; Schubert, D.W. Novel approach towards aligned PCL-collagen nanofibrous constructs from a benign solvent system. Mater. Sci. Eng. C Mater. Biol. Appl. 2017, 72, 278–283. [Google Scholar] [CrossRef]
- Li, D.; Wang, Y.L.; Xia, Y.N. Electrospinning of polymeric and ceramic nanofibers as uniaxially aligned arrays. Nano Lett. 2003, 3, 1167–1171. [Google Scholar] [CrossRef]
- Xie, J.W.; Li, X.R.; Xia, Y.N. Putting electrospun nanofibers to work for biomedical research. Macromol. Rapid Commun. 2008, 29, 1775–1792. [Google Scholar] [CrossRef]
- Piner, R.D.; Zhu, J.; Xu, F.; Hong, S.H.; Mirkin, C.A. “Dip-pen” nanolithography. Science 1999, 283, 661–663. [Google Scholar] [CrossRef]
- Reifenberger, R.G. Fundamentals of Atomic Force Microscopy; World Scientific: Singapore, 2015. [Google Scholar]
- Liu, W.; Bonin, K.; Guthold, M. An easy and direct method for calibrating AFM lateral force measurements. Rev. Sci. Instrum. 2007, 78, 063707. [Google Scholar] [CrossRef]
- Lang, T.A.; Secic, M. How to Report Statistics in Medicine: Annotated Guidelines for Authors, Editors, and Reviewers, 2nd ed.; American College of Physicians: New York, NY, USA, 2006. [Google Scholar]
- Tan, E.P.S.; Ng, S.Y.; Lim, C.T. Tensile testing of a single ultrafine polymeric fiber. Biomaterials 2005, 26, 1453–1456. [Google Scholar] [CrossRef]
- Lim, C.T.; Tan, E.P.S.; Ng, S.Y. Effects of crystalline morphology on the tensile properties of electrospun polymer nanofibers. Appl. Phys. Lett. 2008, 92. [Google Scholar] [CrossRef]
- Wong, S.C.; Baji, A.; Leng, S.W. Effect of fiber diameter on tensile properties of electrospun poly(epsilon-caprolactone). Polymer 2008, 49, 4713–4722. [Google Scholar] [CrossRef]
- Chew, S.Y.; Hufnagel, T.C.; Lim, C.T.; Leong, K.W. Mechanical properties of single electrospun drug-encapsulated nanofibres. Nanotechnology 2006, 17, 3880–3891. [Google Scholar] [CrossRef] [PubMed]
- Croisier, F.; Duwez, A.S.; Jerome, C.; Leonard, A.F.; van der Werf, K.O.; Dijkstra, P.J.; Bennink, M.L. Mechanical testing of electrospun PCL fibers. Acta Biomater. 2012, 8, 218–224. [Google Scholar] [CrossRef]
- Sengupta, D.; Kottapalli, A.G.P.; Chen, S.H.; Miao, J.M.; Kwok, C.Y.; Triantafyllou, M.S.; Warkiani, M.E.; Asadnia, M. Characterization of single polyvinylidene fluoride (PVDF) nanofiber for flow sensing applications. Aip. Adv. 2017, 7, 105205. [Google Scholar] [CrossRef]
- Houser, J.R.; Hudson, N.E.; Ping, L.; O’Brien Iii, E.T.; Superfine, R.; Lord, S.T.; Falvo, M.R. Evidence that αC region is origin of low modulus, high extensibility, and strain stiffening in fibrin fibers. Biophys. J. 2010, 99, 3038–3047. [Google Scholar] [CrossRef] [PubMed]
- Silver, F.H.; Freeman, J.W.; Seehra, G.P. Collagen self-assembly and the development of tendon mechanical properties. J. Biomech. 2003, 36, 1529–1553. [Google Scholar] [CrossRef]
- Liu, W.; Carlisle, C.R.; Sparks, E.A.; Guthold, M. The mechanical properties of single fibrin fibers. J. Thromb. Haemost. 2010, 8, 1030–1036. [Google Scholar] [CrossRef]
- Gosline, J.M.; Guerette, P.A.; Ortlepp, C.S.; Savage, K.N. The mechanical design of spider silks: From fibroin sequence to mechanical function. J. Exp. Biol. 1999, 202, 3295–3303. [Google Scholar]
- Woods, I.; Black, A.; Molloy, E.J.; Jockenhoevel, S.; Flanagan, T.C. Fabrication of blood-derived elastogenic vascular grafts using electrospun fibrinogen and polycaprolactone composite scaffolds for paediatric applications. J. Tissue Eng. Regen. Med. 2020, 15. [Google Scholar] [CrossRef]



| Value | Average +/− Std. Dev. | Data Points, N |
|---|---|---|
| Extensibility (Maximum Strain) | 110 ± 60% | 80 |
| Maximum Stress | 410 ± 210 MPa | 86 |
| Elastic Limit | 5 ± 5% | 51 |
| Energy Loss | 75 ± 10% | 25 |
| Fast Relaxation Time | 1.1 ± 0.4 s | 87 |
| Slow Relaxation Time | 16 ± 6 s | 86 |
| Initial Modulus, single pull (~10% strain) | 1700 ± 800 MPa | 9 |
| Large strain Modulus, single pull (~100% strain) | 110 ± 90 MPa | 9 |
| Total Modulus, incremental (0–25% strain) | 1400 ± 990 MPa | 90 |
| Elastic Modulus, incremental (0–25% strain) | 980 ± 710 MPa | 90 |
| Total Modulus, incremental (~100% strain) | 430 ± 420 MPa | 90 |
| Elastic Modulus, incremental (~100% strain) | 310 ± 250 MPa | 90 |
| Fiber Type | Extensibility (%) | Fast Relax (s) | Slow Relax (s) | Elastic Modulus (MPa) | Total Modulus (MPa) | Diameter (nm) |
|---|---|---|---|---|---|---|
| e-spun 50:50 Fibrinogen:PCL [this paper] | 110 ± 60 | 1.1 ± 0.4 | 16 ± 6 | 980 ± 710 (low strain values) | 1400 ± 990 (low strain values) | 230 ± 90 |
| e-spun PCL Fibers (>30 days) [31] | 98 ± 30 | 0.98 ± 0.26 | 8.79 ± 3.08 | 52.9 ± 36.2 | 62.3 ± 25.6 | 440–1040 |
| e-spun PCL Fibers (<30 days) [31] | 1.69 ± 0.44 | 21.22 ± 8.97 | 61.4 ± 51.1 | 99.2 ± 83.9 | 440–1040 | |
| e-spun Fibrinogen (dry) [32] | 113 ± 22 | 1.2 ± 0.4 | 11 ± 5 | 4200 ± 3400 | 3700 ± 3100 | 30–200 |
| Native Collagen [50] | 12 | 160–7500 | (tendon) | |||
| Cross-linked Fibrin [51] | 147 | 2.1 | 49 | 8.0 | 4.0 | 124–800 |
| Uncrosslinked Fibrin [51] | 226 | 2.9 | 54 | 3.9 | 1.9 | 94–700 |
| Dry e-spun Collagen Fibers [33] | 33 ± 3 | 3 | 50 | 2800 ± 3100 | 200–800 | |
| Spider Silk [52] | 270 | 3 | 1000–5000 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharpe, J.M.; Lee, H.; Hall, A.R.; Bonin, K.; Guthold, M. Mechanical Properties of Electrospun, Blended Fibrinogen: PCL Nanofibers. Nanomaterials 2020, 10, 1843. https://doi.org/10.3390/nano10091843
Sharpe JM, Lee H, Hall AR, Bonin K, Guthold M. Mechanical Properties of Electrospun, Blended Fibrinogen: PCL Nanofibers. Nanomaterials. 2020; 10(9):1843. https://doi.org/10.3390/nano10091843
Chicago/Turabian StyleSharpe, Jacquelyn M., Hyunsu Lee, Adam R. Hall, Keith Bonin, and Martin Guthold. 2020. "Mechanical Properties of Electrospun, Blended Fibrinogen: PCL Nanofibers" Nanomaterials 10, no. 9: 1843. https://doi.org/10.3390/nano10091843
APA StyleSharpe, J. M., Lee, H., Hall, A. R., Bonin, K., & Guthold, M. (2020). Mechanical Properties of Electrospun, Blended Fibrinogen: PCL Nanofibers. Nanomaterials, 10(9), 1843. https://doi.org/10.3390/nano10091843






