The Scattering of Phonons by Infinitely Long Quantum Dislocations Segments and the Generation of Thermal Transport Anisotropy in a Solid Threaded by Many Parallel Dislocations
Abstract
1. Introduction
2. Classical Action
3. Canonical Quantization of the Free Fields
4. The Quadratic Interactions with a Single String
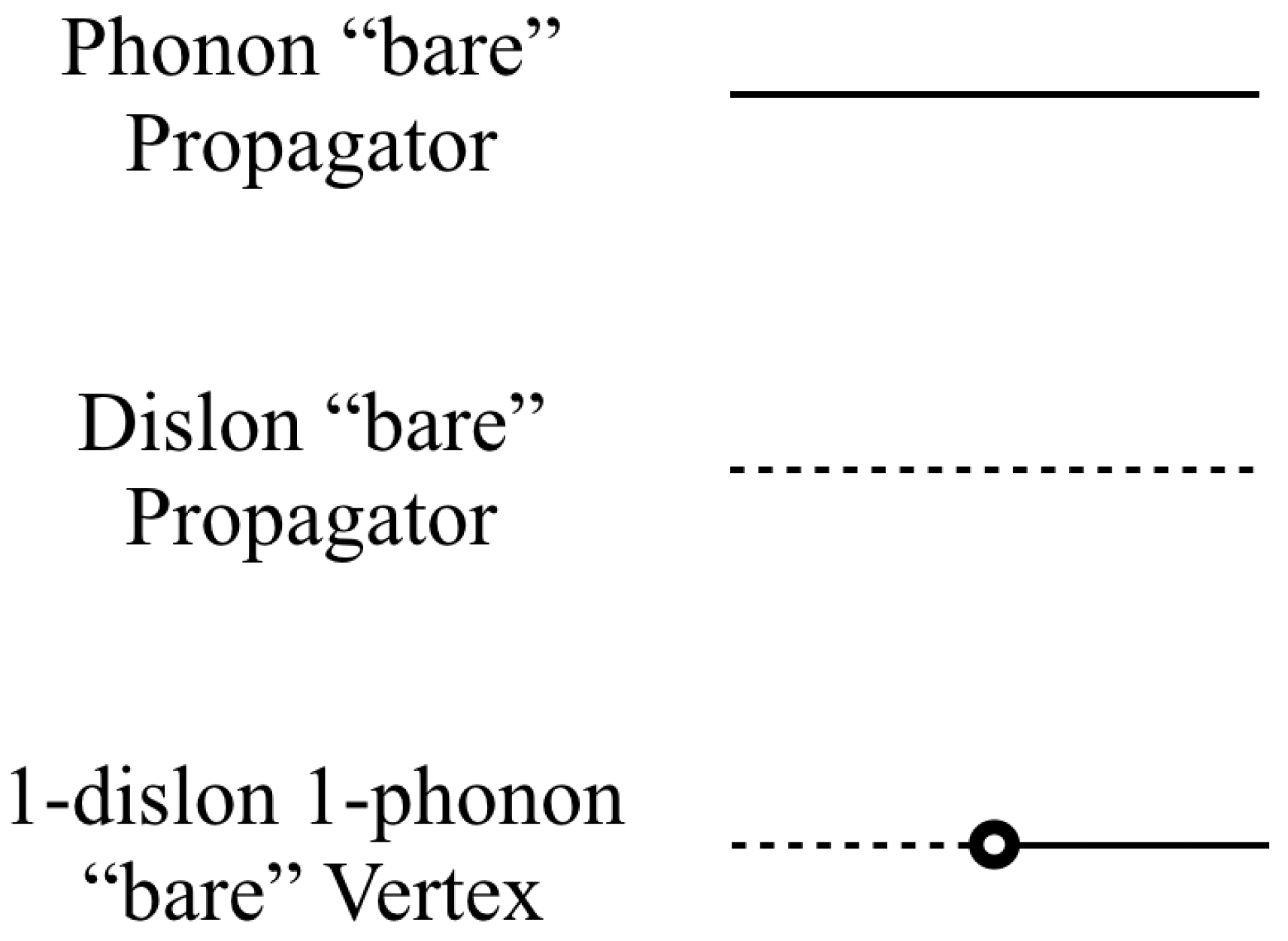
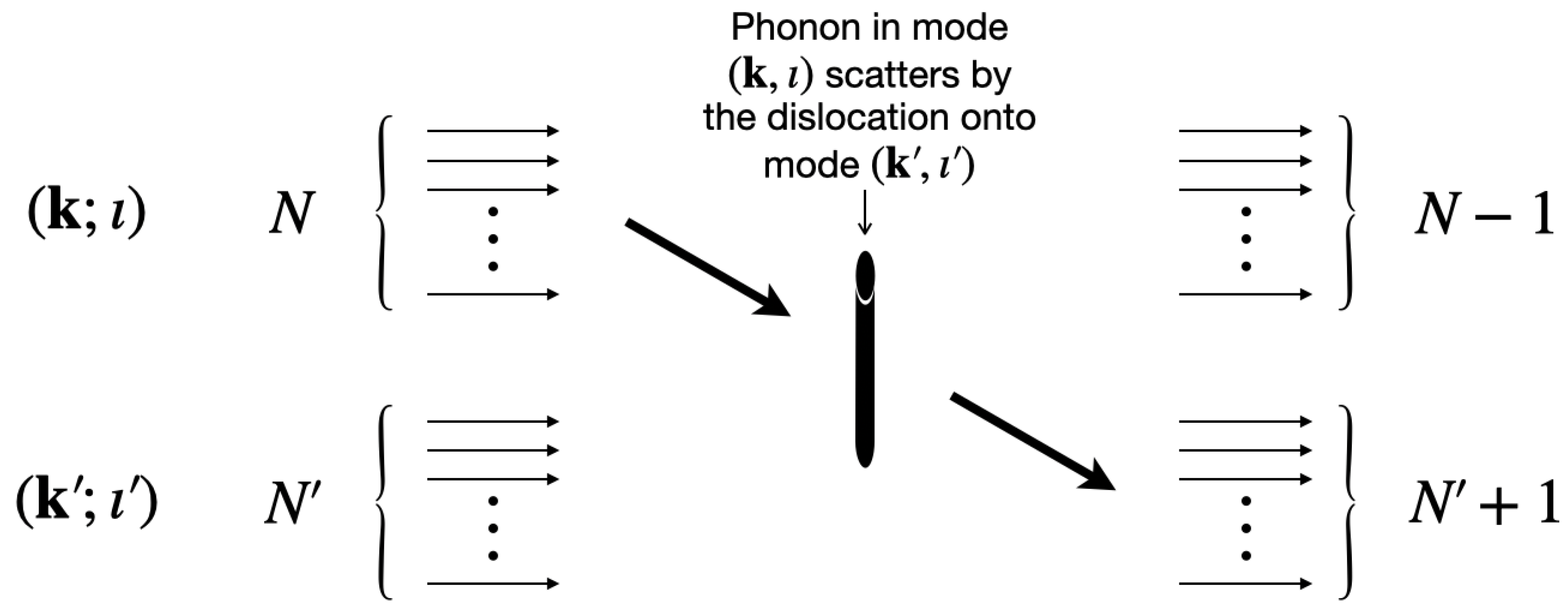
4.1. Phonon by Dislocation Scattering: Amplitudes and Feynman Diagrams
- Phonon “bare” propagator: the phonon Green’s function. In particular, we will be more interested in its derivatives, or the earlier defined whose value in momentum–frequency space is given bywhere we have omitted an overall Dirac delta imposing momentum–frequency conservation .
- Dislon “bare” propagator: the dislon Green’s function. It is given in momentum–frequency space bywhere we have also omitted an overall Dirac delta imposing momentum–frequency conservation .
- 1-dislon 1-phonon “bare” vertex: diagrammatical representation of the quadratic interaction between phonons and dislons. In position space, it instructs to operate over the coincident position coordinate of both adjacent propagators asThis coupling will have important consequences when we examine the exact propagator for the dislocation excitations. Moreover, it enforces momentum (wavenumber) conservation along the direction of the dislocation line, through a factor that appears after integrating over the string coordinate s.
4.2. A Look at the Dislon Dispersion Relation
4.3. The Phonon Propagator in the Presence of a Single Dislocation
5. Implications on Thermal Transport
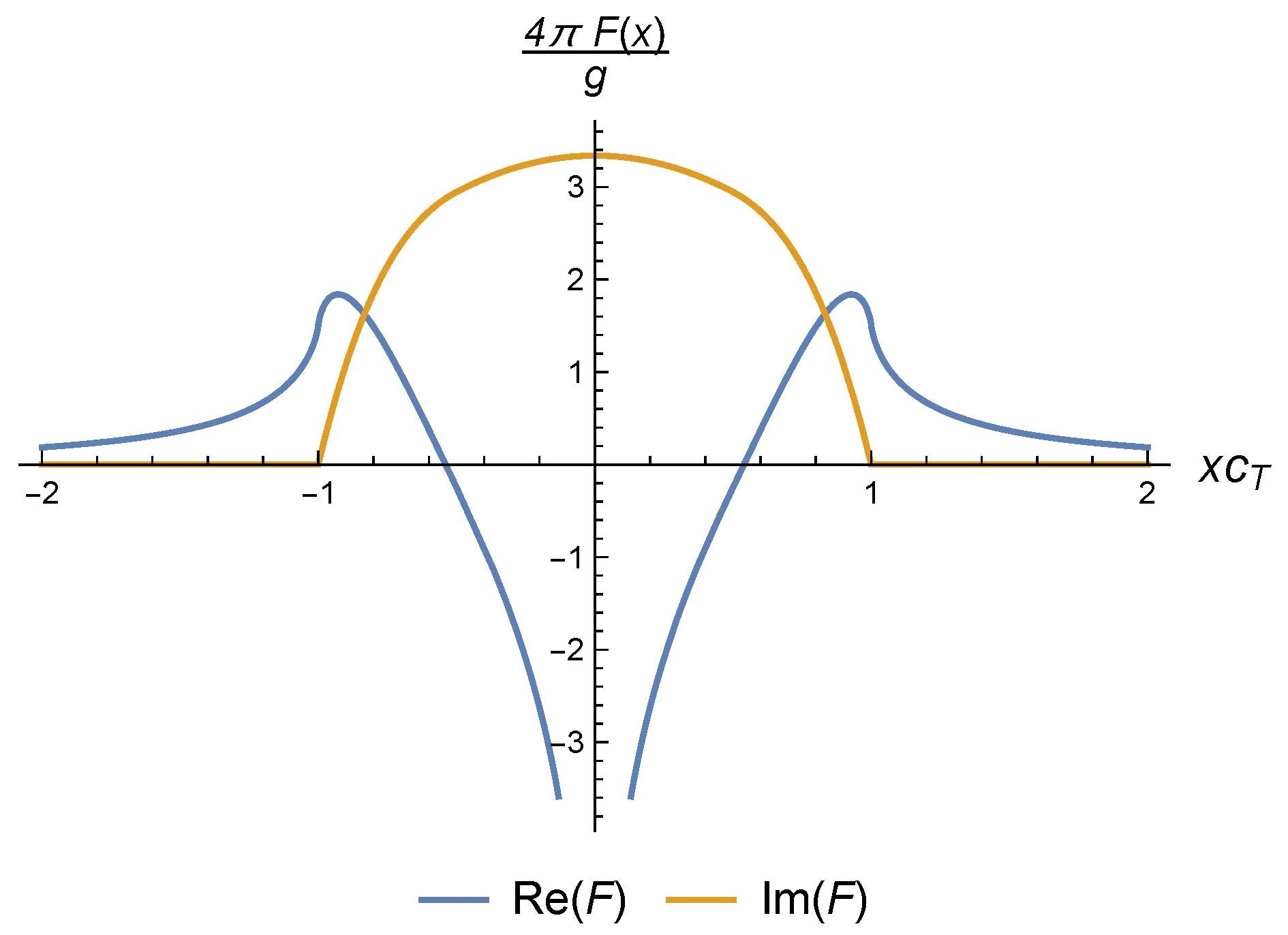
5.1. The Scattering of a Phonon by a Dislocation: Cross Sections
5.2. The Scattering of a Phonon by a Dislocation: Lifetimes
5.3. A Comparison with Klemens’ and Carruthers’ Models
- All models (even though Klemens’ and Caurruthers’ results we have shown here do not make this explicit) have a vanishing phonon decay rate at , i.e., when the phonon is incident parallel to the dislocation line, favoring thermal transport in this direction over the others.
- All models have a linear dependence on the dislocation density, with the observation that Carruthers’ model has an additional logarithmic sensitivity to the dislocation density because of how the strain field is modeled. This makes the interaction strength of Carruthers’ model generically stronger than Klemens’.
- The other parameters that control the magnitude of the phonon lifetime are , the sound speed in the material, and b, the dislocation’s Burgers vector. Incidentally, our model is insensitive to the value of the Burgers vector, being only dependent on the macroscopic parameters and .
- In stark contrast to what both Klemens’ and Carruthers’ models predict, the phonon lifetime in our model is larger at smaller frequencies, depending on the phonon energy as over the range of frequencies where the infinite dislocation line approximation holds . In particular, this means that the thermal transport anisotropy induced by dislocations will become stronger at lower temperatures relative to Carruthers’ and Klemens’ models.
5.4. Thermal Transport Anisotropy
- there is always “intrinsic” phonon scattering due to anharmonicities in the elastic continuum,
- the dislocation lines will usually not be perfectly aligned in a real material,
- the consideration of finite size effects in the material introduces a boundary scattering contribution.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Features of the Dislon Dispersion Relation
Appendix A.1. Dislons as Particles: Evanescent and Propagating Modes
Appendix A.2. Resonances in the Dislon Propagator
Appendix B. Thermal Equilibrium
References
- Takabatake, T.; Suekuni, K.; Nakayama, T.; Kaneshita, E. Phonon-glass electron-crystal thermoelectric clathrates: Experiments and theory. Rev. Mod. Phys. 2014, 86, 669–716. [Google Scholar] [CrossRef]
- Shuai, J.; Geng, H.; Lan, Y.; Zhu, Z.; Wang, C.; Liu, Z.; Bao, J.; Chu, C.W.; Sui, J.; Ren, Z. Higher thermoelectric performance of Zintl phases (Eu0.5Yb0.5)1−xCaxMg2Bi2 by band engineering and strain fluctuation. Proc. Natl. Acad. Sci. USA 2016, 113, E4125–E4132. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Chen, Z.; Nan, P.; Xiong, F.; Lin, S.; Zhang, X.; Chen, Y.; Chen, L.; Ge, B.; Pei, Y. Lattice Strain Advances Thermoelectrics. Joule 2019, 3, 1276–1288. [Google Scholar] [CrossRef]
- You, L.; Liu, Y.; Li, X.; Nan, P.; Ge, B.; Jiang, Y.; Luo, P.; Pan, S.; Pei, Y.; Zhang, W.; et al. Boosting the thermoelectric performance of PbSe through dynamic doping and hierarchical phonon scattering. Energy Environ. Sci. 2018, 11, 1848–1858. [Google Scholar] [CrossRef]
- Xin, J.; Wu, H.; Liu, X.; Zhu, T.; Yu, G.; Zhao, X. Mg vacancy and dislocation strains as strong phonon scatterers in Mg2Si1−xSbx thermoelectric materials. Nano Energy 2017, 34, 428–436. [Google Scholar] [CrossRef]
- Zhou, C.; Lee, Y.K.; Cha, J.; Yoo, B.; Cho, S.P.; Hyeon, T.; Chung, I. Defect Engineering for High-Performance n-Type PbSe Thermoelectrics. J. Am. Chem. Soc. 2018, 140, 9282–9290. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.; Zhang, S.; Mio, A.M.; Gault, B.; Sheskin, A.; Scheu, C.; Raabe, D.; Zu, F.; Wuttig, M.; Amouyal, Y.; et al. Ag-Segregation to Dislocations in PbTe-Based Thermoelectric Materials. ACS Appl. Mater. Interfaces 2018, 10, 3609–3615. [Google Scholar] [CrossRef]
- Giaremis, S.; Kioseoglou, J.; Desmarchelier, P.; Tanguy, A.; Isaiev, M.; Belabbas, I.; Komninou, P.; Termentzidis, K. Decorated Dislocations against Phonon Propagation for Thermal Management. ACS Appl. Energy Mater. 2020, 3, 2682–2694. [Google Scholar] [CrossRef]
- Klemens, P.G. The Scattering of Low-Frequency Lattice Waves by Static Imperfections. Proc. Phys. Soc. Sect. A 1955, 68, 1113. [Google Scholar] [CrossRef]
- Granato, A.; Lücke, K. Theory of Mechanical Damping Due to Dislocations. J. Appl. Phys. 1956, 27, 583–593. [Google Scholar] [CrossRef]
- Granato, A.; Lücke, K. Application of Dislocation Theory to Internal Friction Phenomena at High Frequencies. J. Appl. Phys. 1956, 27, 789–805. [Google Scholar] [CrossRef]
- Anderson, P.; Hirth, J.; Lothe, J. Theory of Dislocations; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Wang, T.; Carrete, J.; Mingo, N.; Madsen, G.K.H. Phonon Scattering by Dislocations in GaN. ACS Appl. Mater. Interfaces 2019, 11, 8175–8181. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Carrete, J.; van Roekeghem, A.; Mingo, N.; Madsen, G.K.H. Ab initio phonon scattering by dislocations. Phys. Rev. B 2017, 95, 245304. [Google Scholar] [CrossRef]
- Sun, B.; Haunschild, G.; Polanco, C.; Ju, J.; Lindsay, L.; Koblmüller, G.; Kan Koh, Y. Dislocation-induced thermal transport anisotropy in single-crystal group-III nitride films. Nat. Mater. 2019, 18, 136–140. [Google Scholar] [CrossRef]
- Carruthers, P. Scattering of Phonons by Elastic Strain Fields and the Thermal Resistance of Dislocations. Phys. Rev. 1959, 114, 995–1001. [Google Scholar] [CrossRef]
- Lund, F.; Scheihing H., B. Scattering of phonons by quantum-dislocation segments in an elastic continuum. Phys. Rev. B 2019, 99, 214102. [Google Scholar] [CrossRef]
- Ninomiya, T. Dislocation Vibration and Phonon Scattering. J. Phys. Soc. Jpn. 1968, 25, 830–840. [Google Scholar] [CrossRef]
- Ninomiya, T. Eigenfrequencies in a dislocated crystal. In Journal of Research of the National Bureau of Standards Section A-Physics and Chemistry; Number 5; US Government Printing Office: Washington, DC, USA, 1969; p. 544. [Google Scholar]
- Li, M.; Cui, W.; Dresselhaus, M.S.; Chen, G. Electron energy can oscillate near a crystal dislocation. New J. Phys. 2017, 19, 013033. [Google Scholar] [CrossRef]
- Li, M.; Ding, Z.; Meng, Q.; Zhou, J.; Zhu, Y.; Liu, H.; Dresselhaus, M.S.; Chen, G. Nonperturbative Quantum Nature of the Dislocation-Phonon Interaction. Nano Lett. 2017, 17, 1587–1594. [Google Scholar] [CrossRef]
- Li, M.; Tsurimaki, Y.; Meng, Q.; Andrejevic, N.; Zhu, Y.; Mahan, G.D.; Chen, G. Theory of electron-phonon–dislon interacting system-toward a quantized theory of dislocations. New J. Phys. 2018, 20, 023010. [Google Scholar] [CrossRef]
- Peach, M.; Koehler, J.S. The Forces Exerted on Dislocations and the Stress Fields Produced by Them. Phys. Rev. 1950, 80, 436–439. [Google Scholar] [CrossRef]
- Granato, A. Thermal Properties of Mobile Defects. Phys. Rev. 1958, 111, 740–746. [Google Scholar] [CrossRef]
- Kneezel, G.A.; Granato, A.V. Effect of independent and coupled vibrations of dislocations on low-temperature thermal conductivity in alkali halides. Phys. Rev. B 1982, 25, 2851–2866. [Google Scholar] [CrossRef]
- Maurel, A.; Pagneux, V.; Barra, F.; Lund, F. Interaction between an elastic wave and a single pinned dislocation. Phys. Rev. B 2005, 72, 174110. [Google Scholar] [CrossRef]
- Lund, F. Response of a stringlike dislocation loop to an external stress. J. Mater. Res. 1988, 3, 280–297. [Google Scholar] [CrossRef]
- Maurel, A.; Pagneux, V.; Barra, F.; Lund, F. Wave propagation through a random array of pinned dislocations: Velocity change and attenuation in a generalized Granato and Lücke theory. Phys. Rev. B 2005, 72, 174111. [Google Scholar] [CrossRef]
- Rodríguez, N.; Maurel, A.; Pagneux, V.; Barra, F.; Lund, F. Interaction between elastic waves and prismatic dislocation loops. J. Appl. Phys. 2009, 106, 054910. [Google Scholar] [CrossRef]
- Churochkin, D.; Barra, F.; Lund, F.; Maurel, A.; Pagneux, V. Multiple scattering of elastic waves by pinned dislocation segments in a continuum. Wave Motion 2016, 60, 220–230. [Google Scholar] [CrossRef]
- Mujica, N.; Cerda, M.T.; Espinoza, R.; Lisoni, J.; Lund, F. Ultrasound as a probe of dislocation density in aluminum. Acta Mater. 2012, 60, 5828–5837. [Google Scholar] [CrossRef]
- Barra, F.; Espinoza-González, R.; Fernández, H.; Lund, F.; Maurel, A.; Pagneux, V. The Use of Ultrasound to Measure Dislocation Density. JOM 2015, 67, 1856–1863. [Google Scholar] [CrossRef]
- Salinas, V.; Aguilar, C.; Espinoza-González, R.; Lund, F.; Mujica, N. In situ monitoring of dislocation proliferation during plastic deformation using ultrasound. Int. J. Plast. 2017, 97, 178–193. [Google Scholar] [CrossRef]
- Espinoza, C.; Feliú, D.; Aguilar, C.; Espinoza-González, R.; Lund, F.; Salinas, V.; Mujica, N. Linear Versus Nonlinear Acoustic Probing of Plasticity in Metals: A Quantitative Assessment. Materials 2018, 11, 2217. [Google Scholar] [CrossRef] [PubMed]
- Srednicki, M. Quantum Field Theory; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Peskin, M.; Schroeder, D. An Introduction To Quantum Field Theory; Frontiers in Physics; Avalon Publishing: New York, NY, USA, 1995. [Google Scholar]
- Ninomiya, T. Frictional Force Acting on a Dislocation—Fluttering Mechanism—. J. Phys. Soc. Jpn. 1974, 36, 399–405. [Google Scholar] [CrossRef]
- Bitzek, E.; Gumbsch, P. Atomistic study of drag, surface and inertial effects on edge dislocations in face-centered cubic metals. In Proceedings of the 13th International Conference on the Strength of Materials, Budapest, Hungary, 25–30 August 2003; pp. 11–15. [Google Scholar]
- Blaschke, D.N. Velocity dependent dislocation drag from phonon wind and crystal geometry. J. Phys. Chem. Solids 2019, 124, 24–35. [Google Scholar] [CrossRef]
- Soto, R. Kinetic Theory and Transport Phenomena; Oxford Master Series in Physics; Oxford University Press: Oxford, UK, 2016. [Google Scholar]
- Luttinger, J.M. Theory of Thermal Transport Coefficients. Phys. Rev. 1964, 135, A1505–A1514. [Google Scholar] [CrossRef]
- Eshelby, J.D.; Mott, N.F. Dislocations as a cause of mechanical damping in metals. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1949, 197, 396–416. [Google Scholar] [CrossRef]
- Nabarro, F.R.N.; Peierls, R.E. The interaction of screw dislocations and sound waves. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1951, 209, 278–290. [Google Scholar] [CrossRef]
- Maurel, A.; Mercier, J.F.; Lund, F. Scattering of an elastic wave by a single dislocation. J. Acoust. Soc. Am. 2004, 115, 2773–2780. [Google Scholar] [CrossRef]
- Asen-Palmer, M.; Bartkowski, K.; Gmelin, E.; Cardona, M.; Zhernov, A.P.; Inyushkin, A.V.; Taldenkov, A.; Ozhogin, V.I.; Itoh, K.M.; Haller, E.E. Thermal conductivity of germanium crystals with different isotopic compositions. Phys. Rev. B 1997, 56, 9431–9447. [Google Scholar] [CrossRef]
- Tan, C.; Cao, X.; Wu, X.J.; He, Q.; Yang, J.; Zhang, X.; Chen, J.; Zhao, W.; Han, S.; Nam, G.H.; et al. Recent Advances in Ultrathin Two-Dimensional Nanomaterials. Chem. Rev. 2017, 117, 6225–6331. [Google Scholar] [CrossRef]
- Gu, X.; Wei, Y.; Yin, X.; Li, B.; Yang, R. Colloquium: Phononic thermal properties of two-dimensional materials. Rev. Mod. Phys. 2018, 90, 041002. [Google Scholar] [CrossRef]
- Zeng, Y.J.; Wu, D.; Cao, X.H.; Zhou, W.X.; Tang, L.M.; Chen, K.Q. Nanoscale Organic Thermoelectric Materials: Measurement, Theoretical Models, and Optimization Strategies. Adv. Funct. Mater. 2020, 30, 1903873. [Google Scholar] [CrossRef]


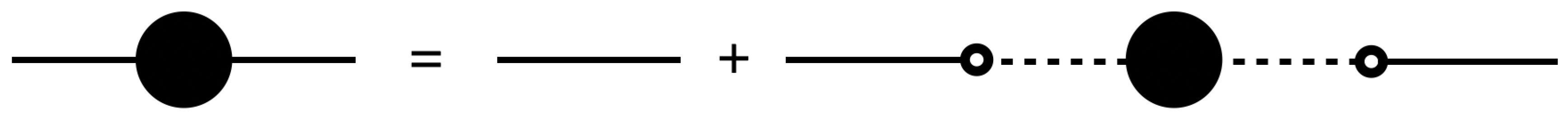


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lund, F.; Scheihing-Hitschfeld, B. The Scattering of Phonons by Infinitely Long Quantum Dislocations Segments and the Generation of Thermal Transport Anisotropy in a Solid Threaded by Many Parallel Dislocations. Nanomaterials 2020, 10, 1711. https://doi.org/10.3390/nano10091711
Lund F, Scheihing-Hitschfeld B. The Scattering of Phonons by Infinitely Long Quantum Dislocations Segments and the Generation of Thermal Transport Anisotropy in a Solid Threaded by Many Parallel Dislocations. Nanomaterials. 2020; 10(9):1711. https://doi.org/10.3390/nano10091711
Chicago/Turabian StyleLund, Fernando, and Bruno Scheihing-Hitschfeld. 2020. "The Scattering of Phonons by Infinitely Long Quantum Dislocations Segments and the Generation of Thermal Transport Anisotropy in a Solid Threaded by Many Parallel Dislocations" Nanomaterials 10, no. 9: 1711. https://doi.org/10.3390/nano10091711
APA StyleLund, F., & Scheihing-Hitschfeld, B. (2020). The Scattering of Phonons by Infinitely Long Quantum Dislocations Segments and the Generation of Thermal Transport Anisotropy in a Solid Threaded by Many Parallel Dislocations. Nanomaterials, 10(9), 1711. https://doi.org/10.3390/nano10091711




