Optical Multistability in the Metal Nanoparticle–Graphene Nanodisk–Quantum Dot Hybrid Systems
Abstract
1. Introduction
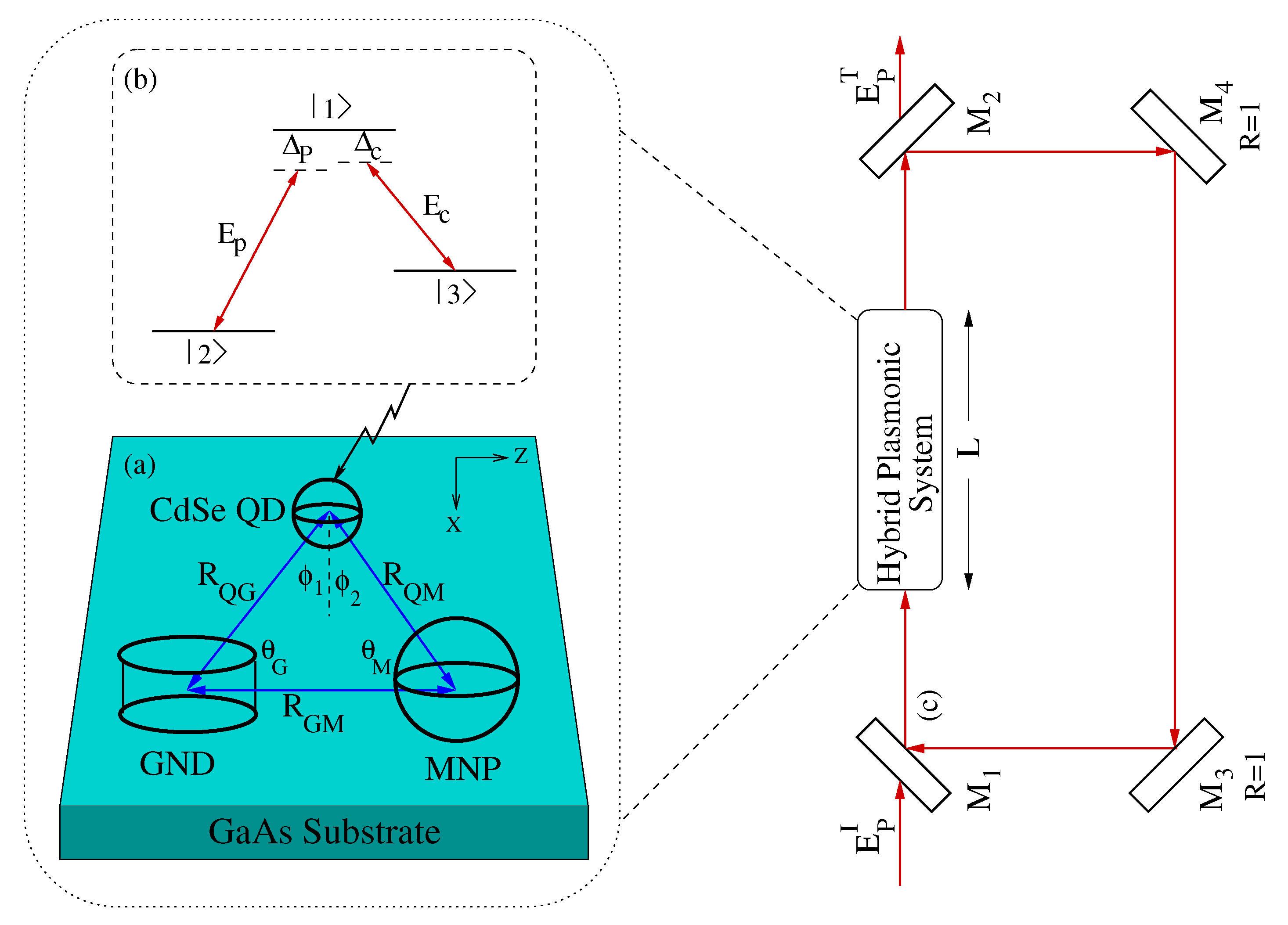
2. Theoretical Model
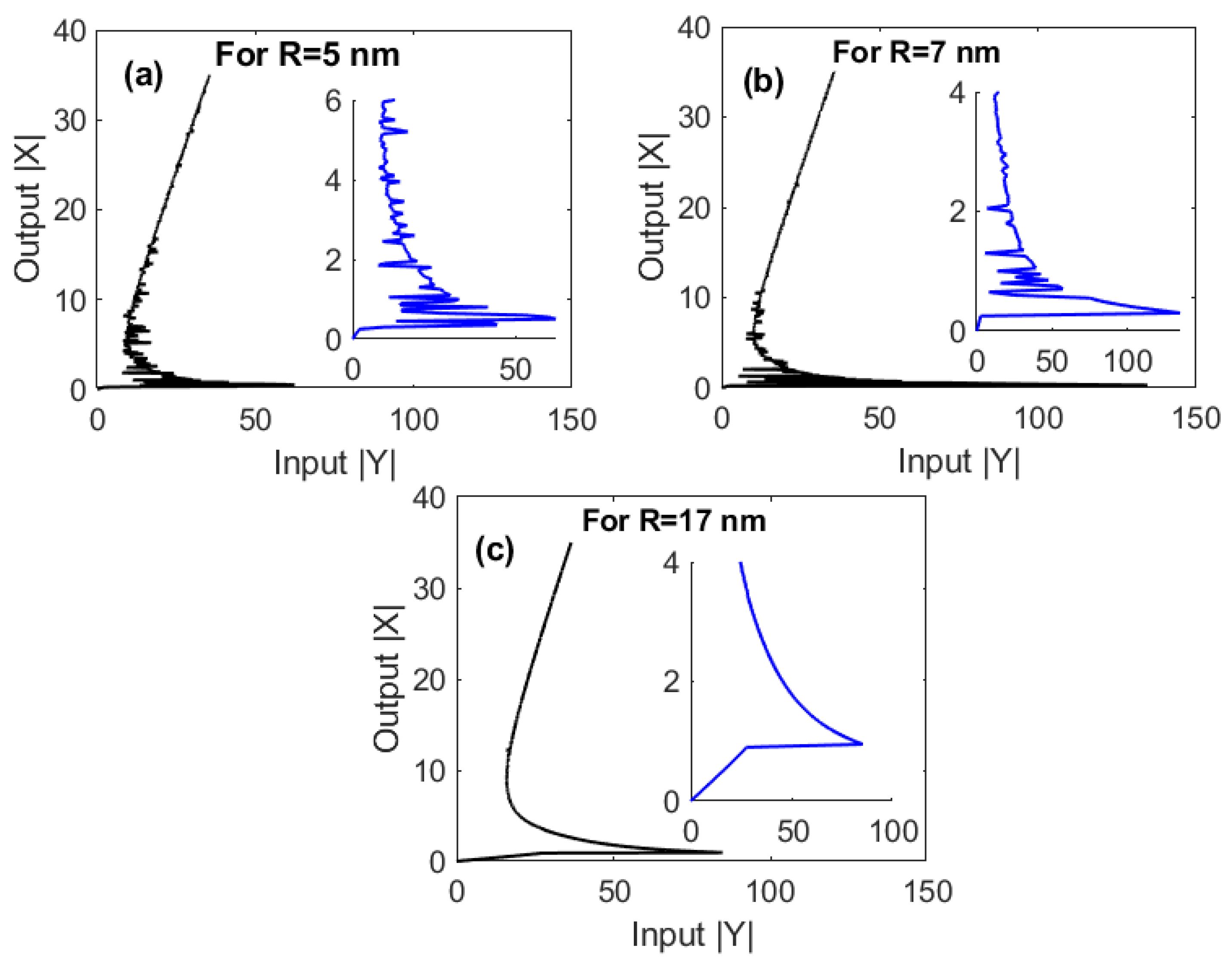
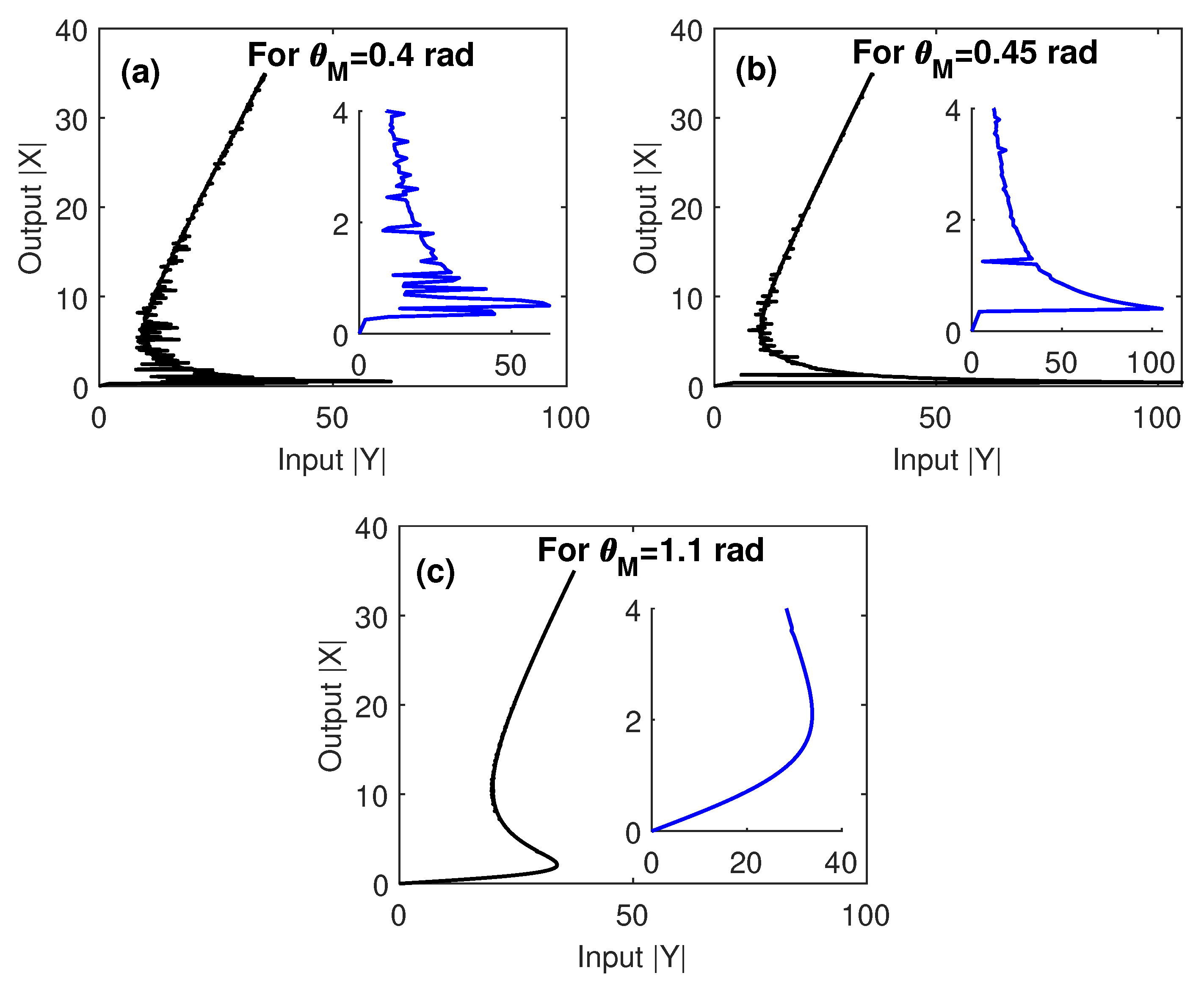
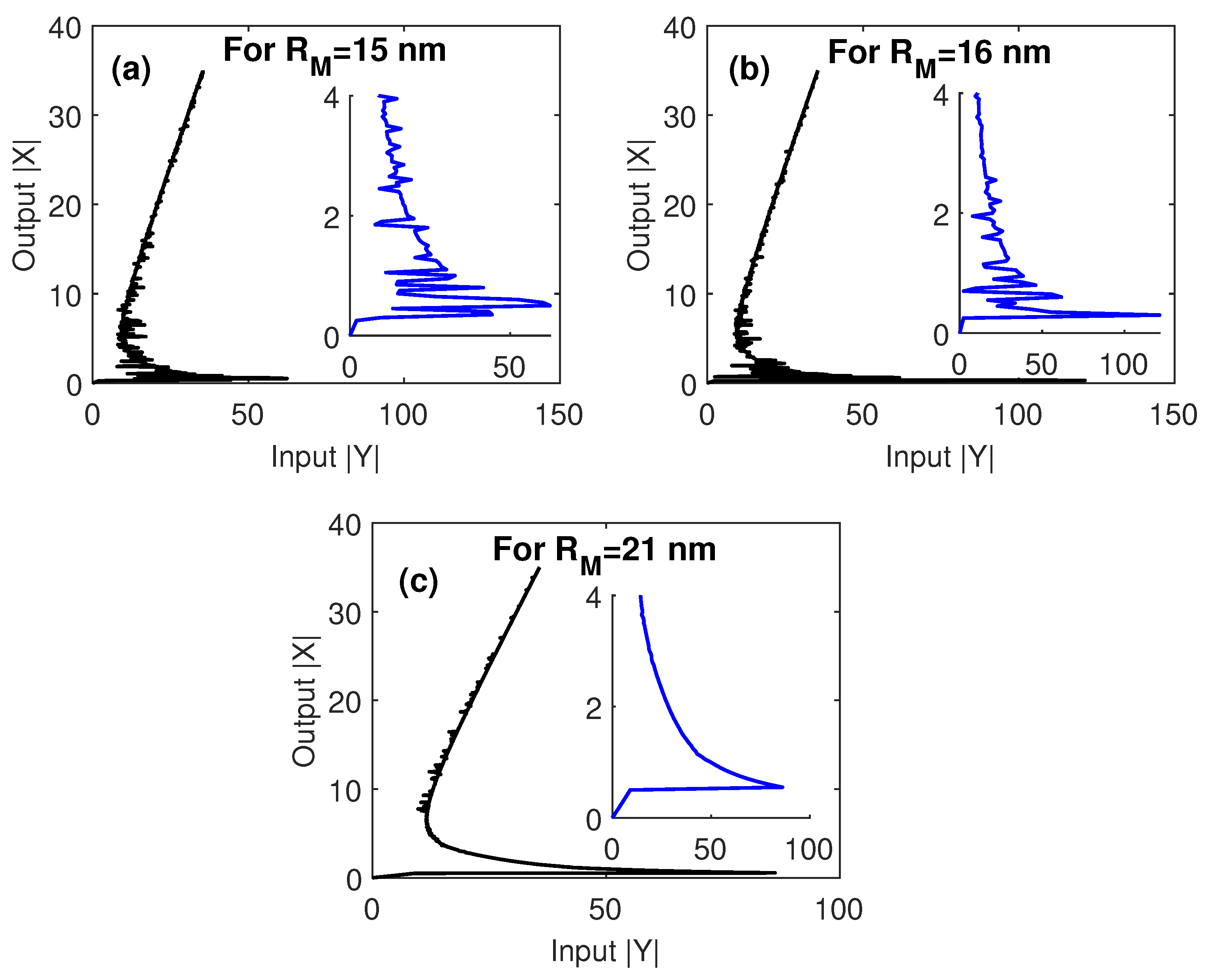
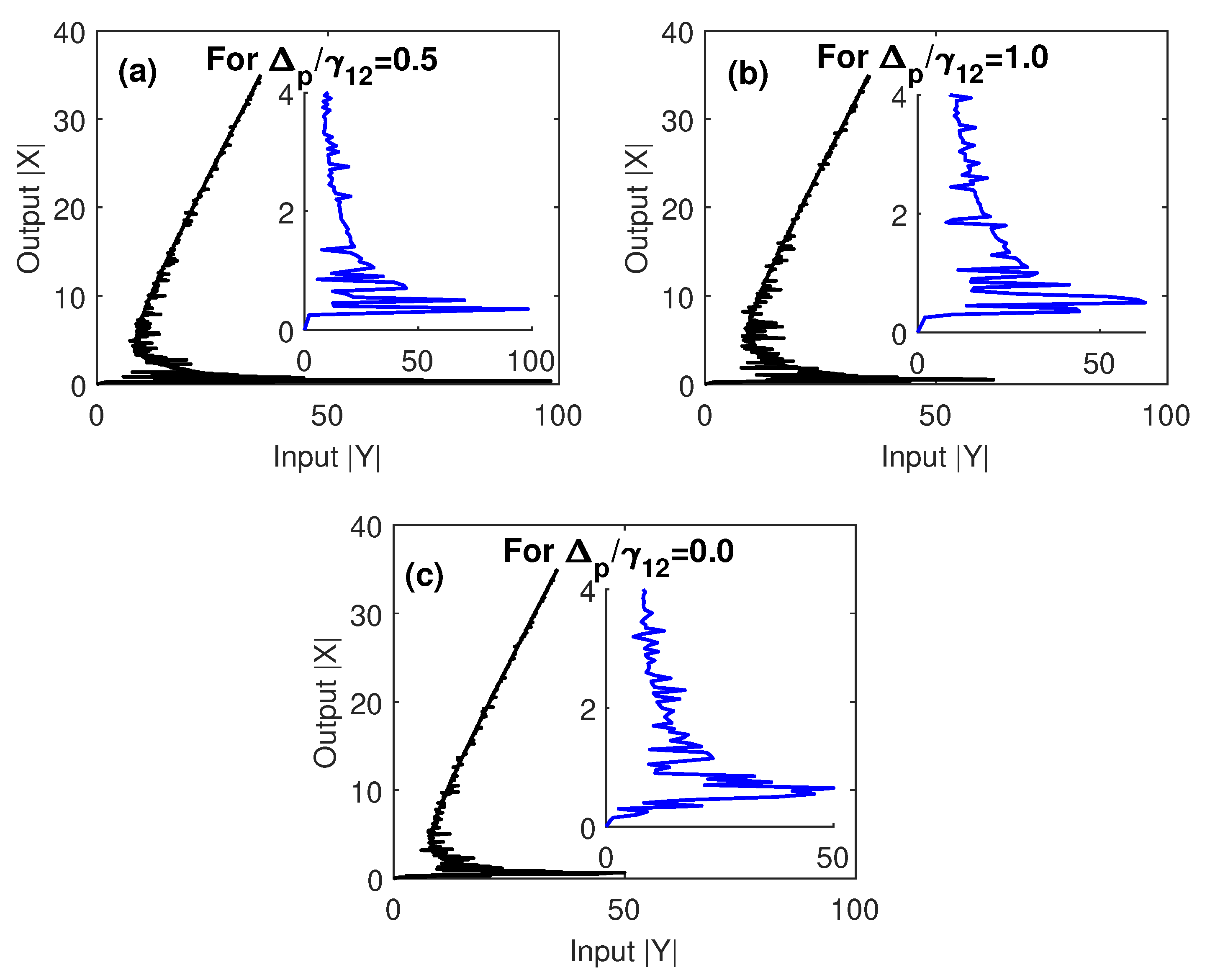
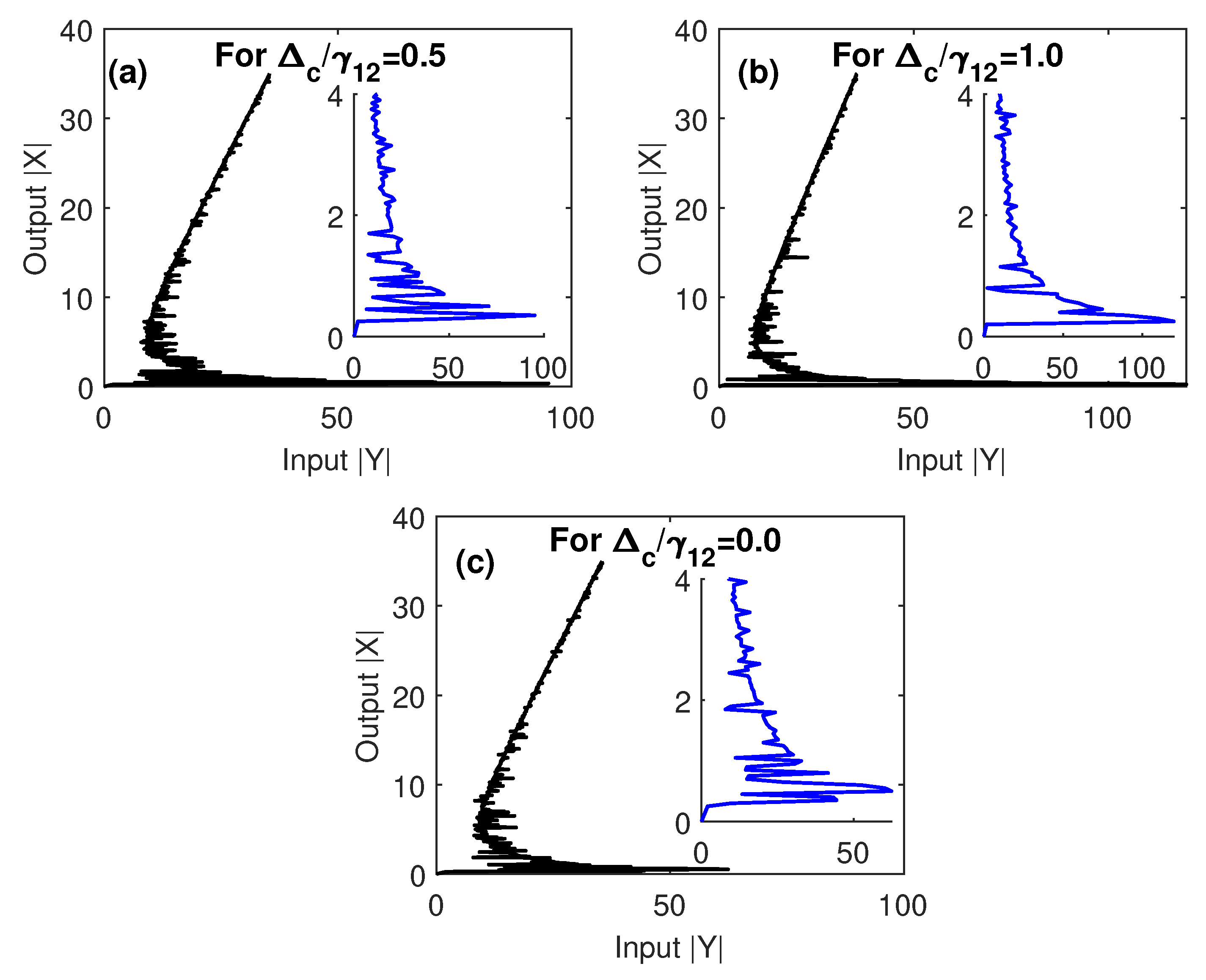
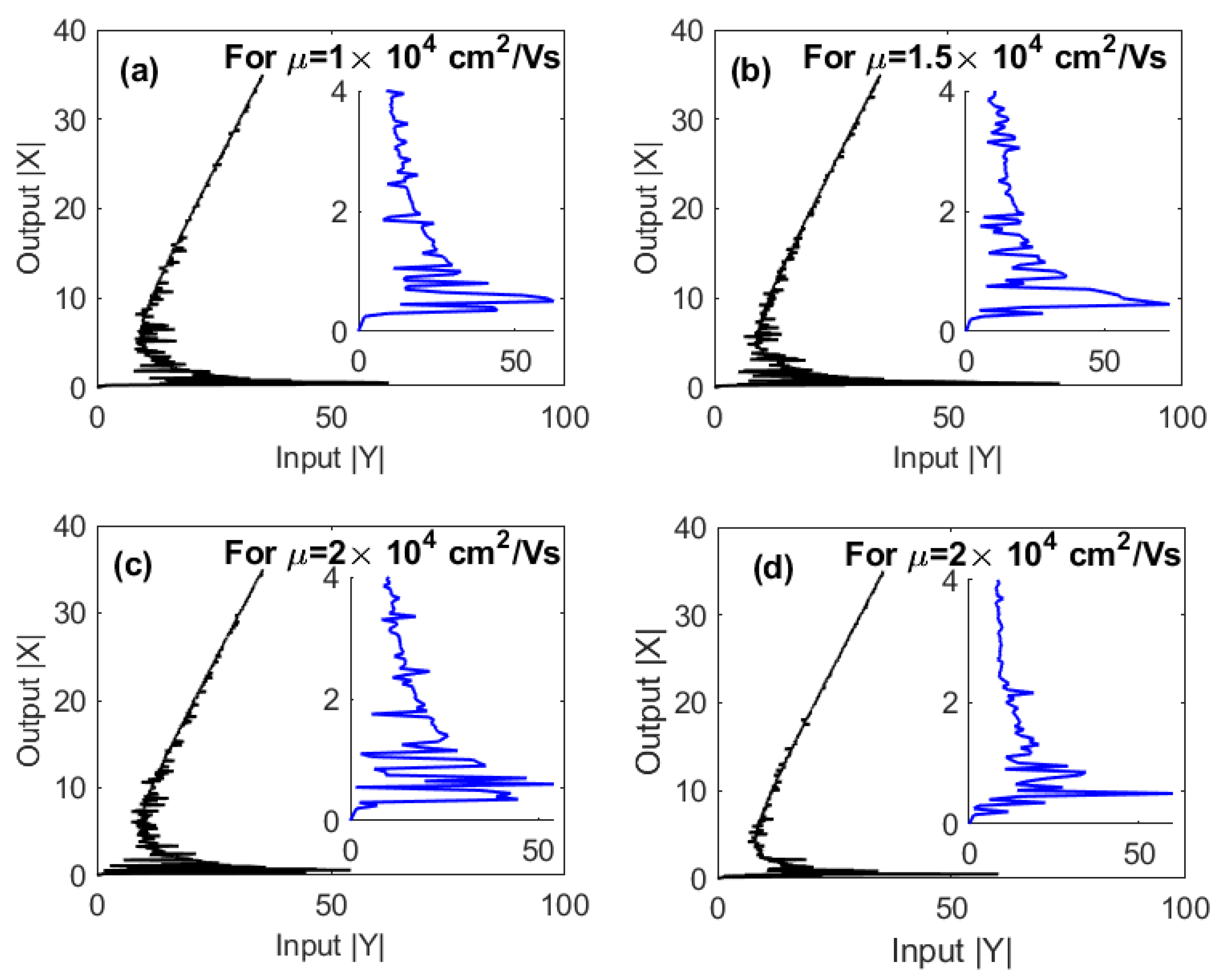
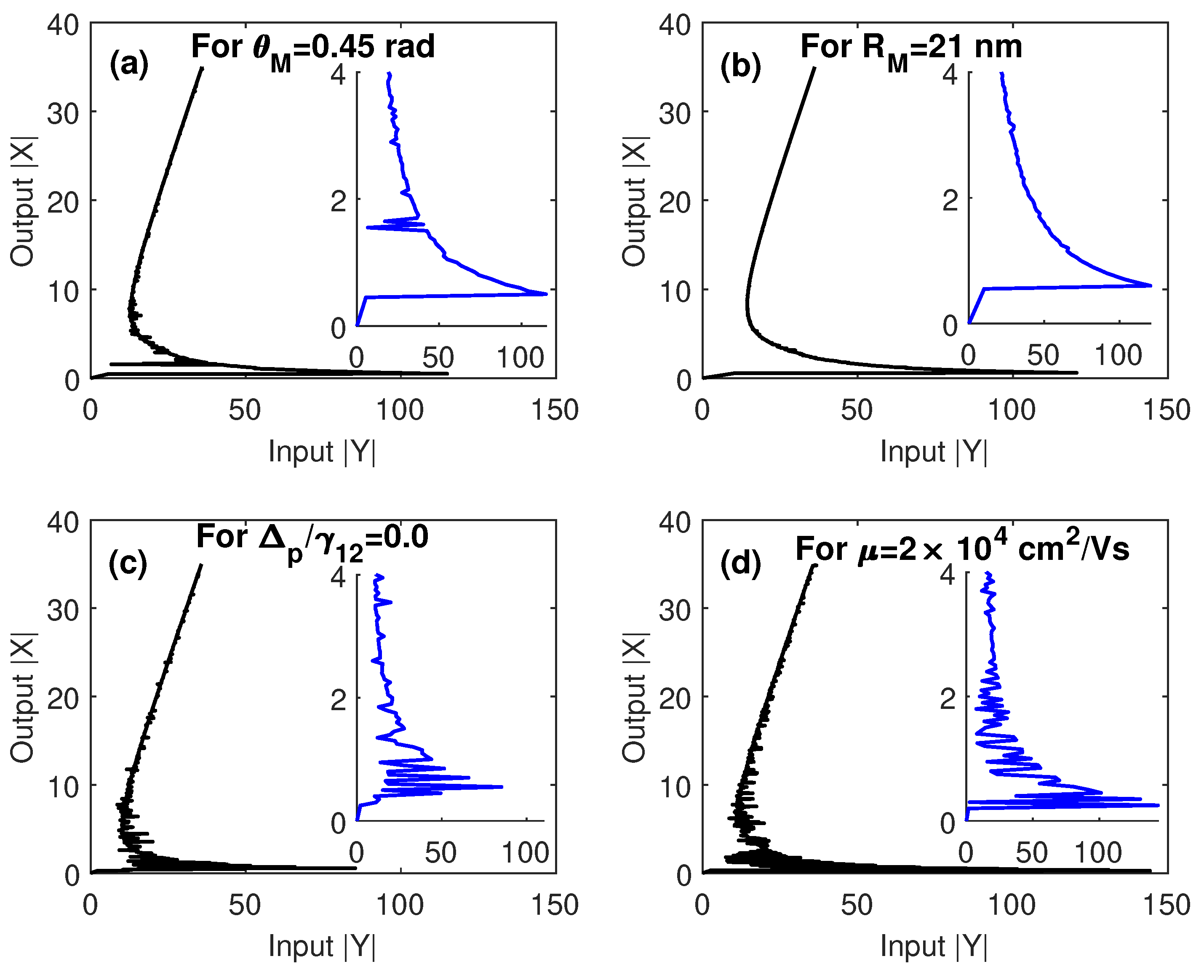
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MNP | Metal nanoparticle |
| GND | Graphene nanodisk |
| QD | Quantum dot |
| EIT | Electromagnetically induced transparency |
References
- Gibbs, H. Optical Bistability: Controlling Light with Light; Academic Press: Cambridge, MA, USA, 1985. [Google Scholar]
- Abraham, E.; Smith, S. Optical bistability and related devices. Rep. Prog. Phys. 1982, 45, 815. [Google Scholar] [CrossRef]
- Li, Y.N.; Chen, Y.Y.; Wan, R.G.; Yan, H.W. Dynamical switching and memory via incoherent pump assisted optical bistability. Phys. Lett. A 2019, 383, 2248–2254. [Google Scholar] [CrossRef]
- Smith, S. Optical bistability, photonic logic, and optical computation. Appl. Opt. 1986, 25, 1550–1564. [Google Scholar] [CrossRef] [PubMed]
- Assanto, G.; Wang, Z.; Hagan, D.; VanStryland, E. All-optical modulation via nonlinear cascading in type II second-harmonic generation. Appl. Phys. Lett. 1995, 67, 2120–2122. [Google Scholar] [CrossRef]
- Mazurenko, D.A.; Kerst, R.; Dijkhuis, J.; Akimov, A.; Golubev, V.; Kurdyukov, D.; Pevtsov, A.; Sel’Kin, A. Ultrafast optical switching in three-dimensional photonic crystals. Phys. Rev. Lett. 2003, 91, 213903. [Google Scholar] [CrossRef] [PubMed]
- Singh, M.R. Theory of all-optical switching based on the Kerr nonlinearity in metallic nanohybrids. Phys. Rev. A 2020, 102, 013708. [Google Scholar] [CrossRef]
- Boyd, R.W. Nonlinear Optics; Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Joshi, A.; Xiao, M. Controlling nonlinear optical processes in multi-level atomic systems. Prog. Opt. 2006, 49, 97. [Google Scholar]
- Nobrega, K.; Da Silva, M.; Sombra, A. Multistable all-optical switching behavior of the asymmetric nonlinear directional coupler. Opt. Commun. 2000, 173, 413–421. [Google Scholar] [CrossRef]
- Miroshnichenko, A.E.; Brasselet, E.; Kivshar, Y.S. All-optical switching and multistability in photonic structures with liquid crystal defects. Appl. Phys. Lett. 2008, 92, 230. [Google Scholar] [CrossRef]
- Sheng, J.; Khadka, U.; Xiao, M. Realization of all-optical multistate switching in an atomic coherent medium. Phys. Rev. Lett. 2012, 109, 223906. [Google Scholar] [CrossRef]
- Martellucci, S.; Chester, A.N. Nonlinear Optics and Optical Computing; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 19. [Google Scholar]
- Wang, Z.; Xu, M. Control of the switch between optical multistability and bistability in three-level V-type atoms. Opt. Commun. 2009, 282, 1574–1578. [Google Scholar] [CrossRef]
- Sahrai, M.; Hamedi, H.; Memarzadeh, M. Kerr nonlinearity and optical multi-stability in a four-level Y-type atomic system. J. Mod. Opt. 2012, 59, 980–987. [Google Scholar] [CrossRef]
- Asadpour, S.H.; Soleimani, H.R. Optical bistability and multistability in a four-level quantum system in the presence of plasmonic nanostructure. Phys. E Low-Dimens. Syst. Nanostructures 2016, 75, 112–117. [Google Scholar] [CrossRef]
- Chen, H.; Ren, J.; Gu, Y.; Zhao, D.; Zhang, J.; Gong, Q. Nanoscale Kerr nonlinearity enhancement using spontaneously generated coherence in plasmonic nanocavity. Sci. Rep. 2015, 5, 18315. [Google Scholar] [CrossRef] [PubMed]
- Terzis, A.; Kosionis, S.; Boviatsis, J.; Paspalakis, E. Nonlinear optical susceptibilities of semiconductor quantum dot–metal nanoparticle hybrids. J. Mod. Opt. 2016, 63, 451–461. [Google Scholar] [CrossRef]
- Ren, J.; Chen, H.; Gu, Y.; Zhao, D.; Zhou, H.; Zhang, J.; Gong, Q. Plasmon-enhanced Kerr nonlinearity via subwavelength-confined anisotropic Purcell factors. Nanotechnology 2016, 27, 425205. [Google Scholar] [CrossRef]
- Tohari, M.; Lyras, A.; AlSalhi, M. Giant Self-Kerr Nonlinearity in the Metal Nanoparticles-Graphene Nanodisks-Quantum Dots Hybrid Systems Under Low-Intensity Light Irradiance. Nanomaterials 2018, 8, 521. [Google Scholar] [CrossRef]
- Kosionis, S.G.; Paspalakis, E. Control of Self-Kerr Nonlinearity in a Driven Coupled Semiconductor Quantum Dot–Metal Nanoparticle Structure. J. Phys. Chem. C 2019, 123, 7308–7317. [Google Scholar] [CrossRef]
- Bao, C.; Qi, Y.; Niu, Y.; Gong, S. Surface plasmon-assisted optical bistability in the quantum dot-metal nanoparticle hybrid system. J. Mod. Opt. 2016, 63, 1280–1285. [Google Scholar] [CrossRef]
- Wang, H.; Goorskey, D.; Xiao, M. Enhanced Kerr nonlinearity via atomic coherence in a three-level atomic system. Phys. Rev. Lett. 2001, 87, 073601. [Google Scholar] [CrossRef]
- Van Doai, L.; Khoa, D.X.; Bang, N.H. EIT enhanced self-Kerr nonlinearity in the three-level lambda system under Doppler broadening. Phys. Scr. 2015, 90, 045502. [Google Scholar] [CrossRef]
- Yan, X.A.; Wang, L.Q.; Yin, B.Y.; Song, J.P. Electromagnetically induced transparency and enhanced self-Kerr nonlinearity in a four-level scheme. Optik 2011, 122, 986–990. [Google Scholar] [CrossRef]
- Solookinejad, G.; Jabbari, M.; Nafar, M.; Ahmadi, E.; Asadpour, S. Incoherent control of optical bistability and multistability in a hybrid system: Metallic nanoparticle-quantum dot nanostructure. J. Appl. Phys. 2018, 124, 063102. [Google Scholar] [CrossRef]
- Hendry, E.; Hale, P.J.; Moger, J.; Savchenko, A.; Mikhailov, S.A. Coherent nonlinear optical response of graphene. Phys. Rev. Lett. 2010, 105, 097401. [Google Scholar] [CrossRef]
- Cheng, J.L.; Vermeulen, N.; Sipe, J. Third order optical nonlinearity of graphene. New J. Phys. 2014, 16, 053014. [Google Scholar] [CrossRef]
- Dai, X.; Jiang, L.; Xiang, Y. Low threshold optical bistability at terahertz frequencies with graphene surface plasmons. Sci. Rep. 2015, 5, 12271. [Google Scholar] [CrossRef]
- Sharif, M.A.; Khodavirdizadeh, M.; Salmani, S.; Mohajer, S.; Ara, M.M. Difference Frequency Generation-based ultralow threshold Optical Bistability in graphene at visible frequencies, an experimental realization. J. Mol. Liq. 2019, 284, 92–101. [Google Scholar] [CrossRef]
- Zhang, D.; Sun, Z.; Ding, C.; Yu, R.; Yang, X. Controllable optical bistability and multistability in a graphene monolayer system. J. Lumin. 2016, 170, 72–77. [Google Scholar] [CrossRef]
- Sadeghi, M.; Ahmadi, V. Multilayer graphene based optical bistability. JOSA B 2018, 35, 528–532. [Google Scholar] [CrossRef]
- Naseri, T.; Daneshfar, N.; Moradi-Dangi, M.; Eynipour-Malaee, F. Terahertz optical bistability of graphene-coated cylindrical core–shell nanoparticles. J. Theor. Appl. Phys. 2018, 12, 257–263. [Google Scholar] [CrossRef]
- Tohari, M.; Lyras, A.; Alsalhi, M. Ultrafast Energy Transfer in the Metal Nanoparticles-Graphene Nanodisks-Quantum Dots Hybrid Systems. Plasmonics 2019, 14, 17–24. [Google Scholar] [CrossRef]
- Singh, J.; Williams, R.T. Excitonic and Photonic Processes in Materials; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Bonifacio, R.; Lugiato, L. Optical bistability and cooperative effects in resonance fluorescence. Phys. Rev. A 1978, 18, 1129. [Google Scholar] [CrossRef]
- Falkovsky, L. Optical properties of graphene. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2008; Volume 129, p. 012004. [Google Scholar]
- Johnson, P.B.; Christy, R.W. Optical constants of the noble metals. Phys. Rev. B 1972, 6, 4370. [Google Scholar] [CrossRef]
- Guo, J.; Jiang, L.; Jia, Y.; Dai, X.; Xiang, Y.; Fan, D. Low threshold optical bistability in one-dimensional gratings based on graphene plasmonics. Opt. Express 2017, 25, 5972–5981. [Google Scholar] [CrossRef]
- Kar, A.; Goswami, N.; Saha, A. Long-range surface plasmon-induced tunable ultralow threshold optical bistability using graphene sheets at terahertz frequency. Appl. Opt. 2017, 56, 2321–2329. [Google Scholar] [CrossRef]
- Berman, P.R.; Lin, C.C.; Arimondo, E. Advances in Atomic, Molecular, and Optical Physics; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
| System Component (s) | Parameter (Symbol) | Value |
|---|---|---|
| The Metal Nanoparticle (MNP) | High-frequency dielectric constant () | |
| Plasma frequency () | (s−1) | |
| Damping rate of plasmon(s) () | (s−1) | |
| The Graphene Nanodisk (GND) | Thickness () | (nm) |
| Radius () | (nm) | |
| Mobility () | (cm2/Vs) | |
| Fermi energy () | (eV) | |
| The CdSe Quantum Dot (CdSe QD) | Dielectric constant () | |
| Dipole moment transition () | (e nm) | |
| Atomic number density (N) | (m−3) | |
| The GaAs substrate (Background) | Dielectric constant () |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tohari, M.M.; Alqahtani, M.M.; Lyras, A. Optical Multistability in the Metal Nanoparticle–Graphene Nanodisk–Quantum Dot Hybrid Systems. Nanomaterials 2020, 10, 1687. https://doi.org/10.3390/nano10091687
Tohari MM, Alqahtani MM, Lyras A. Optical Multistability in the Metal Nanoparticle–Graphene Nanodisk–Quantum Dot Hybrid Systems. Nanomaterials. 2020; 10(9):1687. https://doi.org/10.3390/nano10091687
Chicago/Turabian StyleTohari, Mariam M., Moteb M. Alqahtani, and Andreas Lyras. 2020. "Optical Multistability in the Metal Nanoparticle–Graphene Nanodisk–Quantum Dot Hybrid Systems" Nanomaterials 10, no. 9: 1687. https://doi.org/10.3390/nano10091687
APA StyleTohari, M. M., Alqahtani, M. M., & Lyras, A. (2020). Optical Multistability in the Metal Nanoparticle–Graphene Nanodisk–Quantum Dot Hybrid Systems. Nanomaterials, 10(9), 1687. https://doi.org/10.3390/nano10091687





