Memristive and Synaptic Characteristics of Nitride-Based Heterostructures on Si Substrate
Abstract
:1. Introduction
2. Materials and Methods
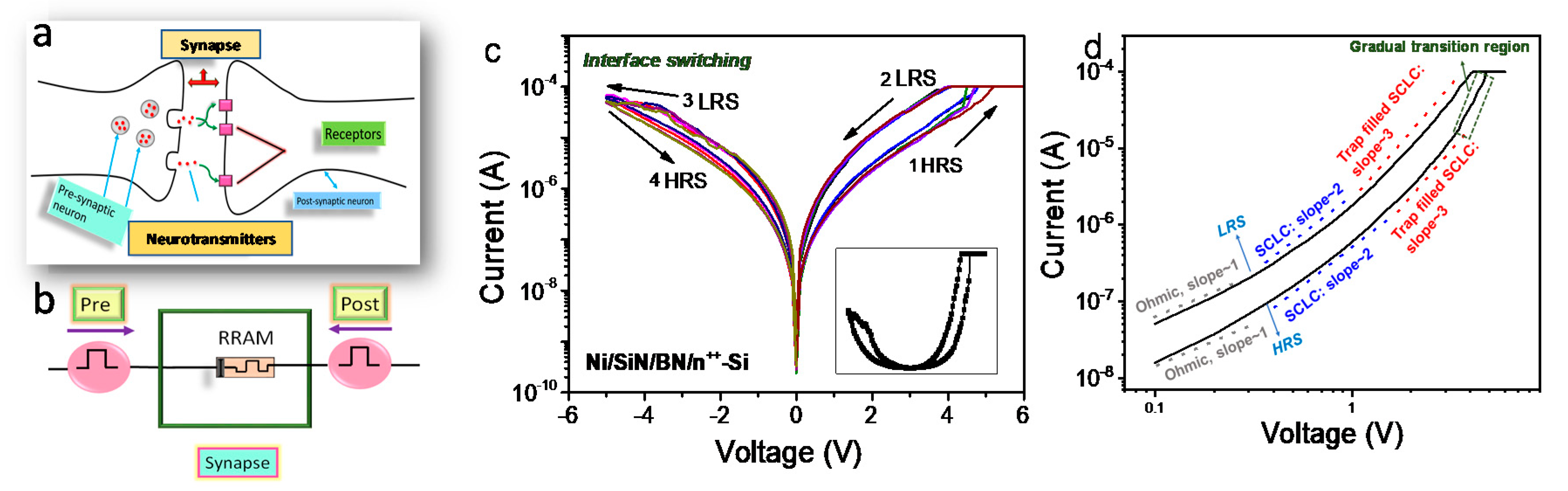
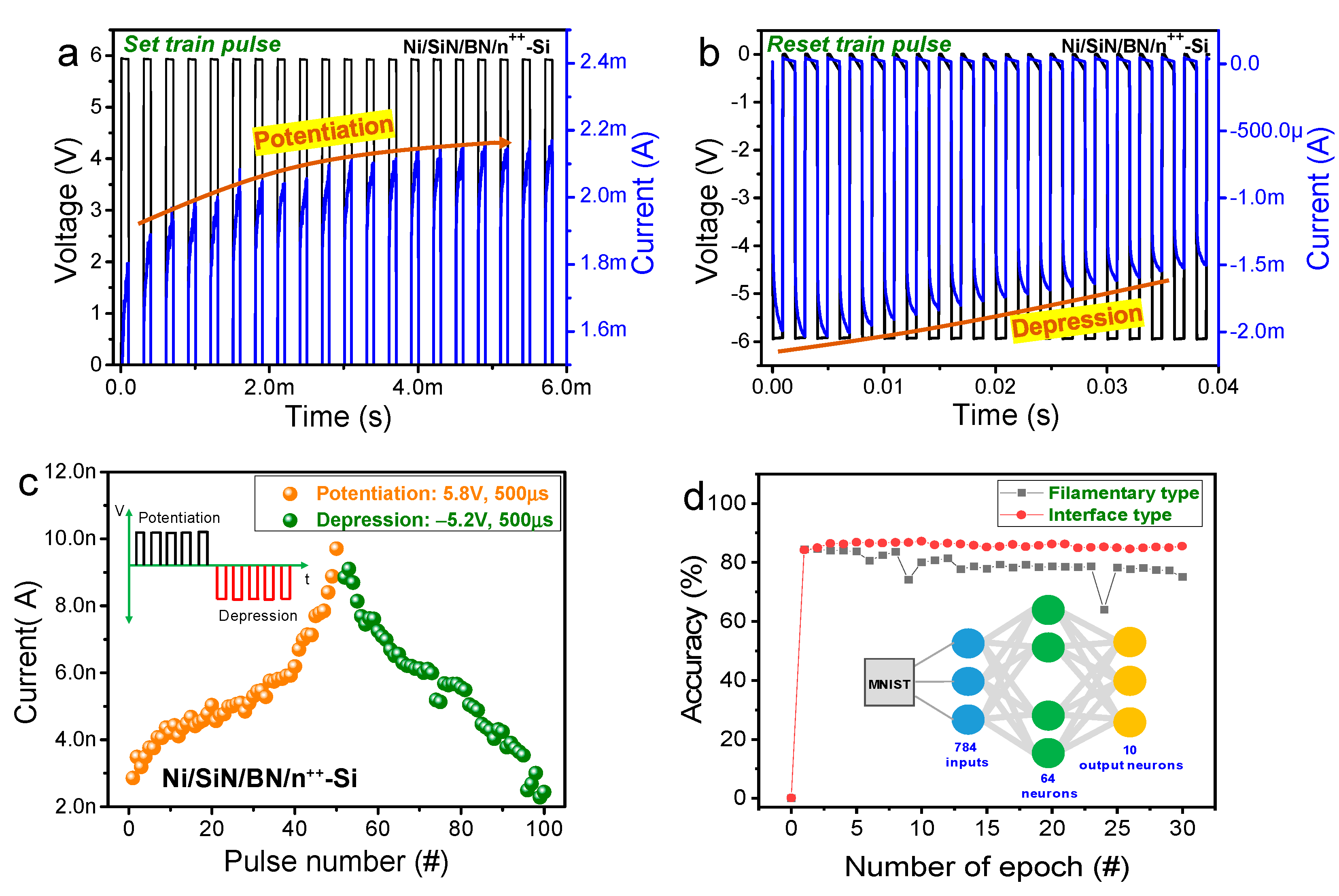
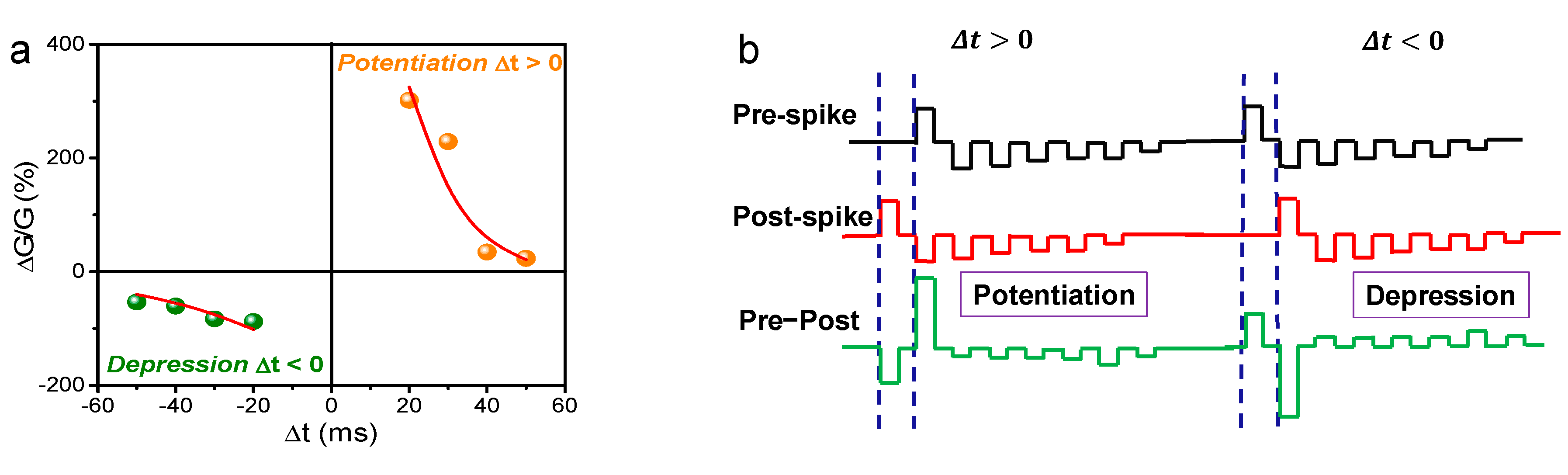
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Apalkov, D.; Khvalkovskiy, A.; Watts, S.; Nikitin, V.; Tang, X.; Lottis, D.; Moon, K.; Luo, X.; Chen, E.; Ong, A.; et al. Spin-transfer torque magnetic random-access memory (STT-MRAM). ACM J. Emerg. Technol. Comput. Syst. 2013, 9, 1–35. [Google Scholar] [CrossRef]
- Fong, S.W.; Neumann, C.M.; Wong, H.S.P. Phase-change memory—Towards a storage-class memory. IEEE Trans. Electron Devices 2017, 64, 4374–4385. [Google Scholar] [CrossRef]
- Balatti, S.; Ambrogio, S.; Ielmini, D. Normally-off Logic Based on Resistive Switches—Part I: Logic Gates. IEEE Trans. Electron Devices 2015, 62, 1831. [Google Scholar] [CrossRef] [Green Version]
- Kim, C.S.; Kim, T.; Min, K.K.; Kim, S.; Park, B.-G. 3D Integrable W/SiNx/n-Si/p-Si 1D1R Unipolar Resistive Random Access Memory Synapse for Suppressing Reverse Leakage in Spiking Neural Network. J. Nanosci. Nanotechnol. 2020, 20, 4735–4739. [Google Scholar] [CrossRef]
- Ielmini, D. Brain-inspired computing with resistive switching memory (RRAM): Devices, synapses and neural networks. Microelectron. Eng. 2018, 190, 44–53. [Google Scholar] [CrossRef]
- Kim, S.; Chen, J.; Chen, Y.C.; Kim, M.-H.; Kim, H.; Kwon, M.-W.; Hwang, S.; Ismail, M.; Li, Y.; Miao, X.-S.; et al. Neuronal dynamics in HfOx/AlOy-based homeothermic synaptic memristors with low-power and homogeneous resistive switching. Nanoscale 2019, 11, 237–245. [Google Scholar] [CrossRef] [Green Version]
- Sawa, A. Resistive switching in transition metal oxides. Mater. Today 2008, 11, 28–37. [Google Scholar] [CrossRef]
- Wong, H.S.P.; Salahuddin, S. Memory leads the way to better computing. Nat. Nanotechnol. 2015, 10, 191–194. [Google Scholar] [CrossRef] [Green Version]
- Walter, F.; Röhrbein, F.; Knoll, A. Neuromorphic implementations of neurobiological learning algorithms for spiking neural networks. Neural Netw. 2015, 72, 152–167. [Google Scholar] [CrossRef] [Green Version]
- Wong, H.S.P.; Lee, H.Y.; Yu, S.; Chen, Y.S.; Wu, Y.; Chen, P.-S.; Lee, B.; Chen, F.T.; Tsai, M.J. Metal-Oxide RRAM. Proc. IEEE 2012, 100, 951–1970. [Google Scholar] [CrossRef]
- Jeon, Y.R.; Abbas, Y.; Sokolov, A.S.; Kim, S.; Ku, B.; Choi, C. Study of in Situ Silver Migration in Amorphous Boron Nitride CBRAM Device. ACS Appl. Mater. Interfaces 2019, 11, 23329. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Chang, Y.F.; Kim, M.H.; Park, B.G. Improved resistive switching characteristics in Ni/SiNx/p++-Si devices by tuning x. Appl. Phys. Lett. 2017, 111, 033509. [Google Scholar] [CrossRef]
- Kim, S.; Cho, S.; Ryoo, K.C.; Park, B.G. Effects of conducting defects on resistive switching characteristics of SiNx-based resistive random-access memory with MIS structure. J. Vac. Sci. Technol. 2015, 33, 0662201. [Google Scholar] [CrossRef]
- Kim, M.H.; Kim, S.; Bang, S.; Kim, T.H.; Lee, D.K.; Cho, S.; Park, B.G. Uniformity Improvement of SiNx-Based Resistive Switching Memory by Suppressed Internal Overshoot Current. IEEE Trans. Nanotechnol. 2018, 17, 824–828. [Google Scholar] [CrossRef]
- Kim, S.; Chang, Y.F.; Park, B.G. Understanding rectifying and nonlinear bipolar resistive switching characteristics in Ni/SiNx/p-Si memory devices. RSC Adv. 2017, 7, 17882–17888. [Google Scholar] [CrossRef] [Green Version]
- Caporale, N.; Dan, Y. Spike timing–dependent plasticity: A Hebbian learning rule. Annu. Rev. Neurosci. 2008, 31, 25–46. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Joshi, S.E.; Savel’ev, S.E.; Jiang, H.; Midya, R.; Lin, P.; Hu, M.; Ge, N.; Strachan, J.P.; Li, Z. Memristors with diffusive dynamics as synaptic emulators for neuromorphic computing. Nat. Mater. 2017, 16, 101–108. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.H.; Huang, J.S.; Lai, C.C.; Huang, H.W.; Lin, S.J.; Chueh, Y.L. Manipulated Transformation of Filamentary and Homogeneous Resistive Switching on ZnO Thin Film Memristor with Controllable Multistate. ACS Appl. Mater. Interfaces 2013, 5, 13. [Google Scholar] [CrossRef]
- Kim, S.; Park, B.G. Power-and Low-Resistance-State-Dependent, Bipolar Reset-Switching Transitions in SiN-Based Resistive Random-Access Memory. Nanoscale Res. Lett. 2016, 11, 360. [Google Scholar] [CrossRef] [Green Version]
- Murgatroyd, P.N. Theory of space-charge-limited current enhanced by Frenkel effect. J. Phys. D-Appl. Phys. 1970, 3, 151. [Google Scholar] [CrossRef]
- Burr, G.W.; Shelby, R.M.; Sidler, S.; Nolfo, C.D.; Jang, J.; Boybat, I.; Shenoy, R.S.; Narayanan, P.; Virwani, K.; Giacometti, E.U.; et al. Experimental demonstration and tolerancing of a large-scale neural network (165 000 synapses) using phase-change memory as the synaptic weight element. IEEE Trans. Electron. Dev. 2015, 62, 3498–3507. [Google Scholar] [CrossRef]
- Feldman, D.E. The spike-timing dependence of plasticity. Neuron 2012, 75, 556–571. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bi, G.Q.; Poo, M.M. Synaptic modifications in cultured hippocampal neurons: Dependence on spike timing, synaptic strength, and postsynaptic cell type. J. Neurosci. 1998, 18, 10464–10472. [Google Scholar] [CrossRef] [PubMed]
- Panwar, N.; Rajendran, B.; Ganguly, U. Arbitrary spike time dependent plasticity (STDP) in memristor by analog waveform engineering. IEEE Electron Device Lett. 2017, 38, 740–743. [Google Scholar] [CrossRef]
- Jackson, B.L.; Rajendran, B.; Corrado, G.S.; Breitwisch, M.; Burr, G.W.; Cheek, R.; Gopalakrishnan, K.; Raoux, S.; Rettner, C.T.; Padilla, A.; et al. Nanoscale electronic synapses using phase change devices. ACM J. Emerg. Technol. Comput. Syst. 2013, 9, 1–20. [Google Scholar] [CrossRef]
- Kubota, S.; Rubin, J.; Kitajima, T. Modulation of LTP/LTD balance in STDP by an activity-dependent feedback mechanism. Neural Netw. 2009, 22, 527–535. [Google Scholar] [CrossRef]
- Babadi, B.; Abbott, L.F. Pairwise analysis can account for network structures arising from spike-timing dependent plasticity. PLoS Comput. Biol. 2013, 9, e1002906. [Google Scholar] [CrossRef] [Green Version]
- Song, S.; Miller, K.D.; Abbott, L.F. Competitive Hebbian learning through spike-timing-dependent synaptic plasticity. Nat. Neurosci. 2000, 3, 919–926. [Google Scholar] [CrossRef]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahmani, M.K.; Kim, M.-H.; Hussain, F.; Abbas, Y.; Ismail, M.; Hong, K.; Mahata, C.; Choi, C.; Park, B.-G.; Kim, S. Memristive and Synaptic Characteristics of Nitride-Based Heterostructures on Si Substrate. Nanomaterials 2020, 10, 994. https://doi.org/10.3390/nano10050994
Rahmani MK, Kim M-H, Hussain F, Abbas Y, Ismail M, Hong K, Mahata C, Choi C, Park B-G, Kim S. Memristive and Synaptic Characteristics of Nitride-Based Heterostructures on Si Substrate. Nanomaterials. 2020; 10(5):994. https://doi.org/10.3390/nano10050994
Chicago/Turabian StyleRahmani, Mehr Khalid, Min-Hwi Kim, Fayyaz Hussain, Yawar Abbas, Muhammad Ismail, Kyungho Hong, Chandreswar Mahata, Changhwan Choi, Byung-Gook Park, and Sungjun Kim. 2020. "Memristive and Synaptic Characteristics of Nitride-Based Heterostructures on Si Substrate" Nanomaterials 10, no. 5: 994. https://doi.org/10.3390/nano10050994
APA StyleRahmani, M. K., Kim, M.-H., Hussain, F., Abbas, Y., Ismail, M., Hong, K., Mahata, C., Choi, C., Park, B.-G., & Kim, S. (2020). Memristive and Synaptic Characteristics of Nitride-Based Heterostructures on Si Substrate. Nanomaterials, 10(5), 994. https://doi.org/10.3390/nano10050994







