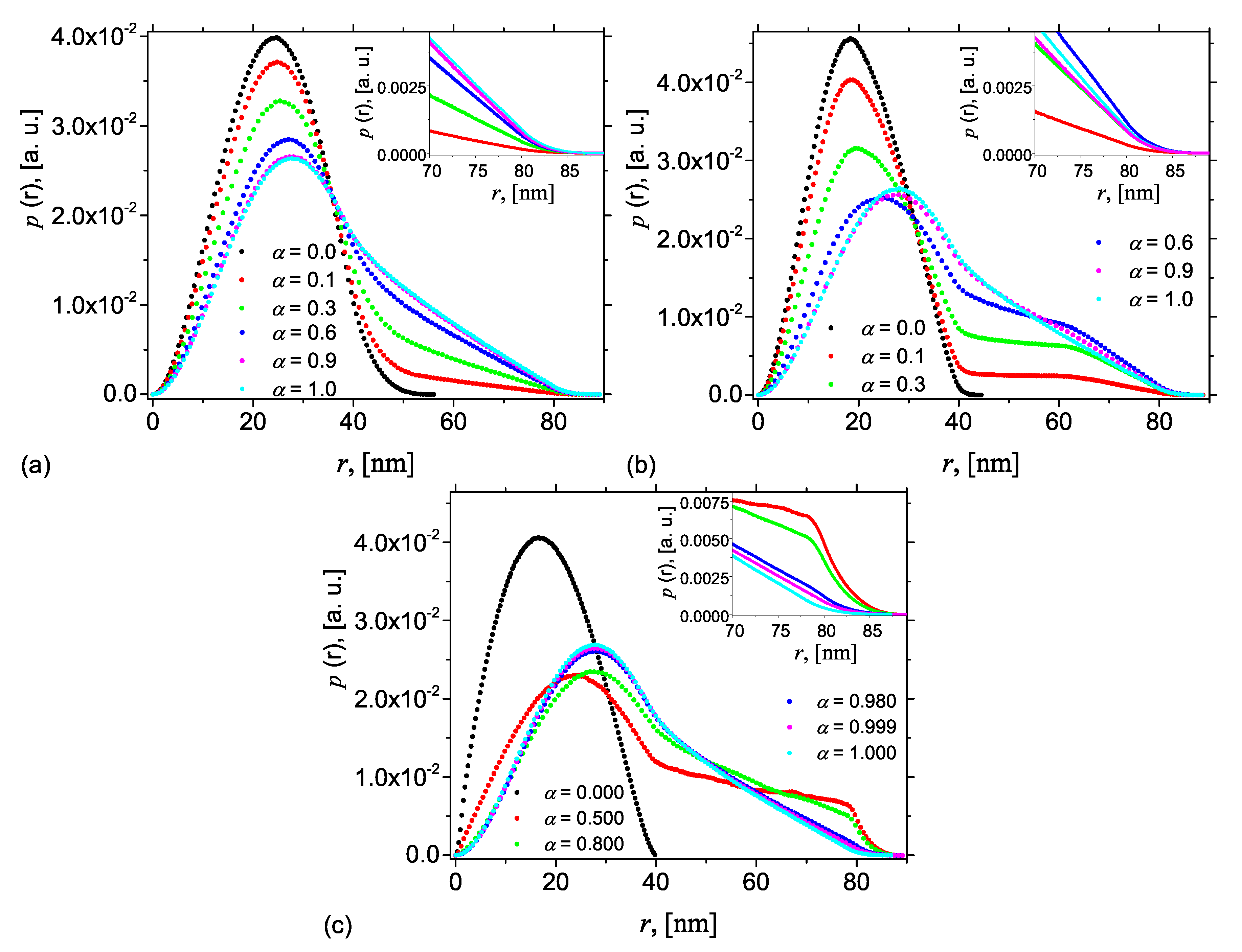
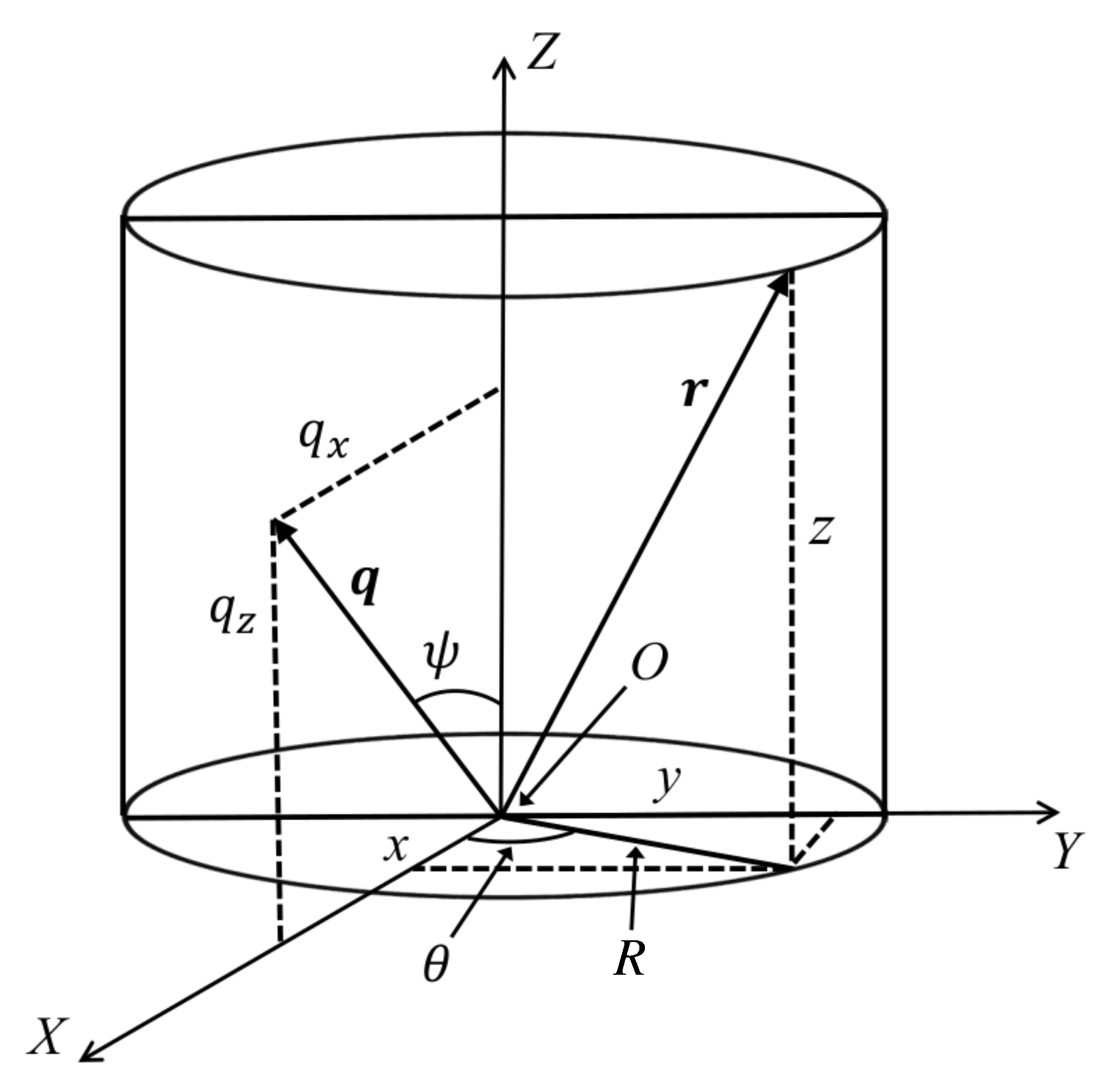
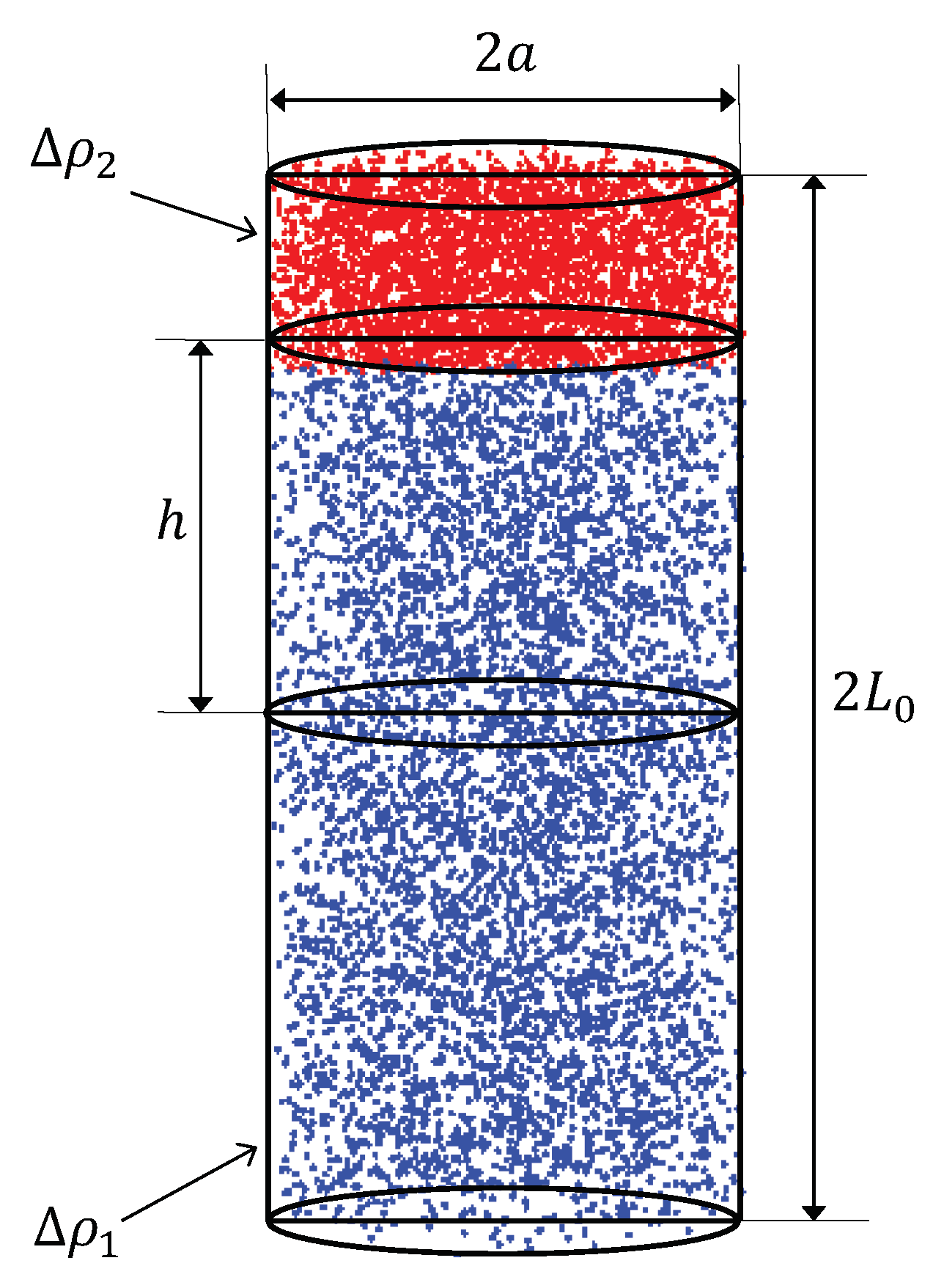
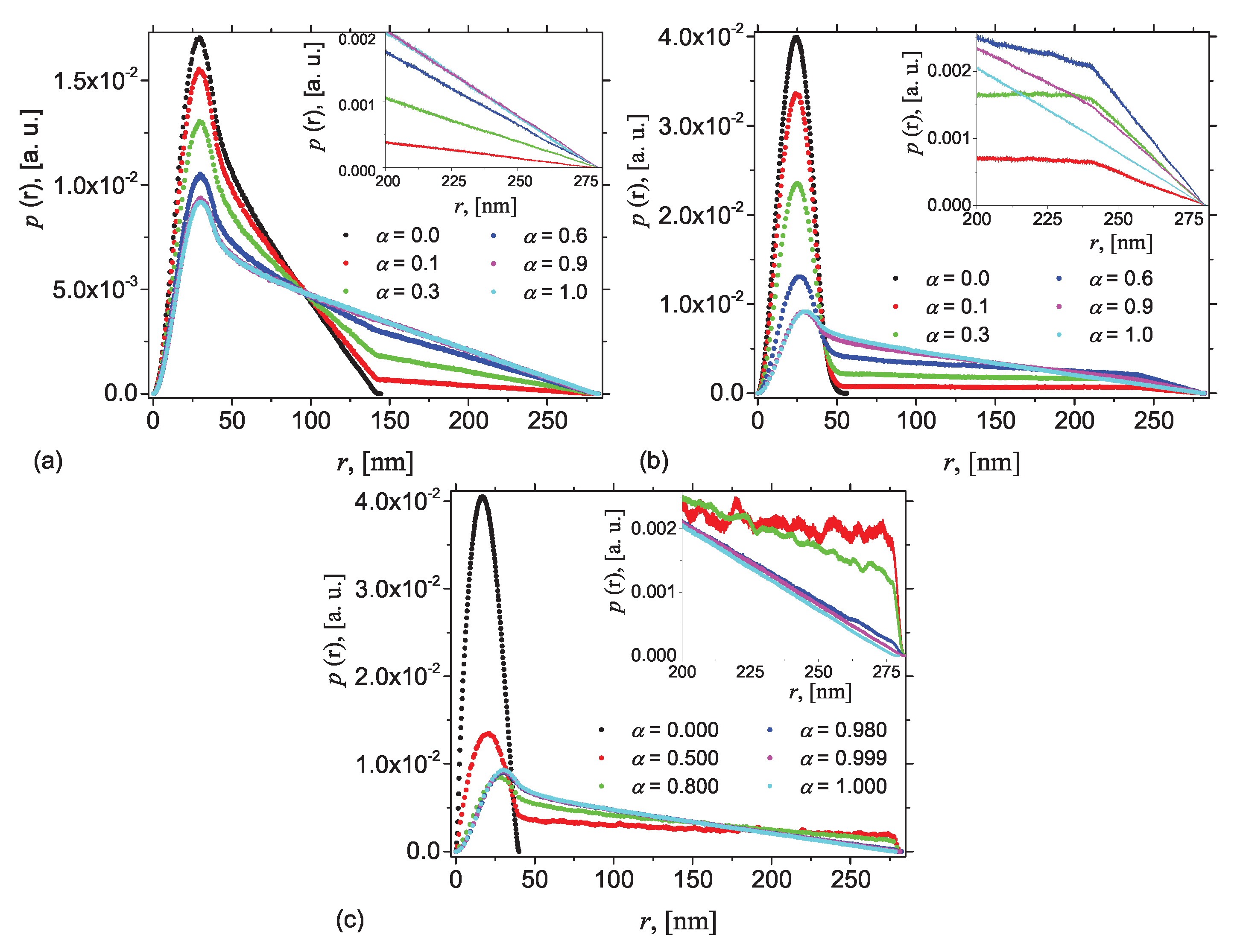
3.2. Pair Distance Distribution from Monte Carlo Simulations
The corresponding pddf at fixed values of the height
h and various values of the contrast parameter
are shown in
Figure 4. The values of
have been obtained by considering that
and
in Equation (
5), while
is varied. For
and
, the AnJPs are reduced to homogeneous cylinders, and the corresponding pddfs are calculated using the classical approach involving a random distribution of points in Region 2 and in Region 1, respectively.
The simplest case is presented in
Figure 4a, which shows the pddfs at
, i.e., when Region 2 is half as compared with Region 1. At
, AnJPs reduces to Region 2 and the corresponding pddf has the well-known behavior where a peak, corresponding to the cross section, gives the largest number of distances that occurs, and is followed by a straight line up to
(black dots). The inflection point at
nm gives a rough indication for the size of the cross section. However, as soon as
, a second inflection point where the pddf increases its slope, occurs at
nm. This is because the density of the complement of Region 2 is different from the density of Region 2 itself. As
is increased further, the differences between the slopes decrease, indicating the formation of a more homogeneous structure, in which the differences between the densities become less. The inset in
Figure 4a shows that at large values of
r, the differences between pddfs corresponding to
and
are almost indistinguishable. Finally, when
, the crossover point disappears, revealing the formation of a completely homogeneous structure. Note that the height of the maxima also decreases with increasing
, reflecting a decreasing of the maximum number of distances when increasing the contribution of Region 1. Thus, the differences between the slopes can be used to quantify the differences between the densities of the two regions in AnJPs.
Figure 4b shows the pddfs when the height
h is increased to 100 nm. This case reflects the situation when, although the two regions of AnJPs have different sizes, both can be considered as 3D objects. This behavior is similar to the previous case in
Figure 4a with the difference that, at the inflection point
nm, the slopes of the pddfs increase. Therefore, the type of transition at this point is an indication of weather the AnJPs is symmetric of not.
Figure 4c presents the case when
nm, i.e., when
. Thus, Region 2 is much smaller than the overall size of AnJP, which implies that
, and thus it can be assimilated to a 2D disk. This induces additional small irregular oscillations in the pddf when
, and with amplitudes slightly increasing with
r. The inset in
Figure 4c clearly shows these oscillations when
and 0.8. Similar results are shown in
Figure A1 for
nm,
nm.
3.2.1. The Scaling Approach
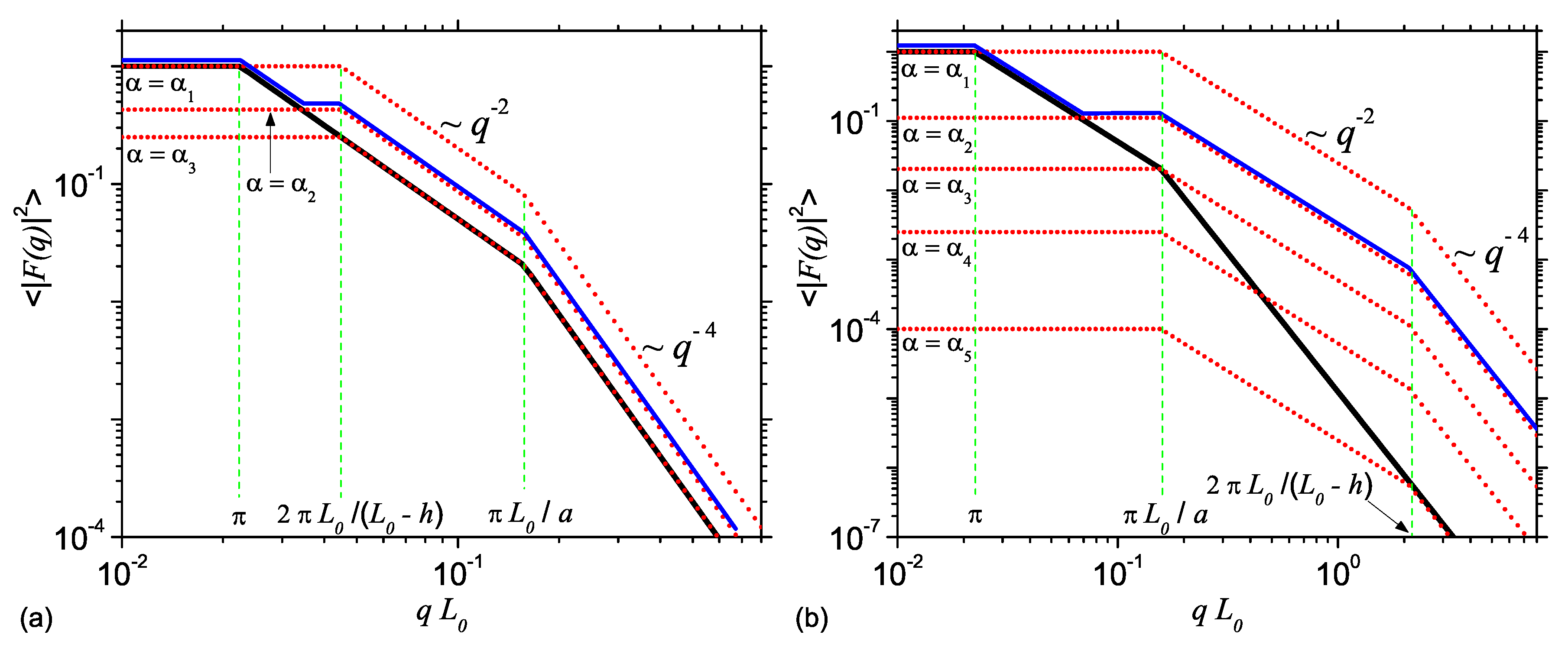
As shown above, features at different scales can be clearly seen in pddfs. To describe all these features also in the reciprocal space, in a unified way, here is presented a scaling description based on comparison of various power-law regimes to the various length scales of AnJPs. Thus, the power-law dependency of the scattering intensity on the scattering vector q is correctly predicted, as well as the crossover position (i.e., the transition point) between two such regimes. However, this approach does not describe the coefficients of these power-law decays and cannot account also for the oscillations present in the scattering curves. However, for practical purposes, these are not of concern since, in most cases, the investigated systems are not monodisperse.
Let us consider that the model-free scattering intensity of Region 1, i.e., of the cylinder with height
h and diameter
, is of the following form:
Here, the coefficients of the power-law decays
,
and
are chosen such that they assure the continuity of the intensity at
and
. Note that, according to the model shown in
Figure 1, the relative values of
and
h can be chosen in such a way that the AnJPs resemble either a 3D object (cylinder) or a 2D one (disk). The behavior of corresponding intensity is presented in
Figure 5a (or
Figure 5b)—black curves. The scattering intensity gives a succession of the type
power-law decays. The transition points are at
and
as expected (see Equation (
14)).
A similar expression as in Equation (
14) can also be written for Region 2. However, since, in this case, either the diameter (
) or the height (
) can have relatively higher values, the intensities corresponding to the cases when
and
can be written as:
and
respectively. These intensities are shown in
Figure 5a,b (red dots), respectively, for various values of the contrast parameter
.
The common feature is the presence of a
transition. When
, the beginning of the
decay is at
(
). However, when
, the beginning of
decay of Region 2 (at
) coincides with the end of the
decay of Region 1. This has important consequences on the overall intensity describing the AnJP. While in the former case, the upper limit is at
, in the later case, this is extended up to
. Thus, since the position of the transition points in Regions 1 and 2 does not coincide, for the contrast parameter values
ranging between
and
(shown in
Figure 5a,b, respectively), the overall intensity of AnJP will be characterized by a more complex type of transition, of the form
, as shown by the blue dash-dotted lines at
. The exact values of
and
depend on the geometrical parameters
and
h of AnJP, and can be found from the conditions
(with
given by Equation (
5)), and by imposing the equality of the two terms containing
and
occurring in Equation (
6) at the point
, respectively.
3.3. Small-Angle Scattering Intensity
By using Equation (
9), the form factor of Region 2 can be written as:
where
,
is the angle between positive direction of axis and scattering vector
.
Therefore, after a little algebra, one finds that the form factor of the AnJPs can be written as:
where the first term corresponds to the form factor of Region 1 (i.e., cylinder of height
and radius
),
and
is the first order Bessel function of the first kind. Note that
depends only on the angle
, and thus the function
in Equation (
3) is independent of the azimuthal angle
. Therefore, the intensity from AnJPs is calculated according to:
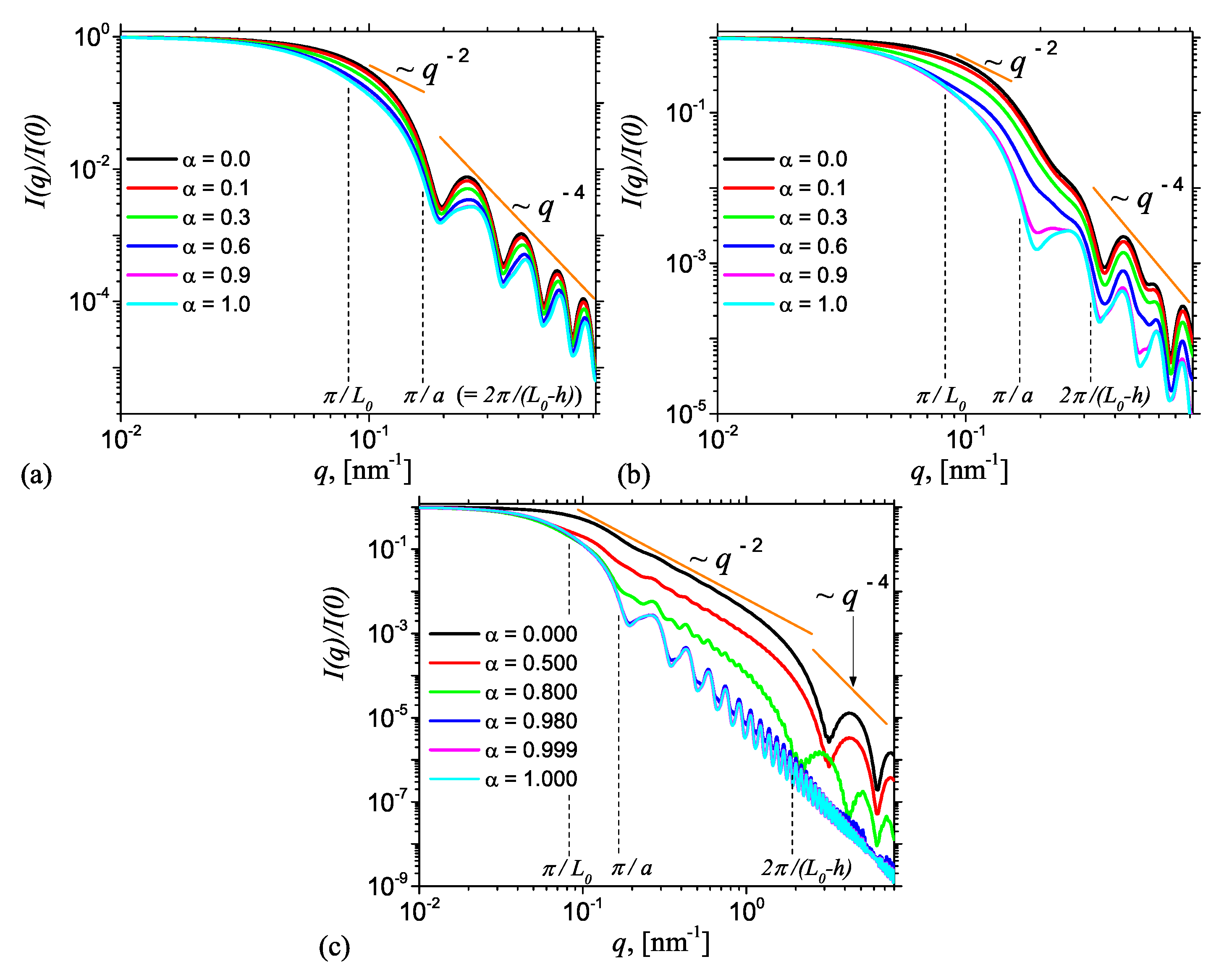
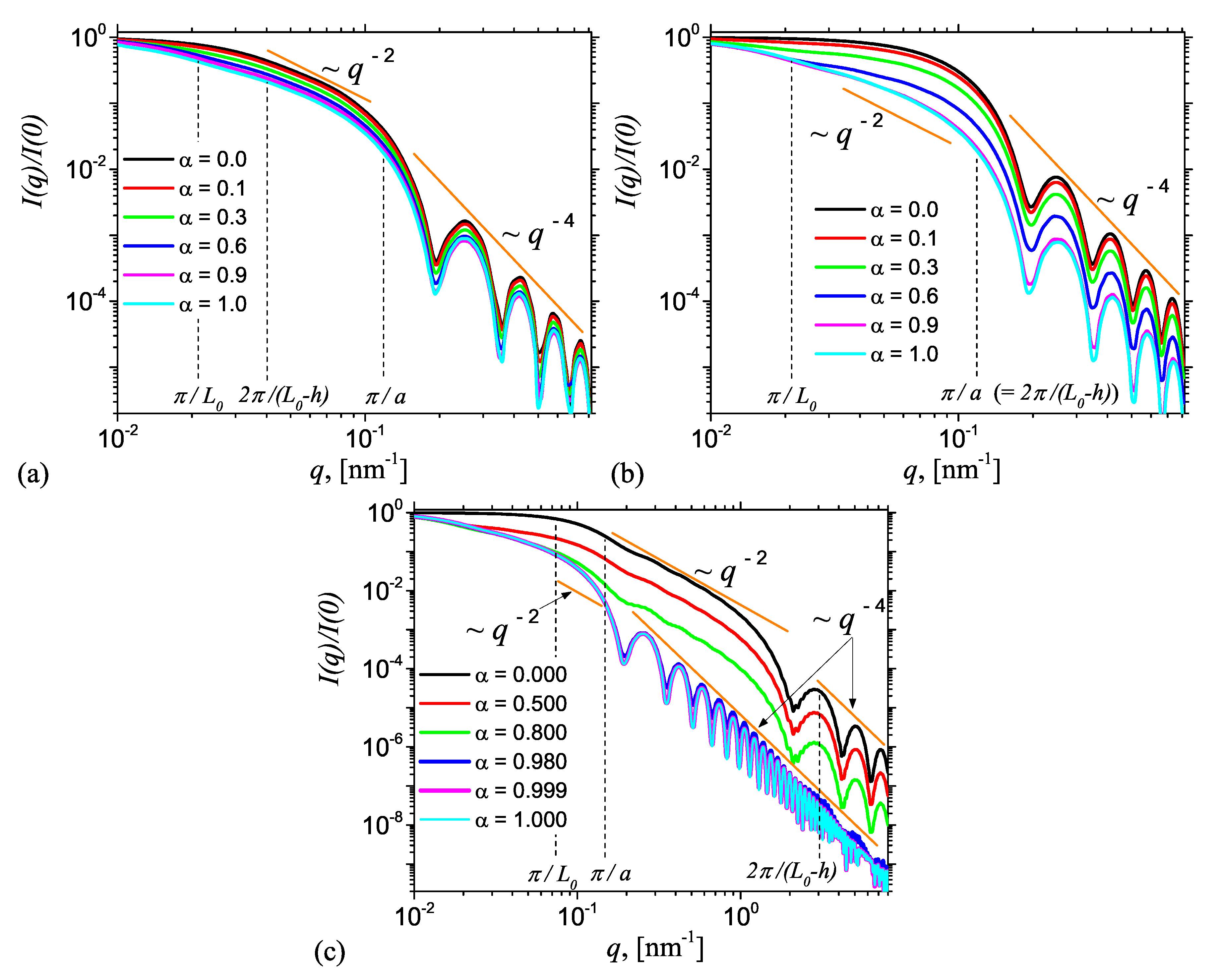
Figure 6 shows the corresponding intensities from AnJPs as a function of height
h and of the contrast parameter
given by Equation (
5). Their numerical values were chosen such that all the cases discussed in
Figure 5 are addressed. The common feature is the presence of a Guinier regime, i.e.,
for
, an intermediate regime where
for
when
and
when
, followed by Porod regime where
. All the curves in
Figure 6 have been reproduced also by performing the Fourier transform given by Equation (
10) of the pddf obtained from Monte-Carlo simulations shown in
Figure 4. The results are presented in the
Appendix A (
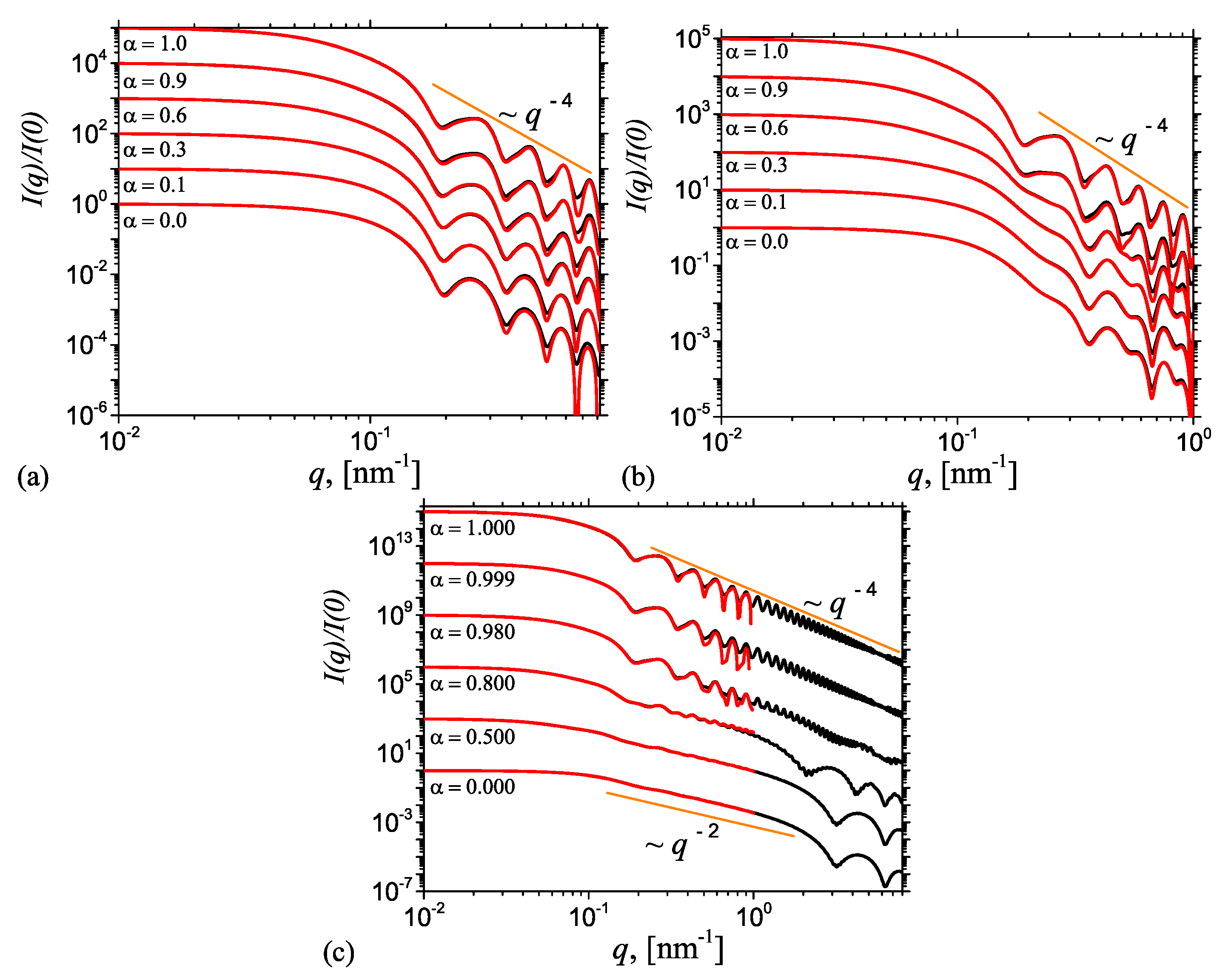
Figure A3) and show a very good agreement between the analytic curves and numerical simulations. This confirms the validity of the developed models.
Figure 6a presents the results when
, corresponding to the case when AnJPs resemble cylinders in which the two regions of different SLDs are situated symmetrically with respect to the middle plane parallel to the bases. For this case, the differences between scattering curves when
varies from zero to one, i.e., when the structure of AnJPs changes from a cylinder of height
and radius
to a cylinder of height
and the same radius, are not very pronounced. The exception is the end of the Guinier regime, which becomes smaller with increasing
due to the increase of the contribution of Region 1. As a consequence, the length of
decay increases with contrast parameter
, and thus it is more reliable for an experimental determination of the cylinder size. Note that the minima positions in the Porod regime are the same, indicating that, in the whole range of
values, the AnJPs preserve their cylindrical structure.
Figure 6b treats the case when the two sides of AnJP are now different in size, but still both resemble 3D objects. The numerical value used for the height
h is 100 nm, and the values of the contrast parameter
are the same as in
Figure 6a. Generally, the results show a transition of the type
. However, the differences between the scattering curves at fixed values of
, are more pronounced in both the Guinier and Porod regimes, due to differences in the overall dimensions of the two regions. As
, the dominant contribution is given by Region 2, i.e., the cylinder of height
nm and diameter
nm, while for
, the dominant contribution comes from Region 1 (see Equation (
6)), i.e., the cylinder of height
nm, and which has the same diameter as Region 2. Therefore, in the former case, we have an almost completely globular particle, and thus the
decay is hardly visible (see black curve). However, as
is increased from 0 to 1, the
decay becomes more clearly visible, with its maximum length occurring at
. In addition, the minima positions in Porod regime coincide for all values of
.
Figure 6c presents the results for a third important case, when the height
nm is almost equal to
(=140 nm). Therefore, Region 2 becomes a disk of height
nm and diameter 40 nm, which closely resemble a 2D structure. Thus, one expects that, for some particular value of
, significant changes in the behavior of the SAS curves shall occur, reflecting the transition from 3D to 2D-like structures. Indeed, numerical investigations show that for the chosen parameters (
and
a) a transition occurs at
. When
the scattering curves show a long
power-law decay, i.e., for
, followed by a Porod regime, thus reflecting the dominant contribution of the 2D-disk, while at
the length of the
decay is significantly reduced, and replaced by a Porod regime, as an effect of the dominance of Region 1, i.e., the 3D cylinder (of height
and diameter
). Thus, the interplay between the relative sizes of the two regions of AnJPs, and the strength of their SLDs on the scattering curve, can be controlled through the values of the scattering parameter
. Note that, in
Figure 6b,c, the scattering curves in the Porod regime are significantly shifted up with decreasing the values of
, and this can be used to extract information about the specific surface [
29].
3.4. Radius of Gyration
One of the most important structural parameters which can be obtained from SAS data shown in
Figure 4 is the radius of gyration
of AnJP. This is a measure of its overall size, and is related to the average of square center-of-mass distances inside the particle, weighted by the SLD. Here,
is obtained from Equation (
11), which makes use of the whole available data in the scattering intensity. The advantage over other methods such as the Guinier plot, is that in the former case is used all the available experimental data.
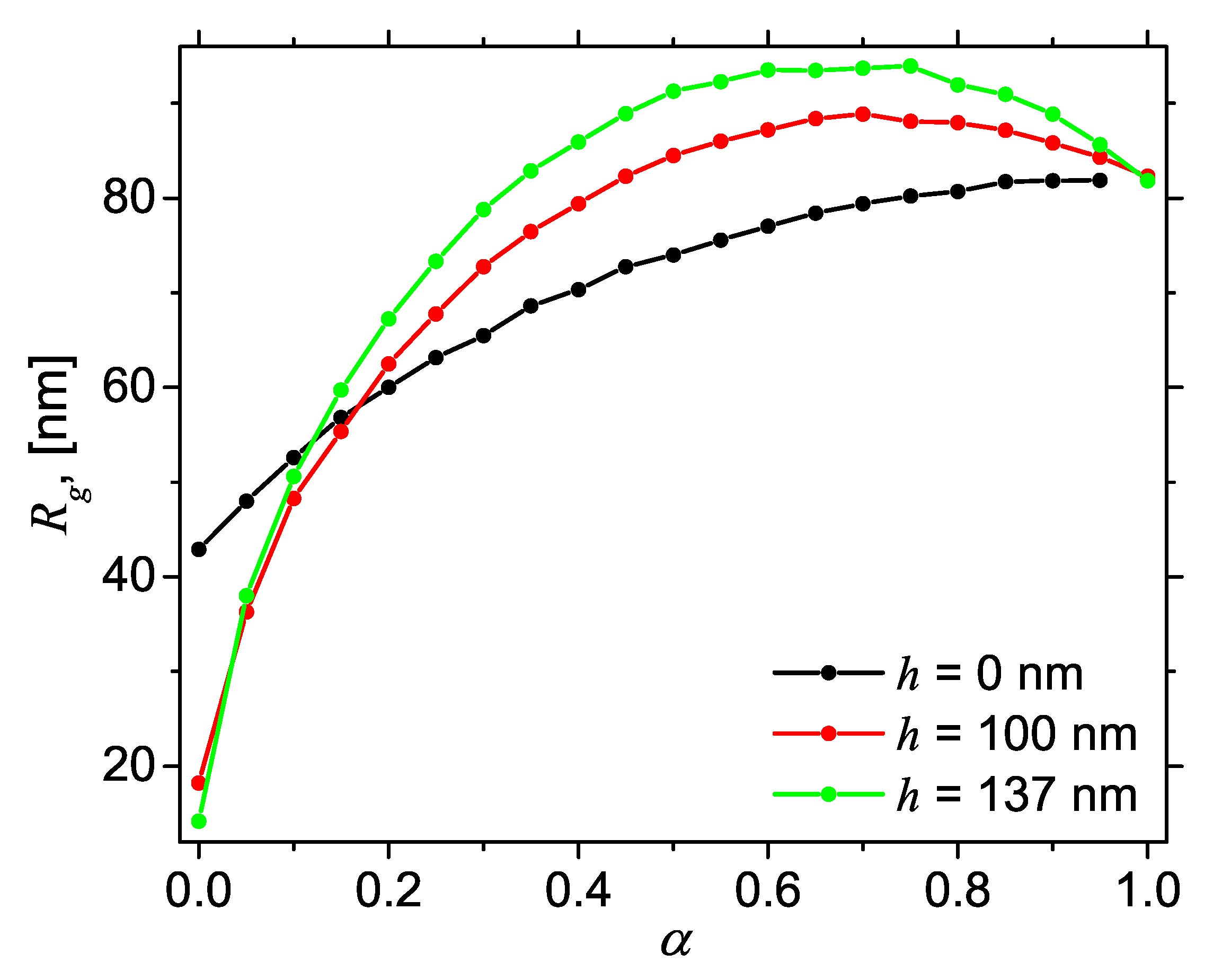
Figure 7 shows the variation of
with the contrast parameter
at the same values of height
h, as in
Figure 4 and
Figure 6. One can distinguish two main types of behavior: when
,
increases asymptotically to a maximum value corresponding to
(black curve), while, for
, the variation of
with
has a downward parabola-like behavior (red and green curves). However, at
, all the curves have a common value, irrespective of the height
h. This property arises since, regardless of the value of
h, when
, we always have a cylinder of diameter
and height
. By using the values
nm and
nm in Equation (
12), one obtains
nm, which is in very good agreement with the numerical value of
given in
Figure 7. This confirms the validity of the proposed approach based on Monte Carlo simulations, to obtain the radius of gyration of AnJPs. Similar results are shown in
Figure A2 for
nm,
nm.
The interplay between geometrical and chemical asymmetries of AnJPs when is manifested through a decrease of at and an increase of the parabola maximum with h. Thus, if one measures vs. for various values of the height h, then one can determine the relative degree of geometrical asymmetry of AnJPs, that is the higher is the value of the more different is the structure compared with a AnJP in which . Similarly, a plot of vs. h at various values of can be used to determine the relative degree of chemical asymmetry.
3.5. Contrast Variation
As shown in Equation (
5), besides the volumes
and
of Regions 2 and Region 1, respectively, the contrast parameter
depends also on the SLD
and
of these regions, as well as on the SLD
of the solvent/matrix in which the AnJPs are embedded. Since this parameter controls the relative contributions of these regions to the total scattering intensity (see Equation (
6)), it leads to a succession of power-law decays with various scattering exponents, as discussed in
Section 3.2.1 and schematically depicted in
Figure 5.
When we are interested in determining the shape, size or the relative arrangement of the different regions composing the AnJPs, then a contrast variation needs to be performed. Generally, for Janus particles consisting from complex, possibly self-similar (fractal) regions, the contrast variation can be applied beyond the Guinier regime. This would also allow distinguishing among various types of structural organization in AnJPs, such as if one region is embedded (immersed) into another one, or if they are non-overlapping [
30]. However, for the AnJPs discussed here, both regions are Euclidean objects, and a contrast variation at
can be performed.
Experimentally, when neutrons are used, the contrast variation can be achieved by preparing a number of several samples which differ in the SLD of each region, as well as in the SLD of the solvent/matrix. Then, the variation of each of these three parameters (
, and
) has its own imprint on the behavior of scattering intensity at
, through Equation (
7). Therefore, in the following, we analyze each of these contributions individually, that is:
Case I: and are fixed, and is variable.
Case II: and are fixed, and is variable.
Case III: and are fixed, and is variable.
Thus, by using the explicit values of
given by Equation (
13), and
in Equation (
5), Equation (
7) can be rewritten as:
Then, the position of the contrast matching point for Case I can be found by taking the derivative with respect to
of Equation (
20), i.e.,
and then equating the last expression with zero. This operation gives the position of the contrast matching point
, as:
Similarly, for Case II, one can find the derivative with respect to
, i.e.,
and the position of the contrast matching point
is:
For Case III, the derivative with respect to
is:
and the position of the contrast matching point
is:
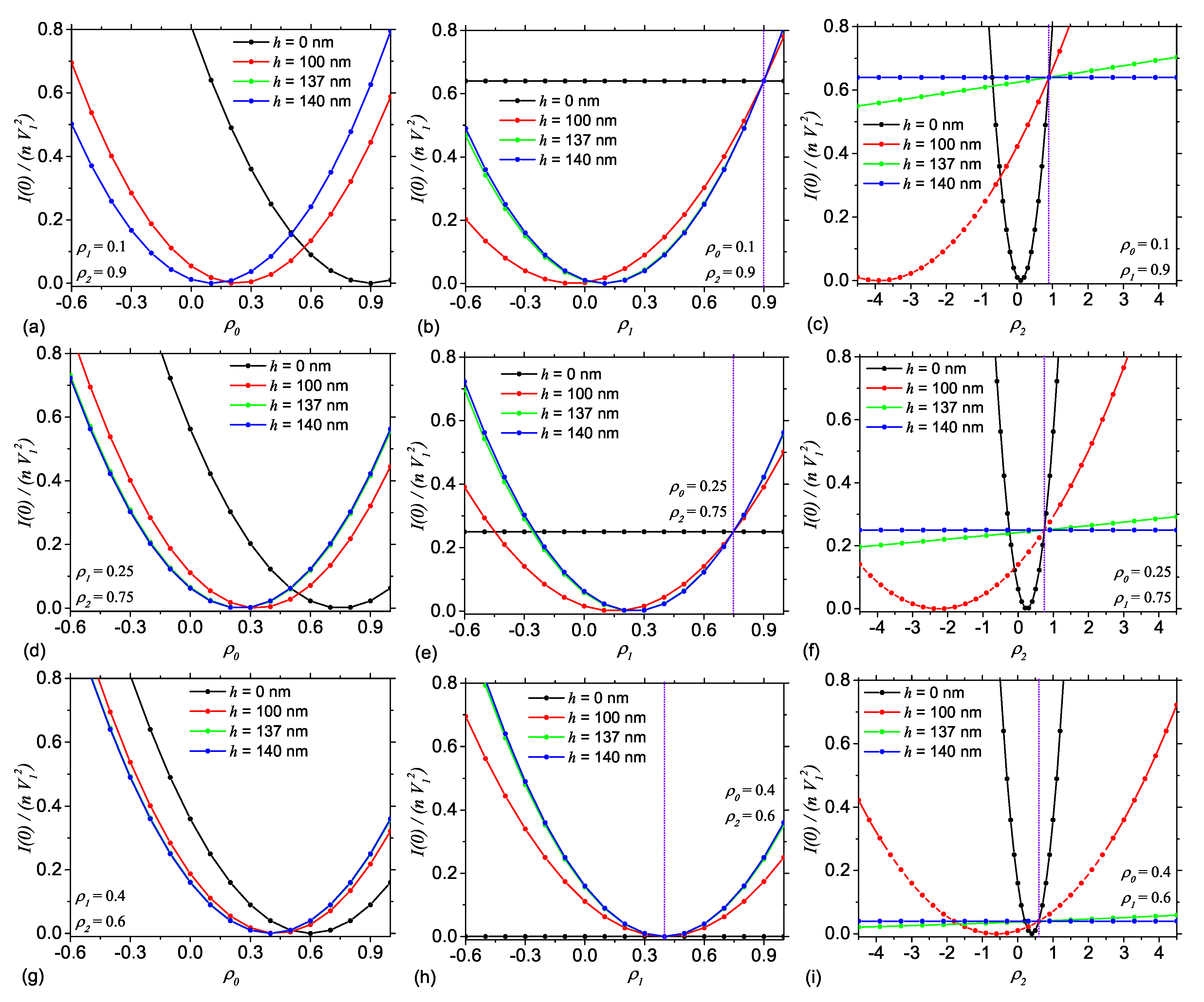
Figure 8a,d,g shows the contrast variation for Case I, with
and
,
and
, and
and
, respectively, for various values of the height
h. In all cases, the variation of
with
have a parabola-like behavior, with minima given by Equation (
22). The common feature is that for each values of the pair
, the minima
satisfy the condition
. These lower and upper limits correspond to
and
, respectively. As the value between
and
decreases, the differences between the positions of the contrast matching points also decrease. In the limiting case when
, we have an AnJP with a single region, and thus the variation of
is independent of the height
h, as expected.
Figure 8b,e,h shows the contrast variation for Case II, with
and
,
and
, and
and
, respectively. Note that, at
, the parabola-like behavior from the previous case is replaced by a straight line (black curve). This is clear from Equation (
24), which has no solution when
. The line intersects the
-axis at
, as indicated by Equation (
20). However, when
the variation of
with
has a parabola-like behavior, with minima
given by Equation (
24). For a given pair of values
, we have
at
. By decreasing the values of
h the minima are shifted to the left, and the parabola opens up, leading to the straight line (black), in the limit
, as discussed above. In addition, when
, all the parabolas reduce to a single one with minimum at
, to which is tangent the straight line corresponding to
(see an approximation in
Figure 8h). The position of the common point is indicated by the vertical violet-dotted line. Such a common point exists for any pair of
values, and the higher the difference between
and
, the point is more shifted to the right (see also vertical lines in
Figure 8b,e). This common points arise when
, that is when AnJP consists from a single region.
Figure 8c,f,i shows the contrast variation for Case III, with
and
,
and
, and
and
, respectively. The overall behavior is similar to the one in Case II, when generally we have a set of parabolas (red, green, and blue curves), while for a limiting value of
h, here at
, we have a straight line (black curve). The minima of the parabolas are given by Equation (
26) and satisfy the condition
. In the limiting case when
, the solvent matches Region 2, and thus at
the position of the contrast matching point is right-most, for a given pair
. By increasing the value of
h, the position of minima are shifted to the left. Note also the presence of a common point to all curves, for a given pair of values
, where the forward scattering intensity is
. Their position on
-axis are indicated by vertical violet dotted lines. As for Case II, these points correspond to AnJPs consisting from a single region.
The above observations illustrate that, in all three cases, contrast variation may be used to obtain the contrast matching points. The parabola describing the overall behavior of
can be further used as basic functions in a more detailed analysis, together with the values of the radii of gyration (see
Figure 7) for a more detailed analysis, to extract additional information such as the relative arrangement of higher and lower density regions within AnJP, with respect to their center of mass, or the deviation of the center of masses of each region of AnJP from the center of mass of the whole AnJP.