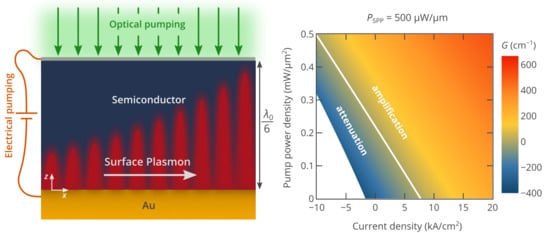
Hybrid Electro-Optical Pumping of Active Plasmonic Nanostructures
Abstract
1. Introduction
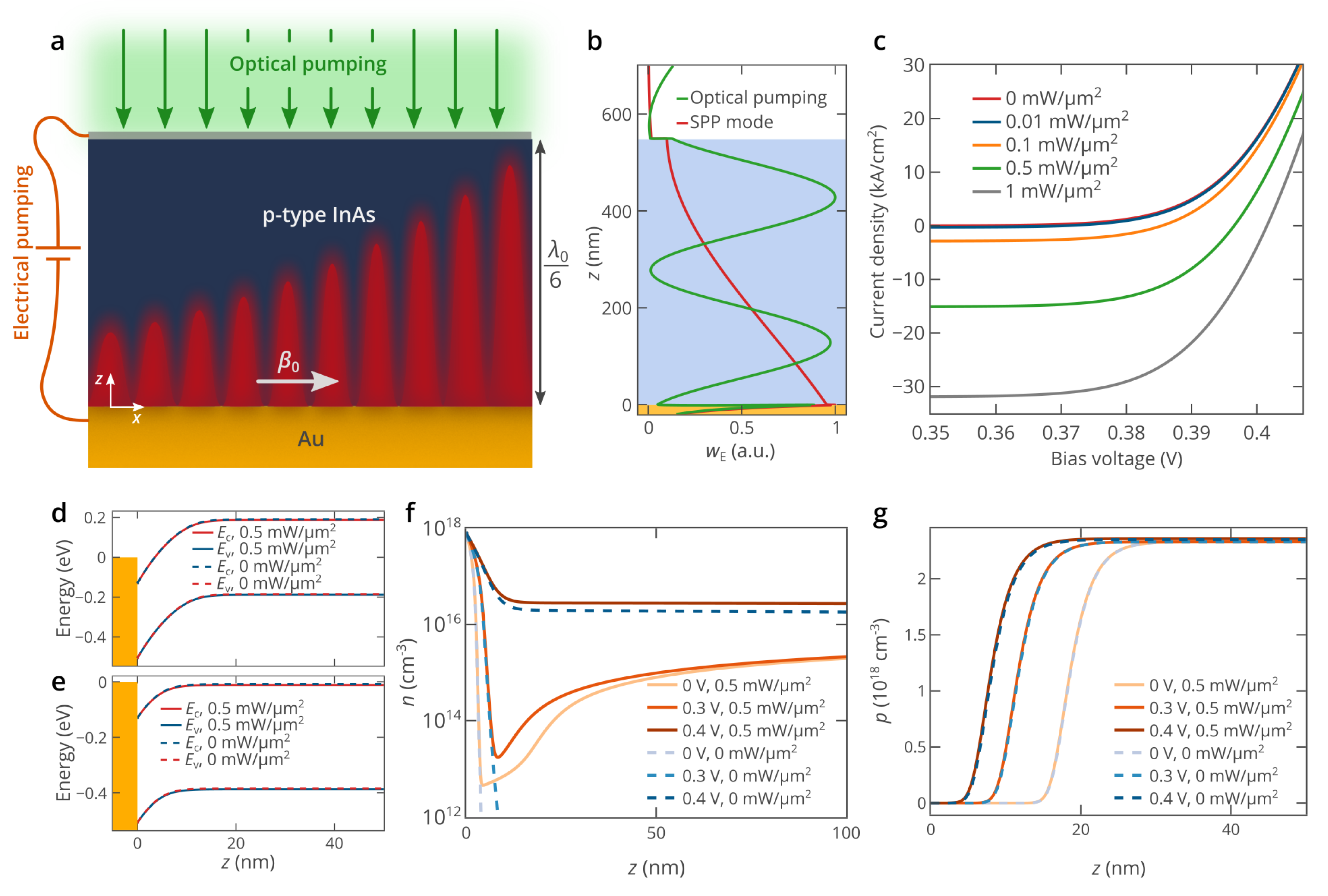
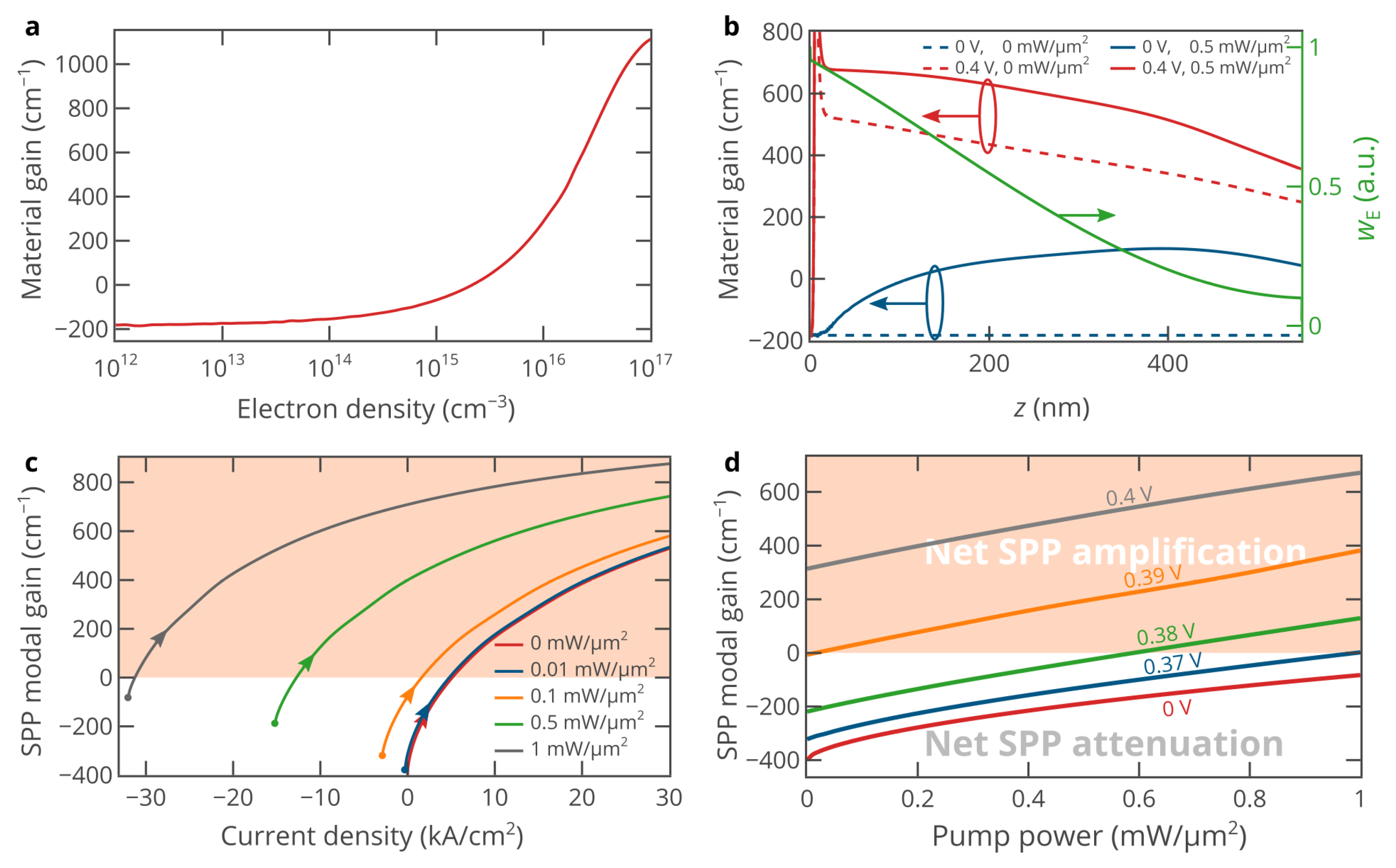
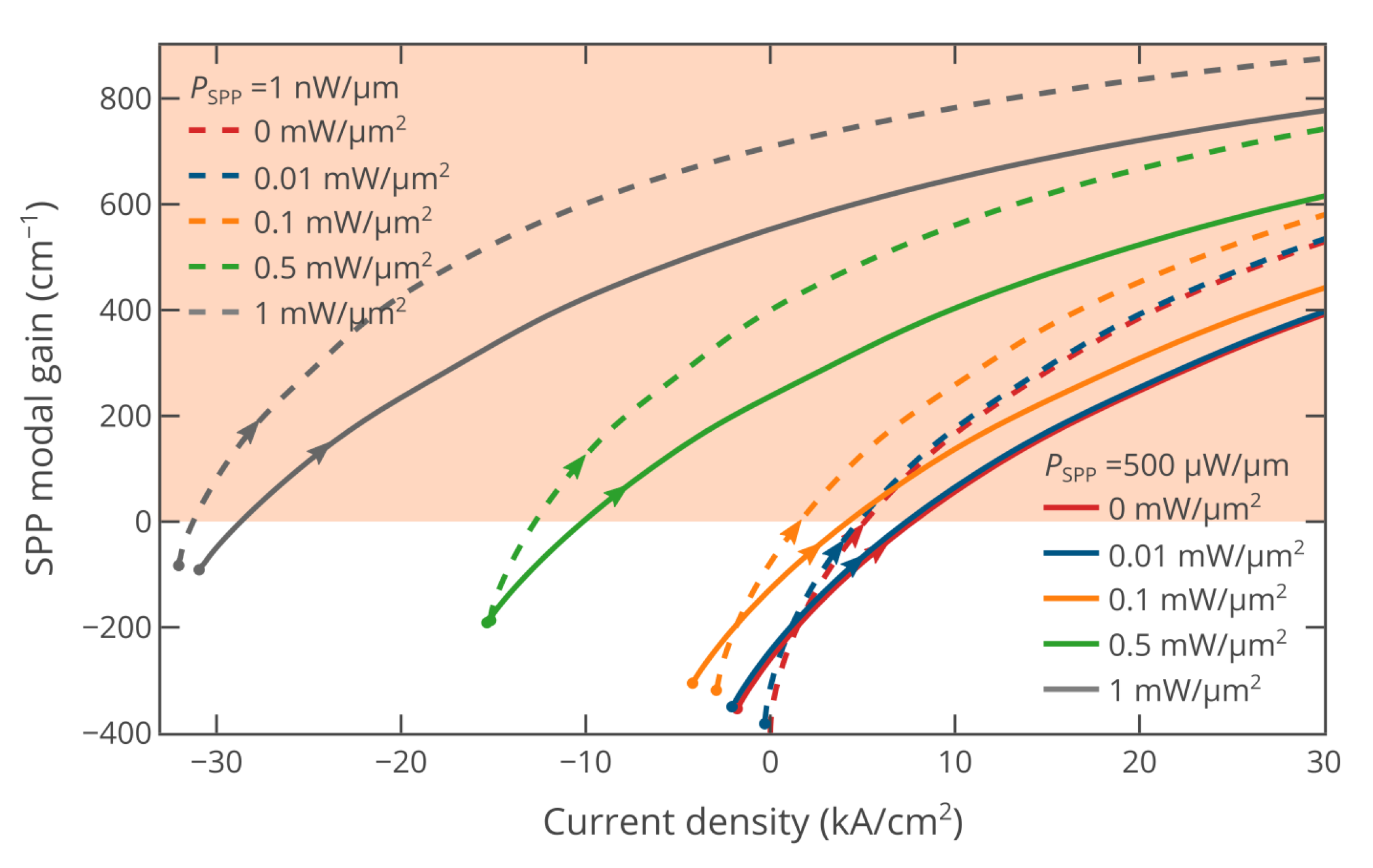
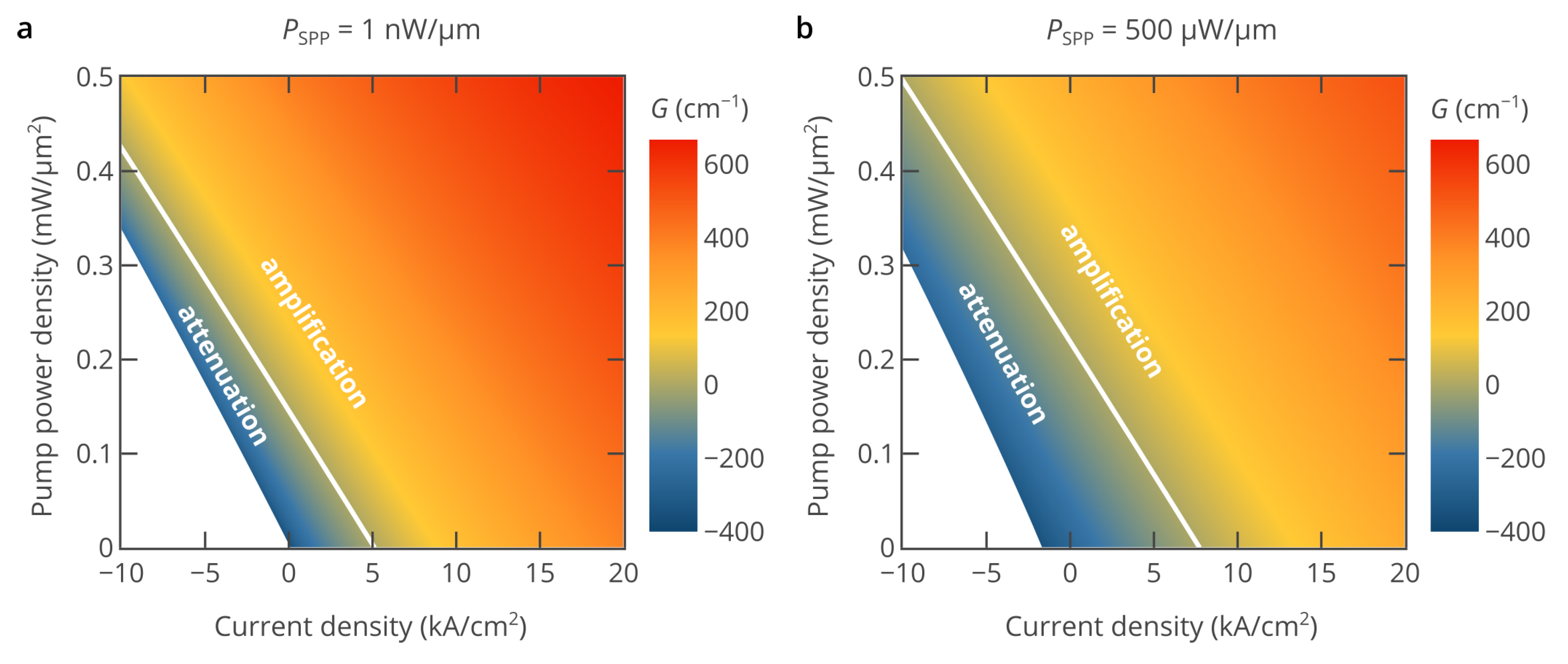
2. Results and Discussion
3. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jiang, N.; Zhuo, X.; Wang, J. Active Plasmonics: Principles, Structures, and Applications. Chem. Rev. 2018, 118, 3054–3099. [Google Scholar] [CrossRef] [PubMed]
- Stockman, M.I.; Kneipp, K.; Bozhevolnyi, S.I.; Saha, S.; Dutta, A.; Ndukaife, J.; Kinsey, N.; Reddy, H.; Guler, U.; Shalaev, V.M.; et al. Roadmap on plasmonics. J. Opt. 2018, 20, 043001. [Google Scholar] [CrossRef]
- Oulton, R.F.; Bartal, G.; Pile, D.F.P.; Zhang, X. Confinement and propagation characteristics of subwavelength plasmonic modes. New J. Phys. 2008, 10, 105018. [Google Scholar] [CrossRef]
- Fang, Y.; Sun, M. Nanoplasmonic waveguides: Towards applications in integrated nanophotonic circuits. Light Sci. Appl. 2015, 4, e294. [Google Scholar] [CrossRef]
- Krasavin, A.V.; Zayats, A.V. Active Nanophotonic Circuitry Based on Dielectric-loaded Plasmonic Waveguides. Adv. Opt. Mater. 2015, 3, 1662–1690. [Google Scholar] [CrossRef]
- McPeak, K.M.; Jayanti, S.V.; Kress, S.J.P.; Meyer, S.; Iotti, S.; Rossinelli, A.; Norris, D.J. Plasmonic Films Can Easily Be Better: Rules and Recipes. ACS Photonics 2015, 2, 326–333. [Google Scholar] [CrossRef]
- Fedyanin, D.Y.; Yakubovsky, D.I.; Kirtaev, R.V.; Volkov, V.S. Ultralow-Loss CMOS Copper Plasmonic Waveguides. Nano Lett. 2016, 16, 362–366. [Google Scholar] [CrossRef]
- Yakubovsky, D.I.; Arsenin, A.V.; Stebunov, Y.V.; Fedyanin, D.Y.; Volkov, V.S. Optical constants and structural properties of thin gold films. Opt. Express 2017, 25, 25574–25587. [Google Scholar] [CrossRef]
- Khurgin, J.B.; Sun, G. In search of the elusive lossless metal. Appl. Phys. Lett. 2010, 96, 181102. [Google Scholar] [CrossRef]
- Yakubovsky, D.I.; Fedyanin, D.Y.; Arsenin, A.V.; Volkov, V.S. Optical constant of thin gold films: Structural morphology determined optical response. AIP Conf. Proc. 2017, 1874, 040057. [Google Scholar]
- Oulton, R.F.; Sorger, V.J.; Genov, D.A.; Pile, D.F.P.; Zhang, X. A hybrid plasmonic waveguide for subwavelength confinement and long-range propagation. Nat. Photonics 2008, 2, 496–500. [Google Scholar] [CrossRef]
- Zenin, V.A.; Choudhury, S.; Saha, S.; Shalaev, V.M.; Boltasseva, A.; Bozhevolnyi, S.I. Hybrid plasmonic waveguides formed by metal coating of dielectric ridges. Opt. Express 2017, 25, 12295–12302. [Google Scholar] [CrossRef]
- Sorger, V.J.; Ye, Z.; Oulton, R.F.; Wang, Y.; Bartal, G.; Yin, X.; Zhang, X. Experimental demonstration of low-loss optical waveguiding at deep sub-wavelength scales. Nat. Commun. 2011, 2, 4674. [Google Scholar] [CrossRef]
- Nezhad, M.; Tetz, K.; Fainman, Y. Gain assisted propagation of surface plasmon polaritons on planar metallic waveguides. Opt. Express 2004, 12, 4072–4079. [Google Scholar] [CrossRef] [PubMed]
- Leosson, K. Optical amplification of surface plasmon polaritons: Review. J. Nanophotonics 2012, 6, 061801. [Google Scholar] [CrossRef][Green Version]
- Sudarkin, A.N.; Demkovic, P.A. Excitation of surface electromagnetic waves on the boundary of a metal with an amplifying medium. Sov. Phys. Tech. Phys. 1989, 34, 764. [Google Scholar]
- Leon, I.D.; De Leon, I.; Berini, P. Amplification of long-range surface plasmons by a dipolar gain medium. Nat. Photonics 2010, 4, 382–387. [Google Scholar] [CrossRef]
- Gather, M.C.; Meerholz, K.; Danz, N.; Leosson, K. Net optical gain in a plasmonic waveguide embedded in a fluorescent polymer. Nat. Photonics 2010, 4, 457–461. [Google Scholar] [CrossRef]
- Oulton, R.F.; Sorger, V.J.; Zentgraf, T.; Ma, R.-M.; Gladden, C.; Dai, L.; Bartal, G.; Zhang, X. Plasmon lasers at deep subwavelength scale. Nature 2009, 461, 629–632. [Google Scholar] [CrossRef]
- Kéna-Cohen, S.; Stavrinou, P.N.; Bradley, D.D.C.; Maier, S.A. Confined surface plasmon-polariton amplifiers. Nano Lett. 2013, 13, 1323–1329. [Google Scholar] [CrossRef][Green Version]
- Fedyanin, D.Y.; Arsenin, A.V. Semiconductor Surface Plasmon Amplifier Based on a Schottky Barrier Diode. AIP Conf. Proc. 2010, 1291, 112–114. [Google Scholar]
- Fedyanin, D.Y.; Arsenin, A.V. Surface plasmon polariton amplification in metal-semiconductor structures. Opt. Express 2011, 19, 12524–12531. [Google Scholar] [CrossRef] [PubMed]
- Hill, M.T.; Marell, M.; Leong, E.S.P.; Smalbrugge, B.; Zhu, Y.; Sun, M.; van Veldhoven, P.J.; Geluk, E.J.; Karouta, F.; Oei, Y.-S.; et al. Lasing in metal-insulator-metal sub-wavelength plasmonic waveguides. Opt. Express 2009, 17, 11107–11112. [Google Scholar] [CrossRef] [PubMed]
- Fedyanin, D.Y.; Krasavin, A.V.; Arsenin, A.V.; Zayats, A.V. Surface plasmon polariton amplification upon electrical injection in highly integrated plasmonic circuits. Nano Lett. 2012, 12, 2459–2463. [Google Scholar] [CrossRef] [PubMed]
- Bergman, D.J.; Stockman, M.I. Surface plasmon amplification by stimulated emission of radiation: Quantum generation of coherent surface plasmons in nanosystems. Phys. Rev. Lett. 2003, 90, 027402. [Google Scholar] [CrossRef]
- Fedyanin, D.Y. Toward an electrically pumped spaser. Opt. Lett. 2012, 37, 404–406. [Google Scholar] [CrossRef]
- Gwo, S.; Shih, C.-K. Semiconductor plasmonic nanolasers: Current status and perspectives. Rep. Prog. Phys. 2016, 79, 086501. [Google Scholar] [CrossRef]
- Ning, C.-Z. Semiconductor nanolasers and the size-energy-efficiency challenge: A review. Adv. Photonics 2019, 1, 1. [Google Scholar] [CrossRef]
- Lee, C.J.; Yeh, H.; Cheng, F.; Su, P.-H.; Her, T.-H.; Chen, Y.-C.; Wang, C.-Y.; Gwo, S.; Bank, S.R.; Shih, C.-K.; et al. Low-Threshold Plasmonic Lasers on a Single-Crystalline Epitaxial Silver Platform at Telecom Wavelength. ACS Photonics 2017, 4, 1431–1439. [Google Scholar] [CrossRef]
- Chou, Y.-H.; Wu, Y.-M.; Hong, K.-B.; Chou, B.-T.; Shih, J.-H.; Chung, Y.-C.; Chen, P.-Y.; Lin, T.-R.; Lin, C.-C.; Lin, S.-D.; et al. High-Operation-Temperature Plasmonic Nanolasers on Single-Crystalline Aluminum. Nano Lett. 2016, 16, 3179–3186. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, G.; Liu, X.; Qian, F.; Li, Y.; Sum, T.C.; Lieber, C.M.; Xiong, Q. A room temperature low-threshold ultraviolet plasmonic nanolaser. Nat. Commun. 2014, 5, 4953. [Google Scholar] [CrossRef] [PubMed]
- Vyshnevyy, A.A.; Fedyanin, D.Y. Self-Heating and Cooling of Active Plasmonic Waveguides. ACS Photonics 2016, 3, 51–57. [Google Scholar] [CrossRef]
- Fedyanin, D.Y. Electrically pumped double-heterostructure surface plasmon polariton amplifier. AIP Conf. Proc. 2012, 1475, 56. [Google Scholar]
- Tiwari, S.; Frank, D.J. Empirical fit to band discontinuities and barrier heights in III–V alloy systems. Appl. Phys. Lett. 1992, 60, 630–632. [Google Scholar] [CrossRef]
- Costantini, D.; Bousseksou, A.; Fevrier, M.; Dagens, B.; Colombelli, R. Loss and Gain Measurements of Tensile-Strained Quantum Well Diode Lasers for Plasmonic Devices at Telecom Wavelengths. IEEE J. Quantum Electron. 2012, 48, 73–78. [Google Scholar] [CrossRef]
- Widmann, M.; Niethammer, M.; Fedyanin, D.Y.; Khramtsov, I.A.; Rendler, T.; Booker, I.D.; Hassan, J.U.; Morioka, N.; Chen, Y.-C.; Ivanov, I.G.; et al. Electrical Charge State Manipulation of Single Silicon Vacancies in a Silicon Carbide Quantum Optoelectronic Device. Nano Lett. 2019, 19, 7173–7180. [Google Scholar] [CrossRef]
- Adachi, S. Optical dispersion relations for GaP, GaAs, GaSb, InP, InAs, InSb, AlxGa1−xAs, and In1−xGaxAsyP1−y. J. Appl. Phys. 1989, 66, 6030. [Google Scholar] [CrossRef]
- Vyshnevyy, A.A.; Fedyanin, D.Y. Spontaneous Emission and Fundamental Limitations on the Signal-to-Noise Ratio in Deep-Subwavelength Plasmonic Waveguide Structures with Gain. Phys. Rev. Appl. 2016, 6, 064024. [Google Scholar] [CrossRef]
- Svintsov, D.A.; Arsenin, A.V.; Fedyanin, D.Y. Full loss compensation in hybrid plasmonic waveguides under electrical pumping. Opt. Express 2015, 23, 19358–19375. [Google Scholar] [CrossRef]
- Aydaraliev, M.; Zotova, N.V.; Karandashov, S.A.; Matveev, B.A.; Stus’, N.M.; Talalakin, G.N. Low-threshold long-wave lasers ( lambda =3.0-3.6 mu m) based on III-V alloys. Semicond. Sci. Technol. 1993, 8, 1575–1580. [Google Scholar] [CrossRef]
- Melngailis, I.; Rediker, R.H. Properties of InAs Lasers. J. Appl. Phys. 1966, 37, 899–911. [Google Scholar] [CrossRef]
- Bhargava, S.; Blank, H.-R.; Narayanamurti, V.; Kroemer, H. Fermi-level pinning position at the Au–InAs interface determined using ballistic electron emission microscopy. Appl. Phys. Lett. 1997, 70, 759–761. [Google Scholar] [CrossRef]
- Visser, T.D.; Blok, H.; Demeulenaere, B.; Lenstra, D. Confinement factors and gain in optical amplifiers. IEEE J. Quantum Electron. 1997, 33, 1763–1766. [Google Scholar] [CrossRef]
- Casey, H.C., Jr.; Stern, F. Concentration-dependent absorption and spontaneous emission of heavily doped GaAs. J. Appl. Phys. 1976, 47, 631–643. [Google Scholar] [CrossRef]
- Miller, D.A.B. Rationale and challenges for optical interconnects to electronic chips. Proc. IEEE 2000, 88, 728–749. [Google Scholar] [CrossRef]
- Manipatruni, S.; Lipson, M.; Young, I.A. Device Scaling Considerations for Nanophotonic CMOS Global Interconnects. IEEE J. Sel. Top. Quantum Electron. 2013, 19, 8200109. [Google Scholar] [CrossRef]
- Vyshnevyy, A.A.; Fedyanin, D.Y. Noise reduction in plasmonic amplifiers. Appl. Phys. Express 2018, 11, 062002. [Google Scholar] [CrossRef]
- Humar, M.; Yun, S.H. Intracellular microlasers. Nat. Photonics 2015, 9, 572–576. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vyshnevyy, A.A.; Fedyanin, D.Y. Hybrid Electro-Optical Pumping of Active Plasmonic Nanostructures. Nanomaterials 2020, 10, 856. https://doi.org/10.3390/nano10050856
Vyshnevyy AA, Fedyanin DY. Hybrid Electro-Optical Pumping of Active Plasmonic Nanostructures. Nanomaterials. 2020; 10(5):856. https://doi.org/10.3390/nano10050856
Chicago/Turabian StyleVyshnevyy, Andrey A., and Dmitry Yu. Fedyanin. 2020. "Hybrid Electro-Optical Pumping of Active Plasmonic Nanostructures" Nanomaterials 10, no. 5: 856. https://doi.org/10.3390/nano10050856
APA StyleVyshnevyy, A. A., & Fedyanin, D. Y. (2020). Hybrid Electro-Optical Pumping of Active Plasmonic Nanostructures. Nanomaterials, 10(5), 856. https://doi.org/10.3390/nano10050856