2.1. Specular Reflection
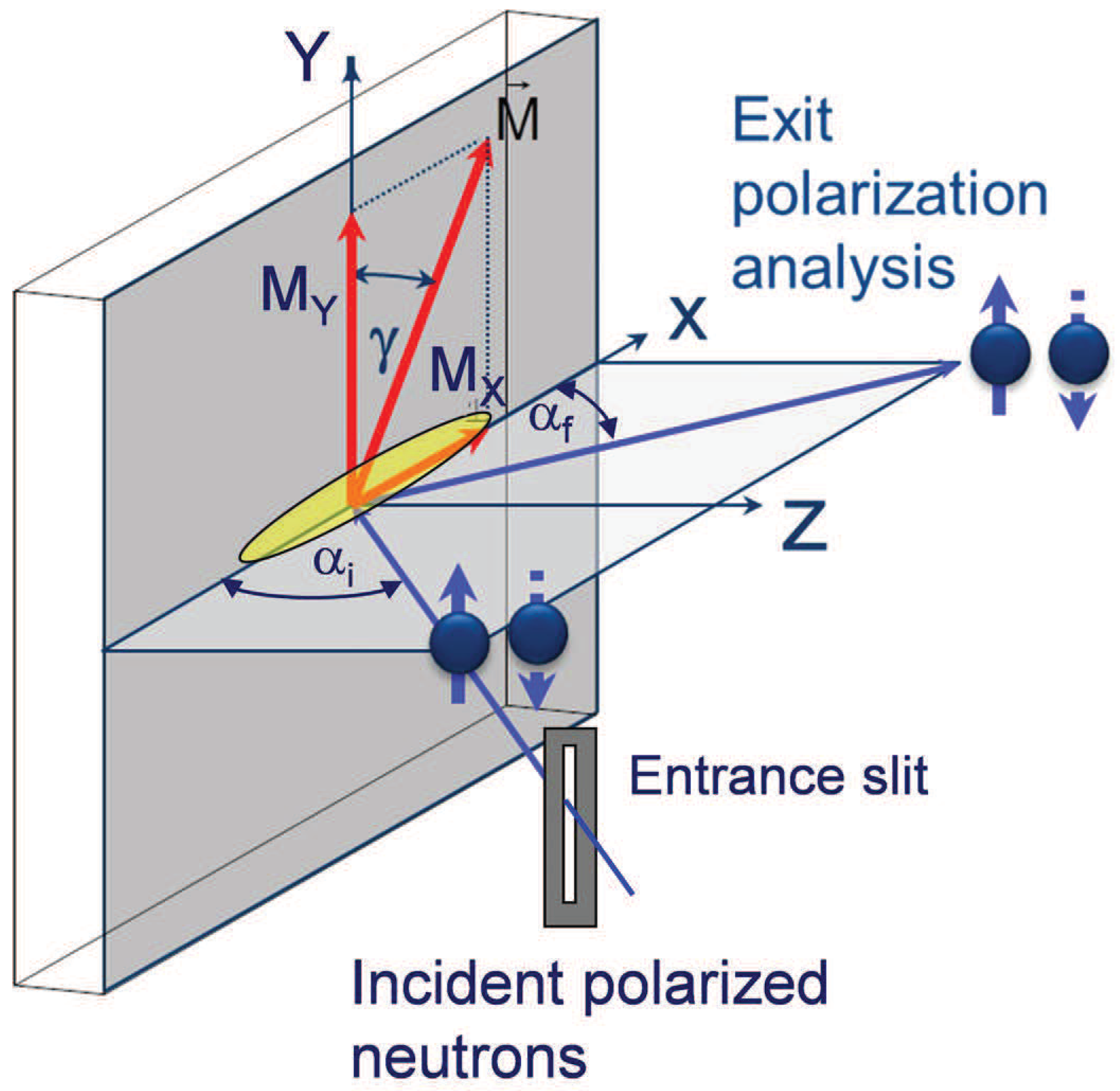
In the most common experimental geometry shown in
Figure 1, the polarization vector of the incident neutron beam is fixed along with, or opposite to the a guide field
parallel to the
Y-direction and perpendicular to the
-scattering plane. Hence the guiding field serves as the quantization axis for the neutron spin whose projection onto this axis may either remain unchanged, or flip during the reflection process. The flat sample is assumed to be parallel to the
-plane with the surface normal parallel to the
Z-direction.
With this set-up, polarized neutron reflectometry allows to determine four specular reflectivities
as a function of the scattering vector
Q by flipping the direction of the polarization of the incident beam and by analyzing the polarization of the reflected beam. Here
Q is the modulus of the scattering vector
defined by
, where
is the neutron wavelength and
is the glancing incident (exit) angle of the neutron beam. In case of specular reflectivity,
is oriented parallel to the film normal or perpendicular to the film plane. In general,
is the Fourier transform of the respective nuclear and magnetic scattering length density profiles
and
in the
Z-direction, and
N is the nuclear number density. For a homogeneously magnetized sample with magnetization vector tilted on the angle
with respect to the
Y-axis and assuming ideal neutron polarization, the non-spin-flip (NSF) reflectivities are defined by the equations [
7]:
while the spin-flip (SF) reflectivities are written as:
Here
are the complex reflection amplitudes determined by the sum or the difference of nuclear and magnetic scattering length densities (SLDs):
, where
is the coherent nuclear scattering length, and
is an effective magnetic scattering length (mSLD). The latter is proportional to the magnetic induction
B [
16]:
where the constant
C is expressed by
Here,
is the neutron mass,
is the neutron magnetic moment, where
= 1.913 is the gyromagnetic ratio of neutrons and
is the nuclear magneton. The Equation (
3) does not depend on the orientation of the sample magnetization vector
with respect to e.g., the direction of the neutron beam polarization.
In contrast, the reflectivities in Equations (
1) and (
2) depend on the angle
between the incident polarization vector collinear with the
Y-axis and the sample magnetization vector
. More specifically, the NSF reflectivities are determined by the projection
of the unit vector
onto the
Y-axis, while the SF reflectivities are due to the component
orthogonal to the
Y-axis.
From Equation (
1) it follows that NSF reflectivities,
, are degenerated under the following conditions: (1) the sample is non-magnetic (
= 0); (2) the sample is totally demagnetized so that its mean magnetization
; (3) the magnetization vector is oriented parallel to the
X-axis (
); (4) the magnetization vector is oriented parallel to the
Z-axis (perpendicular anisotropy). In the latter case, the magnetic induction does not cause any reflection contrast at the surface of homogeneously magnetized film, and therefore PNR is not sensitive to the magnetization. If, alternatively, the magnetization vector
and has a component
collinear with the
Y axis, then
. In contrast, the SF-reflectivities are always equal to each other:
=
. The case
is discussed further below.
In accordance with Equation (
1), the difference of the NSF reflectivities is:
while due to Equation (
2) the SF reflectivities are proportional to
with the proportionality coefficient
. Therefore, only the absolute value, but not the sign of the angle
can be determined. Hence, with 1D polarization analysis it is impossible to determine the sense of the homogeneous magnetization rotation. This is usually not a problem when, for example, the film magnetization is tilted under the action of a magnetic field applied at an angle with respect to the uniaxial, or unidirectional anisotropy axis. On the other hand, homogeneous magnetization rotation is not always a unique mechanism of the magnetization evolution under the action of an external field. Often magnetization rotation competes with domain formation, which may become more favorable at certain field strengths and directions. These two scenarios of magnetization reversal processes can well be discriminated with PNR methods, being one of the main motivations for using PNR as a powerful analytical tool to analyze magnetism in nanostructures.
In case of domains, Equations (
1)–(
5) are also valid after averaging over the sample surface. Such averaging is easy to perform if the domains are sufficiently large so that each of them comprise a number of coherence ellipsoids. We call such domains “large”, in contrast to “small” domains, which fit into one single coherence ellipsoid. Coherence ellipsoids are discussed in the next
Section 2.2. Thus, the scattering events from large domains do not interfere. And therefore, the procedure of incoherent averaging over all domains is just reduced to the substitution of
and
by their mean values
and
, respectively, averaged over angles
between magnetization directions in domains and external field. The subscript
indicates that the averaging is performed incoherently. This averaging can easily be accomplished because the absolute values of magnetization in each of the domains is, by definition, the same and equal to that of the saturation magnetization.
Taking into account that
one can also introduce the dispersion:
which, together with the expectation value
quantifies basic statistical properties of magnetization distribution over an ensemble of domains. Indeed, in a single domain state,
is always zero at any magnetization orientation determined by the parameter
. If, alternatively, the sample is totally demagnetized via a set of
domains so that
, then
. In general a multidomain state is characterized by
and
. For domain magnetizations equally distributed over all in-plane directions, the dispersion
, while
. Note that both
and
are observables that can be gained from fitting the PNR data. Hence, the dispersion
yielding information on the domain state of the sample is a most instructive quantity to be easily extracted from PNR measurements.
It is also important to note that the averaging procedure over large domains does not affect the reflection amplitudes
, which according to Equations (
1)–(
5) are determined by the SLDs
. Here the magnetic SLD
is proportional to the saturation magnetization, in accordance with Equation (
3). Therefore, the location of the critical edges of total reflection
as well as the reflection amplitudes are
independent of the magnetization direction, as is illustrated in
Figure 2. The locations of the critical edges
are marked in the top panels of
Figure 2 and
Figure 3.
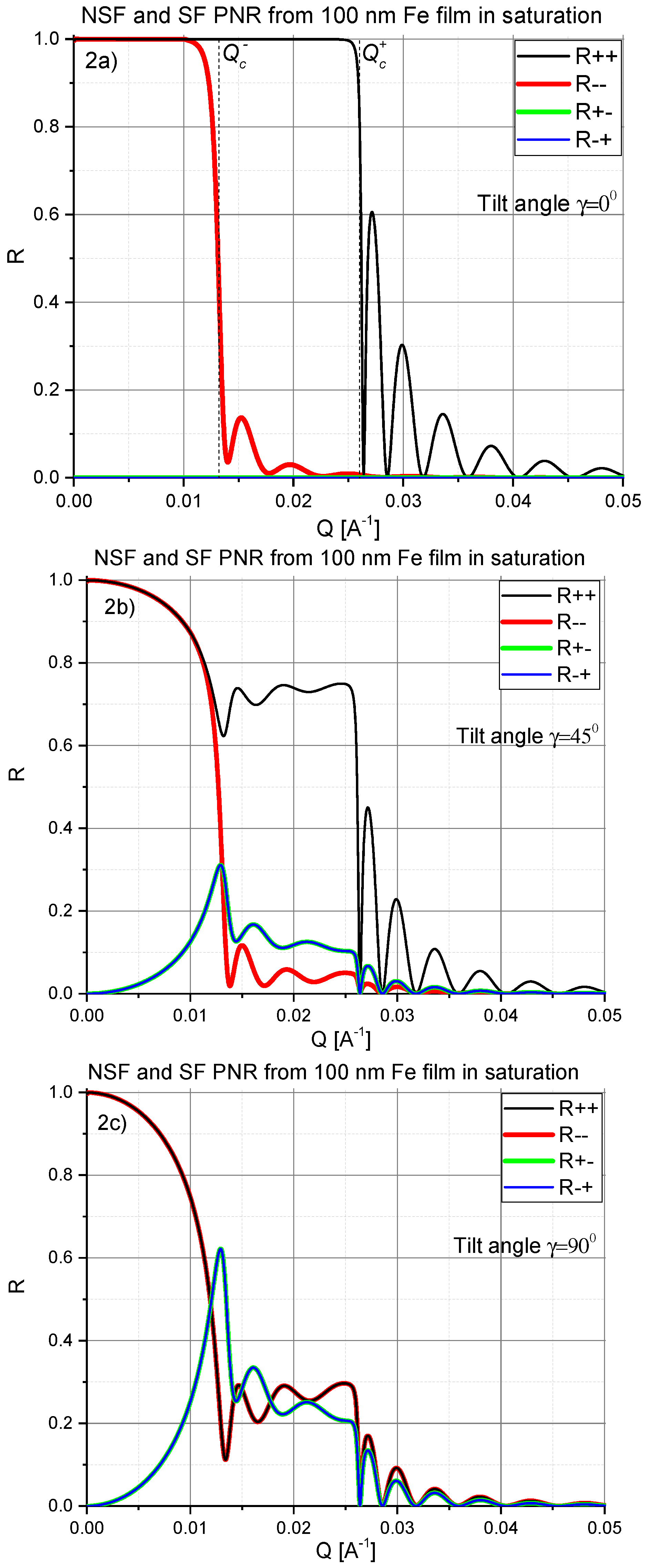
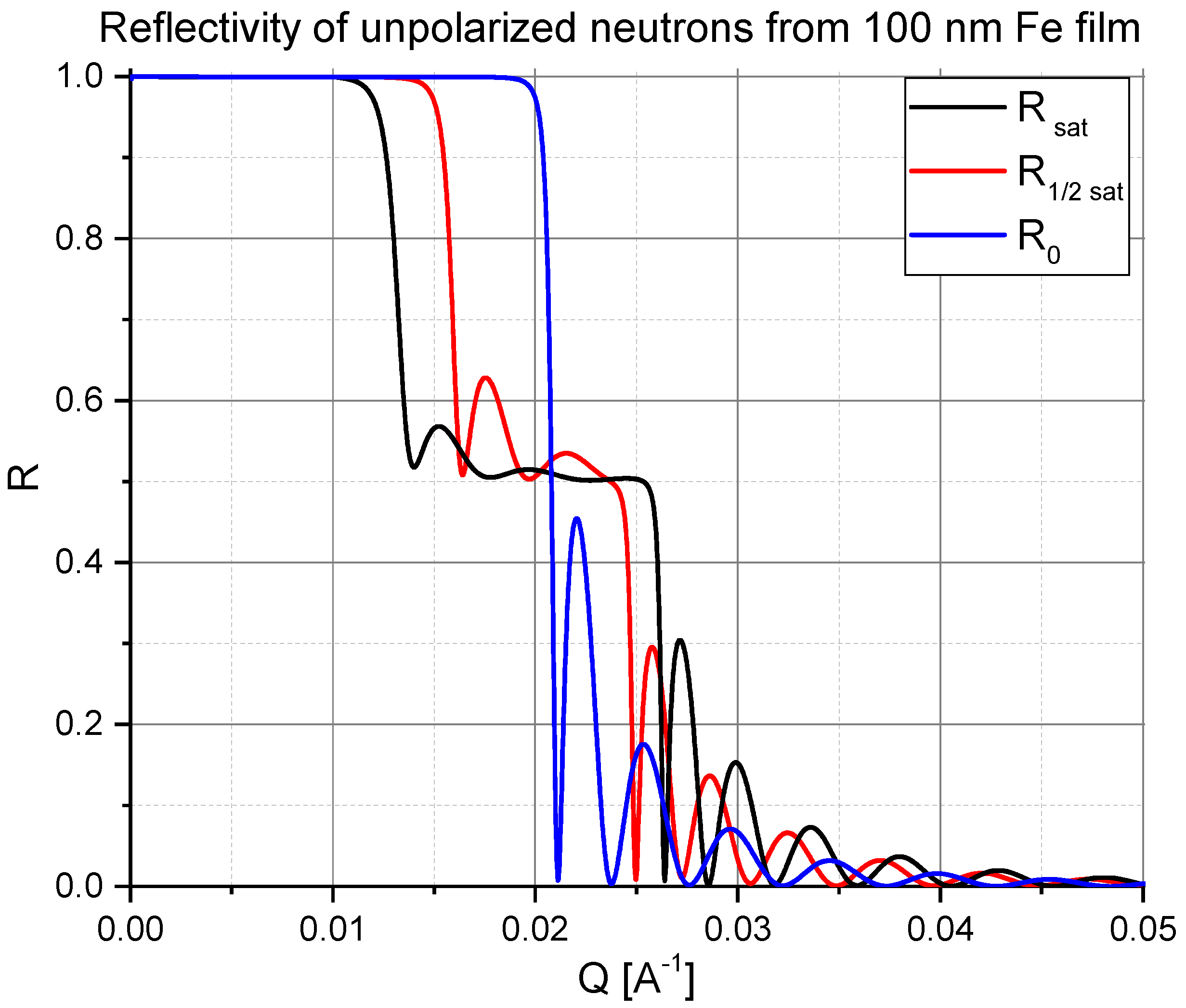
To exemplify our discussion so far, in
Figure 2, a set of reflectivity curves
,
and
are calculated for a 100 nm thick iron film deposited onto a silicon substrate and for magnetization vector orientations: (a) parallel to the axis
Y, (b) tilted to the angle
and (c) to the angle
with respect to the
Y axis. All reflectivities are shown on a linear scale for better visibility of the behavior close to the critical edges, instead of the more common logarithmic scale.
In
Figure 2a one can readily recognize plateaus of totally reflected intensity for each of NSF reflectivity curves, so that
steeply decreases at
, while
abruptly drops down when
, hence indicating positions of corresponding critical reflection edges
. The width of the plateau, or more precisely the difference
is proportional to the saturation magnetization
, according to Equations (
3) and (
7).
Figure 2b,c show that total NSF reflection (
= 1) does not exist at
if the angle between the magnetization direction and the
Y-axis
. However, the positions of the critical edges
, determined by steep descent in reflectivity curves, are
totally independent of the angle
, although the intensity distribution between different NSF and SF reflection channels substantially changes with an angle
. Note, that the position
in
Figure 2b,c is also confirmed by the sharp maximum in SF reflectivities.
If, on the other hand, the magnetic domain sizes turn out to be much smaller than the coherence volume and the latter comprises a number of domains, then two prominent effects emerge. The first and the most distinct one is off-specular scattering (OSS) [
17], which allows to measure e.g., the domain size and will be discussed later. The second effect is a reduction of the mSLD due to the destructive interference of neutron waves scattered from different domains in directions of specular reflection and transmission. Such a reduction is accounted for via replacing the mSLD in Equation (
3) by its mean value. This averaging within a coherence volume is indicated by a overline bar. The equation
then links the mean SLD
and mean magnetization
averaged over the coherence volume. Such averaging can be easily performed in case that the domain magnetization is tilted at angles
to the left or to the right with respect to the direction of the mean magnetization vector
of the coherence volume. Then the cartesian projections of this vector are:
and
. Taking into account that the direction of the vector
is fixed by the condition
, one can conclude that
.
For domains smaller than the coherence volume, the reduction of the magnetic SLD also affects the positions of the critical edges
for total reflections, in contrast to the case of large domains discussed before. Therefore, in Equation (
7) the mSLD
has to be substituted for its mean value
. Consequently, the NSF and SF reflectivities, determined by their mean reflection amplitudes
, depend on the mean mSLD
which, in turn, may also depend on the applied field.
In neutron reflectometry the coherence area, which is the intersectional area of the coherence volume with the sample surface, usually covers only a very small fraction of the sample surface illuminated by the neutron beam, as illustrated in
Figure 1. Therefore, the measured reflection is the result of incoherent averaging over a huge number of coherence ellipsoids. This additional averaging is trivial, as long as the mean magnetization vector
is the same for each coherence ellipsoid and directed along with external field parallel to the polarization axis. Then, instead of Equations (
1) and (
2), one has:
If the vector
, being identical for each of coherence volumes, is not, however, parallel to
Y-axis, but tilted by the angle
with respect to the neutron polarization direction, then NSF and SF reflectivities are determined by the same set of Equations (
1) and (
2) with reflection amplitudes
replaced by their mean values
.
When, alternatively, the angle
is not identical for each coherence ellipsoid varying over distances greater than the coherence length, then Equations (
1) and (
2) NSF and SF reflectivities should be additionally averaged over the angle
incoherently. The result of such averaging of NSF reflectivities can be represented by the sums of two terms:
in which the first terms,
describe reflection of polarized neutrons without analysis of final spin states, while the second terms,
correspond to the SF reflection coefficients.
The PNR mode discussed so far is referred to as full one-dimensional (1D) analysis of the neutron polarization, which yields the most complete information for flat samples with in-plane magnetization. In the reduced mode of PNR, the incident neutron beam can be polarized but polarization analysis of the reflected beam is not available. Then the reflected beam is a sum of both contributions NSF and SF reflectivity and therefore only two reflectivities,
and
, can be determined and described by Equation (
10), while any information related with SF reflection described by Equation (
11) is missing.
For the trivial case of a homogeneously magnetized sample in a single domain state, both modes of PNR are equivalent and yield the same information as both contain the same set of parameters. In either case, the main information to be extracted is the SLDs , and the magnetization tilt angle . However, a homogeneous sample magnetization is rarely a subject of interest for PNR studies, as saturation magnetization and its tilt angle can and should be measured with easier available laboratory magnetometers. Vibrating sample magnetometer (VSM) and SQUID measures the net magnetization projection onto the field direction and are not sensitive to its distribution over the sample surface. On the other hand, PNR carries additional valuable information on domain dimensions and domain dispersion scaled with the neutron coherence range.
Even in the reduced mode of PNR, one may clearly discriminate between a magnetization that is averaged over small domains and a magnetization averaged over dimensions larger than the coherence length. In the first case, the positions of the critical edges for total reflection are affected, while in the second case the critical edges are unaffected while the intensities in the plateau region are different for both spin components.
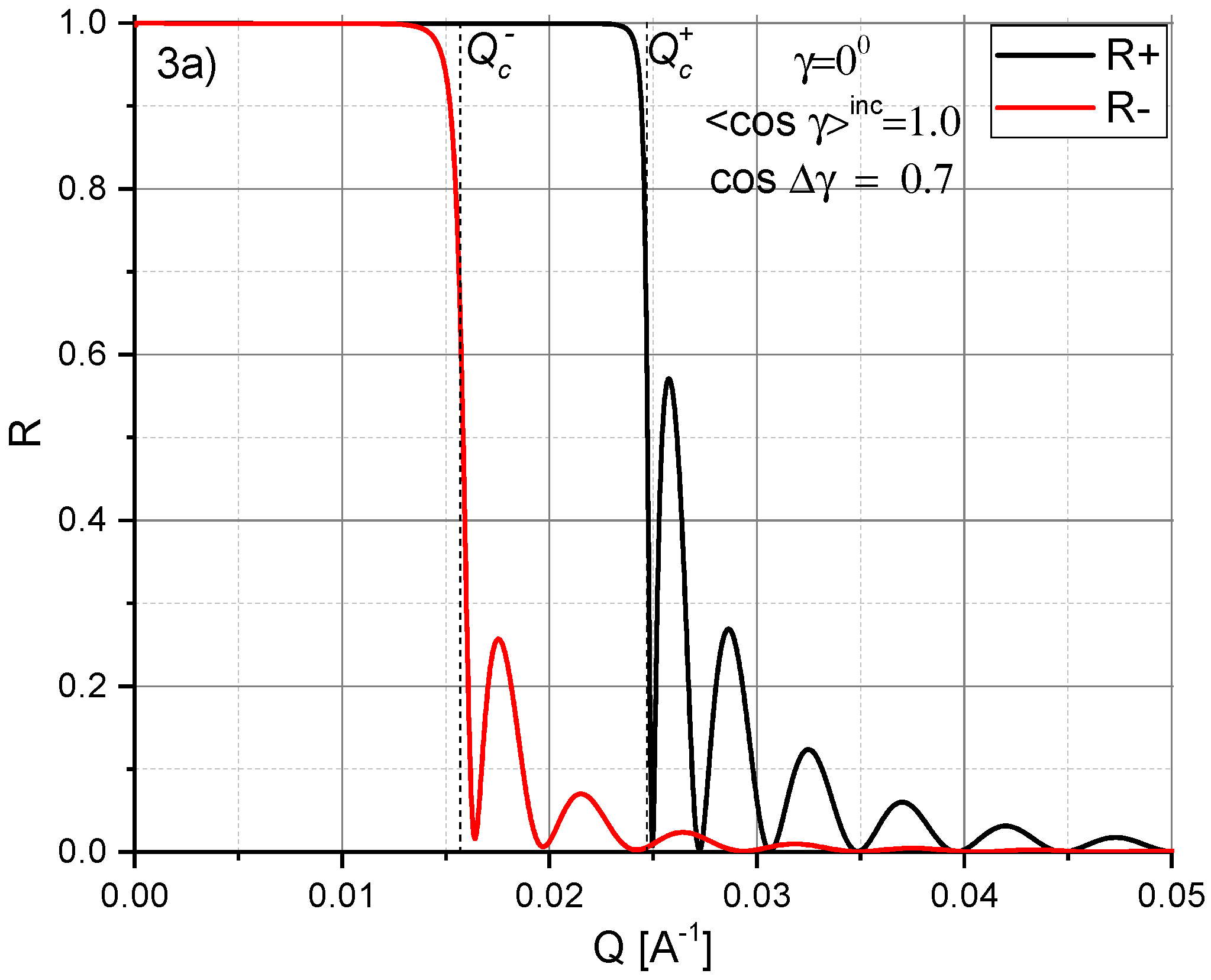
For illustrating the reduced reflectivity mode, we have calculated reflectivity curves in
Figure 3 for the same 100 nm thick iron film as shown in
Figure 2 but without polarization analysis of the reflected neutrons, and for different magnetization conditions, as explained in the following. In
Figure 3a we assume that the iron film is partially demagnetized, so that the mean magnetization parallel to the Y-axis (
,
= 1) is
. The respective reflectivities
(black solid line) and
(red solid line) are similar to those shown in
Figure 2a. However, the difference
-
is reduced because of the decreased mean magnetization
.
In
Figure 3b is similar to
Figure 3a but with the mean magnetization
tilted by the angle
. Again, the difference between
and
is reduced in comparison to the one in
Figure 2b. Furthermore, the sharp maximum seen in
Figure 2b at
is now incorporated in the reflectivity
.
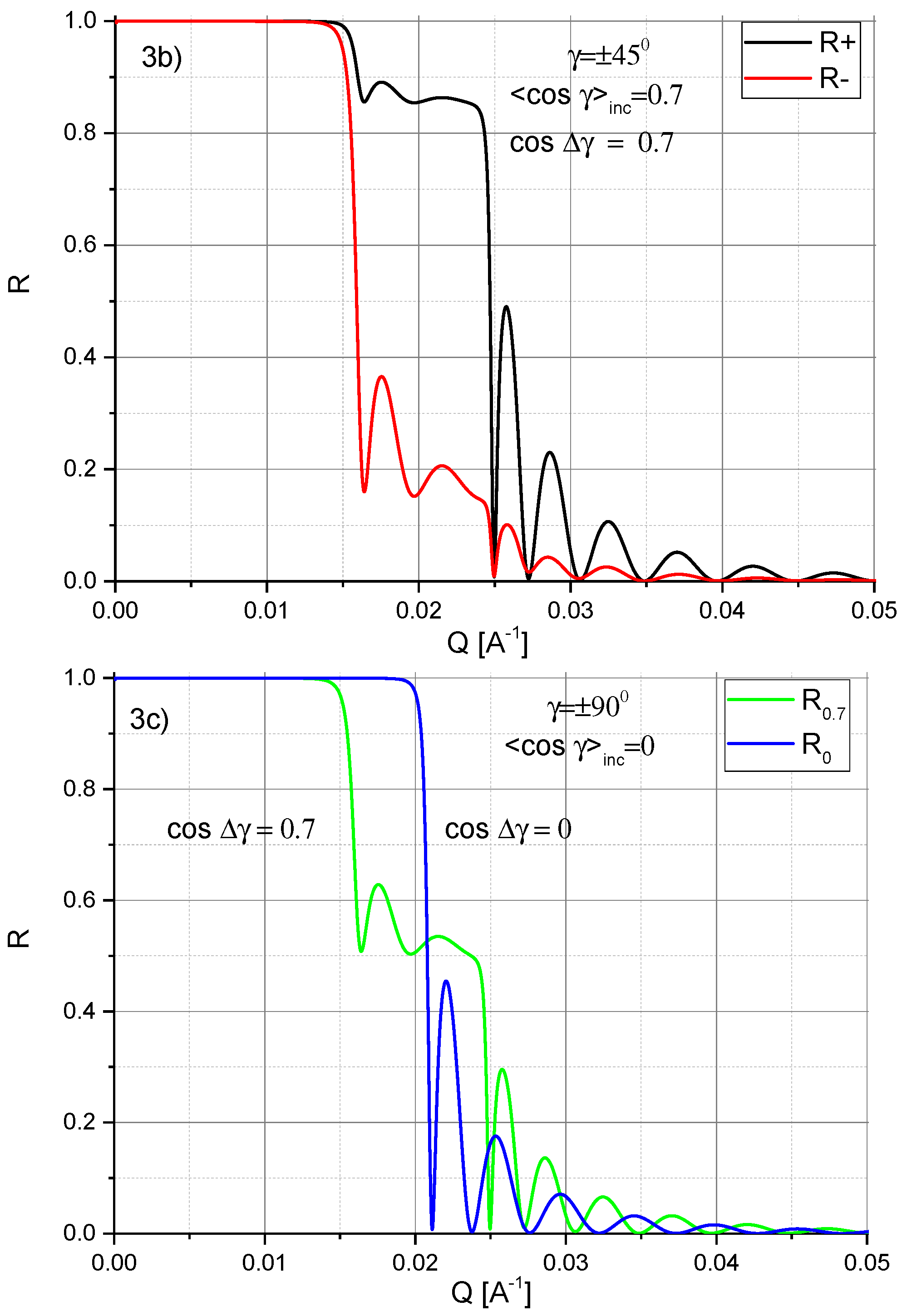
Figure 3c illustrates two cases. The green line shows the reflectivity for a homogeneous magnetization
, tilted by
. The corresponding reflectivities
are merged, but the steep drops of reflected intensity at
and a further drop at
are clear indications for a mean magnetization that is tilted by
. The blue line shows the reflectivity assuming total demagnetization averaged over small domains. Therefore, a tilt of a finite magnetization can clearly be distinguished from a complete demagnetization even without polarization analysis.
Even
unpolarized neutron reflectometry is able to measure the mean magnetization averaged over small domains delivering information that is hardly accessible with bulk magnetometry, and different of that provided either by magneto-optic Kerr effect (MOKE), or Lorentz microscopy and magnetic force microscopy (MFM). Indeed, for an unpolarized neutron beam the reflection coefficient
is described by the mean reflectivity:
averaged over neutron spins states. The results of the spin averaging is illustrated in
Figure 4 where reflectivity curves are plotted for three values of the mean magnetization:
,
and
. For this simulation, the orientation of the mean magnetization does not matter and cannot be resolved. But the steep drop of the reflected intensity to a plateau region and a second drop before reaching the Kiessig fringes unambiguously indicates that the sample exhibits a finite magnetization. Moreover, the finite magnetization is proportional to the width of the plateau region.
As already mentioned, using unpolarized neutron reflectivity we cannot determine the magnetization tilt angle . Strictly speaking, the tilt angle can not be uniquely determined with the reduced mode of PNR since it is sensitive to only the projection of magnetization onto the Y-axis characterized by the parameter , but information on the X-projections is missing. Then one cannot distinguish between random distribution of domain magnetization around some single direction from bi-modal distribution characterized by two alternative magnetization directions. This is only possible with full 1D PNR. Therefore aiming for a full polarization analysis is preferable, provided the experimental conditions allow to do so.
It is worth mentioning that PNR is usually considered as a unique method to be applied to record magnetization depth profiles in e.g., multilayers. This is of particular interest in case of a complex noncollinear depth distribution of a 3D magnetization vector. Despite of appreciable progress in this direction, currently, only 1D polarization analysis is experimentally established, but obviously not sufficient to reliably recover depth profiles of all three components of the magnetization vector. Here we do not discuss advantages of the vector (3D, spherical, etc.) polarization analysis techniques and just mention that theoretical tools for description of such experiments are available [
18].
For a full treatment of the theory of neutron reflectometry we refer to the reviews listed in Refs. [
7,
16,
19]. In short, PNR from thin magnetic films in saturation parallel to the
Y-direction shows three salient features, as illustrated in
Figure 2:
A flat intensity plateau due to total reflection for wave-vectors
, where
is the modulus of the scattering vector,
are the glancing angles with
for specular reflection, and
are the critical wave numbers for total reflection defined by Equation (
7).
If the sample is homogeneously magnetized or decomposed into a set of large magnetic domains then the critical edges, which separate the total reflection region from the rest of reflectivity, are distinctly different for up and down polarized neutrons. The difference being proportional to the saturation magnetization is independent of the angle between magnetization direction and Y-axis. In contrast, the angle determines the reflected intensity distribution between different NSF and SF reflection channels.
In case of domains smaller than the coherence area the difference between and is proportional to the mean magnetization averaged over small domains.
For , oscillatory Kiessig fringes occur, the period of which at is inversely proportional to the film thickness, while the reflected intensity drops according to .
In what follows, we will focus on magnetic thin films broken down into periodic stripe arrays in the lateral direction. But before going into further details, the concept of the coherence volume for neutron reflectivity and its application to stripe arrays will be emphasized, which is essential for interpreting experimental results of patterned samples.
2.3. Stripe Array with Parallel and Perpendicular Orientation
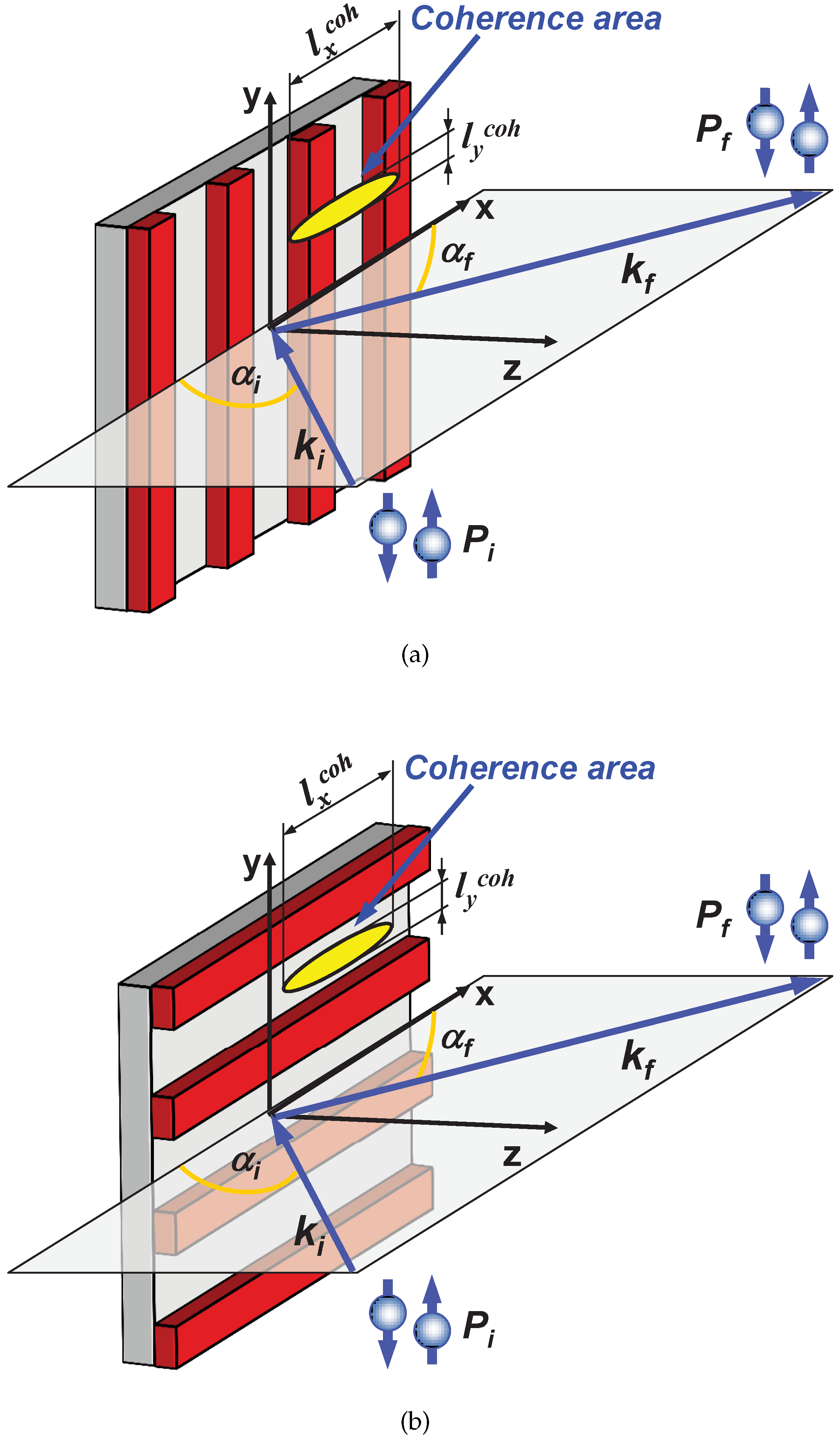
For orientation of the micro-stripes perpendicular to the scattering plane, as depicted in
Figure 5a, the large extension of the coherence volume
covers a number of stripes. This is a prerequisite for coherent enhancement of scattering amplitudes whenever the Bragg equation
is satisfied, where the integer
n numerates the order of Bragg reflection in the lateral direction, and
d is the stripe array period of a few micrometers.
At a given shallow incident angle
, Bragg scattering is excited when the shallow scattering angle
, where
with integer
. Alternatively, Bragg conditions are satisfied when
, where
with
. For
these equations merge with Snell’s law
for specular reflection, the amplitude of which is determined by the mean SLD averaged over the coherence ellipsoid. The Bragg reflections and the diffuse scattering observed at
is referred to as off-specular scattering (OSS). The Bragg reflections are generated by periodic deviations
of SLD from its mean value
, while the diffuse scattering occurs due to random SLD deviations.
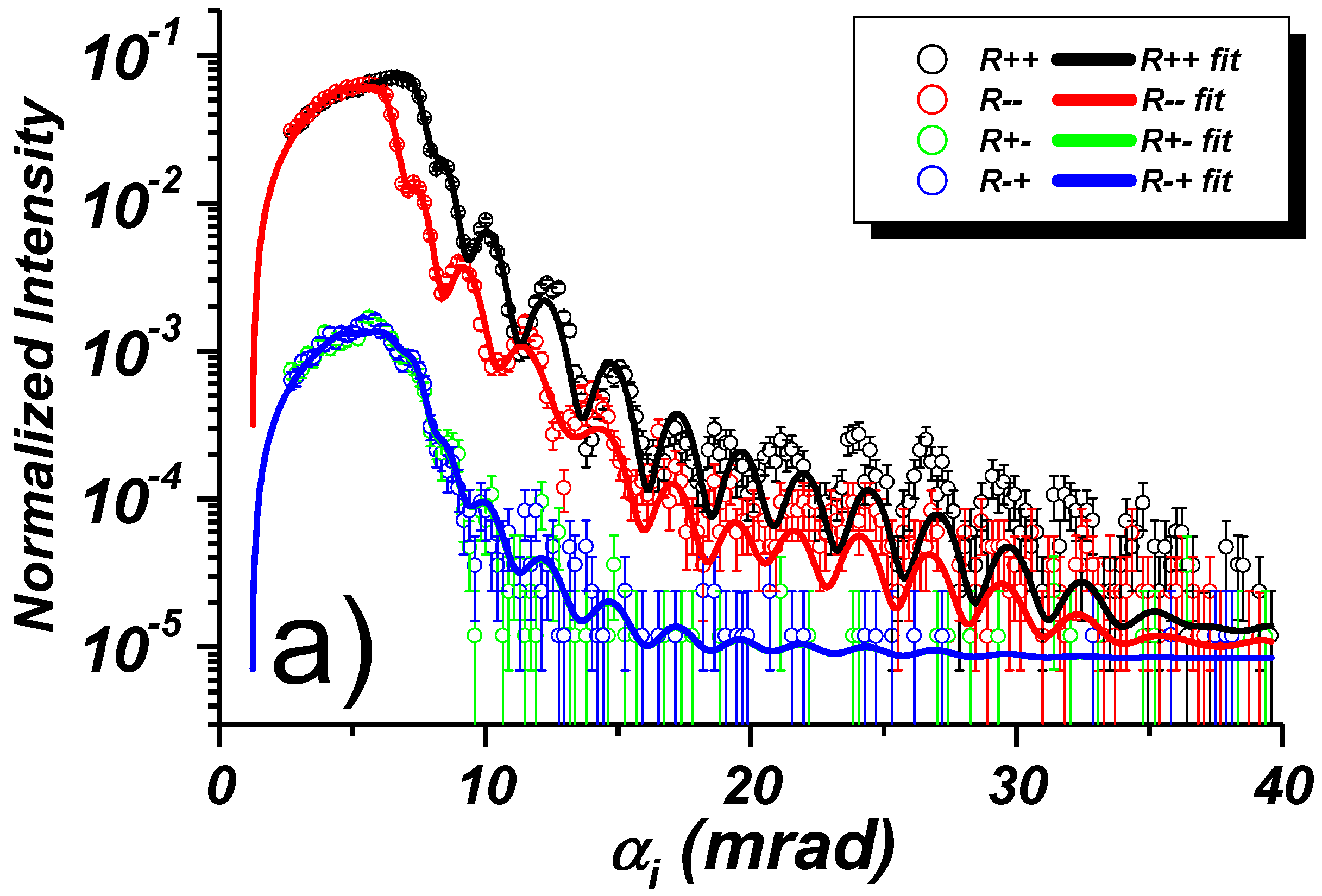
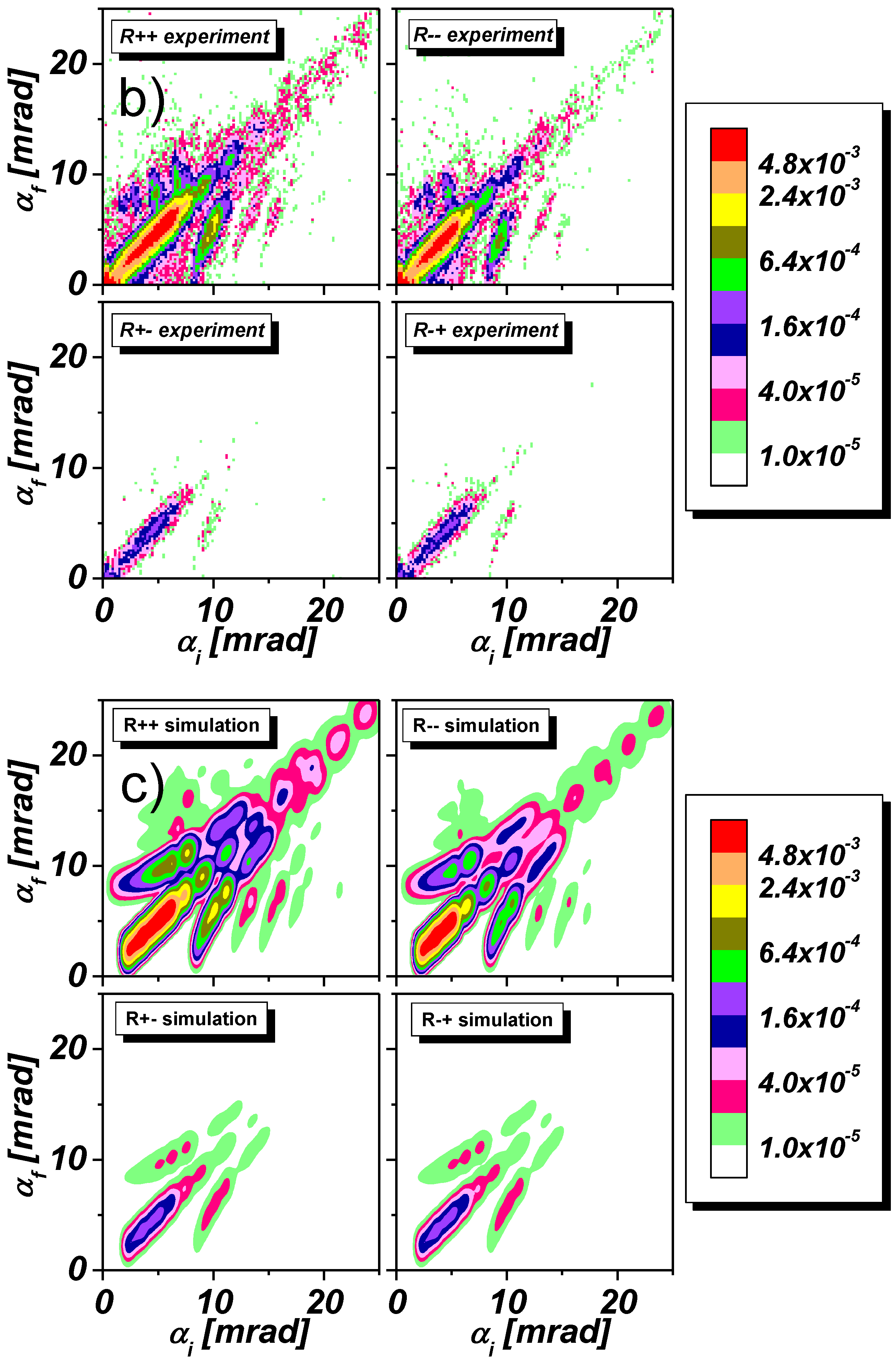
Now we consider the case that an external field H applied parallel to the Y-axis is high enough to saturate the magnetization within the stripes for the parallel and the perpendicular orientation. As the field H is homogeneous along the Y-axis, it does not cause scattering contrast. Therefore we conclude that for perpendicular orientation of the stripes, the mean SLD value is given by , where is the surface fraction covered by the stripes. These reduced mean SLDs are used to calculate the reflection amplitudes for each of the spin states. Then NSF and SF reflection coefficients and corresponding OSS cross sections are averaged over incident and outgoing spin states filtered by the polarizer and analyzer. The result is convoluted with the 3D resolution function and incoherently averaged over all coherence ellipsoids spanning the whole sample surface.
Thus, in perpendicular orientation, specular reflection and Bragg diffraction at shallow angles provides information on width and periodicity of stripe arrays and on magnetic induction within the stripes. In this orientation OSS is, however, less sensitive to the possible inhomogeneity of magnetic flux in stripes with not ideal edges and, especially, in the
inter-space [
21]. Therefore, a complimentary parallel orientation has to be chosen to supplement the remaining information.
In parallel orientation, the stripe pattern is rotated by 90
about the surface normal and the long axis of the coherence ellipsoid lies now parallel to the stripes. In this orientation sketched in
Figure 5b, no Bragg diffraction can be seen as neither of coherence ellipsoids crosses more than a single stripe. Then neutron waves scattered from different stripes do not interfere. Also there is almost no interference between waves reflected from the stripes and from the inter-stripe spaces filled with magnetic field. As a result, the specular reflection coefficients
can be represented as an incoherent sum of reflectivities from individual stripes
and reflectivities
from the inter-stripe regions weighted with the corresponding surface factors
and
, respectively:
This relation holds independent on whether the magnetization of the stripes is in a saturated state parallel or perpendicular to the stripes. But the magnetization orientation will affect the proportion between NSF and SF specular reflectivity and off-specular scattering. If, on the other hand, the magnetization is not constant and split up into domains, in addition off-specular diffuse scattering will be observed that yields information on the domain size and distribution, as already discussed for homogeneous flat magnetic films.
Summarizing, both orientations of stripe arrays, parallel and perpendicular to the scattering plane, are needed for a complete analysis of the stripe patterns. The perpendicular orientation yields information on the geometry of the stripe array, including stripe width and periodicity, whereas the parallel orientation adds information on the magnetic flux distribution in e.g., the inter-space region.