Coulomb Blockade Effect in Well-Arranged 2D Arrays of Palladium Nano-Islands for Hydrogen Detection at Room Temperature: A Modeling Study
Abstract
1. Introduction
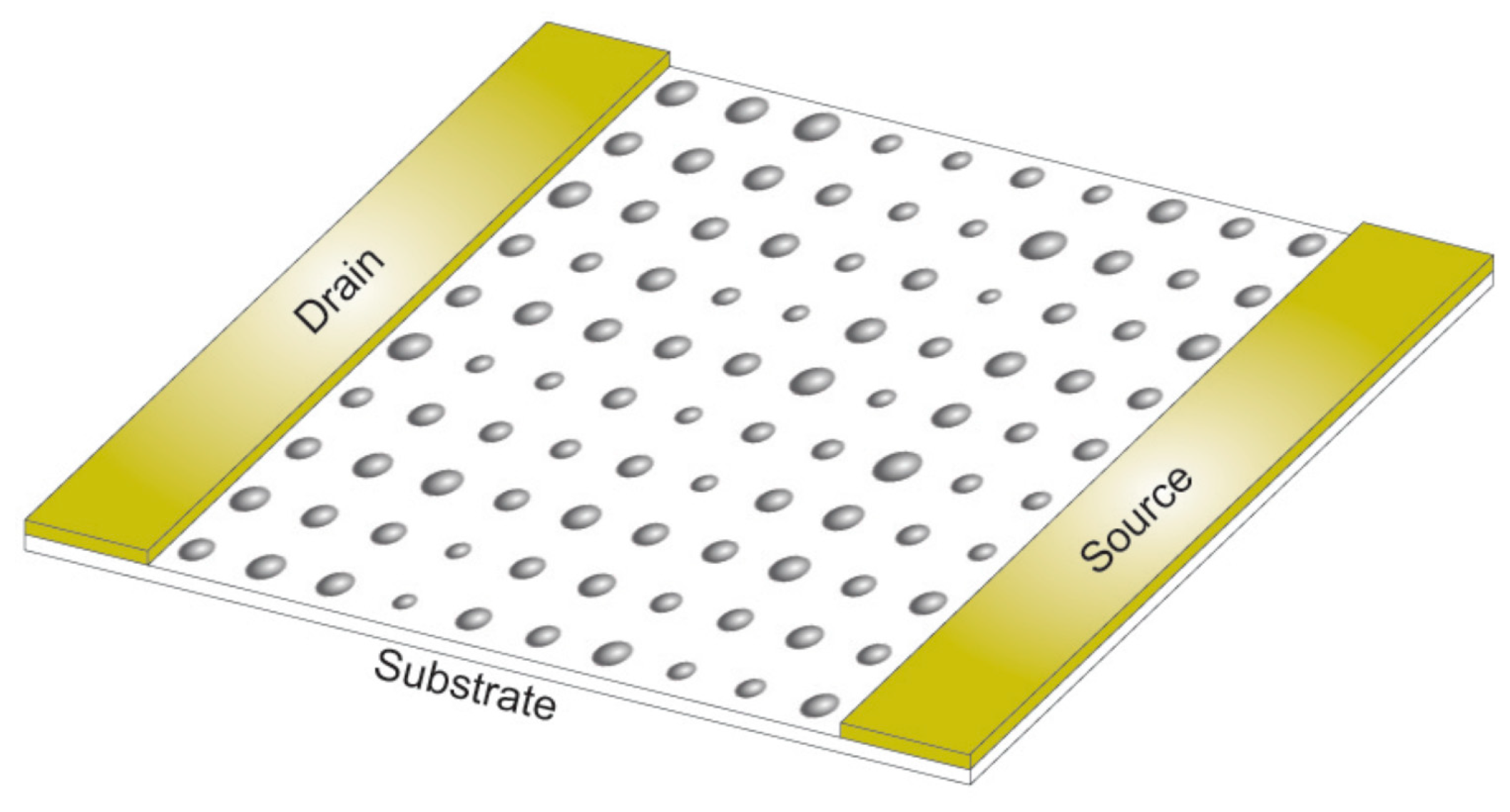
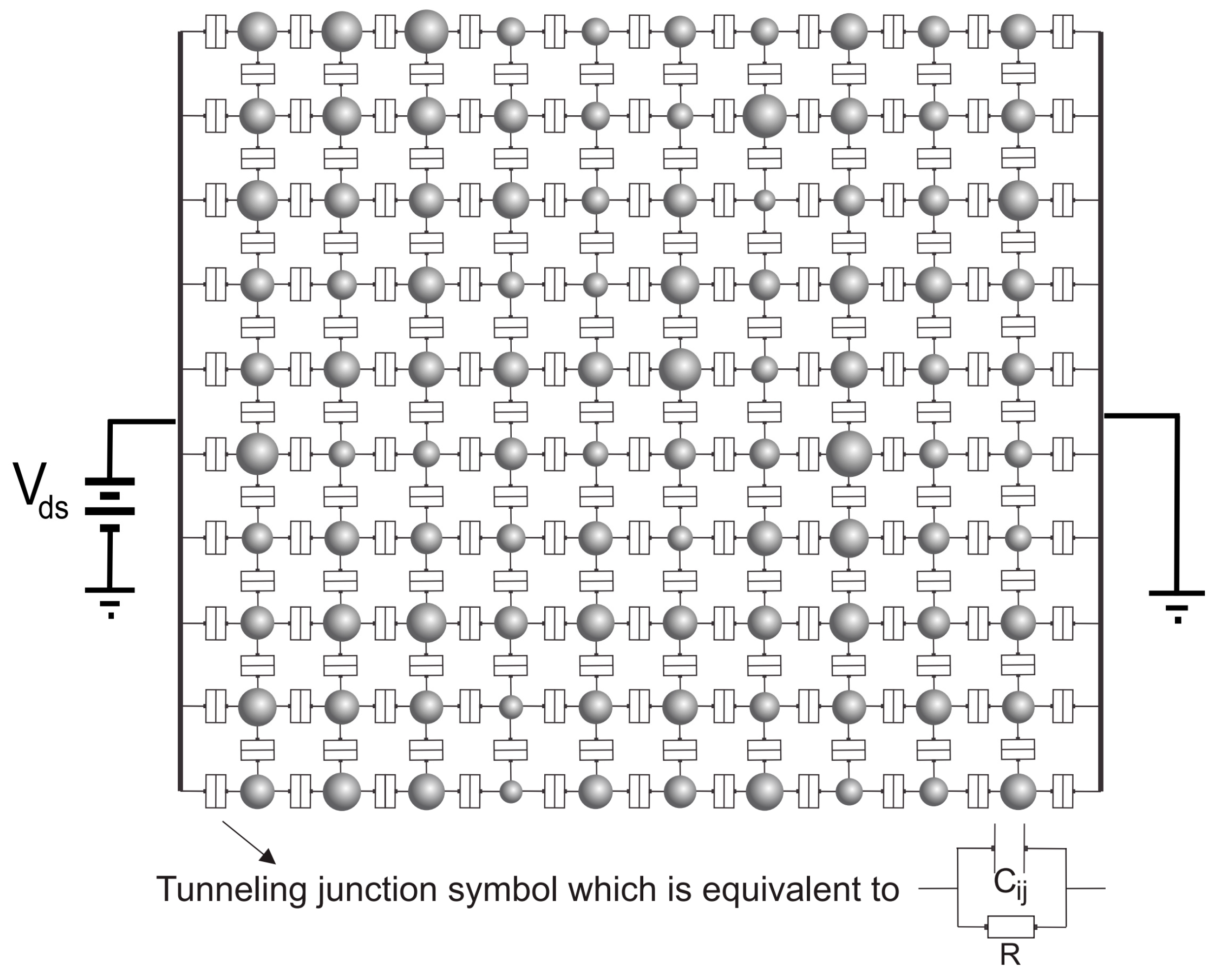
2. Assumptions of the Model and Simulation Method
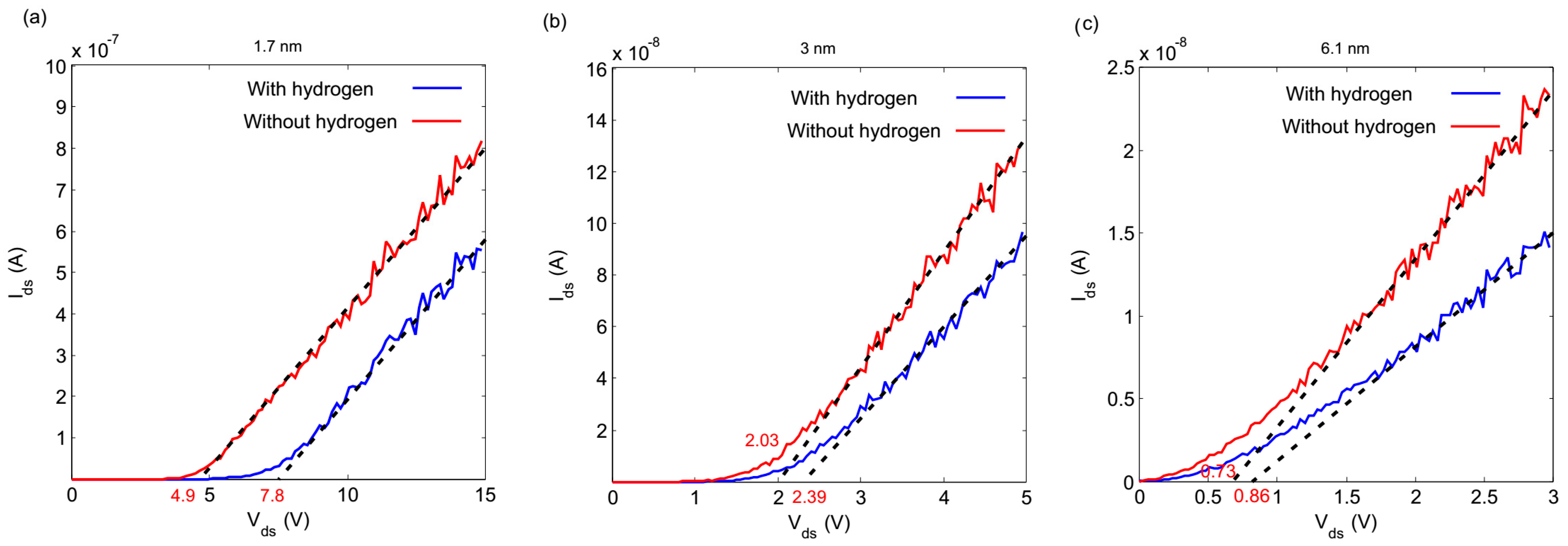
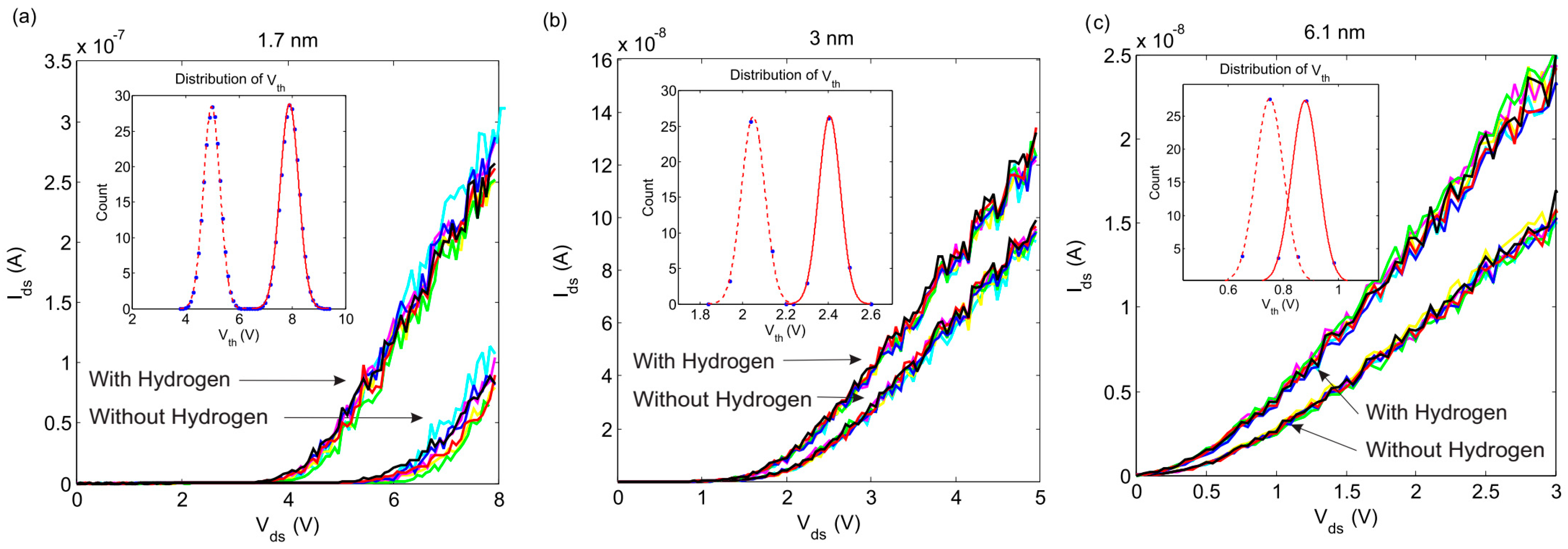
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jacobson, M.Z.; Colella, W.; Golden, D. Cleaning the air and improving health with hydrogen fuel-cell vehicles. Science 2005, 308, 1901–1905. [Google Scholar] [CrossRef]
- Liekhus, K.J.; Zlochower, I.A.; Cashdollar, K.L.; Djordjevic, S.M.; Loehr, C.A. Flammability of gas mixtures containing volatile organic compounds and hydrogen. J. Loss Prev. Process Ind. 2000, 13, 377–384. [Google Scholar] [CrossRef]
- Nakamoto, K.; Kurita, R.; Niwa, O. Electrochemical surface plasmon resonance measurement based on gold nanohole array fabricated by nanoimprinting technique. Anal. Chem. 2012, 84, 3187–3191. [Google Scholar] [CrossRef] [PubMed]
- Yagati, A.K.; Lee, T.; Min, J.; Choi, J.-W. Electrochemical performance of gold nanoparticle–cytochrome c hybrid interface for H2O2 detection. Colloids Surf. B Biointerfaces 2012, 92, 161–167. [Google Scholar] [CrossRef] [PubMed]
- Moafi, A.; Partridge, J.G.; Sadek, A.Z.; Lau, D.W.M.; Kalantar-zadeh, K.; McCulloch, D.G. A Hydrogen Sensor Based on Graphitic Carbon. IEEE Sens. J. 2011, 11, 1913–1916. [Google Scholar] [CrossRef]
- Al-Mashat, L.; Tran, H.D.; Wlodarski, W.; Kaner, R.B.; Kalantar-Zadeh, K. Conductometric Hydrogen Gas Sensor Based on Polypyrrole Nanofibers. IEEE Sens. J. 2008, 8, 365–370. [Google Scholar] [CrossRef]
- Lee, S.P. Electrodes for semiconductor gas sensors. Sensors 2017, 17, 683. [Google Scholar] [CrossRef]
- Becker, E.; Andersson, M.; Eriksson, M.; Spetz, A.L.; Skoglundh, M. Study of the sensing mechanism towards carbon monoxide of platinum-based field effect sensors. IEEE Sens. J. 2010, 11, 1527–1534. [Google Scholar] [CrossRef]
- Westerwaal, R.; Duim, N.; Nieuwenhuijse, I.; Perrotton, C.; Dabirian, A.; van Leeuwen, J.; Palmisano, V.; Dam, B. Thin film based sensors for a continuous monitoring of hydrogen concentrations. Sens. Actuators B Chem. 2012, 165, 88–96. [Google Scholar] [CrossRef]
- Sadek, A.; Wlodarski, W.; Li, Y.; Yu, W.; Li, X.; Yu, X.; Kalantar-Zadeh, K. A ZnO nanorod based layered ZnO/64 YX LiNbO3 SAW hydrogen gas sensor. Thin Solid Films 2007, 515, 8705–8708. [Google Scholar] [CrossRef]
- Atashbar, M.; Sadek, A.; Wlodarski, W.; Sriram, S.; Bhaskaran, M.; Cheng, C.; Kaner, R.; Kalantar-Zadeh, K. Layered SAW gas sensor based on CSA synthesized polyaniline nanofiber on AlN on 64 YX LiNbO3 for H2 sensing. Sens. Actuators B Chem. 2009, 138, 85–89. [Google Scholar] [CrossRef]
- Jakubik, W. Investigations of thin film structures of WO3 and WO3 with Pd for hydrogen detection in a surface acoustic wave sensor system. Thin Solid Films 2007, 515, 8345–8350. [Google Scholar] [CrossRef]
- Abbasi, H.; Sedghi, H.; Khaje, M. Single-Electron Tunneling Based Hydrogen Sensor. Chin. J. Phys. 2015, 53, 120805-1. [Google Scholar]
- Chen, D.; Wang, J.J.; Xu, Y. Hydrogen sensor based on Pd-functionalized film bulk acoustic resonator. Sens. Actuators B Chem. 2011, 159, 234–237. [Google Scholar] [CrossRef]
- Bannenberg, L.J.; Boelsma, C.; Asano, K.; Schreuders, H.; Dam, B. Metal Hydride Based Optical Hydrogen Sensors. J. Phys. Soc. Japan 2020, 89, 051003. [Google Scholar] [CrossRef]
- Bigiani, L.; Zappa, D.; Maccato, C.; Gasparotto, A.; Sada, C.; Comini, E.; Barreca, D. Hydrogen Gas Sensing Performances of p-Type Mn3O4 Nanosystems: The Role of Built-in Mn3O4/Ag and Mn3O4/SnO2 Junctions. Nanomaterials 2020, 10, 511. [Google Scholar] [CrossRef]
- Hübert, T.; Boon-Brett, L.; Black, G.; Banach, U. Hydrogen sensors–A review. Sens. Actuators B Chem. 2011, 157, 329–352. [Google Scholar] [CrossRef]
- Ndaya, C.C.; Javahiraly, N.; Brioude, A. Recent Advances in Palladium Nanoparticles-Based Hydrogen Sensors for Leak Detection. Sensors 2019, 19, 4478. [Google Scholar] [CrossRef]
- Jakubik, W.P. Hydrogen gas-sensing with bilayer structures of WO3 and Pd in SAW and electric systems. Thin Solid Films 2009, 517, 6188–6191. [Google Scholar] [CrossRef]
- Jung, W.B.; Cho, S.Y.; Suh, B.L.; Yoo, H.W.; Jeon, H.J.; Kim, J.; Jung, H.T. Polyelemental Nanolithography via Plasma Ion Bombardment: From Fabrication to Superior H2 Sensing Application. Adv. Mater. 2019, 31, 1805343. [Google Scholar] [CrossRef]
- Yoo, H.-W.; Cho, S.-Y.; Jeon, H.-J.; Jung, H.-T. Well-defined and high resolution Pt nanowire arrays for a high performance hydrogen sensor by a surface scattering phenomenon. Anal. Chem. 2015, 87, 1480–1484. [Google Scholar] [CrossRef]
- Cho, S.-Y.; Ahn, H.; Park, K.; Choi, J.; Kang, H.; Jung, H.-T. Ultrasmall grained Pd nanopattern H2 sensor. ACS Sens. 2018, 3, 1876–1883. [Google Scholar] [CrossRef]
- Thelander, C.; Magnusson, M.H.; Deppert, K.; Samuelson, L.; Poulsen, P.R.; Nygård, J.; Borggreen, J. Gold nanoparticle single-electron transistor with carbon nanotube leads. Appl. Phys. Lett. 2001, 79, 2106–2108. [Google Scholar] [CrossRef]
- Averin, D.; Likharev, K. Coulomb blockade of single-electron tunneling, and coherent oscillations in small tunnel junctions. J. Low Temp. Phys. 1986, 62, 345–373. [Google Scholar] [CrossRef]
- Likharev, K.K. Single-electron devices and their applications. Proc. IEEE 1999, 87, 606–632. [Google Scholar] [CrossRef]
- Sehrawat, P.; Islam, S. Graphene quantum dot arrays: Pros and cons of photodetection in the Coulomb blockade regime. Carbon 2019, 149, 499–511. [Google Scholar]
- Meschke, M.; Kemppinen, A.; Pekola, J. Accurate Coulomb blockade thermometry up to 60 kelvin. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150052. [Google Scholar] [CrossRef]
- Borini, S.; Boarino, L.; Amato, G. Coulomb blockade sensors based on nanostructured mesoporous silicon. Physica E Low Dimens. Syst. Nanostruct. 2007, 38, 197–199. [Google Scholar] [CrossRef]
- Ingham, B.; Toney, M.F.; Hendy, S.C.; Cox, T.; Fong, D.D.; Eastman, J.A.; Fuoss, P.H.; Stevens, K.J.; Lassesson, A.; Brown, S. Particle size effect of hydrogen-induced lattice expansion of palladium nanoclusters. Phys. Rev. B 2008, 78, 245408. [Google Scholar] [CrossRef]
- Offermans, P.; Tong, H.; Van Rijn, C.; Merken, P.; Brongersma, S.; Crego-Calama, M. Ultralow-power hydrogen sensing with single palladium nanowires. Appl. Phys. Lett. 2009, 94, 223110. [Google Scholar] [CrossRef]
- Xu, T.; Zach, M.; Xiao, Z.; Rosenmann, D.; Welp, U.; Kwok, W.; Crabtree, G. Self-assembled monolayer-enhanced hydrogen sensing with ultrathin palladium films. Appl. Phys. Lett. 2005, 86, 203104. [Google Scholar] [CrossRef]
- Mehrara, H.; Erfanian, A.; Khaje, M.; Zahedinejad, M.; Rezvani, F. I–V characteristics of two-dimensional nanodot-array single electron transistors. Superlattices Microstruct. 2013, 53, 1–8. [Google Scholar] [CrossRef]
- Erfanian, A.; Mehrara, H.; Raissi, F.; Khaje, M. Coulomb blockade in PtSi/porous Si Schottky barrier as a two-dimensional multi-tunnelling junction. IET Circuits Devices Syst. 2015, 9, 81–86. [Google Scholar] [CrossRef]
- Abramov, I.; Ignatenko, S.; Novik, E. Model of multi-island single-electron arrays based on the Monte Carlo method. Semiconductors 2003, 37, 564–568. [Google Scholar] [CrossRef]
- Abramov, I.; Ignatenko, S.; Novik, E. Influence of the design and material parameters on the current-voltage characteristics of two-island single-electron chains. Semiconductors 2002, 36, 1192–1197. [Google Scholar] [CrossRef]
- Fujino, H.; Oya, T. Analysis of electron transfer among quantum dots in two-dimensional quantum dot network. Jpn. J. Appl. Phys. 2014, 53, 06JE02. [Google Scholar] [CrossRef]
- Abbasi, H.; Sedghi, H.; Khaje, M. Emergence and Shift of Coulomb Blockade Threshold in Well-Arranged Two-Dimensional Arrays of Nanodots: A Simulation Study. J. Comput. Theor. Nanosci. 2015, 12, 4573–4578. [Google Scholar] [CrossRef]
- Karre, P.S.K.; Acharya, M.; Knudsen, W.R.; Bergstrom, P.L. Single electron transistor-based gas sensing with tungsten nanoparticles at room temperature. IEEE Sens. J. 2008, 8, 797–802. [Google Scholar] [CrossRef]
- Kim, S.-W.; Park, J.; Jang, Y.; Chung, Y.; Hwang, S.; Hyeon, T.; Kim, Y.W. Synthesis of monodisperse palladium nanoparticles. Nano Lett. 2003, 3, 1289–1291. [Google Scholar] [CrossRef]
- Boubaker, A.; Troudi, M.; Sghaier, N.; Souifi, A.; Baboux, N.; Kalboussi, A. Electrical characteristics and modelling of multi-island single-electron transistor using SIMON simulator. Microelectron. J. 2009, 40, 543–546. [Google Scholar] [CrossRef]
- Wasshuber, C.; Kosina, H. A single-electron device and circuit simulator. Superlattices Microstruct. 1997, 21, 37–42. [Google Scholar] [CrossRef]
- Barwiński, B. Temperature dependence of the electrical conduction in discontinuos silver films on sapphire substrates. Thin Solid Films 1987, 148, 233–241. [Google Scholar] [CrossRef]
- Van Lith, J.; Lassesson, A.; Brown, S.; Schulze, M.; Partridge, J.; Ayesh, A. A hydrogen sensor based on tunneling between palladium clusters. Appl. Phys. Lett. 2007, 91, 181910. [Google Scholar] [CrossRef]
- Pisler, E.; Adhikari, T. Numerical calculation of mutual capacitance between two equal metal spheres. Phys. Scr. 1970, 2, 81. [Google Scholar] [CrossRef]
- Lekner, J. Capacitance coefficients of two spheres. J. Electrostat. 2011, 69, 11–14. [Google Scholar] [CrossRef]
- Parthasarathy, R.; Lin, X.-M.; Elteto, K.; Rosenbaum, T.; Jaeger, H.M. Percolating through networks of random thresholds: Finite temperature electron tunneling in metal nanocrystal arrays. Phys. Rev. Lett. 2004, 92, 076801. [Google Scholar] [CrossRef]
- Parthasarathy, R.; Lin, X.-M.; Jaeger, H.M. Electronic Transport in Metal Nanocrystal Arrays: The Effect of Structural Disorder on Scaling Behavior. Phys. Rev. Lett. 2001, 87, 186807. [Google Scholar] [CrossRef]
- Ortiz-Conde, A.; Sánchez, F.G.; Liou, J.J.; Cerdeira, A.; Estrada, M.; Yue, Y. A review of recent MOSFET threshold voltage extraction methods. Microelectron. Reliab. 2002, 42, 583–596. [Google Scholar] [CrossRef]
- Shin, D.H.; Lee, J.S.; Jun, J.; An, J.H.; Kim, S.G.; Cho, K.H.; Jang, J. Flower-like palladium nanoclusters decorated graphene electrodes for ultrasensitive and flexible hydrogen gas sensing. Sci. Rep. 2015, 5, 12294. [Google Scholar] [CrossRef]
- Gupta, D.; Dutta, D.; Kumar, M.; Barman, P.; Sarkar, C.; Basu, S.; Hazra, S. A low temperature hydrogen sensor based on palladium nanoparticles. Sens. Actuators B Chem. 2014, 196, 215–222. [Google Scholar] [CrossRef]



| Mean diameter of nanoparticles, nm | 1.7 | 3 | 6.1 |
| Full width at half maximum, nm | 1.1 | 0.3 | 0.7 |
| Lattice constant before exposing to hydrogen, °A | 3.9167 | 3.9167 | 3.90 |
| Lattice constant after exposing to hydrogen (20 torr), °A | 3.9232 | 3.9217 | 3.92 |
| Tunneling gap between adjacent nano-islands, nm | 2 | 2.25 | 3 |
| Mean Diameter of Nanoparticles, nm | 1.7 | 3 | 6.1 |
| Vth for 10 × 10 arrays of nano-islands before exposing to hydrogen, V | 7.26 | 2.8 | 0.83 |
| Vth for 10 × 10 arrays of nano-islands after exposing to hydrogen (20 torr), V | 4.9 | 2.03 | 0.73 |
| Vth for 15 × 15 arrays of nano-islands, V | 10.4 | 3.4 | 0.81 |
| Vth for 20 × 20 arrays of nano-islands, V | 13.6 | 4.3 | 0.93 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khaje, M.; Sedghi, H.; Goudarzi, H.; Ahmadi, M.T.; Rahimian Koloor, S.S.; Petrů, M. Coulomb Blockade Effect in Well-Arranged 2D Arrays of Palladium Nano-Islands for Hydrogen Detection at Room Temperature: A Modeling Study. Nanomaterials 2020, 10, 835. https://doi.org/10.3390/nano10050835
Khaje M, Sedghi H, Goudarzi H, Ahmadi MT, Rahimian Koloor SS, Petrů M. Coulomb Blockade Effect in Well-Arranged 2D Arrays of Palladium Nano-Islands for Hydrogen Detection at Room Temperature: A Modeling Study. Nanomaterials. 2020; 10(5):835. https://doi.org/10.3390/nano10050835
Chicago/Turabian StyleKhaje, Mahdi, Hassan Sedghi, Hadi Goudarzi, Mohammad Taghi Ahmadi, Seyed Saeid Rahimian Koloor, and Michal Petrů. 2020. "Coulomb Blockade Effect in Well-Arranged 2D Arrays of Palladium Nano-Islands for Hydrogen Detection at Room Temperature: A Modeling Study" Nanomaterials 10, no. 5: 835. https://doi.org/10.3390/nano10050835
APA StyleKhaje, M., Sedghi, H., Goudarzi, H., Ahmadi, M. T., Rahimian Koloor, S. S., & Petrů, M. (2020). Coulomb Blockade Effect in Well-Arranged 2D Arrays of Palladium Nano-Islands for Hydrogen Detection at Room Temperature: A Modeling Study. Nanomaterials, 10(5), 835. https://doi.org/10.3390/nano10050835







