Investigation of AC-Measurements of Epoxy/Ferrite Composites
Abstract
1. Introduction
2. Materials and Methods
2.1. Preparation of Nickel-Zinc Lithium Ferrite Nanoparticles and Epoxy/Ferrite Composites
2.2. Alternating Current (AC) -Measurements
3. Results and Discussion
3.1. Electrical Properties
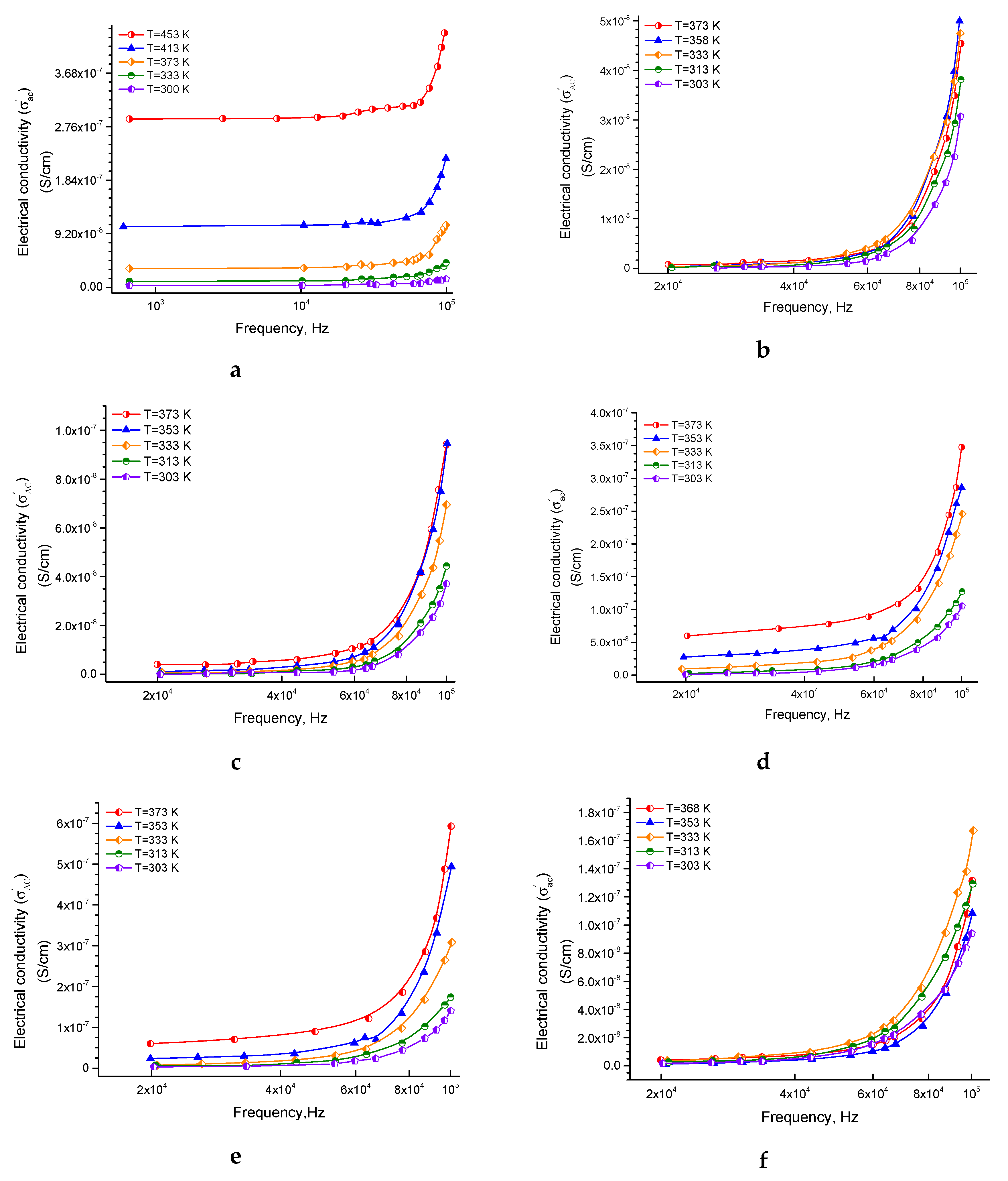
3.1.1. The Behavior of Ac Conductivity
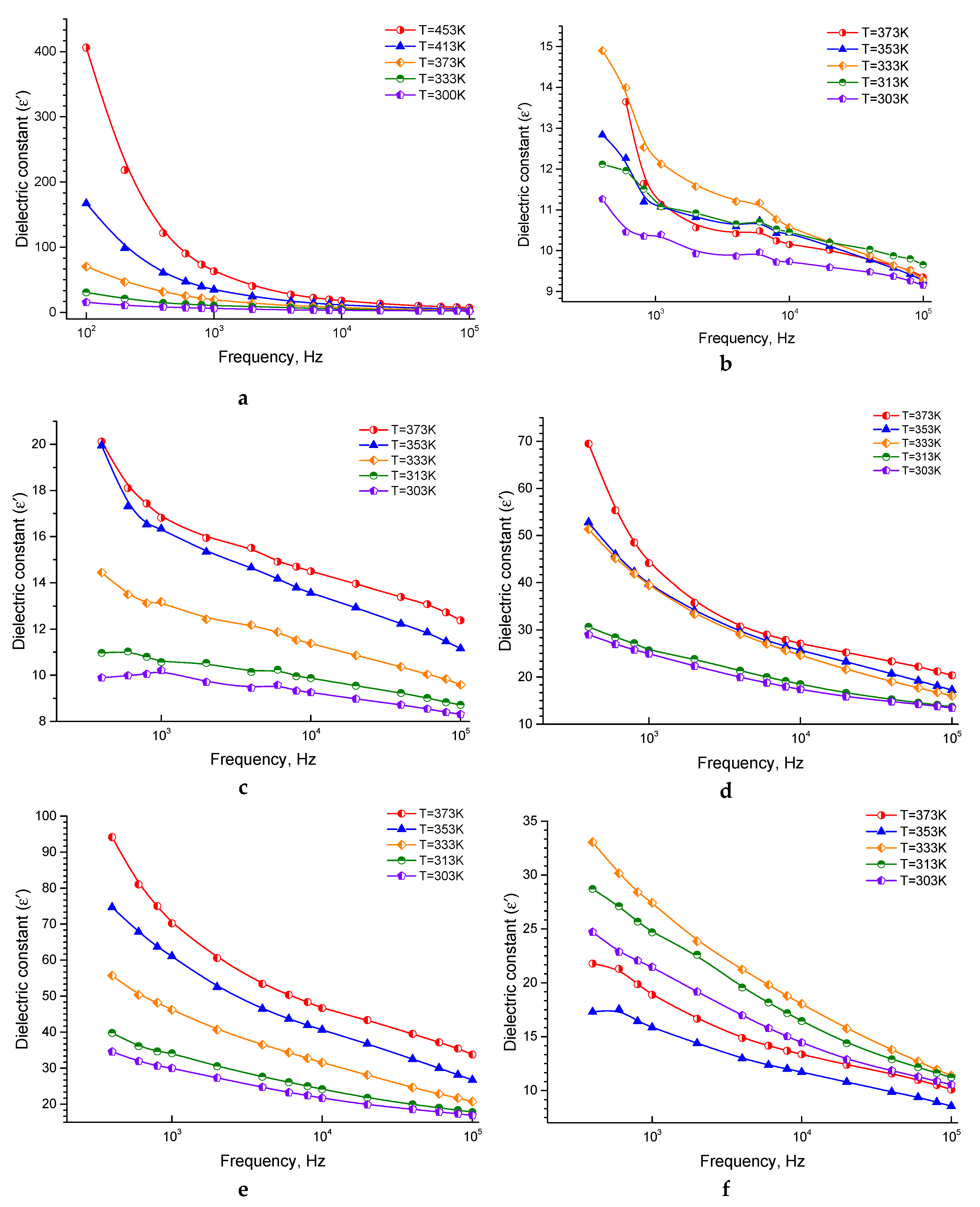
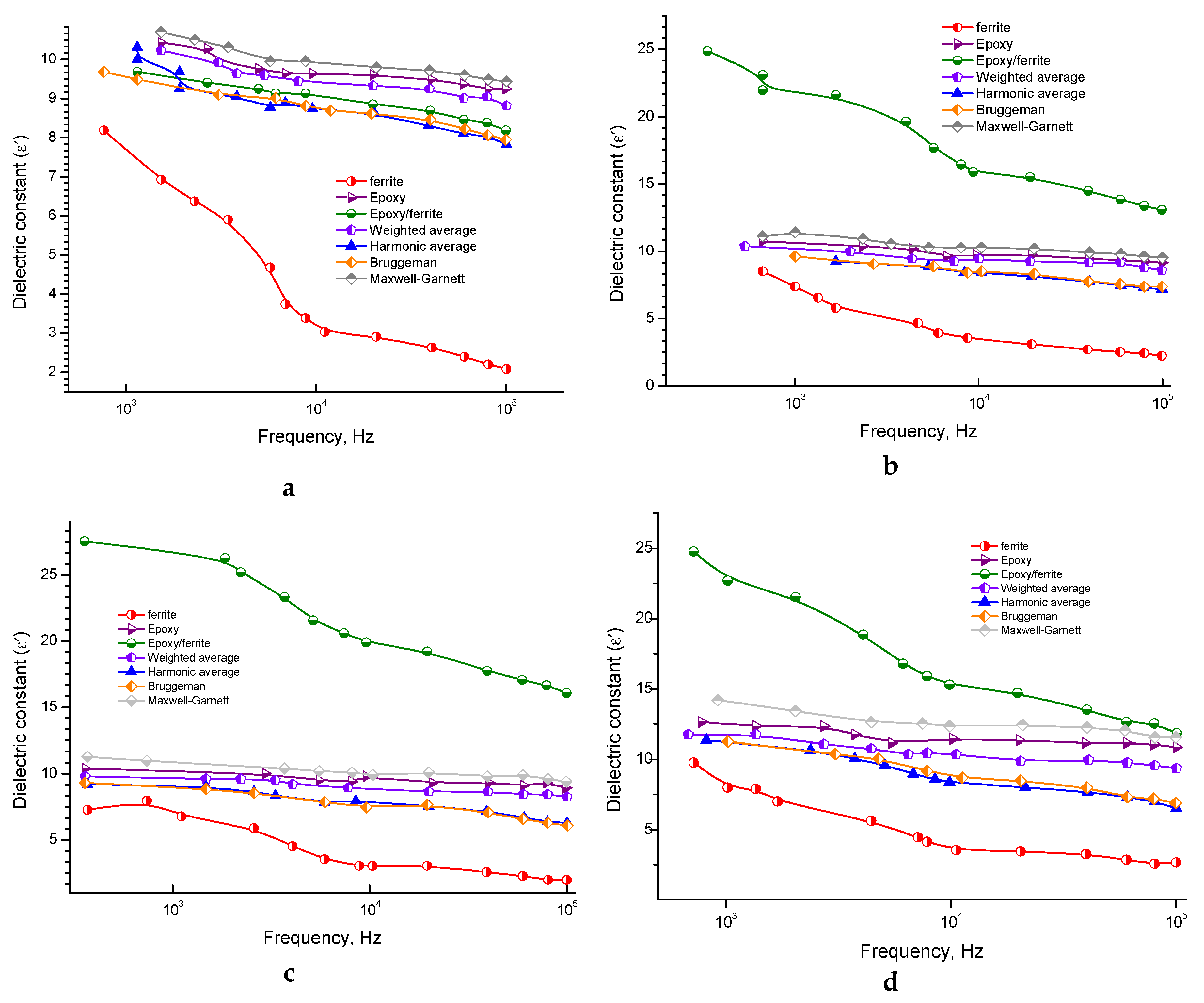
3.1.2. The Behavior of Dielectric Constant
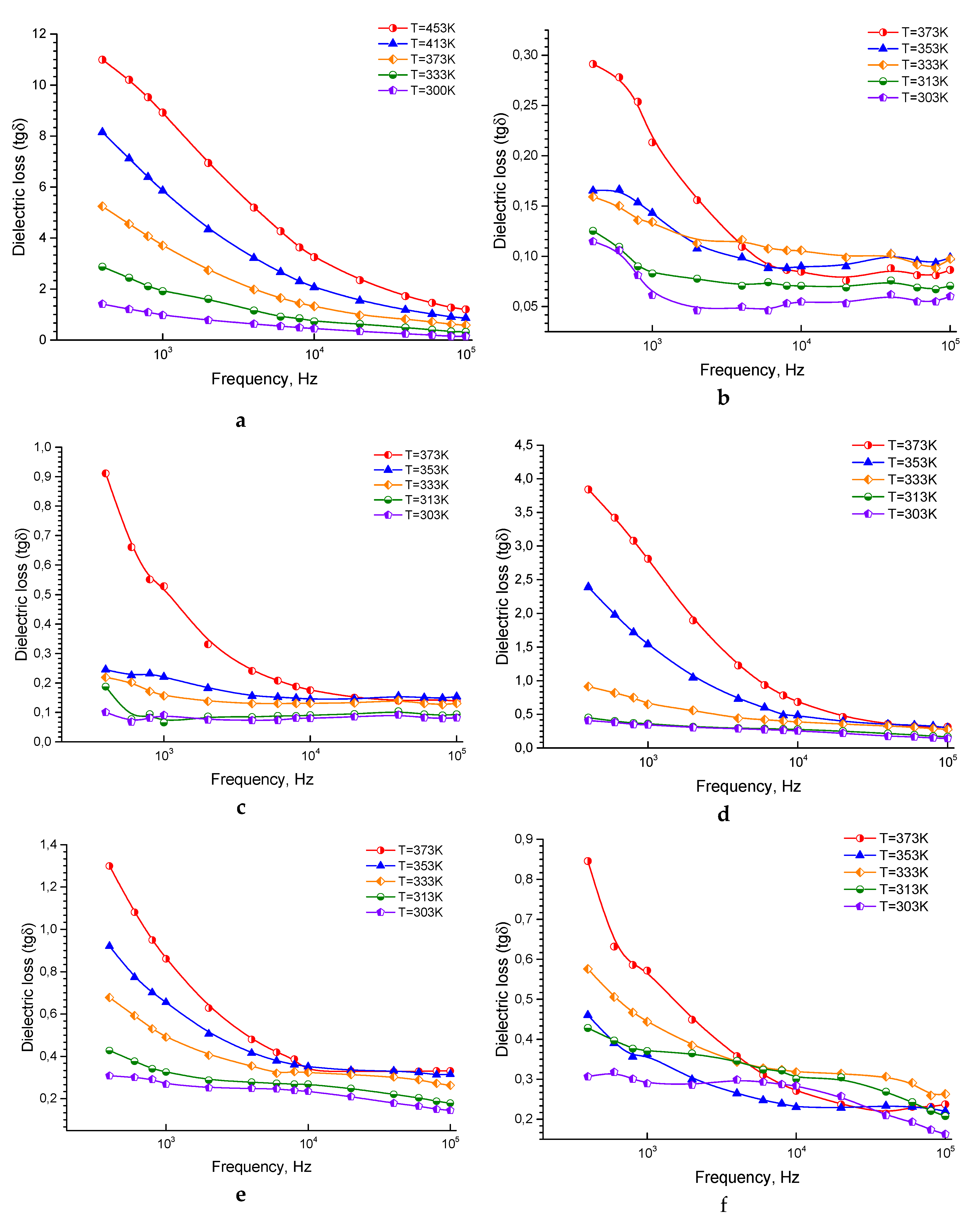
3.1.3. The Behavior of Dielectric Loss tangent
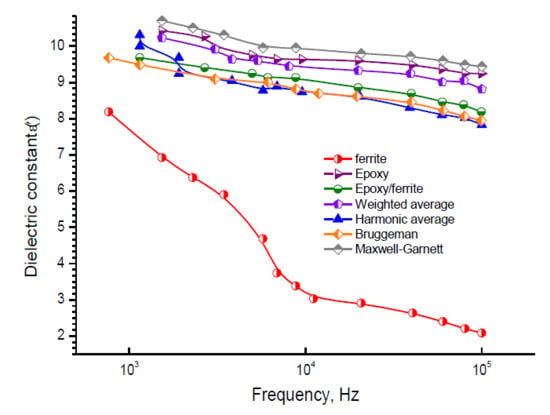
3.2. Modeling Dielectric Constant Behavior by Mixing Formulas
3.2.1. The Maxwell Garnett (MG) Model
3.2.2. The Symmetric Brüggemann Model
3.2.3. Weighted Average Model
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kumar, A.M.; Varma, M.C.; Dube, C.L.; Rao, K.H.; Kashyap, S.C. Development of Ni–Zn nanoferrite core material with improved saturation magnetization and DC resistivity. J. Magn. Magn. Mater. 2008, 320, 1995–2000. [Google Scholar] [CrossRef]
- Mathew, D.S.; Juang, R.-S. An overview of the structure and magnetism of spinel ferrite nanoparticles and their synthesis in microemulsions. Chem. Eng. J. 2007, 129, 51–65. [Google Scholar] [CrossRef]
- Dippong, T.; Levei, E.A.; Cadar, O. Preparation of CoFe2O4/SiO2 Nanocomposites at low temperatures using short chain diols. J. Chem. 2017, 2017, 3. [Google Scholar] [CrossRef]
- Yakovenko, O.S.; Matzui, L.Y.; Vovchenko, L.L.; Trukhanov, A.V.; Kazakevich, I.S.; Trukhanov, S.V.; Prylutskyy, Y.I.; Ritter, U. Magnetic anisotropy of the graphite nanoplatelet–epoxy and MWCNT–epoxy composites with aligned barium ferrite filler. J. Mater. Sci. 2017, 52, 5345–5358. [Google Scholar] [CrossRef]
- Moreau, L.M.; Ha, D.-H.; Zhang, H.; Hovden, R.; Muller, D.A.; Robinson, R.D. Defining crystalline/amorphous phases of nanoparticles through X-ray absorption spectroscopy and X-ray diffraction: The case of nickel phosphide. Chem. Mater. 2013, 25, 2394–2403. [Google Scholar] [CrossRef]
- Hu, C.; Gao, Z.; Yang, X. One-pot low temperature synthesis of MFe2O4 (M=Co, Ni, Zn) superparamagnetic nanocrystals. J. Magn. Magn. Mater. 2008, 320, L70–L73. [Google Scholar] [CrossRef]
- Zhao, H.; Zheng, Z.; Wong, K.W.; Wang, S.; Huang, B.; Li, D. Fabrication and electrochemical performance of nickel ferrite nanoparticles as anode material in lithium ion batteries. Electrochem. Commun. 2007, 9, 2606–2610. [Google Scholar] [CrossRef]
- Sivakumar, M.; Towata, A.; Yasui, K.; Tuziuti, T.; Iida, Y. A new ultrasonic cavitation approach for the synthesis of zinc ferrite nanocrystals. Curr. Appl. Phys. 2006, 6, 591–593. [Google Scholar] [CrossRef]
- Thakur, S.; Katyal, S.C.; Singh, M. Structural and magnetic properties of nano nickel–zinc ferrite synthesized by reverse micelle technique. J. Magn. Magn. Mater. 2009, 321, 1–7. [Google Scholar] [CrossRef]
- Poddar, P.; Srikanth, H.; Morrison, S.A.; Carpenter, E.E. Inter-particle interactions and magnetism in manganese–zinc ferrite nanoparticles. J. Magn. Magn. Mater. 2005, 288, 443–451. [Google Scholar] [CrossRef]
- Ohsaki, S.; Hono, K.; Hidaka, H.; Takaki, S. Characterization of nanocrystalline ferrite produced by mechanical milling of pearlitic steel. Scr. Mater. 2005, 52, 271–276. [Google Scholar] [CrossRef]
- Rao, B.P.; Caltun, O.; Cho, W.S.; Kim, C.-O.; Kim, C. Synthesis and characterization of mixed ferrite nanoparticles. J. Magn. Magn. Mater. 2007, 310, e812–e814. [Google Scholar] [CrossRef]
- Son, S.; Taheri, M.; Carpenter, E.; Harris, V.; McHenry, M. Synthesis of ferrite and nickel ferrite nanoparticles using radio-frequency thermal plasma torch. J. Appl. Phys. 2002, 91, 7589–7591. [Google Scholar] [CrossRef]
- Chu, N.; Wang, X.; Liu, Y.; Jin, H.; Wu, Q.; Li, L.; Wang, Z.; Ge, H. Magnetic properties of low Mn-doped NiCuZn nanocrystalline ferrites. J. Alloys Compd. 2009, 470, 438–442. [Google Scholar] [CrossRef]
- Bhosale, D.N.; Verenkar, V.M.S.; Rane, K.S.; Bakare, P.P.; Sawant, S.R. Initial susceptibility studies on Cu-Mg-Zn ferrites. Mater. Chem. Phys. 1999, 59, 57–62. [Google Scholar] [CrossRef]
- Maletin, M.; Moshopoulou, E.G.; Kontos, A.G.; Devlin, E.; Delimitis, A.; Zaspalis, V.T.; Nalbandian, L.; Srdic, V.V. Synthesis and structural characterization of In-doped ZnFe2O4 nanoparticles. J. Eur. Ceram. Soc. 2007, 27, 4391–4394. [Google Scholar] [CrossRef]
- Stewart, S.J.; Tueros, M.J.; Cernicchiaro, G.; Scorzelli, R.B. Magnetic size growth in nanocrystalline copper ferrite. Solid State Commun. 2004, 129, 347–351. [Google Scholar] [CrossRef]
- Soibam, I.; Phanjoubam, S.; Prakash, C. Mössbauer and magnetic studies of cobalt substituted lithium zinc ferrites prepared by citrate precursor method. J. Alloys Compd. 2009, 475, 328–331. [Google Scholar] [CrossRef]
- Dippong, T.; Levei, E.A.; Tanaselia, C.; Gabor, M.; Nasui, M.; Barbu Tudoran, L.; Borodi, G. Magnetic properties evolution of the CoxFe3−xO4/SiO2 system due to advanced thermal treatment at 700 °C and 1000 °C. J. Magn. Magn. Mater. 2016, 410, 47–54. [Google Scholar] [CrossRef]
- Li, J.; Zhou, D.; Liu, W.-F.; Su, J.-Z.; Fu, M.-S. Novel and facile reduced graphene oxide anchored Ni-Co-Zn-Nd-ferrites composites for microwave absorption. Scr. Mater. 2019, 171, 42–46. [Google Scholar] [CrossRef]
- Vinnik, D.A.; Podgornov, F.V.; Zabeivorota, N.S.; Trofimov, E.A.; Zhivulin, V.E.; Chernukha, A.S.; Gavrilyak, M.V.; Gudkova, S.A.; Zherebtsov, D.A.; Ryabov, A.V.; et al. Effect of treatment conditions on structure and magnetodielectric properties of barium hexaferrites. J. Magn. Magn. Mater. 2020, 498, 166190. [Google Scholar] [CrossRef]
- Gul, I.H.; Ahmed, W.; Maqsood, A. Electrical and magnetic characterization of nanocrystalline Ni–Zn ferrite synthesis by co-precipitation route. J. Magn. Magn. Mater. 2008, 320, 270–275. [Google Scholar] [CrossRef]
- Murugendrappa, M.V.; Ambika Prasad, M.V.N. Dielectric spectroscopy of polypyrrole–γ–Fe2O3 composites. Mater. Res. Bull. 2006, 41, 1364–1369. [Google Scholar] [CrossRef]
- De Morais, J.E.V.; Oliveira, R.G.M.; Silva, M.A.S.; Costa, M.M.; Sales, A.J.M.; Bessa, V.L.; Rodrigues, A.R.; Vasconcelos, I.F.; Goldsmith, J.; Carroll, T.K.; et al. Magneto-dielectric properties studies of the matrix composite [SrFe12O19(SFO)1-X – BiFeO3(BFO)X]. J. Alloys Compd. 2018, 735, 2111–2118. [Google Scholar] [CrossRef]
- Dippong, T.; Goga, F.; Levei, E.A.; Cadar, O. Influence of zinc substitution with cobalt on thermal behaviour, structure and morphology of zinc ferrite embedded in silica matrix. J. Solid State Chem. 2019, 275, 159–166. [Google Scholar] [CrossRef]
- Dippong, T.; Levei, E.A.; Cadar, O.; Deac, I.G.; Diamandescu, L.; Barbu-Tudoran, L. Effect of nickel content on structural, morphological and magnetic properties of NixCo1−xFe2O4/SiO2 nanocomposites. J. Alloys Compd. 2019, 786, 330–340. [Google Scholar] [CrossRef]
- Li, J.; Zhou, D. Influence of Ag doping on the dielectric and magnetic properties of LiFe5O8 ceramics. J. Alloys Compd. 2019, 785, 13–18. [Google Scholar] [CrossRef]
- Vinnik, D.A.; Zhivulin, V.E.; Starikov, A.Y.; Gudkova, S.A.; Trofimov, E.A.; Trukhanov, A.V.; Trukhanov, S.V.; Turchenko, V.A.; Matveev, V.V.; Lahderanta, E.; et al. Influence of titanium substitution on structure, magnetic and electric properties of barium hexaferrites BaFe12−xTixO19. J. Magn. Magn. Mater. 2020, 498, 166117. [Google Scholar] [CrossRef]
- Dippong, T.; Deac, I.G.; Cadar, O.; Levei, E.A.; Diamandescu, L.; Borodi, G. Effect of Zn content on structural, morphological and magnetic behavior of ZnxCo1−xFe2O4/SiO2 nanocomposites. J. Alloys Compd. 2019, 792, 432–443. [Google Scholar] [CrossRef]
- Ismail, I.; Hashim, M.; Ibrahim, I.R.; Nazlan, R.; Mohd Idris, F.; Shafie, S.E.; Manap, M.; Bahmanrokh, G.; Abdullah, N.H.; Wan Rahman, W.N. Crystallinity and magnetic properties dependence on sintering temperature and soaking time of mechanically alloyed nanometer-grain Ni0.5Zn0.5Fe2O4. J. Magn. Magn. Mater. 2013, 333, 100–107. [Google Scholar] [CrossRef]
- Liu, R.; Shen, X.; Jiang, C.; Song, F.; Li, H. Preparation of Ni0.5Zn0.5Fe2O4/SiO2 nanocomposites and their adsorption of bovine serum albumin. J. Alloys Compd. 2012, 511, 163–168. [Google Scholar] [CrossRef]
- Aphesteguy, J.C.; Damiani, A.; DiGiovanni, D.; Jacobo, S.E. Microwave-absorbing characteristics of epoxy resin composites containing nanoparticles of NiZn- and NiCuZn-ferrites. Phys. B Condens. Matter 2009, 404, 2713–2716. [Google Scholar] [CrossRef]
- Almessiere, M.A.; Trukhanov, A.V.; Khan, F.A.; Slimani, Y.; Tashkandi, N.; Turchenko, V.A.; Zubar, T.I.; Tishkevich, D.I.; Trukhanov, S.V.; Panina, L.V.; et al. Correlation between microstructure parameters and anti-cancer activity of the [Mn0.5Zn0.5](EuxNdxFe2-2x)O4 nanoferrites produced by modified sol-gel and ultrasonic methods. Ceram. Int. 2020, 46, 7346–7354. [Google Scholar] [CrossRef]
- Dukenbayev, K.; Korolkov, I.V.; Tishkevich, D.I.; Kozlovskiy, A.L.; Trukhanov, S.V.; Gorin, Y.G.; Shumskaya, E.E.; Kaniukov, E.Y.; Vinnik, D.A.; Zdorovets, M.V.; et al. Fe3O4 nanoparticles for complex targeted delivery and boron neutron capture therapy. Nanomaterials 2019, 9, 494. [Google Scholar] [CrossRef]
- Yakovenko, O.S.; Matzui, L.Y.; Vovchenko, L.L.; Lozitsky, O.V.; Prokopov, O.I.; Lazarenko, O.A.; Zhuravkov, A.V.; Oliynyk, V.V.; Launets, V.L.; Trukhanov, S.V.; et al. Electrophysical properties of epoxy-based composites with graphite nanoplatelets and magnetically aligned magnetite. Mol. Cryst. Liq. Cryst. 2018, 661, 68–80. [Google Scholar] [CrossRef]
- Trukhanov, A.V.; Astapovich, K.A.; Almessiere, M.A.; Turchenko, V.A.; Trukhanova, E.L.; Korovushkin, V.V.; Amirov, A.A.; Darwish, M.A.; Karpinsky, D.V.; Vinnik, D.A.; et al. Pecularities of the magnetic structure and microwave properties in Ba(Fe1−xScx)12O19 (x < 0.1) hexaferrites. J. Alloys Compd. 2020, 822, 153575. [Google Scholar] [CrossRef]
- Almessiere, M.A.; Trukhanov, A.V.; Slimani, Y.; You, K.Y.; Trukhanov, S.V.; Trukhanova, E.L.; Esa, F.; Sadaqat, A.; Chaudhary, K.; Zdorovets, M.; et al. Correlation between composition and electrodynamics properties in nanocomposites based on hard/soft ferrimagnetics with strong exchange coupling. Nanomaterials 2019, 9, 202. [Google Scholar] [CrossRef]
- Matzui, L.Y.; Trukhanov, A.V.; Yakovenko, O.S.; Vovchenko, L.L.; Zagorodnii, V.V.; Oliynyk, V.V.; Borovoy, M.O.; Trukhanova, E.L.; Astapovich, K.A.; Karpinsky, D.V.; et al. Functional magnetic composites based on hexaferrites: Correlation of the composition, magnetic and high-frequency properties. Nanomaterials 2019, 9, 1720. [Google Scholar] [CrossRef]
- Turchenko, V.A.; Trukhanov, A.V.; Bobrikov, I.A.; Trukhanov, S.V.; Balagurov, A.M. Study of the crystalline and magnetic structures of BaFe11.4Al0.6O19 in a wide temperature range. J. Surf. Investig. 2015, 9, 17–23. [Google Scholar] [CrossRef]
- Trukhanov, A.V.; Darwish, M.A.; Panina, L.V.; Morchenko, A.T.; Kostishyn, V.G.; Turchenko, V.A.; Vinnik, D.A.; Trukhanova, E.L.; Astapovich, K.A.; Kozlovskiy, A.L.; et al. Features of crystal and magnetic structure of the BaFe12−xGaxO19 (x ≤ 2) in the wide temperature range. J. Alloys Compd. 2019, 791, 522–529. [Google Scholar] [CrossRef]
- Trukhanov, A.V.; Almessiere, M.A.; Baykal, A.; Trukhanov, S.V.; Slimani, Y.; Vinnik, D.A.; Zhivulin, V.E.; Starikov, A.Y.; Klygach, D.S.; Vakhitov, M.G.; et al. Influence of the charge ordering and quantum effects in heterovalent substituted hexaferrites on their microwave characteristics. J. Alloys Compd. 2019, 788, 1193–1202. [Google Scholar] [CrossRef]
- Ramajo, L.A.; Cristóbal, A.A.; Botta, P.M.; Porto López, J.M.; Reboredo, M.M.; Castro, M.S. Dielectric and magnetic response of Fe3O4/epoxy composites. Compos. Part A Appl. Sci. 2009, 40, 388–393. [Google Scholar] [CrossRef]
- Wang, Y.; Li, L.; Jiang, J.; Liu, H.; Qiu, H.; Xu, F. Conductivity and magnetic properties of Zn0.6Cu0.4Cr0.5La0.04Fe1.46O4/PPy composites prepared by in situ inverse microemulsion polymerization. React. Funct. Polym. 2008, 68, 1587–1593. [Google Scholar] [CrossRef]
- Li, G.; Yan, S.; Zhou, E.; Chen, Y. Preparation of magnetic and conductive NiZn ferrite-polyaniline nanocomposites with core-shell structure. Colloid Surf. A 2006, 276, 40–44. [Google Scholar] [CrossRef]
- Salem, M.M.; Panina, L.V.; Trukhanova, E.L.; Darwish, M.A.; Morchenko, A.T.; Zubar, T.I.; Trukhanov, S.V.; Trukhanov, A.V. Structural, electric and magnetic properties of (BaFe11.9Al0.1O19)1−x - (BaTiO3)x composites. Compos. B Eng. 2019, 174, 107054. [Google Scholar] [CrossRef]
- Saafan, S.A.; Assar, S.T.; Moharram, B.M.; El Nimr, M.K. Comparison study of some structural and magnetic properties of nano-structured and bulk Li–Ni–Zn ferrite samples. J. Magn. Magn. Mater. 2010, 322, 628–632. [Google Scholar] [CrossRef]
- Darwish, M.A.; Saafan, S.A.; El-Kony, D.; Salahuddin, N.A. Preparation and investigation of dc conductivity and relative permeability of epoxy/Li–Ni–Zn ferrite composites. J. Magn. Magn. Mater. 2015, 385, 99–106. [Google Scholar] [CrossRef]
- Trukhanov, S.V.; Trukhanov, A.V.; Kostishin, V.G.; Panina, L.V.; Kazakevich, I.S.; Turchenko, V.A.; Oleinik, V.V.; Yakovenko, E.S.; Matsui, L.Y. Magnetic and absorbing properties of M-type substituted hexaferrites BaFe12−xGaxO19 (0.1 < x < 1.2). JETP 2016, 123, 461–469. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, F.; Shao, J.; Huang, D.; He, H.; Trukhanov, A.V.; Trukhanov, S.V. Influence of Nd-NbZn co-substitution on structural, spectral and magnetic properties of M-type calcium-strontium hexaferrites Ca0.4Sr0.6−xNdxFe12.0−x(Nb0.5Zn0.5)xO19. J. Alloys Compd. 2018, 765, 616–623. [Google Scholar] [CrossRef]
- El Hiti, M.A. Dielectric behavior and ac electrical conductivity of Zn-substituted Ni-Mg ferrites. J. Magn. Magn. Mater. 1996, 164, 187–196. [Google Scholar] [CrossRef]
- Abdeen, A.M. Electric conduction in Ni–Zn ferrites. J. Magn. Magn. Mater. 1998, 185, 199–206. [Google Scholar] [CrossRef]
- Vinnik, D.A.; Klygach, D.S.; Zhivulin, V.E.; Malkin, A.I.; Vakhitov, M.G.; Gudkova, S.A.; Galimov, D.M.; Zherebtsov, D.A.; Trofimov, E.A.; Knyazev, N.S.; et al. Electromagnetic properties of BaFe12O19:Ti at centimeter wavelengths. J. Alloys Compd. 2018, 755, 177–183. [Google Scholar] [CrossRef]
- Elliott, S.R. Ac conduction in amorphous chalcogenide and pnictide semiconductors. Adv. Phys. 1987, 36, 135–217. [Google Scholar] [CrossRef]
- Batoo, K.M.; Kumar, S.; Lee, C.G.; Alimuddin. Finite size effect and influence of temperature on electrical properties of nanocrystalline Ni–Cd ferrites. Curr. Appl. Phys. 2009, 9, 1072–1078. [Google Scholar] [CrossRef]
- Soibam, I.; Phanjoubam, S.; Sharma, H.B.; Sarma, H.N.K.; Laishram, R.; Prakash, C. Effects of cobalt substitution on the dielectric properties of Li–Zn ferrites. Solid State Commun. 2008, 148, 399–402. [Google Scholar] [CrossRef]
- Thakur, A.; Mathur, P.; Singh, M. Study of dielectric behaviour of Mn-Zn nano ferrites. J. Phys. Chem. Solids 2007, 68, 378–381. [Google Scholar] [CrossRef]
- Koops, C.G. On the dispersion of resistivity and dielectric constant of some semiconductors at audiofrequencies. Phys. Rev. 1951, 83, 121–124. [Google Scholar] [CrossRef]
- El Hiti, M.A. Electrical and dielectric properties of NixMg1−xFe2O4. J. Phys. III 1996, 6, 1307–1313. [Google Scholar] [CrossRef]
- Goldman, A. Modern Ferrite Technology; Springer: Pittsburgh, PA, USA, 2006. [Google Scholar] [CrossRef]
- Saafan, S.A.; Assar, S.T. Dielectric behavior of nano-structured and bulk Li Ni Zn ferrite samples. J. Magn. Magn. Mater. 2012, 324, 2989–3001. [Google Scholar] [CrossRef]
- Trukhanov, A.V.; Grabchikov, S.S.; Solobai, A.A.; Tishkevich, D.I.; Trukhanov, S.V.; Trukhanova, E.L. AC and DC-shielding properties for the Ni80Fe20/Cu film structures. J. Magn. Magn. Mater. 2017, 443, 142–148. [Google Scholar] [CrossRef]
- Gul, I.H.; Abbasi, A.Z.; Amin, F.; Anis-ur-Rehman, M.; Maqsood, A. Structural, magnetic and electrical properties of Co1−xZnxFe2O4 synthesized by co-precipitation method. J. Magn. Magn. Mater. 2007, 311, 494–499. [Google Scholar] [CrossRef]
- Ravinder, D. Effect of sintering temperature on electrical conductivity of mixed lithium-cadmium ferrites. Mater. Lett. 1999, 40, 198–203. [Google Scholar] [CrossRef]
- Ramana Reddy, A.V.; Ranga Mohan, G.; Boyanov, B.S.; Ravinder, D. Electrical transport properties of zinc-substituted cobalt ferrites. Mater. Lett. 1999, 39, 153–165. [Google Scholar] [CrossRef]
- Ravinder, D.; Chandrashekhar Reddy, A.; Shalini, P. High-temperature electrical conductivity of Li-Ge ferrites. J. Alloys Compd. 2003, 360, 30–33. [Google Scholar] [CrossRef]
- Almessiere, M.A.; Slimani, Y.; Güngüne, H.; Baykal, A.; Trukhanov, S.V.; Trukhanov, A.V. Manganese/Yttrium codoped strontium nanohexaferrites: Evaluation of magnetic susceptibility and Mössbauer spectra. Nanomaterials 2019, 9, 24. [Google Scholar] [CrossRef] [PubMed]
- Ravinder, D.; Latha, K. Dielectric behaviour of mixed Mg–Zn ferrites at low frequencies. Mater. Lett. 1999, 41, 247–253. [Google Scholar] [CrossRef]
- Salem, M.M.; Morchenko, A.T.; Panina, L.V.; Kostishyn, V.G.; Andreev, V.G.; Bibikov, S.B.; Nikolaev, A.N. Dielectric and magnetic properties of two-phase composite system: Mn-Zn or Ni-Zn ferrites in dielectric matrices. Phys. Proc. 2015, 75, 1360–1369. [Google Scholar] [CrossRef]
- Grabchikov, S.S.; Trukhanov, A.V.; Trukhanov, S.V.; Kazakevich, I.S.; Solobay, A.A.; Erofeenko, V.T.; Vasilenkov, N.A.; Volkova, O.S.; Shakin, A. Effectiveness of the magnetostatic shielding by the cylindrical shells. J. Magn. Magn. Mater. 2016, 398, 49–53. [Google Scholar] [CrossRef]
- Ravinder, D.; Kumar, K.V. Dielectric behaviour of erbium substituted Mn-Zn ferrites. Bull. Mater. Sci. 2001, 24, 505–509. [Google Scholar] [CrossRef]
- Turchenko, V.; Trukhanov, A.; Trukhanov, S.; Balasoiu, M.; Lupu, N. Correlation of crystalline and magnetic structures of barium ferrites with dual ferroic properties. J. Magn. Magn. Mater. 2019, 477, 9–16. [Google Scholar] [CrossRef]
- Assar, S.T.; Abosheiasha, H.F.; Mansour, D.E.A.; Darwish, M.A. Preparation and investigation of epoxy/Li0.5AlxFe2.5−xO4 nanocomposites for electronic packaging applications. J. Alloys Compd. 2020, 821, 153533. [Google Scholar] [CrossRef]
- Yang, Y.; Li, J.; Zhang, H.; Wang, G.; Rao, Y.; Gan, G. TiO2 tailored low loss NiCuZn ferrite ceramics having equivalent permeability and permittivity for miniaturized antenna. J. Magn. Magn. Mater. 2019, 487, 165318. [Google Scholar] [CrossRef]
- Morchenko, A.T. Modeling the structure and conditions of the absorption of electromagnetic radiation in magnetic composites using effective medium approximations. Bull. Russ. Acad. Sci. Phys. 2014, 78, 1209–1217. [Google Scholar] [CrossRef]
- Rozanov, K.N. Frequency-dependent effective material parameters of composites as a function of inclusion shape. In Composites and Their Properties; Koledintseva, M.Y., Ed.; IntechOpen: Rijeka, Croatia, 2012; p. 15. [Google Scholar] [CrossRef]
- Bruggeman, D.A.G. Berechnung verschiedener physikalischer konstanten von heterogenen substanzen. I. Dielektrizitätskonstanten und leitfähigkeiten der mischkörper aus isotropen substanzen. Ann. Phys. 1935, 416, 636–664. [Google Scholar] [CrossRef]
- Polder, D.; van Santen, J.H. The effective permeability of mixtures of solids. Physica 1946, 12, 257–271. [Google Scholar] [CrossRef]
- Barber, P.; Balasubramanian, S.; Anguchamy, Y.; Gong, S.; Wibowo, A.; Gao, H.; Ploehn, H.J.; zur Loye, H.-C. Polymer composite and nanocomposite dielectric materials for pulse power energy storage. Materials 2009, 2, 1697–1733. [Google Scholar] [CrossRef]
- Turchenko, V.; Kostishyn, V.G.; Trukhanov, S.; Damay, F.; Porcher, F.; Balasoiu, M.; Lupu, N.; Bozzo, B.; Fina, I.; Trukhanov, A.; et al. Crystal and magnetic structures, magnetic and ferroelectric properties of strontium ferrite partially substituted with in ions. J. Alloys Compd. 2020, 821, 153412. [Google Scholar] [CrossRef]
- Kaur, H.; Marwaha, A.; Singh, C.; Narang, S.B.; Jotania, R.; Jacobo, S.; Sombra, A.S.B.; Trukhanov, S.V.; Trukhanov, A.V.; Dhruv, P. Investigation of structural, hysteresis and electromagnetic parameters for microwave absorption application in doped Ba-Sr hexagonal ferrites at X-band. J. Alloys Compd. 2019, 806, 1220–1229. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Darwish, M.A.; Trukhanov, A.V.; Senatov, O.S.; Morchenko, A.T.; Saafan, S.A.; Astapovich, K.A.; Trukhanov, S.V.; Trukhanova, E.L.; Pilyushkin, A.A.; Sombra, A.S.B.; et al. Investigation of AC-Measurements of Epoxy/Ferrite Composites. Nanomaterials 2020, 10, 492. https://doi.org/10.3390/nano10030492
Darwish MA, Trukhanov AV, Senatov OS, Morchenko AT, Saafan SA, Astapovich KA, Trukhanov SV, Trukhanova EL, Pilyushkin AA, Sombra ASB, et al. Investigation of AC-Measurements of Epoxy/Ferrite Composites. Nanomaterials. 2020; 10(3):492. https://doi.org/10.3390/nano10030492
Chicago/Turabian StyleDarwish, Moustafa A., Alex V. Trukhanov, Oleg S. Senatov, Alexander T. Morchenko, Samia A. Saafan, Ksenia A. Astapovich, Sergei V. Trukhanov, Ekaterina L. Trukhanova, Andrey A. Pilyushkin, Antonio Sergio B. Sombra, and et al. 2020. "Investigation of AC-Measurements of Epoxy/Ferrite Composites" Nanomaterials 10, no. 3: 492. https://doi.org/10.3390/nano10030492
APA StyleDarwish, M. A., Trukhanov, A. V., Senatov, O. S., Morchenko, A. T., Saafan, S. A., Astapovich, K. A., Trukhanov, S. V., Trukhanova, E. L., Pilyushkin, A. A., Sombra, A. S. B., Zhou, D., Jotania, R. B., & Singh, C. (2020). Investigation of AC-Measurements of Epoxy/Ferrite Composites. Nanomaterials, 10(3), 492. https://doi.org/10.3390/nano10030492