Effects of a Rotating Cone on the Mixed Convection in a Double Lid-Driven 3D Porous Trapezoidal Nanofluid Filled Cavity under the Impact of Magnetic Field
Abstract
1. Introduction
2. Modeling Steps in the Numerical Simulation
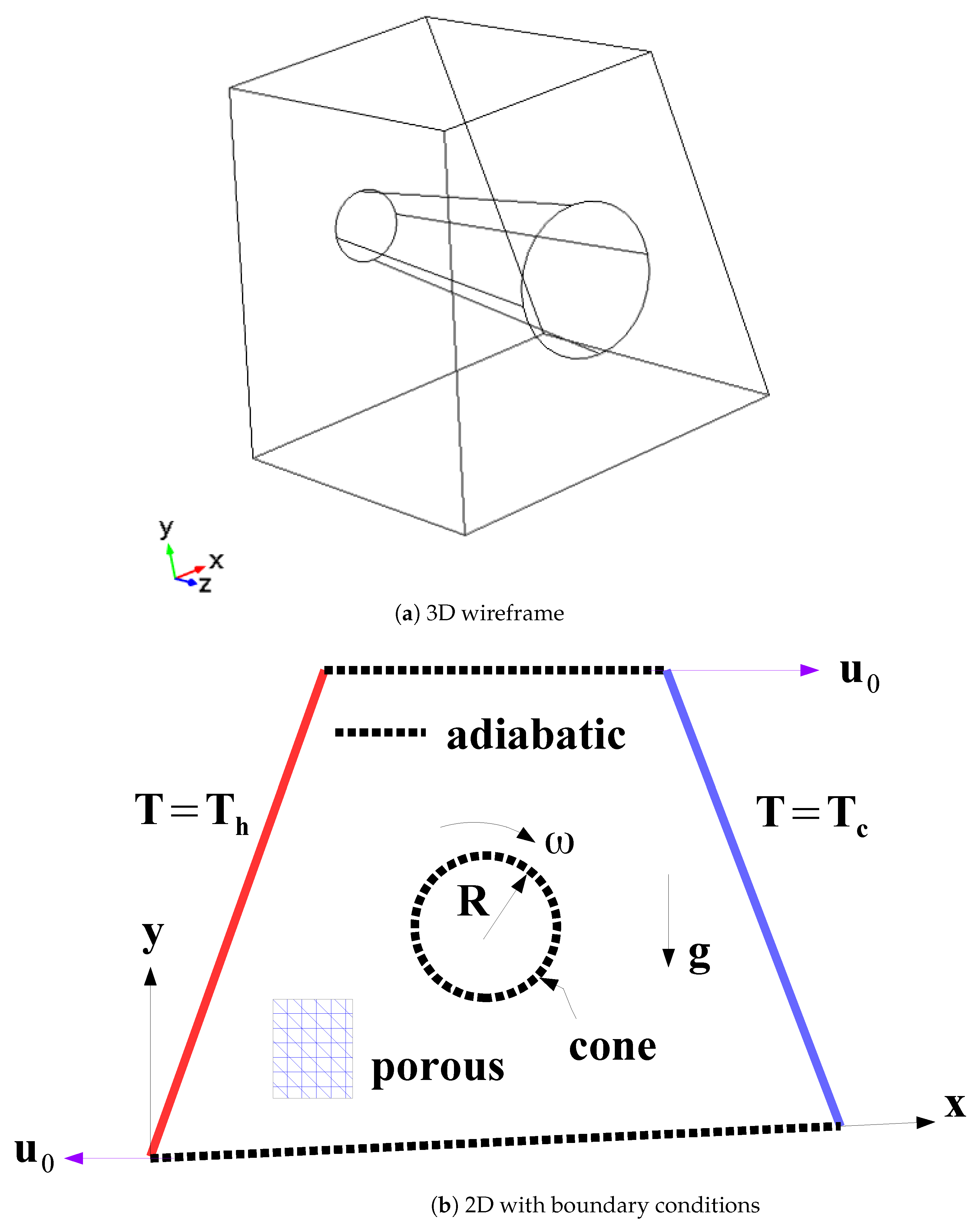
2.1. Geometric Model and Governing Equations
- -
- For horizontal upper moving surface, .
- -
- For left side surface, .
- -
- For right side surface, .
- -
- For horizontal lower moving surface, .
- -
- Along the surface of the cone, .
2.2. CNT-Water Nanofluid Property Equations
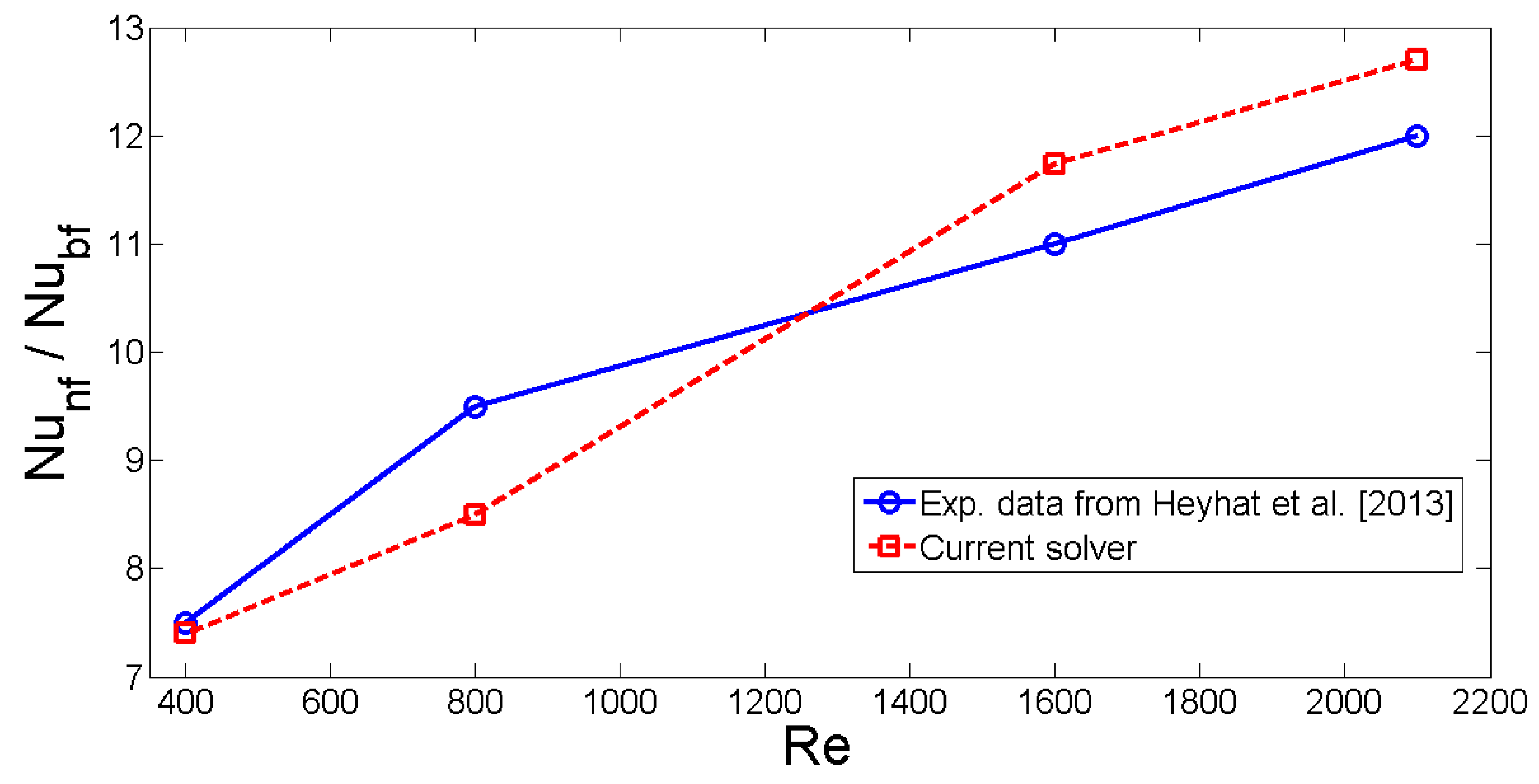
2.3. Mesh Examination and Code Verification
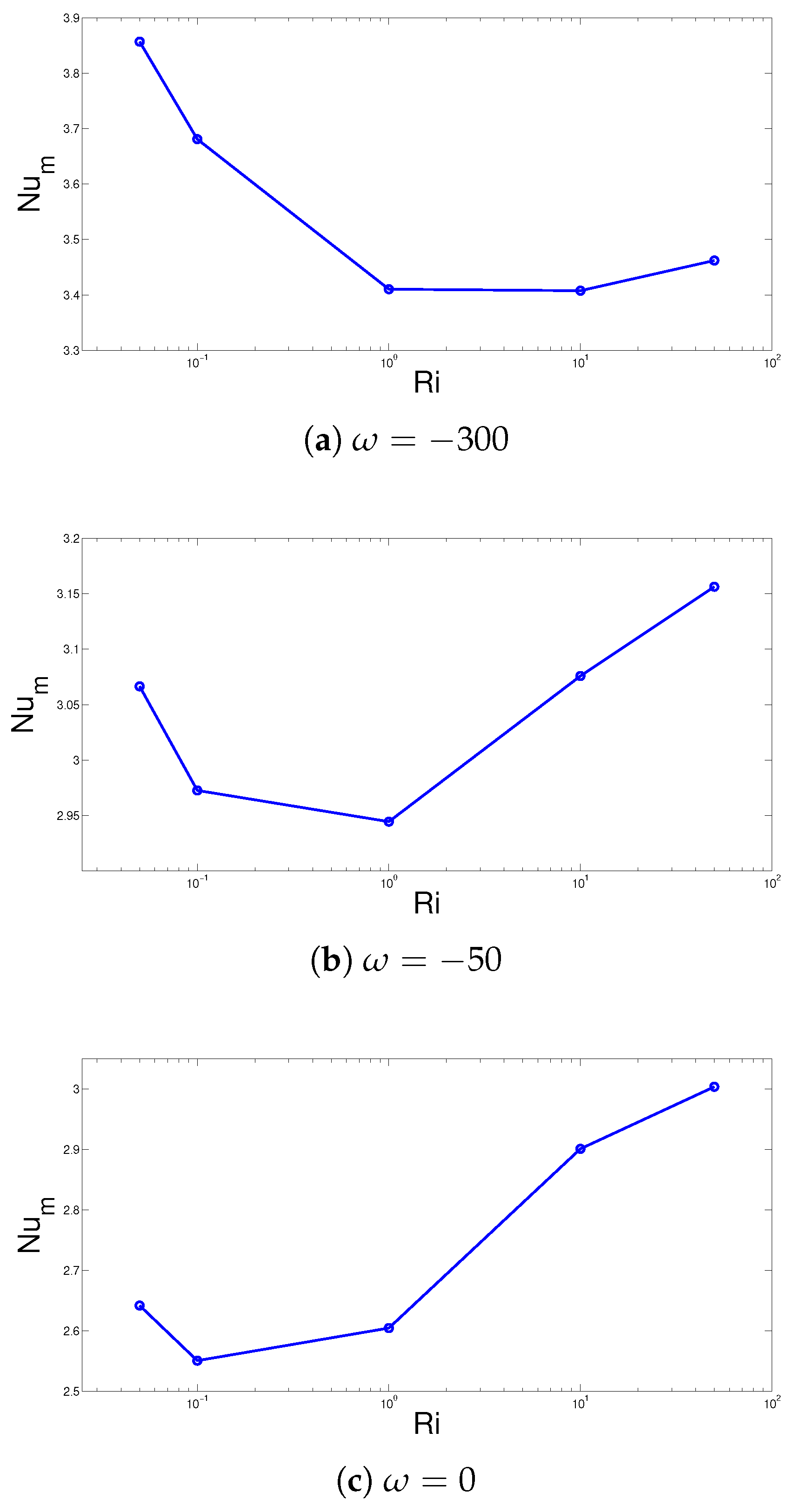
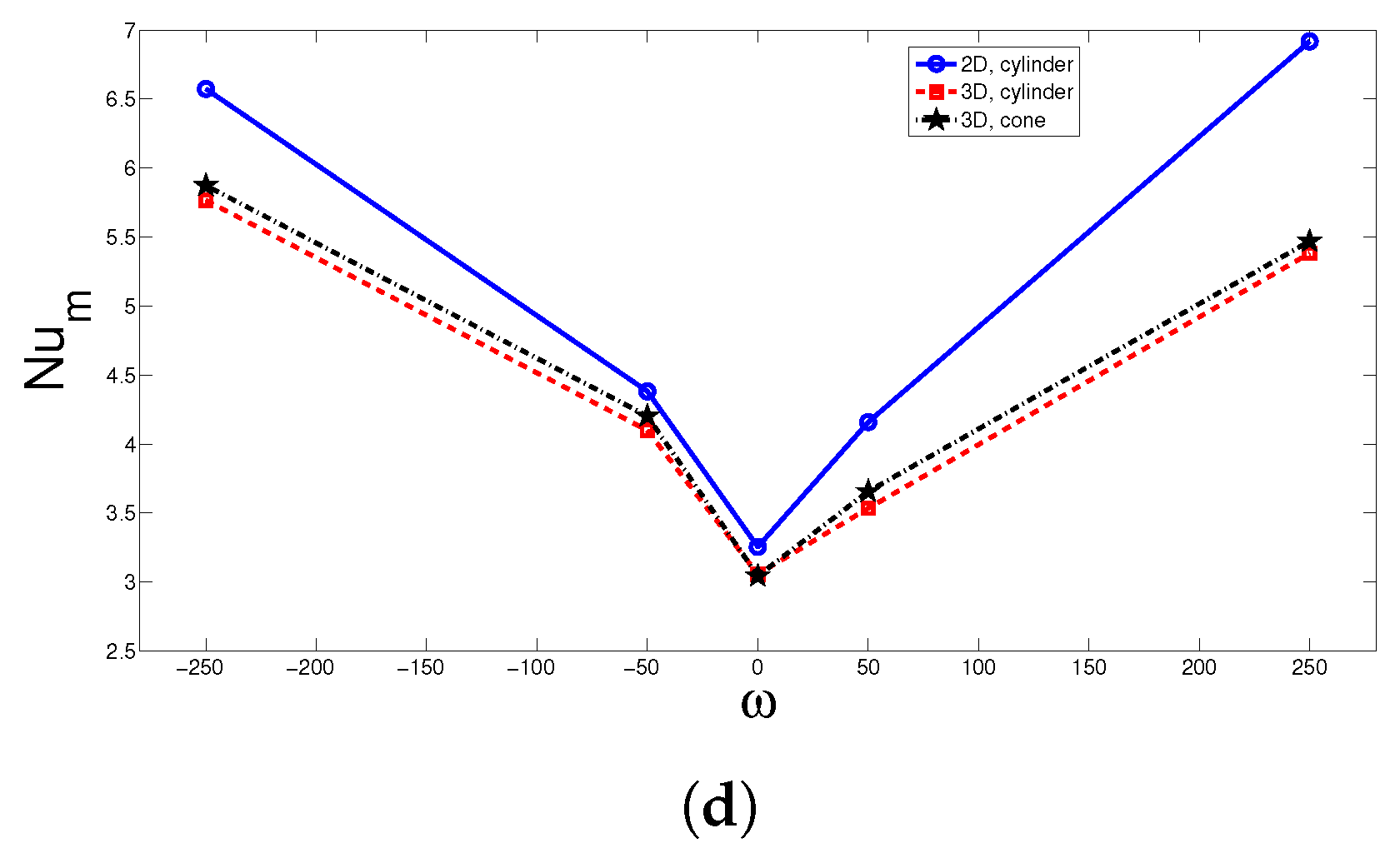
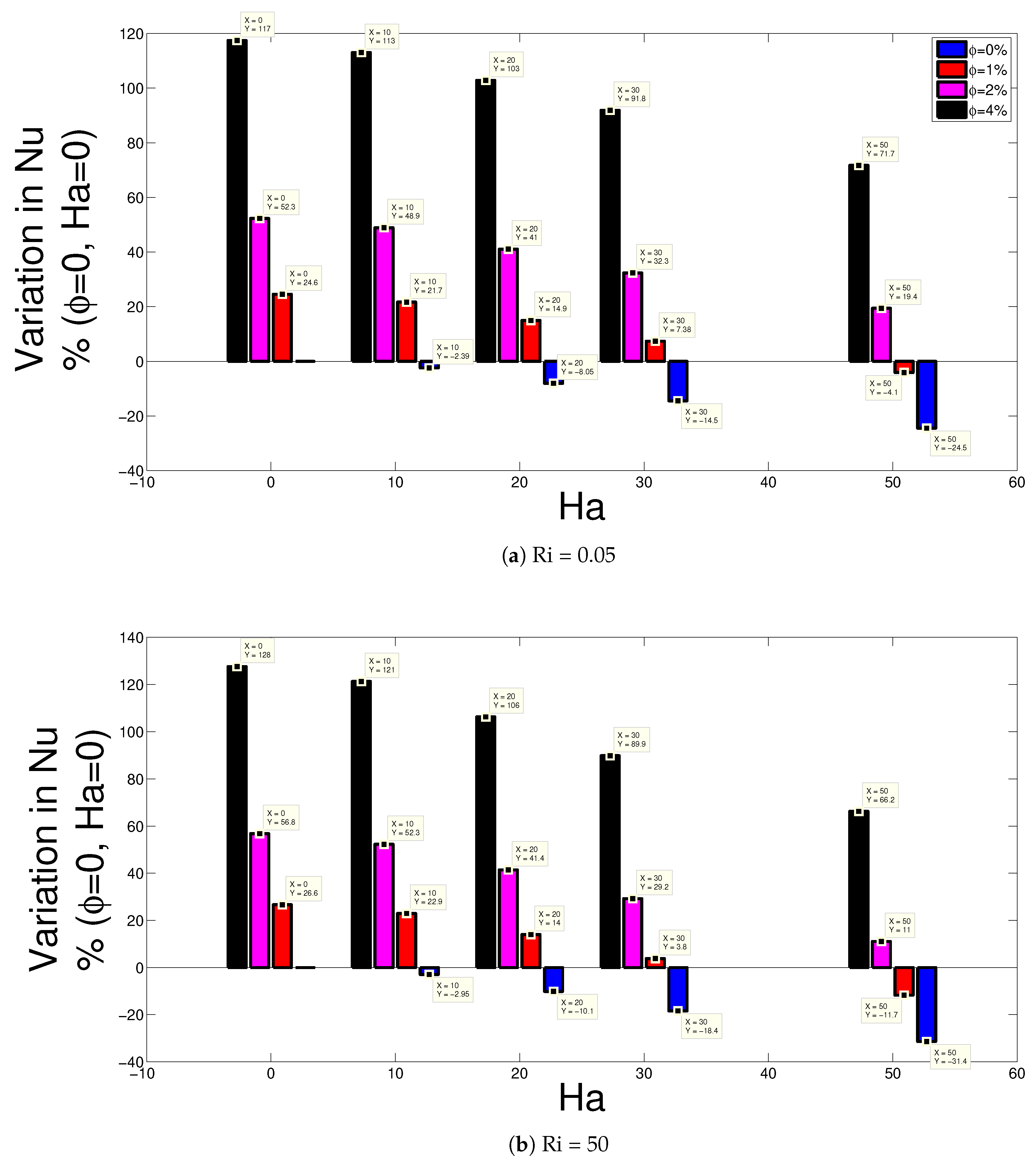
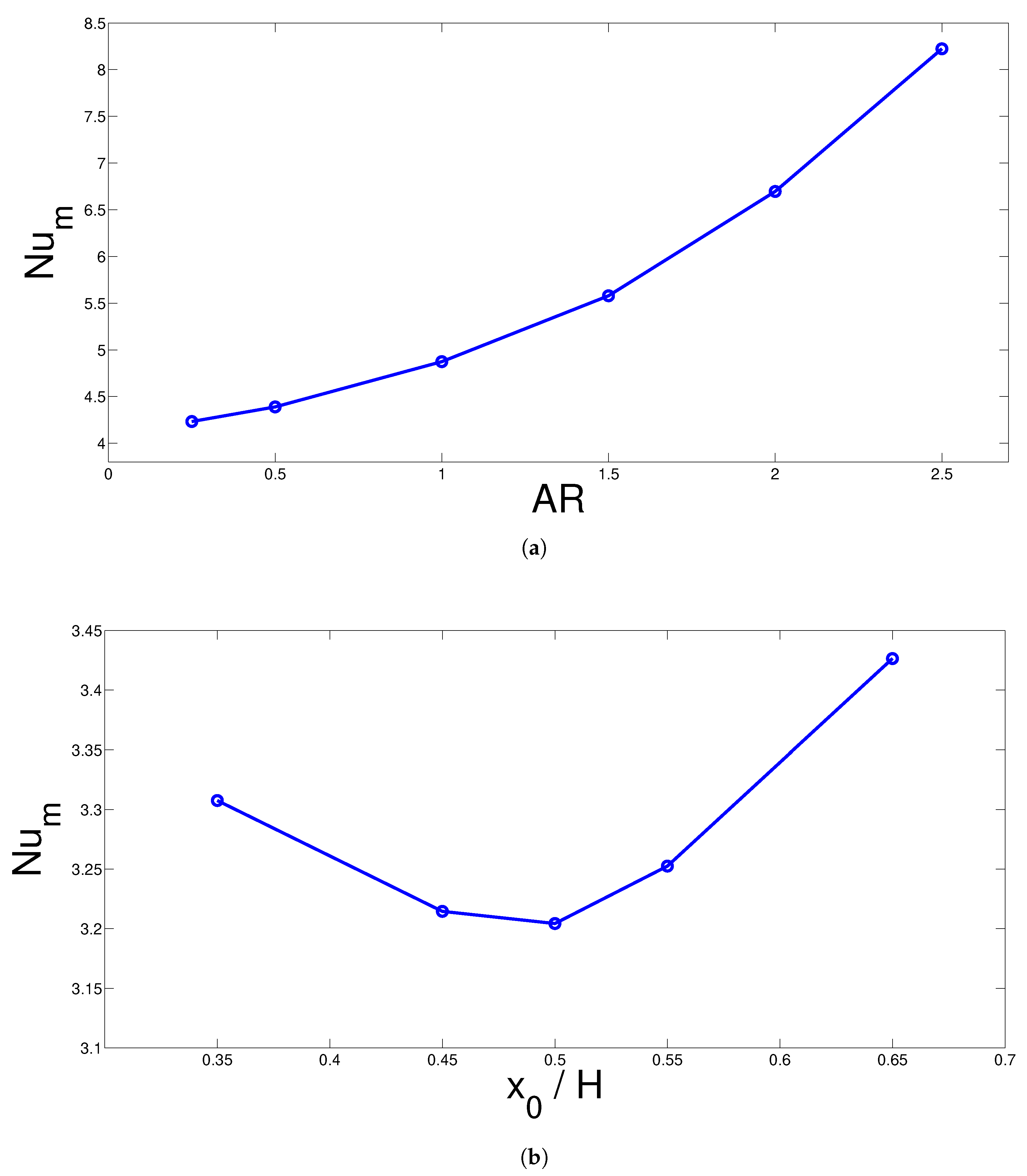
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations/Nomenclature
| x, y | Cartesian coordinates | ||
| AR | aspect ratio | Greek Characters | |
| F | weight function | thermal diffusivity | |
| Gr | Grashof number | expansion coefficient | |
| g | gravitational acceleration | solid volume fraction | |
| h | local heat transfer coefficient | kinematic viscosity | |
| Ha | Hratamnn nunber | non-dimensional temperature | |
| k | thermal conductivity | porosity | |
| n | unit normal vector | permeability | |
| Nu | local Nusselt number | density of the fluid | |
| Nu | average Nusselt number | electrical conductivity | |
| p | pressure | rotational speed of the cone | |
| Pr | Prandtl number | Subscripts | |
| R | normalized residual | c | cold |
| Ra | Rayleigh number | CNT | carbon nanotube |
| Re | Reynolds number | h | hot |
| Ri | Richardson number | m | average |
| T | temperature | nf | nanofluid |
| u, v | x-y velocity components | p | solid particle |
References
- Chamkha, A.J.; Abu-Nada, E. Mixed convection flow in single- and double-lid driven square cavities filled with water—Al2O3 nanofluid: Effect of viscosity models. Eur. J. Mech. B Fluids 2012, 36, 82–96. [Google Scholar] [CrossRef]
- Islam, A.; Sharif, M.; Carlson, E. Mixed convection in a lid driven square cavity with an isothermally heated square blockage inside. Int. J. Heat Mass Transf. 2012, 55, 5244–5255. [Google Scholar] [CrossRef]
- Garmroodi, M.R.D.; Ahmadpour, A.; Talati, F. MHD mixed convection of nanofluids in the presence of multiple rotating cylinders in different configurations: A two-phase numerical study. Int. J. Mech. Sci. 2019, 150, 247–264. [Google Scholar] [CrossRef]
- Barnoon, P.; Toghraie, D.; Dehkordi, R.B.; Abed, H. MHD mixed convection and entropy generation in a lid-driven cavity with rotating cylinders filled by a nanofluid using two phase mixture model. J. Magn. Magn. Mater. 2019, 483, 224–248. [Google Scholar] [CrossRef]
- Lewis, E. Steady flow between a rotating circular cylinder and fixed square cylinder. J. Fluid Mech. 1979, 95, 497–513. [Google Scholar] [CrossRef]
- Khanafer, K.; Aithal, S. Laminar mixed convection flow and heat transfer characteristics in a lid driven cavity with a circular cylinder. Int. J. Heat Mass Transf. 2013, 66, 200–209. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Gorji-Bandpy, M.; Ganji, D.; Soleimani, S.; Seyyedi, S. Natural convection of nanofluids in an enclosure between a circular and a sinusoidal cylinder in the presence of magnetic field. Int. Commun. Heat Mass Transf. 2012, 39, 1435–1443. [Google Scholar] [CrossRef]
- Oztop, H.F.; Zhao, Z.; Yu, B. Fluid flow due to combined convection in lid-driven enclosure having a circular body. Int. J. Heat Fluid Flow 2009, 30, 886–901. [Google Scholar] [CrossRef]
- Costa, V.A.F.; Raimundo, A.M. Steady mixed convection in a differentially heated square enclosure with an active rotating circular cylinder. Int. J. Heat Mass Transf. 2010, 53, 1208–1219. [Google Scholar] [CrossRef]
- Hussain, S.H.; Hussein, A.K. Mixed convection heat transfer in a differentially heated square enclosure with a conductive rotating circular cylinder at different vertical locations. Int. Commun. Heat Mass Transf. 2011, 38, 263–274. [Google Scholar] [CrossRef]
- Ghaddar, N.; Thiele, F. Natural convection over a rotating cylindrical heat source in a rectangular enclosure. Numer. Heat Transf. A Appl. 1994, 26, 701–717. [Google Scholar] [CrossRef]
- Fu, W.; Cheng, C.; Shieh, W. Enhancement of natural convection heat transfer of an enclosure by a rotating circular cylinder. Int. J. Heat Mass Transf. 1994, 37, 1885–1897. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Oztop, H.F. Conjugate mixed convection of nanofluid in a cubic enclosure separated with a conductive plate and having an inner rotating cylinder. Int. J. Heat Mass Transf. 2019, 139, 1000–1017. [Google Scholar] [CrossRef]
- Kareem, A.K.; Gao, S. A comparison study of mixed convection heat transfer of turbulent nanofluid flow in a three-dimensional lid-driven enclosure with a clockwise versus an anticlockwise rotating cylinder. Int. Commun. Heat Mass Transf. 2018, 90, 44–55. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Oztop, H.F. Mixed convection of nanofluids in a three dimensional cavity with two adiabatic inner rotating cylinders. Int. J. Heat Mass Transf. 2018, 117, 331–343. [Google Scholar] [CrossRef]
- Sarris, I.; Zikos, G.; Grecos, A.; Vlachos, N. On the limits of validity of the low magnetic Reynolds number approximation in MHD natural-convection heat transfer. Numer. Heat Transf. Part B 2006, 50, 158–180. [Google Scholar] [CrossRef]
- Sajjadi, H.; Delouei, A.A.; Izadi, M.; Mohebbi, R. Investigation of MHD natural convection in a porous media by double MRT lattice Boltzmann method utilizing MWCNT-Fe3O4/water hybrid nanofluid. Int. J. Heat Mass Transf. 2019, 132, 1087–1104. [Google Scholar] [CrossRef]
- Geridonmez, B.P.; Oztop, H.F. Natural convection in a cavity filled with porous medium under the effect of a partial magnetic field. Int. J. Mech. Sci. 2019, 161, 105077. [Google Scholar] [CrossRef]
- Wang, Z.H.; Zhou, Z.K. External natural convection heat transfer of liquid metal under the influence of the magnetic field. Int. J. Heat Mass Transf. 2019, 134, 175–184. [Google Scholar] [CrossRef]
- Rahman, M.; Oztop, H.F.; Saidur, R.; Mekhilef, S.; Al-Salem, K. Finite element solution of MHD mixed convection in a channel with a fully or partially heated cavity. Comput. Fluids 2013, 79, 53–64. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Oztop, H.F. Numerical study of MHD mixed convection in a nanofluid filled lid driven square enclosure with a rotating cylinder. Int. J. Heat Mass Transf. 2014, 78, 741–754. [Google Scholar] [CrossRef]
- Pekmen, B.; Sezgin, M.T. MHD flow and heat transfer in a lid-driven porous enclosure. Comput. Fluids 2014, 89, 191–199. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Oztop, H.F. Fluid-solid interaction of elastic-step type corrugation effects on the mixed convection of nanofluid in a vented cavity with magnetic field. Int. J. Mech. Sci. 2019, 152, 185–197. [Google Scholar] [CrossRef]
- Abbassi, H.; Nassrallah, S.B. MHD flow and heat transfer in a backward-facing step. Int. Commun. Heat Mass Transf. 2007, 34, 231–237. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Oztop, H.F. Influence of inclination angle of magnetic field on mixed convection of nanofluid flow over a backward facing step and entropy generation. Adv. Powder Technol. 2015, 26, 1663–1675. [Google Scholar] [CrossRef]
- Ma, Y.; Mohebbi, R.; Rashidi, M.M.; Yang, Z.; Sheremet, M.A. Numerical study of MHD nanofluid natural convection in a baffled U-shaped enclosure. Int. J. Heat Mass Transf. 2019, 130, 123–134. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Oztop, H.F. Analysis of MHD mixed convection in a flexible walled and nanofluids filled lid-driven cavity with volumetric heat generation. Int. J. Mech. Sci. 2016, 118, 113–124. [Google Scholar] [CrossRef]
- Mahmoudi, A.; Mejri, I.; Abbassi, M.A.; Omri, A. Analysis of MHD natural convection in a nanofluid-filled open cavity with non uniform boundary condition in the presence of uniform heat generation/absorption. Powder Technol. 2015, 269, 275–289. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Bandpy, M.G.; Ellahi, R.; Zeeshan, A. Simulation of MHD CuO-water nanofluid flow and convective heat transfer considering Lorentz forces. J. Magn. Magn. Mater. 2014, 369, 69–80. [Google Scholar] [CrossRef]
- Salman, S.; Talib, A.R.A.; Saadon, S.; Sultan, M.T.H. Hybrid nanofluid flow and heat transfer over backward and forward steps: A review. Powder Technol. 2020, 363, 448–472. [Google Scholar] [CrossRef]
- Javed, S.; Ali, H.M.; Babar, H.; Khan, M.S.; Janjua, M.M.; Bashir, M.A. Internal convective heat transfer of nanofluids in different flow regimes: A comprehensive review. Phys. A Stat. Mech. Appl. 2020, 538, 122783. [Google Scholar] [CrossRef]
- Huminic, G.; Huminic, A. Entropy generation of nanofluid and hybrid nanofluid flow in thermal systems: A review. J. Mol. Liq. 2020, 302, 112533. [Google Scholar] [CrossRef]
- Mahian, O.; Kianifar, A.; Heris, S.Z.; Wen, D.; Sahin, A.Z.; Wongwises, S. Nanofluids effects on the evaporation rate in a solar still equipped with a heat exchanger. Nano Energy 2017, 36, 134–155. [Google Scholar] [CrossRef]
- Cho, C.C. Heat transfer and entropy generation of natural convection in nanofluid-filled square cavity with partially-heated wavy surface. Int. J. Heat Mass Transf. 2014, 77, 818–827. [Google Scholar] [CrossRef]
- Tiwari, R.; Das, M.K. Heat Transfer Augmentation in a Two-Sided Lid-Driven Differentially Heated Square Cavity Utilizing Nanofluids. Int. J. Heat Mass Transf. 2007, 50, 2002–2018. [Google Scholar] [CrossRef]
- Oztop, H.F.; Abu-Nada, E. Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids. Int. J. Heat Fluid Flow 2008, 29, 1326–1336. [Google Scholar] [CrossRef]
- Koo, J.; Kleinstreuer, C. Laminar nanofluid flow in microheat-sinks. Int. J. Heat Mass Transf. 2005, 48, 2652–2661. [Google Scholar] [CrossRef]
- Hajialigol, N.; Fattahi, A.; Ahmadi, M.H.; Qomi, M.E.; Kakoli, E. MHD mixed convection and entropy generation in a 3-D microchannel using Al2O3 water nanofluid. J. Taiwan Inst. Chem. Eng. 2015, 46, 30–42. [Google Scholar] [CrossRef]
- Drummond, J.; Korpela, S. Natural convection in a shallow cavity. J. Fluid Mech. 1987, 182, 543–564. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Shehzad, S.A.; Li, Z. Water based nanofluid free convection heat transfer in a three dimensional porous cavity with hot sphere obstacle in existence of Lorenz forces. Int. J. Heat Mass Transf. 2018, 125, 375–386. [Google Scholar] [CrossRef]
- Al-Rashed, A.A.; Kalidasan, K.; Kolsi, L.; Aydi, A.; Malekshah, E.H.; Hussein, A.K.; Kanna, P.R. Three-dimensional investigation of the effects of external magnetic field inclination on laminar natural convection heat transfer in CNT water nanofluid filled cavity. J. Mol. Liq. 2018, 252, 454–468. [Google Scholar] [CrossRef]
- Ghasemi, K.; Siavashi, M. Three-dimensional analysis of magnetohydrodynamic transverse mixed convection of nanofluid inside a lid-driven enclosure using MRT-LBM. Int. J. Mech. Sci. 2020, 165, 105199. [Google Scholar] [CrossRef]
- Gibanov, N.S.; Sheremet, M.A.; Oztop, H.F.; Al-Salem, K. MHD natural convection and entropy generation in an open cavity having different horizontal porous blocks saturated with a ferrofluid. J. Magn. Magn. Mater. 2018, 452, 193–204. [Google Scholar] [CrossRef]
- Miroshnichenko, I.V.; Sheremet, M.A.; Oztop, H.F.; Abu-Hamdeh, N. Natural convection of alumina-water nanofluid in an open cavity having multiple porous layers. Int. J. Heat Mass Transf. 2018, 125, 648–657. [Google Scholar] [CrossRef]
- Ghasemi, K.; Siavashi, M. MHD nanofluid free convection and entropy generation in porous enclosures with different conductivity ratios. J. Magn. Magn. Mater. 2017, 442, 474–490. [Google Scholar] [CrossRef]
- Raza, J.; Rohni, A.M.; Omar, Z. MHD flow and heat transfer of Cu-water nanofluid in a semi porous channel with stretching walls. Int. J. Heat Mass Transf. 2016, 103, 336–340. [Google Scholar] [CrossRef]
- Mehryan, S.A.M.; Sheremet, M.A.; Soltani, M.; Izadi, M. Natural convection of magnetic hybrid nanofluid inside a double-porous medium using two-equation energy model. J. Mol. Liq. 2019, 277, 959–970. [Google Scholar] [CrossRef]
- Kumaresan, V.; Velraj, R. Experimental investigation of the thermo-physical properties of water-ethylene glycol mixture based CNT nanofluids. Thermochim. Acta 2012, 545, 180–186. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Oztop, H.F. Corrugated conductive partition effects on MHD free convection of CNT-water nanofluid in a cavity. Int. J. Heat Mass Transf. 2019, 129, 265–277. [Google Scholar] [CrossRef]
- Abu-Nada, E.; Chamkha, A.J. Mixed convection flow in a lid-driven inclined square enclosure filled with a nanofluid. Eur. J. Mech. B Fluids 2010, 29, 472–482. [Google Scholar] [CrossRef]
- Basak, T.; Roy, S.; Pop, I. Heat flow analysis for natural convection within trapezoidal enclosures based on heatline concept. Int. J. Heat Mass Transf. 2009, 52, 2471–2483. [Google Scholar]
- Brinkman, H. The viscosity of concentrated suspensions and solutions. J. Chem. Phys. 1952, 20, 571–581. [Google Scholar] [CrossRef]
- Al-Sayegh, R. Influence of external magnetic field inclination on three-dimensional buoyancy-driven convection in an open trapezoidal cavity filled with CNT-Water nanofluid. Int. J. Mech. Sci. 2018, 148, 756–765. [Google Scholar]
- Al-Rashed, A.A.; Kolsi, L.; Kalidasan, K.; Malekshah, E.H.; Kanna, P.R. Second law analysis of natural convection in a CNT-water nanofluid filled inclined 3D cavity with incorporated Ahmed body. Int. J. Mech. Sci. 2017, 130, 399–415. [Google Scholar] [CrossRef]
- Halelfadl, S.; Estelle, P.; Aladag, B.; Doner, N.; Mare, T. Viscosity of carbon nanotubes water-based nanofluids: Influence of concentration and temperature. Int. J. Therm. Sci. 2013, 71, 111–117. [Google Scholar] [CrossRef]
- Benos, L.T.; Karvelas, E.G.; Sarris, I.E. Crucial effect of aggregations in CNT-water nanofluid magnetohydrodynamic natural convection. Therm. Sci. Eng. Prog. 2019, 11, 263–271. [Google Scholar] [CrossRef]
- Razmara, N.; Namarvari, H.; Meneghini, J.R. A new correlation for viscosity of model water-carbon nanotube nanofluids: Molecular dynamics simulation. J. Mol. Liq. 2019, 293, 111438. [Google Scholar] [CrossRef]
- Ouertatani, N.; Cheikh, N.B.; Beya, B.B.; Lili, T.; Campo, A. Mixed convection in a double lid-driven cubic cavity. Int. J. Therm. Sci. 2009, 48, 1265–1272. [Google Scholar] [CrossRef]
- Heyhat, M.M.; Kowsary, F.; Rashidi, A.M.; Momenpour, M.H.; Amrollahi, A. Experimental investigation of laminar convective heat transfer and pressure drop of water-based Al2O3 nanofluids in fully developed flow regime. Exp. Therm. Fluid Sci. 2013, 44, 483–489. [Google Scholar] [CrossRef]
- Oztop, H.F.; Dagtekin, I. Mixed convection in two-sided lid-driven differentially heated square cavity. Int. J. Heat Mass Transf. 2004, 47, 1761–1769. [Google Scholar] [CrossRef]
- Kaneda, M.; Tagawa, T.; Ozoe, H. Natural convection of liquid metal under a uniform magnetic field with an electric current supplied from outside. Exp. Therm. Fluid Sci. 2006, 30, 243–252. [Google Scholar] [CrossRef]
- Sawada, T.; Kikura, H.; Saito, A.; Tanahashi, T. Natural convection of a magnetic fluid in concentric horizontal annuli under nonuniform magnetic fields. Exp. Therm. Fluid Sci. 1993, 7, 212–220. [Google Scholar] [CrossRef]
- Li, Q.; Xuan, Y. Experimental investigation on heat transfer characteristics of magnetic fluid flow around a fine wire under the influence of an external magnetic field. Exp. Therm. Fluid Sci. 2009, 33, 591–596. [Google Scholar] [CrossRef]
- Sarafraz, M.M.; Hormozi, F.; Nikkhah, V. Thermal performance of a counter-current double pipe heat exchanger working with COOH-CNT/water nanofluids. Exp. Therm. Fluid Sci. 2016, 78, 41–49. [Google Scholar] [CrossRef]
- Rathnakumar, P.; Iqbal, S.M.; Michael, J.J.; Suresh, S. Study on performance enhancement factors in turbulent flow of CNT/water nanofluid through a tube fitted with helical screw louvered rod inserts. Chem. Eng. Process. Process Intensif. 2018, 127, 103–110. [Google Scholar] [CrossRef]

| Property | Water | SWCNT | MWCNT |
|---|---|---|---|
| 997.1 | 2600 | 1600 | |
| 4179 | 425 | 796 | |
| 0.61 | 6600 | 3000 |
| Grid Name | Number of Elements | Nu (Ri = 0.05) | Nu (Ri = 1) | Nu (Ri = 50) |
|---|---|---|---|---|
| G1 | 1923 | 6.45 | 4.06 | 3.47 |
| G2 | 4834 | 5.29 | 3.64 | 3.27 |
| G3 | 7680 | 4.56 | 3.36 | 3.11 |
| G4 | 19298 | 4.23 | 3.26 | 3.06 |
| G5 | 39287 | 3.91 | 3.15 | 3.02 |
| G6 | 69769 | 3.85 | 3.14 | 3.01 |
| G7 | 69769 | 3.84 | 3.13 | 3.01 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chamkha, A.J.; Selimefendigil, F.; Oztop, H.F. Effects of a Rotating Cone on the Mixed Convection in a Double Lid-Driven 3D Porous Trapezoidal Nanofluid Filled Cavity under the Impact of Magnetic Field. Nanomaterials 2020, 10, 449. https://doi.org/10.3390/nano10030449
Chamkha AJ, Selimefendigil F, Oztop HF. Effects of a Rotating Cone on the Mixed Convection in a Double Lid-Driven 3D Porous Trapezoidal Nanofluid Filled Cavity under the Impact of Magnetic Field. Nanomaterials. 2020; 10(3):449. https://doi.org/10.3390/nano10030449
Chicago/Turabian StyleChamkha, Ali J., Fatih Selimefendigil, and Hakan F. Oztop. 2020. "Effects of a Rotating Cone on the Mixed Convection in a Double Lid-Driven 3D Porous Trapezoidal Nanofluid Filled Cavity under the Impact of Magnetic Field" Nanomaterials 10, no. 3: 449. https://doi.org/10.3390/nano10030449
APA StyleChamkha, A. J., Selimefendigil, F., & Oztop, H. F. (2020). Effects of a Rotating Cone on the Mixed Convection in a Double Lid-Driven 3D Porous Trapezoidal Nanofluid Filled Cavity under the Impact of Magnetic Field. Nanomaterials, 10(3), 449. https://doi.org/10.3390/nano10030449






