Effect of Compressive Prestrain on the Anti-Pressure and Anti-Wear Performance of Monolayer MoS2: A Molecular Dynamics Study
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Relaxation Process
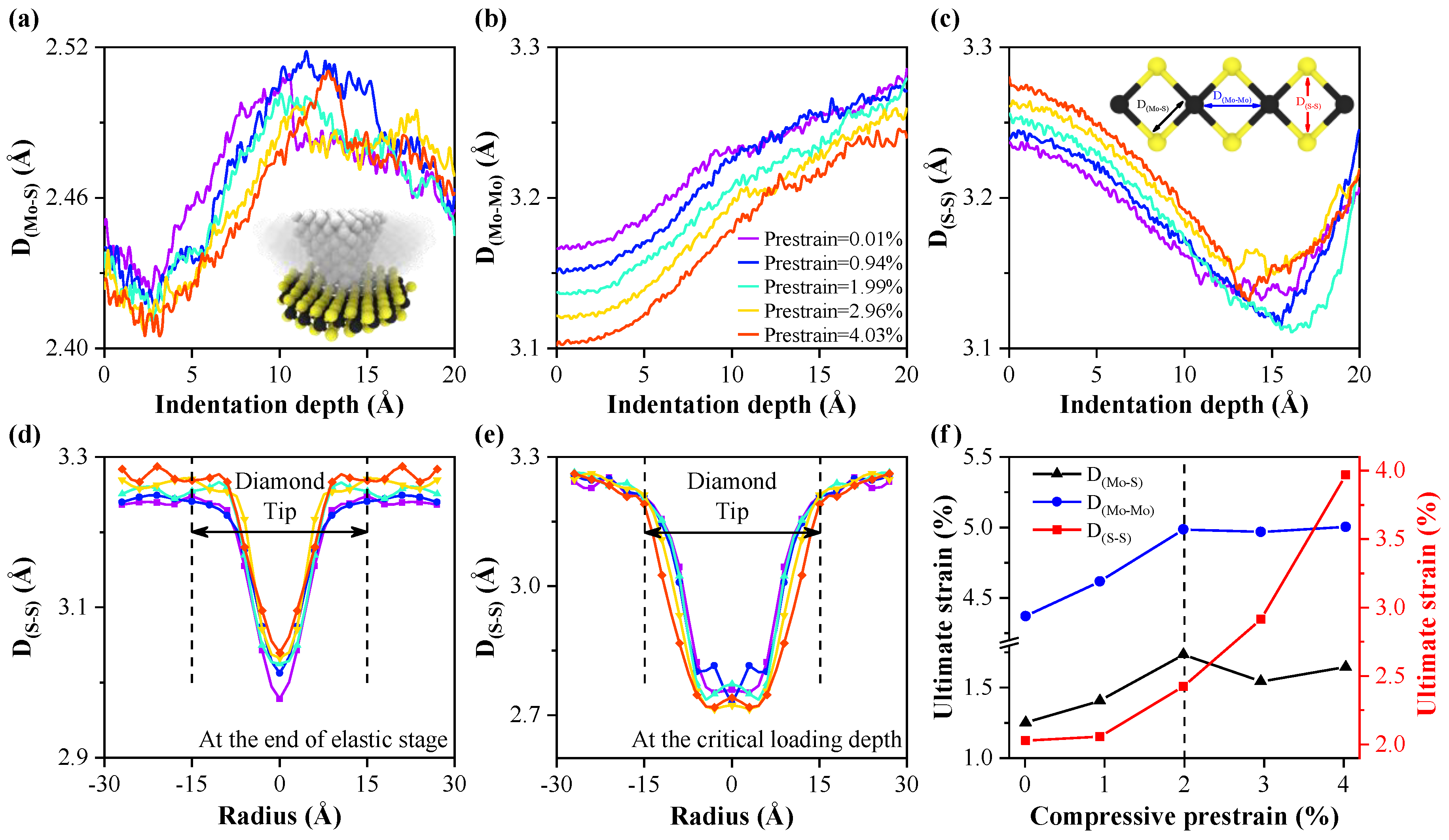
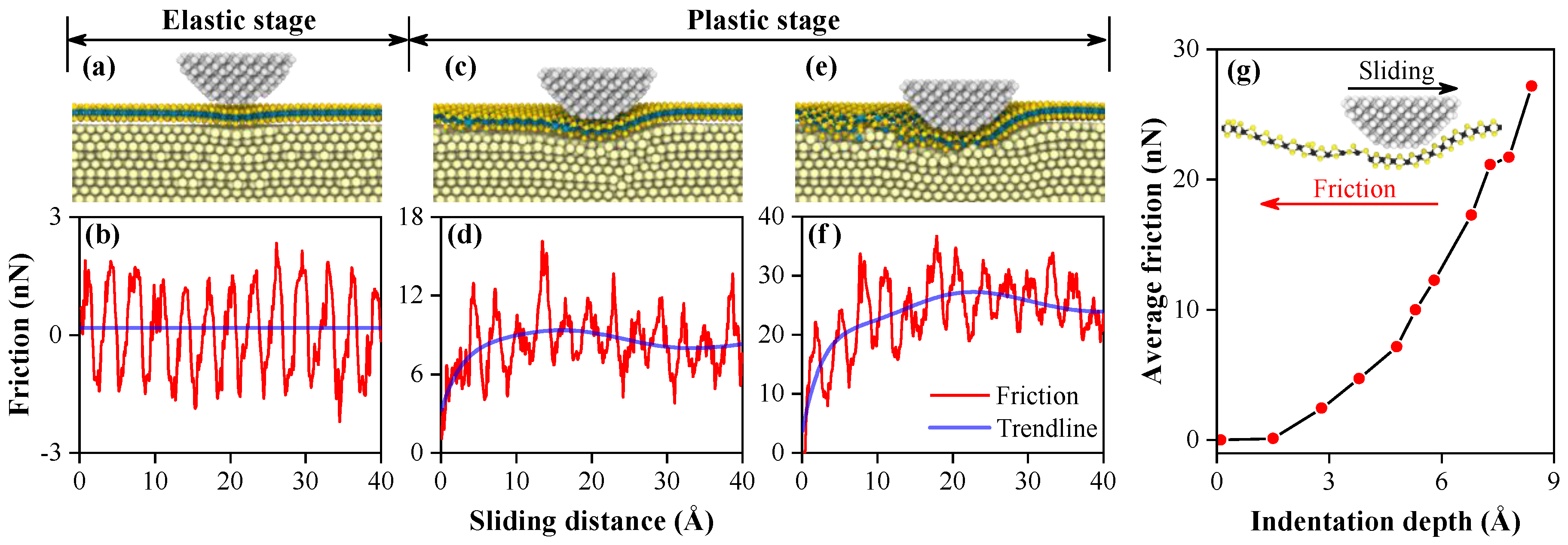
3.2. Indentation Process
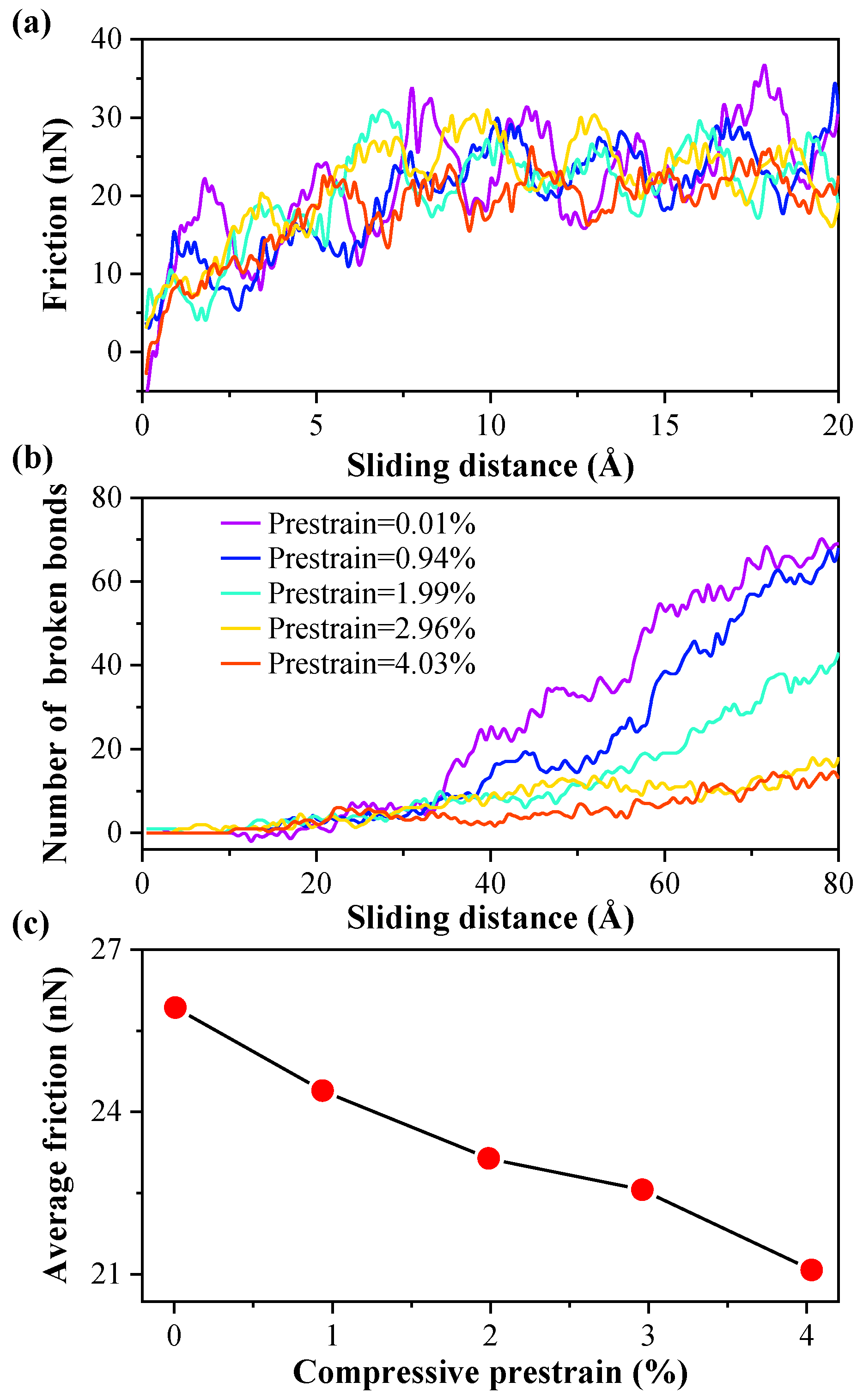
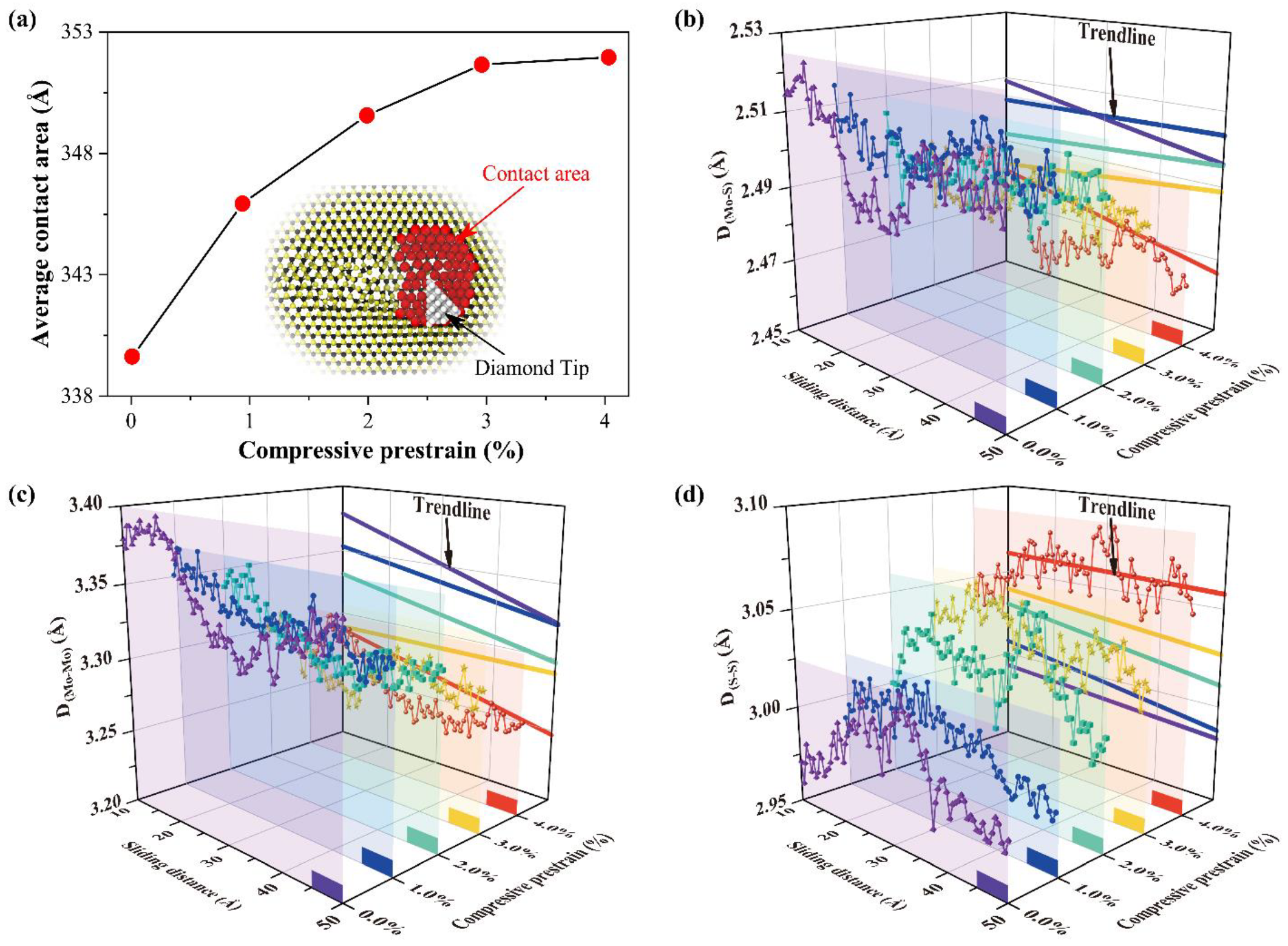
3.3. Sliding Process
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef]
- Lee, G.-H.; Cooper, R.C.; An, S.J.; Lee, S.; van der Zande, A.; Petrone, N.; Hammerherg, A.G.; Lee, C.; Crawford, B.; Oliver, W.; et al. High-Strength Chemical-Vapor Deposited Graphene and Grain Boundaries. Science 2013, 340, 1073–1076. [Google Scholar] [CrossRef]
- Lee, C.; Wei, X.; Kysar, J.W.; Hone, J. Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef] [PubMed]
- Bertolazzi, S.; Brivio, J.; Kis, A. Stretching and Breaking of Ultrathin MoS2. Acs Nano 2011, 5, 9703–9709. [Google Scholar] [CrossRef] [PubMed]
- Cooper, R.C.; Lee, C.; Marianetti, C.A.; Wei, X.; Hone, J.; Kysar, J.W. Nonlinear elastic behavior of two-dimensional molybdenum disulfide. Phys. Rev. B 2013, 87, 035423. [Google Scholar] [CrossRef]
- Jiang, J.-W.; Park, H.S. Mechanical properties of MoS2/graphene heterostructures. Appl. Phys. Lett. 2014, 105, 033108. [Google Scholar] [CrossRef]
- Chhowalla, M.; Amaratunga, G.A.J. Thin films of fullerene-like MoS2 nanoparticles with ultra-low friction and wear. Nature 2000, 407, 164–167. [Google Scholar] [CrossRef]
- Spear, J.C.; Ewers, B.W.; Batteas, J.D. 2D-nanomaterials for controlling friction and wear at interfaces. Nano Today 2015, 10, 301–314. [Google Scholar] [CrossRef]
- Lee, C.; Li, Q.; Kalb, W.; Liu, X.-Z.; Berger, H.; Carpick, R.W.; Hone, J. Frictional Characteristics of Atomically Thin Sheets. Science 2010, 328, 76–80. [Google Scholar] [CrossRef]
- Miura, K.; Kamiya, S. Observation of the Amontons-Coulomb law on the nanoscale: Frictional forces between MoS2 flakes and MoS2 surfaces. Europhys. Lett. 2002, 58, 610–615. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, X.; Xu, Q.; Ma, T.; Hu, Y.; Wang, H.; Tieu, A.K.; Luo, J. Effects of grain boundary on wear of graphene at the nanoscale: A molecular dynamics study. Carbon 2019, 143, 578–586. [Google Scholar] [CrossRef]
- Cao, X.A.; Gan, X.; Lang, H.; Yu, K.; Ding, S.; Peng, Y.; Yi, W. Anisotropic nanofriction on MoS2 with different thicknesses. Tribol. Int. 2019, 134, 308–316. [Google Scholar] [CrossRef]
- Castellanos-Gomez, A.; Poot, M.; Steele, G.A.; van der Zant, H.S.J.; Agrait, N.; Rubio-Bollinger, G. Elastic Properties of Freely Suspended MoS2 Nanosheets. Adv. Mater. 2012, 24, 772–775. [Google Scholar] [CrossRef] [PubMed]
- Xiong, S.; Cao, G. Molecular dynamics simulations of mechanical properties of monolayer MoS2. Nanotechnology 2015, 26, 185705. [Google Scholar] [CrossRef] [PubMed]
- Serpini, E.; Rota, A.; Valeri, S.; Ukraintsev, E.; Rezek, B.; Polcar, T.; Nicolini, P. Nanoscale frictional properties of ordered and disordered MoS2. Tribol. Int. 2019, 136, 67–74. [Google Scholar] [CrossRef]
- Li, H.; Wang, J.; Gao, S.; Chen, Q.; Peng, L.; Liu, K.; Wei, X. Superlubricity between MoS2 Monolayers. Adv. Mater. 2017, 29, 1701474. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, G.; Wang, L.; Xue, Q. The Tribological Mechanism of MoS2 Film under Different Humidity. Tribol. Lett. 2017, 65, 64. [Google Scholar] [CrossRef]
- Donnet, C.; Martin, J.M.; Le Mogne, T.; Belin, M. Super-low friction of MoS2 coatings in various environments. Tribol. Int. 1996, 29, 123–128. [Google Scholar] [CrossRef]
- Quan, X.; Zhang, S.; Hu, M.; Gao, X.; Jiang, D.; Sun, J. Tribological properties of WS2/MoS2-Ag composite films lubricated with ionic liquids under vacuum conditions. Tribol. Int. 2017, 115, 389–396. [Google Scholar] [CrossRef]
- Li, Z.-Y.; Yang, W.-J.; Wu, Y.-P.; Wu, S.-B.; Cai, Z.-B. Role of humidity in reducing the friction of graphene layers on textured surfaces. Appl. Surf. Sci. 2017, 403, 362–370. [Google Scholar] [CrossRef]
- Yen, B.K. Influence of water vapor and oxygen on the tribology of carbon materials with sp2 valence configuration. Wear 1996, 192, 208–215. [Google Scholar] [CrossRef]
- Li, W.; Fan, X.Q.; Li, H.; Zhu, M.H.; Wang, L.P. Probing carbon-based composite coatings toward high vacuum lubrication application. Tribol. Int. 2018, 128, 386–396. [Google Scholar] [CrossRef]
- Kim, S.H.; Asay, D.B.; Dugger, M.T. Nanotribology and MEMS. Nano Today 2007, 2, 22–29. [Google Scholar] [CrossRef]
- Nian, J.; Si, Y.; Guo, Z. Advances in atomic-scale tribological mechanisms of solid interfaces. Tribol. Int. 2016, 94, 1–13. [Google Scholar] [CrossRef]
- Najmaei, S.; Liu, Z.; Zhou, W.; Zou, X.; Shi, G.; Lei, S.; Yakobson, B.I.; Idrobo, J.-C.; Ajayan, P.M.; Lou, J. Vapour phase growth and grain boundary structure of molybdenum disulphide atomic layers. Nat. Mater. 2013, 12, 754–759. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.H.; Zhang, X.Q.; Zhang, W.J.; Chang, M.T.; Lin, C.T.; Chang, K.D.; Yu, Y.C.; Wang, J.T.W.; Chang, C.S.; Li, L.J.; et al. Synthesis of Large-Area MoS2 Atomic Layers with Chemical Vapor Deposition. Adv. Mater. 2012, 24, 2320–2325. [Google Scholar] [CrossRef]
- Van der Zande, A.M.; Huang, P.Y.; Chenet, D.A.; Berkelbach, T.C.; You, Y.; Lee, G.-H.; Heinz, T.F.; Reichman, D.R.; Muller, D.A.; Hone, J.C. Grains and grain boundaries in highly crystalline monolayer molybdenum disulphide. Nat. Mater. 2013, 12, 554–561. [Google Scholar] [CrossRef]
- Liu, H.; Chi, D. Dispersive growth and laser-induced rippling of large-area singlelayer MoS2 nanosheets by CVD on c-plane sapphire substrate. Sci. Rep. 2015, 5, 11756. [Google Scholar] [CrossRef]
- Ji, Q.; Zhang, Y.; Gao, T.; Zhang, Y.; Ma, D.; Liu, M.; Chen, Y.; Qiao, X.; Tan, P.-H.; Kan, M.; et al. Epitaxial Monolayer MoS2 on Mica with Novel Photoluminescence. Nano Lett. 2013, 13, 3870–3877. [Google Scholar] [CrossRef]
- Song, I.; Park, C.; Choi, H.C. Synthesis and properties of molybdenum disulphide: From bulk to atomic layers. RSC Adv. 2015, 5, 7495–7514. [Google Scholar] [CrossRef]
- Liu, Z.; Amani, M.; Najmaei, S.; Xu, Q.; Zou, X.; Zhou, W.; Yu, T.; Qiu, C.; Birdwell, A.G.; Crowne, F.J.; et al. Strain and structure heterogeneity in MoS2 atomic layers grown by chemical vapour deposition. Nat. Commun. 2014, 5, 5246. [Google Scholar] [CrossRef] [PubMed]
- Kataria, S.; Wagner, S.; Cusati, T.; Fortunelli, A.; Iannaccone, G.; Pandey, H.; Fiori, G.; Lemme, M.C. Growth-Induced Strain in Chemical Vapor Deposited Monolayer MoS2: Experimental and Theoretical Investigation. Adv. Mater. Interfaces 2017, 4, 1700031. [Google Scholar] [CrossRef]
- Hui, Y.Y.; Liu, X.; Jie, W.; Chan, N.Y.; Hao, J.; Hsu, Y.-T.; Li, L.-J.; Guo, W.; Lau, S.P. Exceptional Tunability of Band Energy in a Compressively Strained Trilayer MoS2 Sheet. Acs Nano 2013, 7, 7126–7131. [Google Scholar] [CrossRef] [PubMed]
- Luo, S.; Hao, G.; Fan, Y.; Kou, L.; He, C.; Qi, X.; Tang, C.; Li, J.; Huang, K.; Zhong, J. Formation of ripples in atomically thin MoS2 and local strain engineering of electrostatic properties. Nanotechnology 2015, 26, 105705. [Google Scholar] [CrossRef] [PubMed]
- Lin, X.; Zhang, H.; Guo, Z.; Chang, T. Strain engineering of friction between graphene layers. Tribol. Int. 2019, 131, 686–693. [Google Scholar] [CrossRef]
- Wang, C.; Li, H.; Zhang, Y.; Sun, Q.; Jia, Y. Effect of strain on atomic-scale friction in layered MoS2. Tribol. Int. 2014, 77, 211–217. [Google Scholar] [CrossRef]
- Yang, L.; Guo, Y.; Zhang, Q. Frictional behavior of strained multilayer graphene: Tuning the atomic scale contact area. Diam. Relat. Mater. 2017, 73, 273–277. [Google Scholar] [CrossRef]
- Liang, T.; Phillpot, S.R.; Sinnott, S.B. Parametrization of a reactive many-body potential for Mo-S systems. Phys. Rev. B 2009, 79, 245110. [Google Scholar] [CrossRef]
- Stewart, J.A.; Spearot, D.E. Atomistic simulations of nanoindentation on the basal plane of crystalline molybdenum disulfide (MoS2). Model. Simul. Mater. Sci. Eng. 2013, 21, 045003. [Google Scholar] [CrossRef]
- Lee, B.J.; Shim, J.H.; Baskes, M.I. Semiempirical atomic potentials for the fcc metals Cu, Ag, Au, Ni, Pd, Pt, Al, and Pb based on first and second nearest-neighbor modified embedded atom method. Phys. Rev. B 2003, 68, 144112. [Google Scholar] [CrossRef]
- Girifalco, L.A.; Hodak, M.; Lee, R.S. Carbon nanotubes, buckyballs, ropes, and a universal graphitic potential. Phys. Rev. B 2000, 62, 13104–13110. [Google Scholar] [CrossRef]
- Varshney, V.; Patnaik, S.S.; Muratore, C.; Roy, A.K.; Voevodin, A.A.; Farmer, B.L. MD simulations of molybdenum disulphide (MoS2): Force-field parameterization and thermal transport behavior. Comput. Mater. Sci. 2010, 48, 101–108. [Google Scholar] [CrossRef]
- Toghraie, D.; Mokhtari, M.; Afrand, M. Molecular dynamic simulation of copper and platinum nanoparticles poiseuille flow in a nanochannels. Phys. E-Low-Dimens. Syst. Nanostructures 2016, 84, 152–161. [Google Scholar] [CrossRef]
- Li, L.; Xia, Z.H.; Curtin, W.A.; Yang, Y.Q. Molecular dynamics simulations of interfacial sliding in carbon-nanotube/diamond nanocomposites. J. Am. Ceram. Soc. 2009, 92, 2331–2336. [Google Scholar] [CrossRef]
- Dong, Y.; Li, Q.; Martini, A. Molecular dynamics simulation of atomic friction: A review and guide. J. Vac. Sci. Technol. A 2013, 31, 033108. [Google Scholar] [CrossRef]
- Le, D.; Sun, D.; Lu, W.; Bartels, L.; Rahman, T.S. Single layer MoS2 on the Cu(111) surface: First-principles electronic structure calculations. Phys. Rev. B 2012, 85, 075429. [Google Scholar] [CrossRef]
- Jiang, J.W.; Qi, Z.N.; Park, H.S.; Rabczuk, T. Elastic bending modulus of single-layer molybdenum disulfide (MoS2): Finite thickness effect. Nanotechnology 2013, 24, 435705. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Y.; Ma, T.; Luo, J. Atomic Scale Simulation on the Anti-Pressure and Friction Reduction Mechanisms of MoS2 Monolayer. Materials 2018, 11, 683. [Google Scholar] [CrossRef]
- Klemenz, A.; Pastewka, L.; Balakrishna, S.G.; Caron, A.; Bennewitz, R.; Moseler, M. Atomic Scale Mechanisms of Friction Reduction and Wear Protection by Graphene. Nano Lett. 2014, 14, 7145–7152. [Google Scholar] [CrossRef]
- Mo, Y.; Turner, K.T.; Szlufarska, I. Friction laws at the nanoscale. Nature 2009, 457, 1116–1119. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, Y.; Cao, G. Boundary condition and pre-strain effects on the free standing indentation response of graphene monolayer. J. Phys. Condens. Matter 2013, 25, 475303. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, F. Maximum asymmetry in strain induced mechanical instability of graphene: Compression versus tension. Appl. Phys. Lett. 2011, 99, 241908. [Google Scholar] [CrossRef]
- Pena-Alvarez, M.; del Corro, E.; Morales-Garcia, A.; Kavan, L.; Kalbac, M.; Frank, O. Single Layer Molybdenum Disulfide under Direct Out-of-Plane Compression: Low-Stress Band-Gap Engineering. Nano Lett. 2015, 15, 3139–3146. [Google Scholar] [CrossRef]
- Lorenz, T.; Joswig, J.-O.; Seifert, G. Stretching and breaking of monolayer MoS2-an atomistic simulation. 2d Mater. 2014, 1, 011007. [Google Scholar] [CrossRef]
- Li, S.; Li, Q.; Carpick, R.W.; Gumbsch, P.; Liu, X.Z.; Ding, X.; Sun, J.; Li, J. The evolving quality of frictional contact with graphene. Nature 2016, 539, 541–545. [Google Scholar] [CrossRef]
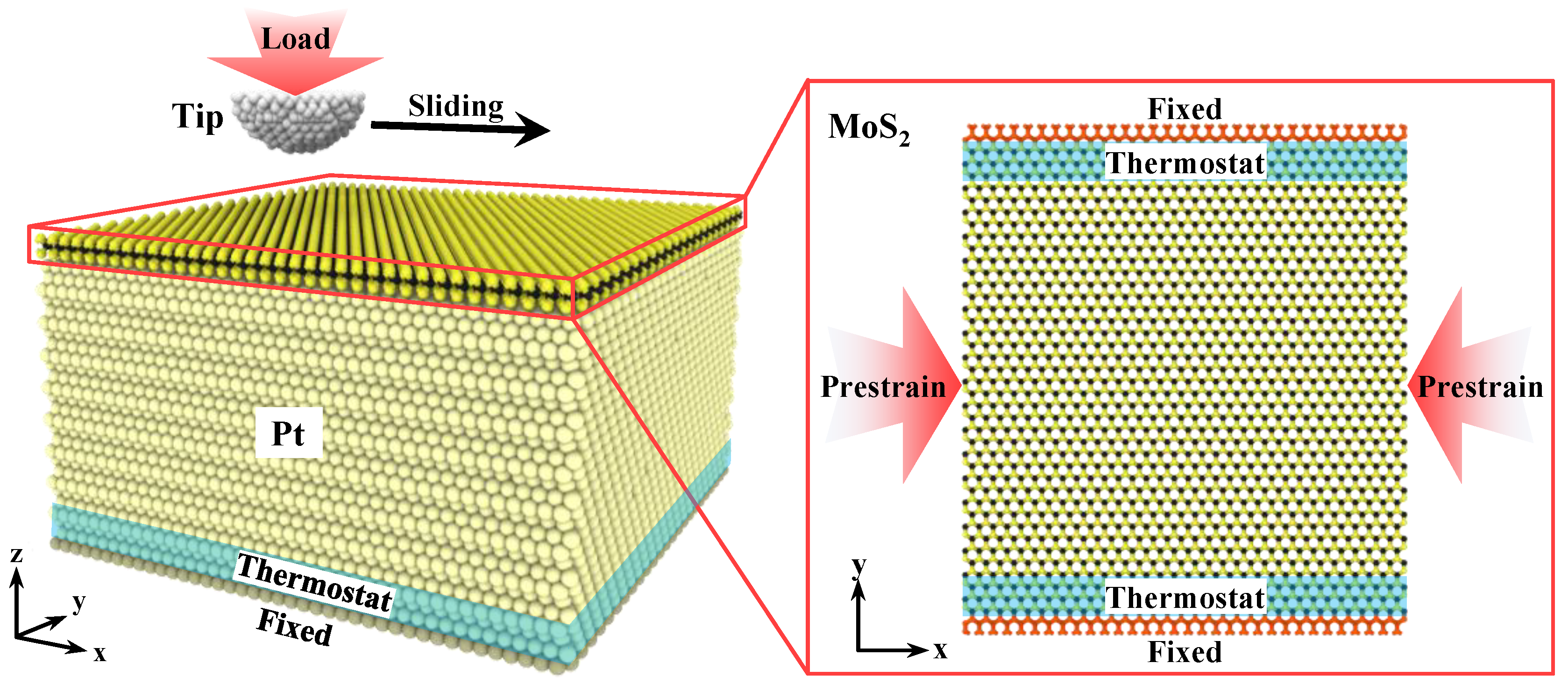
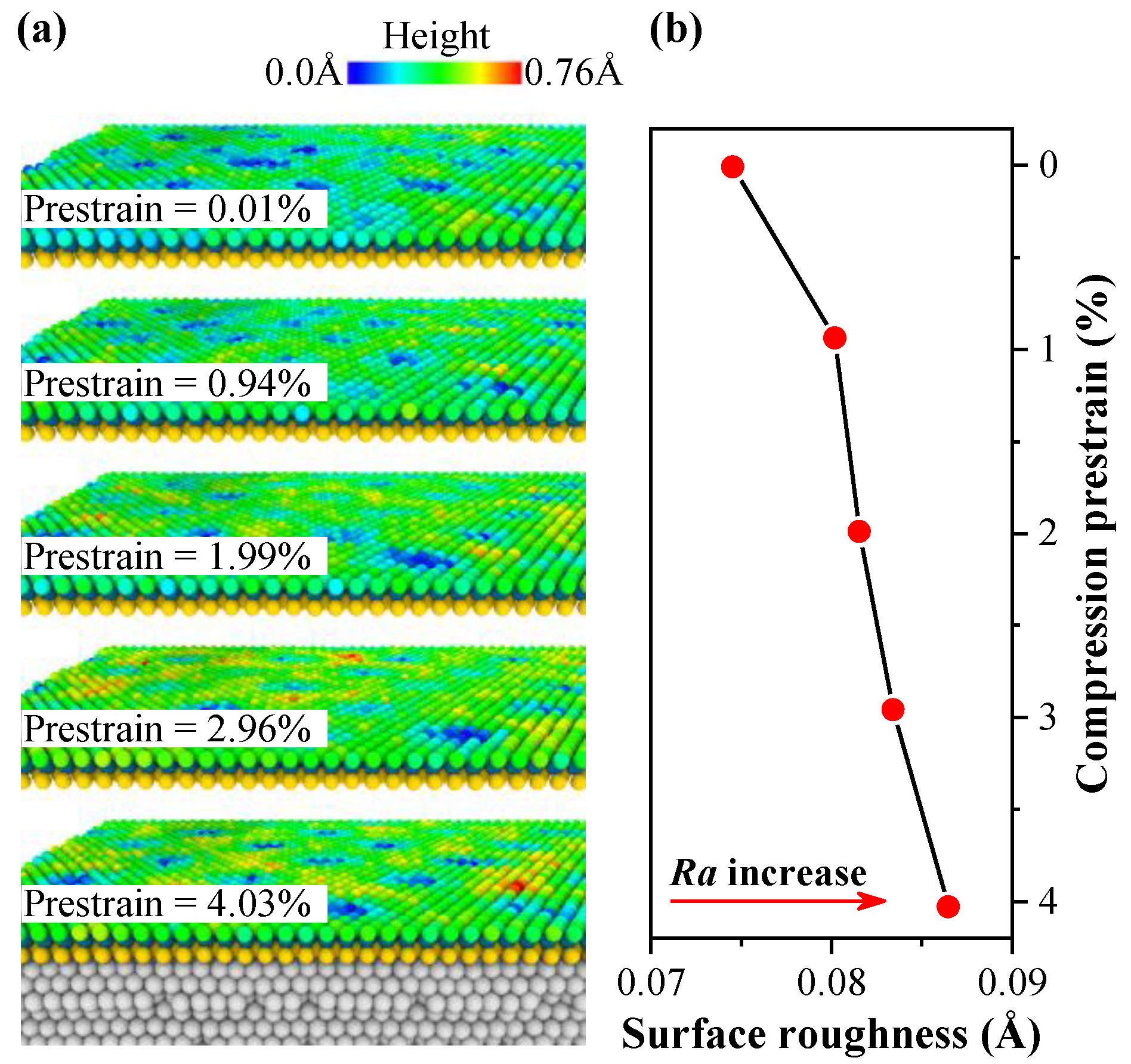
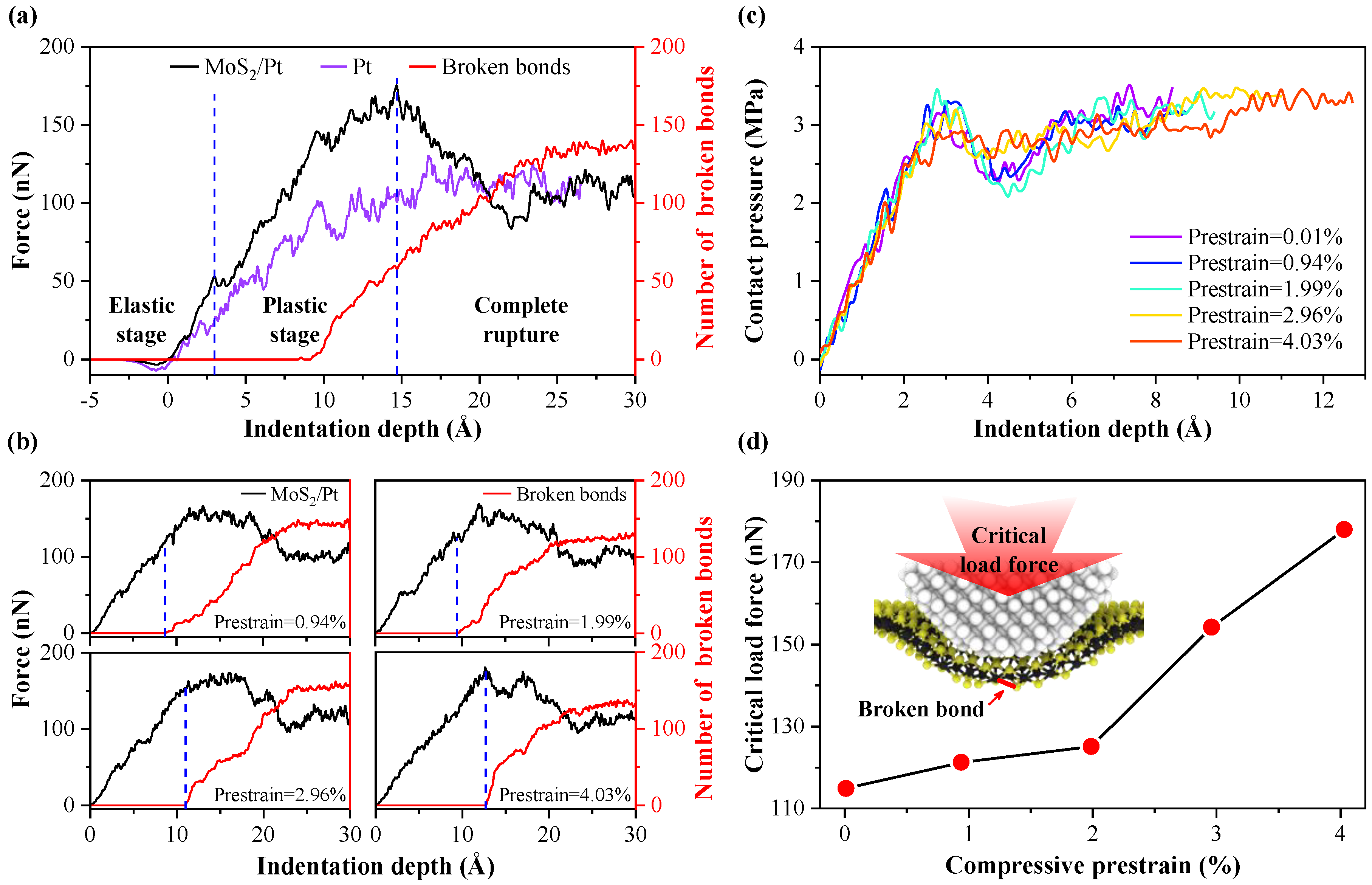
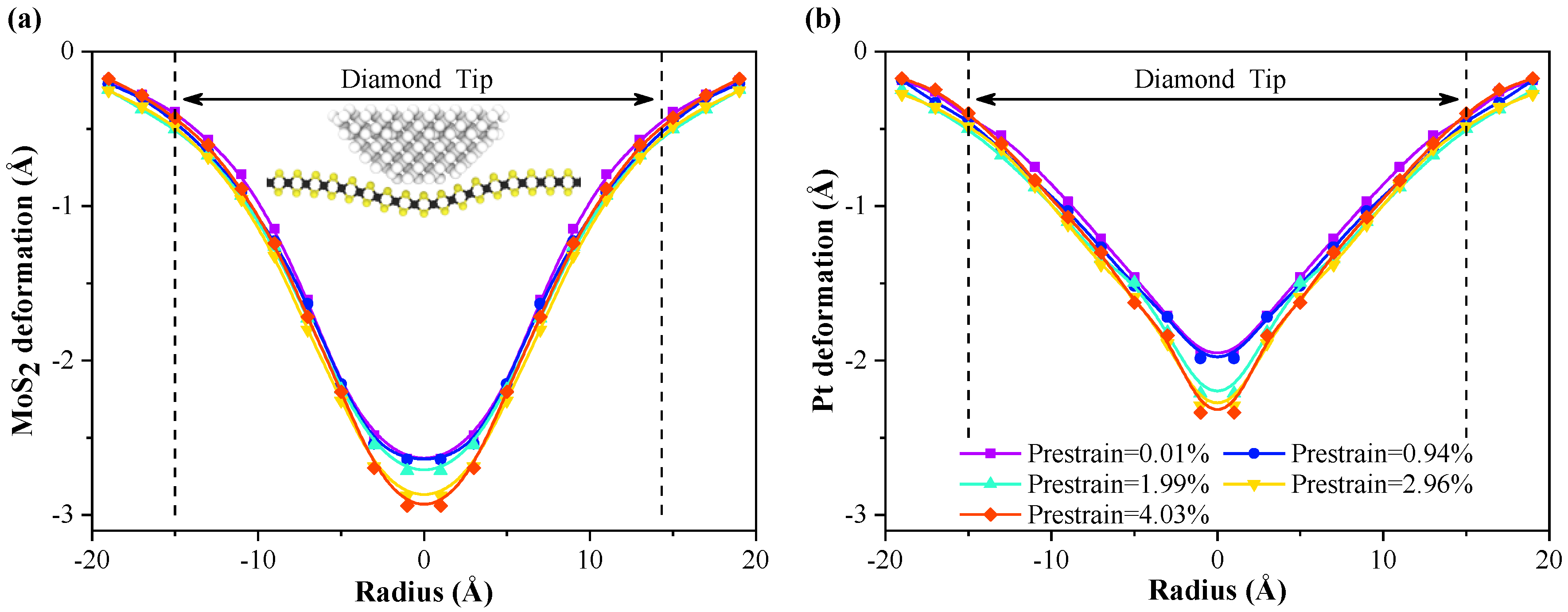
| Model | Compressive Prestrain | x Size Before Compression (Å) | x Size After Compression (Å) |
|---|---|---|---|
| Ⅰ | 0.01% | 113.774 | 113.768 |
| Ⅱ | 0.99% | 148.539 | 147.066 |
| Ⅲ | 1.99% | 135.897 | 133.192 |
| Ⅳ | 2.96% | 120.095 | 116.543 |
| Ⅴ | 4.03% | 135.897 | 130.417 |
| Parameter | C–S | C–Mo | C–Pt | S–Pt | Mo–Pt |
|---|---|---|---|---|---|
| ε (meV) | 13.165 | 48.962 | 38.635 | 177.840 | 661.41 |
| σ (Å) | 3.418 | 3.009 | 2.971 | 2.922 | 2.513 |
| Rcutoff (Å) | 8.545 | 7.523 | 7.428 | 7.305 | 6.283 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kong, N.; Wei, B.; Zhuang, Y.; Zhang, J.; Li, H.; Wang, B. Effect of Compressive Prestrain on the Anti-Pressure and Anti-Wear Performance of Monolayer MoS2: A Molecular Dynamics Study. Nanomaterials 2020, 10, 275. https://doi.org/10.3390/nano10020275
Kong N, Wei B, Zhuang Y, Zhang J, Li H, Wang B. Effect of Compressive Prestrain on the Anti-Pressure and Anti-Wear Performance of Monolayer MoS2: A Molecular Dynamics Study. Nanomaterials. 2020; 10(2):275. https://doi.org/10.3390/nano10020275
Chicago/Turabian StyleKong, Ning, Boyu Wei, Yuan Zhuang, Jie Zhang, Hongbo Li, and Bo Wang. 2020. "Effect of Compressive Prestrain on the Anti-Pressure and Anti-Wear Performance of Monolayer MoS2: A Molecular Dynamics Study" Nanomaterials 10, no. 2: 275. https://doi.org/10.3390/nano10020275
APA StyleKong, N., Wei, B., Zhuang, Y., Zhang, J., Li, H., & Wang, B. (2020). Effect of Compressive Prestrain on the Anti-Pressure and Anti-Wear Performance of Monolayer MoS2: A Molecular Dynamics Study. Nanomaterials, 10(2), 275. https://doi.org/10.3390/nano10020275





