High-Order Harmonic Generation in Au Nanoparticle-Contained Plasmas
Abstract
1. Introduction
2. Materials and Methods
Experiment
3. Results
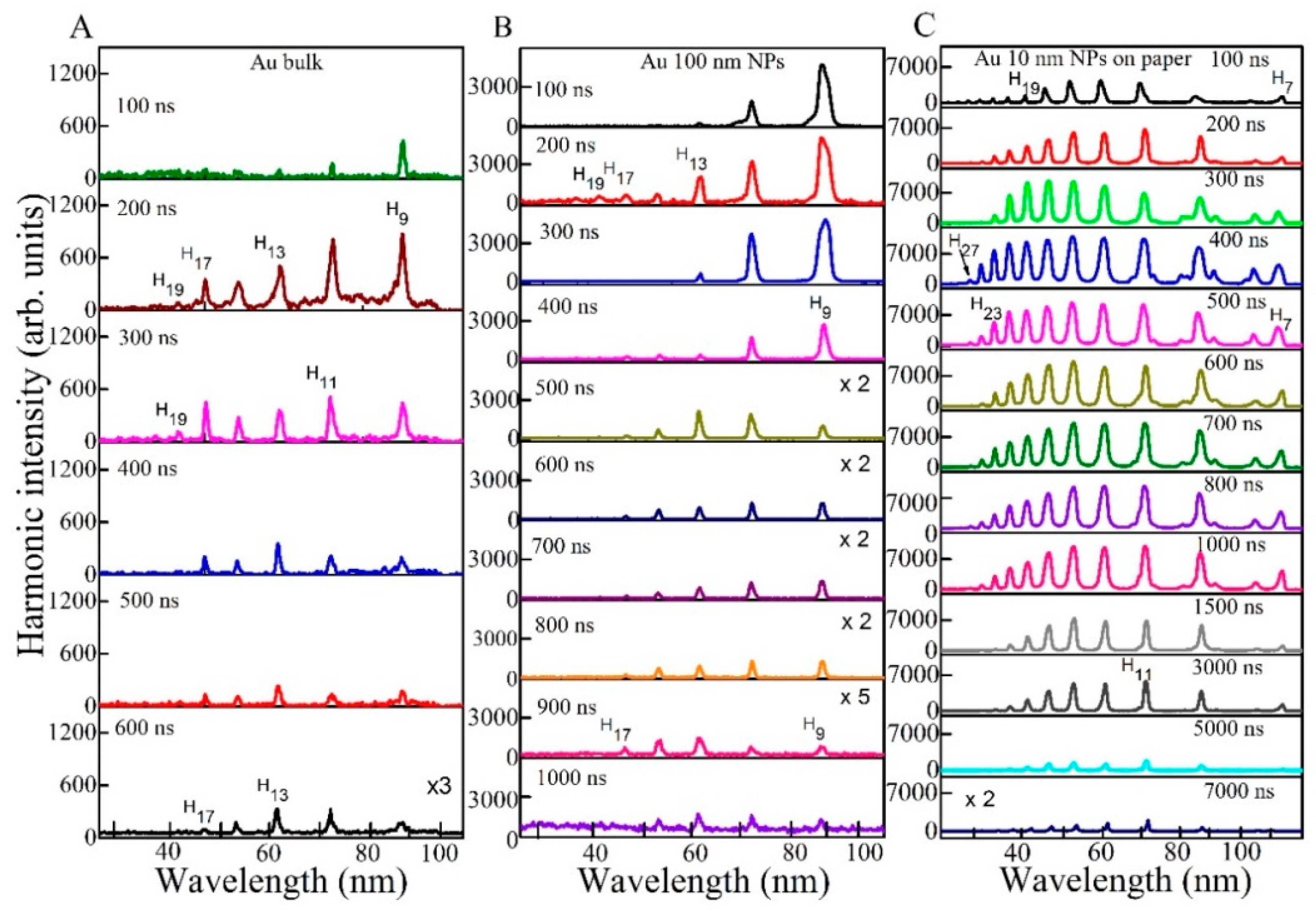
3.1. Comparison of Harmonic Emission from Different Plasmas Containing Gold Nanoparticles
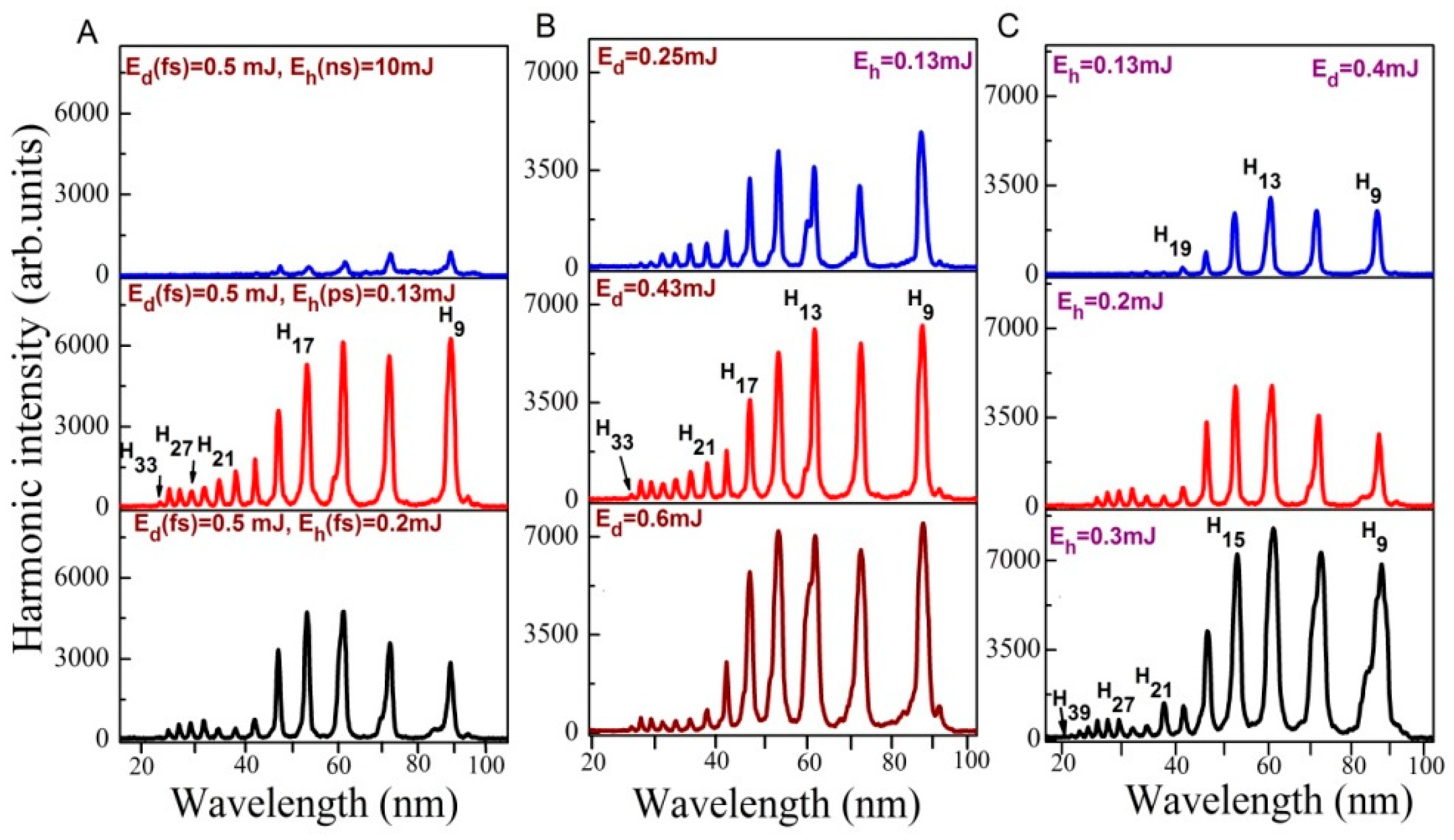
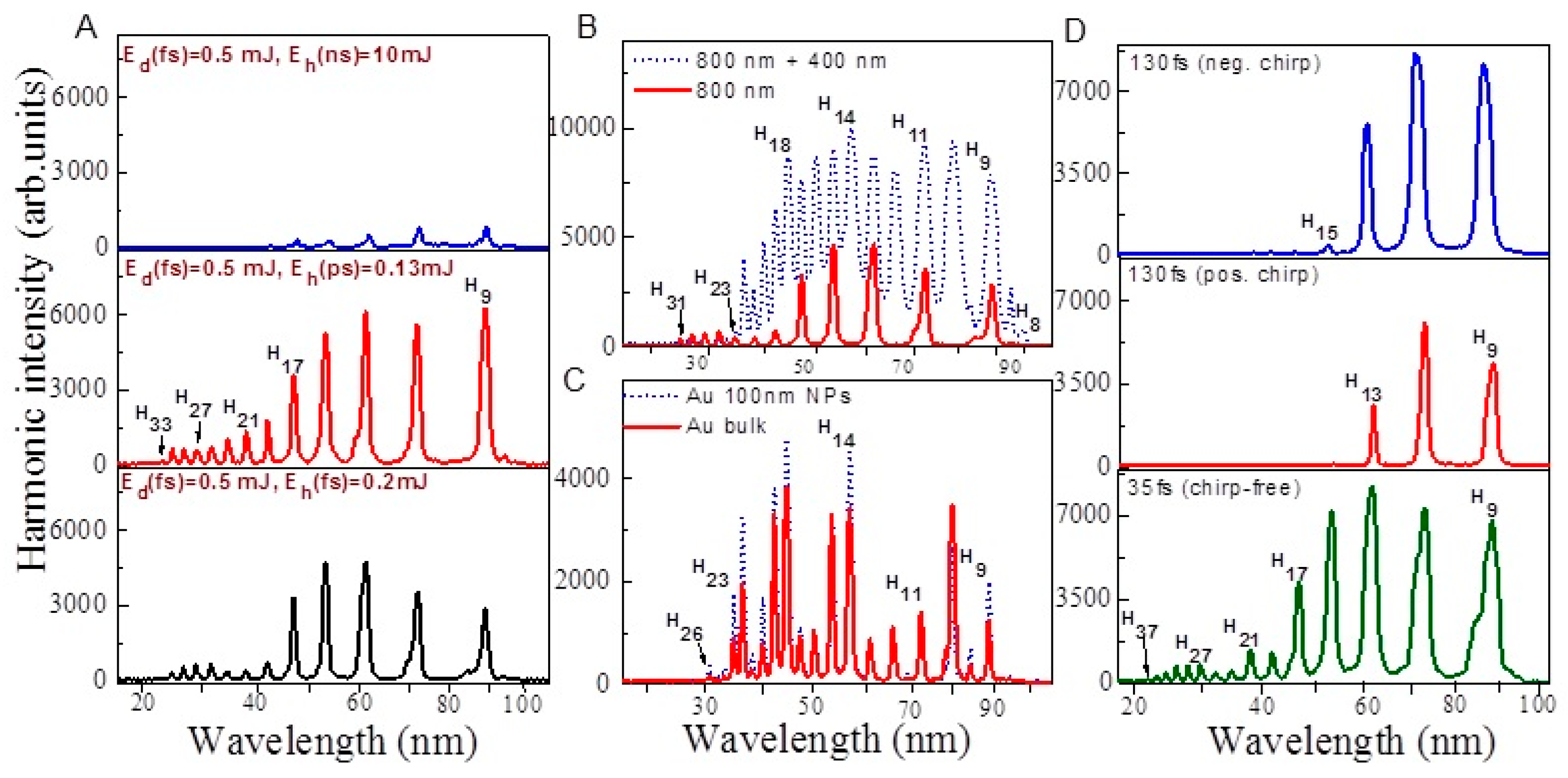
3.2. Role of Different Parameters of Driving and Heating Pulses on the HHG Efficiency in Au NP Containing Plasmas
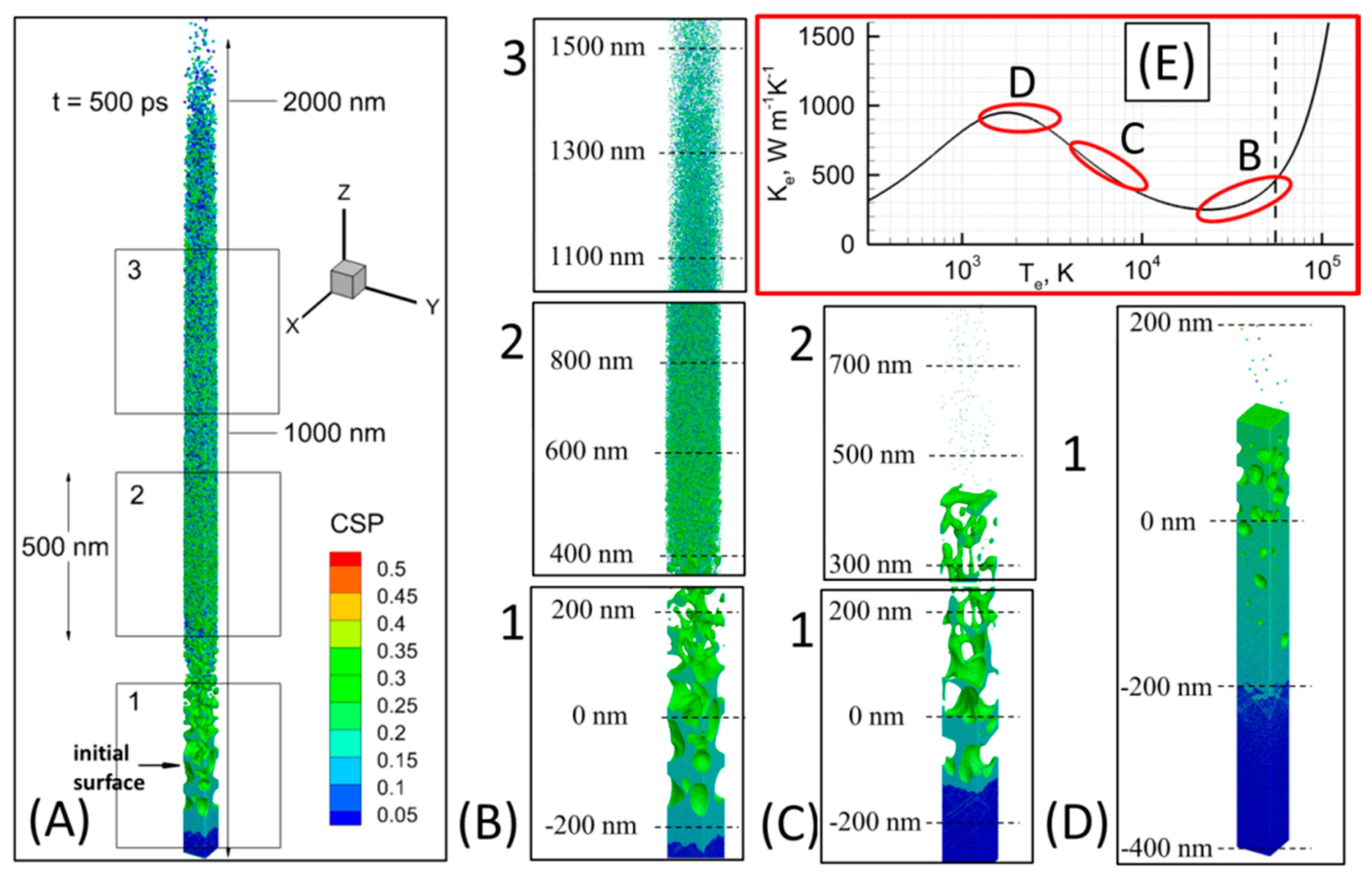
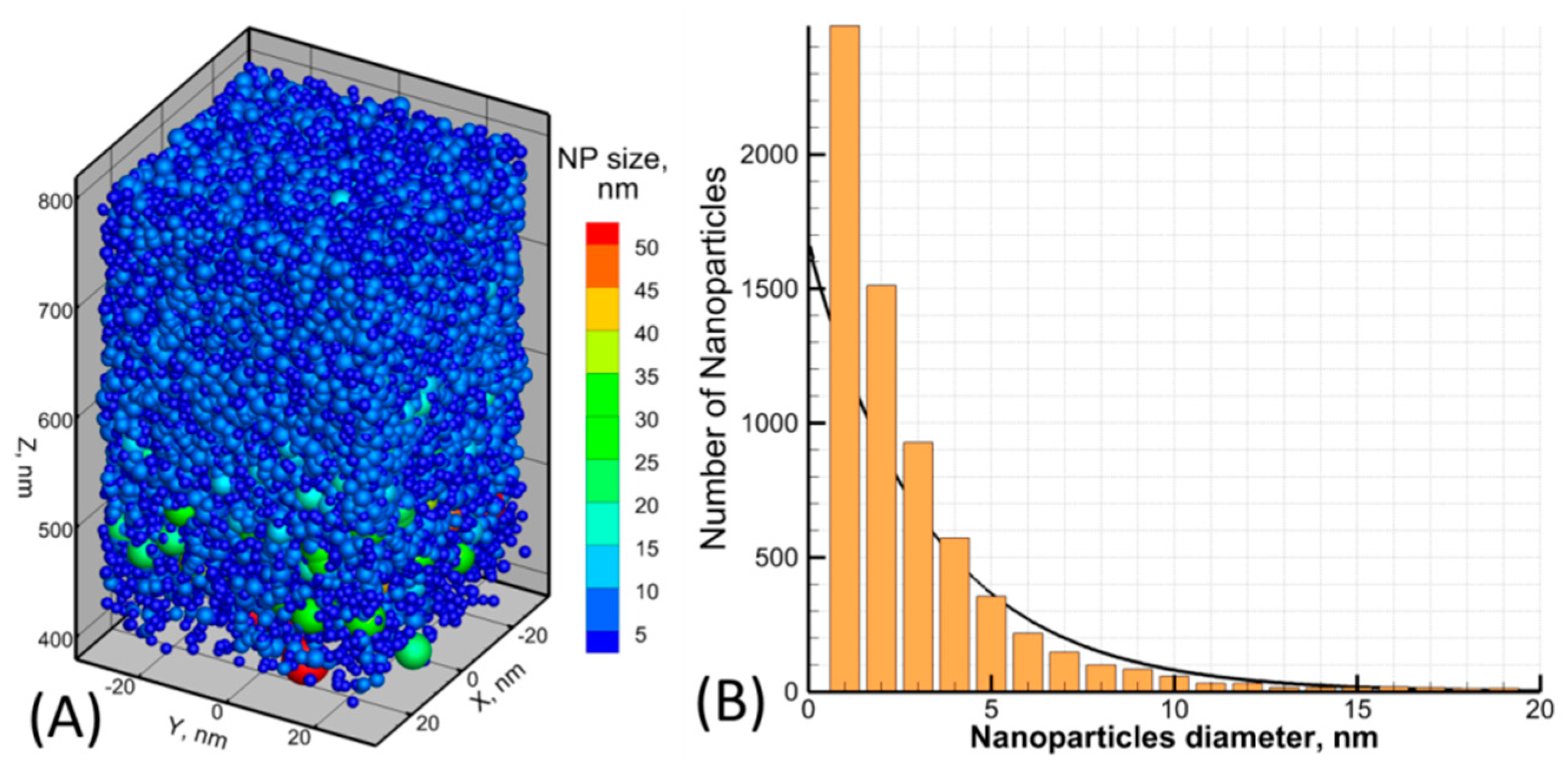
3.3. Numerical Simulations of Au Nanoparticles Formation During Laser Ablation
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Corkum, P.B.; Krausz, F. Attosecond science. Nat. Phys. 2007, 3, 381. [Google Scholar] [CrossRef]
- Ganeev, R.A. High-Order Harmonic Generation in Laser Plasma Plumes; Imperial College Press: London, UK, 2012. [Google Scholar]
- Tsakiris, G.D.; Eidmann, K.; Meyer-ter-Vehn, J.; Krausz, F. Route to intense single attosecond pulses. New J. Phys. 2006, 8, 1–20. [Google Scholar] [CrossRef]
- Ganeev, R.A.; Suzuki, M.; Baba, M.; Kuroda, H. High-order harmonic generation from laser plasma produced by pulses of different duration. Phys. Rev. A 2007, 76, 023805. [Google Scholar] [CrossRef]
- Akiyama, Y.; Midorikawa, K.; Matsunawa, Y.; Nagata, Y.; Obara, M.; Tashiro, T.; Toyoda, K. Generation of high-order harmonics using laser-produced rare-gas-like ions. Phys. Rev. Lett. 1992, 69, 2176. [Google Scholar] [CrossRef]
- Kubodera, S.; Nagata, Y.; Akiyama, Y.; Midorikawa, K.; Obara, M.; Tashiro, H.; Toyoda, K. High-order harmonic generation in laser-produced ions. Phys. Rev. A 1993, 48, 4576. [Google Scholar] [CrossRef]
- de Nalda, R.; Lopez-Arias, M.; Sanz, M.; Oujja, M.; Castillejo, M. Harmonic generation in ablation plasmas of wide bandgap semiconductors. Phys. Chem. Chem. Phys. 2011, 13, 10755–10760. [Google Scholar] [CrossRef]
- Ganeev, R.A.; Singhal, H.; Naik, P.A.; Arora, V.; Chakravarty, U.; Chakera, J.A.; Khan, R.A.; Redkin, P.V.; Raghuramaiah, M.; Gupta, P.D. Single harmonic enhancement by controlling the chirp of the driving laser pulse during high-order harmonic generation from GaAs plasma. J. Opt. Soc. Am. B 2006, 23, 2535–2540. [Google Scholar] [CrossRef]
- Pertot, Y.; Chen, S.; Khan, S.D.; Bom, L.B.E.; Ozaki, T.; Chang, Z. Generation of continuum high-order harmonics from carbon plasma using double optical gating. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 074017. [Google Scholar] [CrossRef]
- Lopez-Quintas, I.; Oujja, M.; Sanz, M.; Martin, M.; Ganeev, R.A.; Castillejo, M. Low-order harmonic generation in nanosecond laser ablation plasmas of carbon containing materials. Appl. Surf. Sci. 2013, 278, 33–37. [Google Scholar] [CrossRef]
- Haessler, S.; Strelkov, V.V.; Bom, L.B.E.; Khokhlova, M.; Gobert, O.; Hergott, J.-F.; Lepetit, F.; Perdrix, M.; Ozaki, T.; Salières, P. Phase distortions of attosecond pulses produced by resonance-enhanced high harmonic generation. New J. Phys. 2013, 15, 013051. [Google Scholar] [CrossRef]
- Rosenthal, N.; Marcus, G. Discriminating between the role of phase matching and that of the single atom response in resonance plasma-plume high-order harmonic generation. Phys. Rev. Lett. 2015, 115, 133901. [Google Scholar] [CrossRef] [PubMed]
- Fareed, M.A.; Thiré, N.; Mondal, S.; Schmidt, B.E.; Légaré, F.; Ozaki, T. Efficient generation of sub-100 eV high-order harmonics from carbon molecules using infrared laser pulses. Appl. Phys. Lett. 2016, 108, 124104. [Google Scholar] [CrossRef]
- Fareed, M.A.; Strelkov, V.V.; Thiré, N.; Mondal, S.; Schmidt, B.E.; Légaré, F.; Ozaki, T. High-order harmonic generation from the dressed autoionizing states. Nat. Commun. 2017, 8, 16061. [Google Scholar] [CrossRef] [PubMed]
- Oujja, M.; Izquierdo, J.G.; Bañares, L.; de Nalda, R.; Castillejo, M. Observation of middle-sized metal clusters in femtosecond laser ablation plasmas through nonlinear optics. Phys. Chem. Chem. Phys. 2018, 20, 16956–16965. [Google Scholar] [CrossRef]
- Fareed, M.A.; Strelkov, V.V.; Singh, M.; Thire, N.; Mondal, S.; Schmidt, B.E.; Légaré, F.; Ozaki, T. Harmonic generation from neutral manganese atoms in the vicinity of the giant autoionization resonance. Phys. Rev. Lett. 2018, 121, 023201. [Google Scholar] [CrossRef]
- Ganeev, R.A.; Boltaev, G.S.; Kim, V.V.; Venkatesh, M.; Guo, C. Comparison studies of high-order harmonic generation in argon gas and different laser-produced plasmas. OSA Continuum 2019, 2, 2381–2390. [Google Scholar] [CrossRef]
- Han, S.; Kim, H.; Kim, Y.W.; Kim, Y.J.; Kim, S.; Park, I.Y.; Kim, S.W. High-harmonic generation by field enhanced femtosecond pulses in metal-sapphire nanostructure. Nat. Commun. 2016, 7, 13105. [Google Scholar] [CrossRef]
- Liu, H.; Guo, C.; Vampa, G.; Zhang, J.L.; Sarmiento, T.; Xiao, M.; Bucksbaum, P.H.; Vučković, J.; Fan, S.; Reis, D.A. Enhanced high-harmonic generation from an all-dielectric metasurface. Nat. Phys. 2018, 14, 1006–1010. [Google Scholar] [CrossRef]
- Rout, A.; Boltaev, G.S.; Ganeev, R.A.; Fu, Y.; Maurya, S.K.; Kim, V.V.; Rao, K.S.; Guo, C. Nonlinear optical studies of gold nanoparticle films. Nanomaterials 2019, 9, 291. [Google Scholar] [CrossRef]
- Hutchison, C.; Ganeev, R.A.; Witting, T.; Frank, F.; Okell, W.A.; Tisch, J.W.G.; Marangos, J.P. Stable generation of high-order harmonics of femtosecond laser radiation from laser produced plasma plumes at 1 kHz pulse repetition rate. Opt. Lett. 2012, 37, 2064–2066. [Google Scholar] [CrossRef]
- NIST Atomic Spectra Database Lines Form. Available online: https://physics.nist.gov/PhysRefData/ASD/lines_form.html (accessed on 27 January 2020).
- Ganeev, R.A.; Witting, T.; Hutchison, C.; Frank, F.; Redkin, P.V.; Okell, W.A.; Lei, D.Y.; Roschuk, T.; Maier, S.A.; Marangos, J.P.; et al. Enhanced high-order harmonic generation in a carbon ablation plume. Phys. Rev. A 2012, 85, 015807. [Google Scholar] [CrossRef]
- Bom, L.B.E.; Pertot, Y.; Bhardwaj, V.R.; Ozaki, T. Multi-μJ coherent extreme ultraviolet source generated from carbon using the plasma harmonic method. Opt. Express 2011, 19, 3077–3085. [Google Scholar] [CrossRef] [PubMed]
- Ganeev, R.A.; Naik, P.A.; Singhal, H.; Chakera, J.A.; Kumar, M.; Chakravarty, U.; Gupta, P.D. Use of carbon containing materials for efficient high order harmonic generation with femtosecond pulses. Opt. Commun. 2012, 285, 2934–2941. [Google Scholar] [CrossRef]
- Ganeev, R.A.; Hutchison, C.; Witting, T.; Frank, F.; Okell, W.A.; Zaïr, A.; Weber, S.; Redkin, P.V.; Lei, D.Y.; Roschuk, T.; et al. High-order harmonic generation in graphite plasma plumes using ultrashort laser pulses: A systematic analysis of harmonic radiation and plasma conditions. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 165402. [Google Scholar] [CrossRef]
- Olmon, R.L.; Slovick, B.; Johnson, T.W.; Shelton, D.; Oh, S.-H.; Boreman, G.D.; Raschke, M.B. Optical dielectric function of gold. Phys. Rev. B 2012, 86, 235147. [Google Scholar] [CrossRef]
- Kim, S.; Jin, J.; Kim, Y.-J.; Park, I.-Y.; Kim, Y.; Kim, S.-W. High-harmonic generation by resonant plasmon field enhancement. Nature 2008, 453, 757–760. [Google Scholar] [CrossRef]
- Park, I.-Y.; Kim, S.; Choi, J.; Lee, D.-H.; Kim, Y.-J.; Kling, M.F.; Stockman, M.I.; Kim, S.-W. Plasmonic generation of ultrashort extreme-ultraviolet light pulses. Nat. Photonics 2011, 5, 677–681. [Google Scholar] [CrossRef]
- Ciappina, M.F.; Aćimović, S.S.; Shaaran, T.; Biegert, J.; Quidant, R.; Lewenstein, M. Enhancement of high harmonic generation by confining electron motion in plasmonic nanostructures. Opt. Express 2012, 20, 26261–26271. [Google Scholar] [CrossRef]
- Chen, K.; Durak, C.; Heflin, J.R.; Robinson, H.D. Plasmon-enhanced second-harmonic generation from ionic self-assembled multilayer films. Nano Lett. 2007, 7, 254–258. [Google Scholar] [CrossRef]
- Ren, F.; Wang, X.; Li, Z.; Luo, J.; Jang, S.-H.; Jen, A.K.-Y.; Wang, A.X. Enhanced third harmonic generation by organic materials on high-Q plasmonic photonic crystals. Opt. Express 2014, 22, 20292–20297. [Google Scholar] [CrossRef]
- Ulriksen, H.U.; Pedersen, K. Field enhancement at silicon surfaces by gold ellipsoids probed by optical second-harmonic generation spectroscopy. J. Appl. Phys. 2016, 120, 235307. [Google Scholar] [CrossRef]
- Dong, Z.; Asbahi, M.; Lin, J.; Zhu, D.; Wang, Y.M.; Hippalgaonkar, K.; Chu, H.-S.; Goh, W.P.; Wang, F.; Huang, Z.; et al. Second-harmonic generation from sub-5 nm gaps by directed self-assembly of nanoparticles onto template-stripped gold substrates. Nano Lett. 2015, 15, 5976–5981. [Google Scholar] [CrossRef] [PubMed]
- Shi, L.; Nicolas, R.; Andrade, J.R.C.; Boutu, W.; Franz, D.; Heidenblut, T.; Reinhardt, C.; Morgner, U.; Merdji, H.; Kovacev, M. Impact of plasmon-induced atoms migration in harmonic generation. ACS Photonics 2018, 5, 1208–1214. [Google Scholar] [CrossRef]
- Vampa, G.; Ghamsari, B.G.; Siadat Mousavi, S.; Hammond, T.J.; Olivieri, A.; Lisicka-Skrek, E.; Naumov, A.Y.; Villeneuve, D.M.; Staudte, A.; Berini, P.; et al. Plasmon-enhanced high-harmonic generation from silicon. Nat. Phys. 2017, 13, 659–662. [Google Scholar] [CrossRef]
- Ganeev, R.A. Controlling single harmonic enhancement in laser produced plasmas. J. Appl. Phys. 2017, 121, 133108. [Google Scholar] [CrossRef]
- Franz, D.; Kaassamani, S.; Gauthier, D.; Nicolas, R.; Kholodtsova, M.; Douillard, L.; Gomes, J.-T.; Lavoute, L.; Gaponov, D.; Ducros, N.; et al. All semiconductor enhanced high-harmonic generation from a single nanostructured cone. Sci. Rep. 2019, 9, 5663. [Google Scholar] [CrossRef]
- Ganeev, R.A.; Baba, M.; Suzuki, M.; Kuroda, H. High-order harmonic generation from silver plasma. Phys. Lett. A 2005, 339, 103–109. [Google Scholar] [CrossRef]
- Ganeev, R.A.; Boltaev, G.S.; Kim, V.V.; Guo, C. Effects of laser plasma formation on quasi-phase matching of high-order harmonics from nanoparticles and atoms. Nanomaterials 2019, 9, 572. [Google Scholar] [CrossRef]
- Ganeev, R.A. Harmonic generation from partially ionized plasma. J. Opt. Soc. Am. B 2014, 31, 2221–2231. [Google Scholar] [CrossRef]
- Lai, C.-J.; Kärtner, F.X. The influence of plasma defocusing in high harmonic generation. Opt. Express 2011, 19, 22377. [Google Scholar] [CrossRef][Green Version]
- Ganeev, R.A. On- and off-axis studies of the quasi-phase-matching-enhanced harmonics generated in the multi-jet laser-produced plasmas. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 095402. [Google Scholar] [CrossRef]
- Kan, C.; Burnett, N.H.; Capjack, C.E.; Rankin, R. Coherent XUV generation from gases ionized by several cycle optical pulses. Phys. Rev. Lett. 1997, 79, 2971–2974. [Google Scholar] [CrossRef]
- Kim, I.J.; Lee, G.H.; Park, S.B.; Lee, Y.S.; Kim, T.K.; Nam, C.H.; Mocek, T.; Jakubczak, K. Generation of submicrojoule high harmonics using a long gas jet in a two-color laser field. Appl. Phys. Lett. 2008, 92, 021125. [Google Scholar] [CrossRef]
- Brandi, F.; Giammanco, F.; Ubachs, W. Spectral redshift in harmonic generation from plasma dynamics in the laser focus. Phys. Rev. Lett. 2006, 96, 123904. [Google Scholar] [CrossRef] [PubMed]
- Ganeev, R.A.; Bom, L.B.E.; Kieffer, J.-C.; Ozaki, T. Systematic investigation of resonance-induced single-harmonic enhancement in the extreme-ultraviolet range. Phys. Rev. A 2007, 75, 063806. [Google Scholar] [CrossRef]
- Holian, B.L.; Lomdahl, P.S. Plasticity induced by shock waves in nonequilibrium molecular-dynamics simulations. Science 1998, 280, 2085–2088. [Google Scholar] [CrossRef]
- Hohlfeld, J.; Wellershoff, S.-S.; Guedde, J.; Conrad, U.; Jaehnke, V.; Matthias, E. Electron and lattice dynamics following optical excitation of metals. Chem. Phys. 2000, 251, 237–258. [Google Scholar] [CrossRef]
- Anisimov, S.I.; Kapeliovich, B.L.; Perel’man, T.L. Electron emission from metal surfaces exposed to ultrashort laser pulses. Zh. Eksp. Teor. Fiz. 1974, 66, 776. [Google Scholar]
- Ivanov, D.S.; Zhigilei, L.V. Combined atomistic-continuum modelling of short-pulse laser melting 659 and disintegration of metal films. Phys. Rev. B 2003, 68, 064114. [Google Scholar] [CrossRef]
- Ivanov, D.S.; Kuznetsov, A.I.; Lipp, V.P.; Rethfeld, B.; Chichkov, B.N.; Garcia, M.E.; Schulz, W. Short laser pulse surface nanostructuring on thin metal films: Direct comparison of molecular dynamics modeling and experiment. Appl. Phys. A 2013, 111, 675. [Google Scholar] [CrossRef]
- Zhakhovskii, V.V.; Inogamov, N.A.; Petrov, Y.V.; Ashitkov, S.I.; Nishihara, K. Molecular dynamics simulation of femtosecond ablation and spallation with different interatomic potentials. Appl. Surf. Sci. 2009, 55, 9592–9596. [Google Scholar] [CrossRef]
- The World’s Sales Leader in Thin-Film Thickness Measurement. Available online: https://www.filmetrics.com (accessed on 27 January 2020).
- Corkum, P.B.; Brunel, F.; Sherman, N.; Srinivasan-Rao, T.J. Thermal response of metals to ultrashort-pulse laser excitation. Phys. Rev. Lett. 1988, 61, 2886. [Google Scholar] [CrossRef] [PubMed]
- Ivanov, D.S.; Rethfeld, B. The effect of pulse duration on the interplay of electron heat conduction and electron–phonon interaction: Photo-mechanical versus photo-thermal damage of metal targets. Appl. Surf. Sci. 2009, 255, 9724–9728. [Google Scholar] [CrossRef]
- Bom, L.B.E.; Kieffer, J.-C.; Ganeev, R.A.; Suzuki, M.; Kuroda, H.; Ozaki, T. Influence of the main pulse and prepulse intensity on high-order harmonic generation in silver plasma ablation. Phys. Rev. A 2007, 75, 033804. [Google Scholar]
- Ganeev, R.A.; Hutchison, C.; Castillejo, M.; Lopez-Quintas, I.; McGrath, F.; Lei, D.Y.; Marangos, J.P. Ablation of nanoparticles and efficient harmonic generation using a 1-kHz laser. Phys. Rev. A 2013, 88, 033803. [Google Scholar] [CrossRef]
- Wöstmann, M.; Redkin, P.V.; Zheng, J.; Witte, H.; Ganeev, R.A.; Zacharias, H. High-order harmonic generation in plasmas from nanoparticle and mixed metal targets at 1-kHz repetition rate. Appl. Phys. B 2015, 120, 17–24. [Google Scholar] [CrossRef]
- Ganeev, R.A.; Suzuki, M.; Kuroda, H. High-order harmonic generation in Ag, Sn, fullerene, and graphene nanoparticle-contained plasmas using two-color mid-infrared pulses. Eur. Phys. J. 2016, 70, 21. [Google Scholar] [CrossRef]




© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Venkatesh, M.; Ganeev, R.A.; Ivanov, D.S.; Boltaev, G.S.; Kim, V.V.; Liang, J.; Samokhvalov, A.A.; Kabashin, A.V.; Klimentov, S.M.; Garcia, M.E.; et al. High-Order Harmonic Generation in Au Nanoparticle-Contained Plasmas. Nanomaterials 2020, 10, 234. https://doi.org/10.3390/nano10020234
Venkatesh M, Ganeev RA, Ivanov DS, Boltaev GS, Kim VV, Liang J, Samokhvalov AA, Kabashin AV, Klimentov SM, Garcia ME, et al. High-Order Harmonic Generation in Au Nanoparticle-Contained Plasmas. Nanomaterials. 2020; 10(2):234. https://doi.org/10.3390/nano10020234
Chicago/Turabian StyleVenkatesh, Mottamchetty, Rashid A. Ganeev, Dmitry S. Ivanov, Ganjaboy S. Boltaev, Vyacheslav V. Kim, Jingguang Liang, Andrey A. Samokhvalov, Andrei V. Kabashin, Sergey M. Klimentov, Martin E. Garcia, and et al. 2020. "High-Order Harmonic Generation in Au Nanoparticle-Contained Plasmas" Nanomaterials 10, no. 2: 234. https://doi.org/10.3390/nano10020234
APA StyleVenkatesh, M., Ganeev, R. A., Ivanov, D. S., Boltaev, G. S., Kim, V. V., Liang, J., Samokhvalov, A. A., Kabashin, A. V., Klimentov, S. M., Garcia, M. E., & Guo, C. (2020). High-Order Harmonic Generation in Au Nanoparticle-Contained Plasmas. Nanomaterials, 10(2), 234. https://doi.org/10.3390/nano10020234






