Review and Mechanism of the Thickness Effect of Solid Dielectrics
Abstract
1. Introduction
2. Review on Reported Relations about EBD on d
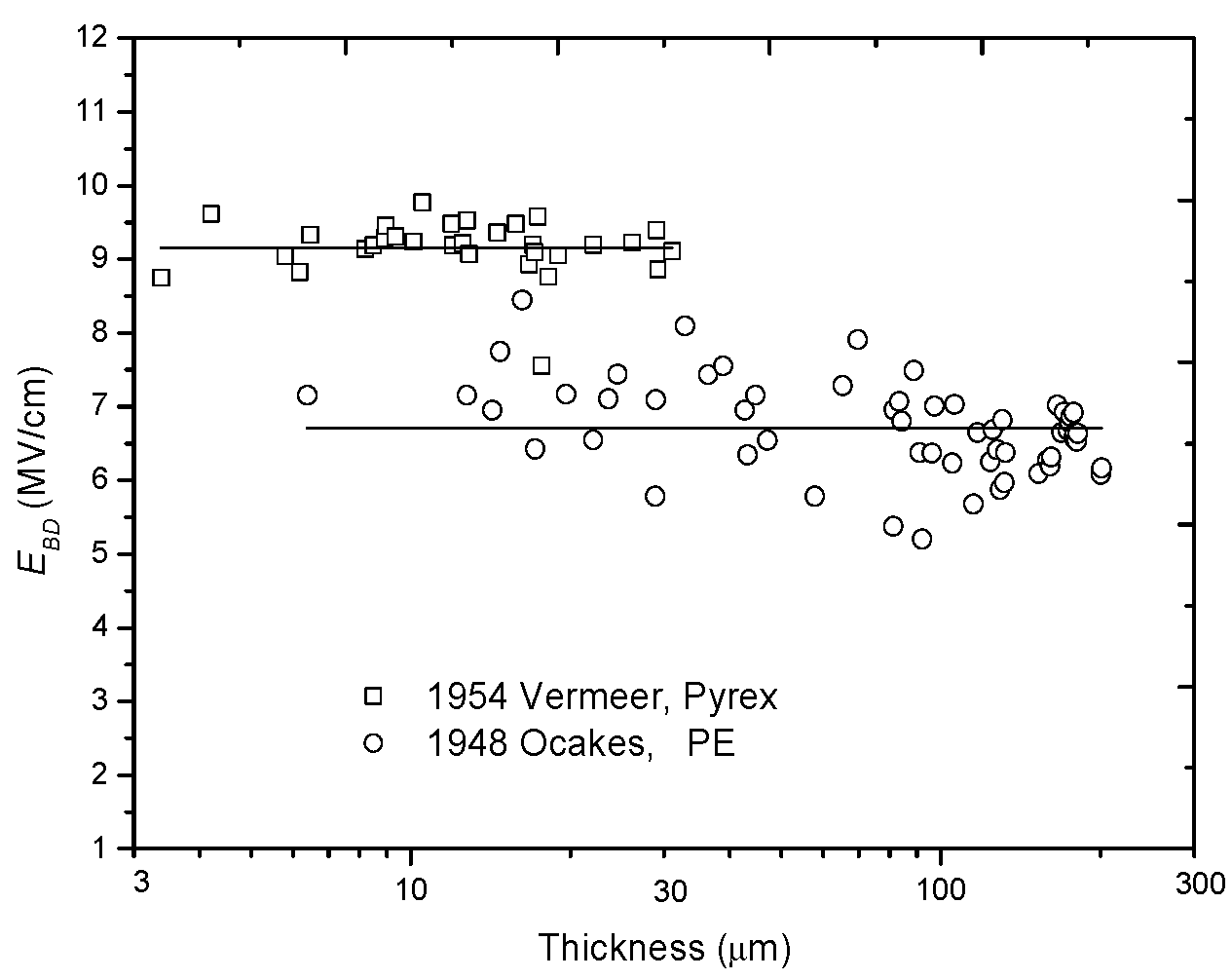
2.1. Constant Relation
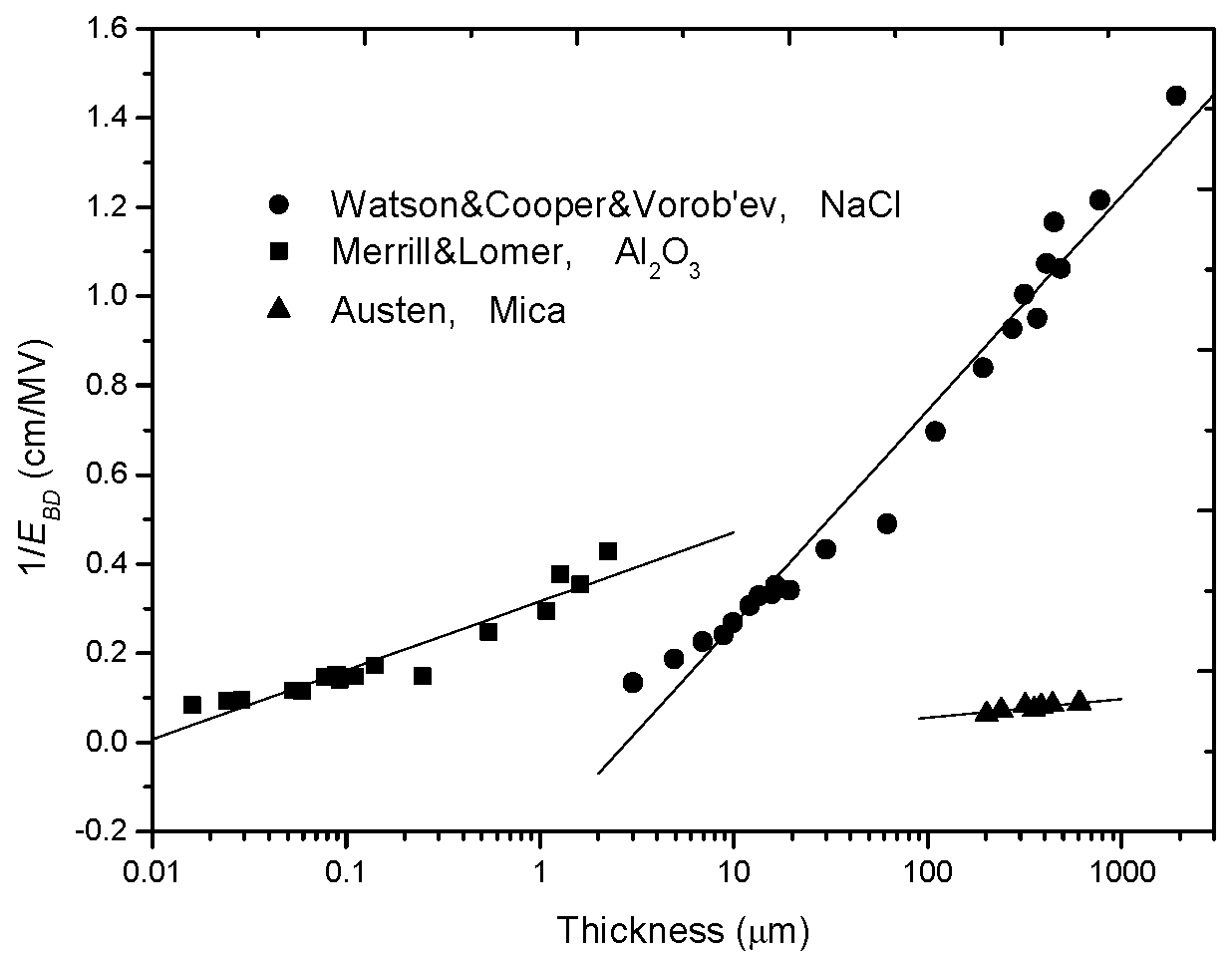
2.2. Reciprocal-Single-Logarithm Relation
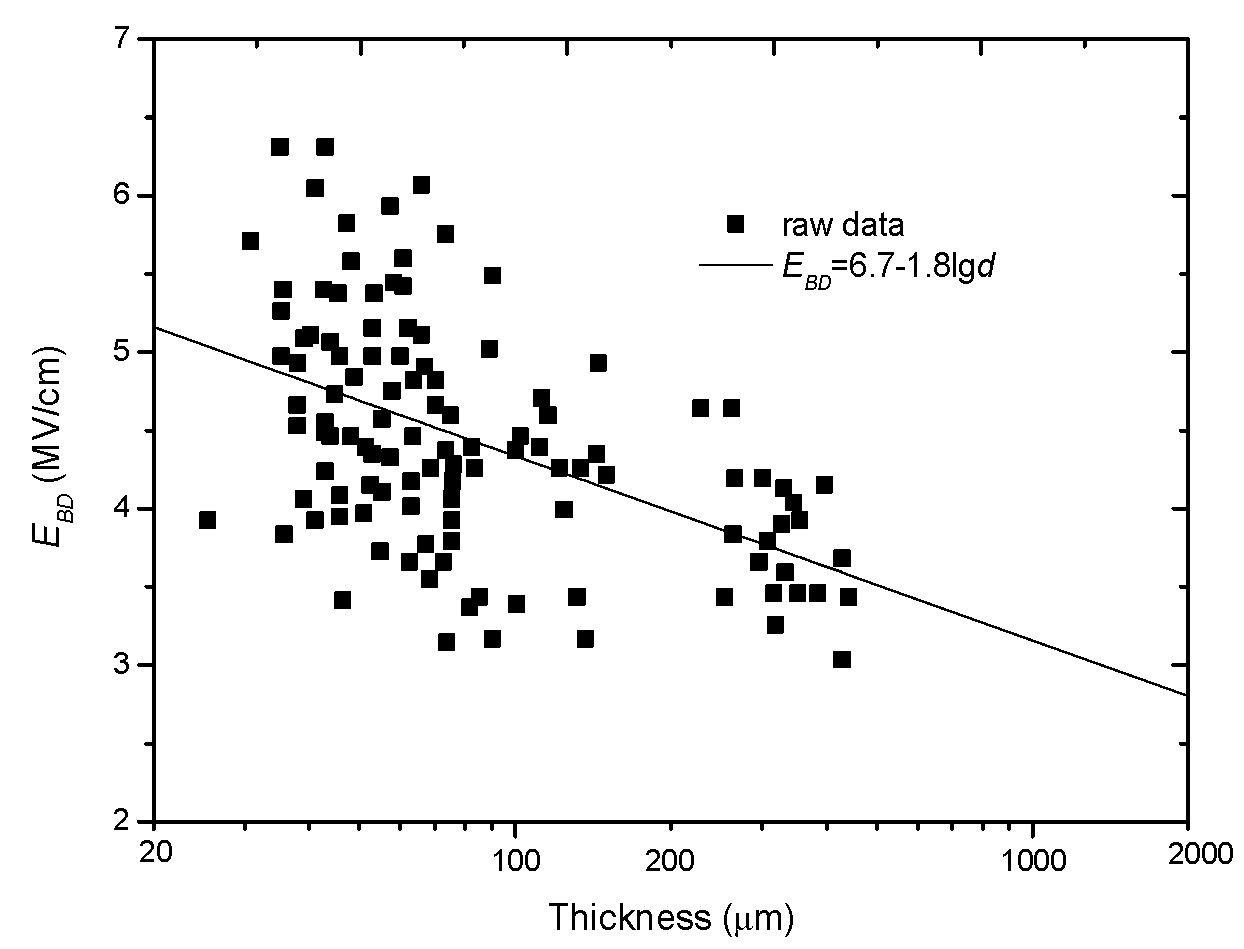
2.3. Minus-Single-Logarithm Relation
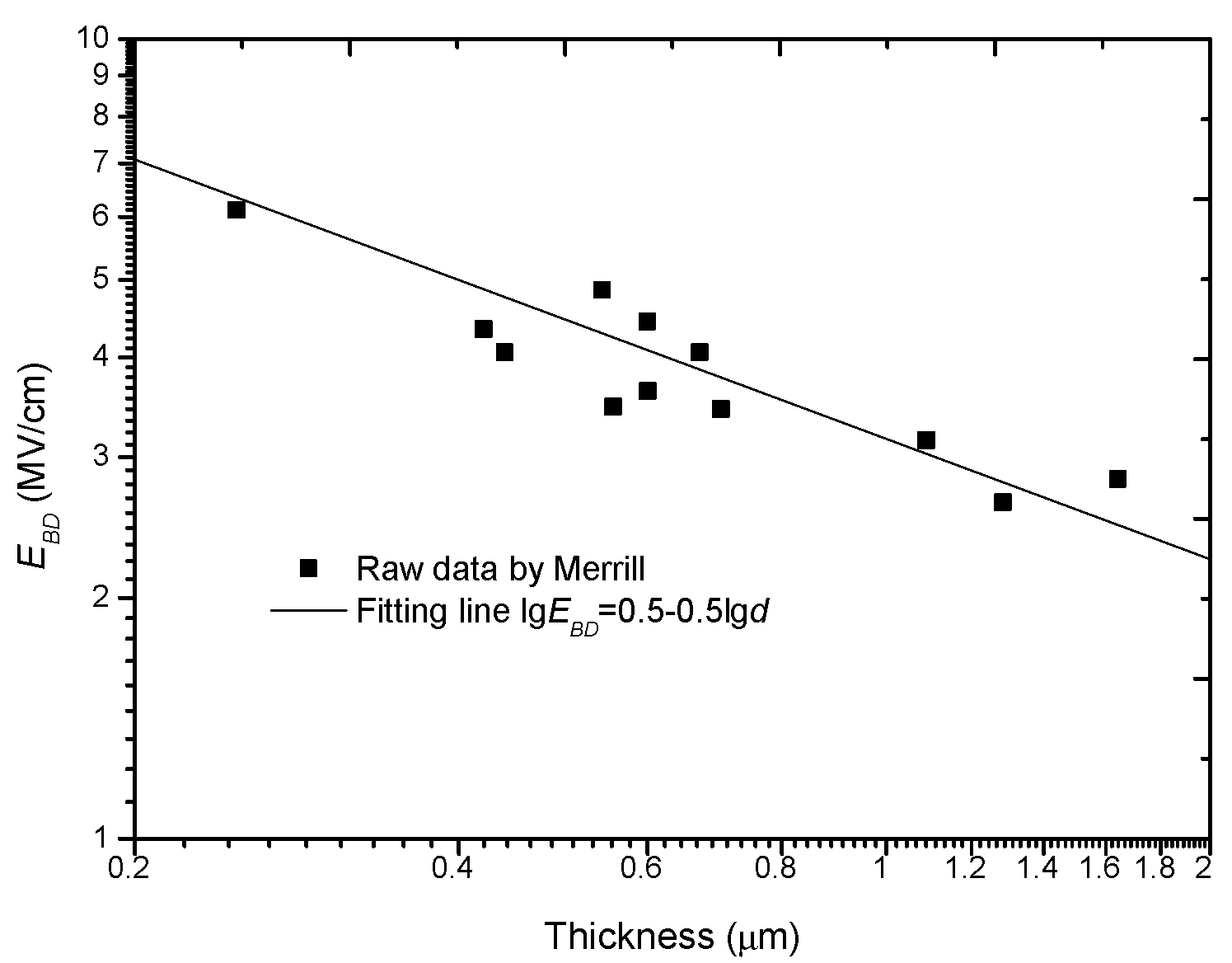
2.4. Double-Logarithm Relation
3. Comparison of Different EBD-d Relations
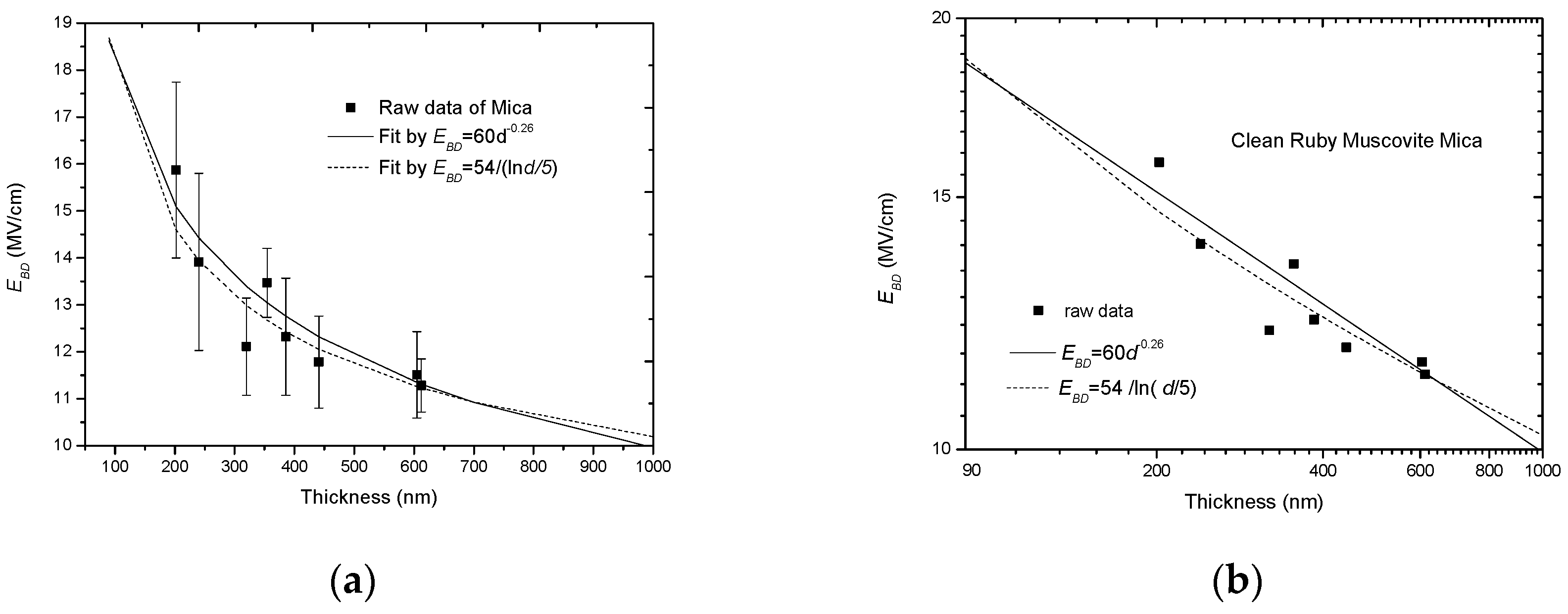
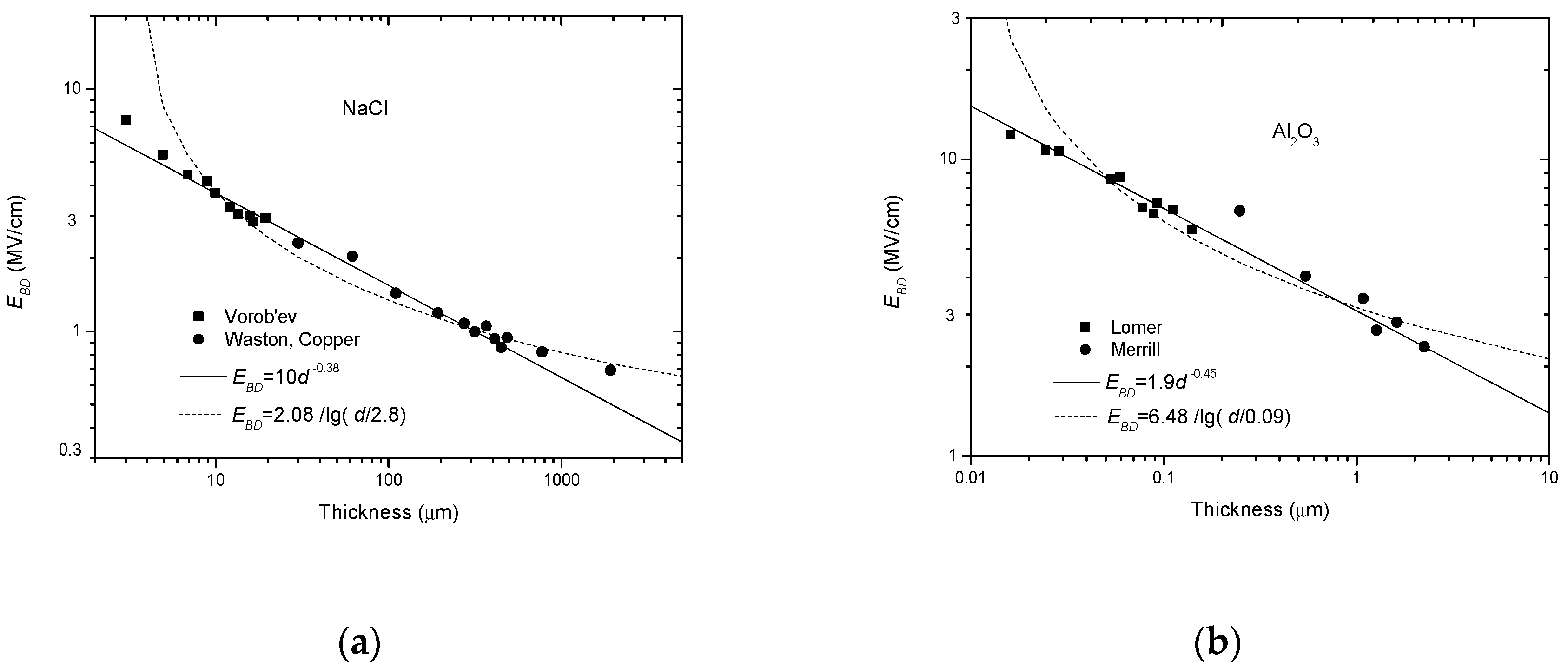
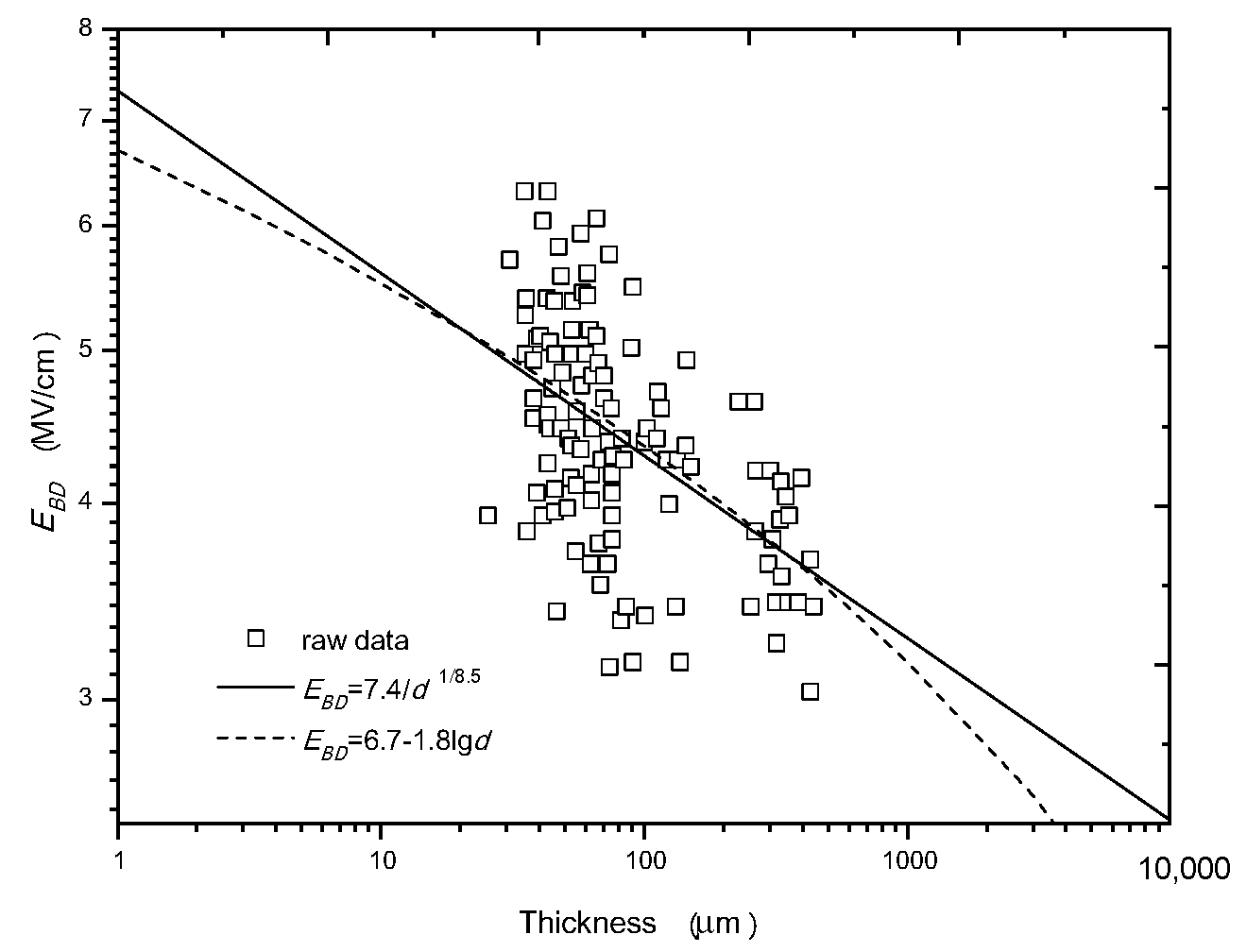
3.1. More Results on lgEBD-lgd Relation
3.2. Comparison between Minus Power Relation and Other Three Types of Relations
3.2.1. Comparison with the Reciprocal-Single-Logarithm Relation
3.2.2. Comparison with the Minus-Single-Logarithm Relation
3.2.3. Comparison with the Constant Relation
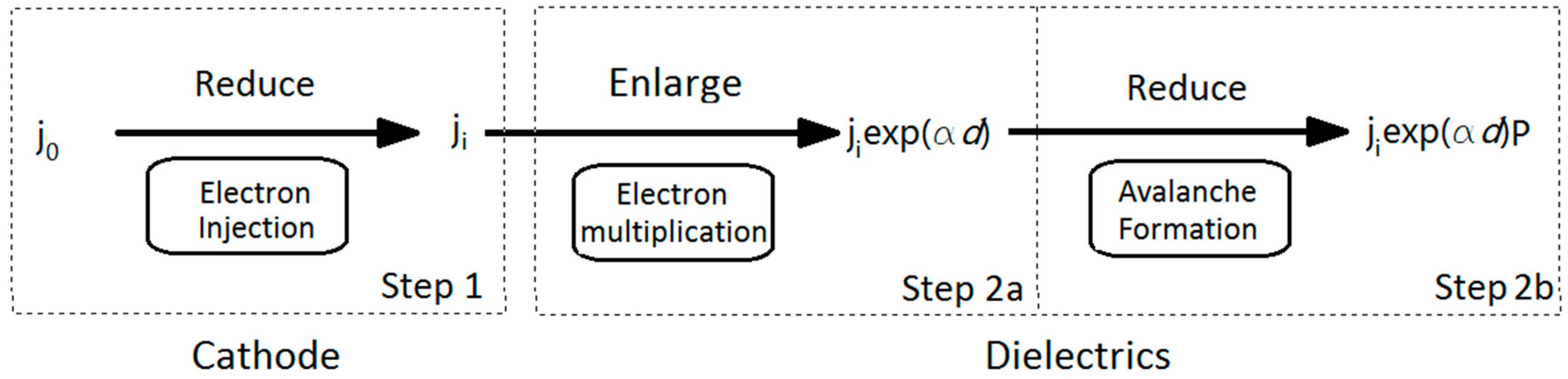
4. Mechanism for the Minus Power Relation
4.1. Review on Model Suggested by F. Forlani
4.2. Solution and Improvements for Forlani’ Model
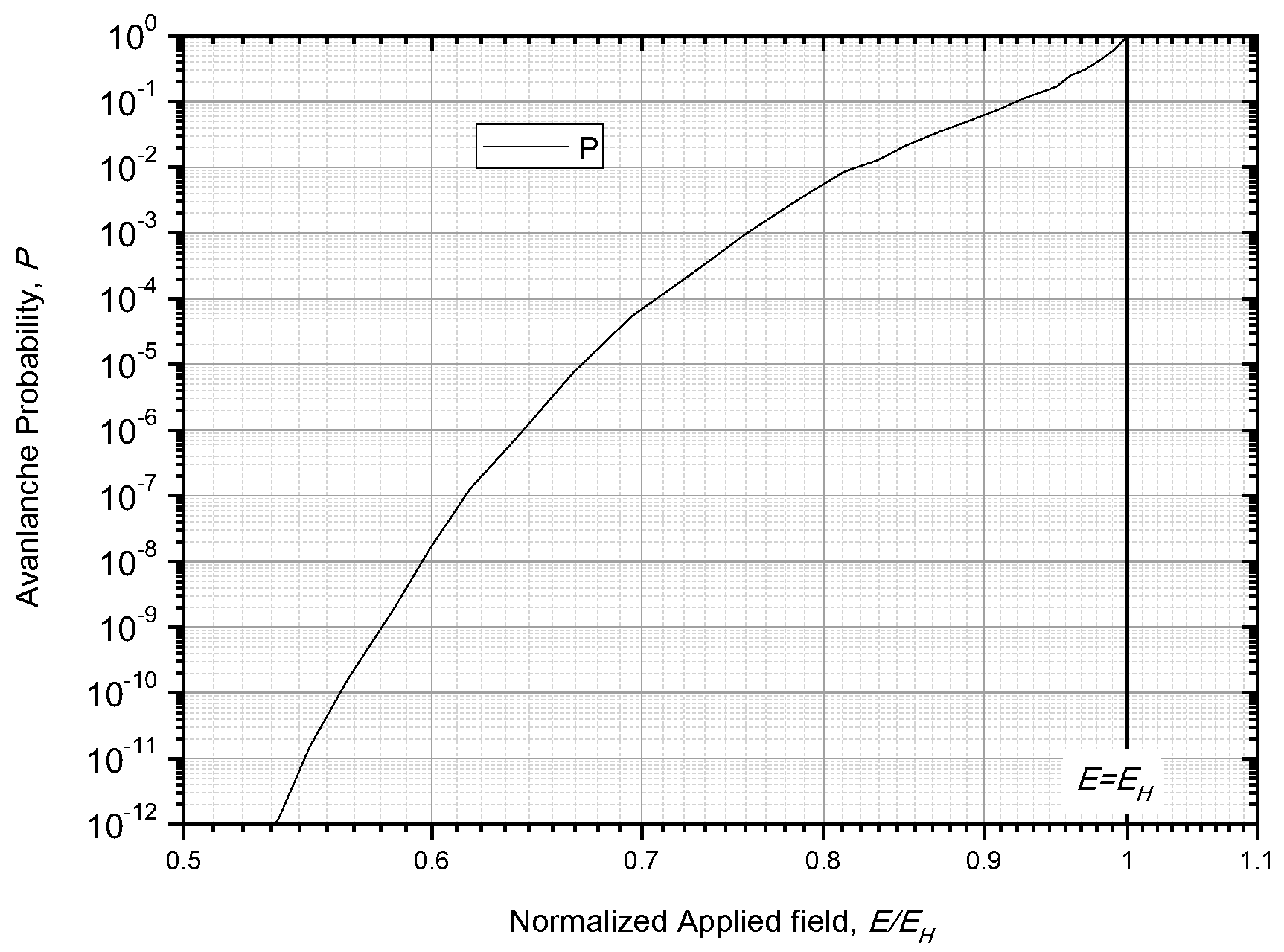
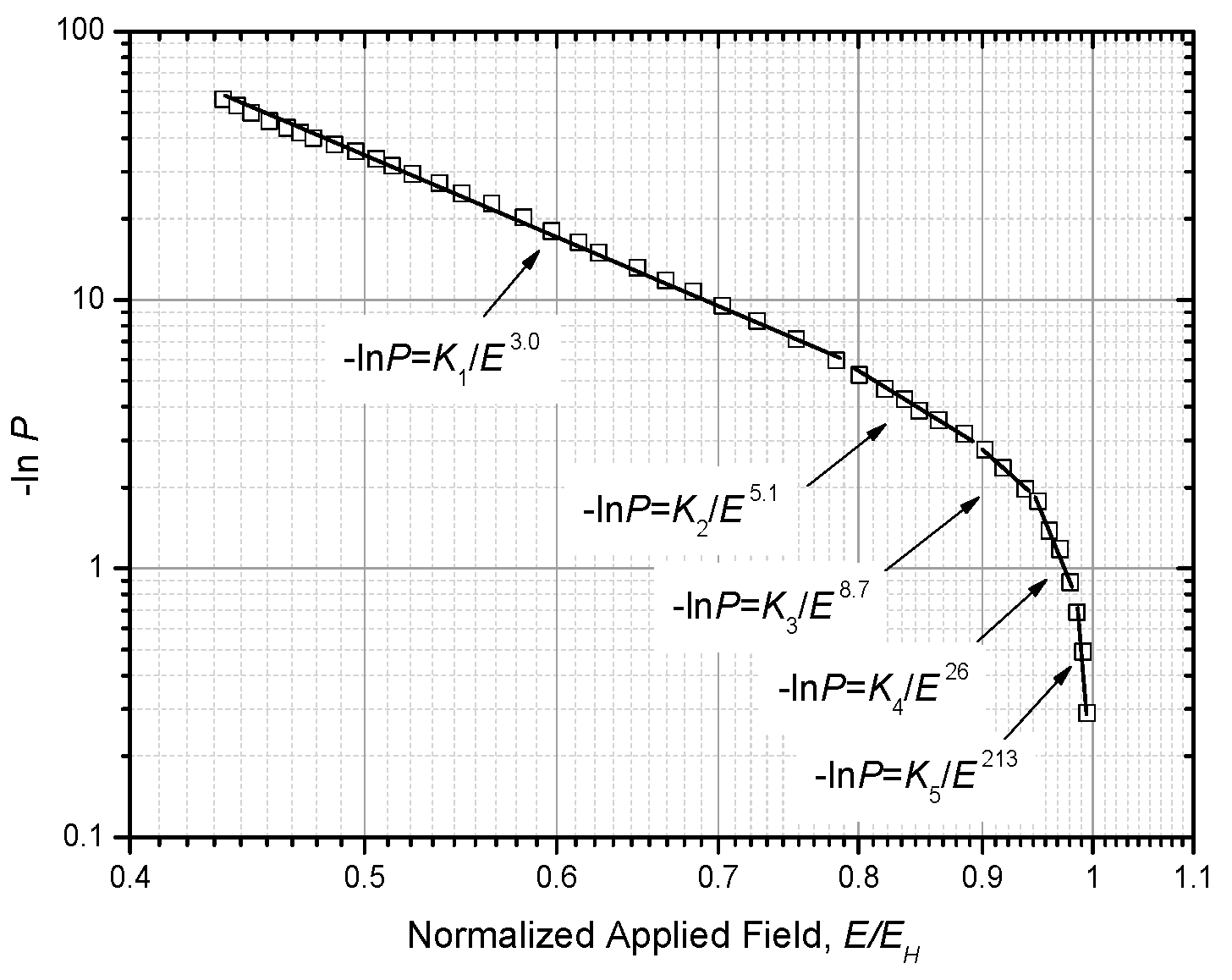
5. Minus Power Relation from Weibull Statistics
5.1. Deduction for the Minus Power Relation
5.2. Expectation and Standard Error of Weibull Distribution
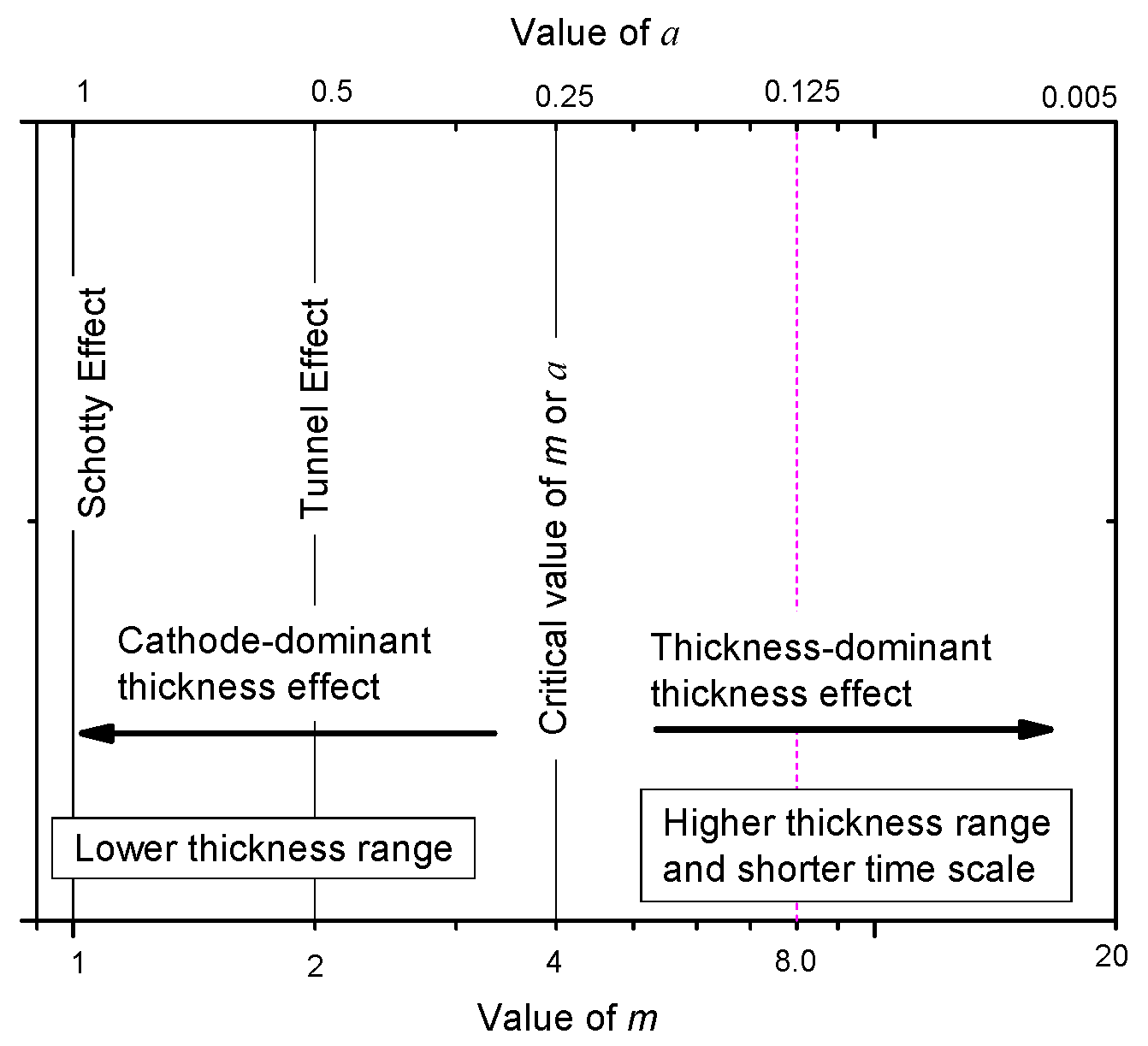
5.3. Physical Meaning of a or 1/m
6. Discussion on the Power Exponent of a or 1/m in Minus Power Relation
6.1. Factors Influencing a
6.1.1. Temperature
6.1.2. Time Scale
6.1.3. Electrode Configuration and Ambient Liquid
6.1.4. Thickness Range
6.2. What Does m Betray When m > 4 (or a < 0.25)?
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Korovin, S.D.; Rostov, V.V.; Polevin, S.D.; Pegel, I.V.; Schamiloglu, E.; Fuks, M.I.; Barker, R.J. Pulsed power-driven high-power microwave sources. Proc. IEEE 2004, 92, 1082–1095. [Google Scholar] [CrossRef]
- Roth, I.S.; Sincerny, P.S.; Mandelcorn, L.; Mendelsohn, M.; Smith, D.; Engel, T.G.; Schlitt, L.; Cooke, C.M. Vacuum insulator coating development. In Proceedings of the 11th IEEE International Pulsed Power Conference, Baltimore, MD, USA, 29 June 1997; IEEE: Piscataway, NJ, USA, 1997; pp. 537–542. [Google Scholar]
- Stygar, W.A.; Lott, J.A.; Wagoner, T.C.; Anaya, V.; Harjes, H.C. Improved design of a high-voltage vacuum-insulator interface. Phys. Rev. Spec. Top. Accel. Beams 2005, 8, 050401. [Google Scholar] [CrossRef]
- Zhao, L.; Peng, J.C.; Pan, Y.F.; Zhang, X.B.; Su, J.C. Insulation Analysis of a Coaxial High-Voltage Vacuum Insulator. IEEE Trans. Plasma Sci. 2010, 38, 1369–1374. [Google Scholar] [CrossRef]
- Mesyats, G.A.; Korovin, S.D.; Gunin, A.V.; Gubanov, V.P.; Stepchenko, A.S.; Grishin, D.M.; Landl, V.F.; Alekseenko, P.I. Repetitively pulsed high-current accelerators with transformer charging of forming lines. Laser Part. Beams 2003, 21, 198–209. [Google Scholar] [CrossRef]
- Oakes, W.G. The intrinsic electric strength of polythene and its variation with temperature. J. Inst. Electr. Eng. 1948, 95, 36–44. [Google Scholar] [CrossRef]
- von Hippel, A. Electric Breakdown of Solid and Liquid Insulators. J. Appl. Phys. 1937, 8, 815–832. [Google Scholar] [CrossRef]
- von Hippel, A. Electronic conduction in insulating crystals under very high field strength. Phys. Rev. 1938, 54, 1096–1102. [Google Scholar] [CrossRef]
- von Hippel, A.; Davisson, J.W. The propagation of electron waves in ionic single crystals. Phys. Rev. 1940, 57, 156–157. [Google Scholar] [CrossRef]
- von Hippel, A.; Lee, G.M. Scattering, trapping, and release of electrons in NaCl and in mixed crystals of NaCl and AgCl. Phys. Rev. 1941, 59, 824–826. [Google Scholar] [CrossRef]
- von Hippel, A.; Maurer, R.J. Electric breakdown of glasses and crystals as a function of temperature. Phys. Rev. 1941, 59, 820–823. [Google Scholar] [CrossRef]
- von Hippel, A.; Schulman, J.H.; Rittner, E.S. A New Electrolytic Selenium Photo-Cell. J. Appl. Phys. 1946, 17, 215–224. [Google Scholar] [CrossRef]
- von Hippel, A.V.; Auger, R.S. Breakdown of Ionic Crystals by Electron Avalanches. Phys. Rev. 1949, 76, 127–133. [Google Scholar] [CrossRef]
- von Hippel, A.R. From ferroelectrics to living systems. IEEE Trans. Electron. Dev. 1969, 16, 602. [Google Scholar] [CrossRef]
- Frohlich, H. Theory of electrical breakdown in ionic crystals. In Proceedings of Royal Society of London; Series A: Mathematical and Physical Sciences; Royal Society: London, UK, 1937; Volume 160, pp. 230–241. [Google Scholar]
- Frohlich, H. Theory of electrical breakdown in ionic crystals. II. In Proceedings of Royal Society of London; Series A: Mathematical and Physical Sciences; Royal Society: London, UK, 1939; Volume 172, pp. 94–106. [Google Scholar]
- Frohlich, H. Dielectric breakdown in ionic crystals. Phys. Rev. 1939, 56, 349–352. [Google Scholar] [CrossRef]
- Frohlich, H. Electric breakdown of ionic crystals. Phys. Rev. 1942, 61, 200–201. [Google Scholar] [CrossRef]
- Frohlich, H. Theory of dielectric breakdown. Nature 1943, 151, 339–340. [Google Scholar] [CrossRef]
- Frohlich, H. On the Theory of Dielectric Breakdown in Solids. In Proceedings of Royal Society of London; Series A: Mathematical and Physical Sciences; Royal Society: London, UK, 1947; pp. 521–532. [Google Scholar]
- Frohlich, H.; Seitz, F. Notes on the Theory of Dielectric Breakdown in Ionic Crystals. Phys. Rev. 1950, 79, 526–527. [Google Scholar] [CrossRef]
- Seitz, F.; Johnson, R.P. Modern Theory of Solids. I. J. Appl. Phys. 1937, 8, 84–97. [Google Scholar] [CrossRef]
- Seitz, F.; Johnson, R.P. Modern Theory of Solids. III. J. Appl. Phys. 1937, 8, 246–260. [Google Scholar] [CrossRef]
- Seitz, F.; Johnson, R.P. Modern Theory of Solids. II. J. Appl. Phys. 1937, 8, 186–199. [Google Scholar] [CrossRef]
- Seitz, F.; Read, T.A. Theory of the Plastic Properties of Solids. I. J. Appl. Phys. 1941, 12, 100–118. [Google Scholar] [CrossRef]
- Seitz, F.; Read, T.A. Theory of the Plastic Properties of Solids. III. J. Appl. Phys. 1941, 12, 470–486. [Google Scholar] [CrossRef]
- Seitz, F.; Read, T.A. Theory of the Plastic Properties of Solids. II. J. Appl. Phys. 1941, 12, 170–186. [Google Scholar] [CrossRef]
- Seitz, F.; Read, T.A. Theory of the Plastic Properties of Solids. IV. J. Appl. Phys. 1941, 12, 538–554. [Google Scholar] [CrossRef]
- Stark, K.H.; Garton, G.C. Electrical Strength of Irradiation Polymers. Nature 1955, 176, 1225–1226. [Google Scholar] [CrossRef]
- Austen, A.E.W.; Whitehead, S. The electric strength of some solid dielectrics. In Proceedings Royal Society in London; Royal Society: London, UK, 1940; Volume 176, pp. 33–50. [Google Scholar]
- Whitehead, S. Dielectric Breakdown of Solid; Clarendon Press: Oxford, UK, 1951. [Google Scholar]
- O’Dwyer, J.J. Dielectric breakdown in solid. Adv. Phys. 1958, 7, 349–394. [Google Scholar] [CrossRef]
- O’Dwyer, J.J. The theory of avalanche breakdown in solid dielectrics. J. Phys. Chem. Solids 1967, 7, 1137–1144. [Google Scholar] [CrossRef]
- O’Dwyer, J.J. Theory of High Field Conduction in a Dielectric. J. Appl. Phys. 1969, 40, 3887–3890. [Google Scholar] [CrossRef]
- Zurlo, G.; Destrade, M.; DeTommasi, D.; Puglisi, G. Catastrophic Thinning of Dielectric Elastomers. Phys. Rev. Lett. 2017, 118, 078001. [Google Scholar] [CrossRef]
- Christensen, L.R.; Hassager, O.; Skov, A.L. Electro-Thermal and -Mechanical Model of Thermal Breakdown in Multilayered Dielectric Elastomers. AIChE J. 2020, 66. [Google Scholar] [CrossRef]
- Vermeer, J. The impulse breadown strength of pyrex glass. Phys. X X 1954, 20, 313–326. [Google Scholar]
- Seitz, F. On the Theory of Electron Multiplication in Crystals. Phys. Rev. 1949, 76, 1376–1393. [Google Scholar] [CrossRef]
- Cooper, R.; Rowson, C.H.; Waston, D.B. Intrinsic electric strength of polythene. Nature 1963, 197, 663–664. [Google Scholar] [CrossRef]
- Forlani, F.; Minnaja, N. Thickness influence in breakdown phenomena of thin dielectric films. Phys. Stat. Sol. 1964, 4, 311–324. [Google Scholar] [CrossRef]
- Cooper, R. The dielectric strength of solid dielectrics. Br. J. Appl. Phys. 1966, 17, 149–166. [Google Scholar] [CrossRef]
- Merrill, R.C.; West, R.A. A New Dried Anodized Aluminum Capacitor. IEEE Trans. Parts Mater. Packag. 1965, 1, 224–229. [Google Scholar] [CrossRef]
- Mason, J.H. Breakdown of insulation by discharges. Proc. IEE Part IIA Insul. Mater. 1953, 100, 149–158. [Google Scholar] [CrossRef]
- Mason, J.H. Effects of thickness and area on the electric strength of polymers. IEEE Trans. Electr. Insul. 1991, 26, 318–322. [Google Scholar] [CrossRef]
- Mason, J.H. Effects of frequency on the electric strength of polymers. IEEE Trans. Electr. Insul. 1992, 27, 1213–1216. [Google Scholar] [CrossRef]
- Yilmaz, G.; Kalenderli, O. The effect of thickness and area on the electric strength of thin dielectric films. In Proceedings of the IEEE International Symposium on Electrical Insulation, Montreal, QC, Canada, 16–19 June 1996; pp. 478–481. [Google Scholar]
- Yilmaz, G.; Kalenderli, O. Dielectric behavior and electric strength of polymer films in varying thermal conditions for 5 Hz to 1 MHz frequency range. In Proceedings of the Electrical Insulation Conference and Electrical Manufacturing and Coil Winding, Rosemont, IL, USA, 22–25 September 1997; pp. 269–271. [Google Scholar]
- Singh, A.; Pratap, R. AC electrial breakdown in thin magnesium oxide. Thin Solid Films 1982, 87, 147–150. [Google Scholar] [CrossRef]
- Singh, A. Dielectric breakdown study of thin La2O3 Films. Thin Solid Films 1983, 105, 163–168. [Google Scholar] [CrossRef]
- Ye, Y.; Zhang, S.C.; Dogan, F.; Schamiloglu, E.; Gaudet, J.; Castro, P.; Roybal, M.; Joler, M.; Christodoulou, C. Influence of nanocrystalline grain size on the breakdown strength ceramic dielectrics. In Digest of Technical Papers, PPC-2003. 14th IEEE International Pulsed Power Conference; IEEE: Piscataway, NJ, USA, 2003; pp. 719–722. [Google Scholar]
- Yoshino, K.; Harada, S.; Kyokane, J.; Inuishi, Y. Electrical properties of hexatriacontane single crystal. J. Phys. D Appl. Phys. 1979, 12, 1535–1540. [Google Scholar] [CrossRef]
- Theodosiou, K.; Vitellas, I.; Gialas, I.; Agoris, D.P. Polymer film degradation and breakdown in high voltage ac fields. J. Electr. Eng. 2004, 55, 225–231. [Google Scholar]
- Chen, G.; Zhao, J.; Li, S.; Zhong, L. Origin of thickness dependent dc electrical breakdown in dielectrics. Appl. Phys. Lett. 2012, 100, 222904. [Google Scholar]
- Agwal, V.K.; Srivastava, V.K. Thickness dependence of breakdown filed in thin films. Thin Solid Films 1971, 1971, 377–381. [Google Scholar] [CrossRef]
- Forlani, F.; Minnaja, N. Electrical Breakdown in Thin Dielectric Films. J. Vac. Sci. Technol. 1969, 6, 518–525. [Google Scholar] [CrossRef]
- Mason, J.H. Breakdown of Solid Dielectrics in Divergent Fields. Proc. IEE Part C Monogr. 1955, 102, 254–263. [Google Scholar] [CrossRef]
- Mason, J.H. Comments on ‘Electric breakdown strength of aromatic polymers-dependence on film thickness and chemical structure’. IEEE Trans. Electr. Insul. 1992, 27, 1061. [Google Scholar] [CrossRef]
- Helgee, B.; Bjellheim, P. Electric breakdown strength of aromatic polymers: Dependence on film thickness and chemical structure. IEEE Trans. Electr. Insul. 1991, 26, 1147–1152. [Google Scholar] [CrossRef]
- Yilmaz, G.; Kalenderli, O. Dielectric Properties of Aged Polyester Films. In Proceedings of the IEEE Annual Report—Conference on Electrical Insulation and Dielectric Phenomena, Minneapolis, MN, USA, 19–22 October 1997; pp. 444–446. [Google Scholar]
- Diaham, S.; Zelmat, S.; Locatelli, M.L.; Dinculescu, S.; Decup, M.; Lebey, T. Dielectric Breakdown of Polyimide Films: Area, Thickness and Temperature Dependence. IEEE Trans. Dielectr. Electr. Insul. 2010, 17, 18–27. [Google Scholar] [CrossRef]
- Zhao, L.; Liu, G.Z.; Su, J.C.; Pan, Y.F.; Zhang, X.B. Investigation of Thickness Effect on Electric Breakdown Strength of Polymers under Nanosecond Pulses. IEEE Trans. Plasma Sci. 2011, 39, 1613–1618. [Google Scholar] [CrossRef]
- Neusel, B.C.; Schneider, G.A. Size-dependence of the dielectric breakdown strength from nano- to millimeter scale. J. Mech. Phys. Solids 2013, 63, 201–213. [Google Scholar] [CrossRef]
- Weibull, W. A statistical distribution function of wide applicability. J. Appl. Mech. 1951, 18, 293–297. [Google Scholar]
- Kiyan, T.; Ihara, T.; Kameda, S.; Furusato, T.; Hara, M.; Akiyama, H. Weibull Statistical Analysis of Pulsed Breakdown Voltages in High-Pressure Carbon Dioxide Including Supercritical Phase. IEEE Trans. Plasma Sci. 2011, 39, 1792. [Google Scholar] [CrossRef]
- Dissado, L.A.; Fothergill, J.C.; Wolfe, S.V.; Hill, R.M. Weibull Statistics in Dielectric Breakdown: Theoretical Basis, Applications and Implications. IEEE Trans. Electr. Insul. 1984, EI-19, 227–233. [Google Scholar] [CrossRef]
- Tsuboi, T.; Takami, J.; Okabe, S.; Inami, K.; Aono, K. Weibull Parameter of Oil-immersed Transformer to Evaluate Insulation Reliability on Temporary Overvoltage. IEEE Trans. Dielectr. Electr. Insul. 2010, 17, 1863–1868. [Google Scholar] [CrossRef]
- Wilson, M.P.; Given, M.J.; Timoshkin, I.V.; MacGregor, S.J.; Wang, T.; Sinclair, M.A.; Thomas, K.J.; Lehr, J.M. Impulse-driven Surface Breakdown Data: A Weibull Statistical Analysis. IEEE Trans. Plasma Sci. 2012, 40, 2449–2457. [Google Scholar] [CrossRef]
- Hauschild, W.; Mosch, W. Statistical Techniques for High Voltage Engineering; IET: London, UK, 1992. [Google Scholar]
- Zhao, L.; Su, J.C.; Zhang, X.B.; Pan, Y.F.; LI, R.; Zeng, B.; Cheng, J.; Yu, B.X.; Wu, X.L. A Method to design composite insulation structures based on reliability for pulsed power systems. Laser Part. Beams 2014, 32, 1–8. [Google Scholar] [CrossRef]
- Zhao, L.; Su, J.C.; Pan, Y.F.; Li, R.; Zeng, B.; Cheng, J.; Yu, B.X. Correlation between volume effect and lifetime effect of solid dielectrics on nanosecond time scale. IEEE Trans. Dielectr. Electr. Insul. 2014, 22, 1769–1776. [Google Scholar] [CrossRef]
- Zhao, L. Theoretical Calculation on Formative Time Lag in Polymer Breakdown on a Nanosecond Time Scale. IEEE Trans. Dielectr. Electr. Insul. 2020, 27, 1051–1058. [Google Scholar] [CrossRef]
- Ludeke, R.; Cuberes M., T.; Cartier, E. Hot carrier transport effects in Al2O3-based metal-oxide-semiconductor structures. J. Vac. Sci. Technol. B Microelectron. Nanom. Struct. 2000, 18, 2153–2159. [Google Scholar] [CrossRef]
- Ludeke, R.; Cuberes, M.T.; Cartier, E. Local transport and trapping issues in Al2O3 gate oxide structures. Appl. Phys. Lett. 2000, 76, 2886–2888. [Google Scholar] [CrossRef]
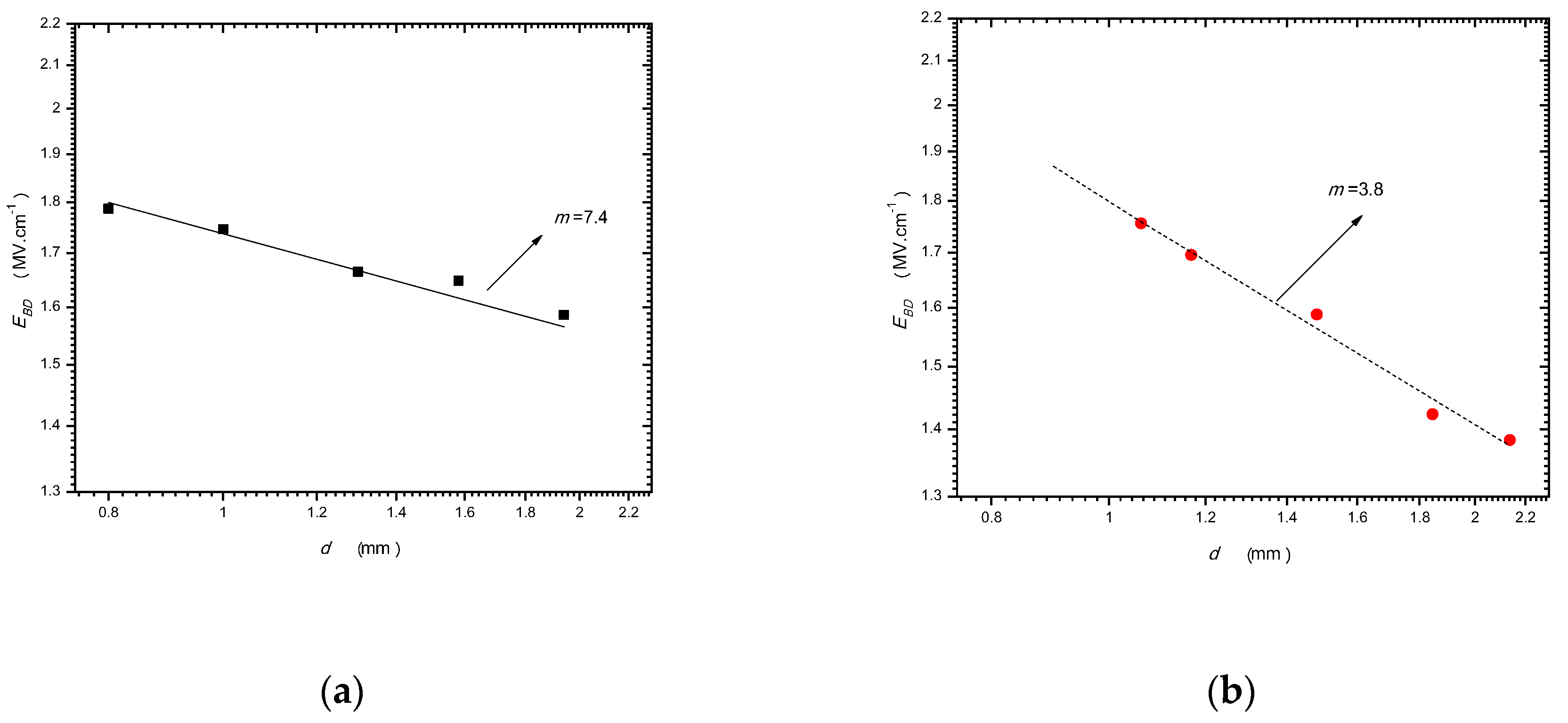
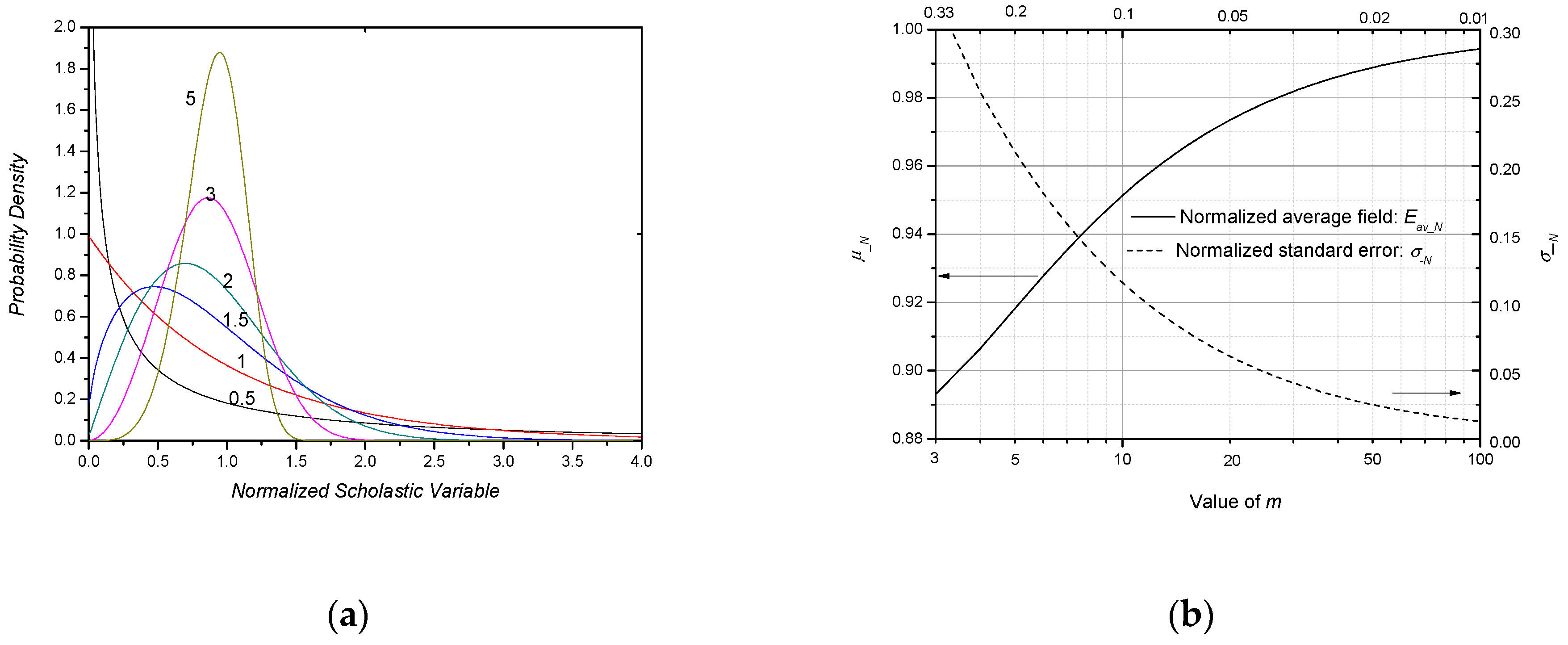
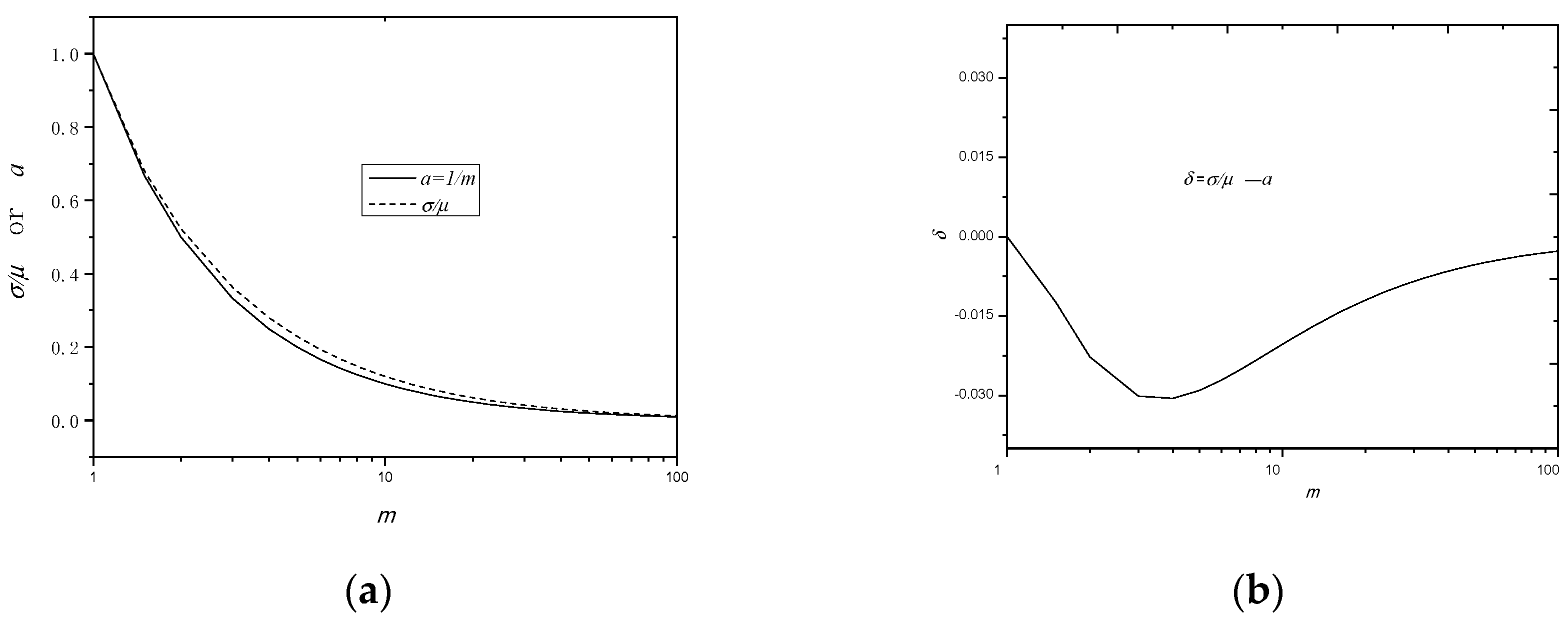

| Breakdown Type | General Mechanism | Basic Characteristics |
|---|---|---|
| Intrinsic breakdown | “Electron instability” | 1. EBD is independent of d. 2. The breakdown time is in the nanosecond time scale. 3. The breakdown happens in a low temperature range. |
| Avalanche breakdown | Electron impact and ionization | 1. EBD is dependent on d and the electrode configuration. 2. The breakdown time is in the nanosecond time scale. 3. The breakdown happens in a low temperature range. |
| Thermal breakdown | “Heat instability” | 1. The breakdown time is longer (in the microsecond time scale or longer). 2. EBD is related to sample and electrode waveform. 3. The breakdown happens in a high temperature range. |
| Electro-mechanical breakdown | Electro-mechanical force | 1. It is common for plastics and crystals. 2. It happens easily when defects exist in dielectrics. |
| Typical Relation | Mathematical Expression | Mechanism | Researcher/Year |
|---|---|---|---|
| Constant relation | Intrinsic breakdown | Oakes/1948 [6] Vermeer/1954 [37] | |
| Reciprocal-single-logarithm relation | Avalanche breakdown | Austen/1940 [30] O’Dwyer/1967 [33] | |
| Minus-single-logarithm relation | / | Cooper/1963 [39] | |
| Double-logarithm relation or minus power relation | Electron injection and avalanche | Forlani/1964 [40] Merrill/1963 [42] |
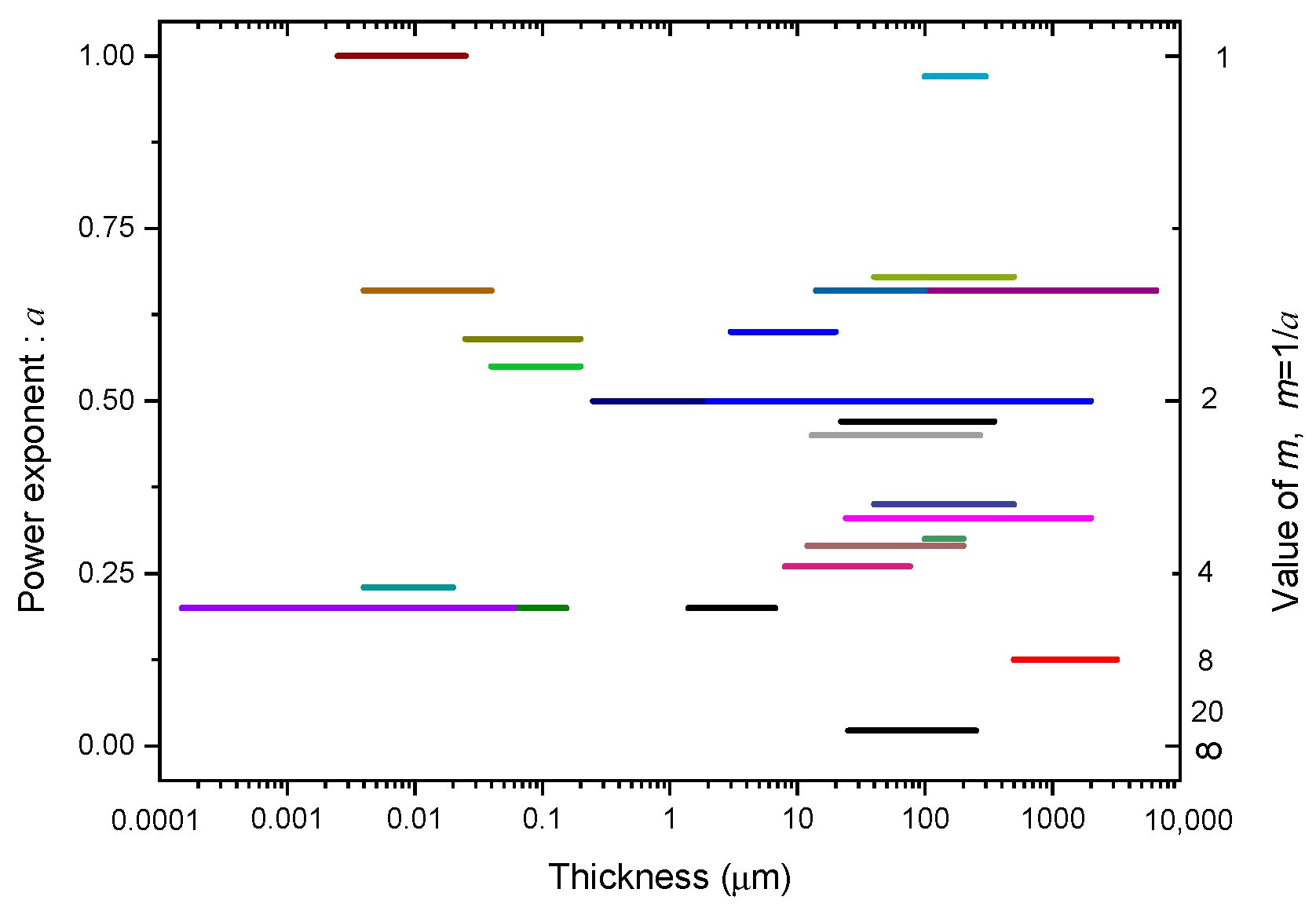
| Year/Researcher | Test Object and Condition | Thickness Range | Value of a | Comments/Feature |
|---|---|---|---|---|
| 1948/Oakes | PE, ac | 22 μm–350 μm | a = 0.47 [6] | |
| 1961/Cooper | NaCl | 236 μm–544 μm | a = 0.33 [55] | |
| 1963/Vorob’ev | NaCl | 3 μm–20 μm | a = 0.60 [55] | |
| 1965/Watson | NaCl | 24 μm–2000 μm | a = 0.33 [55] | In mm range. |
| 1950/Lomer | Al2O3 | 13 nm–0.154 μm | a = 0.20 [55] | |
| 1963/Merrill | Al2O3 | 0.25 μm–2.5 μm | a = 0.50 [42] | |
| 1968/Nicol | Al2O3 | 0.15 nm–60 nm | a = 0.20 [55] | In Å range. |
| 1955/Mason | PE, 1/25 μs pulse | 0.1 mm–6.5 mm | a = 0.66 [56,57] | In mm range. |
| 1971/Agarwal | Bariμm stearate, dc | 2.5 nm–25 nm | a = 1.0 [54] | a is the largest. |
| 1971/Agarwal | Bariμm stearate, dc | 25 nm–200 nm | a = 0.59 [54] | |
| 1979/Yoshino | Hexatriacontane, 6 μs | 14 μm–100 μm | α = 0.66 [51] | |
| 1982/Singh | MgO, ac | 4 nm–20 nm | a = 0.23 [48] | In nm range. |
| 1983/Singh | La2O3, ac | 4 nm–40 nm | a = 0.66 [48] | |
| 1983/Baguji | TiO2, ac | 40 nm–200 nm | a = 0.55 [49] | |
| 1991/Mason | PP, ac, φ63.5 mm | 8 μm–76 μm | a = 0.24 [44] | Reflecting the factor of electrode on EBD. |
| 1991/Mason | PP, ac, φ12.5 mm | 8 μm–76 μm | a = 0.33 [44] | |
| 1991/Mason | PP, ac, φ10 mm v.s. φ10 mm | 100 μm–500 μm | a = 0.5 [44] | |
| 1991/Mason | PVC, dc, εr of liquid is 9. | 40 μm–500 μm | a = 0.33, 0.38 [44] | Reflecting factor of ambient liquid. |
| 1991/Mason | PVC, dc, εr of liquid is 5. | 40 μm–500 μm | a = 0.66, 0.70 [44] | |
| 1992/Helgee | PI, ac | 13 μm–27 0μm | a = 0.39 [58] | |
| 1992/Helgee | PEI, ac | 13 μm–270 μm | a = 0.44 [58] | |
| 1992/Helgee | PET, ac | 13 μm–270 μm | a = 0.47 [58] | |
| 1992/Helgee | PEEK, ac | 13 μm–270 μm | a = 0.48 [58] | |
| 1992/Helgee | PES, ac | 13 μm–270 μm | a = 0.51 [58] | |
| 1996/Yilmaz | PES, ac | 12 μm–200 μm | a = 0.26–0.32 [59] | |
| 1997/Yilmaz | PES, ac (0 °C) | 100 μm–200 μm | a = 0.28 [47] | Focusing on the factor of temperature. |
| 1997/Yilmaz | PES, ac (80 °C) | 100 μm–200 μm | a = 0.30 [47] | |
| 1997/Yilmaz | PES, ac (120°C) | 100 μm–200 μm | a = 0.32 [47] | |
| 2003/Yang | TiO2, dc | 100 μm–300 μm | a = 0.97 [50] | a is the largest. |
| 2004/Theodosiou | PET, dc | 25 μm–350 μm | a = 0.50 [52] | |
| 2010/Diaham | PI, dc | 1.4 μm–6.7 μm | a = 0.16–0.25 [60] | |
| 2011/Zhao | PMMA, PE, Nylon, PTFE *, ns pulse | 0.5 mm–3.2 mm | a = 0.125 [61] | In nanosecond pulse |
| 2012/Chen | PE, dc | 25 μm–250 μm | a = 0.022 [53] | a is the smallest. |
| 2013/Neusel | Al2O3, TiO2, BaTiO, SrTiO3 | 2 μm–2 mm | a = 0.5 [62] | Plenty of dielectrics were tested. |
| 2013/Neusel | PMMA, PS **, PVC ***, PE | 2 μm–2 mm | a = 0.5 [62] |
| Perspective | A Larger m (or a Smaller a) Means: |
|---|---|
| Breakdown mechanism | A larger P and a larger EBD. |
| Dielectric purity | A better dielectric purity. |
| Statistics | A higher EBD and a smaller σ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, L.; Liu, C.L. Review and Mechanism of the Thickness Effect of Solid Dielectrics. Nanomaterials 2020, 10, 2473. https://doi.org/10.3390/nano10122473
Zhao L, Liu CL. Review and Mechanism of the Thickness Effect of Solid Dielectrics. Nanomaterials. 2020; 10(12):2473. https://doi.org/10.3390/nano10122473
Chicago/Turabian StyleZhao, Liang, and Chun Liang Liu. 2020. "Review and Mechanism of the Thickness Effect of Solid Dielectrics" Nanomaterials 10, no. 12: 2473. https://doi.org/10.3390/nano10122473
APA StyleZhao, L., & Liu, C. L. (2020). Review and Mechanism of the Thickness Effect of Solid Dielectrics. Nanomaterials, 10(12), 2473. https://doi.org/10.3390/nano10122473




