Intrinsic Control in Defects Density for Improved ZnO Nanorod-Based UV Sensor Performance
Abstract
1. Introduction
2. Materials and Methods
2.1. Substrate Preparation and Cleaning
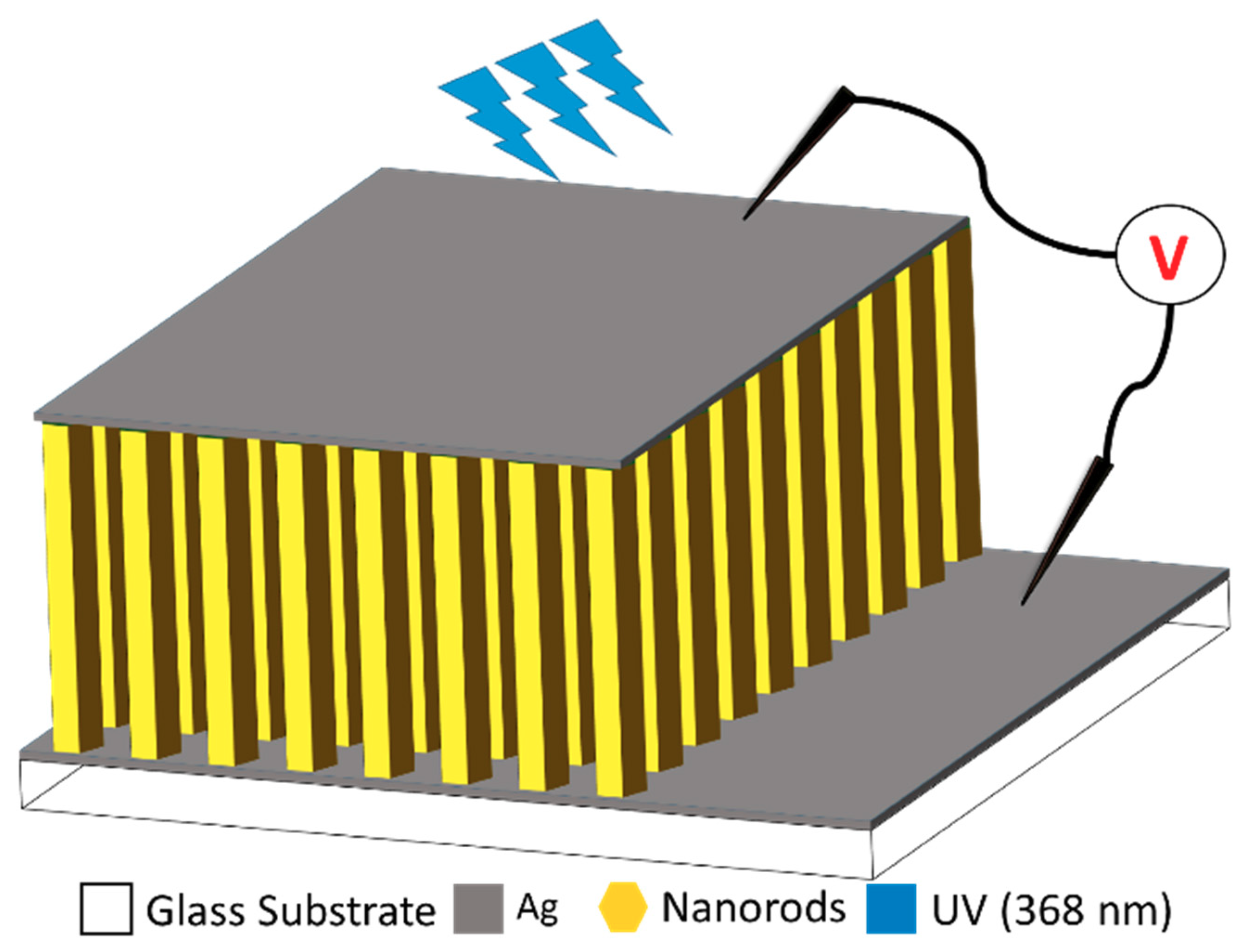
2.2. Device Fabrication
2.3. Characterization Tools
3. Results and Discussion
3.1. ZnO Nanorods Morphology and Physical Characteristics
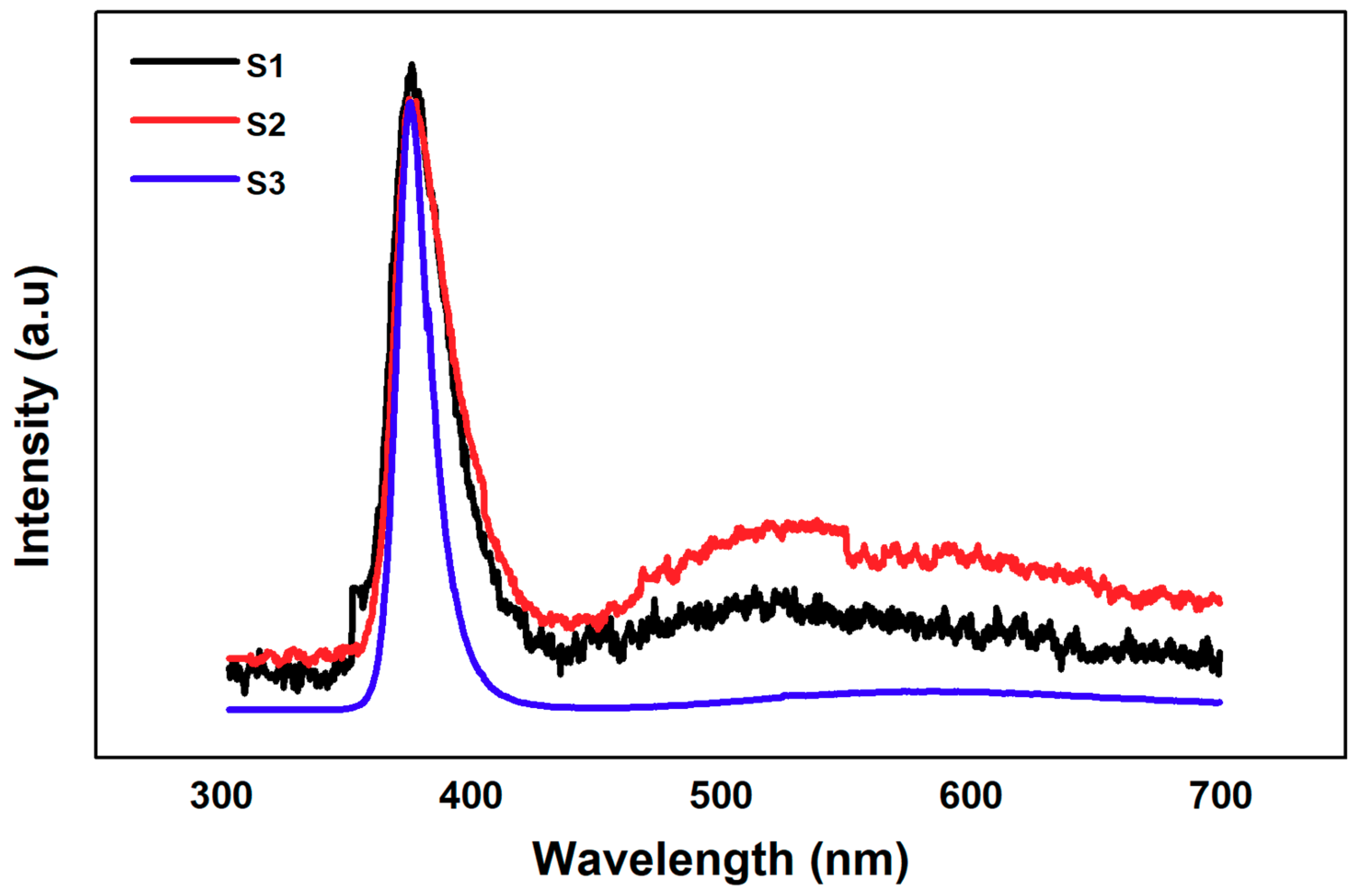
3.2. XRD Structural and PL Optical Characteristics
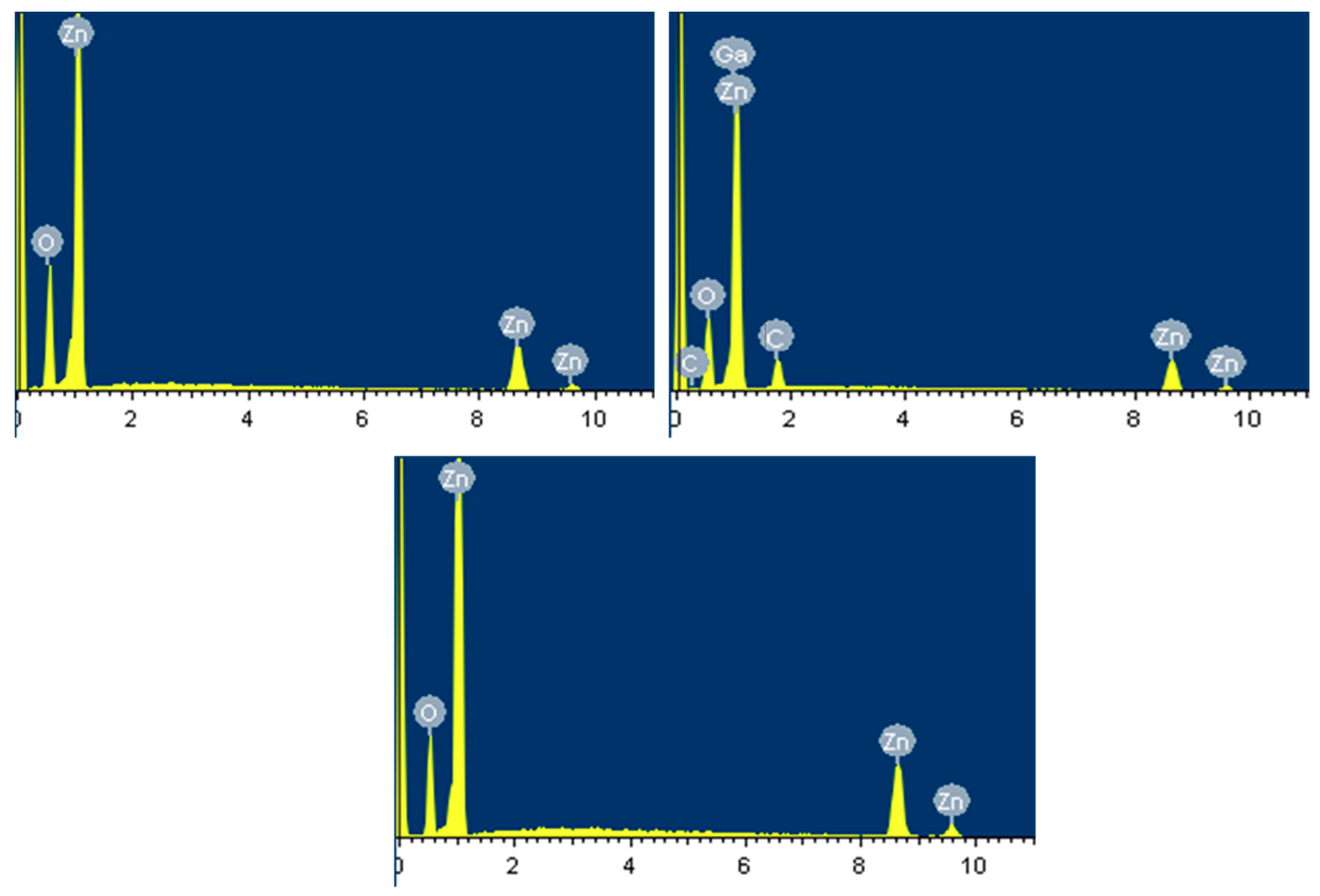
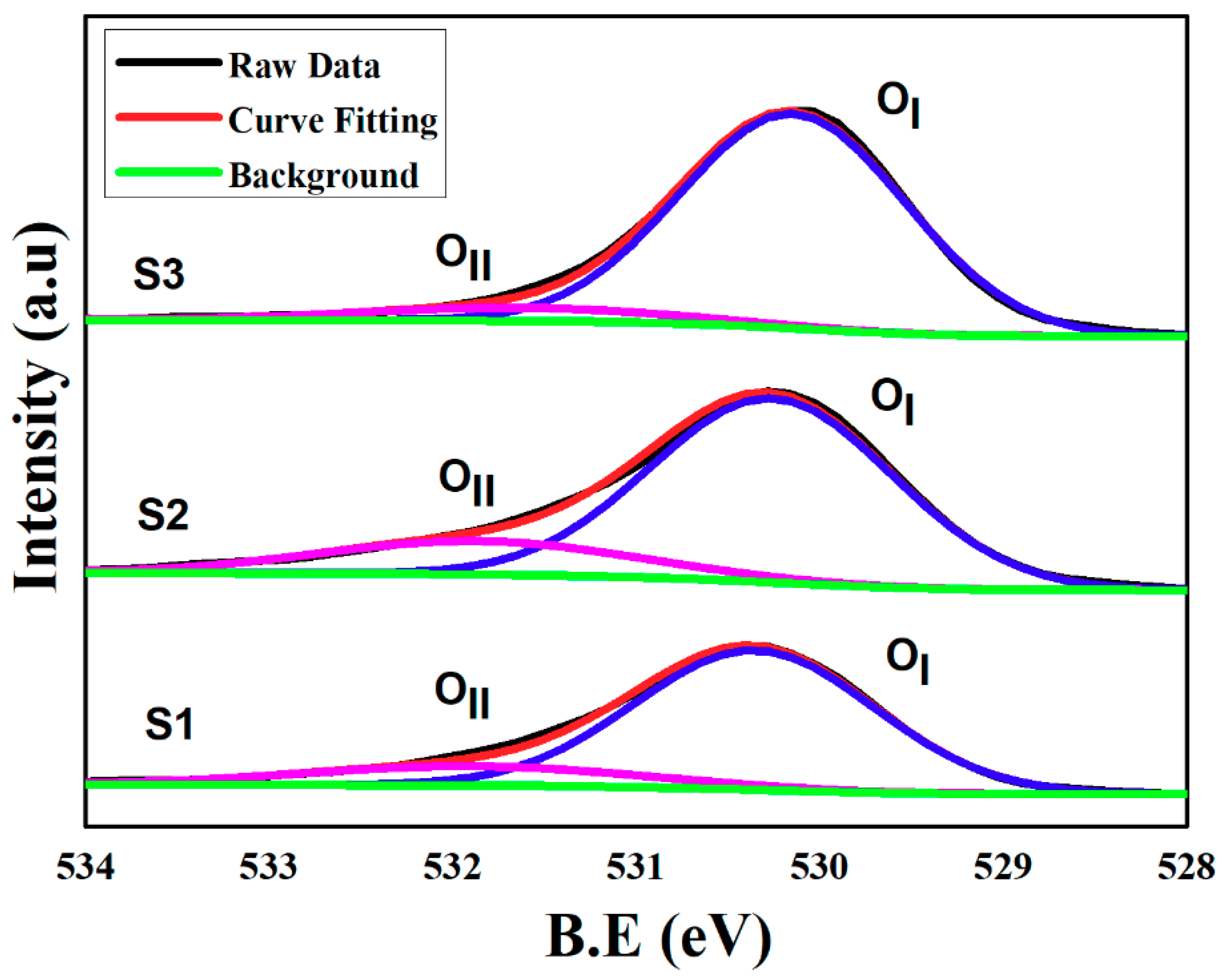
3.3. EDXMA and XPS Analyses
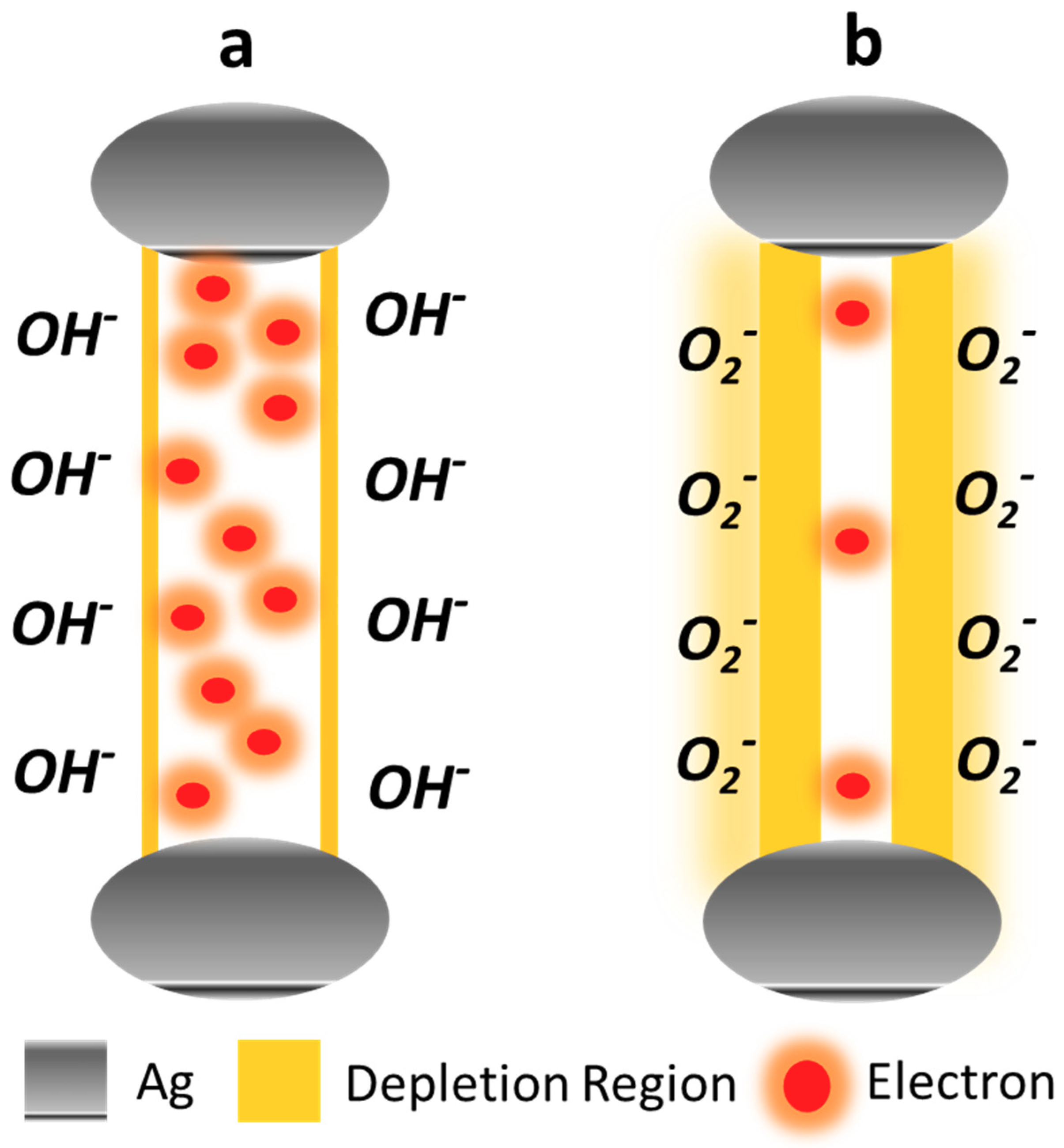
3.4. Proposed UV Sensor Mechanism
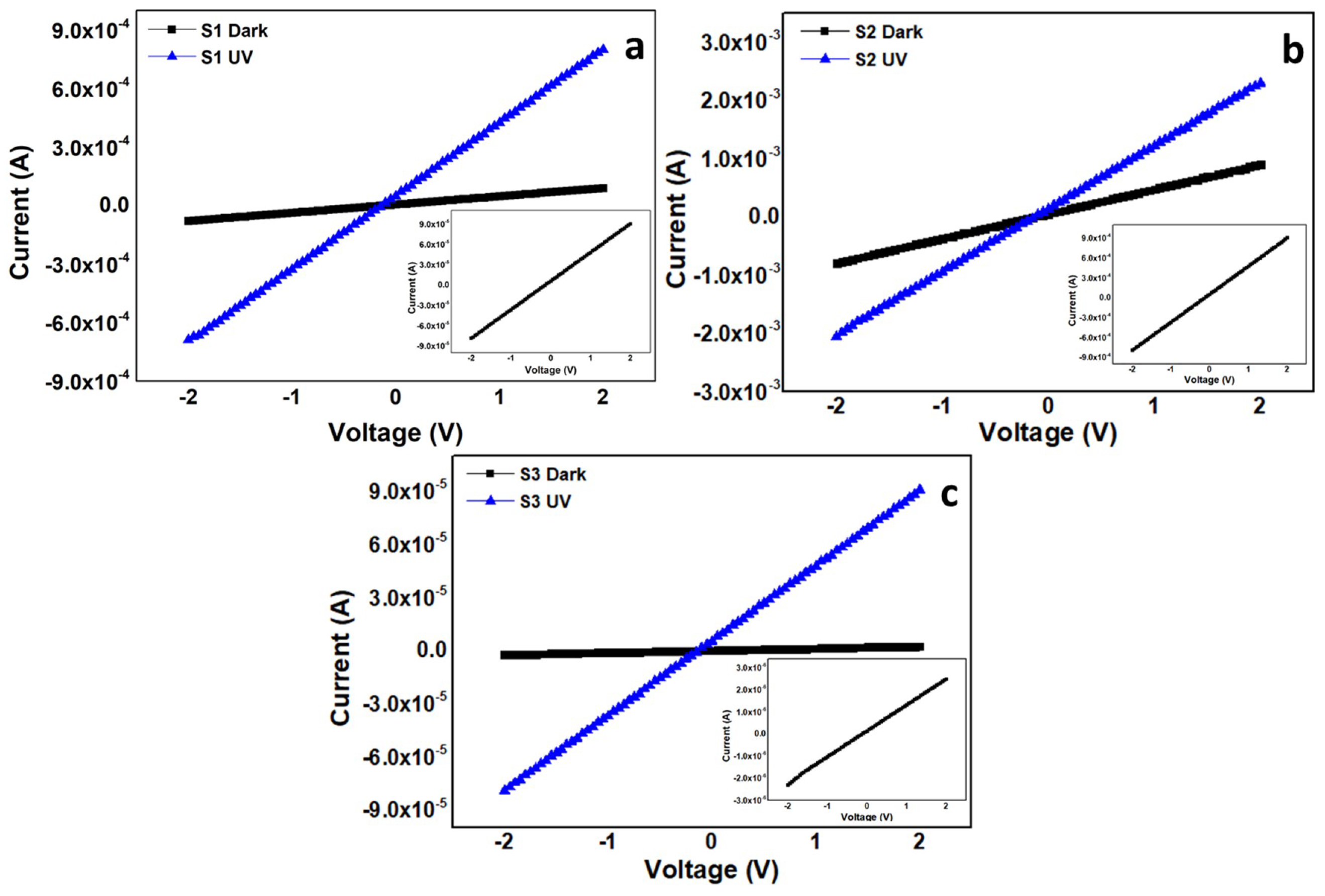
3.5. Current–Voltage (I–V) Characteristics
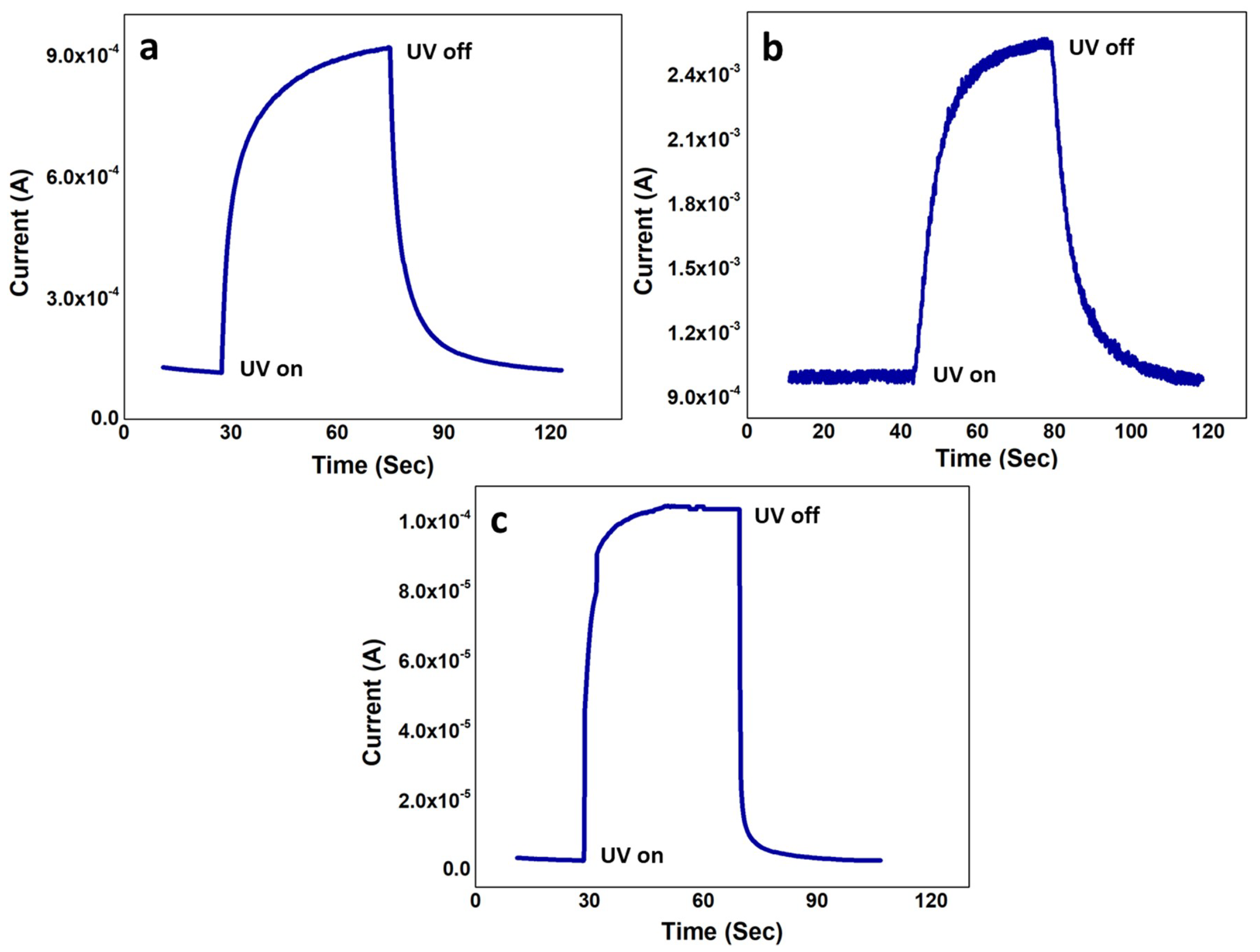
3.6. Impulse Response as a Function of Time
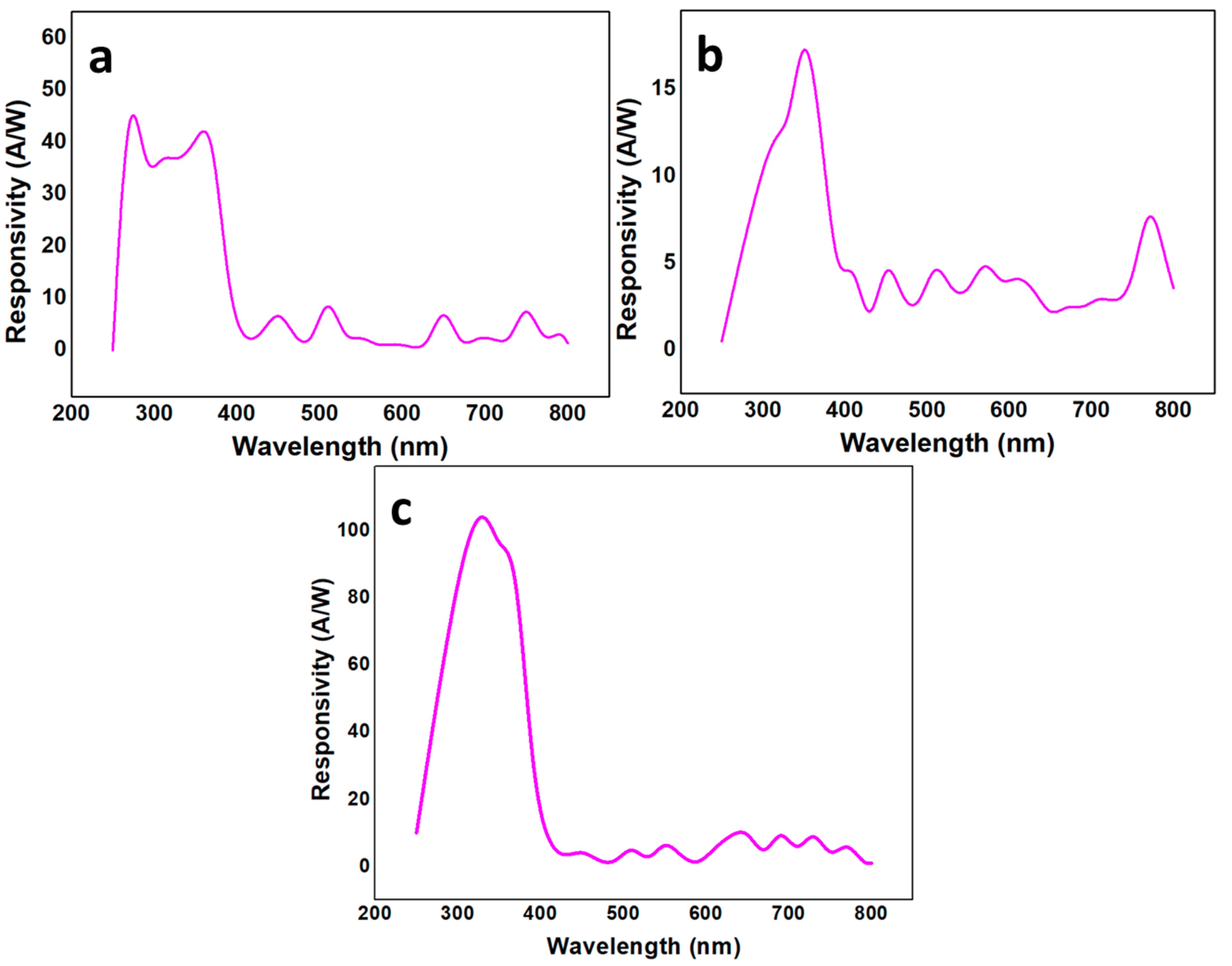
3.7. Quantum Efficiency, Responsivity, and Photoconductive Gain
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Amin, M.; Shah, N.A.; Bhatti, A.S. Development of highly sensitive UV sensor using morphology tuned ZnO nanostructures. Appl. Phys. A 2015, 118, 595–603. [Google Scholar] [CrossRef]
- Cole, J.J.; Wang, X.; Knuesel, R.J.; Jacobs, H.O. Integration of ZnO microcrystals with tailored dimensions forming light emitting diodes and UV photovoltaic cells. Nano Lett. 2008, 8, 1477–1481. [Google Scholar] [CrossRef]
- Caruge, J.M.; Halpert, J.E.; Wood, V.; Bulovic, V.; Bawendi, M.G. Colloidal quantum-dot light-emitting diodes with metal-oxide charge transport layers. Nat. Photonics 2008, 2, 247–250. [Google Scholar] [CrossRef]
- Anikeeva, P.O.; Halpert, J.E.; Bawendi, M.G.; Bulovic, V. Electroluminescence from a mixed red–green–blue colloidal quantum dot monolayer. Nano Lett. 2007, 7, 2196–2200. [Google Scholar] [CrossRef] [PubMed]
- Rana, A.S.; Chang, S.B.; Kim, H.S. NH4OH-Oriented and pH-Dependent Growth of ZnO Nanostructures via Microwave-Assisted Growth Method. J. Nanosci. Nanotechnol. 2018, 18, 2125–2127. [Google Scholar] [CrossRef] [PubMed]
- Somvanshi, D.; Jit, S. Analysis of temperature-dependent electrical characteristics of n-ZnO nanowires (NWs)/p-Si heterojunction diodes. IEEE Trans. Nanotechnol. 2014, 13, 62–69. [Google Scholar] [CrossRef]
- Rana, A.S.; Kang, M.; Jeong, E.S.; Kim, H.S. Transition between ZnO Nanorods and ZnO Nanotubes with Their Antithetical Properties. J. Nanosci. Nanotechnol. 2016, 16, 10772–10776. [Google Scholar] [CrossRef]
- Vinod, R.; Sajan, P.; Achary, S.R.; Tomas, C.M.; Munoz-Sanjose, V.; Bushiri, M.J. Enhanced UV emission from ZnO nanoflowers synthesized by the hydrothermal process. J. Phys. D: Appl. Phys. 2012, 45, 425103. [Google Scholar] [CrossRef]
- Rana, A.S.; Shahid, A.; Lee, J.Y.; Kim, H.S. High-Power Microwave-Assisted Ga Doping, an Effective Method to Tailor n-ZnO/p-Si Heterostructure Optoelectronic Characteristics. Phys. Status Solidi A 2018, 215, 1700763. [Google Scholar] [CrossRef]
- Rana, A.S.; Kim, H.S. Growth Condition-Oriented Defect Engineering for Changes in Au-ZnO Contact Behavior from Schottky to Ohmic and Vice Versa. Nanomaterials 2018, 8, 12. [Google Scholar] [CrossRef]
- Yang, P.; Yan, H.; Mao, S.; Russo, R.; Johnson, J.; Saykally, R.; Morris, N.; Pham, J.; He, R.; Choi, H.J. Controlled growth of ZnO nanowires and their optical properties. Adv. Funct. Mater. 2002, 12, 323–331. [Google Scholar] [CrossRef]
- Park, W.I.; Yi, G.C.; Kim, M.; Pennycook, S.J. ZnO Nanoneedles Grown Vertically on Si Substrates by Non-Catalytic Vapor-Phase Epitaxy. Adv. Mater. 2002, 14, 1841–1843. [Google Scholar] [CrossRef]
- Sun, Y.; Fuge, G.M.; Ashfold, M.N. Growth of aligned ZnO nanorod arrays by catalyst-free pulsed laser deposition methods. Chem. Phys. Lett. 2004, 396, 21–26. [Google Scholar] [CrossRef]
- Yao, B.D.; Chan, Y.F.; Wang, N. Formation of ZnO nanostructures by a simple way of thermal evaporation. Appl. Phys. Lett. 2002, 81, 757–759. [Google Scholar] [CrossRef]
- Rana, A.S.; Ko, K.; Hong, S.; Kang, M.; Kim, H.S. Fabrication and characterization of ZnO nanorods on multiple substrates. J. Nanosci. Nanotechnol. 2015, 15, 8375–8380. [Google Scholar] [CrossRef]
- Rana, A.S.; Kang, M.; Kim, H.S. Microwave-assisted facile and ultrafast growth of ZnO nanostructures and proposition of alternative microwave-assisted methods to address growth stoppage. Sci. Rep. 2016, 6, 24870. [Google Scholar] [CrossRef]
- Weber, M.; Kim, J.H.; Lee, J.H.; Kim, J.Y.; Iatsunskyi, I.; Coy, E.; Drobek, M.; Julbe, A.; Bechelany, M.; Kim, S.S. High-performance nanowire hydrogen sensors by exploiting the synergistic effect of Pd nanoparticles and metal–organic framework membranes. ACS Appl. Mater. Interfaces 2018, 10, 34765–34773. [Google Scholar] [CrossRef]
- Weber, M.; Kim, J.Y.; Lee, J.H.; Kim, J.H.; Iatsunskyi, I.; Coy, E.; Miele, P.; Bechelany, M.; Kim, S.S. Highly efficient hydrogen sensors based on Pd nanoparticles supported on boron nitride coated ZnO nanowires. J. Mater. Chem. A 2019, 7, 8107–8116. [Google Scholar] [CrossRef]
- Rana, A.S.; Lee, J.Y.; Hong, Y.P.; Kim, H.S. Transient Current Response for ZnO Nanorod-Based Doubly Transparent UV Sensor Fabricated on Flexible Substrate. Phys. Status Solidi RRL 2018, 12, 1800001. [Google Scholar] [CrossRef]
- Boscarino, S.; Filice, S.; Sciuto, A.; Libertino, S.; Scuderi, M.; Galati, C.; Scalese, S. Investigation of ZnO-decorated CNTs for UV light detection applications. Nanomaterials 2019, 9, 1099. [Google Scholar] [CrossRef]
- Luo, L.; Zhang, Y.; Mao, S.S.; Lin, L. Fabrication and characterization of ZnO nanowires based UV photodiodes. Sens. Actuators A-Phys. 2006, 127, 201–206. [Google Scholar] [CrossRef]
- Zhou, J.; Gu, Y.; Hu, Y.; Mai, W.; Yeh, P.H.; Bao, G.; Sood, A.K.; Polla, D.L.; Wang, Z.L. Gigantic enhancement in response and reset time of ZnO UV nanosensor by utilizing Schottky contact and surface functionalization. Appl. Phys. Lett. 2009, 94, 191103. [Google Scholar] [CrossRef] [PubMed]
- Bai, S.; Wu, W.; Qin, Y.; Cui, N.; Bayerl, D.J.; Wang, X. High-performance integrated ZnO nanowire UV sensors on rigid and flexible substrates. Adv. Funct. Mater. 2011, 21, 4464–4469. [Google Scholar] [CrossRef]
- Alenezi, M.R.; Henley, S.J.; Silva, S.R.P. On-chip fabrication of high performance nanostructured ZnO UV detectors. Sci. Rep. 2015, 5, 8516. [Google Scholar] [CrossRef]
- Rana, A.S.; Chang, S.B.; Chae, H.U.; Kim, H.S. Structural, optical, electrical and morphological properties of different concentration sol-gel ZnO seeds and consanguineous ZnO nanostructured growth dependence on seeds. J. Alloys Compd. 2017, 729, 571–582. [Google Scholar] [CrossRef]
- Sahdan, M.Z.; Mamat, M.H.; Salina, M.; Khusaimi, Z.; Noor, U.M.; Rusop, M. Heat treatment effects on the surface morphology and optical properties of ZnO nanostructures. Phys. Status Solidi C 2010, 7, 2286–2289. [Google Scholar] [CrossRef]
- Keskenler, E.F.; Tomakin, M.; Dogan, S.; Turgut, G.; Aydın, S.; Duman, S.; Gurbulak, B. Growth and characterization of Ag/n-ZnO/p-Si/Al heterojunction diode by solegel spin technique. J. Alloys Compd. 2013, 550, 129–132. [Google Scholar] [CrossRef]
- Shklovskii, B.I.; Efros, A.L. Electronic Properties of Doped Semiconductors; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 45. [Google Scholar]
- Moormann, H.; Kohl, D.; Heiland, G. Variations of work function and surface conductivity on clean cleaved zinc oxide surfaces by annealing and by hydrogen adsorption. Surf. Sci. 1980, 100, 302–314. [Google Scholar] [CrossRef]
- Heiland, G.; Kunstmann, P. Polar surfaces of zinc oxide crystals. Surf. Sci. 1969, 13, 72–84. [Google Scholar] [CrossRef]
- Nakagawa, M.; Mitsudo, H. Anomalous temperature dependence of the electrical conductivity of zinc oxide thin films. Surf. Sci. 1986, 175, 157–176. [Google Scholar] [CrossRef]
- Lany, S.; Zunger, A. Anion vacancies as a source of persistent photoconductivity in II-VI and chalcopyrite semiconductors. Phys. Rev. B 2005, 72, 035215. [Google Scholar] [CrossRef]
- Look, D.C.; Hemsky, J.W.; Sizelove, J.R. Residual native shallow donor in ZnO. Phys. Rev. Lett. 1999, 82, 2552. [Google Scholar] [CrossRef]
- Janotti, A.; Van deWalle, C.G. Hydrogen multicentre bonds. Nat. Mater. 2007, 6, 44–47. [Google Scholar] [CrossRef]
- Shinde, S.S.; Rajpure, K.Y. High-performance UV detector based on Ga-doped zinc oxide thin films. Appl. Surf. Sci. 2011, 257, 9595–9599. [Google Scholar] [CrossRef]
- Shinde, S.S.; Rajpure, K.Y. Fast response ultraviolet Ga-doped ZnO based photoconductive detector. Mater. Res. Bull. 2011, 46, 1734–1737. [Google Scholar] [CrossRef]
- Sun, J.; Liu, F.J.; Huang, H.Q.; Zhao, J.W.; Hu, Z.F.; Zhang, X.Q.; Wang, Y.S. Fast response ultraviolet photoconductive detectors based on Ga-doped ZnO films grown by radio-frequency magnetron sputtering. Appl. Surf. Sci. 2010, 257, 921–924. [Google Scholar] [CrossRef]
- Seeger, K. Semiconductor Physics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Chapter 6. [Google Scholar]
- McLean, T.P.; Paige, E.G.S. A theory of the effects of carrier-carrier scattering on mobility in semiconductors. J. Phys. Chem. Solids 1960, 16, 220–236. [Google Scholar] [CrossRef]
- Rodwihok, C.; Choopun, S.; Ruankham, P.; Gardchareon, A.; Phadungdhitidhada, S.; Wongratanaphisan, D. UV sensing properties of ZnO nanowires/nanorods. Appl. Surf. Sci. 2019, 477, 159–165. [Google Scholar] [CrossRef]
- Eom, T.H.; Han, J.I. Single fiber UV detector based on hydrothermally synthesized ZnO nanorods for wearable computing devices. Appl. Surf. Sci. 2018, 428, 233–241. [Google Scholar] [CrossRef]
- Makhlouf, H.; Karam, C.; Lamouchi, A.; Tingry, S.; Miele, P.; Habchi, R.; Chtourou, R.; Bechelany, M. Analysis of ultraviolet photo-response of ZnO nanostructures prepared by electrodeposition and atomic layer deposition. Appl. Surf. Sci. 2018, 444, 253–259. [Google Scholar] [CrossRef]

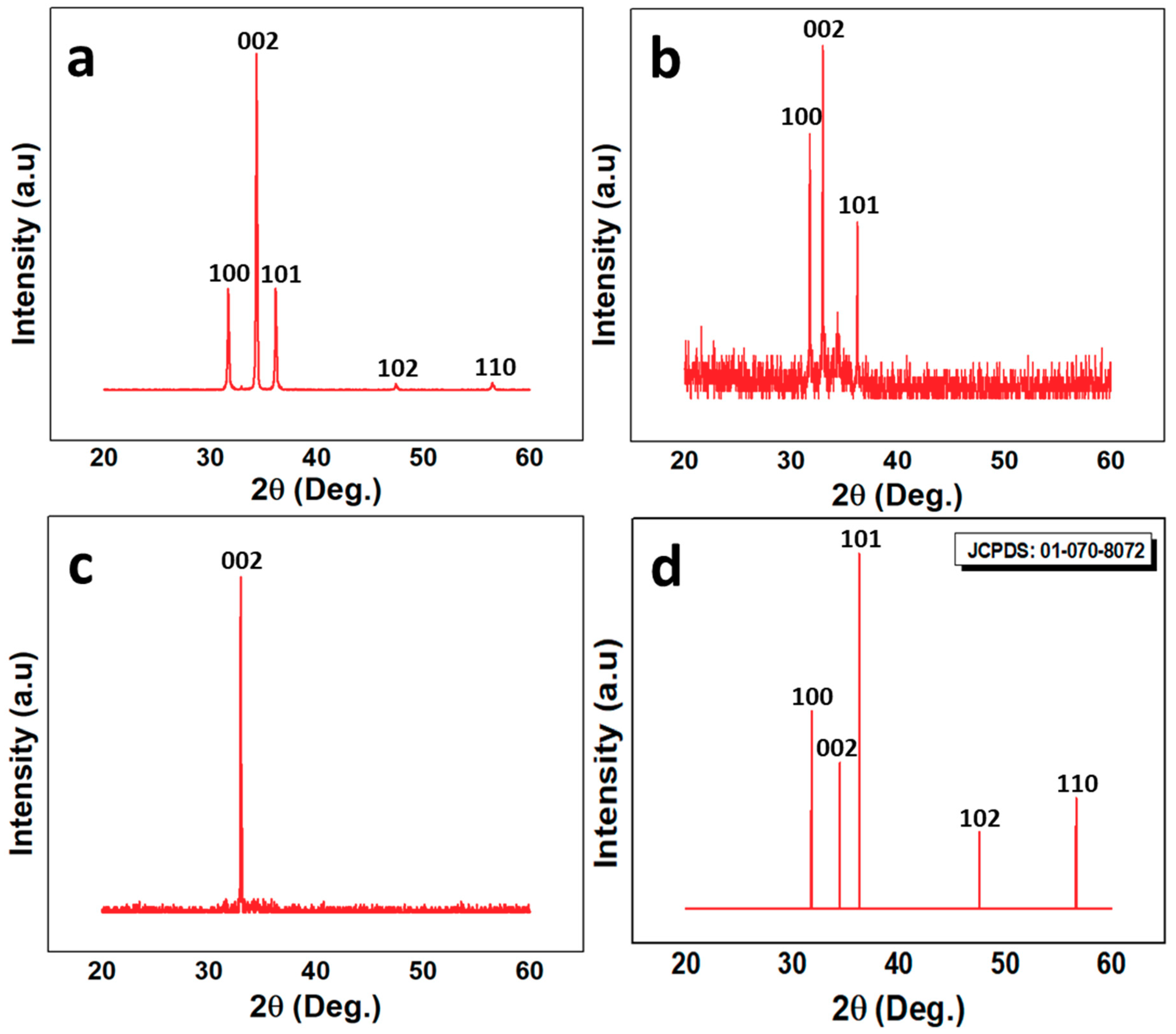
| Sample | 2θ (Degree) | FWHM (Radian) | D (nm) | C (Å) | ε |
|---|---|---|---|---|---|
| S1 | 34.63 (±0.04) | 0.0046 (±0.0002) | 30.93 | 5.284 | 1.62 |
| S2 | 34.80 (±0.08) | 0.0054 (±0.0004) | 24.07 | 5.299 | 2.9 |
| S3 | 34.48 (±0.01) | 0.0021 (±0.0002) | 67.16 | 5.204 | 0.25 |
| Element | Weight % | Atomic % |
|---|---|---|
| S1 | ||
| O | 27.10 (±0.92) | 31.68 |
| C | 4.01 (±2.06) | 11.84 |
| Zn | 66.71 (±0.29) | 53.84 |
| Ga | 2.18 (±1.42) | 2.64 |
| Total | 100.00 | 100.00 |
| S2 | ||
| O | 19.93 (±0.81) | 38.87 |
| Zn | 80.07 (±0.36) | 61.13 |
| Total | 100.00 | 100.00 |
| S3 | ||
| O | 24.47 (±0.20) | 48.56 |
| Zn | 75.53 (±0.16) | 51.44 |
| Total | 100.00 | 100.00 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rana, A.u.H.S.; Shaikh, S.F.; Al-Enizi, A.M.; Agyeman, D.A.; Ghani, F.; Nah, I.W.; Shahid, A. Intrinsic Control in Defects Density for Improved ZnO Nanorod-Based UV Sensor Performance. Nanomaterials 2020, 10, 142. https://doi.org/10.3390/nano10010142
Rana AuHS, Shaikh SF, Al-Enizi AM, Agyeman DA, Ghani F, Nah IW, Shahid A. Intrinsic Control in Defects Density for Improved ZnO Nanorod-Based UV Sensor Performance. Nanomaterials. 2020; 10(1):142. https://doi.org/10.3390/nano10010142
Chicago/Turabian StyleRana, Abu ul Hassan Sarwar, Shoyebmohamad F. Shaikh, Abdullah M. Al-Enizi, Daniel Adjei Agyeman, Faizan Ghani, In Wook Nah, and Areej Shahid. 2020. "Intrinsic Control in Defects Density for Improved ZnO Nanorod-Based UV Sensor Performance" Nanomaterials 10, no. 1: 142. https://doi.org/10.3390/nano10010142
APA StyleRana, A. u. H. S., Shaikh, S. F., Al-Enizi, A. M., Agyeman, D. A., Ghani, F., Nah, I. W., & Shahid, A. (2020). Intrinsic Control in Defects Density for Improved ZnO Nanorod-Based UV Sensor Performance. Nanomaterials, 10(1), 142. https://doi.org/10.3390/nano10010142








