Evaluating the Surface Topography of Pyrolytic Carbon Finger Prostheses through Measurement of Various Roughness Parameters
Abstract
:1. Introduction
2. Results and Discussion
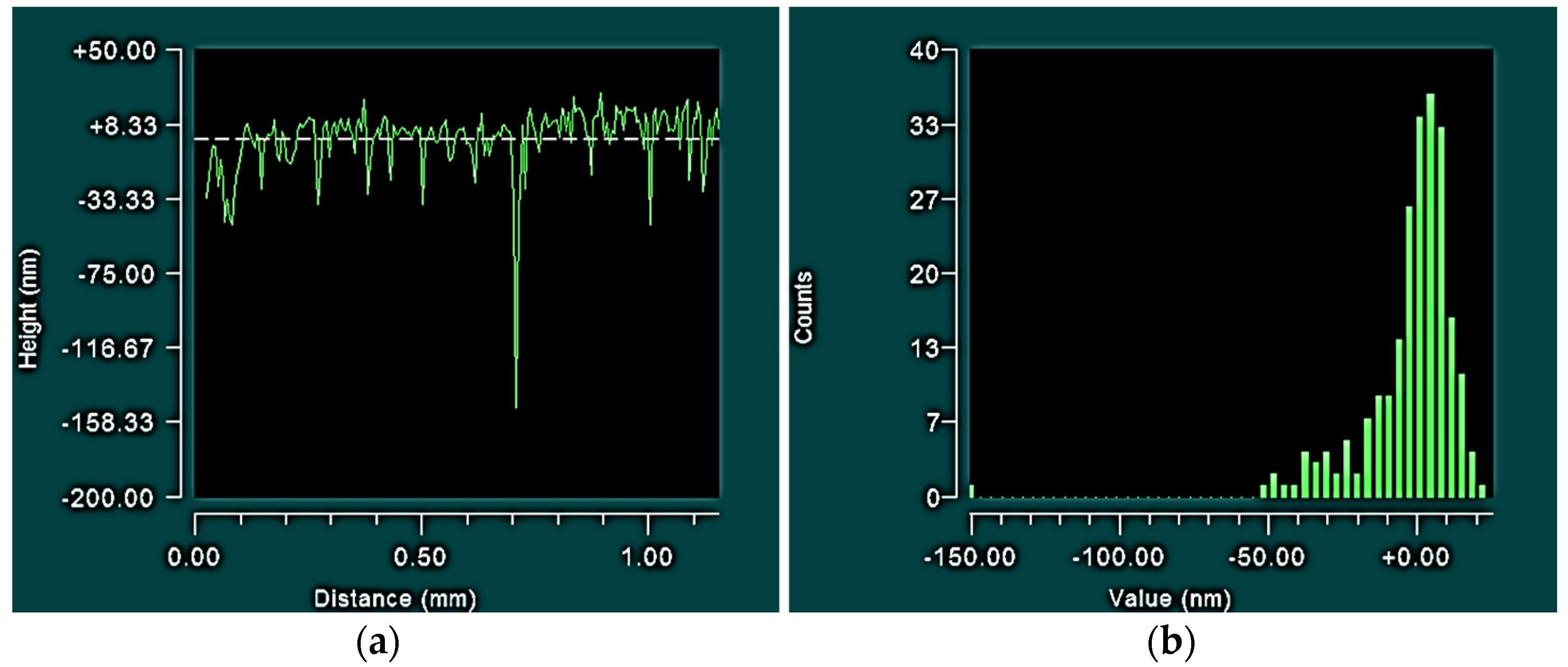
2.1. Topographical Results
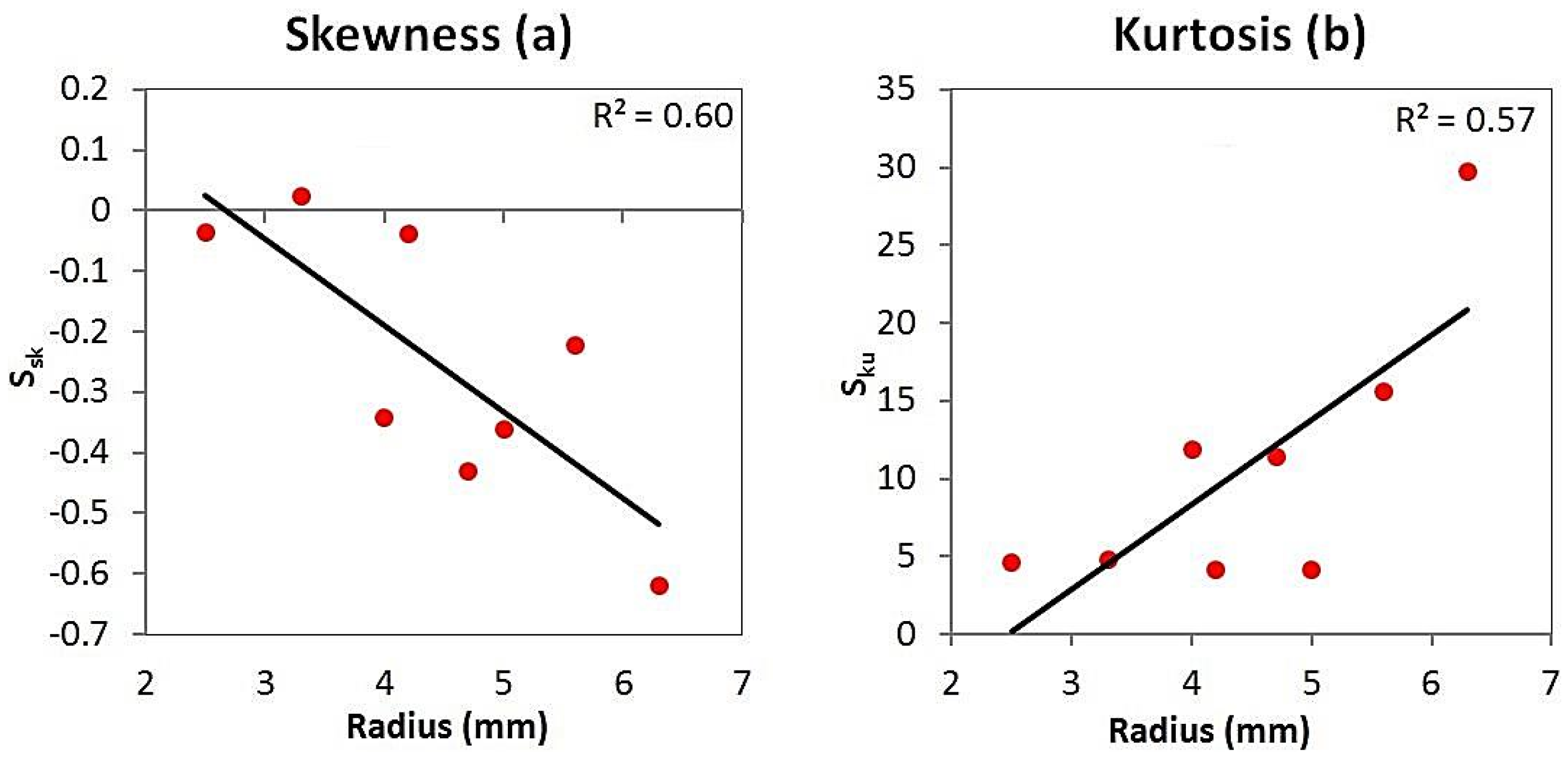
2.2. Linear Regression and ANOVA
2.3. Prior Assessment of Joint Prostheses of the Hand
2.4. What Are the Most Appropriate Topographical Parameters?
3. Experimental Section
3.1. Roughness Parameters
3.2. Samples
3.3. Statistical Methods
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Adams, J.; Ryall, C.; Pandyan, A.; Metcalf, C.; Stokes, M.; Bradley, S.; Warwick, D.J. Proximal interphalangeal joint replacement in patients with arthritis of the hand: A meta-analysis. J. Bone Joint Surg. Br. 2012, 94, 1305–1312. [Google Scholar] [CrossRef] [PubMed]
- Wijk, U.; Wollmark, M.; Kopylov, P.; Tagil, M. Outcomes of proximal interphalangeal joint pyrocarbon implants. J Hand Surg. Am. 2010, 35, 38–43. [Google Scholar] [CrossRef] [PubMed]
- Chung, K.C.; Ram, A.N.; Shauver, M.J. Outcomes of pyrolytic carbon arthroplasty for the proximal interphalangeal joint. Plast. Reconstr. Surg. 2009, 123, 1521–1532. [Google Scholar] [CrossRef] [PubMed]
- Herren, D.B.; Schindele, S.; Goldhahn, J.; Simmen, B.R. Problematic bone fixation with pyrocarbon implants in proximal interphalangeal joint replacement: Short-term results. J. Hand Surg. Br. 2006, 31, 643–651. [Google Scholar] [CrossRef] [PubMed]
- Nunley, R.M.; Boyer, M.I.; Goldfarb, C.A. Pyrolytic carbon arthroplasty for posttraumatic arthritis of the proximal interphalangeal joint. J. Hand Surg. Am. 2006, 31, 1468–1474. [Google Scholar] [CrossRef] [PubMed]
- Bone, M.C.; Giddins, G.; Joyce, T.J. An analysis of explanted pyrolytic carbon prostheses. J. Hand Surg. Eur. Vol. 2014, 39, 666–667. [Google Scholar] [CrossRef] [PubMed]
- Naylor, A.; Bone, M.C.; Unsworth, A.; Talwalkar, S.C.; Trail, I.A.; Joyce, T.J. In vitro wear testing of the pyrocarbon proximal interphalangeal joint replacement: Five million cycles of flexion and extension. Proc. Inst. Mech. Eng. H 2015, 229, 362–368. [Google Scholar] [CrossRef] [PubMed]
- Smith, S.L.; Li, B.L.; Buniya, A.; Lin, S.H.; Scholes, S.C.; Johnson, G.; Joyce, T.J. In vitro wear testing of a contemporary design of reverse shoulder prosthesis. J. Biomech. 2015, 48, 3072–3079. [Google Scholar] [CrossRef] [PubMed]
- Scholes, S.C.; Kennard, E.; Gangadharan, R.; Weir, D.; Holland, J.; Deehan, D.; Joyce, T.J. Topographical analysis of the femoral components of ex vivo total knee replacements. J. Mater. Sci. Mater. Med. 2013, 24, 547–554. [Google Scholar] [CrossRef] [PubMed]
- Naylor, A.; Talwalkar, S.C.; Trail, I.A.; Joyce, T.J. In vitro wear testing of a CoCr-UHMWPE finger prosthesis with hydroxyapatite coated cocr stems. Lubricants 2015, 3, 244–255. [Google Scholar] [CrossRef]
- Joyce, T.J.; Langton, D.J.; Jameson, S.S.; Nargol, A.V.F. Tribological analysis of failed resurfacing hip prostheses and comparison with clinical data. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2009, 223, 317–323. [Google Scholar] [CrossRef]
- Joyce, T.J. Wear testing of a DJOA finger prosthesis in vitro. J. Mater. Sci. Mater. Med. 2010, 21, 2337–2343. [Google Scholar] [CrossRef] [PubMed]
- Hall, R.M.; Siney, P.; Unsworth, A.; Wroblewski, B.M. The effect of surface topography of retrieved femoral heads on the wear of uhmwpe sockets. Med. Eng. Phys. 1997, 19, 711–719. [Google Scholar] [CrossRef]
- Hailey, J.L.; Ingham, E.; Stone, M.; Wroblewski, B.M.; Fisher, J. Ultra-high molecular weight polyethylene wear debris generated in vivo and in laboratory tests; the influence of counterface roughness. Proc. Inst. Mech. Eng. H 1996, 210, 3–10. [Google Scholar] [CrossRef] [PubMed]
- Gadelmawla, E.S.; Koura, M.M.; Maksoud, T.M.A.; Elewa, I.M.; Soliman, H.H. Roughness parameters. J. Mater. Process. Technol. 2002, 123, 133–145. [Google Scholar] [CrossRef]
- Sedlaček, M.; Podgornik, B.; Vižintin, J. Correlation between standard roughness parameters skewness and kurtosis and tribological behaviour of contact surfaces. Tribol. Int. 2012, 48, 102–112. [Google Scholar] [CrossRef]
- BS EN ISO 7206–2: Implants for Surgery—Partial and Total Hip Joint Prostheses. Part 2: Articulating Surfaces Made of Metallic, Ceramic and Plastics Materials; British Standards Institute: London, UK, 2011.
- Surface Measurement Parameters for Wyko® Optical Profilers: An505-5-0403; Veeco Instruments: Terminal Drive Plainview, NY, USA, 2003.
- Naylor, A.; Trail, I.A.; Talwalkar, S.C.; Joyce, T.J. Evaluating the Articulating Surface Roughness of New Pyrocarbon Proximal Interphalangeal Prostheses. In Proceedings of the British Society for Surgery of the Hand: Autumn Scientific Meeting, London, UK, 15–16 October 2015.
- Gelinck, E.R.M.; Schipper, D.J. Calculation of stribeck curves for line contacts. Tribol. Int. 2000, 33, 175–181. [Google Scholar] [CrossRef]
- Etsion, I. State of the art in laser surface texturing. J. Tribol. 2005, 127, 248–253. [Google Scholar] [CrossRef]
- BS EN ISO 25178–2: Geometric Product Specification, Surface Texture (Areal). Part 2: Terms, Definitions and Surface Texture Parameters; British Standards Institute: London, UK, 2012.

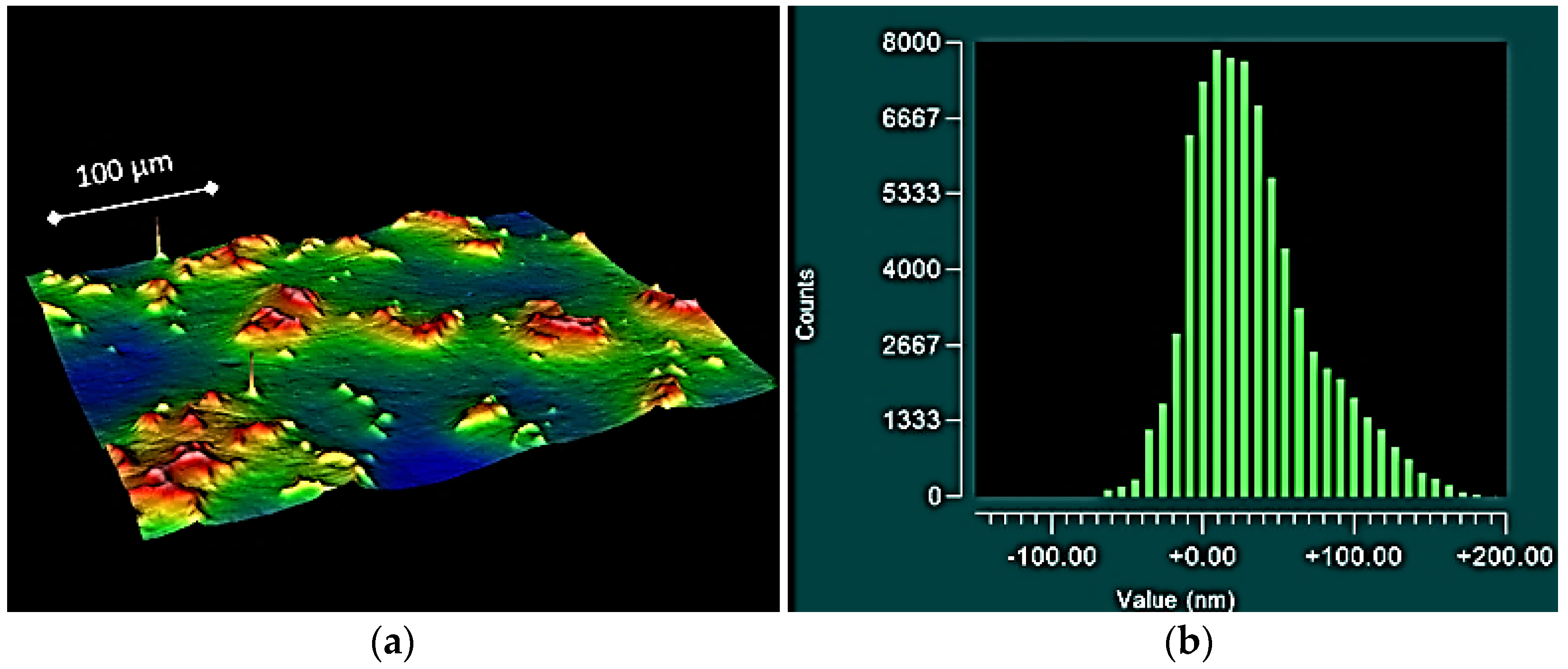
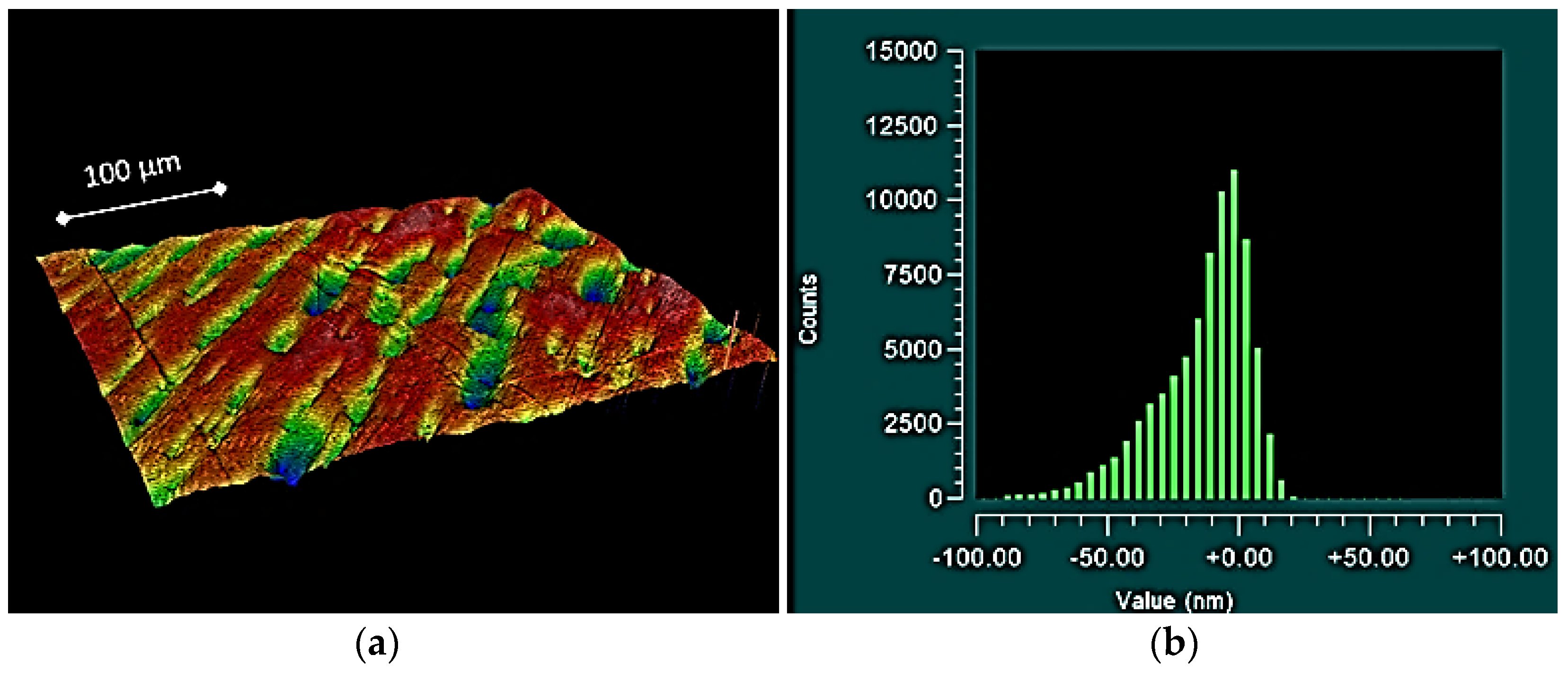
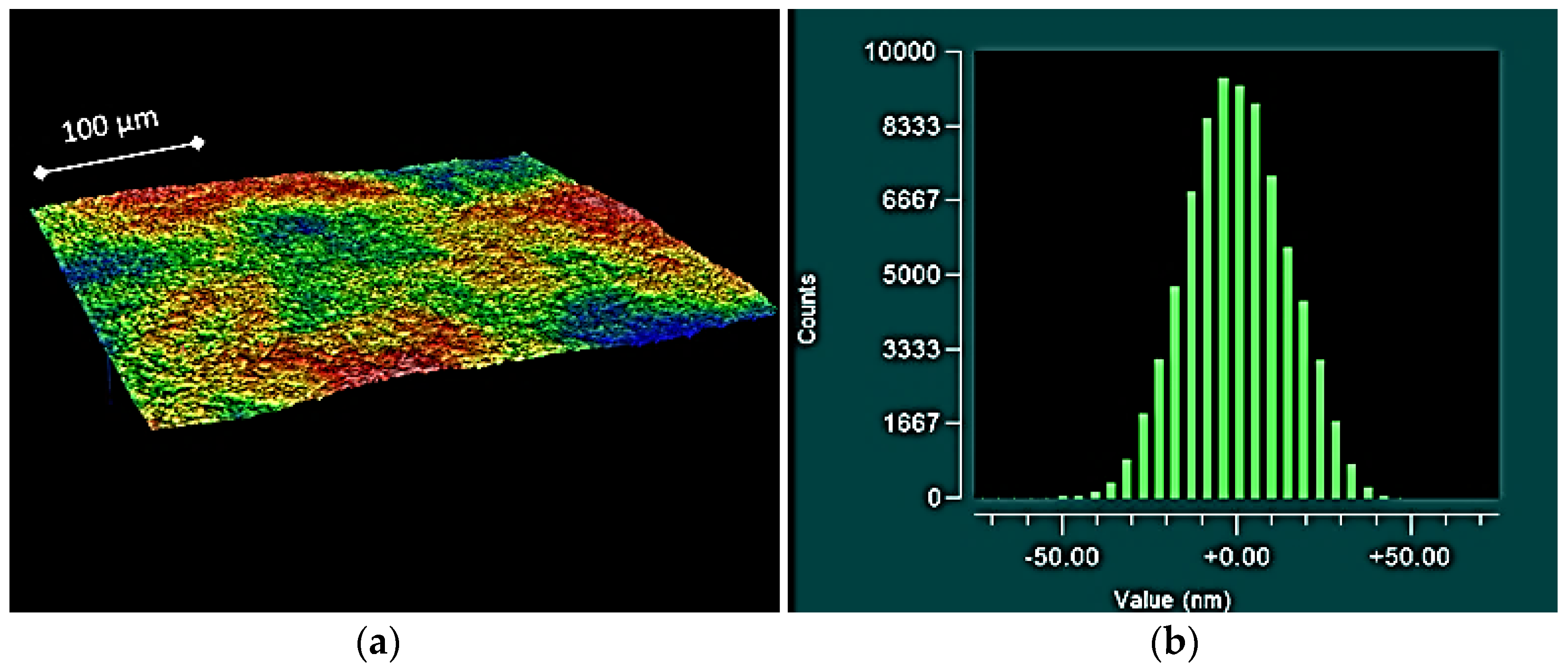
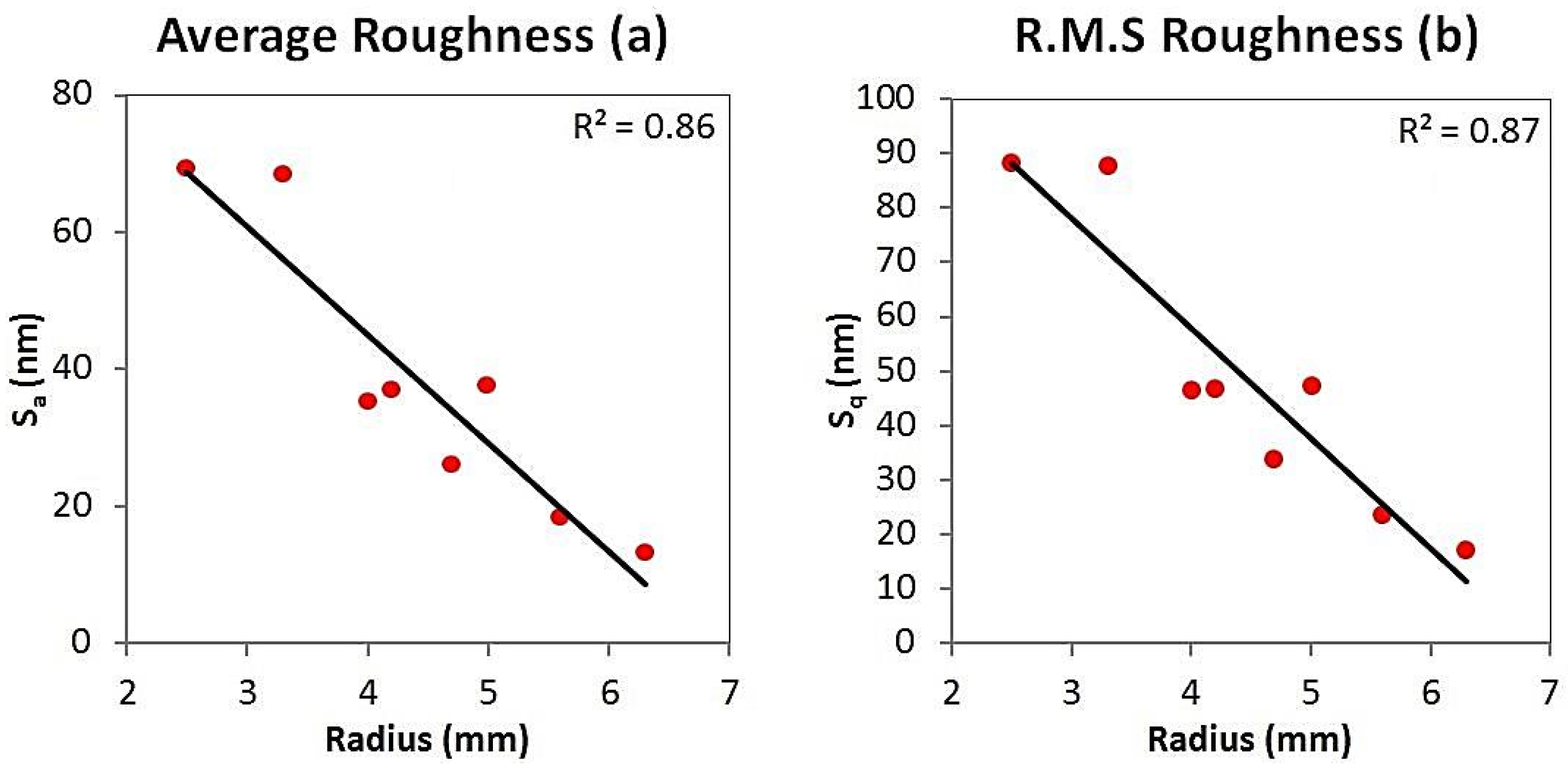
| Parameter | Size | Proximal Component | Medial Component | ||||
|---|---|---|---|---|---|---|---|
| Mean (95% CI) | z-Score | p-Value | Mean (95% CI) | z-Score | p-Value | ||
| Sa (nm) | Size 10 | 69.2 (63.4–74.8) | 6.52 | 0.00 | 34.9 (25.6–44.1) | −3.20 | 0.00 |
| Size 20 | 68.1 (62.1–74) | 5.96 | 0.00 | 37.4 (33.9–40.9) | −7.10 | 0.00 | |
| Size 30 | 36.8 (30.8–41.2) | −5.30 | 0.00 | 18.1 (16.4–19.8) | −36.10 | 0.00 | |
| Size 40 | 25.9 (23.6–28.3) | −20.10 | 0.00 | 13 (11.9–14) | −71.10 | 0.00 | |
| Sq (nm) | Size 10 | 88 (80.7–95.3) | 10.26 | 0.00 | 46.4 (34–58.7) | −5.80 | 0.56 |
| Size 20 | 87.9 (80.5–95.2) | 10.10 | 0.00 | 47.1 (42.6–51.6) | −1.27 | 0.20 | |
| Size 30 | 46.7 (40.2–53.2) | −0.99 | 0.32 | 23.4 (21.3–25.5) | −24.87 | 0.00 | |
| Size 40 | 33.7 (30.1–36.5) | −11.32 | 0.00 | 17 (15.7–18.3) | −48.77 | 0.00 | |
| Ssk | Size 10 | −0.036 (−0.149–0.078) | −0.62 | 0.53 | −0.342 (−0.646 to −0.038) | −2.20 | 0.05 |
| Size 20 | 0.024 (−0.176–0.128) | 0.31 | 0.76 | 0.036 (−0.126 to 0.182) | 0.44 | 0.66 | |
| Size 30 | −0.038 (−0.148–0.072) | −0.68 | 0.50 | −0.222 (−0.486 to 0.046) | −1.62 | 0.10 | |
| Size 40 | −0.43 (−0.685 to −0.175) | −3.31 | 0.00 | −0.62 (−1.08 to −0.161) | −2.65 | 0.01 | |
| Sku | Size 10 | 4.65 (4.23–5.06) | 8.20 | 0.00 | 11.86 (7.37–16.34) | 3.87 | 0.00 |
| Size 20 | 4.77 (4.1–5.44) | 5.210 | 0.00 | 4.16 (3.73–4.59) | 5.340 | 0.00 | |
| Size 30 | 4.16 (3.72–4.59) | 5.310 | 0.00 | 15.61 (8.94–22.28) | 3.710 | 0.00 | |
| Size 40 | 11.4 (7.84–14.97) | 4.620 | 0.00 | 29.74 (15.22–44.26) | 3.610 | 0.00 | |
| Parameter | Source of Variation | Degrees of Freedom | Sum of Squares | Mean Square | F-Statistic | p-Value |
|---|---|---|---|---|---|---|
| Sa (nm) | Regression | 1 | 2632 | 2632 | 37 | 0.001 |
| Error | 6 | 426 | 71 | – | – | |
| Total | 7 | 3058 | – | – | – | |
| Sq (nm) | Regression | 1 | 4303 | 4303 | 39 | 0.001 |
| Error | 6 | 660 | 110 | – | – | |
| Total | 7 | 4963 | – | – | – | |
| Ssk | Regression | 1 | 0.215 | 0.215 | 9.1 | 0.023 |
| Error | 6 | 0.142 | 0.204 | – | – | |
| Total | 7 | 0.356 | – | – | – | |
| Ssk | Regression | 1 | 311 | 311 | 7.8 | 0.03 |
| Error | 6 | 243 | 39 | – | – | |
| Total | 7 | 546 | – | – | – |
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naylor, A.; Talwalkar, S.C.; Trail, I.A.; Joyce, T.J. Evaluating the Surface Topography of Pyrolytic Carbon Finger Prostheses through Measurement of Various Roughness Parameters. J. Funct. Biomater. 2016, 7, 9. https://doi.org/10.3390/jfb7020009
Naylor A, Talwalkar SC, Trail IA, Joyce TJ. Evaluating the Surface Topography of Pyrolytic Carbon Finger Prostheses through Measurement of Various Roughness Parameters. Journal of Functional Biomaterials. 2016; 7(2):9. https://doi.org/10.3390/jfb7020009
Chicago/Turabian StyleNaylor, Andrew, Sumedh C. Talwalkar, Ian A. Trail, and Thomas J. Joyce. 2016. "Evaluating the Surface Topography of Pyrolytic Carbon Finger Prostheses through Measurement of Various Roughness Parameters" Journal of Functional Biomaterials 7, no. 2: 9. https://doi.org/10.3390/jfb7020009
APA StyleNaylor, A., Talwalkar, S. C., Trail, I. A., & Joyce, T. J. (2016). Evaluating the Surface Topography of Pyrolytic Carbon Finger Prostheses through Measurement of Various Roughness Parameters. Journal of Functional Biomaterials, 7(2), 9. https://doi.org/10.3390/jfb7020009







