Optimisation of 3D Printing Parameters and Surface Modification for Porous Gyroid Structures in Beta Titanium Alloy Ti25Nb4Ta8Sn
Abstract
1. Introduction
2. Material and Methods
2.1. Material Preparation and Printing Parameters
2.2. Gyroid Structure
2.3. Evaluation Methods and Equipment Used
2.4. Etching as a Post-Printing Surface Refinement Method
3. Results and Discussion
3.1. Porosity Evaluation
3.2. Evaluation of the Area of a 3D Printed Sample
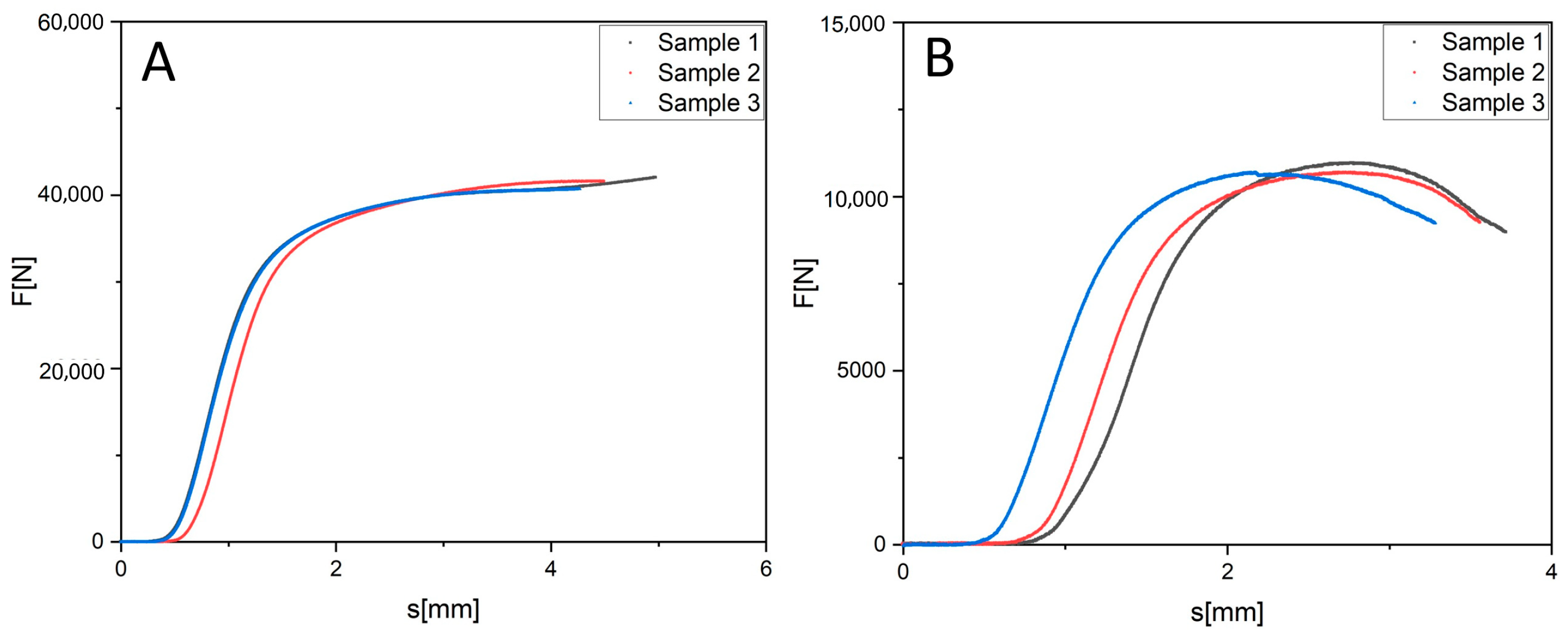
3.3. Pressure Test
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, Y.; Xu, L.; Qiu, C. Development of an Additively Manufactured Metastable Beta Titanium Alloy with A Fully Equiaxed Grain Structure and Ultrahigh Yield Strength. Addit. Manuf. 2022, 60, 103208. [Google Scholar] [CrossRef]
- Vandrovcova, M.; Tolde, Z.; Vanek, P.; Nehasil, V.; Doubková, M.; Trávníčková, M.; Drahokoupil, J.; Buixaderas, E.; Borodavka, F.; Novakova, J.; et al. Beta-Titanium Alloy Covered by Ferroelectric Coating–Physicochemical Properties and Human Osteoblast-Like Cell Response. Coatings 2021, 11, 210. [Google Scholar] [CrossRef]
- Tolde, Z.; Smola, V.; Šebová, E.; Budinská, Z.; Bumba, J.; Vlčák, P. Characterization and Bioactivity Of Β-Tricalcium Phosphate Powder Sol–Gel Coatings on Titanium Substrates. J. Sol-Gel Sci. Technol. 2025. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, T. Laser Powder Bed Fusion of Powder Material: A Review. 3D Print. Addit. Manuf. 2023, 10, 1439–1454. [Google Scholar] [CrossRef] [PubMed]
- Onder, M.E.; Culhaoglu, A.; Ozgul, O.; Tekin, U.; Atıl, F.; Taze, C.; Yasa, E. Biomimetic Dental Implant Production Using Selective Laser Powder Bed Fusion Melting: In-Vitro Results. J. Mech. Behav. Biomed. Mater. 2024, 151, 106360. [Google Scholar] [CrossRef]
- Salim, A.A.; Bakhtiar, H.; Ghoshal, S.K.; Aziz, M.S.A. 3D-Printed Titanium-Aluminum-Vanadium Alloy Produced at Various Laser Powers: Evaluation of Microstructures and Mechanical Characteristics. Int. J. Adv. Manuf. Technol. 2024, 132, 3671–3681. [Google Scholar] [CrossRef]
- Wang, Z.; Xiao, Z.; Tse, Y.; Huang, C.; Zhang, W. Optimization of Processing Parameters and Establishment of a Relationship Between Microstructure and Mechanical Properties of Slm Titanium Alloy. Opt. Laser Technol. 2019, 112, 159–167. [Google Scholar] [CrossRef]
- Cho, K.; Sakata, M.; Yasuda, H.Y.; Todai, M.; Ueda, M.; Takeyama, M.; Nakano, T. Effect of Scan Speed on Microstructure and Tensile Properties of Ti–48Al–2Cr–2Nb Alloys Fabricated Via Additive Manufacturing. Mater. Trans. 2023, 64, 1112–1118. [Google Scholar] [CrossRef]
- Tekumalla, S.; Chew, J.E.; Tan, S.W.; Krishnan, M.; Seita, M. Towards 3-D Texture Control in A Β Titanium Alloy Via Laser Powder Bed Fusion and Its Implications on Mechanical Properties. Addit. Manuf. 2022, 59, 103111. [Google Scholar] [CrossRef]
- Wu, Q.; Wang, X.; Li, K.; Zhou, Y.; Wen, S.; Shi, Y. Microstructure and Mechanical Properties of Ti6Al4V/W Bimetallic Structure Via Selective Laser Melting. Int. J. Refract. Met. Hard Mater. 2024, 121, 106683. [Google Scholar] [CrossRef]
- Abramczyk, I.; Ligaj, B. Influence of the Etching Time of Ti6Al4V Titanium Alloy with Selected Acid Solutions on Changes in Physical Parameters of the Element. In Proceedings of the Engineering Mechanics, Brno, Czech Republic, 16 May 2024; pp. 38–41. [Google Scholar]
- Sheng, X.; Wang, A.; Wang, Z.; Liu, H.; Wang, J.; Li, C. Advanced Surface Modification For 3D-Printed Titanium Alloy Implant Interface Functionalization. Front. Bioeng. Biotechnol. 2022, 10, 850110. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Zhang, J.; Shi, Y.; Tang, J.; Huang, D.; Yan, M.; Dargusch, M.S. Surface Modification of Biomedical Ti and Ti Alloys: A Review on Current Advances. Materials 2022, 15, 1749. [Google Scholar] [CrossRef] [PubMed]
- Thenard, T.; Catapano, A.; Allena, R.; El May, M.; Saintier, N.; Mesnard, M. Topography and Wettability Characterization of Surfaces Manufactured by Slm and Treated by Chemical Etching. Mech. Adv. Mater. Struct. 2020, 29, 1674–1691. [Google Scholar] [CrossRef]
- Shaboldo, O.P.; Vitorskii, Y.M.; Sagaradze, V.V.; Pecherkina, N.L.; Skotnikova, M.A. Formation of the Structure and Properties of Β-Type Titanium Alloy Upon Thermomechanical Treatment. Phys. Met. Metallogr. 2017, 118, 75–80. [Google Scholar] [CrossRef]
- Takase, A.; Ishimoto, T.; Suganuma, R.; Nakano, T. Surface Residual Stress and Phase Stability in Unstable Β-Type Ti–15Mo–5Zr–3Al Alloy Manufactured by Laser and Electron Beam Powder Bed Fusion Technologies. Addit. Manuf. 2021, 47, 102257. [Google Scholar] [CrossRef]
- Yang, X.; Sun, Z.; Hu, Y.; Mi, C. Multi-Parameter Design of Triply Periodic Minimal Surface Scaffolds: From Geometry Optimization to Biomechanical Simulation. Biomed. Mater. 2024, 19, 055005. [Google Scholar] [CrossRef]
- Ziaie, B.; Velay, X.; Saleem, W. Exploring the Optimal Mechanical Properties of Triply Periodic Minimal Surface Structures for Biomedical Applications: A Numerical Analysis. J. Mech. Behav. Biomed. Mater. 2024, 160, 106757. [Google Scholar] [CrossRef]
- Lv, X.; Yang, X.; Liu, W.; Zhou, R.; Zhou, H.; Chen, Y.; Xing, Z.; Li, W. Gyroid Minimal Surface-Based Composite Porous Structure with Superior Mechanical Property Via Triangular Grid Design and Stress Distribution Optimization. Mater. Today Commun. 2022, 33, 104550. [Google Scholar] [CrossRef]
- Gawronska, E.; Dyja, R. A Numerical Study of Geometry’s Impact on the Thermal and Mechanical Properties of Periodic Surface Structures. Materials 2021, 14, 427. [Google Scholar] [CrossRef]
- Szymczyk, P.; Hoppe, V.; Ziółkowski, G.; Smolnicki, M.; Madeja, M. The Effect of Geometry on Mechanical Properties of Ti6Al4V Eli Scaffolds Manufactured Using Additive Manufacturing Technology. Arch. Civ. Mech. Eng. 2020, 20, 11. [Google Scholar] [CrossRef]
- Jíra, A.; Šejnoha, M.; Krejčí, T.; Vorel, J.; Řehounek, L.; Marseglia, G. Mechanical Properties of Porous Structures for Dental Implants: Experimental Study and Computational Homogenization. Materials 2021, 14, 4592. [Google Scholar] [CrossRef] [PubMed]
- Schoen, A.H. Infinite Periodic Minimal Surfaces Without Self-Intersections; NASA TN D—Svazek 5541; National Aeronautics and Space Administration: Washington, DC, USA, 1970.
- Araya-Calvo, M.; Järvenpää, A.; Rautio, T.; Morales-Sanchez, J.E.; Guillen-Girón, T. Comparative Fatigue Performance of As-Built vs. Etched Ti64 in Tpms-Gyroid and Stochastic Structures Fabricated Via Pbf-Lb for Biomedical Applications. Rapid Prototyp. J. 2024, 30, 217–230. [Google Scholar] [CrossRef]
- Ahmed, N.; Barsoum, I.; Abu Al-Rub, R.K. Numerical Investigation on the Effect of Residual Stresses on the Effective Mechanical Properties Of 3D-Printed Tpms Lattices. Metals 2022, 12, 1344. [Google Scholar] [CrossRef]
- Ali, B.; Heider, Y.; Markert, B. Modeling the Thermomechanical Processes and Residual Stresses in Additive Manufacturing of Metallic Components. Proc. Appl. Math. Mech. 2023, 22, e202200089. [Google Scholar] [CrossRef]
- Polley, C.; Radlof, W.; Hauschulz, F.; Benz, C.; Sander, M.; Seitz, H. Morphological and Mechanical Characterisation of Three-Dimensional Gyroid Structures Fabricated by Electron Beam Melting for the Use as a Porous Biomaterial. J. Mech. Behav. Biomed. Mater. 2022, 125, 104882. [Google Scholar] [CrossRef]
- Ren, J.; Huang, R.; Huang, L.; Yang, S.; Pan, C.; Sun, Y.; Tian, S.; Wu, X.; Wang, D.; Yang, Y. A Functionally Graded Gyroid-Type Three-Periodic Minimal Surface Framework Applied to Implant-Supported Fixed Complete Dentures. Int. J. Bioprinting 2024, 10, 3453. [Google Scholar] [CrossRef]
- Wang, N.; Meenashisundaram, G.K.; Chang, S.; Fuh, J.Y.H.; Dheen, S.T.; Senthil Kumar, A. A Comparative Investigation on the Mechanical Properties and Cytotoxicity of Cubic, Octet, and Tpms Gyroid Structures Fabricated by Selective Laser Melting of Stainless Steel 316L. J. Mech. Behav. Biomed. Mater. 2022, 129, 105151. [Google Scholar] [CrossRef]
- Isaacson, N.; Lopez-Ambrosio, K.; Chubb, L.; Waanders, N.; Hoffmann, E.; Witt, C.; James, S.; Prawel, D.A. Compressive Properties and Failure Behavior of Photocast Hydroxyapatite Gyroid Scaffolds Vary with Porosity. J. Biomater. Appl. 2022, 37, 55–76. [Google Scholar] [CrossRef]
- Baumer, V.; Gunn, E.; Riegle, V.; Bailey, C.; Shonkwiler, C.; Prawel, D. Robocasting of Ceramic Fischer–Koch S Scaffolds for Bone Tissue Engineering. J. Funct. Biomater. 2023, 14, 251. [Google Scholar] [CrossRef]
- Spece, H.; Yu, T.; Law, A.W.; Marcolongo, M.; Kurtz, S.M. 3D Printed Porous Peek Created Via Fused Filament Fabrication for Osteoconductive Orthopaedic Surfaces. J. Mech. Behav. Biomed. Mater. 2020, 109, 103850. [Google Scholar] [CrossRef]
- Sabahi, N.; Farajzadeh, E.; Roohani, I.; Wang, C.H.; Li, X. Material Extrusion 3D Printing of Polyether-Ether-Ketone Scaffolds Based on Triply Periodic Minimal Surface Designs: A Numerical and Experimental Investigation. Appl. Mater. Today 2024, 39, 102262. [Google Scholar] [CrossRef]
- Verma, R.; Kumar, J.; Singh, N.K.; Rai, S.K.; Saxena, K.K.; Xu, J. Design and Analysis of Biomedical Scaffolds Using Tpms-Based Porous Structures Inspired from Additive Manufacturing. Coatings 2022, 12, 839. [Google Scholar] [CrossRef]
- Naghavi, S.A.; Tamaddon, M.; Marghoub, A.; Wang, K.; Babamiri, B.B.; Hazeli, K.; Xu, W.; Lu, X.; Sun, C.; Wang, L.; et al. Mechanical Characterisation and Numerical Modelling of Tpms-Based Gyroid and Diamond Ti6Al4V Scaffolds for Bone Implants: An Integrated Approach for Translational Consideration. Bioengineering 2022, 9, 504. [Google Scholar] [CrossRef]
- Zaharin, H.A.; Abdul Rani, A.M.; Azam, F.I.; Ginta, T.L.; Sallih, N.; Ahmad, A.; Yunus, N.A.; Zulkifli, T.Z.A. Effect of Unit Cell Type and Pore Size on Porosity and Mechanical Behavior of Additively Manufactured Ti6Al4V Scaffolds. Materials 2018, 11, 2402. [Google Scholar] [CrossRef] [PubMed]
- Yapa, P.; Munaweera, I. Functionalized Nanoporous Architectures Derived from Sol–Gel Processes for Advanced Biomedical Applications. J. Mater. Chem. B 2025, 13, 10715–10742. [Google Scholar] [CrossRef] [PubMed]
- Liang, W.; Zhou, C.; Bai, J.; Zhang, H.; Long, H.; Jiang, B.; Wang, J.; Huang, X.; Zhang, H.; Zhao, J. Prospective Applications of Bioactive Materials in Orthopedic Therapies: A Review. Heliyon 2024, 10, e36152. [Google Scholar] [CrossRef] [PubMed]
- Sebastiani, S.; Buccino, F.; Qin, Z.; Vergani, L.M. Structural Influences on Bone Tissue Engineering: A Review and Perspective. Matter 2025, 8, 102252. [Google Scholar] [CrossRef]
- Krčil, J.; Mára, V.; Šimota, J. The Evaluation of Ti-24Nb-8Ta-4Sn Alloy Prepared By 3D Printing. Solid State Phenom. 2022, 334, 43–48. [Google Scholar] [CrossRef]
- Jíra, A.; Kruis, J.; Tolde, Z.; Krčil, J.; Jírů, J.; Fojt, J. Effect of Sample Thickness and Post-Processing on Mechanical Properties of 3D-Printed Titanium Alloy. Materials 2025, 18, 5008. [Google Scholar] [CrossRef]
- Bahl, S.; Das, S.; Suwas, S.; Chatterjee, K. Engineering the Next-Generation Tin Containing Β Titanium Alloys with High Strength and Low Modulus for Orthopedic Applications. J. Mech. Behav. Biomed. Mater. 2018, 78, 124–133. [Google Scholar] [CrossRef]
- Al-Ketan, O.; Abu Al-Rub, R.K. Mslattice: A Free Software for Generating Uniform and Graded Lattices Based on Triply Periodic Minimal Surfaces. Mater. Des. Process. Commun. 2020, 3, e205. [Google Scholar] [CrossRef]
- Nandhakumar, R.; Venkatesan, K. A Process Parameters Review on Selective Laser Melting-Based Additive Manufacturing of Single and Multi-Material: Microstructure, Physical Properties, Tribological, And Surface Roughness. Mater. Today Commun. 2023, 35, 105538. [Google Scholar] [CrossRef]




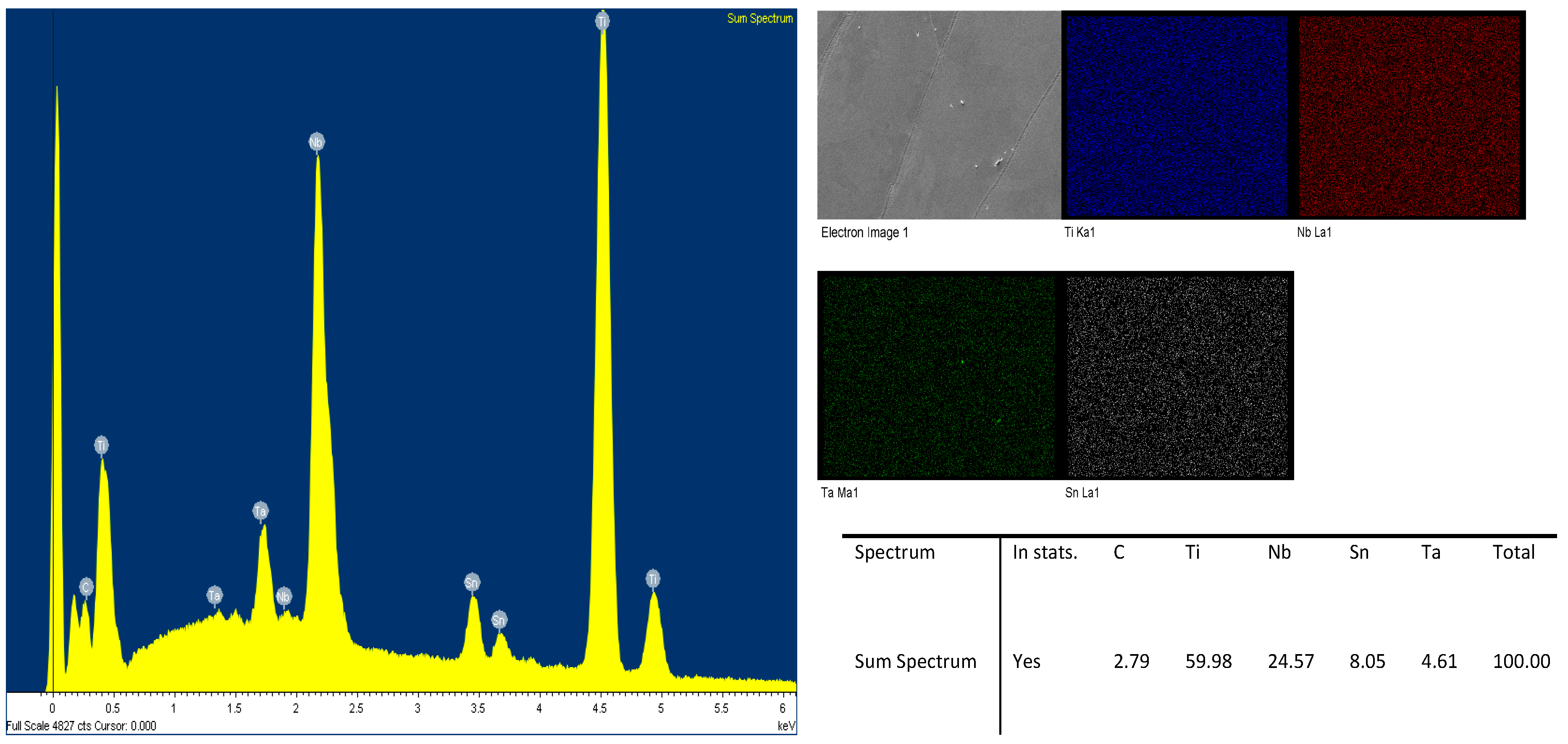


| Sample ID | Modification Type | Description of Printing Parameters/Strategy |
|---|---|---|
| T1 | Reference sample | Default parameters: laser power 180 W, melting rate 550 mm/s (based on previous optimisation). |
| T2 | Scanning strategy | Changed to chessboard scanning. |
| T3 | Scanning strategy | Offset filling “In → Out” (from centre to edge). |
| T4 | Scanning strategy | Offset filling “Out → In” (from edge to centre). |
| T5 | Scanning strategy | Stripe filling (“Zigzag—Connected”). |
| T6 | Border parameters | Melting rate for border paths adjusted to 600 mm/s and laser power at 180 W. |
| T7 | Contour removal | No contour; border distance = 0 mm; other parameters as T1. |
| T8 | Contour removal | No contour; border distance = 0 mm; other parameters as T2. |
| T9 | Contour removal | No contour; border distance = 0 mm; other parameters as T3. |
| T10 | Contour removal | No contour; border distance = 0 mm; other parameters as T4. |
| T11 | Contour removal | No contour; border distance = 0 mm; other parameters as T5. |
| T12 | Contour removal | No contour; border distance = 0 mm; other parameters as T6. |
| T13 | Beam compensation | Beam compensation = 0.001 mm; other parameters as T1. |
| T14 | Beam compensation | Beam compensation = 0.001 mm; other parameters as T7. |
| T15 | Beam compensation | Beam compensation = 0.12 mm; other parameters as T1. |
| T16 | Beam compensation | Beam compensation = 0.12 mm; other parameters as T7. |
| T17 | Hatch distance | Hatch distance = 0.08 mm; other parameters as T1. |
| T18 | Hatch distance | Hatch distance = 0.12 mm; other parameters as T1. |
| T19 | Hatch distance | Hatch distance = 0.06 mm; other parameters as T7. |
| T20 | Hatch distance | Hatch distance = 0.08 mm; other parameters as T7. |
| T21 | Hatch distance | Hatch distance = 0.12 mm; other parameters as T7. |
| Density | Size [mm] | Cells | Wall Thickness [mm] |
|---|---|---|---|
| 20% | 15 × 15 × 15 | 3 × 3 × 3 | 0.35 |
| 40% | 0.72 |
| Sample (Percentage of Pores) | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | |
| first grinding | |||||||||||||||||||||
| 1 | 1.8 | 1.4 | 4.3 | 1.1 | 1.6 | 0.1 | 0.7 | 0.3 | 0.9 | 15.9 | 0.4 | 0.2 | 1.2 | 0.1 | 1.6 | 0.2 | 0.4 | 2 | 0.2 | 0 | 0.2 |
| 2 | 0.6 | 0.7 | 2.9 | 0.2 | 1.5 | 0.1 | 0.3 | 0 | 0.7 | 12.9 | 0.6 | 0.1 | 2.1 | 0.2 | 1 | 0.1 | 0.3 | 2.1 | 0.2 | 0.3 | 0.2 |
| 3 | 0.4 | 0.4 | 0.3 | 0.2 | 0.8 | 0 | 0.2 | 0 | 0.1 | 7.9 | 0.5 | 0.1 | 1.7 | 0.2 | 0.9 | 0.1 | 0.4 | 0.8 | 0.2 | 0 | 0.3 |
| Average | 0.9 | 0.8 | 2.5 | 0.5 | 1.3 | 0.1 | 0.4 | 0.1 | 0.6 | 12.2 | 0.5 | 0.1 | 1.7 | 0.2 | 1.2 | 0.1 | 0.4 | 1.6 | 0.2 | 0.1 | 0.2 |
| SD | ±0.62 | ±0.42 | ±1.66 | ±0.42 | ±0.36 | ±0.05 | ±0.22 | ±0.14 | ±0.34 | ±3.30 | ±0.08 | ±0.05 | ±0.37 | ±0.05 | ±0.31 | ±0.05 | ±0.05 | ±0.59 | ±0.00 | ±0.14 | ±0.05 |
| 1 | 0.3 | 0.6 | 0.3 | 0.1 | 0.3 | 0.1 | 0.1 | 0.3 | 0.2 | 1.5 | 0.1 | 0.2 | 1 | 0.3 | 1 | 0.1 | 0.1 | 1.1 | 0.1 | 0 | 0.1 |
| 2 | 0.7 | 0.9 | 0.9 | 0.3 | 0.7 | 0.1 | 0.1 | 0 | 0.1 | 2.5 | 0.1 | 0.3 | 1.5 | 0.3 | 0.8 | 0.1 | 0.5 | 2.1 | 0 | 0 | 0.3 |
| 3 | 1 | 0.5 | 0.6 | 0.7 | 0.9 | 0.1 | 0 | 0.4 | 0.1 | 1.4 | 0.1 | 0.2 | 1.2 | 0.4 | 1.8 | 0.1 | 0.4 | 2.3 | 0.1 | 0.1 | 0.1 |
| Average | 0.7 | 0.7 | 0.6 | 0.4 | 0.6 | 0.1 | 0.1 | 0.2 | 0.1 | 1.8 | 0.1 | 0.2 | 1.2 | 0.3 | 1.2 | 0.1 | 0.3 | 1.8 | 0.1 | 0 | 0.2 |
| SD | ±0.29 | ±0.17 | ±0.24 | ±0.25 | ±0.25 | ±0.00 | ±0.05 | ±0.17 | ±0.05 | ±0.50 | ±0.00 | ±0.05 | ±0.21 | ±0.05 | ±0.43 | ±0.00 | ±0.17 | ±0.52 | ±0.05 | ±0.05 | ±0.09 |
| OverallAverage | 0.80 | 0.75 | 1.55 | 0.43 | 0.97 | 0.08 | 0.23 | 0.17 | 0.35 | 7.02 | 0.30 | 0.18 | 1.45 | 0.25 | 1.18 | 0.12 | 0.35 | 1.73 | 0.13 | 0.07 | 0.20 |
| SD | ±0.1 | ±0.05 | ±0.95 | ±0.05 | ±0.35 | ±0 | ±0.15 | ±0.05 | ±0.25 | ±5.2 | ±0.2 | ±0.05 | ±0.25 | ±0.05 | ±0 | ±0 | ±0.05 | ±0.1 | ±0.05 | ±0.05 | ±0 |
| Sample | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T1 | T2 | T3 | T4 | T5 | T6 | T7 | T8 | T9 | T10 | T11 | T12 | T13 | T14 | T15 | T16 | T17 | T18 | T19 | T20 | T21 | |
| First grinding—area after printing (image size 2560 × 1920 px) defined sample size is 182,667 px | |||||||||||||||||||||
| px | 176,268 | 158,677 | 146,192 | 169,162 | 166,902 | 212,628 | 177,437 | 171,482 | 197,589 | 190,472 | 201,802 | 167,009 | 197,443 | 167,134 | 105,948 | 124,022 | 152,936 | 158,706 | 148110 | 165,789 | 164,297 |
| Percentage Representation (%) | 96.5 | 86.9 | 80 | 92.6 | 91.4 | 116.4 | 97.1 | 93.9 | 108.2 | 104.3 | 110.5 | 91.4 | 108.1 | 91.5 | 58 | 67.9 | 83.7 | 86.9 | 81.1 | 90.8 | 89.9 |
| Second grinding area after printing (image size 2560 × 1920 px) defined sample size is 286,785 px | |||||||||||||||||||||
| px | 258,586 | 253,528 | 245,797 | 258,300 | 265,992 | 352,570 | 283,770 | 278,352 | 323,231 | 304,861 | 324,914 | 284,108 | 320,053 | 322,965 | 172,380 | 188,896 | 243,935 | 248,251 | 237,097 | 237,329 | 256,766 |
| Percentage Representation (%) | 90.2 | 88.4 | 85.7 | 90.1 | 92.7 | 122.9 | 98.9 | 97.1 | 112.7 | 106.3 | 113.3 | 99.1 | 111.6 | 112.6 | 60.1 | 65.9 | 85.1 | 86.6 | 82.7 | 82.8 | 89.5 |
| Overall Average (%) | 93.3 | 87.6 | 82.9 | 91.3 | 92.1 | 119.7 | 98 | 95.5 | 110.4 | 105.3 | 111.9 | 95.2 | 109.8 | 102.1 | 59.1 | 66.9 | 84.4 | 86.7 | 81.9 | 86.8 | 89.7 |
| SD | ±3.15 | ±0.75 | ±2.85 | ±1.25 | ±0.65 | ±3.25 | ±0.9 | ±1.6 | ±2.25 | ±1 | ±1.4 | ±3.85 | ±1.75 | ±10.55 | ±1.05 | ±1 | ±0.7 | ±0.15 | ±0.8 | ±4 | ±0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tolde, Z.; Jíra, A.; Jírů, J.; Hybášek, V.; Smola, V.; Vlčák, P. Optimisation of 3D Printing Parameters and Surface Modification for Porous Gyroid Structures in Beta Titanium Alloy Ti25Nb4Ta8Sn. J. Funct. Biomater. 2025, 16, 416. https://doi.org/10.3390/jfb16110416
Tolde Z, Jíra A, Jírů J, Hybášek V, Smola V, Vlčák P. Optimisation of 3D Printing Parameters and Surface Modification for Porous Gyroid Structures in Beta Titanium Alloy Ti25Nb4Ta8Sn. Journal of Functional Biomaterials. 2025; 16(11):416. https://doi.org/10.3390/jfb16110416
Chicago/Turabian StyleTolde, Zdeněk, Aleš Jíra, Jitřenka Jírů, Vojtěch Hybášek, Vojtěch Smola, and Petr Vlčák. 2025. "Optimisation of 3D Printing Parameters and Surface Modification for Porous Gyroid Structures in Beta Titanium Alloy Ti25Nb4Ta8Sn" Journal of Functional Biomaterials 16, no. 11: 416. https://doi.org/10.3390/jfb16110416
APA StyleTolde, Z., Jíra, A., Jírů, J., Hybášek, V., Smola, V., & Vlčák, P. (2025). Optimisation of 3D Printing Parameters and Surface Modification for Porous Gyroid Structures in Beta Titanium Alloy Ti25Nb4Ta8Sn. Journal of Functional Biomaterials, 16(11), 416. https://doi.org/10.3390/jfb16110416







