Finite Element Method for the Evaluation of the Human Spine: A Literature Overview
Abstract
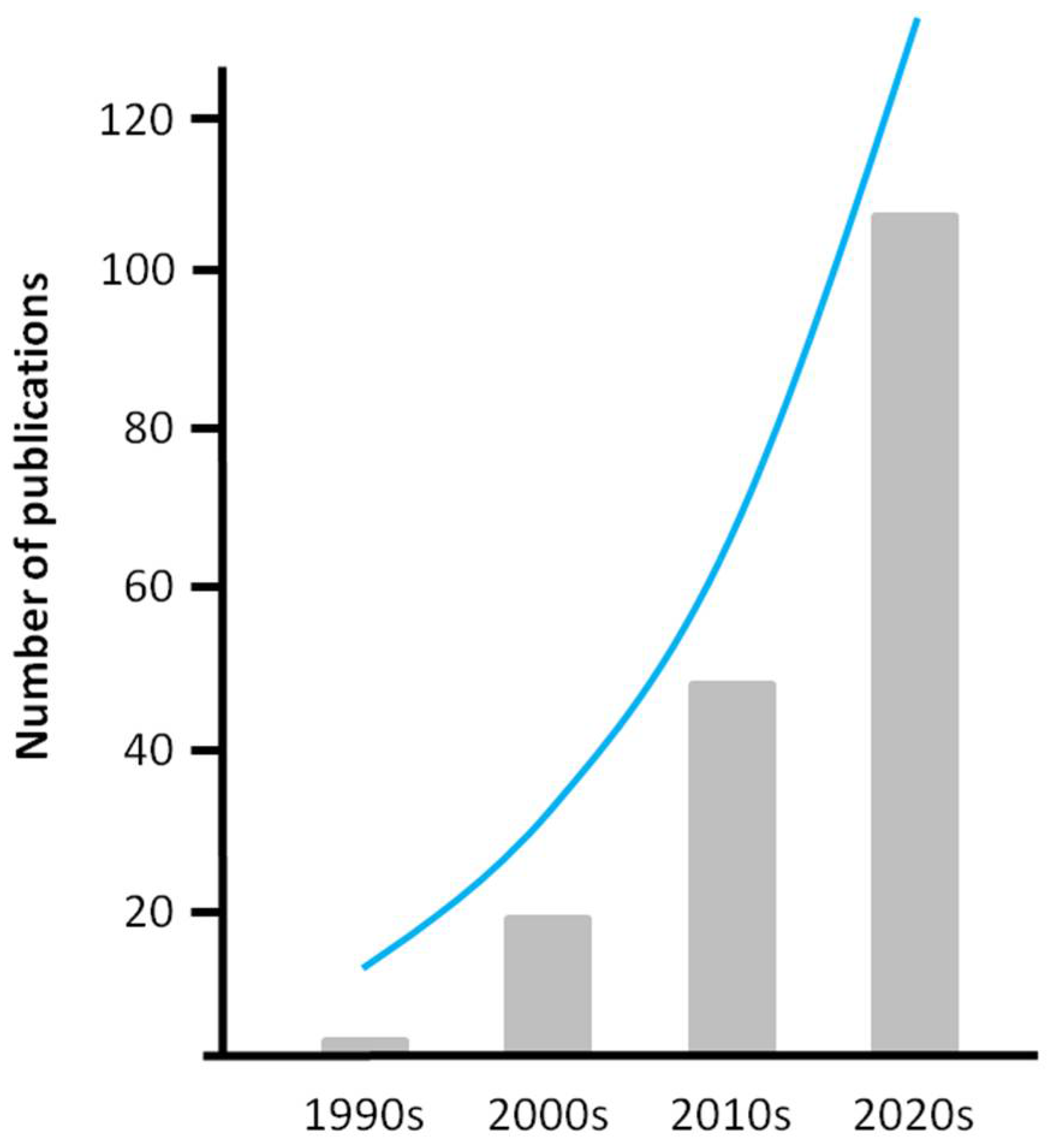
1. Introduction
2. Functional Anatomy of the Spine
3. Pathology of the Spine
3.1. Scoliosis
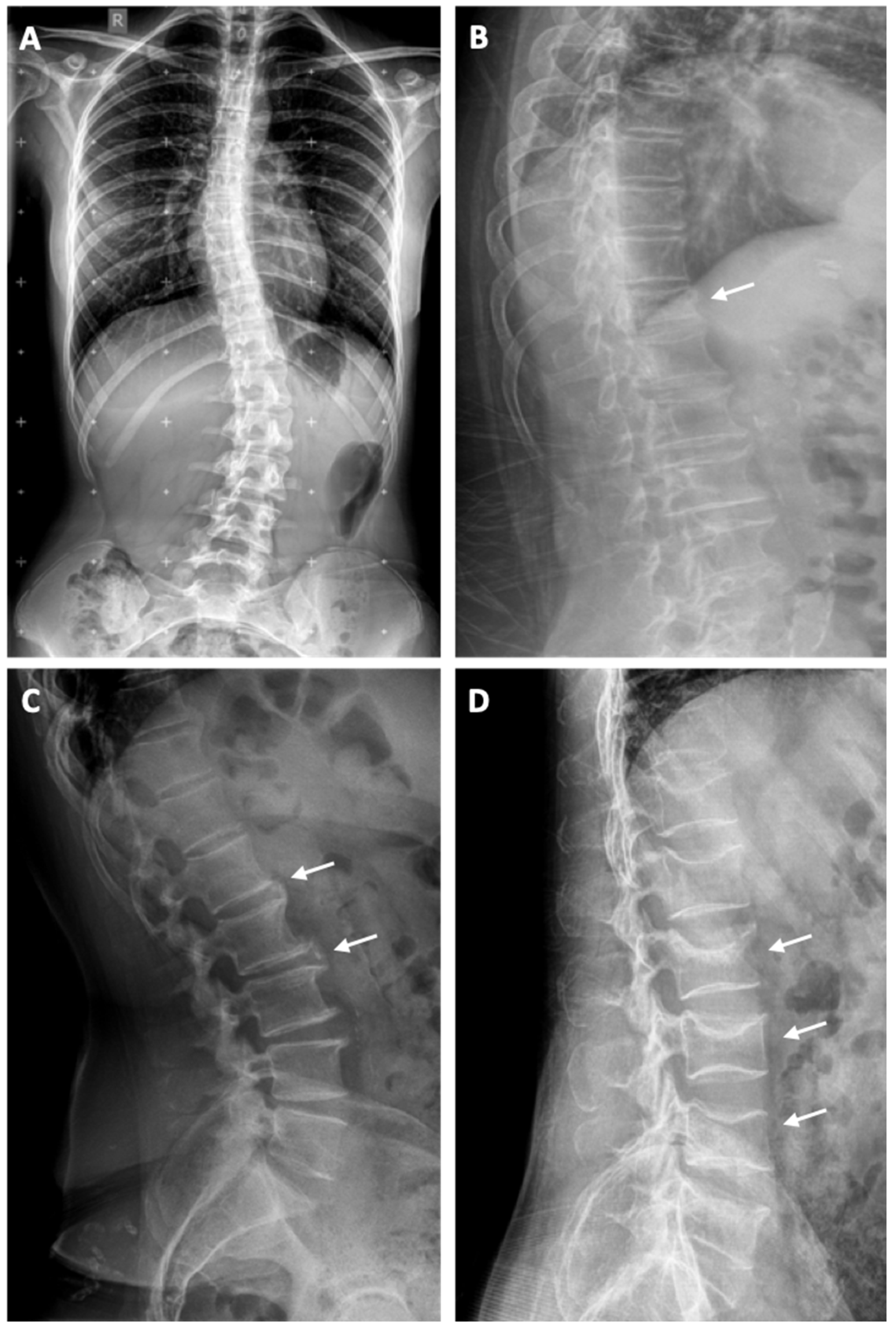
3.2. Fracture
3.3. Degenerative Disc Disease
3.4. Osteoporosis
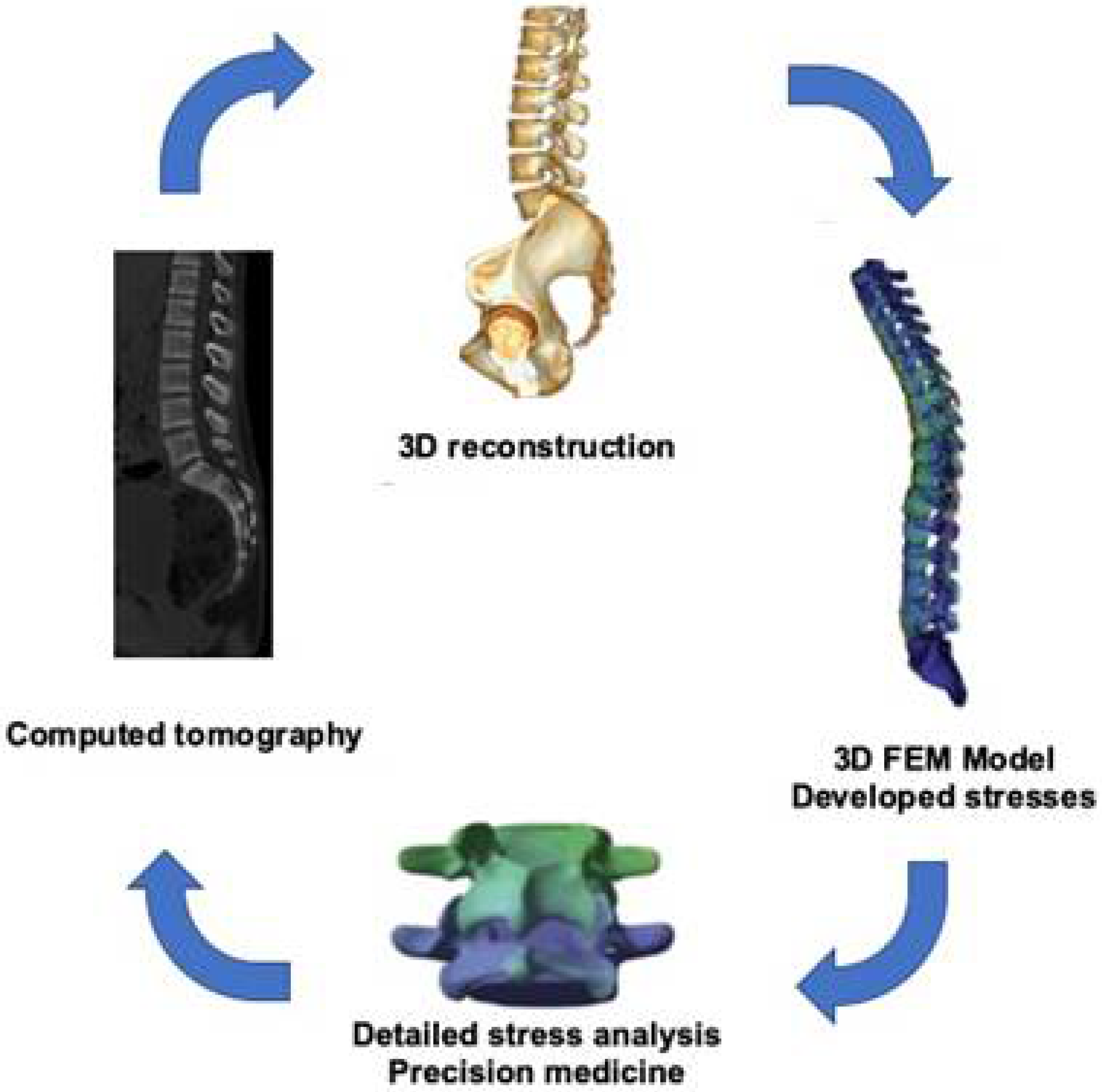
4. Application of FEM in the Spine
4.1. Scoliosis
4.2. Fracture
4.3. Degenerative Disc Disease
4.4. Osteoporosis
5. Future Development
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Holland, I. Fundamentals of the finite element method. Comput. Struct. 1974, 4, 3–15. [Google Scholar] [CrossRef]
- Welch-Phillips, A.; Gibbons, D.; Ahern, D.P.; Butler, J.S. What Is Finite Element Analysis? Clin. Spine Surg. 2020, 33, 323–324. [Google Scholar] [CrossRef]
- Benca, E.; Amini, M.; Pahr, D.H. Effect of CT imaging on the accuracy of the finite element modelling in bone. Eur. Radiol. Exp. 2020, 4, 51. [Google Scholar] [CrossRef]
- Lu, Y.; Yang, Z.; Wang, Y. A critical review on the three-dimensional finite element modelling of the compression therapy for chronic venous insufficiency. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2019, 233, 1089–1099. [Google Scholar] [CrossRef]
- Parashar, S.K.; Sharma, J.K. A review on application of finite element modeling in bone biomechanics. Perspect. Sci. 2016, 8, 696–698. [Google Scholar] [CrossRef]
- Saha, S.; Roychowdhury, A. Application of the finite element method in orthopedic implant design. J. Long Term Eff. Med. Implant. 2009, 19, 55–82. [Google Scholar]
- Fagan, M.J.; Julian, S.; Mohsen, A.M. Finite element analysis in spine research. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2002, 216, 281–298. [Google Scholar] [CrossRef] [PubMed]
- Herrera, A.; Ibarz, E.; Cegoñin, O.J.; Lobo-Escolar, A.; Puértolas, S.; López, E.; Mateo, J.; Gracia, L. Applications of finite element simulation in orthopedic and trauma surgery. World J. Orthop. 2012, 3, 25–41. [Google Scholar] [CrossRef]
- Miele, V.J.; Panjabi, M.M.; Benzel, E.C. Anatomy and biomechanics of the spinal column and cord. Handb. Clin. Neurol. 2012, 109, 31–43. [Google Scholar] [PubMed]
- Musapoor, A.; Nikkhoo, M.; Haghpanahi, M. A finite element study on intra-operative corrective forces and evaluation of screw density in scoliosis surgeries. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2018, 232, 1245–1254. [Google Scholar] [CrossRef]
- Blevins, K.; Battenberg, A.; Beck, A. Management of Scoliosis. Adv. Pediatr. 2018, 65, 249–266. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Cai, H.; Zhang, G.; Zheng, F.; Wu, C.; Lin, H. The construction of the scoliosis 3D finite element model and the biomechanical analysis of PVCR orthopaedy. Saudi J. Biol. Sci. 2020, 27, 695–700. [Google Scholar] [CrossRef]
- Looby, S.; Flanders, A. Spine trauma. Radiol. Clin. N. Am. 2011, 49, 129–163. [Google Scholar] [CrossRef]
- Kim, H.S.; Wu, P.H.; Jang, I.T. Lumbar Degenerative Disease Part 1: Anatomy and Pathophysiology of Intervertebral Discogenic Pain and Radiofrequency Ablation of Basivertebral and Sinuvertebral Nerve Treatment for Chronic Discogenic Back Pain: A Prospective Case Series and Review of Literature. Int. J. Mol. Sci. 2020, 21, 1483. [Google Scholar]
- Todd, A.G. Cervical spine: Degenerative conditions. Curr. Rev. Musculoskelet. Med. 2011, 4, 168–174. [Google Scholar] [CrossRef]
- Kamal, Z.; Rouhi, G.; Arjmand, N.; Adeeb, S. A stability-based model of a growing spine with adolescent idiopathic scoliosis: A combination of musculoskeletal and finite element approaches. Med. Eng. Phys. 2019, 64, 46–55. [Google Scholar] [CrossRef] [PubMed]
- Guan, T.; Zhang, Y.; Anwar, A.; Zhang, Y.; Wang, L. Determination of Three-Dimensional Corrective Force in Adolescent Idiopathic Scoliosis and Biomechanical Finite Element Analysis. Front. Bioeng. Biotechnol. 2020, 8, 963. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Xin, D.; Lei, Z.; Zuo, Y.; Zhao, Y. Comparative Three-Dimensional Finite Element Analysis of 4 Kinds of Pedicle Screw Schemes for Treatment of Adult Degenerative Scoliosis. Med. Sci. Monit. 2020, 26, e922050. [Google Scholar] [CrossRef] [PubMed]
- Johnston, C.B.; Dagar, M. Osteoporosis in Older Adults. Med. Clin. N. Am. 2020, 104, 873–884. [Google Scholar] [CrossRef]
- Jia, S.; Lin, L.; Yang, H.; Fan, J.; Zhang, S.; Han, L. The influence of the rib cage on the static and dynamic stability responses of the scoliotic spine. Sci. Rep. 2020, 10, 16916. [Google Scholar] [CrossRef] [PubMed]
- Haddas, R.; Xu, M.; Lieberman, I.; Yang, J. Finite Element Based-Analysis for Pre and Post Lumbar Fusion of Adult Degenerative Scoliosis Patients. Spine Deform. 2019, 7, 543–552. [Google Scholar] [CrossRef]
- Wang, W.; Baran, G.R.; Betz, R.R.; Samdani, A.F.; Pahys, J.M.; Cahill, P.J. The use of finite element models to assist understanding and treatment for scoliosis: A review paper. Spine Deform. 2014, 2, 10–27. [Google Scholar] [CrossRef]
- Basaran, R.; Efendioglu, M.; Kaksi, M.; Celik, T.; Mutlu, İ.; Ucar, M. Finite Element Analysis of Short- Versus Long-Segment Posterior Fixation for Thoracolumbar Burst Fracture. World Neurosurg. 2019, 128, e1109–e1117. [Google Scholar] [CrossRef]
- Zhu, R.; Chen, Y.H.; Yu, Q.Q.; Liu, S.Q.; Wang, J.J.; Zeng, Z.L.; Cheng, L.M. Effects of contusion load on cervical spinal cord: A finite element study. Math. Biosci. Eng. 2020, 17, 2272–2283. [Google Scholar] [CrossRef]
- Tang, X.M.; Liu, C.; Huang, K.; Zhu, G.T.; Sun, H.L.; Dai, J.; Tian, J.W. Analysis of a three-dimensional finite element model of atlas and axis complex fracture. Zhonghua Yi Xue Za Zhi 2018, 98, 1484–1488. [Google Scholar]
- Zeng, Z.L.; Zhu, R.; Li, S.Z.; Yu, Y.; Wang, J.J.; Jia, Y.W.; Chen, B.; Cheng, L.M. Formative mechanism of intracanal fracture fragments in thoracolumbar burst fractures: A finite element study. Chin. Med. J. (Engl.) 2013, 126, 2852–2858. [Google Scholar]
- Liao, J.C. Impact of Osteoporosis on Different Type of Short-Segment Posterior Instrumentation for Thoracolumbar Burst Fracture-A Finite Element Analysis. World Neurosurg. 2020, 139, e643–e651. [Google Scholar] [CrossRef] [PubMed]
- Westbury, L.D.; Shere, C.; Edwards, M.H.; Cooper, C.; Dennison, E.M.; Ward, K.A. Cluster Analysis of Finite Element Analysis and Bone Microarchitectural Parameters Identifies Phenotypes with High Fracture Risk. Calcif. Tissue Int. 2019, 105, 252–262. [Google Scholar] [CrossRef] [PubMed]
- Zhou, F.; Yang, S.; Liu, J.; Lu, J.; Shang, D.; Chen, C.; Wang, H.; Ma, J. Finite element analysis comparing short-segment instrumentation with conventional pedicle screws and the Schanz pedicle screw in lumbar 1 fractures. Neurosurg. Rev. 2020, 43, 301–312. [Google Scholar] [CrossRef]
- Nakashima, D.; Kanchiku, T.; Nishida, N.; Ito, S.; Ohgi, J.; Suzuki, H.; Imajo, Y.; Funaba, M.; Chen, X.; Taguchi, T. Finite element analysis of compression fractures at the thoracolumbar junction using models constructed from medical images. Exp. Ther. Med. 2018, 15, 3225–3230. [Google Scholar] [CrossRef]
- Diotalevi, L.; Bailly, N.; Wagnac, É.; Mac-Thiong, J.M.; Goulet, J.; Petit, Y. Dynamics of spinal cord compression with different patterns of thoracolumbar burst fractures: Numerical simulations using finite element modelling. Clin. Biomech. 2020, 72, 186–194. [Google Scholar] [CrossRef]
- Sterba, M.; Aubin, C.É.; Wagnac, E.; Fradet, L.; Arnoux, P.J. Effect of impact velocity and ligament mechanical properties on lumbar spine injuries in posterior-anterior impact loading conditions: A finite element study. Med. Biol. Eng. Comput. 2019, 57, 1381–1392. [Google Scholar] [CrossRef]
- Nishida, N.; Ohgi, J.; Jiang, F.; Ito, S.; Imajo, Y.; Suzuki, H.; Funaba, M.; Nakashima, D.; Sakai, T.; Chen, X. Finite Element Method Analysis of Compression Fractures on Whole-Spine Models Including the Rib Cage. Comput. Math. Methods Med. 2019, 2019, 8348631. [Google Scholar] [CrossRef]
- Giambini, H.; Qin, X.; Dragomir-Daescu, D.; An, K.N.; Nassr, A. Specimen-specific vertebral fracture modeling: A feasibility study using the extended finite element method. Med. Biol. Eng. Comput. 2016, 54, 583–593. [Google Scholar] [CrossRef][Green Version]
- Liu, H.; Wang, H.; Liu, J.; Li, C.; Zhou, Y.; Xiang, L. Biomechanical comparison of posterior intermediate screw fixation techniques with hybrid monoaxial and polyaxial pedicle screws in the treatment of thoracolumbar burst fracture: A finite element study. J. Orthop. Surg. Res. 2019, 14, 122. [Google Scholar] [CrossRef]
- Guo, L.X.; Li, W.J. A biomechanical investigation of thoracolumbar burst fracture under vertical impact loads using finite element method. Clin. Biomech. 2019, 68, 29–36. [Google Scholar] [CrossRef]
- Bashkuev, M.; Reitmaier, S.; Schmidt, H. Relationship between intervertebral disc and facet joint degeneration: A probabilistic finite element model study. J. Biomech. 2020, 102, 109518. [Google Scholar] [CrossRef]
- Fan, W.; Guo, L.X. The influence of bilateral pedicle screw fixation on vibration response of the disc degenerated human lumbar spine: A finite element stress analysis. Technol. Health Care 2019, 27, 441–450. [Google Scholar] [CrossRef]
- Guan, W.; Sun, Y.; Qi, X.; Hu, Y.; Duan, C.; Tao, H.; Yang, X. Spinal biomechanics modeling and finite element analysis of surgical instrument interaction. Comput. Assist. Surg. 2019, 24 (Suppl. 1), 151–159. [Google Scholar] [CrossRef]
- Cao, L.; Liu, Y.; Mei, W.; Xu, J.; Zhan, S. Biomechanical changes of degenerated adjacent segment and intact lumbar spine after lumbosacral topping-off surgery: A three-dimensional finite element analysis. BMC Musculoskelet. Disord. 2020, 21, 104. [Google Scholar] [CrossRef]
- Wang, H.H.; Wang, K.; Deng, Z.; Li, X.F.; Qin, Y.X.; Zhan, H.S.; Niu, W.X. Effects of facet joint degeneration on stress alterations in cervical spine C5–C6: A finite element analysis. Math. Biosci. Eng. 2019, 16, 7447–7457. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Yuchi, C.X.; Gao, Z.; Ma, X.; Zhao, D.; Li, J.W.; Xu, B.; Zhang, C.Q.; Wang, Z.; Du, C.F.; et al. Comparative analysis of the biomechanics of the adjacent segments after minimally invasive cervical surgeries versus anterior cervical discectomy and fusion: A finite element study. J. Orthop. Transl. 2020, 23, 107–112. [Google Scholar] [CrossRef]
- Mengoni, M. Biomechanical modelling of the facet joints: A review of methods and validation processes in finite element analysis. Biomech. Model. Mechanobiol. 2021, 20, 389–401. [Google Scholar] [CrossRef]
- Manickam, P.S.; Roy, S. The biomechanical study of cervical spine: A Finite Element Analysis. Int. J. Artif. Organs 2021, 2021. [Google Scholar] [CrossRef]
- Gandhi, A.A.; Grosland, N.M.; Kallemeyn, N.A.; Kode, S.; Fredericks, D.C.; Smucker, J.D. Biomechanical Analysis of the Cervical Spine Following Disc Degeneration, Disc Fusion, and Disc Replacement: A Finite Element Study. Int. J. Spine Surg. 2019, 13, 491–500. [Google Scholar] [CrossRef]
- Cai, X.Y.; Sang, D.; Yuchi, C.X.; Cui, W.; Zhang, C.; Du, C.F.; Liu, B. Using finite element analysis to determine effects of the motion loading method on facet joint forces after cervical disc degeneration. Comput. Biol. Med. 2020, 116, 103519. [Google Scholar] [CrossRef] [PubMed]
- Jain, P.; Khan, M.R. Selection of suitable pedicle screw for degenerated cortical and cancellous bone of human lumbar spine: A finite element study. Int. J. Artif. Organs 2021, 44, 361–366. [Google Scholar] [CrossRef]
- Cai, X.Y.; Sun, M.S.; Huang, Y.P.; Liu, Z.X.; Liu, C.-J.; Du, C.-F.; Yang, Q. Biomechanical Effect of L4–L5 Intervertebral Disc Degeneration on the Lower Lumbar Spine: A Finite Element Study. Orthop. Surg. 2020, 12, 917–930. [Google Scholar] [CrossRef]
- Sun, X.; Sun, S.; Zhang, T.; Kong, C.; Wang, W.; Lu, S. Biomechanical comparison of noncontiguous cervical disc arthroplasty and noncontiguous cervical discectomy and fusion in the treatment of noncontinuous cervical degenerative disc disease: A finite element analysis. J. Orthop. Surg. Res. 2020, 15, 36. [Google Scholar] [CrossRef]
- Li, Z.; Liu, H.; Yang, M.; Zhang, W. A biomechanical analysis of four anterior cervical techniques to treating multilevel cervical spondylotic myelopathy: A finite element study. BMC Musculoskelet. Disord. 2021, 22, 278. [Google Scholar]
- Ouyang, P.; Li, J.; He, X.; Dong, H.; Zang, Q.; Li, H.; Jin, Z. Biomechanical Comparison of 1-Level Corpectomy and 2-Level Discectomy for Cervical Spondylotic Myelopathy: A Finite Element Analysis. Med. Sci. Monit. 2020, 26, e919270. [Google Scholar] [CrossRef]
- Stoner, K.E.; Abode-Iyamah, K.O.; Fredericks, D.C.; Viljoen, S.; Howard, M.A.; Grosland, N.M. A comprehensive finite element model of surgical treatment for cervical myelopathy. Clin. Biomech. 2020, 74, 79–86. [Google Scholar] [CrossRef]
- Wang, X.D.; Feng, M.S.; Hu, Y.C. Establishment and Finite Element Analysis of a Three-dimensional Dynamic Model of Upper Cervical Spine Instability. Orthop. Surg. 2019, 11, 500–509. [Google Scholar] [CrossRef] [PubMed]
- Hu, B.W.; Lv, X.; Chen, S.F.; Shao, Z.W. Application of Finite Element Analysis for Investigation of Intervertebral Disc Degeneration: From Laboratory to Clinic. Curr. Med. Sci. 2019, 39, 7–15. [Google Scholar] [CrossRef]
- Imai, K. Computed tomography-based finite element analysis to assess fracture risk and osteoporosis treatment. World J. Exp. Med. 2015, 5, 182–187. [Google Scholar] [CrossRef]
- Zhang, W.; Zhao, J.; Li, L.; Yu, C.; Zhao, Y.; Si, H. Modelling tri-cortical pedicle screw fixation in thoracic vertebrae under osteoporotic condition: A finite element analysis based on computed tomography. Comput. Methods Programs Biomed. 2020, 187, 105035. [Google Scholar] [CrossRef] [PubMed]
- Guo, H.Z.; Guo, D.Q.; Tang, Y.C.; Liang, D.; Zhang, S.C. Selective cement augmentation of cranial and caudal pedicle screws provides comparable stability to augmentation on all segments in the osteoporotic spine: A finite element analysis. Ann. Transl. Med. 2020, 8, 1384. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Li, Y.; Yin, H.; Li, J.; Qu, J.; Jiang, M.; Tian, J. Three-Dimensional finite element analysis of optimal distribution model of vertebroplasty. Ann. Palliat. Med. 2020, 9, 1062–1072. [Google Scholar] [CrossRef] [PubMed]
- Fei, Q.; Li, Q.J.; Yang, Y.; Li, D.; Tang, H.; Li, J.J.; Wang, B.Q.; Wang, Y.P. Three-dimensional finite element model of thoracolumbar spine with osteoporotic vertebral compression fracture. Zhonghua Yi Xue Za Zhi 2010, 90, 2943–2946. [Google Scholar]
- Wang, T.; Zhao, Y.; Cai, Z.; Wang, W.; Xia, Y.; Zheng, G.; Liang, Y.; Wang, Y. Effect of osteoporosis on internal fixation after spinal osteotomy: A finite element analysis. Clin. Biomech. 2019, 69, 178–183. [Google Scholar] [CrossRef] [PubMed]
- Zysset, P.; Qin, L.; Lang, T.; Khosla, S.; Leslie, W.D.; Shepherd, J.A.; Schousboe, J.T.; Engelke, K. Clinical Use of Quantitative Computed Tomography-Based Finite Element Analysis of the Hip and Spine in the Management of Osteoporosis in Adults: The 2015 ISCD Official Positions-Part II. J. Clin. Densitom. 2015, 18, 359–392. [Google Scholar] [CrossRef]
- John, J.D.; Kumar, G.S.; Yoganandan, N. Cervical spine morphology and ligament property variations: A finite element study of their influence on sagittal bending characteristics. J. Biomech. 2019, 85, 18–26. [Google Scholar] [CrossRef] [PubMed]
- Rayudu, N.M.; Dieckmeyer, M.; Löffler, M.T.; Noël, P.B.; Kirschke, J.S.; Baum, T.; Subburaj, K. Predicting Vertebral Bone Strength Using Finite Element Analysis for Opportunistic Osteoporosis Screening in Routine Multidetector Computed Tomography Scans-A Feasibility Study. Front. Endocrinol. 2021, 11, 526332. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Shi, J.; Chang, M.; Yuan, X.; Zhang, R.; Huang, H.; Tang, S. Does Osteoporosis Affect the Adjacent Segments Following Anterior Lumbar Interbody Fusion? A Finite Element Study. World Neurosurg. 2021, 146, e739–e746. [Google Scholar] [CrossRef] [PubMed]
- Allaire, B.T.; Lu, D.; Johannesdottir, F.; Kopperdahl, D.; Keaveny, T.M.; Jarraya, M.; Guermazi, A.; Bredella, M.A.; Samelson, E.J.; Kiel, D.P.; et al. Prediction of incident vertebral fracture using CT-based finite element analysis. Osteoporos. Int. 2019, 30, 323–331. [Google Scholar] [CrossRef]
- Anitha, D.P.; Baum, T.; Kirschke, J.S.; Subburaj, K. Effect of the intervertebral disc on vertebral bone strength prediction: A finite-element study. Spine J. 2020, 20, 665–671. [Google Scholar] [CrossRef]
- Ono, K.; Ohashi, S.; Oka, H.; Kadono, Y.; Yasui, T.; Matsumoto, T.; Omata, Y.; Tanaka, S. Evaluations of daily teriparatide using finite-element analysis over 12 months in rheumatoid arthritis patients. J. Bone Miner. Metab. 2021, 39, 270–277. [Google Scholar] [CrossRef] [PubMed]
- Matsukawa, K.; Yato, Y.; Imabayashi, H. Impact of Screw Diameter and Length on Pedicle Screw Fixation Strength in Osteoporotic Vertebrae: A Finite Element Analysis. Asian Spine J. 2020, 20, 665–671. [Google Scholar]
- Wu, Y.; Chen, C.H.; Tsuang, F.Y.; Lin, Y.C.; Chiang, C.J.; Kuo, Y.J. The stability of long-segment and short-segment fixation for treating severe burst fractures at the thoracolumbar junction in osteoporotic bone: A finite element analysis. PLoS ONE 2019, 14, e0211676. [Google Scholar] [CrossRef]
- Sawa, A.G.U.; Lehrman, J.N.; Crawford, N.R.; Kelly, B.P. Variations Among Human Lumbar Spine Segments and Their Relationships to In Vitro Biomechanics: A Retrospective Analysis of 281 Motion Segments From 85 Cadaveric Spines. Int. J. Spine Surg. 2020, 14, 140–150. [Google Scholar] [CrossRef]
- Lafon, Y.; Lafage, V.; Steib, J.P.; Dubousset, J.; Skalli, W. In vivo distribution of spinal intervertebral stiffness based on clinical flexibility tests. Spine 2010, 35, 186–193. [Google Scholar] [CrossRef] [PubMed]
- Calvo-Echenique, A.; Cegoñino, J.; Chueca, R.; Palomar, A.P.-D. Stand-Alone lumbar cage subsidence: A biomechanical sensitivity study of cage design and placement. Comput. Methods Programs Biomed. 2018, 162, 211–219. [Google Scholar] [CrossRef] [PubMed]
- Bohn, T.; Lang, S.A.J.; Roll, S.; Schrader, H.; Pumberger, M.; Büttner-Janz, K. Meta-analyses comparing spine simulators with cadavers and finite element models by analysing range-of-motion data before and after lumbar total disc replacement. J. Adv. Res. 2020, 26, 29–41. [Google Scholar] [CrossRef] [PubMed]
- Sun, M.S.; Cai, X.Y.; Liu, Q.; Du, C.F.; Mo, Z.J. Application of Simulation Methods in Cervical Spine Dynamics. J. Health Eng. 2020, 2020, 7289648. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Khuyagbaatar, B.; Kim, K. Recent advances in finite element modeling of the human cervical spine. J. Mech. Sci. Technol. 2018, 32, 1–10. [Google Scholar] [CrossRef]
- Martínez, J.; Casanova, E.; Graciano, C.; Estrada, O.A. Sensitivity analysis of a member under compression via Monte Carlo method. Rev. UIS Ing. 2018, 17, 179–184. [Google Scholar] [CrossRef]
- Stadelmann, M.A.; Stocker, R.; Maquer, G.; Hoppe, S.; Vermathen, P.; Alkalay, R.N.; Zysset, P.K. Finite element models can reproduce the effect of nucleotomy on the multi-axial compliance of human intervertebral discs. Comput. Methods Biomech. Biomed. Eng. 2020, 23, 934–944. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.; Han, Z.; Hu, B.; Du, C.; Xing, Z.; Zhang, C.; Gao, J.; Shan, B.; Chen, C. A graphical guide for constructing a finite element model of the cervical spine with digital orthopedic software. Ann. Transl. Med. 2021, 9, 169. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naoum, S.; Vasiliadis, A.V.; Koutserimpas, C.; Mylonakis, N.; Kotsapas, M.; Katakalos, K. Finite Element Method for the Evaluation of the Human Spine: A Literature Overview. J. Funct. Biomater. 2021, 12, 43. https://doi.org/10.3390/jfb12030043
Naoum S, Vasiliadis AV, Koutserimpas C, Mylonakis N, Kotsapas M, Katakalos K. Finite Element Method for the Evaluation of the Human Spine: A Literature Overview. Journal of Functional Biomaterials. 2021; 12(3):43. https://doi.org/10.3390/jfb12030043
Chicago/Turabian StyleNaoum, Symeon, Angelo V. Vasiliadis, Christos Koutserimpas, Nikolaos Mylonakis, Michail Kotsapas, and Konstantinos Katakalos. 2021. "Finite Element Method for the Evaluation of the Human Spine: A Literature Overview" Journal of Functional Biomaterials 12, no. 3: 43. https://doi.org/10.3390/jfb12030043
APA StyleNaoum, S., Vasiliadis, A. V., Koutserimpas, C., Mylonakis, N., Kotsapas, M., & Katakalos, K. (2021). Finite Element Method for the Evaluation of the Human Spine: A Literature Overview. Journal of Functional Biomaterials, 12(3), 43. https://doi.org/10.3390/jfb12030043







