Effect Sizes, Power, and Biases in Intelligence Research: A Meta-Meta-Analysis
Abstract
1. Introduction
2. Method
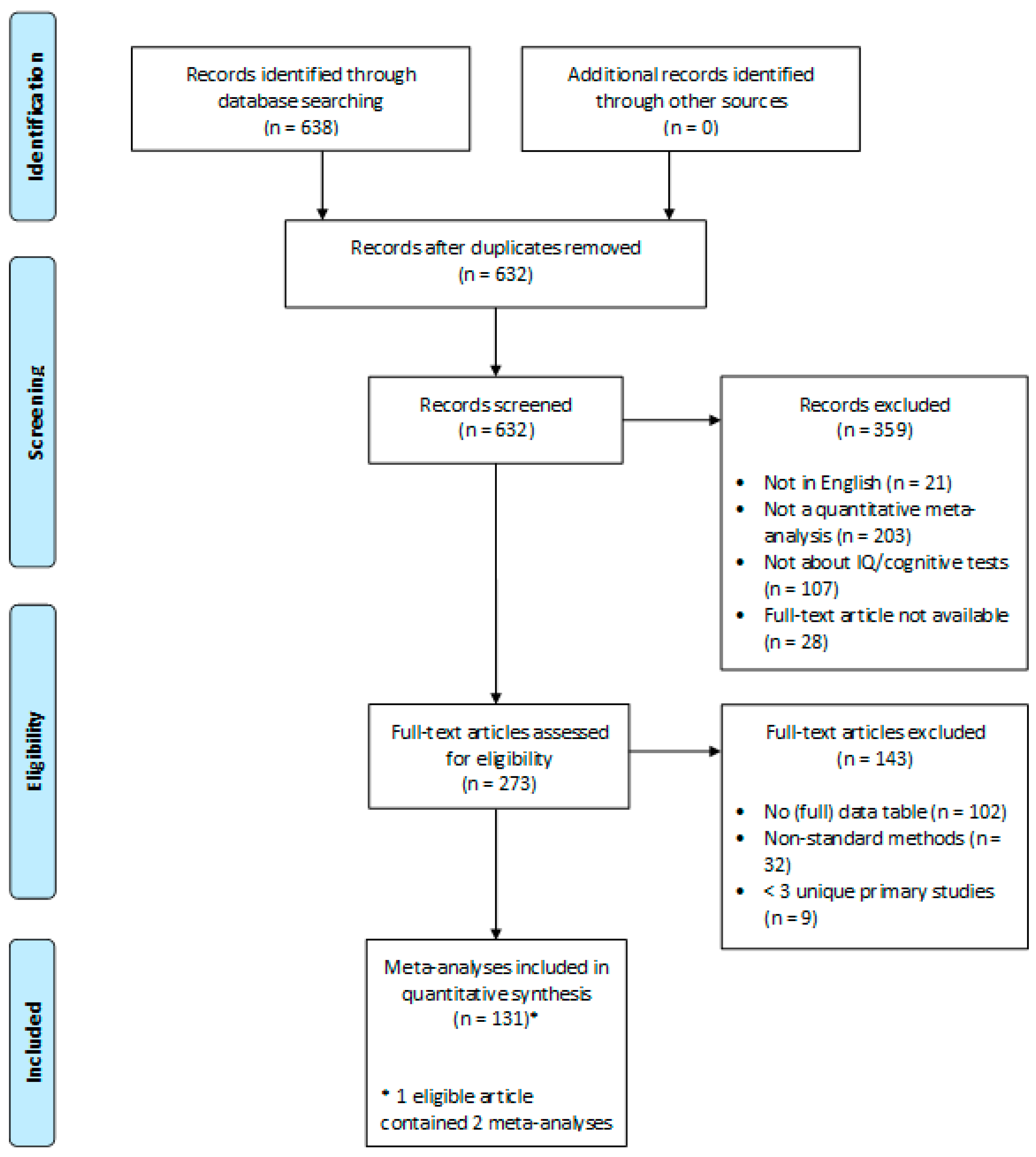
2.1. Sample
2.2. Procedure
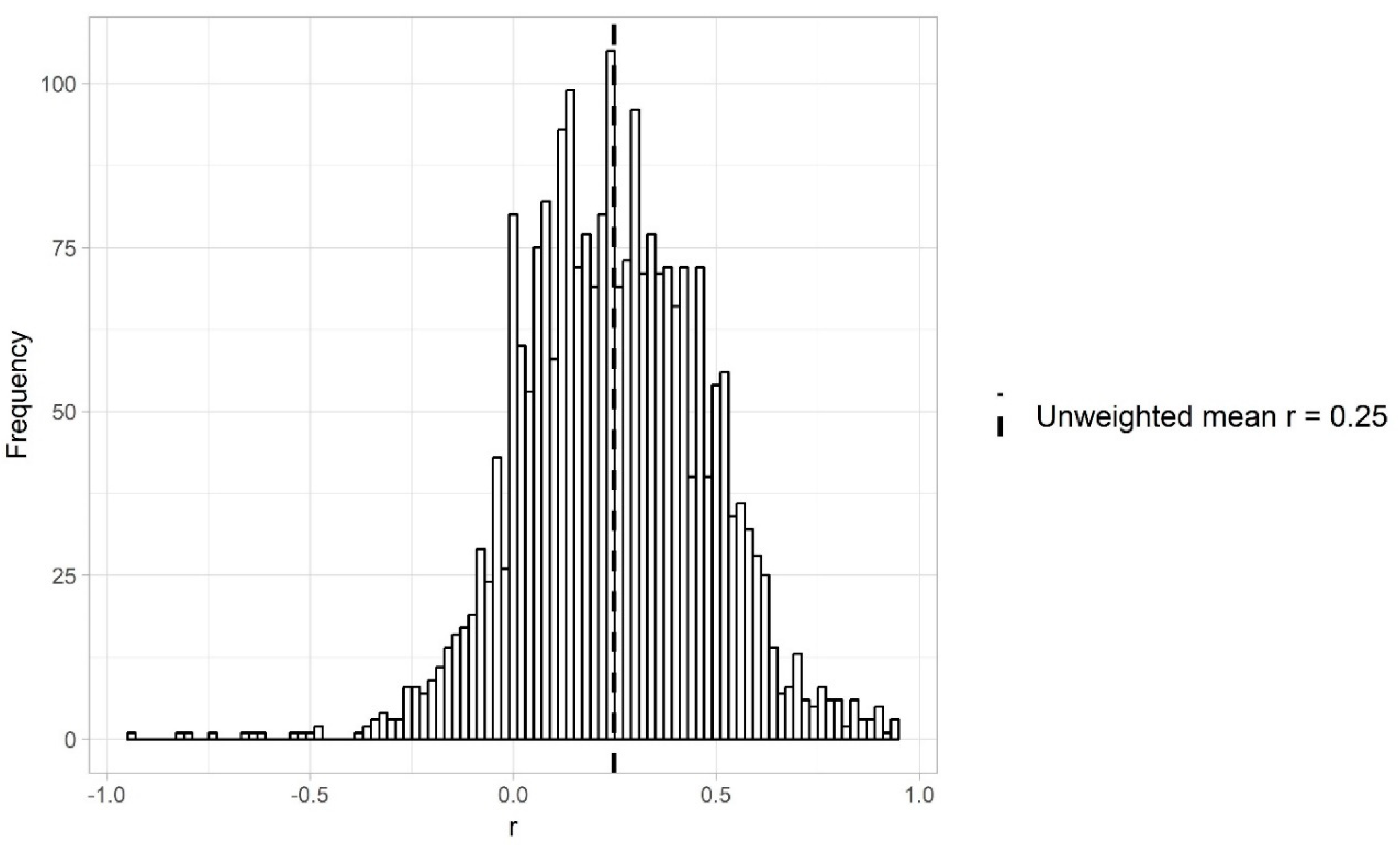
3. Effect Sizes in Intelligence Research
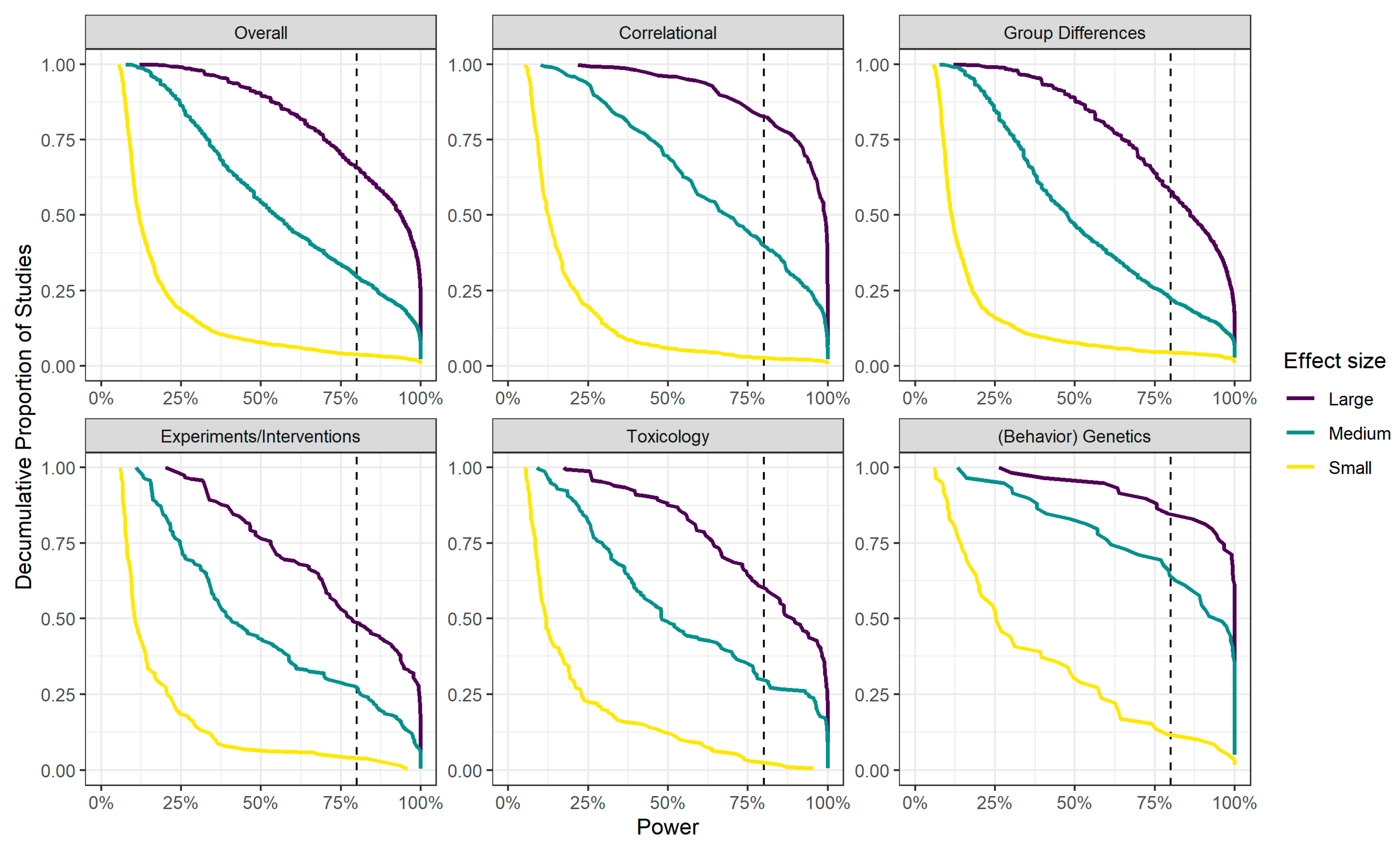
4. Power in Intelligence Research
5. Bias-Related Patterns in Effect Sizes
5.1. Two-Step Meta-Regression
5.2. Results of Small-Study Effect
5.3. Other Bias-Related Patterns
6. Discussion
6.1. Limitations
6.1.1. Sample
6.1.2. Analyses
6.2. Conclusion and Recommendations
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Agnoli, Franca, Jelte M. Wicherts, Coosje L. S. Veldkamp, Paolo Albiero, and Roberto Cubelli. 2017. Questionable research practices among Italian research psychologists. PLoS ONE 12: 1–17. [Google Scholar] [CrossRef] [PubMed]
- Anderson, Samantha F., Ken Kelley, and Scott E. Maxwell. 2017. Sample-size planning for more accurate statistical power: A method adjusting sample effect sizes for publication bias and uncertainty. Psychological Science 28: 1547–62. [Google Scholar] [CrossRef] [PubMed]
- Asendorpf, Jens B., Mark Conner, Filip De Fruyt, Jan De Houwer, Jaap J. A. Denissen, Klaus Fiedler, Susann Fiedler, David C. Funder, Reinhold Kliegl, Brian A. Nosek, and et al. 2013. Recommendations for increasing replicability in psychology. European Journal of Personality 27: 108–19. [Google Scholar] [CrossRef]
- Aylward, Elizabeth, Elaine Walker, and Barbara Bettes. 1984. Intelligence in schizophrenia: Meta-analysis of the research. Schizophrenia Bulletin 10: 430–59. [Google Scholar] [CrossRef]
- Baker, Monya. 2016. 1500 scientists lift the lid on reproducibility. Nature News 533: 452. [Google Scholar] [CrossRef]
- Bakermans-Kranenburg, Marian J., Marinus H. van IJzendoorn, and Femmie Juffer. 2008. Earlier is better: A meta-analysis of 70 years of intervention improving cognitive development in institutionalized children. Monographs of the Society for Research in Child Development 73: 279–93. [Google Scholar] [CrossRef]
- Bakker, Marjan, and Jelte M. Wicherts. 2011. The (mis)reporting of statistical results in psychology journals. Behavior Research Methods 43: 666–78. [Google Scholar] [CrossRef]
- Bakker, Marjan, Annette van Dijk, and Jelte M. Wicherts. 2012. The rules of the game called psychological science. Perspectives on Psychological Science 7: 543–54. [Google Scholar] [CrossRef]
- Beaujean, A. Alexander. 2005. Heritability of cognitive abilities as measured by mental chronometric tasks: A meta-analysis. Intelligence 33: 187–201. [Google Scholar] [CrossRef]
- Binet, Alfred, and Th Simon. 1905. New methods for the diagnosis of the intellectual level of subnormals. L’annee Psychologique 12: 191–244. [Google Scholar]
- Borenstein, Michael, L. V. Hedges, J. P. T. Higgins, and H. R. Rothstein. 2009a. Random-effects model. In Introduction to Meta-Analysis. Edited by Michael Borenstein, L. V. Hedges, J. P. T. Higgins and H. R. Rothstein. New York: Wiley, pp. 69–76. [Google Scholar]
- Borenstein, Michael, L. V. Hedges, J. P. T. Higgins, and H. R. Rothstein. 2009b. Fixed-effect versus random-effects models. In Introduction to Meta-Analysis. Edited by Michael Borenstein, L. V. Hedges, J. P. T. Higgins and H. R. Rothstein. New York: Wiley, pp. 77–86. [Google Scholar]
- Brandt, Mark J., Hans IJzerman, Ap Dijksterhuis, Frank J. Farach, Jason Geller, Roger Giner-Sorolla, James A. Grange, Marco Perugini, Jeffrey R. Spies, and Anna Van’t Veer. 2014. The replication recipe: What makes for a convincing replication? Journal of Experimental Social Psychology 50: 217–24. [Google Scholar] [CrossRef]
- Button, Katherine S., John P. A. Ioannidis, Claire Mokrysz, Brian A. Nosek, Jonathan Flint, Emma S. J. Robinson, and Marcus R. Munafo. 2013. Power failure: Why small sample size undermines the reliability of neuroscience. Nature Reviews Neuroscience 14: 1–12. [Google Scholar] [CrossRef]
- Carlisle, James C., Kathryn C. Dowling, David M. Siegel, and George V. Alexeeff. 2009. A blood lead benchmark for assessing risks from childhood lead exposure. Journal of Environmental Science and Health Part a-Toxic/Hazardous Substances & Environmental Engineering 44: 1200–08. [Google Scholar] [CrossRef]
- Carroll, John B. 1993. Human Cognitive Abilities: A Survey of Factor-Analytic Studies. New York: Cambridge University Press. [Google Scholar]
- Chambers, Chris, and Marcus Munafo. 2013. Trust in Science Would Be Improved by Study Pre-Registration. Available online: http://www.theguardian.com/science/blog/2013/jun/05/trust-in-science-study-pre-registration (accessed on 25 September 2020).
- Champely, Stephane. 2017. Pwr: Basic Functions for Power Analysis. R Package Version 1.2–1. Available online: https://CRAN.R-project.org/package=pwr (accessed on 25 September 2020).
- Christensen-Szalanski, Jay J. J., and Lee Roy Beach. 1984. The citation bias: Fad and fashion in the judgment and decision literature. American Psychologist 39: 75–78. [Google Scholar] [CrossRef]
- Cohen, Jacob. 1962. The statistical power of abnormal-social psychological research: A review. The Journal of Abnormal and Social Psychology 65: 145–53. [Google Scholar] [CrossRef]
- Cohn, Lawrence D., and P. Michiel Westenberg. 2004. Intelligence and maturity: Meta-analytic evidence for the incremental and discriminant validity of Loevinger’s measure of ego development. Journal of Personality and Social Psychology 86: 760–72. [Google Scholar] [CrossRef]
- Dickersin, Kay. 2005. Publication bias: Recognizing the problem, understanding its origins and scope, and preventing harm. In Publication Bias in Meta-Analysis: Prevention, Assessment and Adjustments. Edited by Hannah R. Rothstein, Alexander J Sutton and Michael Borenstein. New York: Wiley, pp. 11–33. [Google Scholar]
- Doucouliagos, Hristos, Patrice Laroche, and Tom D. Stanley. 2005. Publication bias in union-productivity research? Relations Industrielles/Industrial Relations 60: 320–47. [Google Scholar] [CrossRef]
- Duyx, Bram, Miriam J. E. Urlings, Gerard M. H. Swaen, Lex M. Bouter, and Maurice P. Zeegers. 2017. Scientific citations favor positive results: A systematic review and meta-analysis. Journal of Clinical Epidemiology 88: 92–101. [Google Scholar] [CrossRef]
- Eerland, Anita, Andrew M. Sherrill, Joseph P. Magliano, Rolf A. Zwaan, J. D. Arnal, Philip Aucoin, Stephanie A. Berger, A. R. Birt, Nicole Capezza, and Marianna Carlucci. 2016. Registered replication report: Hart & Albarracín (2011). Perspectives on Psychological Science 11: 158–71. [Google Scholar] [CrossRef]
- Ellis, Paul D. 2010. The Essential Guide to Effect Sizes: Statistical Power, Meta-Analysis, and the Interpretation of Research Results. New York: Cambridge University Press. [Google Scholar]
- Falkingham, Martin, Asmaa Abdelhamid, Peter Curtis, Susan Fairweather-Tait, Louise Dye, and Lee Hooper. 2010. The effects of oral iron supplementation on cognition in older children and adults: A systematic review and meta-analysis. Nutrition Journal 9: 4. [Google Scholar] [CrossRef]
- Fanelli, Daniele. 2010. “Positive” results increase down the hierarchy of the sciences. PLoS ONE 5: e10068. [Google Scholar] [CrossRef] [PubMed]
- Fanelli, Daniele, and John P. A. Ioannidis. 2013. US studies may overestimate effect sizes in softer research. Proceedings of the National Academy of Sciences of the United States of America 110: 15031–36. [Google Scholar] [CrossRef] [PubMed]
- Fanelli, Daniele, and John P. A. Ioannidis. 2014. Reanalyses actually confirm that US studies overestimate effects in softer research. Proceedings of the National Academy of Sciences the United States of America 1117: E714–15. [Google Scholar] [CrossRef]
- Fanelli, Daniele, Rodrigo Costas, and John P. A. Ioannidis. 2017. Meta-assessment of bias in science. Proceedings of the National Academy of Sciences the United States of America 114: 3714–19. [Google Scholar] [CrossRef]
- Fiedler, Klaus, and Norbert Schwarz. 2016. Questionable research practices revisited. Social Psychological and Personality Science 7: 45–52. [Google Scholar] [CrossRef]
- Fraley, R. Chris, and Simine Vazire. 2014. The N-pact factor: Evaluating the quality of empirical journals with respect to sample size and statistical power. PLoS ONE 9: e109019. [Google Scholar] [CrossRef]
- Francis, Gregory. 2014. The frequency of excess success for articles in psychological science. Psychonomic Bulletin & Review 21: 1180–87. [Google Scholar] [CrossRef]
- Franco, Annie, Neil Malhotra, and Gabor Simonovits. 2014. Publication bias in the social sciences: Unlocking the file drawer. Science 345: 1502–05. [Google Scholar] [CrossRef]
- Freund, Philipp Alexander, and Nadine Kasten. 2012. How smart do you think you are? A meta-analysis on the validity of self-estimates of cognitive ability. Psychological Bulletin 138: 296–321. [Google Scholar] [CrossRef]
- Gignac, Gilles E., and Eva T. Szodorai. 2016. Effect size guidelines for individual differences researchers. Personality and Individual Differences 102: 74–78. [Google Scholar] [CrossRef]
- Glass, Gene V., Mary Lee Smith, and Barry McGaw. 1981. Meta-Analysis in Social Research. Beverly Hills: Sage Publications, Incorporated. [Google Scholar]
- Gøtzsche, Peter C., Asbjørn Hróbjartsson, Katja Marić, and Britta Tendal Tendal. 2007. Data extraction errors in meta-analyses that use standardized mean differences. Journal of the American Medical Association 298: 430–37. [Google Scholar] [CrossRef] [PubMed]
- Greenwald, Anthony G. 1975. Consequences of prejudice against the null hypothesis. Psychological Bulletin 82: 1–20. [Google Scholar] [CrossRef]
- Hagger, Martin S., Nikos L. D. Chatzisarantis, Hugo Alberts, Calvin Octavianus Anggono, Cédric Batailler, Angela R. Birt, Ralf Brand, Mark J. Brandt, Gene Brewer, Sabrina Bruyneel, and et al. 2016. A multilab preregistered replication of the ego-depletion effect. Perspectives on Psychological Science 11: 546–73. [Google Scholar] [CrossRef]
- Hartgerink, Chris H. J., Jelte M. Wicherts, and M. A. L. M. Van Assen. 2017. Too good to be false: Non-significant results revisited. Collabra: Psychology 3: 1–18. [Google Scholar] [CrossRef]
- Hunt, Earl. 2010. Human intelligence. New York: Cambridge University Press. [Google Scholar]
- Ioannidis, John P. A. 1998. Effect of the statistical significance of results on the time to completion and publication of randomized efficacy trials. Journal of the American Medical Association 279: 281–86. [Google Scholar] [CrossRef] [PubMed]
- Ioannidis, John P. A., Evangelia E. Ntzani, Thomas A. Trikalinos, and Despina G. Contopoulos-Ioannidis. 2001. Replication validity of genetic association studies. Nature Genetics 29: 306–9. [Google Scholar] [CrossRef]
- Ioannidis, John P. A. 2005. Why most published research findings are false. PLoS Medicine 2: e124. [Google Scholar] [CrossRef]
- Ioannidis, John P. A., and Thomas A. Trikalinos. 2005. Early extreme contradictory estimates may appear in published research: The Proteus phenomenon in molecular genetics research and randomized trials. Journal of Clinical Epidemiology 58: 543–49. [Google Scholar] [CrossRef]
- Ioannidis, John P. A. 2016. The mass production of redundant, misleading, and conflicted systematic reviews and meta-analyses. The Milbank Quarterly 94: 485–514. [Google Scholar] [CrossRef]
- Ioannidis, John P. A., Tom D. Stanley, and Hristos Doucouliagos. 2017. The power of bias in economics research. The Economic Journal 127: F236–F265. [Google Scholar] [CrossRef]
- Irwing, Paul, and Richard Lynn. 2005. Sex differences in means and variability on the progressive matrices in university students: A meta-analysis. British Journal of Psychology 96: 505–24. [Google Scholar] [CrossRef] [PubMed]
- Jannot, Anne-Sophie, Thomas Agoritsas, Angèle Gayet-Ageron, and Thomas V. Perneger. 2013. Citation bias favoring statistically significant studies was present in medical research. Journal of Clinical Epidemiology 66: 296–301. [Google Scholar] [CrossRef] [PubMed]
- Jennions, Michael D., and Anders P. Moeller. 2002. Publication bias in ecology and evolution: An empirical assessment using the trim and fill method. Biological Reviews 77: 211–22. [Google Scholar] [CrossRef] [PubMed]
- Jennions, Michael D., and Anders P. Moeller. 2003. A survey of the statistical power of research in behavioral ecology and animal behavior. Behavioral Ecology 14: 438–45. [Google Scholar] [CrossRef]
- John, Leslie K., George Loewenstein, and Drazen Prelec. 2012. Measuring the prevalence of questionable research practices with incentives for truth-telling. Psychological Science 23: 524–32. [Google Scholar] [CrossRef]
- Kenny, David A., and Charles M. Judd. 2019. The unappreciated heterogeneity of effect sizes: Implications for power, precision, planning of research, and replication. Psychological Methods 24: 578. [Google Scholar] [CrossRef]
- Klein, Richard A., Kate A. Ratliff, Michelangelo Vianello, Reginald B. Adams, Jr., Štěpán Bahník, Michael J. Bernstein, Konrad Bocian, Mark J. Brandt, Beach Brooks, Claudia Chloe Brumbaugh, and et al. 2014. Investigating variation in replicability: A “Many Labs” Replication Project. Social Psychology 45: 142–52. [Google Scholar] [CrossRef]
- Kraemer, Helena Chmura, Christopher Gardner, John O. Brooks, III, and Jerome A. Yesavage. 1998. Advantages of excluding underpowered studies in meta-analysis: Inclusionist versus exclusionist viewpoints. Psychological Methods 3: 23–31. [Google Scholar] [CrossRef]
- Kvarven, Amanda, Eirik Strømland, and Magnus Johannesson. 2019. Comparing meta-analyses and preregistered multiple-laboratory replication projects. Nature Human Behaviour, 1–12. [Google Scholar] [CrossRef]
- Langan, Dean, Julian Higgins, and Mark Simmonds. 2017. Comparative performance of heterogeneity variance estimators in meta-analysis: A review of simulation studies. Research Synthesis Methods 8: 181–98. [Google Scholar] [CrossRef]
- LeBel, Etienne P., Denny Borsboom, Roger Giner-Sorolla, Fred Hasselman, Kurt R. Peters, Kate A. Ratliff, and Colin Tucker Smith. 2013. PsychDisclosure.Org: Grassroots support for reforming reporting standards in psychology. Perspectives on Psychological Science 8: 424–32. [Google Scholar] [CrossRef]
- Lester, Barry M., Linda L. LaGasse, and Ronald Seifer. 1998. Cocaine exposure and children: The meaning of subtle effects. Science 282: 633–34. [Google Scholar] [CrossRef] [PubMed]
- Lexchin, Joel, Lisa A. Bero, Benjamin Djulbegovic, and Otavio Clark. 2003. Pharmaceutical industry sponsorship and research outcome and quality: Systematic review. British Medical Journal 326: 1167–70. [Google Scholar] [CrossRef] [PubMed]
- Maassen, Esther, Marcel ALM van Assen, Michèle B. Nuijten, Anton Olsson-Collentine, and Jelte M. Wicherts. 2020. Reproducibility of individual effect sizes in meta-analyses in psychology. PLoS ONE 15: e0233107. [Google Scholar] [CrossRef]
- Mackintosh, Nicholas John. 2011. IQ and Human Intelligence. New York: Oxford University Press. [Google Scholar]
- Maddock, Jason E., and Joseph S. Rossi. 2001. Statistical power of articles published in three health-psychology related journals. Health Psychology 20: 76–78. [Google Scholar] [CrossRef] [PubMed]
- Marszalek, Jacob M., Carolyn Barber, Julie Kohlhart, and B. Holmes Cooper. 2011. Sample size in psychological research over the past 30 years. Perceptual and Motor Skills 112: 331–48. [Google Scholar] [CrossRef] [PubMed]
- Mathes, Tim, Pauline Klaßen, and Dawid Pieper. 2017. Frequency of data extraction errors and methods to increase data extraction quality: A methodological review. BMC Medical Research Methodology 17: 152. [Google Scholar] [CrossRef]
- Maxwell, Scott E. 2004. The persistence of underpowered studies in psychological research: Causes, consequences, and remedies. Psychological Methods 9: 147–63. [Google Scholar] [CrossRef]
- McAuley, Laura, Peter Tugwell, and David Moher. 2000. Does the inclusion of grey literature influence estimates of intervention effectiveness reported in meta-analyses? The Lancet 356: 1228–31. [Google Scholar] [CrossRef]
- McDaniel, Michael A. 2005. Big-brained people are smarter: A meta-analysis of the relationship between in vivo brain volume and intelligence. Intelligence 33: 337–46. [Google Scholar] [CrossRef]
- McGrew, Kevin S. 2009. CHC theory and the human cognitive abilities project: Standing on the shoulders of the giants of psychometric intelligence research. Intelligence 37: 1–10. [Google Scholar] [CrossRef]
- McShane, Blakeley B., and Ulf Böckenholt. 2014. You Cannot Step Into the Same River Twice:When Power Analyses Are Optimistic. Perspectives on Psychological Science 9: 612–25. [Google Scholar] [CrossRef] [PubMed]
- McShane, Blakeley B., Ulf Böckenholt, and Karsten T. Hansen. 2020. Average power: A cautionary note. Advances in Methods and Practices in Psychological Science, 1–15. [Google Scholar] [CrossRef]
- Moher, David, Alessandro Liberati, Jennifer Tetzlaff, Douglas G. Altman, and The Prisma Group. 2009. Preferred reporting items for systematic reviews and meta-analyses: The prisma statement. PLoS Medicine 6: e1000097. [Google Scholar] [CrossRef] [PubMed]
- Munafò, Marcus R., Brian A. Nosek, Dorothy V.M. Bishop, Katherine S. Button, Christopher D. Chambers, Nathalie Percie du Sert, Uri Simonsohn, Eric-Jan Wagenmakers, Jennifer J. Ware, and John P.A. Ioannidis. 2017. A manifesto for reproducible science. Nature Human Behaviour 1: 0021. [Google Scholar] [CrossRef]
- Niemeyer, Helen, Jochen Musch, and Reinhard Pietrowsky. 2012. Publication bias in meta-analyses of the efficacy of psychotherapeutic interventions for schizophrenia. Schizophrenia Research 138: 103–12. [Google Scholar] [CrossRef]
- Niemeyer, Helen, Jochen Musch, and Reinhard Pietrowsky. 2013. Publication bias in meta-analyses of the efficacy of psychotherapeutic interventions for depression. Journal of Consulting and Clinical Psychology 81: 58–74. [Google Scholar] [CrossRef]
- Nord, Camilla L., Vincent Valton, John Wood, and Jonathan P. Roiser. 2017. Power-up: A reanalysis of power failure in neuroscience using mixture modeling. The Journal of Neuroscience 37: 8051–61. [Google Scholar] [CrossRef]
- Nosek, Brian A., and Yoav Bar-Anan. 2012. Scientific utopia: I. Opening scientific communication. Psychological Inquiry 23: 217–43. [Google Scholar] [CrossRef]
- Nuijten, Michèle B., Marcel ALM van Assen, Robbie CM van Aert, and Jelte M. Wicherts. 2014. Standard analyses fail to show that US studies overestimate effect sizes in softer research. Proceedings of the National Academy of Sciences 111: E712–E713. [Google Scholar] [CrossRef]
- Nuijten, Michèle B., Marcel A.L.M. van Assen, Coosje L.S. Veldkamp, and Jelte M. Wicherts. 2015. The replication paradox: Combining studies can decrease accuracy of effect size estimates. Review of General Psychology 19: 172–82. [Google Scholar] [CrossRef]
- Nuijten, Michèle B., Chris H.J. Hartgerink, Marcel A.L.M. van Assen, Sacha Epskamp, and Jelte M. Wicherts. 2016. The prevalence of statistical reporting errors in psychology (1985–2013). Behavior Research Methods 48: 1205–26. [Google Scholar] [CrossRef] [PubMed]
- Nuijten, Michèle. 2017. Share analysis plans and results. Nature 551: 559. [Google Scholar] [CrossRef]
- Nuijten, Michèle B. 2018. Practical tools and strategies for researchers to increase replicability. Developmental Medicine & Child Neurology 61: 535–39. [Google Scholar] [CrossRef]
- Open Science Collaboration. 2015. Estimating the reproducibility of psychological science. Science 349: aac4716. [Google Scholar] [CrossRef]
- Pashler, Harold, and Eric–Jan Wagenmakers. 2012. Editors’ introduction to the special section on replicability in psychological science a crisis of confidence? Perspectives on Psychological Science 7: 528–30. [Google Scholar] [CrossRef]
- Perugini, Marco, Marcello Galucci, and Giulio Constantini. 2014. Safeguard power as a protection against imprecise power estimates. Perspectives on Psychological Science 9: 319–32. [Google Scholar] [CrossRef]
- Petrocelli, John, Joshua Clarkson, Melanie Whitmire, and Paul Moon. 2012. When ab ≠ c – c′: Published errors in the reports of single-mediator models: Published errors in the reports of single-mediator models. Behavior Research Methods 45: 595–601. [Google Scholar] [CrossRef][Green Version]
- Pietschnig, Jakob, Martin Voracek, and Anton K. Formann. 2010. Mozart effect–Shmozart effect: A meta-analysis. Intelligence 38: 314–23. [Google Scholar] [CrossRef]
- Pietschnig, Jakob, Lars Penke, Jelte M. Wicherts, Michael Zeiler, and Martin Voracek. 2015. Meta-analysis of associations between human brain volume and intelligence differences: How strong are they and what do they mean? Neuroscience & Biobehavioral Reviews 57: 411–32. [Google Scholar] [CrossRef]
- Pietschnig, Jakob, Magdalena Siegel, Junia Sophia Nur Eder, and Georg Gittler. 2019. Effect declines are systematic, strong, and ubiquitous: A meta-meta-analysis of the decline effect in intelligence research. Frontiers in Psychology 10: 2874. [Google Scholar] [CrossRef] [PubMed]
- R Core Team. 2019. R: A Language and Environment for Statistical Computing. Available online: https://www.R-project.org/ (accessed on 25 September 2020).
- Ritchie, Stuart. 2015. Intelligence: All that Matters. London: Hodder & Stoughton. [Google Scholar]
- Rosenthal, Robert, and M. Robin DiMatteo. 2001. Meta-analysis: Recent developments in quantitative methods for literature reviews. Annual Review of Psychology 52: 59–82. [Google Scholar] [CrossRef] [PubMed]
- Rossi, Joseph S. 1990. Statistical power of psychological research: What have we gained in 20 years? Journal of Consulting and Clinical Psychology 58: 646–56. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, Frank L. 2017. Statistical and measurement pitfalls in the use of meta-regression in meta-analysis. Career Development International 22: 469–76. [Google Scholar] [CrossRef]
- Sedlmeier, Peter, and Gerd Gigerenzer. 1989. Do studies of statistical power have an effect on the power of studies? Psychological Bulletin 105: 309–16. [Google Scholar] [CrossRef]
- Simmons, Joseph P., Leif D. Nelson, and Uri Simonsohn. 2011. False-positive psychology: Undisclosed flexibility in data collection and analysis allows presenting anything as significant. Psychological Science 22: 1359–66. [Google Scholar] [CrossRef]
- Song, Fujian, Sheetal Parekh, Lee Hooper, Yoon K Loke, J Ryder, Alex J Sutton, C Hing, Chun Shing Kwok, Chun Pang, and Ian Harvey. 2010. Dissemination and publication of research findings: An updated review of related biases. Health Technology Assessment 14: 1–193. [Google Scholar] [CrossRef]
- Spitz, Herman H. 1986. The Raising of Intelligence: A Selected History of Attempts to Raise Retarded Intelligence. Hillsdale: Lawrence Erlbaum Associates, Inc., Publishers. [Google Scholar]
- Stanley, T. D., Evan C. Carter, and Hristos Doucouliagos. 2018. What meta-analyses reveal about the replicability of psychological research. Psychological Bulletin 144: 1325–46. [Google Scholar] [CrossRef]
- Stern, Jerome M., and R. John Simes. 1997. Publication bias: Evidence of delayed publication in a cohort study of clinical research projects. British Medical Journal 315: 640–45. [Google Scholar] [CrossRef]
- Sterne, Jonathan AC, Betsy Jane Becker, and Matthias Egger. 2005. The funnel plot. In Publication Bias in Meta-Analysis: Prevention, Assessment and Adjustments. Edited by Hannah R. Rothstein, Alexander J. Sutton and Michael Borenstein. New York: Wiley, pp. 75–98. [Google Scholar]
- Sterne, Jonathan A.C., and Matthias Egger. 2005. Regression methods to detect publication and other bias in meta-analysis. In Publication Bias in Meta-Analysis: Prevention, Assessment and Adjustments. Edited by Hannah R. Rothstein, Alexander J. Sutton and Michael Borenstein. New York: Wiley, pp. 99–110. [Google Scholar]
- Szucs, Denes, and John PA Ioannidis. 2017. Empirical assessment of published effect sizes and power in the recent cognitive neuroscience and psychology literature. PLoS Biology 15: e2000797. [Google Scholar] [CrossRef]
- Trikalinos, Thomas A., and John PA Ioannidis. 2005. Assessing the evolution of effect sizes over time. In Publication Bias in Meta-analysis: Prevention, ASSESSMENT and Adjustments. Edited by H. R. Rothstein, A. J. Sutton and Michael Borenstein. New York: Wiley, pp. 241–59. [Google Scholar]
- Van Aert, Robbie CM, Jelte M. Wicherts, and Marcel ALM Van Assen. 2019. Publication bias examined in meta-analyses from psychology and medicine: A meta-meta-analysis. PLoS ONE 14: e0215052. [Google Scholar] [CrossRef] [PubMed]
- Van Assen, Marcel A.L.M., Robbie van Aert, and Jelte M. Wicherts. 2015. Meta-analysis using effect size distributions of only statistically significant studies. Psychological Methods 20: 293–309. [Google Scholar] [CrossRef] [PubMed]
- Van Dalen, Hendrik P., and Kene Henkens. 2012. Intended and unintended consequences of a publish-or-perish culture: A worldwide survey. Journal of the American Society for Information Science and Technology 63: 1282–93. [Google Scholar] [CrossRef]
- Van Der Maas, Han L.J., Conor V. Dolan, Raoul P.P.P. Grasman, Jelte M. Wicherts, Hilde M. Huizenga, and Maartje E.J. Raijmakers. 2006. A dynamical model of general intelligence: The positive manifold of intelligence by mutualism. Psychological Review 113: 842–61. [Google Scholar] [CrossRef]
- Veroniki, Areti Angeliki, Dan Jackson, Wolfgang Viechtbauer, Ralf Bender, Jack Bowden, Guido Knapp, Oliver Kuss, Julian Higgins, Dean Langan, and Georgia Salanti. 2016. Methods to estimate the between-study variance and its uncertainty in meta-analysis. Research Synthesis Methods 7: 55–79. [Google Scholar] [CrossRef]
- Vevea, Jack L., and Larry V. Hedges. 1995. A general linear model for estimating effect size in the presence of publication bias. Psychometrika 60: 419–35. [Google Scholar] [CrossRef]
- Viechtbauer, Wolfgang. 2010. The Metafor Package: A Meta-Analysis Package for R (Version 1.3-0). Available online: http://cran.r-project.org/web/packages/metafor/index.html (accessed on 25 September 2020).
- Wagenmakers, Eric-Jan, Ruud Wetzels, Denny Borsboom, Han L.J. van der Maas, and Rogier A. Kievit. 2012. An agenda for purely confirmatory research. Perspectives on Psychological Science 7: 632–38. [Google Scholar] [CrossRef]
- Wagenmakers, E. J., Titia Beek, Laura Dijkhoff, Quentin F. Gronau, A. Acosta, R. B. Adams, Jr., D.N. Albohn, E.S. Allard, S.D. Benning, and E-M Blouin-Hudon. 2016. Registered Replication Report: Strack, Martin, & Stepper (1988). Perspectives on Psychological Science 11: 917–28. [Google Scholar] [CrossRef]
- Wicherts, Jelte. 2013. Science revolves around the data. Journal of Open Psychology Data 1: e1. [Google Scholar] [CrossRef]
- Wicherts, Jelte M., Coosje L.S. Veldkamp, Hilde E.M. Augusteijn, Marjan Bakker, Robbie Van Aert, and Marcel A.L.M. Van Assen. 2016. Degrees of freedom in planning, running, analyzing, and reporting psychological studies: A checklist to avoid p-hacking. Frontiers in Psychology 7: 1832. [Google Scholar] [CrossRef]
- Zhang, Jian-Ping, Katherine E. Burdick, Todd Lencz, and Anil K. Malhotra. 2010. Meta-analysis of genetic variation in DTNBP1 and general cognitive ability. Biological Psychiatry 68: 1126–33. [Google Scholar] [CrossRef] [PubMed]
| 1 | None of the included primary studies used a within-subjects design. |
| 2 | It is also possible to investigate a small-study effect with multilevel weighted regression analyses that take into account that primary studies are nested within meta-analyses (Fanelli et al. 2017; Fanelli and Ioannidis 2013). A downside to this method is that it requires strong statistical assumptions that are difficult to meet with these data. For the sake of completeness, we intended to run such a multilevel analysis on our data as well, but the model was too complex for the amount of data and failed to converge. |
| 3 | In a previous discussion about estimating bias in meta-analyses (Fanelli and Ioannidis 2013; Fanelli and Ioannidis 2014; Nuijten et al. 2014) Fanelli and Ioannidis argued that choosing a random effects model at both levels unnecessarily reduces power, and they advocated the use of fixed effect models within each of the meta-analyses to decrease the amount of random fluctuation in the estimates. However, we argue that the choice for a fixed effect or random effects model is a theoretical choice, not a statistical one (Borenstein et al. 2009b). |
| 4 | For an overview of alternative explanations of a decline effect, see Trikalinos and Ioannidis 2005. |
| Type of Research | Explanation | # Meta-Analyses | # Unique Primary Studies |
|---|---|---|---|
| 1. Correlational studies | (a) Selected IQ test is correlated with other, continuous measurement of psychological construct; (b) test–retest correlation. | 31 | 781 |
| 2. Group differences (clinical and non-clinical) | Correlation IQ test and categorical, demographical variables or clinical diagnoses (e.g., male/female, schizophrenia yes/no). | 59 | 1249 |
| 3. Experiments and interventions | Studies in which participants are randomly assigned to conditions to see if the intervention affects IQ. | 20 | 188 |
| 4. Toxicology | Studies in which IQ is correlated to exposure to possibly harmful substances. | 16 | 169 |
| 5. Behavior genetics | Genetic analyses and twin designs. | 5 | 59 |
| # Meta-Analyses | # Unique Primary Studies | Total N | Median N | Range N | Median Unweighted Pearson’s r | Median Meta-Analytic Effect (r) | |
|---|---|---|---|---|---|---|---|
| 1. Predictive validity and correlational studies | 31 | 779 | 367,643 | 65 | [7; 116,053] | 0.26 | 0.24 |
| 2. Group differences (clinical and non-clinical) | 59 | 1247 | 19,757,277 | 59 | [6; 1530,128] | 0.26 | 0.19 |
| 3. Experiments and interventions | 20 | 188 | 24,371 | 49 | [10; 1358] | 0.18 | 0.17 |
| 4. Toxicology | 16 | 169 | 25,720 a | 60 | [6; 1333] | 0.15 | 0.19 |
| 5. (Behavior) genetics | 5 | 59 | 30,545 | 169 | [12; 8707] | 0.07 | 0.08 |
| Total | 131 | 2442 | 20,205,556 | 60 | [6; 1530,128] | 0.24 | 0.18 |
| Study Type | Median Power to Detect a … Effect * | ||
|---|---|---|---|
| Small | Medium | Large | |
| 1. Predictive validity and correlational studies | 12.5% | 68.2% | 99.1% |
| 2. Group differences (clinical and non-clinical) | 11.4% | 47.7% | 86.1% |
| 3. Experiments and interventions | 10.5% | 39.9% | 77.9% |
| 4. Toxicology | 11.9% | 47.9% | 88.2% |
| 5. (Behavior) genetics | 25.1% | 92.0% | 100.0% |
| Total | 11.9% | 54.5% | 93.3% |
| Type of Bias | “Predictor” in | Included Number of Meta-Analyses (m) and Number of Primary Effect Sizes (k) | Estimate of the Mean Parameter Across Meta-Analyses [99% CI] | Variance in the Meta-Regression Slopes (SE) |
|---|---|---|---|---|
| 1. Small-study effect | Standard error of primary study’s effect size (SE) | m = 130; k = 2432 | 0.67 [0.35; 0.99] | var = 0.73 (0.25) |
| 2. Decline effect | Order of publication | m = 131; k = 2442 | 0.001 [−0.003; 0.005] | var = 0.00 (0.00) |
| 3. US effect | US × SE | m = 92; k = 2114 | 0.46 [−0.15; 1.06] | var = 0.20 (0.75) |
| 4. Citation bias | Citations per year (log transformed) | m = 126; k = 2405 | 0.008 [−0.004; 0.020] | var = 0.00 (0.00) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nuijten, M.B.; van Assen, M.A.L.M.; Augusteijn, H.E.M.; Crompvoets, E.A.V.; Wicherts, J.M. Effect Sizes, Power, and Biases in Intelligence Research: A Meta-Meta-Analysis. J. Intell. 2020, 8, 36. https://doi.org/10.3390/jintelligence8040036
Nuijten MB, van Assen MALM, Augusteijn HEM, Crompvoets EAV, Wicherts JM. Effect Sizes, Power, and Biases in Intelligence Research: A Meta-Meta-Analysis. Journal of Intelligence. 2020; 8(4):36. https://doi.org/10.3390/jintelligence8040036
Chicago/Turabian StyleNuijten, Michèle B., Marcel A. L. M. van Assen, Hilde E. M. Augusteijn, Elise A. V. Crompvoets, and Jelte M. Wicherts. 2020. "Effect Sizes, Power, and Biases in Intelligence Research: A Meta-Meta-Analysis" Journal of Intelligence 8, no. 4: 36. https://doi.org/10.3390/jintelligence8040036
APA StyleNuijten, M. B., van Assen, M. A. L. M., Augusteijn, H. E. M., Crompvoets, E. A. V., & Wicherts, J. M. (2020). Effect Sizes, Power, and Biases in Intelligence Research: A Meta-Meta-Analysis. Journal of Intelligence, 8(4), 36. https://doi.org/10.3390/jintelligence8040036





