Understanding the Role of Cognitive Abilities and Math Anxiety in Adolescent Math Achievement
Abstract
1. Introduction
1.1. Higher-Order Cognitive Abilities
1.2. Executive Functions
1.3. Working Memory
1.4. Math Anxiety
1.5. Aim and Hypotheses
2. Materials and Methods
2.1. Participants
2.2. Design and Procedure
2.3. Measures
2.3.1. Math
2.3.2. Higher-Order Cognitive Abilities
Spatial Ability Test (PMA-S)
Verbal Ability Test (PMA-V)
Reasoning Ability Test (PMA-R)
2.3.3. Inhibitory Control
Stroop Task
Flanker Task
Simon Task
2.3.4. Working Memory
Verbal WM
Visuo-Spatial WM
2.3.5. Math Anxiety
2.4. Data Analysis
3. Results
3.1. Preliminary Analyses
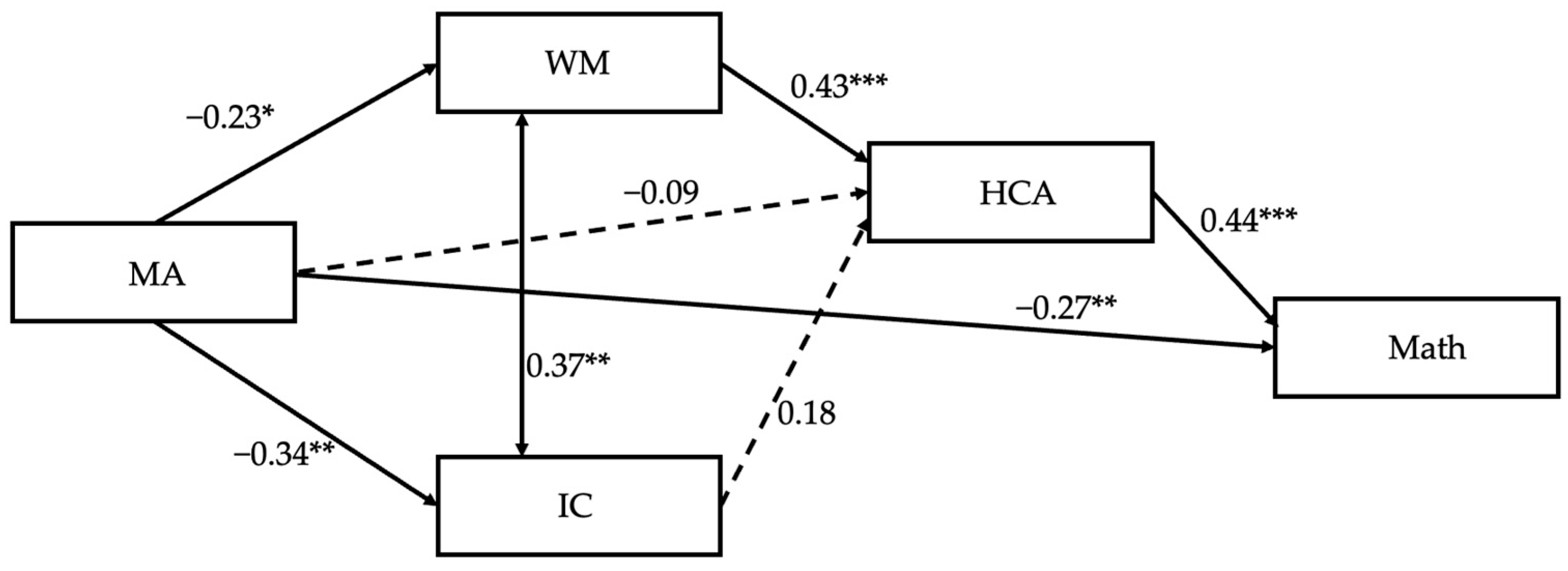
3.2. Path Analysis
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Agostino, Alba, Janice Johnson, and Juan Pascual-Leone. 2010. Executive functions underlying multiplicative reasoning: Problem type matters. Journal of Experimental Child Psychology 105: 286–305. [Google Scholar] [CrossRef] [PubMed]
- Allen, Katie, David Giofrè, Steve Higgins, and John Adams. 2020. Working memory predictors of mathematics across the middle primary school years. British Journal of Educational Psychology 90: 848–69. [Google Scholar] [CrossRef] [PubMed]
- Alloway, Tracy Packiam, and Ross G. Alloway. 2010. Investigating the predictive roles of working memory and IQ in academic attainment. Journal of Experimental Child Psychology 106: 20–29. [Google Scholar] [CrossRef] [PubMed]
- Amoretti, Guido, Luciana Bazzini, Angela Pesci, and Maria Reggiani. 1997. MAT-2. Test di Matematica. Firenze: GIUNTI O.S.Organizzazioni Speciali. [Google Scholar]
- Andersson, Ulf. 2007. The Contribution of Working Memory to Children’s Mathematical Mathematical Word Problem Solving. Applied Cognitive Psychology 21: 1201–16. [Google Scholar] [CrossRef]
- Andersson, Ulf. 2008. Working memory as a predictor of written arithmetical skills in children: The importance of central executive functions. British Journal of Educational Psychology 78: 181–203. [Google Scholar] [CrossRef]
- Ashcraft, Mark H. 2002. Math anxiety: Personal, educational, and cognitive consequences. Current Directions in Psychological Science 11: 181–85. [Google Scholar] [CrossRef]
- Ashcraft, Mark H., and Alex M. Moore. 2009. Mathematics anxiety and the affective drop in performance. Journal of Psychoeducational Assessment 27: 197–205. [Google Scholar] [CrossRef]
- Baddeley, Alan. 2000. The episodic buffer: A new component of working memory? Trends in Cognitive Sciences 4: 417–23. [Google Scholar] [CrossRef]
- Beilock, Sian L., and Erin A. Maloney. 2015. Math Anxiety: A Factor in Math Achievement Not to Be Ignored. Policy Insights from the Behavioral and Brain Sciences 2: 4–12. [Google Scholar] [CrossRef]
- Berg, Derek H. 2008. Working memory and arithmetic calculation in children: The contributory roles of processing speed, short-term memory, and reading. Journal of Experimental Child Psychology 99: 288–308. [Google Scholar] [CrossRef]
- Bonato, Mario, Sara Fabbri, Carlo Umiltà, and Marco Zorzi. 2007. The Mental Representation of Numerical Fractions: Real or Integer? Journal of Experimental Psychology: Human Perception and Performance 33: 1410–19. [Google Scholar] [CrossRef] [PubMed]
- Borella, Erika, and Anik de Ribaupierre. 2014. The role of working memory, inhibition, and processing speed in text comprehension in children. Learning and Individual Differences 34: 86–92. [Google Scholar] [CrossRef]
- Borst, Grégoire, Grégory Simon, Julie Vidal, and Olivier Houdé. 2013. Inhibitory control and visuo-spatial reversibility in piaget’s seminal number conservation task: A high-density ERP study. Frontiers in Human Neuroscience 7: 920. [Google Scholar] [CrossRef]
- Brookman-Byrne, Annie, Denis Mareschal, Andrew K. Tolmie, and Iroise Dumontheil. 2018. Inhibitory control and counterintuitive science and maths reasoning in adolescence. PLoS ONE 13: e0198973. [Google Scholar] [CrossRef]
- Bull, Rebecca, and Georgia Scerif. 2001. Executive functioning as a predictor of children’s mathematics ability: Inhibition, switching, and working memory. Developmental Neuropsychology 19: 273–93. [Google Scholar] [CrossRef]
- Bull, Rebecca, and Kerry Lee. 2014. Executive functioning and mathematics achievement. Child Development Perspectives 8: 36–41. [Google Scholar] [CrossRef]
- Burgoyne, Alexander P., Jason S. Tsukahara, Cody A. Mashburn, Richard Pak, and Randall W. Engle. 2023. Nature and Measurement of Attention Control. Journal of Experimental Psychology: General 152: 2369–402. [Google Scholar] [CrossRef]
- Burnham, Kenneth, and David Anderson. 2004. Model Selection and Multimodel Inference. A Practical Information-Theoretic Approach 63: 10. [Google Scholar] [CrossRef]
- Campos, Isabel S., Leandro S. Almeida, Aristides I. Ferreira, Luis F. Martinez, and Glória Ramalho. 2013. Cognitive processes and math performance: A study with children at third grade of basic education. European Journal of Psychology of Education 28: 421–36. [Google Scholar] [CrossRef]
- Carey, Emma, Amy Devine, Francesca Hill, and Dénes Szucs. 2017. Differentiating anxiety forms and their role in academic performance from primary to secondary school. PLoS ONE 12: e0174418. [Google Scholar] [CrossRef]
- Carey, Emma, Francesca Hill, Amy Devine, and Dénes Szücs. 2016. The chicken or the egg? The direction of the relationship between mathematics anxiety and mathematics performance. Frontiers in Psychology 6: 1987. [Google Scholar] [CrossRef] [PubMed]
- Caviola, Sara, Caterina Primi, Francesca Chiesi, and Irene C. Mammarella. 2017. Psychometric properties of the Abbreviated Math Anxiety Scale (AMAS) in Italian primary school children. Learning and Individual Differences 55: 174–82. [Google Scholar] [CrossRef]
- Caviola, Sara, Enrico Toffalini, David Giofrè, Jessica Mercader Ruiz, Dénes Szűcs, and Irene C. Mammarella. 2022. Math Performance and Academic Anxiety Forms, from Sociodemographic to Cognitive Aspects: A Meta-analysis on 906,311 Participants. Educational Psychology Review 34. [Google Scholar] [CrossRef]
- Caviola, Sara, Irene C. Mammarella, Daniela Lucangeli, and Cesare Cornoldi. 2014. Working memory and domain-specific precursors predicting success in learning written subtraction problems. Learning and Individual Differences 36: 92–100. [Google Scholar] [CrossRef]
- Caviola, Sara, Lincoln J. Colling, Irene C. Mammarella, and Dénes Szűcs. 2020. Predictors of mathematics in primary school: Magnitude comparison, verbal and spatial working memory measures. Developmental Science 23: e12957. [Google Scholar] [CrossRef]
- Chen, Edward H., and Drew H. Bailey. 2021. Dual-task studies of working memory and arithmetic performance: A meta-analysis. Journal of Experimental Psychology: Learning Memory and Cognition 47: 220–33. [Google Scholar] [CrossRef]
- Choe, Kyoung Whan, Jalisha B. Jenifer, Christopher S. Rozek, Marc G. Berman, and Sian L. Beilock. 2019. Calculated avoidance: Math anxiety predicts math avoidance in effort-based decision-making. Science Advances 5: eaay1062. [Google Scholar] [CrossRef]
- Cragg, Lucy, and Camilla Gilmore. 2014. Skills underlying mathematics: The role of executive function in the development of mathematics proficiency. Trends in Neuroscience and Education 3: 63–68. [Google Scholar] [CrossRef]
- Cragg, Lucy, Sarah Keeble, Sophie Richardson, Hannah E. Roome, and Camilla Gilmore. 2017. Direct and indirect influences of executive functions on mathematics achievement. Cognition 162: 12–26. [Google Scholar] [CrossRef]
- Daker, Richard J., Sylvia U. Gattas, H. Moriah Sokolowski, Adam E. Green, and Ian M. Lyons. 2021. First-year students’ math anxiety predicts STEM avoidance and underperformance throughout university, independently of math ability. NPJ Science of Learning 6: 17. [Google Scholar] [CrossRef]
- Deary, Ian J., Steve Strand, Pauline Smith, and Cres Fernandes. 2007. Intelligence and educational achievement. Intelligence 35: 13–21. [Google Scholar] [CrossRef]
- Demetriou, Andreas, and George Spanoudis. 2017. Mind and Intelligence: Integrating Developmental, Psychometric, and Cognitive Theories of Human Mind BT—Cognitive Abilities and Educational Outcomes: A Festschrift in Honour of Jan-Eric Gustafsson. Edited by Monica Rosén, Kajsa Yang Hansen and Ulrika Wolff. New York: Springer International Publishing, pp. 39–60. [Google Scholar] [CrossRef]
- Demetriou, Andreas, George Spanoudis, Michael Shayer, Antigoni Mouyi, Smaragda Kazi, and Maria Platsidou. 2013. Cycles in speed-working memory-G relations: Towards a developmental-differential theory of the mind. Intelligence 41: 34–50. [Google Scholar] [CrossRef]
- Demetriou, Andreas, George Spanoudis, Michael Shayer, Sanne Van der Ven, Christopher R. Brydges, Evelyn Kroesbergen, Gal Podjarny, and H. Lee Swanson. 2014. Relations between speed, working memory, and intelligence from preschool to adulthood: Structural equation modeling of 14 studies. Intelligence 46: 107–21. [Google Scholar] [CrossRef]
- Diamond, Adele. 2013. Executive functions. Annual Review of Psychology 64: 135–68. [Google Scholar] [CrossRef]
- Distefano, Christine, Min Zhu, and Diana Mindrila. 2008. Understanding and Using Factor Scores: Considerations for the Applied Researcher. Practical Assessment, Research, and Evaluation 14: 20. [Google Scholar] [CrossRef]
- Donolato, Enrica, Enrico Toffalini, David Giofrè, Sara Caviola, and Irene C. Mammarella. 2020. Going Beyond Mathematics Anxiety in Primary and Middle School Students: The Role of Ego-Resiliency in Mathematics. Mind, Brain, and Education 14: 255–66. [Google Scholar] [CrossRef]
- Emslander, Valentin, and Ronny Scherer. 2022. The Relation Between Executive Functions and Math Intelligence in Preschool Children: A Systematic Review and Meta-Analysis. Psychological Bulletin 148: 337–69. [Google Scholar] [CrossRef]
- Enders, Craig K. 2020. Applied Missing Data Analysis, 2nd ed. New York: Guilford Press. Available online: https://www.guilford.com/books/Applied-Missing-Data-Analysis/Craig-Enders/9781462549863 (accessed on 1 March 2025).
- Eysenck, Michael W., Nazanin Derakshan, Rita Santos, and Manuel G. Calvo. 2007. Anxiety and cognitive performance: Attentional control theory. Emotion 7: 336–53. [Google Scholar] [CrossRef]
- Foley, Alana E., Julianne B. Herts, Francesca Borgonovi, Sonia Guerriero, Susan C. Levine, and Sian L. Beilock. 2017. The Math Anxiety-Performance Link: A Global Phenomenon. Current Directions in Psychological Science 26: 52–58. [Google Scholar] [CrossRef]
- Frey, Meredith C., and Douglas K. Detterman. 2004. Scholastic Assessment or g? Psychological Science 15: 373–78. [Google Scholar] [CrossRef]
- Friso-Van Den Bos, Ilona, Sanne H. G. Van Der Ven, Evelyn H. Kroesbergen, and Johannes E.H. Van Luit. 2013. Working memory and mathematics in primary school children: A meta-analysis. Educational Research Review 10: 29–44. [Google Scholar] [CrossRef]
- Giofrè, David, Erika Borella, and Irene Cristina Mammarella. 2017. The relationship between intelligence, working memory, academic self-esteem, and academic achievement. Journal of Cognitive Psychology 29: 731–47. [Google Scholar] [CrossRef]
- Giofrè, David, Irene C. Mammarella, and Cesare Cornoldi. 2013a. The structure of working memory and how it relates to intelligence in children. Intelligence 41: 396–406. [Google Scholar] [CrossRef]
- Giofrè, David, Irene C. Mammarella, Lucia Ronconi, and Cesare Cornoldi. 2013b. Visuospatial working memory in intuitive geometry, and in academic achievement in geometry. Learning and Individual Differences 23: 114–22. [Google Scholar] [CrossRef]
- Giofrè, David, Irene Cristina Mammarella, and Cesare Cornoldi. 2014. The relationship among geometry, working memory, and intelligence in children. Journal of Experimental Child Psychology 123: 112–28. [Google Scholar] [CrossRef]
- Hill, Francesca, Irene C Mammarella, Amy Devine, Sara Caviola, Maria Chiara Passolunghi, and Dénes Szűcs. 2016. Maths anxiety in primary and secondary school students: Gender differences, developmental changes and anxiety specificity. Learning & Individual Differences 48: 45–53. [Google Scholar] [CrossRef]
- Hornung, Caroline, Christine Schiltz, Martin Brunner, and Romain Martin. 2014. Predicting first-grade mathematics achievement: The contributions of domain-general cognitive abilities, nonverbal number sense, and early number competence. Frontiers in Psychology 5: 272. [Google Scholar] [CrossRef]
- Hu, Li Tze, and Peter M. Bentler. 1999. Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Structural Equation Modeling 6: 1–55. [Google Scholar] [CrossRef]
- Jacob, Robin, and Julia Parkinson. 2015. The Potential for School-Based Interventions That Target Executive Function to Improve Academic Achievement: A Review. Review of Educational Research 85: 512–52. [Google Scholar] [CrossRef]
- Johnson, Heather Lynn. 2015. Secondary Students’ Quantification of Ratio and Rate: A Framework for Reasoning about Change in Covarying Quantities. Mathematical Thinking and Learning 17: 64–90. [Google Scholar] [CrossRef]
- Johnson, Wendy, and Thomas J. Bouchard. 2005. The structure of human intelligence: It is verbal, perceptual, and image rotation (VPR), not fluid and crystallized. Intelligence 33: 393–416. [Google Scholar] [CrossRef]
- Johnson, Wendy, Jan te Nijenhuis, and Thomas J. Bouchard. 2008. Still just 1 g: Consistent results from five test batteries. Intelligence 36: 81–95. [Google Scholar] [CrossRef]
- Jorgensen, Terrence D., Sunthud Pornprasertmanit, Alexander M. Schoemann, and Yves Rosseel. 2022. semTools: Useful Tools for Structural Equation Modeling. Available online: https://cran.r-project.org/package=semTools (accessed on 1 March 2025).
- Kline, Rex B. 2011. Principles and Practice of Structural Equation Modeling. New York: Guilford Press. [Google Scholar]
- Krajewski, Kristin, and Wolfgang Schneider. 2009. Exploring the impact of phonological awareness, visual-spatial working memory, and preschool quantity-number competencies on mathematics achievement in elementary school: Findings from a 3-year longitudinal study. Journal of Experimental Child Psychology 103: 516–31. [Google Scholar] [CrossRef]
- Kroesbergen, Evelyn H., Johannes E. H. Van Luit, Ernest C. D. M. Van Lieshout, Erik Van Loosbroek, and Bas A. M. Van de Rijt. 2009. Individual Differences in Early Numeracy. Journal of Psychoeducational Assessment 27: 226–36. [Google Scholar] [CrossRef]
- Lee, Kerry, and Hon Wah Lee. 2019. Inhibition and Mathematical Performance: Poorly Correlated, Poorly Measured, or Poorly Matched? Child Development Perspectives 13: 28–33. [Google Scholar] [CrossRef]
- Lee, Kerry, Rebecca Bull, and Ringo M.H. Ho. 2013. Developmental changes in executive functioning. Child Development 84: 1933–53. [Google Scholar] [CrossRef]
- Lee, Kerry, Swee Fong Ng, Ee Lynn Ng, and Zee Ying Lim. 2004. Working memory and literacy as predictors of performance on algebraic word problems. Journal of Experimental Child Psychology 89: 140–58. [Google Scholar] [CrossRef]
- Lerner, Matthew D., and Christopher J. Lonigan. 2014. Executive Function Among Preschool Children: Unitary Versus Distinct Abilities. Journal of Psychopathology and Behavioral Assessment 36: 626–39. [Google Scholar] [CrossRef]
- Li, Jingguang, Yajun Zhao, Shan Zhou, Yuling Pu, Hongyu He, and Ming Zhao. 2020. Set-shifting ability is specifically linked to high-school science and math achievement in Chinese adolescents. PsyCh Journal 9: 327–38. [Google Scholar] [CrossRef]
- Lubin, Amélie, Julie Vidal, Céline Lanoë, Olivier Houdé, and Grégoire Borst. 2013. Inhibitory control is needed for the resolution of arithmetic word problems: A developmental negative priming study. Journal of Educational Psychology 105: 701–8. [Google Scholar] [CrossRef]
- Miller, Heather, and Jacqueline Bichsel. 2004. Anxiety, working memory, gender, and math performance. Personality and Individual Differences 37: 591–606. [Google Scholar] [CrossRef]
- Miller, Michael R., Gerald F. Giesbrecht, Ulrich Müller, Robert J. McInerney, and Kimberly A. Kerns. 2012. A Latent Variable Approach to Determining the Structure of Executive Function in Preschool Children. Journal of Cognition and Development 13: 395–423. [Google Scholar] [CrossRef]
- Miyake, Akira, and Naomi P. Friedman. 2012. The nature and organization of individual differences in executive functions: Four general conclusions. Current Directions in Psychological Science 21: 8–14. [Google Scholar] [CrossRef] [PubMed]
- Miyake, Akira, Naomi P. Friedman, Michael J. Emerson, Alexander H. Witzki, Amy Howerter, and Tor D. Wager. 2000. The Unity and Diversity of Executive Functions and Their Contributions to Complex “Frontal Lobe” Tasks: A Latent Variable Analysis. Cognitive Psychology 41: 49–100. [Google Scholar] [CrossRef]
- Navarro, Jose I., Manuel Aguilar, Concepcion Alcalde, Gonzalo Ruiz, Esperanza Marchena, and Inmaculada Menacho. 2011. Inhibitory Processes, Working Memory, Phonological Awareness, Naming Speed, and Early Arithmetic Achievement. The Spanish Journal of Psychology 14: 580–88. [Google Scholar] [CrossRef]
- Nelwan, Michel, Ilona Friso-van den Bos, Constance Vissers, and Evelyn Kroesbergen. 2022. The relation between working memory, number sense, and mathematics throughout primary education in children with and without mathematical difficulties. Child Neuropsychology 28: 143–70. [Google Scholar] [CrossRef]
- Nunes, Terezinha, Peter Bryant, Deborah Evans, and Rossana Barros. 2015. Assessing Quantitative Reasoning in Young Children. Mathematical Thinking and Learning 17: 178–96. [Google Scholar] [CrossRef]
- Passolunghi, Maria Chiara, and Silvia Lanfranchi. 2012. Domain-specific and domain-general precursors of mathematical achievement: A longitudinal study from kindergarten to first grade. British Journal of Educational Psychology 82: 42–63. [Google Scholar] [CrossRef]
- Paxton, Pamela, Patrick J. Curran, Kenneth A. Bollen, Jim Kirby, and Feinian Chen. 2001. Monte Carlo Experiments: Design and Implementation. Structural Equation Modeling: A Multidisciplinary Journal 8: 287–312. [Google Scholar] [CrossRef]
- Peng, Peng, Jessica Namkung, Marcia Barnes, and Congying Sun. 2016. A meta-analysis of mathematics and working memory: Moderating effects of working memory domain, type of mathematics skill, and sample characteristics. Journal of Educational Psychology 108: 455–73. [Google Scholar] [CrossRef]
- Pokropek, Artur, Gary N. Marks, and Francesca Borgonovi. 2022. How Much Do Students’ Scores in PISA Reflect General Intelligence and How Much Do They Reflect Specific Abilities? Journal of Educational Psychology 114: 1121–35. [Google Scholar] [CrossRef]
- Purpura, David J., Arthur J. Baroody, and Christopher J. Lonigan. 2013. The transition from informal to formal mathematical knowledge: Mediation by numeral knowledge. Journal of Educational Psychology 105: 453–64. [Google Scholar] [CrossRef]
- Purpura, David J., Sara A. Schmitt, and Colleen M. Ganley. 2017. Foundations of mathematics and literacy: The role of executive functioning components. Journal of Experimental Child Psychology 153: 15–34. [Google Scholar] [CrossRef] [PubMed]
- Qi, Yue, Yinghe Chen, Xiao Yu, Xiujie Yang, Xinyi He, and Xiaoyu Ma. 2024. The relationships among working memory, inhibitory control, and mathematical skills in primary school children: Analogical reasoning matters. Cognitive Development 70: 101437. [Google Scholar] [CrossRef]
- R Core Team. 2024. R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing. Available online: https://www.r-project.org/ (accessed on 1 March 2025).
- Rivella, Carlotta, Cesare Cornoldi, Sara Caviola, and David Giofrè. 2021. Learning a new geometric concept: The role of working memory and of domain-specific abilities. British Journal of Educational Psychology 91: 1537–54. [Google Scholar] [CrossRef]
- Rochat, Philippe. 2023. The Evolution of Developmental Theories Since Piaget: A Metaview. Perspectives on Psychological Science. [Google Scholar] [CrossRef]
- Rosseel, Yves. 2012. {lavaan}: An {R} Package for Structural Equation Modeling. Journal of Statistical Software 48: 1–36. [Google Scholar] [CrossRef]
- Roth, Bettina, Nicolas Becker, Sara Romeyke, Sarah Schäfer, Florian Domnick, and Frank M. Spinath. 2015. Intelligence and school grades: A meta-analysis. Intelligence 53: 118–37. [Google Scholar] [CrossRef]
- RStudio Team. 2024. RStudio: Integrated Development for R. Boston: RStudio, PBC. Available online: https://posit.co/ (accessed on 1 March 2025).
- Simanowski, Stefanie, and Kristin Krajewski. 2019. Specific Preschool Executive Functions Predict Unique Aspects of Mathematics Development: A 3-Year Longitudinal Study. Child Development 90: 544–61. [Google Scholar] [CrossRef]
- Sorvo, Riikka, Noona Kiuru, Tuire Koponen, Tuija Aro, Helena Viholainen, Timo Ahonen, and Mikko Aro. 2022. Longitudinal and situational associations between math anxiety and performance among early adolescents. Annals of the New York Academy of Sciences 1514: 174–86. [Google Scholar] [CrossRef]
- Stavy, Ruth, and Dina Tirosh. 2000. How Students (Mis-)Understand Science and Mathematics: Intuitive Rules. New York: Teachers College Press. [Google Scholar]
- Suárez-Pellicioni, Macarena, María Isabel Núñez-Peña, and Àngels Colomé. 2016. Math anxiety: A review of its cognitive consequences, psychophysiological correlates, and brain bases. Cognitive, Affective and Behavioral Neuroscience 16: 3–22. [Google Scholar] [CrossRef] [PubMed]
- Thurstone, Louis L. 1937. The Primary Mental Abilities of Children. Journal of Educational Psychology 28: 217–32. [Google Scholar] [CrossRef]
- Tourva, Anna, and George Spanoudis. 2020. Speed of processing, control of processing, working memory and crystallized and fluid intelligence: Evidence for a developmental cascade. Intelligence 83: 101503. [Google Scholar] [CrossRef]
- Usai, Maria Carmen, Paola Viterbori, and Laura Traverso. 2018. Preschool Executive Function Profiles: Implications for Math Achievement in Grades 1 and 3. Journal of Research in Childhood Education 32: 404–18. [Google Scholar] [CrossRef]
- Usai, M. Carmen, Paola Viterbori, Laura Traverso, and Valentina De Franchis. 2014. Latent structure of executive function in five- and six-year-old children: A longitudinal study. European Journal of Developmental Psychology 11: 447–62. [Google Scholar] [CrossRef]
- Van den Bussche, Eva, Katrien Vanmeert, Bram Aben, and Dries Sasanguie. 2020. Too anxious to control: The relation between math anxiety and inhibitory control processes. Scientific Reports 10: 19922. [Google Scholar] [CrossRef]
- van Dijck, Jean-Philippe, and Wim Fias. 2011. A working memory account for spatial-numerical associations. Cognition 119: 114–19. [Google Scholar] [CrossRef]
- Viterbori, Paola, Laura Traverso, and M. Carmen Usai. 2017. The Role of Executive Function in Arithmetic Problem-Solving Processes: A Study of Third Graders. Journal of Cognition and Development 18: 595–616. [Google Scholar] [CrossRef]
- Wiebe, Sandra A, Tiffant Sheffield, Jennifer Mize Nelson, Caron A C Clark, Nicolas Chevalier, and Andrews Espy Kimberly. 2010. The structure of executive function in 3-year-old children. Journal of Experimental Child Psychology 108: 436–52. [Google Scholar] [CrossRef]
- Wilkinson, Hannah R., Claudia Smid, Sarah Morris, Emily K. Farran, Iroise Dumontheil, Susan Mayer, Andrew Tolmie, David Bell, Katarzyna Porayska-Pomsta, Wayne Holmes, and et al. 2020. Domain-Specific Inhibitory Control Training to Improve Children’s Learning of Counterintuitive Concepts in Mathematics and Science. Journal of Cognitive Enhancement 4: 296–314. [Google Scholar] [CrossRef]
- Yeniad, Nihal, Maike Malda, Judi Mesman, Marinus H. Van Ijzendoorn, and Suzanne Pieper. 2013. Shifting ability predicts math and reading performance in children: A meta-analytical study. Learning and Individual Differences 23: 1–9. [Google Scholar] [CrossRef]
- Zeidner, Moshe. 2007. Test Anxiety in Educational Contexts. Concepts, Findings, and Future Directions. Emotion in Education, 165–84. [Google Scholar] [CrossRef]
- Zhang, Yuxin, Andrew Tolmie, and Rebecca Gordon. 2023. The Relationship between Working Memory and Arithmetic in primary school children: A meta-analysis. Brain Sciences 13: 22. [Google Scholar] [CrossRef] [PubMed]
| 1. | 2. | 3. | 4. | 5. | |
|---|---|---|---|---|---|
| 1. Math | - | ||||
| 2. HCA | 0.51 | - | |||
| 3. IC | 0.33 | 0.39 | - | ||
| 4. WM | 0.41 | 0.53 | 0.41 | - | |
| 5. MA | −0.38 | −0.25 | −0.34 | −0.23 | - |
| M | 13.05 | 28.62 | 47.52 | 66.13 | 23.32 |
| SD | 5.67 | 10.59 | 14.08 | 12.82 | 6.18 |
| Model | χ2 | df | CFI | TLI | RMSEA | SRMR | AIC | ΔAIC |
|---|---|---|---|---|---|---|---|---|
| Measurement model | ||||||||
| Model 0 | 75.94 | 68 | 0.97 | 0.96 | 0.04 | 0.07 | 6240.47 | |
| Path analysis | ||||||||
| Model 1 | 0 | 0 | 1 | 1 | <0.001 | <0.001 | 2073.91 | |
| Model 2 | 3.74 | 2 | 0.97 | 0.91 | 0.11 | 0.06 | 2073.66 | −0.47 |
| Model 3 | 2.19 | 2 | 1.00 | 0.99 | 0.04 | 0.03 | 2064.62 | −9.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Esposito, L.; Tonizzi, I.; Usai, M.C.; Giofrè, D. Understanding the Role of Cognitive Abilities and Math Anxiety in Adolescent Math Achievement. J. Intell. 2025, 13, 44. https://doi.org/10.3390/jintelligence13040044
Esposito L, Tonizzi I, Usai MC, Giofrè D. Understanding the Role of Cognitive Abilities and Math Anxiety in Adolescent Math Achievement. Journal of Intelligence. 2025; 13(4):44. https://doi.org/10.3390/jintelligence13040044
Chicago/Turabian StyleEsposito, Lorenzo, Irene Tonizzi, Maria Carmen Usai, and David Giofrè. 2025. "Understanding the Role of Cognitive Abilities and Math Anxiety in Adolescent Math Achievement" Journal of Intelligence 13, no. 4: 44. https://doi.org/10.3390/jintelligence13040044
APA StyleEsposito, L., Tonizzi, I., Usai, M. C., & Giofrè, D. (2025). Understanding the Role of Cognitive Abilities and Math Anxiety in Adolescent Math Achievement. Journal of Intelligence, 13(4), 44. https://doi.org/10.3390/jintelligence13040044





