Can Generative AI and ChatGPT Break Human Supremacy in Mathematics and Reshape Competence in Cognitive-Demanding Problem-Solving Tasks?
Abstract
1. Introduction
- RQ1. Are ChatGPT-4o and GPT-4 capable of scoring better than average human students of the same age group in NAEP mathematics tests?
- RQ2. How do ChatGPT-4o and GPT-4 perform at different levels of cognitive demand in NAEP mathematics tests compared to average students of the same age group?
2. Literature Review
2.1. Cognitive Load Effects on Mathematics Problem-Solving Efficiency
2.2. GAI, AI, and ChatGPT Models
2.3. Higher-Order Thinking
2.4. GAI Technologies and Commonsense Problem-Solving
2.5. Research Gap and Study Contribution
3. Materials and Methods
3.1. Study Design
3.2. Population and Sampling
3.3. Instruments and Materials
3.4. Data Analysis
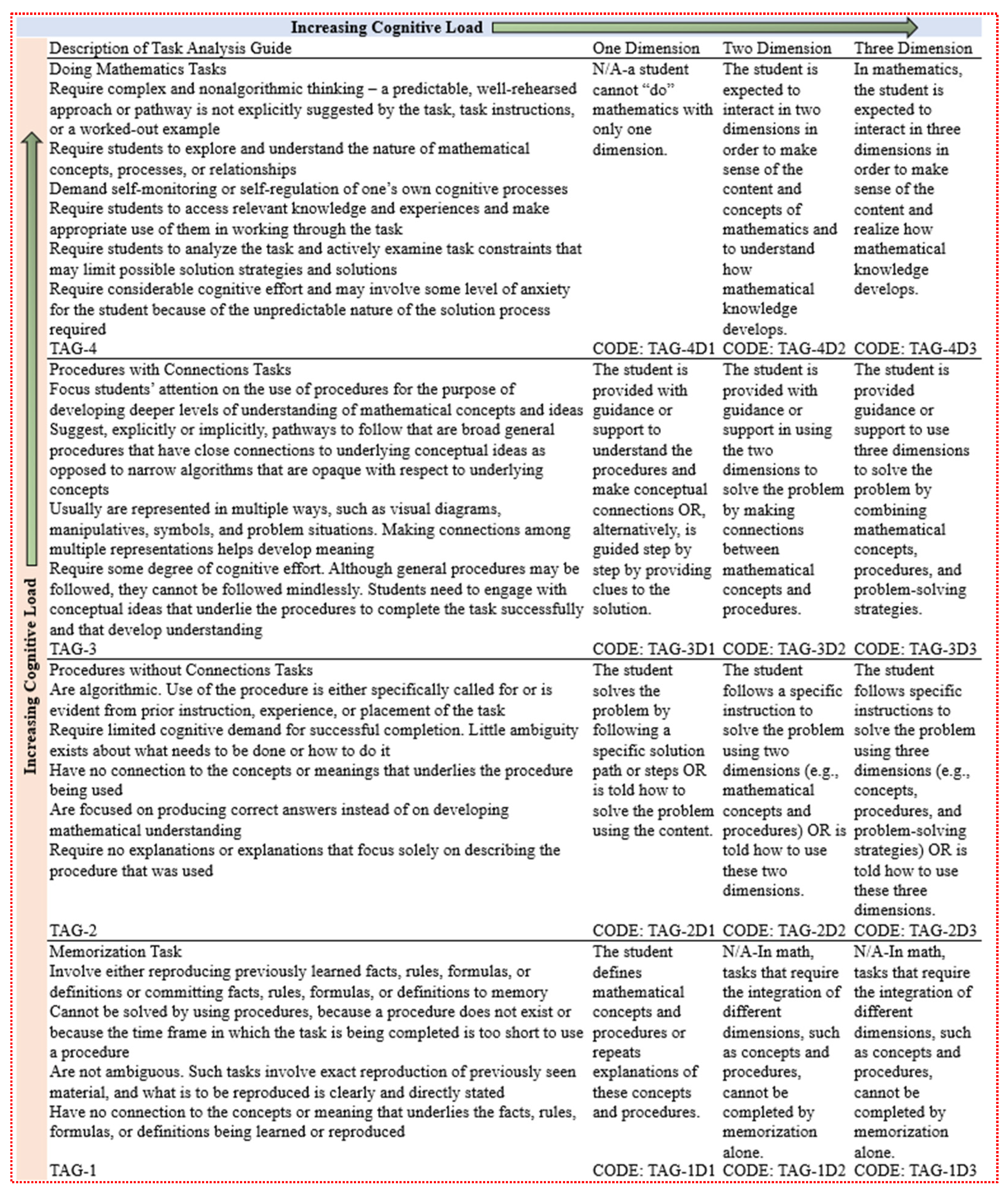
3.4.1. Detailed Coding Framework and Procedures for Cognitive Load in NAEP Tasks
3.4.2. Coding Outcomes
3.4.3. Statistical Analysis
4. Results
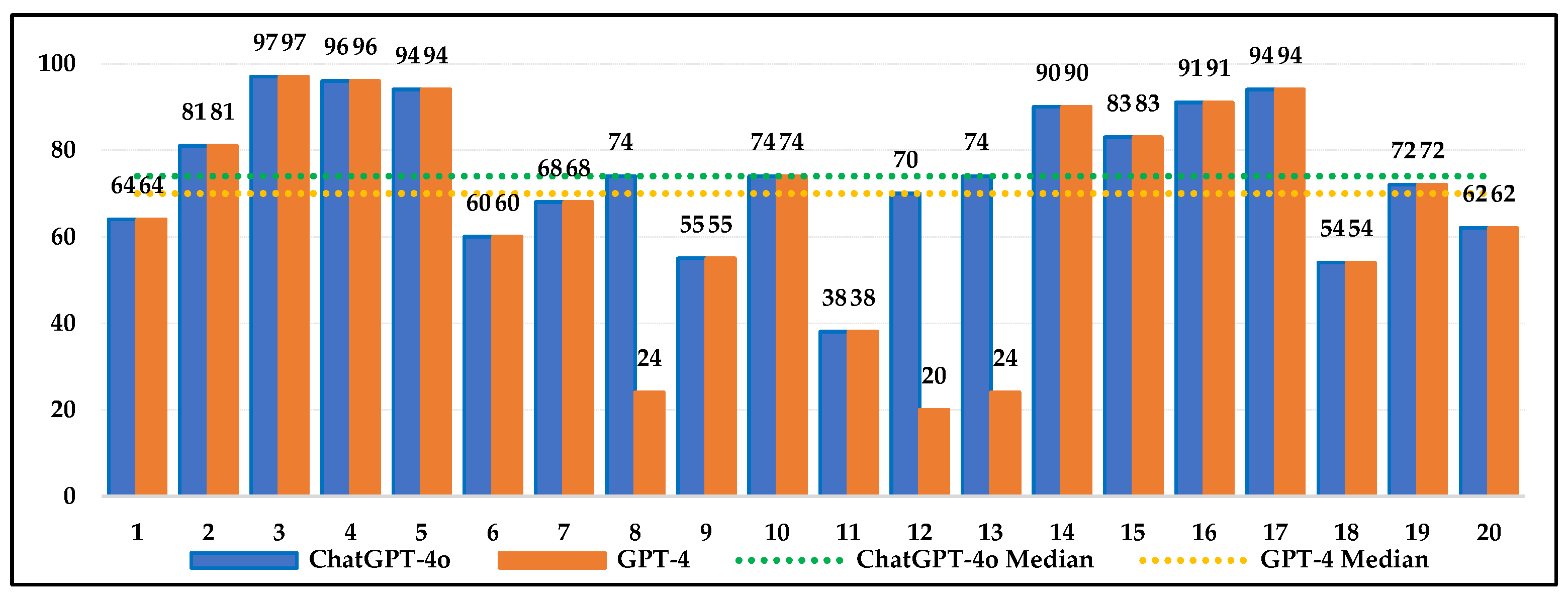
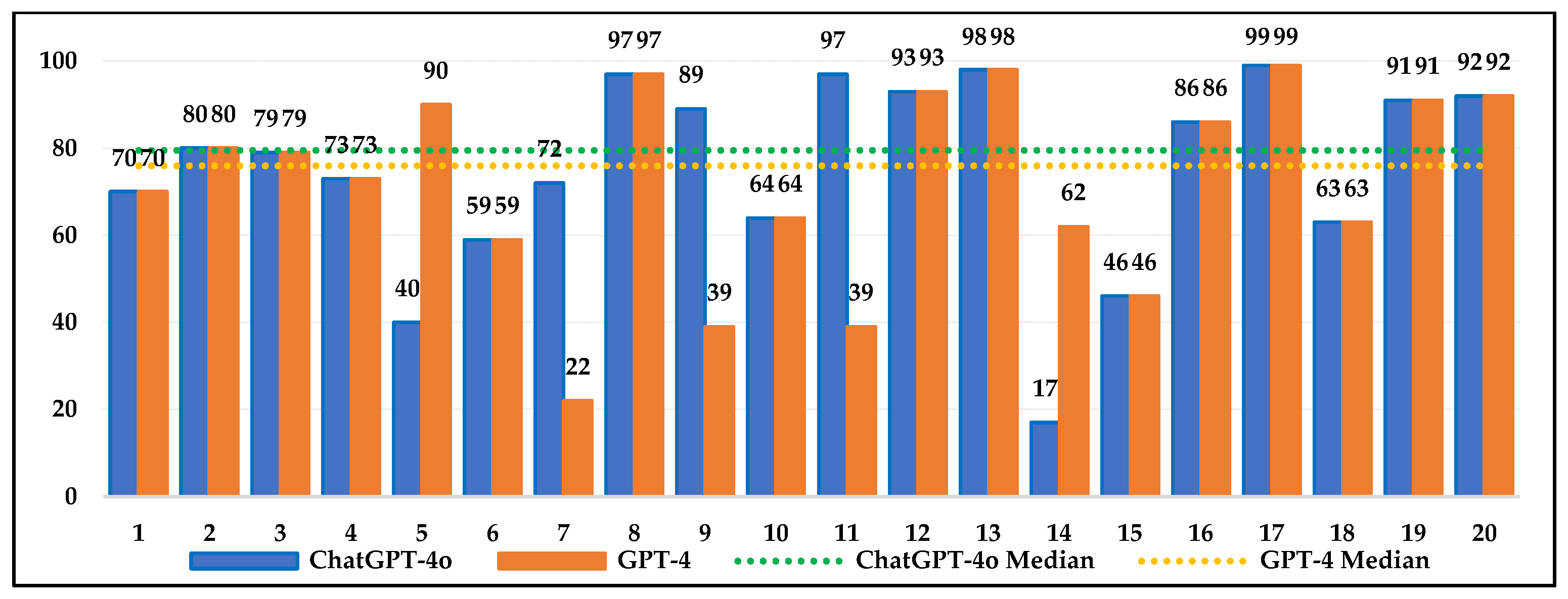
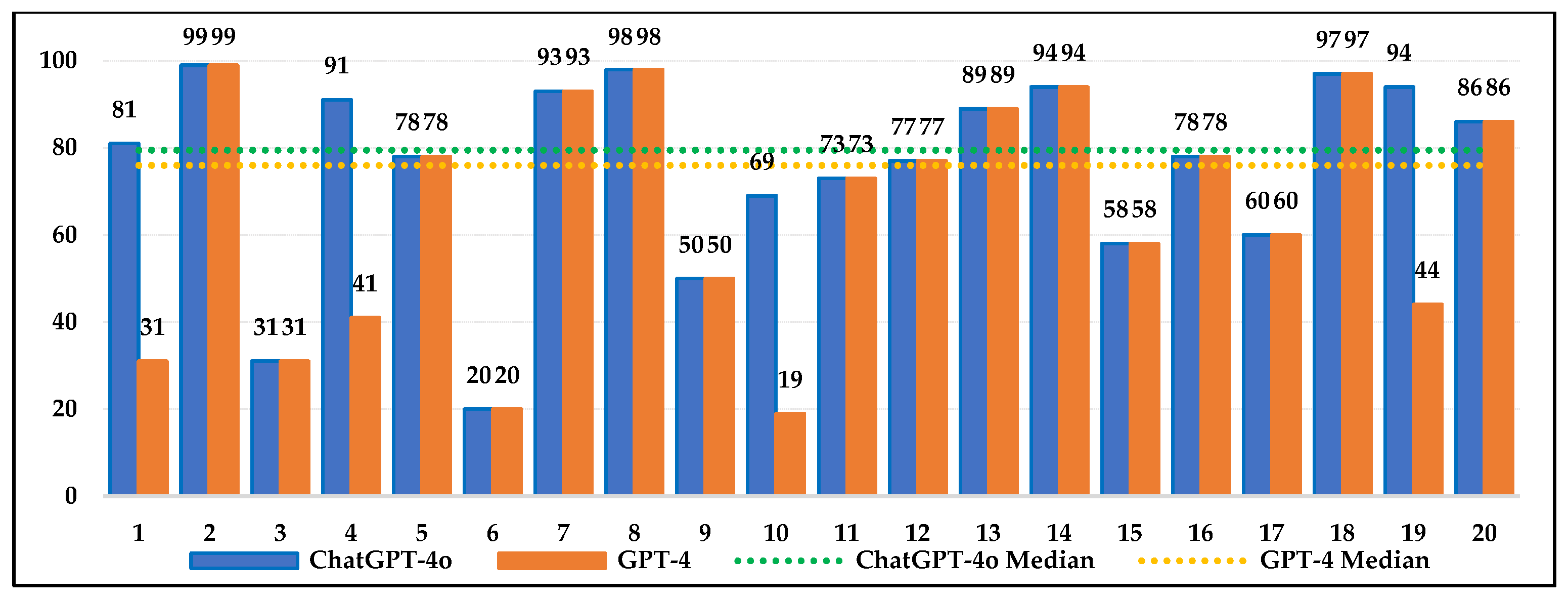
4.1. Can ChatGPT-4o and GPT-4 Surpass Human Performance on NAEP Mathematics Assessments?
4.2. How Well Do ChatGPT-4o and GPT-4 Address Cognitive Demands on NAEP Mathematics Assessments Compared to Humans?
5. Discussion
5.1. Cognitive Load, Grade Levels, and AI Performance
5.2. AI as a Supplementary Educational Tool
5.3. Balancing AI and Human Guidance in Mathematics Education
5.4. Rethinking Assessment Strategies in an AI-Driven Era
5.5. Limitations and Trends for Future Research
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AI | Artificial Intelligence |
| EASPS | Essential Average Student Performance Score |
| ECL | Extraneous Cognitive Load |
| GAI | Generative Artificial Intelligence |
| GPT | Generative Pre-trained Transformer |
| ICC | Intraclass Correlation Coefficient |
| ICL | Intrinsic Cognitive Load |
| IQR | Interquartile Range |
| IRT | Item Response Theory |
| MC | Multiple Choice |
| NAEP | National Assessment of Educational Progress |
| NAGB | National Assessment Governing Board |
| NCES | National Center for Education Statistics |
| NCTM | National Council of Teachers of Mathematics |
| NGSS | Next Generation Science Standards |
| SCR | Short Constructed Response |
| SR | Selected Response |
| TAG | Task Analysis Guide |
References
- Agresti, Alan. 2013. Categorical Data Analysis, 3rd ed. New Jersey: Wiley & Sons Inc. [Google Scholar]
- Asare, Bright, Yarhands D. Arthur, and Francis O. Boateng. 2023. Exploring the impact of ChatGPT on mathematics performance: The influential role of student interest. Education Science and Management 1: 158–68. [Google Scholar] [CrossRef]
- Ayres, Paul. 2006. Using subjective measures to detect variations of intrinsic cognitive load within problems. Learning and Instruction 16: 389–400. [Google Scholar] [CrossRef]
- Bahroun, Zied, Chiraz Anane, Vian Ahmed, and Andrew Zacca. 2023. Transforming education: A comprehensive review of generative artificial intelligence in educational settings through bibliometric and content analysis. Sustainability 15: 12983. [Google Scholar] [CrossRef]
- Bommasani, Rishi, Drew A. Hudson, Ehsan Adeli, Russ Altman, Simran Arora, Sydney von Arx, Michael S. Bernstein, Jeannette Bohg, Antoine Bosselut, Emma Brunskill, and et al. 2021. On the opportunities and risks of foundation models. arXiv arXiv:2108.07258. [Google Scholar] [CrossRef]
- Brown, Tom B., Benjamin Mann, Nick Ryder, Melanie Subbiah, Jared Kaplan, Prafulla Dhariwal, Arvind Neelakantan, Pranav Shyam, Girish Sastry, Amanda Askell, and et al. 2020. Language models are few-shot learners. Advances in Neural Information Processing Systems 33: 1877–901. [Google Scholar] [CrossRef]
- Brüggemann, Thomas, Ulrich Ludewig, Ramona Lorenz, and Nele McElvany. 2023. Effects of mode and medium in reading comprehension tests on cognitive load. Computers & Education 192: 1–13. [Google Scholar] [CrossRef]
- Center for Standards, Assessment, and Accountability (CSAA). 2019. Cognitive Loading in Three-Dimensional NGSS Assessment: Knowledge, Skills, and Know-How. Available online: https://csaa.wested.org/wp-content/uploads/2019/11/CSAI-Whitepaper_Cog-Load-3D-NGSS-1.pdf (accessed on 13 January 2024).
- Chen, Lijia, Pingping Chen, and Zhijian Lin. 2020. Artificial intelligence in education: A review. IEEE Access 8: 75264–78. [Google Scholar] [CrossRef]
- Daher, Wajeeh, Hussam Diab, and Anwar Rayan. 2023. Artificial intelligence generative tools and conceptual knowledge in problem solving in chemistry. Information 14: 409. [Google Scholar] [CrossRef]
- Dao, Xuan-Quy, and Ngoc-Bich Le. 2023. Investigating the effectiveness of ChatGPT in mathematical reasoning and problem solving: Evidence from the Vietnamese national high school graduation examination. arXiv arXiv:2306.06331. [Google Scholar] [CrossRef]
- Davis, Ernest, and Gary Marcus. 2015. Commonsense reasoning and commonsense knowledge in artificial intelligence. Communications of the ACM 58: 92–103. [Google Scholar] [CrossRef]
- Floridi, Luciano, and Massimo Chiriatti. 2020. GPT-3: Its nature, scope, limits, and consequences. Minds and Machines 30: 681–94. [Google Scholar] [CrossRef]
- Frieder, Simon, Luca Pinchetti, Alexis Chevalier, Ryan-Rhys Grifths, Tommaso Salvatori, Thomas Lukasiewicz, Philipp C. Petersen, and Julius Berner. 2023. Mathematical capabilities of ChatGPT. arXiv arXiv:2301.13867. [Google Scholar] [CrossRef]
- Jordan, Michael-Irwin, and Tom-Michael Mitchell. 2015. Machine learning: Trends, perspectives, and prospects. Science 349: 255–60. [Google Scholar] [CrossRef] [PubMed]
- Kalyuga, Slava. 2011. Cognitive load theory: How many types of load does it really need? Educational Psychology Review 23: 1–19. [Google Scholar] [CrossRef]
- Kirschner, A. Paul, John Sweller, and Richard E. Clark. 2006. Why minimal guidance during instruction does not work: An analysis of the failure of constructivist, discovery, problem-based, experiential, and inquiry-based teaching. Educational Psychologist 41: 75–86. [Google Scholar] [CrossRef]
- Lake, M. Brenden, Tomer D. Ullman, Joshua B. Tenenbaum, and Samuel J. Gershman. 2016. Building machines that learn and think like people. Behavioral and Brain Sciences 40: 1–58. [Google Scholar] [CrossRef]
- Levesque, Hector-Joseph. 2017. Common Sense, the Turing Test, and the Quest for Real AI. Cambridge: MIT Press. [Google Scholar]
- Marcus, Gary, and Ernest Davis. 2019. Rebooting AI: Building Artificial Intelligence We Can Trust. New York: Pantheon Books. [Google Scholar]
- Minsky, Marvin. 2006. The Emotion Machine: Commonsense Thinking, Artificial Intelligence, and the Future of the Human Mind. New York: Simon & Schuster. [Google Scholar]
- National Assessment Governing Board [NAGB]. 2005. 2005 National Assessment of Educational Progress Mathematics Assessment Framework. Available online: https://files.eric.ed.gov/fulltext/ED512550.pdf (accessed on 19 March 2024).
- National Assessment Governing Board [NAGB]. 2022. Mathematics Assessment Framework for the 2022 and 2024 National Assessment of Educational Progress. Available online: https://www.nagb.gov/naep-subject-areas/mathematics.html (accessed on 13 March 2024).
- National Center for Education Statistics [NCES]. 2020. Digitally Based Assessments. Transition to Digitally Based Assessments. Available online: https://nces.ed.gov/nationsreportcard/dba/ (accessed on 3 March 2024).
- National Center for Education Statistics [NCES]. 2023. About NAEP. A Common Measure of Student Achievement. Available online: https://nces.ed.gov/nationsreportcard/about/ (accessed on 11 March 2024).
- National Council of Teachers of Mathematics [NCTM]. 2014. Principles to Actions: Ensuring Mathematical Success for All. Available online: https://www.nctm.org/PtA/ (accessed on 3 April 2024).
- Ogunleye, Bayode, Kudirat-Ibilola Zakariyyah, Oluwaseun Ajao, Olakunle Olayinka, and Hemlata Sharma. 2024. A systematic review of generative AI for teaching and learning practice. Education Sciences 14: 636. [Google Scholar] [CrossRef]
- OpenAI. 2023. GPT-4 Technical Report. Available online: https://ar5iv.labs.arxiv.org/html/2303.08774 (accessed on 5 May 2024).
- OpenAI. 2024. GPT-4o Technical Report. Available online: https://openai.com/index/gpt-4o-system-card/ (accessed on 26 May 2024).
- Owoseni, Adebowale, Oluwaseun Kolade, and Abiodun Egbetokun. 2024. Enhancing personalised learning and student engagement using generative AI. In Generative AI in Higher Education: Innovation Strategies for Teaching and Learning. Edited by Adebowale Owoseni, Oluwaseun Kolade and Abiodun Egbetokun. Berlin: Springer, pp. 123–50. [Google Scholar] [CrossRef]
- Paas, Fred, Alexander Renkl, and John Sweller. 2003. Cognitive load theory and instructional design: Recent developments. Educational Psychologist 38: 1–4. [Google Scholar] [CrossRef]
- Paas, Fred, and Jeroen J. G. van Merriënboer. 2020. Cognitive-load theory: Methods to manage working memory load in the learning of complex tasks. Current Directions in Psychological Science 29: 394–98. [Google Scholar] [CrossRef]
- Paas, Fred, Tamara van Gog, and John Sweller. 2010. Cognitive load theory: New conceptualizations, specifications, and integrated research perspectives. Educational Psychology Review 22: 115–21. [Google Scholar] [CrossRef]
- Pallant, Julie. 2020. SPSS Survival Manual: A Step by Step Guide to Data Analysis Using IBM SPSS. New York: McGraw-Hill, Open University Press. [Google Scholar]
- Parra-Martinez, F. Andres, Ophélie A. Desmet, and Jonathan Wai. 2023. The Evolution of intelligence: Analysis of the Journal of Intelligence and intelligence. Journal of Intelligence 11: 35. [Google Scholar] [CrossRef]
- Pesovski, Ivica, Ricardo Santos, Roberto Henriques, and Vladimir Trajkovik. 2024. Generative AI for customizable learning experiences. Sustainability 16: 3034. [Google Scholar] [CrossRef]
- Prisacari, Anna-Agripina, and Jared Danielson. 2017. Computer-based versus paper-based testing: Investigating testing mode with cognitive load and scratch paper use. Computers in Human Behavior 77: 1–10. [Google Scholar] [CrossRef]
- Rahman, Md.-Mostafizer, and Yutaka Watanobe. 2023. ChatGPT for education and research: Opportunities, threats, and strategies. Applied Sciences 13: 5783. [Google Scholar] [CrossRef]
- Rittle-Johnson, Bethany, Jon R. Star, and Kelley Durkin. 2009. The importance of prior knowledge when comparing examples: Influences on conceptual and procedural knowledge of equation solving. Journal of Educational Psychology 101: 836–52. [Google Scholar] [CrossRef]
- Sánchez-Ruiz, L. Manuel, Santiago Moll-López, Adolfo Nuñez-Pérez, José A. Moraño-Fernández, and Erika Vega-Fleitas. 2023. ChatGPT challenges blended learning methodologies in engineering education: A case study in mathematics. Applied Sciences 13: 6039. [Google Scholar] [CrossRef]
- Sandu, Raj, Ergun Gide, and Mahmoud Elkhodr. 2024. The role and impact of ChatGPT in educational practices: Insights from an Australian higher education case study. Discover Education 3: 1–16. [Google Scholar] [CrossRef]
- Schorcht, Sebastian, Nils Buchholtz, and Lukas Baumanns. 2024. Prompt the problem—Investigating the mathematics educational quality of AI-supported problem solving by comparing prompt techniques. Frontiers in Education 9: 1–15. [Google Scholar] [CrossRef]
- Stanovich, E. Keith. 2014. Assessing cognitive abilities: Intelligence and more. Journal of Intelligence 2: 8. [Google Scholar] [CrossRef]
- Stein, Mary-Kay, Margaret S. Smith, Marjorie A. Henningsen, and Edward A. Silver. 2000. Implementing Standards-Based Mathematics Instruction: A Casebook for Professional Development. New York: Teachers College Press. [Google Scholar]
- Sternberg, J. Robert. 2021. Adaptive intelligence: Its nature and implications for education. Education Sciences 11: 823. [Google Scholar] [CrossRef]
- Sullivan, Peter, Doug Clarke, and Barbara Clarke. 2012. Teaching with Tasks for Effective Mathematics Learning. Berlin: Springer. [Google Scholar]
- Supriyadi, Edi, and Krida Singgih Kuncoro. 2023. Exploring the future of mathematics teaching: Insight with ChatGPT. Union: Jurnal Ilmiah Pendidikan Matematika 11: 305–16. [Google Scholar] [CrossRef]
- Sweller, John. 1988. Cognitive load during problem solving: Effects on learning. Cognitive Science 12: 257–85. [Google Scholar] [CrossRef]
- Sweller, John. 2011. Cognitive load theory. In The Psychology of Learning and Motivation: Cognition in Education. Edited by José Mestre and Brian H. Ross. Amsterdam: Elsevier Academic Press, pp. 37–76. [Google Scholar] [CrossRef]
- Sweller, John. 2020. Cognitive load theory and educational technology. Educational Technology Research and Development 68: 1–16. [Google Scholar] [CrossRef]
- Sweller, John, and Paul Chandler. 1991. Evidence for cognitive load theory. Cognition and Instruction 8: 351–62. [Google Scholar] [CrossRef]
- Sweller, John, Paul Ayres, and Slava Kalyuga. 2011. Cognitive Load Theory. New York: Springer. [Google Scholar]
- The Nation’s Report Card. 2022. Data Tools: Questions Tool. Explore the Questions Library. Available online: https://www.nationsreportcard.gov/nqt/ (accessed on 1 February 2024).
- van Gog, Tamara, Liesbeth Kester, and Fred Paas. 2011. Effects of worked examples, example-problem, and problem-example pairs on novices’ learning. Contemporary Educational Psychology 36: 212–18. [Google Scholar] [CrossRef]
- van Merriënboer, Jereon J. G., and John Sweller. 2010. Cognitive load theory in health professional education: Design principles and strategies. Medical Education 44: 85–93. [Google Scholar] [CrossRef]
- Wardat, Yousef, Mohammad A. Tashtoush, Rommel AlAli, and Adeeb M. Jarrah. 2023. ChatGPT: A revolutionary tool for teaching and learning mathematics. Eurasia Journal of Mathematics, Science and Technology Education 19: 1–18. [Google Scholar] [CrossRef]
- Webb, Lott-Norman. 2007. Issues related to judging the alignment of curriculum standards and assessments. Applied Measurement in Education 20: 7–25. [Google Scholar] [CrossRef]
- Weld, Daniel-Sabey, and Gagan Bansal. 2019. The challenge of crafting intelligible intelligence. Communications of the ACM 62: 70–79. [Google Scholar] [CrossRef]
- Yoon, Hyunkyoung, Jihye Hwang, Kyungwon Lee, Kyeong Hah-Roh, and Oh Nam Kwon. 2024. Students’ use of generative artificial intelligence for proving mathematical statements. ZDM–Mathematics Education 56: 1531–51. [Google Scholar] [CrossRef]
- Zhai, Xiaoming, and Eric Wiebe. 2023. Technology-based innovative assessment. In Classroom-Based STEM Assessment. Edited by Christopher J. Harris, Eric Wiebe, Shuchi Grover and James W. Pellegrino. Waltham: Community for Advancing Discovery Research in Education, Education Development Center, Inc., pp. 99–125. [Google Scholar]
- Zhai, Xiaoming, and James W. Pellegrino. 2023. Large-scale assessment in science education. In Handbook of Research on Science Education. Edited by Norman G. Lederman, Dana L. Zeidler and Judith S. Lederman. London: Foutledge, pp. 1045–98. [Google Scholar]
- Zhai, Xiaoming, Matthew Nyaaba, and Wenchao Ma. 2024. Can generative AI and ChatGPT outperform humans on cognitive demanding problem-solving tasks in science? Science & Education, in press. [Google Scholar] [CrossRef]
- Zhai, Xiaoming, Yue Yin, James W. Pellegrino, Kevin C. Haudek, and Lehong Shi. 2020. Applying machine learning in science assessment: A systematic review. Studies in Science Education 56: 111–51. [Google Scholar] [CrossRef]

| Grade Level | SR 1 | SCR 2 | ECR 3 | MC 4 | Sum (SR + SCR + ECR + MC) | |
|---|---|---|---|---|---|---|
| Number properties and operations | 4 | 3 | 1 | 1 | - | 5 |
| 8 | 3 | 2 | - | - | 5 | |
| 12 | - | - | 1 | 1 | 2 | |
| Total | 6 | 3 | 2 | 1 | 12 | |
| Measurement | 4 | 5 | 1 | - | - | 6 |
| 8 | 2 | 2 | - | - | 4 | |
| 12 | - | - | - | 2 | 2 | |
| Total | 7 | 3 | 0 | 2 | 12 | |
| Geometry | 4 | 2 | 1 | - | - | 3 |
| 8 | 2 | 1 | 1 | - | 4 | |
| 12 | - | 1 | 2 | 2 | 5 | |
| Total | 4 | 3 | 3 | 2 | 12 | |
| Data analysis, statistics, and probability | 4 | 2 | - | 1 | - | 3 |
| 8 | 2 | 2 | - | - | 4 | |
| 12 | - | 3 | - | 2 | 5 | |
| Total | 4 | 5 | 1 | 2 | 12 | |
| Algebra | 4 | 2 | 1 | - | - | 3 |
| 8 | 2 | 1 | - | - | 3 | |
| 12 | - | 2 | 1 | 3 | 6 | |
| Total | 4 | 4 | 1 | 3 | 12 | |
| Grand total | Sum | 25 | 18 | 7 | 10 | 60 |
| Intraclass Correlation b | 95% Confidence Interval | F Test with True Value 0 | ||||
|---|---|---|---|---|---|---|
| Lower Bound | Upper Bound | Value | ||||
| Single rater measures | 0.905 a | 0.888 | 0.917 | 29.827 | 59 | 120 |
| Average measure for all raters | 0.966 c | 0.948 | 0.978 | 27.827 | 59 | 120 |
| ID | Grade | Subject | Difficulty | Type | Cognitive Load | ||
|---|---|---|---|---|---|---|---|
| Dimension | Task | Aggregated | |||||
| 1 | 4 | Number Properties | Easy | SCR | 1 | 2 | 2 |
| 2 | 4 | Number Properties | Medium | SR | 3 | 2 | 6 |
| 3 | 4 | Number Properties | Medium | SR | 3 | 3 | 9 |
| 4 | 4 | Number Properties | Hard | SR | 3 | 3 | 9 |
| 5 | 4 | Number Properties | Hard | ECR | 3 | 2 | 6 |
| 6 | 8 | Number Properties | Easy | SR | 1 | 2 | 2 |
| 7 | 8 | Number Properties | Medium | SCR | 2 | 2 | 4 |
| 8 | 8 | Number Properties | Medium | SR | 2 | 2 | 4 |
| 9 | 8 | Number Properties | Medium | SR | 3 | 2 | 6 |
| 10 | 8 | Number Properties | Hard | SCR | 3 | 3 | 9 |
| 11 | 12 | Number Properties | Hard | MC | 2 | 2 | 4 |
| 12 | 12 | Number Properties | Hard | ECR | 3 | 3 | 9 |
| 13 | 4 | Measurement | Easy | SR | 2 | 2 | 4 |
| 14 | 4 | Measurement | Easy | SR | 2 | 2 | 4 |
| 15 | 4 | Measurement | Easy | SR | 3 | 2 | 6 |
| 16 | 4 | Measurement | Medium | SR | 2 | 2 | 4 |
| 17 | 4 | Measurement | Medium | SR | 3 | 2 | 6 |
| 18 | 4 | Measurement | Hard | SCR | 3 | 3 | 9 |
| 19 | 8 | Measurement | Easy | SCR | 2 | 2 | 4 |
| 20 | 8 | Measurement | Medium | SR | 2 | 3 | 6 |
| 21 | 8 | Measurement | Hard | SR | 3 | 3 | 9 |
| 22 | 8 | Measurement | Hard | SCR | 2 | 2 | 4 |
| 23 | 12 | Measurement | Hard | MC | 3 | 3 | 9 |
| 24 | 12 | Measurement | Hard | MC | 3 | 3 | 9 |
| 25 | 4 | Geometry | Medium | SR | 2 | 2 | 4 |
| 26 | 4 | Geometry | Medium | SCR | 2 | 2 | 4 |
| 27 | 4 | Geometry | Hard | SR | 3 | 3 | 9 |
| 28 | 8 | Geometry | Easy | SR | 2 | 3 | 6 |
| 29 | 8 | Geometry | Hard | SR | 3 | 3 | 9 |
| 30 | 8 | Geometry | Hard | SCR | 3 | 3 | 9 |
| 31 | 8 | Geometry | Hard | ECR | 3 | 3 | 9 |
| 32 | 12 | Geometry | Medium | MC | 2 | 3 | 6 |
| 33 | 12 | Geometry | Medium | MC | 3 | 3 | 9 |
| 34 | 12 | Geometry | Hard | SCR | 3 | 2 | 6 |
| 35 | 12 | Geometry | Hard | ECR | 3 | 4 | 12 |
| 36 | 12 | Geometry | Hard | ECR | 3 | 3 | 9 |
| 37 | 4 | Data Analysis | Hard | SR | 2 | 2 | 4 |
| 38 | 4 | Data Analysis | Hard | SR | 3 | 2 | 6 |
| 39 | 4 | Data Analysis | Hard | ECR | 3 | 3 | 9 |
| 40 | 8 | Data Analysis | Easy | SR | 2 | 2 | 4 |
| 41 | 8 | Data Analysis | Medium | SCR | 2 | 3 | 6 |
| 42 | 8 | Data Analysis | Hard | SR | 3 | 2 | 6 |
| 43 | 8 | Data Analysis | Hard | SCR | 3 | 3 | 9 |
| 44 | 12 | Data Analysis | Easy | MC | 3 | 3 | 9 |
| 45 | 12 | Data Analysis | Medium | MC | 2 | 3 | 6 |
| 46 | 12 | Data Analysis | Medium | SCR | 3 | 3 | 9 |
| 47 | 12 | Data Analysis | Hard | SCR | 3 | 3 | 9 |
| 48 | 12 | Data Analysis | Hard | SCR | 3 | 4 | 12 |
| 49 | 4 | Algebra | Easy | SR | 1 | 2 | 2 |
| 50 | 4 | Algebra | Medium | SR | 2 | 3 | 6 |
| 51 | 4 | Algebra | Medium | SCR | 2 | 3 | 6 |
| 52 | 8 | Algebra | Easy | SR | 3 | 2 | 6 |
| 53 | 8 | Algebra | Medium | SR | 3 | 3 | 9 |
| 54 | 8 | Algebra | Hard | SCR | 3 | 4 | 12 |
| 55 | 12 | Algebra | Easy | MC | 2 | 2 | 4 |
| 56 | 12 | Algebra | Medium | SCR | 3 | 3 | 9 |
| 57 | 12 | Algebra | Medium | MC | 3 | 2 | 6 |
| 58 | 12 | Algebra | Hard | SCR | 3 | 4 | 12 |
| 59 | 12 | Algebra | Hard | ECR | 3 | 3 | 9 |
| 60 | 12 | Algebra | Hard | MC | 3 | 3 | 9 |
| 95% Confidence Intervals (2-Tailed) a | |||||
|---|---|---|---|---|---|
| Grade Level | Variables_CL | Significance (2-Tailed) | Lower | Upper | |
| 4 | EASPS_CL | 0.664 *** | 0.000 | 0.661 | 0.668 |
| ChatGPT-4o-score_CL | −0.502 ** | 0.005 | −0.507 | −0.498 | |
| GPTscore_CL | −0.469 ** | 0.008 | −0.474 | −0.464 | |
| 8 | EASPS_CL | 0.557 ** | 0.001 | 0.152 | 0.802 |
| ChatGPT-4o-score_CL | −0.412 * | 0.021 | −0.722 | 0.037 | |
| GPTscore_CL | −0.430 * | 0.015 | −0.733 | 0.015 | |
| 12 | EASPS_CL | 0.469 ** | 0.009 | 0.034 | 0.755 |
| ChatGPT-4o-score_CL | −0.332 | 0.066 | −0.675 | 0.128 | |
| GPTscore_CL | −0.280 | 0.121 | −0.643 | 0.184 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaya, D.; Yavuz, S. Can Generative AI and ChatGPT Break Human Supremacy in Mathematics and Reshape Competence in Cognitive-Demanding Problem-Solving Tasks? J. Intell. 2025, 13, 43. https://doi.org/10.3390/jintelligence13040043
Kaya D, Yavuz S. Can Generative AI and ChatGPT Break Human Supremacy in Mathematics and Reshape Competence in Cognitive-Demanding Problem-Solving Tasks? Journal of Intelligence. 2025; 13(4):43. https://doi.org/10.3390/jintelligence13040043
Chicago/Turabian StyleKaya, Deniz, and Selim Yavuz. 2025. "Can Generative AI and ChatGPT Break Human Supremacy in Mathematics and Reshape Competence in Cognitive-Demanding Problem-Solving Tasks?" Journal of Intelligence 13, no. 4: 43. https://doi.org/10.3390/jintelligence13040043
APA StyleKaya, D., & Yavuz, S. (2025). Can Generative AI and ChatGPT Break Human Supremacy in Mathematics and Reshape Competence in Cognitive-Demanding Problem-Solving Tasks? Journal of Intelligence, 13(4), 43. https://doi.org/10.3390/jintelligence13040043






