Deterministic Input, Noisy Mixed Modeling for Identifying Coexisting Condensation Rules in Cognitive Diagnostic Assessments
Abstract
1. Introduction
2. Background
2.1. Deterministic Input, Noisy Models with Typical Condensation Rules
2.2. Mixture Item Response Models
3. Deterministic Input, Noisy Mixed Model
3.1. Model Formulation
3.2. Bayesian Parameter Estimation
3.3. Relationship with Existing CDMs
3.4. Parameter Identifiability
4. Simulation Studies
4.1. Study 1
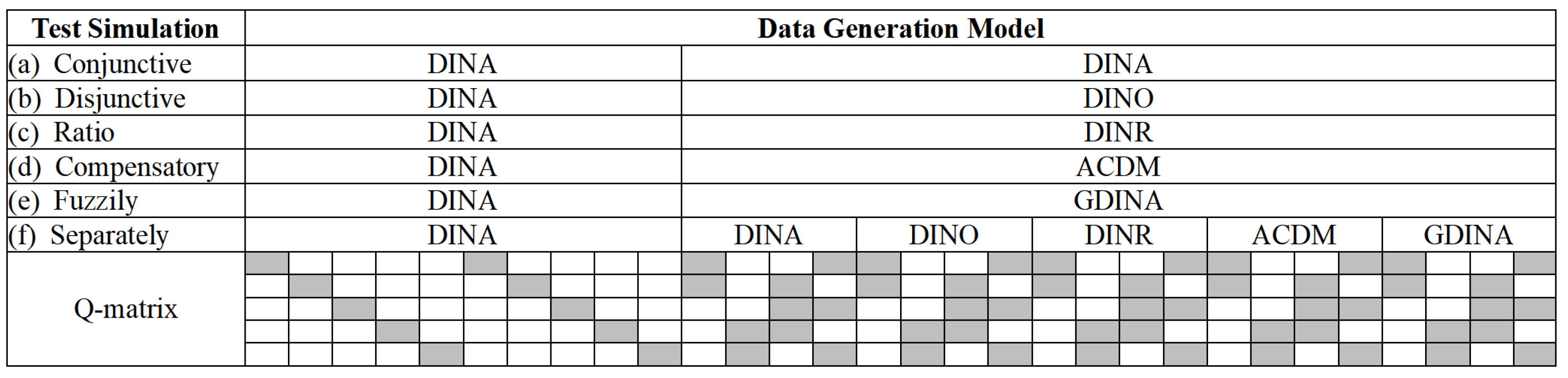
4.1.1. Design and Data Generation
4.1.2. Analysis
4.1.3. Results
4.2. Study 2
4.2.1. Design and Data Generation
4.2.2. Analysis
4.2.3. Results
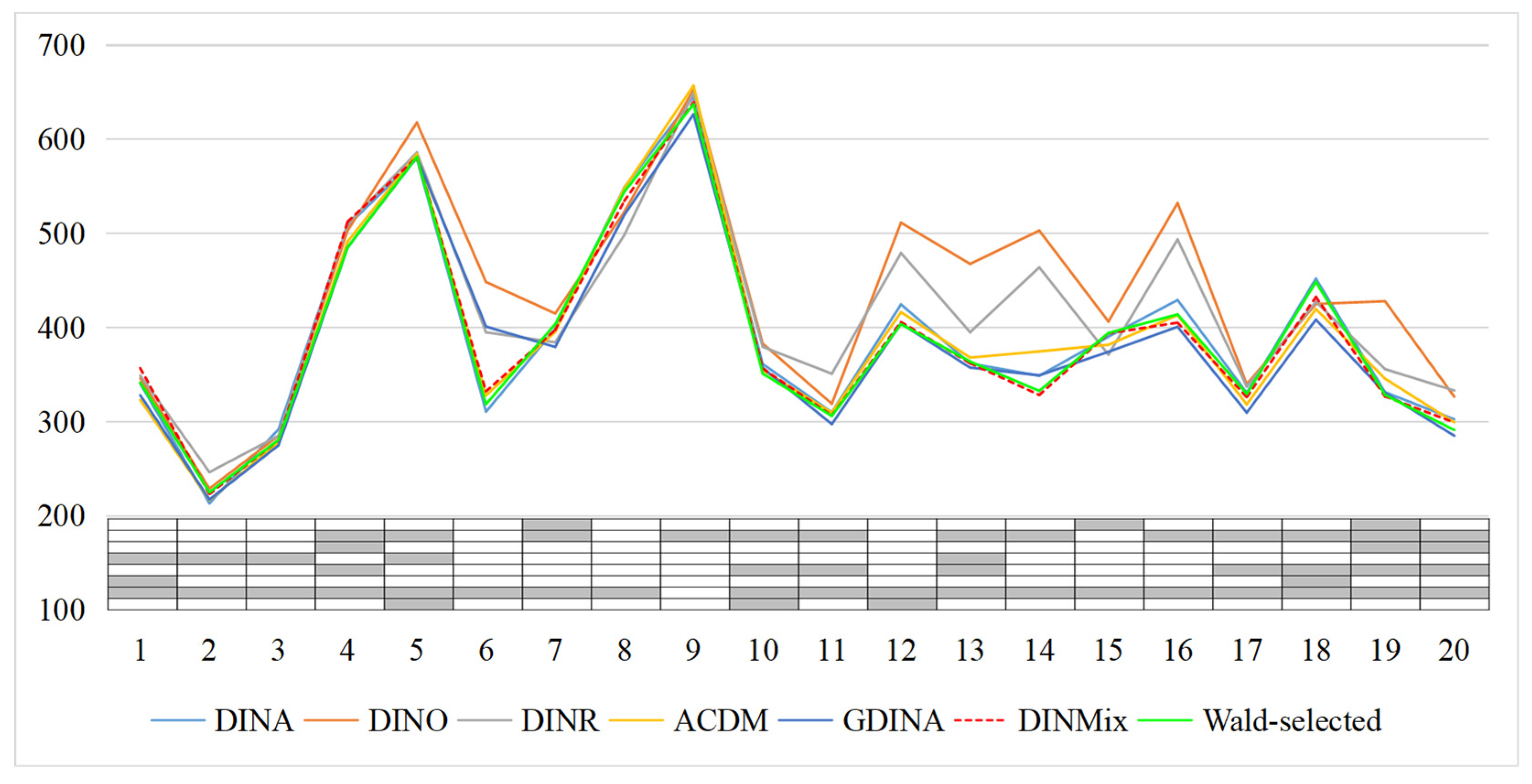
5. An Empirical Example
6. Summary and Discussion
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
| 1 | Specifically, it follows the data-first philosophy (i.e., by developing more complex models to realize the analysis of data in complex situations). In contrast, for the perspective of measurement, considering the viewpoint of garbage-in, garbage-out for predetermined measurement objects (e.g., attributes and cognitive processes) to ensure the reliability and validity of measurement, factors unrelated to the measurement should be excluded (i.e., be revised or be deleted) as much as possible. |
| 2 | Any one element in τi can be set to 1 because all CDMs (for binary attributes) are identical to each other for unidimensional items. |
| 3 | According to the p-values of the Wald test, items 1, 4, 12, 14, and 16 are applicable to the GDINA model, while the remaining items are applicable to the DINA model. |
| 4 | The author does, however, note that this Q-matrix has been suggested to be revised by some previous studies (e.g., Chen et al. 2018). However, it is still fair to compare several models with the same Q-matrix, especially when there is no definite conclusion about the revision of this Q-matrix. |
| 5 |
References
- Beck, Lewis White. 1943. The principle of parsimony in empirical science. The Journal of Philosophy 40: 617–33. [Google Scholar] [CrossRef]
- Brooks, Stephen P., and Andrew Gelman. 1998. General methods for monitoring convergence of iterative simulations. Journal of Computational and Graphical Statistics 7: 434–55. [Google Scholar]
- Chen, Yinghan, Steven Andrew Culpepper, Yuguo Chen, and Jeffrey Douglas. 2018. Bayesian estimation of the DINA Q matrix. Psychometrika 83: 89–108. [Google Scholar] [CrossRef] [PubMed]
- Chiu, Chia-Yi, Jeffrey Douglas, and Xiaodong Li. 2009. Cluster analysis for cognitive diagnosis: Theory and applications. Psychometrika 74: 633–65. [Google Scholar] [CrossRef]
- Choi, Hye-Jeong. 2010. A Model That Combines Diagnostic Classification Assessment with Mixture Item Response Theory Models. Ph.D. dissertation, University of Georgia, Athens, GA, USA. [Google Scholar]
- Cohen, Allan S., and Daniel M. Bolt. 2005. A mixture model analysis of differential item functioning. Journal of Educational Measurement 42: 133–48. [Google Scholar] [CrossRef]
- Culpepper, Steven Andrew. 2015. Bayesian estimation of the DINA model with Gibbs Sampling. Journal of Educational and Behavioral Statistics 40: 454–76. [Google Scholar] [CrossRef]
- de la Torre, Jimmy. 2011. The generalized DINA model framework. Psychometrika 76: 179–99. [Google Scholar] [CrossRef]
- de la Torre, Jimmy, and Chia-Yi Chiu. 2016. A general method of empirical Q-matrix validation. Psychometrika 81: 253–73. [Google Scholar] [CrossRef]
- de la Torre, Jimmy, and Jeffrey Douglas. 2004. Higher-order latent trait models for cognitive diagnosis. Psychometrika 69: 333–53. [Google Scholar] [CrossRef]
- de la Torre, Jimmy, and Jeffrey Douglas. 2008. Model evaluation and multiple strategies in cognitive diagnosis: An analysis of fraction subtraction data. Psychometrika 73: 595–624. [Google Scholar] [CrossRef]
- de la Torre, Jimmy, and Young-Sun Lee. 2013. Evaluating the Wald test for item-level comparison of saturated and reduced models in cognitive diagnosis. Journal of Educational Measurement 50: 355–73. [Google Scholar] [CrossRef]
- DeCarlo, Lawrence. 2011. On the analysis of fraction subtraction data: The DINA model, classification, latent class sizes, and the Q-matrix. Applied Psychological Measurement 35: 8–26. [Google Scholar] [CrossRef]
- DiBello, Louis, William Stout, and Louis Roussos. 1995. Unified cognitive/psychometric assessment likelihood-based classification techniques. In Cognitively Diagnostic Assessment. Edited by Paul D. Nichols, Susan F. Chipman and Robert L. Brennan. Hillsdale: Erlbaum, pp. 361–90. [Google Scholar]
- Embretson, Susan. 1984. A general latent trait model for response processes. Psychometrika 49: 175–86. [Google Scholar] [CrossRef]
- Gu, Yuqi, and Gongjun Xu. 2019. The sufficient and necessary condition for the identifiability and estimability of the DINA model. Psychometrika 84: 468–83. [Google Scholar] [CrossRef] [PubMed]
- Gu, Yuqi, and Gongjun Xu. 2020. Partial identifiability of restricted latent class models. The Annals of Statistics 48: 2082–107. [Google Scholar] [CrossRef]
- Hartz, Sarah, and Louis Roussos. 2008. The fusion model for skills diagnosis: Blending theory with practicality. ETS Research Report Series 2008: i-57. [Google Scholar] [CrossRef]
- Henson, Robert, Jonathan Templin, and John Willse. 2009. Defining a family of cognitive diagnosis models using log-linear models with latent variables. Psychometrika 74: 191–210. [Google Scholar] [CrossRef]
- Jang, Eunice Eunhee. 2009. Cognitive diagnostic assessment of L2 reading comprehension ability: Validity arguments for Fusion Model application to LanguEdge assessment. Language Testing 26: 31–73. [Google Scholar] [CrossRef]
- Jiang, Zhehan, and Wenchao Ma. 2018. Integrating differential evolution optimization to cognitive diagnostic model estimation. Frontiers in Psychology 9: 2142. [Google Scholar] [CrossRef]
- Junker, Brian, and Klaas Sijtsma. 2001. Cognitive assessment models with few assumptions, and connections with nonparametric item response theory. Applied Psychological Measurement 25: 258–72. [Google Scholar] [CrossRef]
- Kim, Jee-Seon, and Daniel Bolt. 2007. Estimating item response theory models using Markov chain Monte Carlo methods. Educational Measurement: Issues and Practice 26: 38–51. [Google Scholar] [CrossRef]
- Levy, Roy, and Robert Mislevy. 2016. Bayesian Psychometric Modeling. Boca Raton: CRC Press. [Google Scholar]
- Liu, Ying, Jeffrey Douglas, and Robert Henson. 2009. Testing person fit in cognitive diagnosis. Applied Psychological Measurement 33: 579–98. [Google Scholar] [CrossRef]
- Ma, Wenchao. 2022. A higher-order cognitive diagnosis model with ordinal attributes for dichotomous response data. Multivariate Behavioral Research 57: 408–21. [Google Scholar] [CrossRef]
- Ma, Wenchao, and Jimmy de la Torre. 2016. A sequential cognitive diagnosis model for polytomous responses. British Journal of Mathematical and Statistical Psychology 69: 253–75. [Google Scholar] [CrossRef] [PubMed]
- Ma, Wenchao, and Jimmy de la Torre. 2020. GDINA: An R package for cognitive diagnosis modeling. Journal of Statistical Software 93: 1–26. [Google Scholar] [CrossRef]
- Ma, Wenchao, and Wenjing Guo. 2019. Cognitive diagnosis models for multiple strategies. British Journal of Mathematical and Statistical Psychology 72: 370–92. [Google Scholar] [CrossRef]
- Ma, Wenchao, Iaconangelo Charies, and Jimmy de la Torre. 2016. Model similarity, model selection, and attribute classification. Applied Psychological Measurement 40: 200–17. [Google Scholar] [CrossRef] [PubMed]
- Man, Kaiwen, and Jeffrey Harring. 2022. Detecting preknowledge cheating via innovative measures: A mixture hierarchical model for jointly modeling item responses, response times, and visual fixation counts. Educational and Psychological Measurement. [Google Scholar] [CrossRef]
- Maris, Eric. 1995. Psychometric latent response models. Psychometrika 60: 523–47. [Google Scholar] [CrossRef]
- Maris, Eric. 1999. Estimating multiple classification latent class models. Psychometrika 64: 187–212. [Google Scholar] [CrossRef]
- Mislevy, Robert. 1996. Test theory reconceived. Journal of Educational Measurement 33: 379–416. [Google Scholar] [CrossRef]
- Mislevy, Robert, and Norman Verhelst. 1990. Modeling item responses when different subjects employ different solution strategies. Psychometrika 55: 195–215. [Google Scholar] [CrossRef]
- Ravand, Hamdollah, Hossein Barati, and Wahyu Widhiarso. 2013. Exploring diagnostic capacity of a high stakes reading comprehension test: A pedagogical demonstration. Iranian Journal of Language Testing 3: 1–27. [Google Scholar]
- Reckase, Mark. 2009. Multidimensional Item Response Theory. New York: Springer. [Google Scholar]
- Rost, Jürgen. 1990. Rasch models in latent classes: An integration of two approaches to item analysis. Applied Psychological Measurement 3: 271–82. [Google Scholar] [CrossRef]
- Rupp, André, Jonathan Templin, and Robert Henson. 2010. Diagnostic Measurement: Theory, Methods, and Applications. New York: Guilford Press. [Google Scholar]
- Spiegelhalter, David, Nicola Best, Bradley Carlin, and Angelika van der Linde. 2002. Bayesian measures of model complexity and fit. Journal of the Royal Statistical Society Series B 64: 583–639. [Google Scholar] [CrossRef]
- Tatsuoka, Curtis. 2002. Data analytic methods for latent partially ordered classification models. Journal of the Royal Statistical Society, Series C Applied Statistics 51: 337–50. [Google Scholar] [CrossRef]
- Tatsuoka, Kikumi. 1983. Rule space: An approach for dealing with misconceptions based on item response theory. Journal of Educational Measurement 20: 345–54. [Google Scholar] [CrossRef]
- Templin, Jonathan, and Robert Henson. 2006. Measurement of psychological disorders using cognitive diagnosis models. Psychological Methods 11: 287–305. [Google Scholar] [CrossRef]
- von Davier, Matthias. 2008a. A general diagnostic model applied to language testing data. British Journal of Mathematical and Statistical Psychology 61: 287–307. [Google Scholar] [CrossRef]
- von Davier, Matthias. 2008b. The mixture general diagnostic model. In Advances in Latent Variable Mixture Models. Edited by Gregory Hancock and Karen Samuelson. Charlotte: Information Age Publishing, pp. 255–76. [Google Scholar]
- von Davier, Matthias, and Young-Sun Lee. 2019. Handbook of Diagnostic Classification Models: Models and Model Extensions, Applications, Software Packages. New York: Springer. [Google Scholar]
- Wang, Chun, and Gongjun Xu. 2015. A mixture hierarchical model for response times and response accuracy. British Journal of Mathematical and Statistical Psychology 68: 456–77. [Google Scholar] [CrossRef]
- Xu, Gongjun. 2017. Identifiability of restricted latent class models with binary responses. The Annals of Statistics 45: 675–707. [Google Scholar] [CrossRef]
- Xu, Gongjun, and Stephanie Zhang. 2016. Identifiability of diagnostic classification models. Psychometrika 81: 625–49. [Google Scholar] [CrossRef] [PubMed]
- Yamaguchi, Kazuhiro, and Kensuke Okada. 2020. Hybrid cognitive diagnostic model. Behaviormetrika 2020: 1–22. [Google Scholar] [CrossRef]
- Yamamoto, Kentaro. 1989. HYBRID Model of IRT and Latent Class Models. ETS Research Report Series (RR-89-41); Princeton: Educational Testing Service. [Google Scholar]
- Zhan, Peida. 2020. A Markov estimation strategy for longitudinal learning diagnosis: Providing timely diagnostic feedback. Educational and Psychological Measurement 80: 1145–67. [Google Scholar] [CrossRef] [PubMed]
- Zhan, Peida, Hong Jiao, Kaiwen Man, and Lijun Wang. 2019a. Using JAGS for Bayesian cognitive diagnosis modeling: A tutorial. Journal of Educational and Behavioral Statistics 44: 473–503. [Google Scholar] [CrossRef]
- Zhan, Peida, Hong Jiao, Manqian Liao, and Yufang Bian. 2019b. Bayesian DINA modeling incorporating within-item characteristics dependency. Applied Psychological Measurement 43: 143–58. [Google Scholar] [CrossRef]
- Zhan, Peida, Wen-Chung Wang, and Xiaomin Li. 2020. A partial mastery, higher-order latent structural model for polytomous attributes in cognitive diagnostic assessments. Journal of Classification 37: 328–51. [Google Scholar] [CrossRef]




| Attribute Profile | Number of Mastered Attributes | DINA | DINO | DINR | DINMix |
|---|---|---|---|---|---|
| (0, 0, 0) | 0 | 0.1 | 0.1 | 0.1 | 0.1 |
| (1, 0, 0) | 1 | 0.1 | 0.9 | 0.367 | 0.207 |
| (0, 1, 0) | 1 | 0.1 | 0.9 | 0.367 | 0.207 |
| (0, 0, 1) | 1 | 0.1 | 0.9 | 0.367 | 0.207 |
| (1, 1, 0) | 2 | 0.1 | 0.9 | 0.633 | 0.233 |
| (1, 0, 1) | 2 | 0.1 | 0.9 | 0.633 | 0.233 |
| (0, 1, 1) | 2 | 0.1 | 0.9 | 0.633 | 0.233 |
| (1, 1, 1) | 3 | 0.9 | 0.9 | 0.9 | 0.9 |
| LSM | IQ | N | I | TM | g | s | τ1 | τ2 | τ3 | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bias | RMSE | Bias | RMSE | Bias | RMSE | Bias | RMSE | Bias | RMSE | |||||
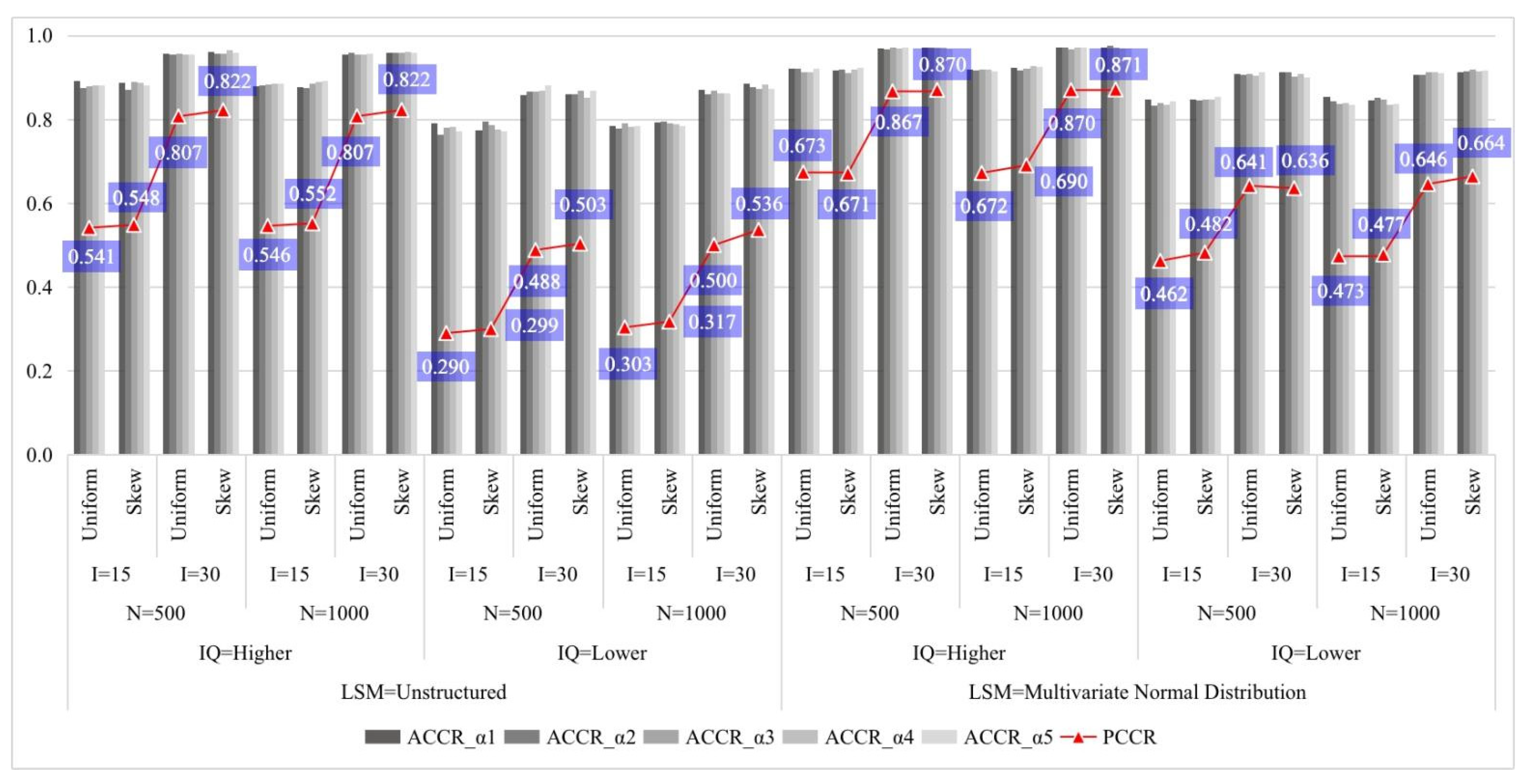
| Un | High | 500 | 15 | Unif | 0.017 | 0.048 | 0.020 | 0.054 | −0.041 | 0.100 | −0.048 | 0.107 | 0.089 | 0.150 |
| Skew | 0.015 | 0.049 | 0.020 | 0.049 | 0.039 | 0.089 | 0.023 | 0.107 | −0.061 | 0.154 | ||||
| 30 | Unif | 0.013 | 0.037 | 0.013 | 0.035 | −0.036 | 0.083 | −0.041 | 0.090 | 0.077 | 0.121 | |||
| Skew | 0.009 | 0.036 | 0.011 | 0.035 | −0.023 | 0.089 | −0.013 | 0.084 | 0.037 | 0.134 | ||||
| 1000 | 15 | Unif | 0.009 | 0.040 | 0.014 | 0.038 | −0.029 | 0.085 | −0.024 | 0.093 | 0.053 | 0.132 | ||
| Skew | 0.008 | 0.036 | 0.007 | 0.036 | 0.013 | 0.076 | 0.013 | 0.087 | −0.026 | 0.130 | ||||
| 30 | Unif | 0.005 | 0.025 | 0.008 | 0.026 | −0.042 | 0.078 | −0.035 | 0.075 | 0.077 | 0.126 | |||
| Skew | 0.006 | 0.024 | 0.007 | 0.024 | −0.025 | 0.073 | −0.026 | 0.072 | 0.050 | 0.119 | ||||
| Low | 500 | 15 | Unif | 0.012 | 0.059 | 0.022 | 0.065 | −0.019 | 0.080 | −0.020 | 0.085 | 0.039 | 0.077 | |
| Skew | 0.013 | 0.063 | 0.018 | 0.064 | 0.084 | 0.117 | 0.054 | 0.153 | −0.138 | 0.215 | ||||
| 30 | Unif | 0.011 | 0.049 | 0.017 | 0.048 | −0.030 | 0.096 | −0.015 | 0.099 | 0.045 | 0.081 | |||
| Skew | 0.008 | 0.050 | 0.012 | 0.047 | −0.009 | 0.121 | 0.003 | 0.124 | 0.006 | 0.167 | ||||
| 1000 | 15 | Unif | 0.006 | 0.048 | 0.015 | 0.055 | −0.026 | 0.099 | −0.012 | 0.097 | 0.039 | 0.087 | ||
| Skew | 0.001 | 0.052 | 0.010 | 0.049 | 0.081 | 0.131 | 0.036 | 0.144 | −0.117 | 0.200 | ||||
| 30 | Unif | 0.006 | 0.037 | 0.010 | 0.039 | −0.034 | 0.092 | −0.031 | 0.094 | 0.065 | 0.104 | |||
| Skew | 0.001 | 0.036 | 0.008 | 0.036 | −0.013 | 0.099 | −0.009 | 0.107 | 0.022 | 0.145 | ||||
| MVN | High | 500 | 15 | Unif | 0.007 | 0.031 | 0.007 | 0.031 | −0.039 | 0.089 | −0.039 | 0.090 | 0.078 | 0.130 |
| Skew | 0.009 | 0.032 | 0.006 | 0.030 | 0.052 | 0.104 | 0.036 | 0.113 | −0.089 | 0.173 | ||||
| 30 | Unif | 0.005 | 0.026 | 0.004 | 0.025 | −0.043 | 0.086 | −0.039 | 0.086 | 0.083 | 0.125 | |||
| Skew | 0.005 | 0.026 | 0.005 | 0.026 | −0.017 | 0.095 | −0.014 | 0.089 | 0.031 | 0.147 | ||||
| 1000 | 15 | Unif | 0.004 | 0.023 | 0.005 | 0.023 | −0.037 | 0.087 | −0.038 | 0.093 | 0.076 | 0.156 | ||
| Skew | 0.002 | 0.021 | 0.006 | 0.022 | 0.019 | 0.085 | 0.027 | 0.094 | −0.046 | 0.146 | ||||
| 30 | Unif | 0.003 | 0.018 | 0.004 | 0.018 | −0.040 | 0.079 | −0.044 | 0.080 | 0.084 | 0.133 | |||
| Skew | 0.002 | 0.018 | 0.003 | 0.018 | −0.019 | 0.077 | −0.019 | 0.078 | 0.037 | 0.132 | ||||
| Low | 500 | 15 | Unif | −0.001 | 0.040 | 0.002 | 0.041 | −0.032 | 0.097 | −0.036 | 0.097 | 0.069 | 0.095 | |
| Skew | −0.004 | 0.041 | −0.001 | 0.039 | 0.087 | 0.134 | 0.041 | 0.141 | −0.128 | 0.201 | ||||
| 30 | Unif | 0.004 | 0.034 | 0.007 | 0.034 | −0.033 | 0.096 | −0.028 | 0.097 | 0.061 | 0.090 | |||
| Skew | 0.002 | 0.034 | 0.006 | 0.033 | −0.008 | 0.126 | 0.001 | 0.124 | 0.007 | 0.167 | ||||
| 1000 | 15 | Unif | 0.000 | 0.031 | 0.001 | 0.029 | −0.040 | 0.105 | −0.029 | 0.103 | 0.069 | 0.110 | ||
| Skew | −0.003 | 0.031 | 0.004 | 0.031 | 0.057 | 0.109 | 0.044 | 0.127 | −0.102 | 0.176 | ||||
| 30 | Unif | 0.001 | 0.025 | 0.005 | 0.024 | −0.037 | 0.096 | −0.033 | 0.092 | 0.071 | 0.106 | |||
| Skew | 0.001 | 0.023 | 0.005 | 0.023 | −0.011 | 0.099 | −0.007 | 0.098 | 0.018 | 0.149 | ||||
| Test Situation | Analysis Model | DIC | Test_–2LCPO | RMSE_g | RMSE_s | PCCR | RMSE_α |
|---|---|---|---|---|---|---|---|
| Conjunctive | DINA | 20,748.69 | 21,201.02 | 0.012 | 0.021 | 0.805 | 0.006 |
| DINMix | 20,852.34 | 21,256.41 | 0.024 | 0.022 | 0.804 | 0.006 | |
| Disjunctive | DINO | 20,746.62 | 21,200.64 | 0.022 | 0.013 | 0.806 | 0.006 |
| DINMix | 20,827.94 | 21,251.88 | 0.022 | 0.024 | 0.803 | 0.006 | |
| Ratio | DINR | 29,963.85 | 30,625.57 | 0.020 | 0.020 | 0.853 | 0.004 |
| DINMix | 30,020.02 | 30,676.92 | 0.021 | 0.021 | 0.852 | 0.004 | |
| Compensatory | ACDM | 29,613.86 | 30,390.21 | 0.020 | 0.020 | 0.853 | 0.003 |
| DINMix | 30,084.68 | 30,713.51 | 0.022 | 0.021 | 0.844 | 0.004 | |
| Fuzzily | GDINA | 28,541.86 | 29,260.53 | 0.020 | 0.022 | 0.845 | 0.004 |
| DINMix | 28,743.04 | 29,372.46 | 0.023 | 0.024 | 0.840 | 0.004 | |
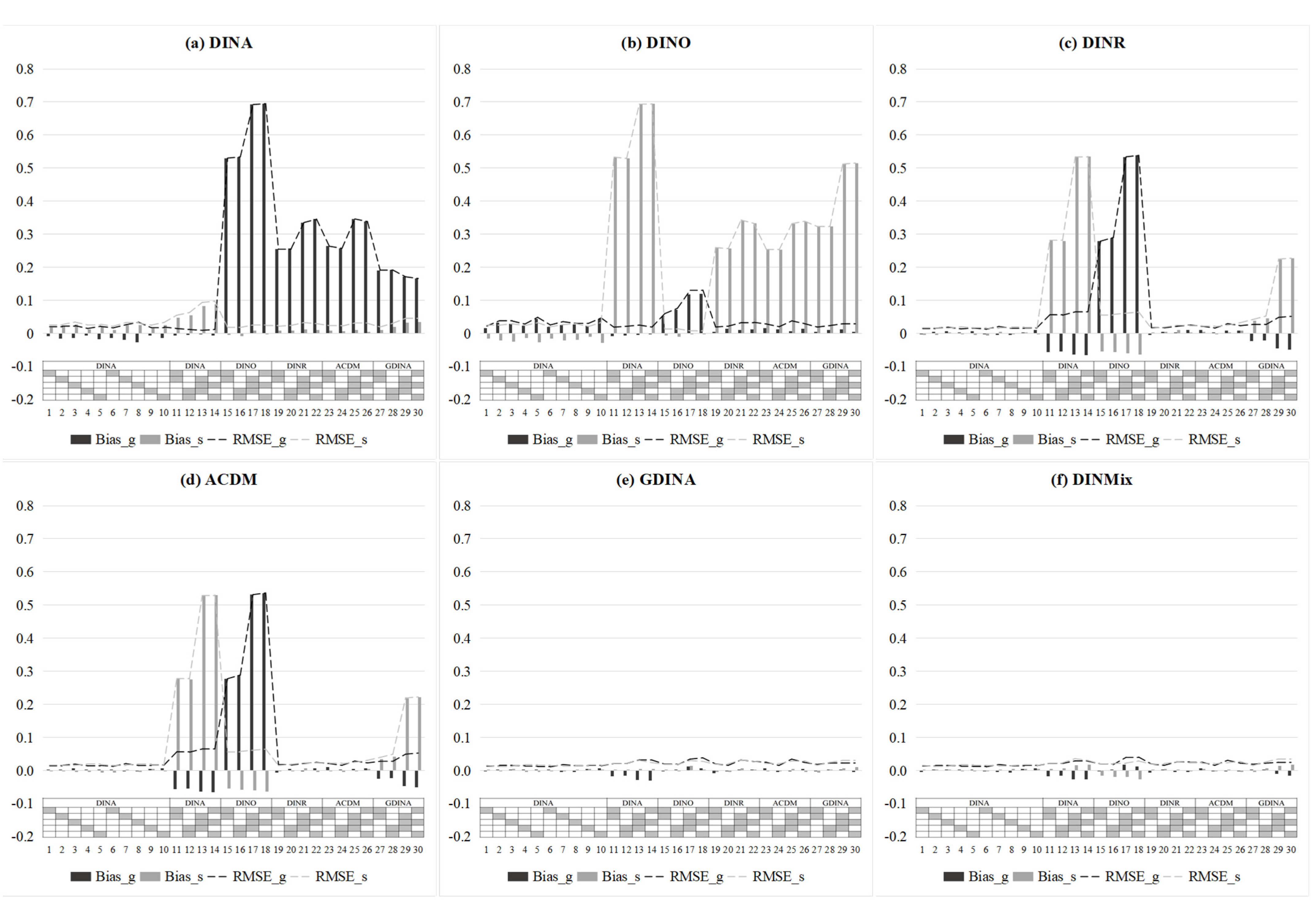
| Separately | DINA | 29,348.12 | 29,971.11 | 0.195 | 0.035 | 0.746 | 0.007 |
| DINO | 30,078.30 | 30,616.86 | 0.039 | 0.227 | 0.726 | 0.008 | |
| DINR | 28,386.28 | 28,972.58 | 0.079 | 0.093 | 0.827 | 0.004 | |
| ACDM | 28,266.83 | 28,911.75 | 0.079 | 0.092 | 0.828 | 0.004 | |
| GDINA | 25,595.61 | 26,341.86 | 0.022 | 0.022 | 0.900 | 0.003 | |
| DINMix | 25,744.26 | 26,397.83 | 0.021 | 0.022 | 0.899 | 0.003 |
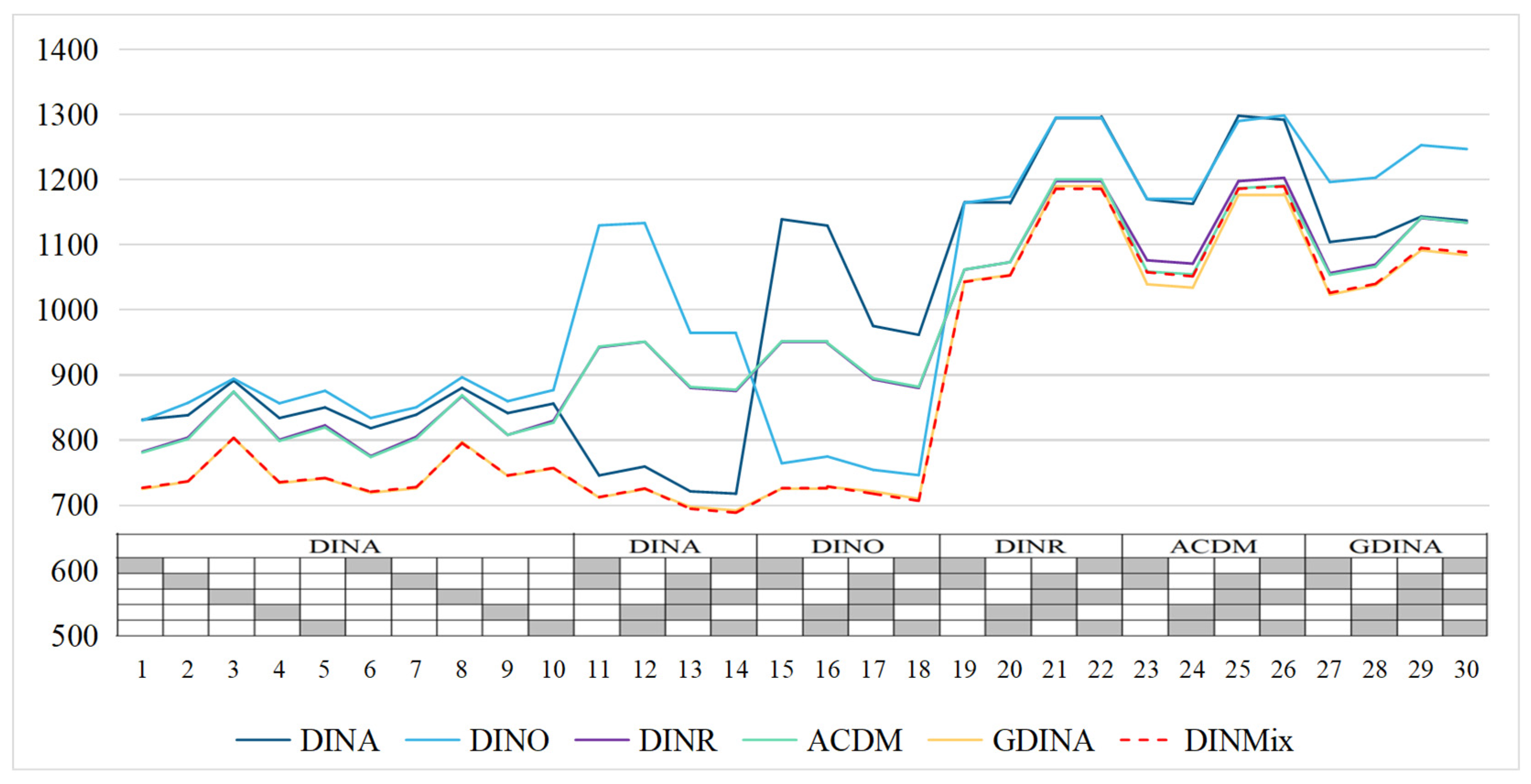
| Analysis Model | DIC | Test-Level –2LCPO |
|---|---|---|
| DINA | 8347.341 | 7882.304 |
| DINO | 9038.505 | 8665.394 |
| DINR | 8911.684 | 8293.461 |
| ACDM | 10,528.705 | 7826.567 |
| GDINA | 11,096.800 | 7690.248 |
| DINMix | 8330.826 | 7803.378 |
| Wald-selected | 8785.672 | 7783.750 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhan, P. Deterministic Input, Noisy Mixed Modeling for Identifying Coexisting Condensation Rules in Cognitive Diagnostic Assessments. J. Intell. 2023, 11, 55. https://doi.org/10.3390/jintelligence11030055
Zhan P. Deterministic Input, Noisy Mixed Modeling for Identifying Coexisting Condensation Rules in Cognitive Diagnostic Assessments. Journal of Intelligence. 2023; 11(3):55. https://doi.org/10.3390/jintelligence11030055
Chicago/Turabian StyleZhan, Peida. 2023. "Deterministic Input, Noisy Mixed Modeling for Identifying Coexisting Condensation Rules in Cognitive Diagnostic Assessments" Journal of Intelligence 11, no. 3: 55. https://doi.org/10.3390/jintelligence11030055
APA StyleZhan, P. (2023). Deterministic Input, Noisy Mixed Modeling for Identifying Coexisting Condensation Rules in Cognitive Diagnostic Assessments. Journal of Intelligence, 11(3), 55. https://doi.org/10.3390/jintelligence11030055





