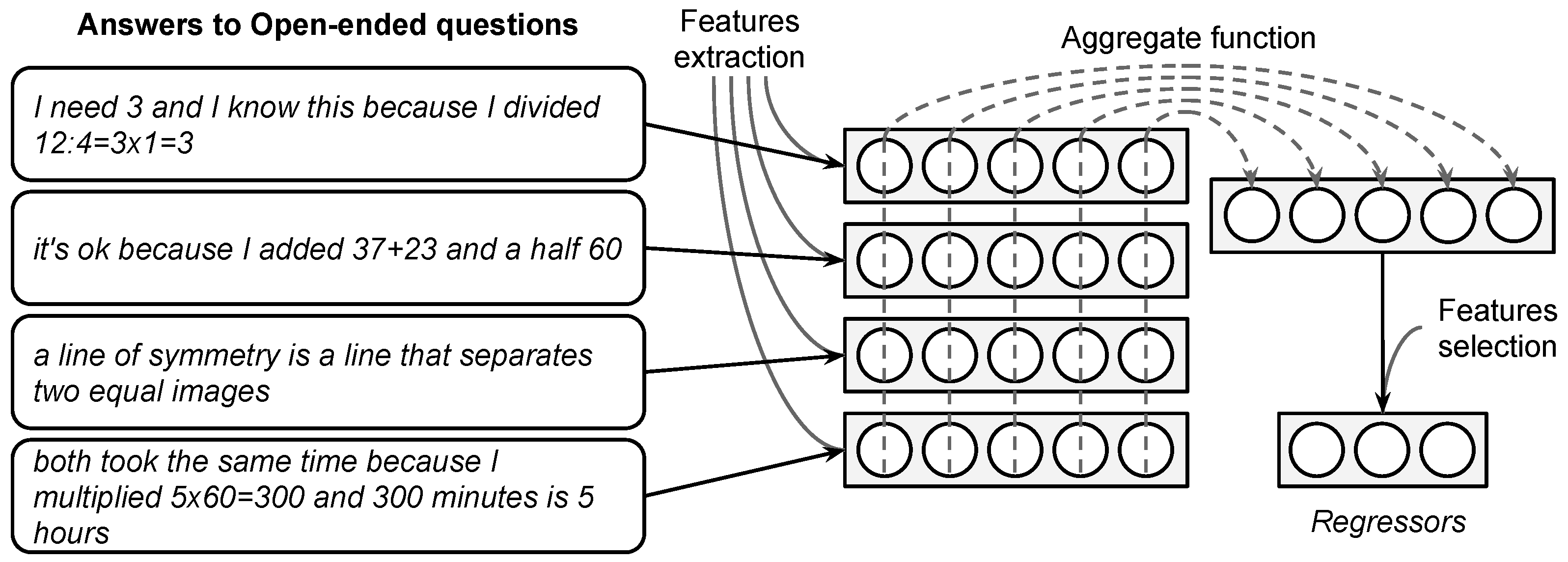
Appendix A.1. Genetic Algorithm to Feature Selection
This appendix describes in detail what the genetic algorithm used for the selection of variables (or regressors) of the Open-ended model consists of and how it is implemented. The Algorithm A1, is the main pseudocode of the genetic algorithm. The following sections define and explain each auxiliary function present in the pseudocode.
| Algorithm A1 (Main) Genetic algorithm to feature selection |
| Require: Vector of zeros and ones that indicate whether the regressor is in the baseline model, Maximum number of iterations, Data compatible with , Stratified indexes of D, with length , of the form |
| Ensure: |
| 1: | ▹ Initial report station |
| 2: |
| 3: |
| 4: |
| 5: while do | ▹ Recursive stage |
| 6: | ▹ Evolution station |
| 7: |
| 8: |
| 9: |
| 10: |
| 11: if then | ▹ Update new status |
| 12: |
| 13: else | ▹ Report station |
| 14: |
| 15: |
| 16: |
| 17: |
| 18: end if |
| 19: end while |
Broadly speaking, the algorithm is composed of two main stations: (R) reporting station and (E) evolution station. Each of these stations is used in key areas of the code. (R) is used to evaluate a model for a specific selection of variables, and (E) is used to modify a current selection of variables. To have a starting point, (R) is used. Then, a recursive process is performed that uses (E) to move forward and (R) to evaluate and decide whether to continue.
Appendix A.1.1. SeedsGenerator
The objective of variable selection is to find those variables that best generalize the linear model to a set of unobserved data. To quantify this notion of generalization, the data are traditionally divided into two disjoint groups of data, which are called training and testing; here, each set is used to train and test a model, resp. In our case, the way of dividing the data cannot be completely random, since some of the variables are not independent per student (e.g., the school’s SIMCE mean score in the previous year). A split that avoids this type of data contamination is called a stratified data split. The stratification we will use is by school; i.e., there cannot be students from the same school but in different training–test sets.
On the other hand, estimating the performance of a model is usually completed with a cross-validation using specific blocks of training and testing, which is a technique called k-fold cross-validation. This consists of dividing the data into
k blocks, with similar sizes, where one of them is used as a test set and the rest is used for training. For a given partition, there are
k ways to do this. To automatically construct each partition in a random way, we used the python library
random with the function
sample (documentation for
sample:
https://docs.python.org/3/library/random.html#random.sample, accesed on 16 March 2022).
In summary, the function SeedsGenerator receives a stratification of the students by establishment (I) and returns the N randomizations (or seeds) of the data, which are grouped by k blocks where one of them corresponds to testing. In our experiments, , with emulating the typical division of 25/75 test/train. Thus, the output of the function is of the form , where each has k splits of the data. Specifically, each is an array of zeros and ones of equal length to I, where those indices in with ones indicate whether such a stratification is used for testing, and it is zero otherwise (hence for training).
Appendix A.1.2. Metrics
To evaluate the performance of a model on a particular randomization of the data, a k-fold cross-validation is used to estimate this value. In the case of linear regression, the coefficient of determination, commonly denoted as , is used. Since it is desired to evaluate performance in terms of generalization, this metric is used only on the test set.
Now, to evaluate the performance over any possible randomness of the data, it is necessary to compute the metrics over all potential randomness. In our case, we are reduced to estimate each quantity using the seeds generated by the function SeedsGenerator described in the previous part.
In summary, the function Metrics receives a set of regressor selectors, which is a collection of randomizations of the data where each of them corresponds to a possible k-fold cross-validation of the data. With this, the function returns the performance of the model (using a each regressor selector) on each collection and on each k-fold. For this, internally, the function Metrics queries a function that receives a k-fold cross-validation and returns the performance of a linear model trained and tested on each k-fold split. This function is called EvalModel, and it is defined in the next section.
Appendix A.1.3. EvalModel
In the previous section, we talked about estimating the performance of a model (defined by a regressor selector) on a particular randomness of the data using the k-fold cross-validation technique. Briefly, this consists of using the k splits of the data (proposed by the k-fold) and determining the of the linear model over each test set using its respective training set. Unlike a linear model fit with all variables, these will be filtered according to the regressor selector provided, i.e., training and testing the model with only a subset of the variables.
A regressor selector consists of a vector with zeros and ones of the same length as the total number of variables present in the data. Here, the components with ones represent which regressors are selected, and those with zeros represent those that are not selected. This is a vector x where are the selected variables, and are those that are not. For a data set , the variable selection simplifies to reduce X with those columns indented by , that is, to eliminate those in . We will denote as the selection of variables with selector x.
On the other hand, a k-fold cross-validation is of the form with k splits of the data. Each is a split of the data in training and test. Those components in with ones indicate which subset of rows of is used for test and with zeros indicate those used for training, that is and , resp. Similar with y. We will denote by and those portions of the data filtered according to .
According to a typical preprocessing, the data (both training and test) are transformed using standardization, i.e., translated with the mean and scale with the standard deviation, both with the training data. For this, we use from the python module
sklearn.preprocessing the function
StandardScaler (documentation for
StandardScaler:
https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.StandardScaler.html, accesed on 16 March 2022). The preprocessed training and test data, respectively, will be denoted by
y
. For interpretability, the variable
y is not standardized in the process.
After pre-processing the data, a linear model is trained with
. Subsequently, this model is evaluated according to
with
. Here,
corresponds to the prediction of the model with
. To achieve this, we used the python module
sklearn.linear_model with the function
LinearRegression (documentation for
LinearRegression:
https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html, accesed on 16 March 2022).
In summary, the function EvalModel receives a regressor selector x, a stratification of the data (I), the data and a possible k-fold cross-validation of the data. With this, the function returns the value of on test over each k-fold split. This value is determined using the model that chooses those variables selected by x, which is trained with the preprocessed training blocks and tested in the test block. This is the same procedure as described in the previous paragraphs.
Appendix A.1.4. SelectIndividuals
For a regressor selector (x) and a seed collection of data (z), the metrics obtained over each k-fold in z can be averaged. We denote this value by . Given the randomness of seed choice, the values of each are almost certainly different. Potentially, there exist k-folds such that is maximum. However, these values are optimistic, since they do not fully represent the performance of the model defined by x over any randomness in the data. At the same time, there exist k-folds such that is minimum. By the same argument, this time, these values are pessimistic, since they are not representative. Thus, the random choice of some will tend to be a better representative of the actual distribution of expected value of performance . However, the choice of one of each type (optimistic, pessimistic and random) summarizes globally the performance of the model in any of the possible cases, i.e., best, worst, and normal case, respectively.
Now, as each was defined, its value is conditionally dependent on the model that uses the regressors selected by x. That is, if x is modified (e.g., adding regressors), there is a non-zero probability that will change value, and potentially, this value will increase. Following this idea, each possible case for (best, worst and normal) characterizes a starting point for modifying the variables selected by x. Under certain conditions, the random choice of only the normal case could increase the number of iterations to find an optimal set of variables. This hypothesis is no more than a design assumption; this paper does not study whether this hypothesis is true or false.
Another view of the choice of only three cases, defined as best, worst, and normal case, follows from informative assumptions
Leardi et al. (
1992). A worst case is potentially more informative than a normal case. This is because the associated seed describes a case where the variables selected by
x do not perform well. On the other hand, for the best case, the information loaded by the variables selected by
x are valuable, since they allow a good performance. As this performance of the selected variables may not be representative, the normal case regularizes the performance to the possible superfluous performance of the worst and best case.
In summary, the function SelectIndividuals receives the metrics obtained by a linear model (with a subset of selected variables) on a randomization of the data. With this, three indices are returned corresponding to the seeds (or k-fold) where the model obtained the best-, worst- and normal value of the average over the k-fold.
Appendix A.1.5. Mutation
As suggested in the previous section, given a regressor selector (x) and a possible k-fold cross-validation of the data, x can be modified such that the metrics improve over the k-fold. It is not clear how to perform a clever modification of the regressors selected by x. This is due to the number of possible variants of a selection of variables, since this is exponential in the total number of variables. There are several ways to modify x, among these are: adding an unselected variable, removing a selected variable, replacing a selected variable with unselected variables, versions of the above operations but with pairs of variables, etc. In this work, we reduced ourselves to use only two operations, adding and removing variables.
The procedure chosen using these operations to modify a regressor selector to a better one consists of a recursive process that interleaves operations that add and remove variables in such a way that a variable is added as long as the previous performance is improved, analogously with the operations of removing variables. This procedure eventually ends, since the number of variables is finite, so at most, the attribute selector adds all variables or is left with at least one variable. These are cases where the model achieves over-fitting or under-fitting, respectively.
Now, testing all combinations of finding a variable in which adding (or removing) it will improve performance consumes a considerable amount of time. Therefore, at each iteration, the algorithm randomly chooses a subset of candidate variables to add (or remove, respectively). In our experiments, we consider a subset of size at most 20 variables. This simplification is equivalent to the probability of mutation defined by
Leardi et al. (
1992). To automatically construct each subset in a random way with a specific size, we used the python library
random with the function
sample. To evaluate the performance of the model when adding (or removing) a variable, the already defined function
EvalModel is used.
In summary, the function Mutation receives a selector of regressors and a set of k-folds (or individuals) where the modifications will be performed. It returns the mutations of x using each individual according to the procedure described in the previous paragraphs, i.e., a recursive process of adding–removing variables with random subsamples.
Appendix A.1.6. CrossOver
So far, we have one regressor selector (x), or parent, and three regressor selectors ( and ), or potential offsprings. Here, each potential child corresponds to the modified version of x with mutations on its associated k-folds (best, worst, and normal case) obtained with the function Mutation defined in the previous section. If we select any of the potential offsprings as the next generation, the selected regressors are likely to encode information biased to the associated seed that was used for the mutation, which only saves local information from the data. This is because at that stage, the variables selected are such that the performance is maximal. To avoid bias in the decision of the candidate offsprings, a cross-over is performed.
When the mutation step is performed, two things usually happen: (a) between each potential offspring, the variables chosen are mostly different and (b) the same, but between each potential offspring with the parent. This is a problem, since the information from each potential offspring and parent is equally valuable. However, it is necessary to choose a single offspring that retains the most information from both the potential offsprings and the parent. To solve this, the potential offsprings can be mixed with each other and with the parent. This technique serves both to regularize the optimization and to explore other untested regressor selectors.
Now, to explain how to mix regressor selectors, we will consider and as two example regressor selectors. Suppose and are different but share at least one selected variable. If and share a selected variable, then the mixture also selects it, i.e., the common information holds. If selects a variable that does not select, then with probability p, the mixture also selects that variable. This allows the mixture to be randomized without privileging the origin of the variable and avoid that indiscriminately adding all the variables. If matters as much as , then the probability p is equal to . However, in our experiments, we consider , privileging . This process repeats itself, but with probability when selects a variable that does not select.
With this scheme, we can mix two regressor selectors. For simplicity, we will consider this way of mixing and not with trios, quartets, etc. On the other hand, for four regressor selectors (a parent and three potential offsprings), there are six possible pairs of regressor selectors. These are , and . Then, each pair of regressors can be mixed, obtaining the following six new regressor selectors . Here, for each , corresponds to the cross-over (or mixing) between the regressor selectors in .
In summary, the function CrossOver receives a set of three regressor selectors (or potential offspring) and a reference regressor selector (or parent), which will be mixed together. The function returns six new selector regressors, which correspond to the cross-overs between each potential offspring and between each potential offspring with the parent. The mixing (or cross-over) procedure follows the logic described in the previous paragraphs, i.e., keeping common information and randomly withholding information that is not common.
Appendix A.1.7. SelectBest
After performing a cross-over, one of the new selector regressors (or new individuals) must be chosen to become the offspring (or new parent). To do this, given the seed collection of data (z), the performance of each new individual on z is evaluated. The performance is calculated with the already defined function Metrics. Then, for each new individual, we average all its local performance ( in each k-fold), estimating the global performance over z. With these values, the individual with the highest global performance is chosen.
In summary, the function SelectBest receives a set of metrics associated to cross-over individuals over a seed collection of data and returns the individual with the best global performance.
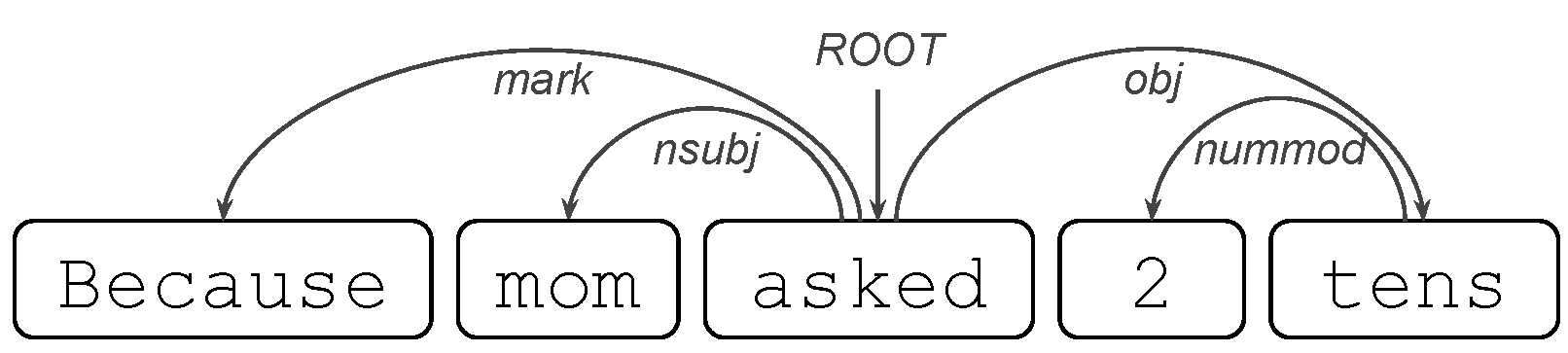 where tens is the object that undergoes the movement of the verb asked.
where tens is the object that undergoes the movement of the verb asked.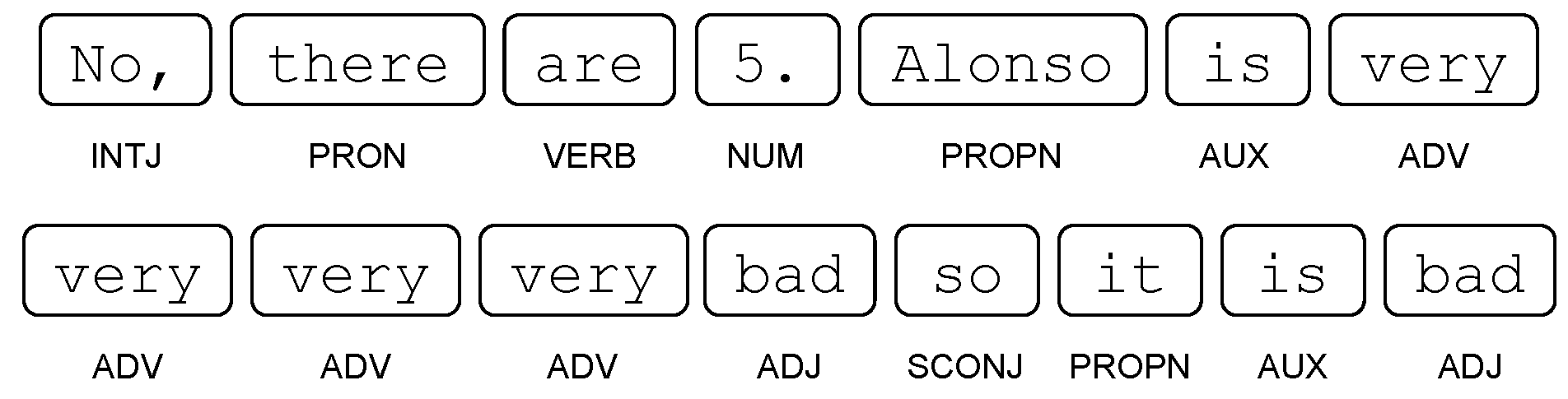 where the word very repeatedly modifies the adjective bad.
where the word very repeatedly modifies the adjective bad.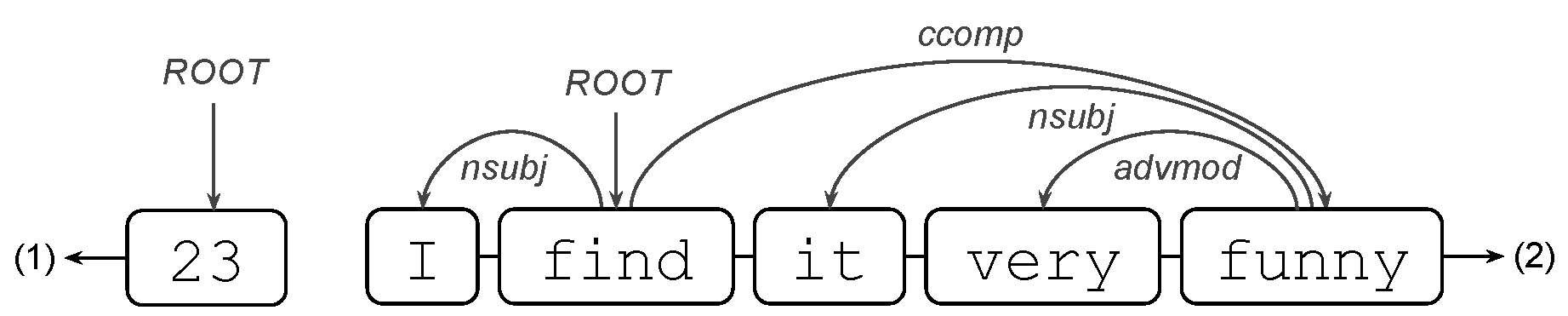 where in (1), the only token 23 will have the ROOT tag, while in (2), the token will be find.
where in (1), the only token 23 will have the ROOT tag, while in (2), the token will be find.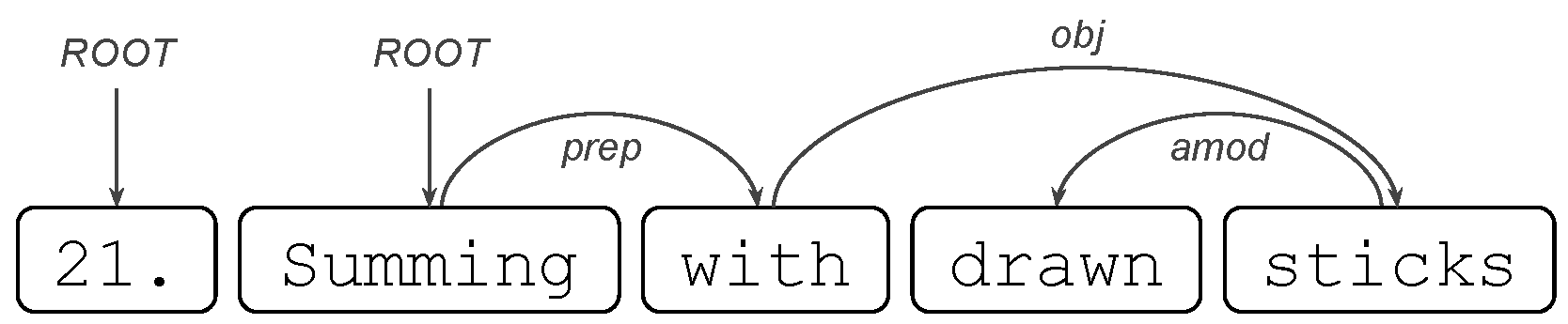 where drawn is an adjectival modifier of the noun sticks.
where drawn is an adjectival modifier of the noun sticks.