The Reasonable Effectiveness of Randomness in Scalable and Integrative Gene Regulatory Network Inference and Beyond

Abstract

Gene regulation is orchestrated by a vast number of molecules, including transcription factors and co-factors, chromatin regulators, as well as epigenetic mechanisms, and it has been shown that transcriptional misregulation, e.g., caused by mutations in regulatory sequences, is responsible for a plethora of diseases, including cancer, developmental or neurological disorders. As a consequence, decoding the architecture of gene regulatory networks has become one of the most important tasks in modern (computational) biology. However, to advance our understanding of the mechanisms involved in the transcriptional apparatus, we need scalable approaches that can deal with the increasing number of large-scale, high-resolution, biological datasets. In particular, such approaches need to be capable of efficiently integrating and exploiting the biological and technological heterogeneity of such datasets in order to best infer the underlying, highly dynamic regulatory networks, often in the absence of sufficient ground truth data for model training or testing. With respect to scalability, randomized approaches have proven to be a promising alternative to deterministic methods in computational biology. As an example, one of the top performing algorithms in a community challenge on gene regulatory network inference from transcriptomic data is based on a random forest regression model. In this concise survey, we aim to highlight how randomized methods may serve as a highly valuable tool, in particular, with increasing amounts of large-scale, biological experiments and datasets being collected. Given the complexity and interdisciplinary nature of the gene regulatory network inference problem, we hope our survey maybe helpful to both computational and biological scientists. It is our aim to provide a starting point for a dialogue about the concepts, benefits, and caveats of the toolbox of randomized methods, since unravelling the intricate web of highly dynamic, regulatory events will be one fundamental step in understanding the mechanisms of life and eventually developing efficient therapies to treat and cure diseases.

1. Introduction

“… So there are very complex different ways that genes are regulated. I kind of look at it as playing music: You have chords on a guitar, or you play with a right and a left hand on the piano. It depends what strings you push down and what strings you strum, or what keys are up and what keys are down, that determine what the profile of the gene expression will be or the sound that you hear.”

David M. Bodine [1]

Gene regulatory networks lie at the core of all biological processes of organisms and—in their most basic form—describe the intricate orchestration of transcription factor proteins binding to regulatory sequences of their respective target genes in order to affect their temporal and spatial expression [2]. Gene regulation is the driver behind the emergence of specific cell types with individual gene expression profiles, all derived from a differential utilization of the same underlying genomic sequences. It is also pivotal in enabling an organism to cope with changes in its environment, especially for sessile organisms, such as plants [3]. As a consequence, advancing our understanding of these regulatory systems can directly impact (personalized) medicine as many traits and diseases are associated with variation of regulatory sequences or dysfunctional regulators [2]. In agriculture, targeted alteration of transcriptional regulation has been essential to improve modern crop yields [4], and its elucidation may further help increase metabolite production rates as well as resilience against environmental stresses [5,6].

As a consequence, computational reverse engineering of gene regulatory networks has gained a lot of attention over the last decades, not least driven by the emergence of large-scale gene expression datasets [7,8,9]. However, gene regulatory network inference remains challenging. While inference methods for in silico or prokaryotic data perform well, inferring regulatory networks from eukaryotic datasets is more difficult [8]. This may in part be due to experimental noise in the data itself. To a larger extent, however, eukaryotic regulation of gene function is further affected by chromatin remodeling, post-transcriptional and/or post-translational processes [10]. Fortunately, heterogeneous data integration methods have emerged to construct more reliable models of eukaryotic gene regulation [11,12,13] or gene function prediction [14,15,16].

To advance our understanding of the mechanisms involved in the transcriptional apparatus, we need scalable approaches that can deal with the increasing number of large-scale, high-resolution, biological datasets. Such approaches need to be capable of efficiently integrating and exploiting the biological heterogeneity captured by these datasets in order to best infer the context-specific underlying network architectures. Such heterogeneity includes different datatypes, experimental treatments, developmental stages, cell types, and even organisms. Often, the analysis is further challenged by the absence of sufficient ground truth data for systematic model training or testing. With respect to scalability, randomized approaches have proven to be a promising alternative to deterministic methods in computational biology (and beyond). As an example, one of the top performers in a community challenge [8] on gene regulatory network inference from gene expression data was based on a random forest regression model [17].

In this survey, we aim to: (i) introduce some fundamental molecular biology as it relates to gene regulation as well as the technologies that drive its discovery; (ii) present the basic concepts behind randomness and randomized algorithms; and (iii) discuss three types of randomized methodologies that are among the most frequently used in computational biology and gene regulatory network inference research in particular. Given the complexity and interdisciplinary nature of the gene regulatory network inference problem, we hope our survey may be helpful to both computational and biological scientists, as well as provide a starting point for a dialogue about the concepts, benefits, and caveats of the toolbox of randomized methods.

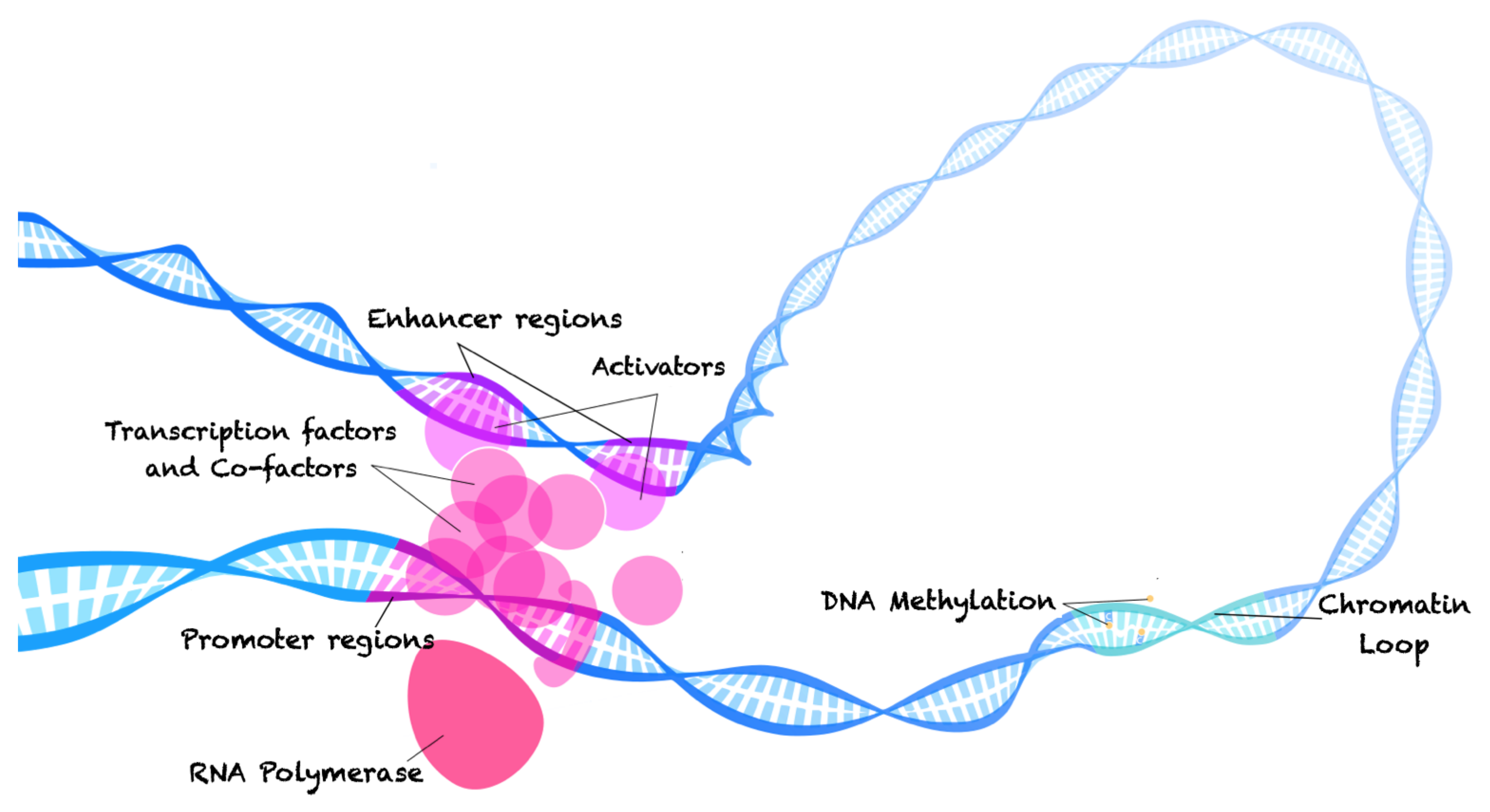
2. The Molecular Biology of Gene Regulation and the Technologies Used to Study It

Although Barbara McClintock discovered the interaction of two genetic loci already in 1951 by showing that differentially pigmented sectors of the maize kernel’s pericarp were due to mobile elements, now known as transposons [18], the first discovery of a gene regulation system is widely considered to be that of the lac operon in Escherichia coli in 1961 by Francois Jacob and Jacques Monod [19]. It involves a negative feedback loop, in which the enzymes of the lactose metabolism are expressed only in the presence of lactose and simultaneous absence of glucose [19]. Generally speaking, transcriptional regulation requires numerous key players, such as the polymerase complex, transcription factors, co-factors, and chromatin modulators to be at the right place at the right time (see Figure 1). Transcription factors thereby bind specific sequence motifs either in promoter regions, i.e., genomic regions proximal to their target gene, or further distant within so-called distal enhancer regions. While activating transcription factors recruit the transcription machinery, which then initiates a gene’s transcription to messenger RNAs (mRNA), repressing transcription factors recruit transcriptional co-repressors such as topless [20]. Functional genomic assays such as chromatin immuno-precipitation followed by sequencing (ChIP-Seq) [21,22,23]) and poly-A mRNA sequencing (RNA-seq) [24] have been instrumental in allowing for the mapping of transcription factor binding sites and steady state gene transcript measurements, respectively.

Virtually all steps of gene expression regulation can be modulated, beginning with the initiation of transcription, RNA processing, up to post-translational modifications of the protein. For example, aforementioned enhancer regions represent important regulator sequence elements bound by transcription factors thereafter directing them to the promoters of target genes [26]. As recent evidence indicates that mutations in enhancers may cause genetic diseases and cancer [26,27,28], there is a great need for their genome-wide analysis. However, their low predictability and distant location relative to their corresponding target genes have been challenging obstacles for the genome-wide discovery of functional enhancers. It had long been known that the genome’s heavily condense structure, organized with protein-complexes together referred to as chromatin, was essential for the spatial compression into nuclei. Until the last decade, however, there was a lack of tools to appreciate the importance of the genome’s dynamic accessibility in fine control of gene expression, or to study the chromatin structure at sites accessible for transcription, including the three-dimensional co-localization of enhancer and promoter elements. To this end, Chromosome Conformation Capture assays [29], such as Hi-C [30], HiChIP [31] or ChIA-PET [32], have been developed to identify spatial proximities across an entire genome. That said, the computational tools for pairing enhancers and target genes are still evolving [33,34].

An example of post-transcriptional gene regulation are microRNAs (miRNA), i.e., endogenous, short (e.g., 24 bp), non-coding RNAs that negatively regulate mRNA abundance by binding to the complementary sequences throughout the target mRNAs, thereby targeting it for RNA silencing [35]. The important role of miRNAs in cancer development has long been established [36,37]. For example, in breast cancer, transcriptional repression of BRCA1 (BReast CAncer gene 1) is caused by over-expressed microRNA-182 [38].

In general, the binding of transcription factors to sequence motifs depends on chromatin accessibility [39,40,41]. Most of the chromatin exists as tightly packed condense DNA (heterochromatin), although two forms, constitutive heterochromatin and facultative heterochromatin, are distinguished based on its accessibility, or lack thereof, to most proteins including transcription factors [42]. This structure is achieved by winding the genomic sequences around protein octamers, called histones, which affects the physical accessibility of the DNA [39]. Hence, through post-translational modifications to the tails of these histone proteins, significant portions of the genome can (dynamically) be silenced, and thus become inaccessible to transcription factors or polymerases [43,44]. Such modifications are facilitated by specialized enzymes, such as histone methyltransferases, acetyltransferases and deacetylases. These specialized enzymes remove or add a diverse range of covalent modifications including ubiquitin, phosphates, methyl or acetyl groups to histone side chains. Together these modifications, referred to as the histone code, serve to recruit other proteins to change chromatin accessibility. For example, pioneer transcription factors play an important role in opening chromatin, which allows transcription factor and polymerase access, whereas histone methylation is often associated with reduced accessibility and sequestering of transcription factors binding elements [45]. Techniques such as MNase-Seq, FAIRE-Seq, DNase-Seq, and ATAC-Seq [39,41,46,47] are used to assess chromatin accessibility, or very recently, MOA-Seq to identify all transcription factor binding sites genome-wide [48].

Aside from chromatin inaccessibility, methylation of the DNA itself is also often associated with the silencing of gene expression [49], although the effect is dependent upon the type of methylation as well as its genomic context [50]. DNA methylation is facilitated by methyltransferase enzymes on cytosine nucleotides. While in animal systems cytosine methylation is predominantly found in CG dinucleotide sequences, also called CpG islands, in plants, methylation occurs in symmetric (i.e., CG and CHG, where H can be A, C, or T) as well as asymmetric (i.e., CHH) genomic contexts [51]. Patches of methylated CG and CHG in promoter and enhancer regions are predominantly associated with a reduction of a gene’s expression [49]. However, they are also found in promotors of microRNAs, which can indirectly increase a gene’s mRNA translation [52]. In addition, the interplay between histone modifications and genome methylation has been characterized to cooperatively control gene regulation [49]. The classical way to measure DNA methylation is bisulfite sequencing [53]. The sodium bisulfite treatment converts unmethylated cytosines into thymines, which allows the quantification of genome-wide methylation levels at single nucleotide resolution [51].

Finally, mutations or natural variation within gene promoters or enhancers are of particular interest for gene regulation analysis [54]. Single nucleotide polymorphisms (SNPs) may cause the loss or creation of promoter binding elements and enhancers. While this is an essential element of evolution, it is also associated with transcriptional miss-regulation, cancer, and genetic diseases [33,34]. Given the plethora of biological layers affecting gene regulation and the heterogeneity of the technologies used to capture them, there has been a considerable amount of work focusing on the computational integration of these diverse functional genomic assays [50,55,56,57,58,59,60,61,62,63,64,65,66,67,68].

3. A Primer on Randomness and Randomized Algorithms

Randomness is a fascinating and powerful concept. Historically, two main worldviews have been postulated regarding its nature. The first one thinks of the world as being basically deterministic, and therefore argues that what we perceive as (apparent) randomness is a mere lack of knowledge of the exact state or description of a system of interest. Throughout history, following this kind of reasoning, randomness has been defined as a sort of antipode of absolute (observational) power. Probably the most famous characterization of this kind of deterministic worldview may be the one given by Laplace in 1814: "... intelligence which could comprehend all the forces that set nature in motion, and all positions of all items of which nature is composed—an intelligence sufficiently vast to submit these data to analysis—it would embrace in the same formula the movements of the greatest bodies in the universe and those of the lightest atom; for it, nothing would be uncertain and the future, as well as the past, would be present to its eyes." [69]. Paradigmatic examples include, e.g., many-body systems in classical mechanics too complex to be considered in all detail and leading to the development of statistical mechanics and thermodynamics, or deterministic chaos [70] where varying initial conditions, even for dynamical systems involving few degrees of freedom, lead to an exponential separation of trajectories, making longtime predictions impossible. In contrast, the second view sees the world as inherently non-deterministic, hence, randomness is an intrinsic property, independent of our knowledge about the system. Intrinsic here means that this kind of randomness cannot be understood in terms of a deterministic, hidden variable model [71]. A prime example of such worldview would be quantum mechanics, where, contrary to Einsteins famous statement: “God does not play dice!” [72], Born’s interpretation of the wave function implies that one may count only on an intrinsically probabilistic description of reality [73], and, as a consequence, has to acknowledge that quantum mechanics could be inherently random [74,75].

Another area in which randomness plays an essential, inherent role is game theory, here in the form of mixed strategy games. A mixed strategy describes the randomization over multiple strategies as opposed to playing merely a single (pure) strategy [76], that is, one randomly chooses among several options to avoid developing a pattern that other players might exploit. It has been proven that if mixed strategies are allowed, every (finite) game has a Nash equilibrium [76], i.e., none of the players has an incentive to change her or his strategy given the opponent’s strategy. However, this is not the case for pure, i.e., deterministic, strategies. As a consequence, randomness guarantees the existence of a Nash equilibrium that would not exist otherwise. Note that playing with a mixed strategy leads to unpredictable outcomes in each play, yet the strategy is rational, i.e., it is meant to maximize a given objective’s expected value. Hence, as long as not humanly predictable, in practice, it makes no difference as to whether an outcome is genuinely unpredictable as in quantum mechanics, or predictable by an outside, more powerful observer [77].

As a final example, in genetics, randomness plays another fundamental role, e.g., in the form of random variations in heritable traits as introduced in Darwin’s theory of evolution by natural selection [78]. Here, one might refer to the definition given by geneticist Theodosius Dobzhansky: “Mutations are random changes because they occur independently of whether they are beneficial or harmful.” [79]. Similarly, the Hardy–Weinberg equilibrium law in population genetics [80], which gives the relative frequencies of genotypes and alleles in a given (infinite) population, is based on the assumption of random mating, i.e., mating irrespective of genetic traits as a selection criterion.

Just these few examples should suffice to convey the important role of randomness, be it apparent or inherent, in nature as well as in numerous scientific and practical applications. Given its importance, in particular within the field of computation theory, we will give a brief account of the mathematical theory of randomness, as well as how it translates into randomized algorithms.

3.1. A Mathematical Theory of Randomness

Gregory Chaitin stated that “randomness is the true foundation of mathematics” [81]. The mathematical theory of randomness, may be seen as an extension of classical probability theory in order to introduce individual random objects [82]. As an example, let’s say a fair coin is flipped ten times and the resulting sequence contains five tails in succession, e.g., 0000011111. The experiment is then repeated, yielding the same number of heads and tails as in the previous one, yet in a more unordered fashion, such as 0010100111. One may have an immediate intuition about the first outcome to appear more special than the second one. However, is such an intuition justified, given that, according to classical probability theory, the probability for both outcomes is exactly the same? Classical probability theory may not be as helpful to transform such intuitions into meaningful mathematical notions given that it is a theory about sets of objects, not of individual objects. The theory of randomness, however, often referred to as algorithmic randomness, was founded based on the theory of computation, in order to give meaning to these individual random objects, specifically random individual sequences.

Early attempts to define randomness in terms of individual random objects date back to Von Mises [83] who formalized already in 1919 the notion that random sequences should be unpredictable. This definition was later extended by Wald [84] and Church [85] giving rise to the notion of what is known as Mises–Wald–Church randomness. It already contains several key ingredients of the modern theory of randomness, including: (i) an insight that randomness is a relative concept, rather than an absolute one, i.e., it depends on choosing a set of selection rules; and (ii) its definition is founded on the theory of computation, thereby restricting to computable selection functions. Other approaches such as Kolmogorov complexity [86] define the intuition that random sequences, given their lack of any inherent, observable structure, are hard to describe by an algorithm, while the approach to define randomness as proposed by Martin-Löf [87] formalizes intuitions underlying measure theory and classical probability. Here, we describe the definition proposed by Kolmogorov and refer the reader to [82] and [88] for excellent overviews of the variety of approaches to define algorithmic randomness.

Kolmogorov theory [86] measures the complexity of random objects in terms of the length of the shortest program needed to generate or describe it. In contrast to information theory, where the entropy measures the randomness for a distribution [89], Kolmogorov’s ideas allow for the evaluation of the randomness of an individual sequence and the theory of computation can be effectively used for its definition.

The Theory of Computation and Kolmogorov’s Definition of Randomness

The theory of computation emerged out of concerns about provability in mathematics in the early 1930s. Gödel’s famous incompleteness theorem states that in any formal system powerful enough to perform arithmetic reasoning, there are always true statements that cannot be proved within the system [90]. Although being a statement about mathematical provability, the proof of the incompleteness theorem is in its core a statement about computability, as the recursive functions utilized by Gödel, were later shown by Turing [91] to define the same class of functions computable by a Turing machine, i.e., there exists a finite step-by-step process, that is able to computes them. Therefore, having a precise mathematical definition of the notion of computability facilitates proving that certain functions or problems cannot be computed, with its prime example being Turing’s Halting Problem. The Halting Problem describes the possibility to decide, given a Turing machine and an input, whether the machine will produces an output in a finite number of steps, as opposed to continuing indefinitely. Turing [91] showed that the Halting Problem is undecidable, that is, that there is no algorithm deciding it.

In order to derive a definition of randomness of sequences in the sense of Kolmogorov, i.e., the length of the shortest program needed to generate it, in a more formal way the notion of a Turing machine is well suited. Note that for illustrative purposes, we only discuss algorithmic randomness in the context of finite binary sequences, which is not a severe restriction, given that many objects, including numbers or graphs, may be naturally represented as such sequences. Further, our example constitutes more than just a toy problem given that, e.g., the verification of binary sequences with respect to the degree of their randomness lies at the heart of applications in cryptography [88]. Following Kolmogorov’s reasoning with respect to the two sequences example given in the beginning of the section, one might be tempted to say that the first one, consisting of consecutive heads followed by the same number of tails, is simpler than the second, because it has a shorter description. More formally, given a Turing machine M, one may define a sequence y to be a description of another sequence x if $M\left(y\right)=x$, i.e., M produces x when given y as input, i.e., the length of the sequence y becomes a measure of the complexity of x. However, this definition still depends on the choice of M. Kolmogorov recognized that a canonical choice for M would be a universal Turing machine, that is, a machine that is able to simulate all other Turing machines. Hence, Kolmogorov complexity of sequence x is denoted as $C\left(x\right)$, i.e., $C\left(x\right)=n$ means that there is a sequence y of length n such that $M\left(y\right)=x$, and that there is no other description sequence y smaller than n. Hence, a sequence x is considered to be (Kolmogorov) random if it has no description y that is shorter than the sequence itself, that is, if there is no way to describe the sequence more efficiently than by listing it completely. In contrast, a sequence of 500 tails would not be considered to be random, since its shortest description is much shorter than the sequence itself. Note that the practical application of Kolmogorov complexity is generally hindered by the fact that the complexity function C is not computable, which is intuitively plausible, since to estimate the complexity of y one would have to evaluate for which inputs x the universal Turing machine M produces y as an output, which itself is impossible due to the undecidability of the Halting Problem. As a consequence, aside a beautiful theoretical advancement of a definition of algorithmic randomness, one might not expect such a definition to be of much practical relevance. It turns out, however, that it does have genuine applications nonetheless, many of which are described in [92]. Leaning more towards the practical application side, we will, however, now discuss how randomness is actually used to define algorithms giving rise to the field of randomized algorithms, and how it can be implemented using stochastic simulations and probabilistic modeling.

3.2. Randomized Algorithms

Besides its fascinating, fundamental role in nature and the attempts to its rigorous, conceptional definition, it is equally intriguing that randomness can be used as an effective strategy for designing algorithms. By the deliberate introduction of randomness into computations [93], randomized algorithms have shown to outperform some of the best deterministic approaches and, furthermore, even allowed for the computation of previously infeasible problems. Monte Carlo methods, introduced by Stan Ulam, Nick Metropolis and John von Neumann [94], rank among the most prominent randomized approaches and have been listed among the best algorithms of the 20th century [95]. Randomized algorithms typically exploit a certain amount of randomness as auxiliary input to their core logic, expecting to achieve reasonable performance on average, that is over all possible choices of randomization. For example, the randomized variant of the Quick Sort algorithm [96] uses random numbers to pick the next pivot. Similarly, Karger’s algorithm for minimum cut detection on graphs randomly selects individual edges for contraction [97]. For a more comprehensive introduction to randomized methods, we refer the reader to [98] or [93].

The two aforementioned examples, that is randomized sorting or the mininum cut algorithm, also exemplify two general design patterns of randomized algorithms. The sorting algorithm refers to a class of randomized algorithms known as Las Vegas algorithms, which are designed to guarantee to always produce a correct or optimum result; however, their time complexity is dependent on a random variable itself. The minimum cut algorithm, on the other hand, belongs to the aforementioned class of algorithms, known as Monte Carlo methods, which are designed to exhibit deterministic time complexity, but a non-zero probability for the output to be incorrect. Hence, Monte Carlo algorithms are typically easier to analyze with respect to their worst case time complexity, as opposed to Las Vegas algorithms, where time complexity is evaluated as the expected value over all possible values of the input random variables. Due to the potential erroneous outputs of Monte Carlo algorithms, the success probability can be amplified by running the algorithm several times with different random sub-samples of the input, and comparing their results, thereby sacrificing runtime, a technique known as amplification. Due to these design patterns, randomized algorithms are of particular interest when certain time or memory constraints exist, and an average case solution is acceptable. In addition, as already hinted at in the elucidation of amplification, an underlying assumption that is pervasive throughout the field of randomized methods is that small random samples taken from a population can be seen to be representative of the entire population. This is of particular interest, since computations involving small samples are less expensive, but may still help to determine characteristic features or latent factors of the whole population [99].

As a side note, in computational complexity theory, randomized algorithms are typically modeled as probabilistic Turing machines, i.e., non-deterministic Turing machines that make random selections between a set of available transitions at each step according to some probability distribution. As a consequence, a probabilistic Turing machine—unlike a deterministic one—may have statistical outcomes; that is, on some given input and instruction state machine, the run times may differ, or the algorithm may even not halt at all [100]. However, there is a large body of work on studying the class of problems solvable in polynomial time by randomized approaches, and given the probabilistic nature of guarantees on performances of randomized algorithms, a variety of class definitions have been proposed [98].

4. On the History and Current Applications of Randomness and Randomized Methods in Computational Biology and Gene Regulation Inference

Randomness has become a key ingredient in several areas of designing algorithms for computational biology and beyond, for example, parameter inference and model selection [101,102,103,104] (see Section 4.1), in data sampling [105] and model building [105,106] (see Section 4.2 and Section 4.3) or data dimensionality reduction and manifold learning [107] (see Section 4.4). Despite aforementioned, theoretical definitions of (algorithmic) randomness as individual random objects, thus separating it from classical probability theory, the actual representation and implementation within individual algorithms as stochastic events is typically based on probabilistic modeling. For example, Bayesian statistical learning provides a coherent probabilistic framework for modeling uncertainty in systems [108]. In particular, sophisticated sampling methodologies, such as Markov Chain Monte Carlo based sampling algorithms [108,109], are typically integrated with probabilistic frameworks [101,102,104,111,112,113].

One of the earlier examples of applying randomized algorithms in computational biology, in particular the inference of gene regulation, is the identification of conserved, transcription factor binding or consensus sequence motifs [114,115]. In their paper Wang et al. adopt a model of consensus pattern detection, showing that with high probability, their randomized algorithm is able to find such a pattern in polynomial time, a problem previously proven to be NP-hard [115]. The aforementioned concepts of random sampling and Monte Carlo based approaches have also been heavily applied in gene network inference, e.g., to predict the effect of single-nucleotide polymorphisms on transcription factor binding affinity [34]. Similarly a plethora of Bayesian modeling approaches based on using Markov Chain Monte Carlo (MCMC) [116] exist for parameter inference or selecting between multiple plausible gene regulatory network architectures given the data, such as (perturbed) gene expression datasets [102,109,111,112,113,117,118].

Other sophisticated methods include randomized tree-based approaches, which rank among the best performing ensemble-based machine learning methodologies for classification or regression tasks [119,120]. As an example, a random forest regression based gene regulatory network inference model [17] was one of the top performers in the DREAM5 network inference challenge [8], as well as on a benchmark on network inference from single-cell transcriptomic data [121]. Other applications of random forest based regression include, e.g., the mapping of genetic variants accounting for confounding factors, such as population structure, and nonlinear interactions between individual causal variants [122]. An example for the design of a random forest-based classification approach for the prediction of high impact cis-regulatory mutations on transcription factor binding is given in [123]. Randomized methods have also been shown to be highly effective for graph clustering and module detection problems. In a recent community challenge that performed a comprehensive assessment of module identification methods across diverse gene networks [124] one of the top performers has been a random walk based approach [125] originally proposed to cluster protein–protein interaction networks [126]. In particular, with the emergence of ever increasing large-scale, high-dimensional datasets, the field of randomized numerical linear algebra [127,128], and in particular randomized matrix decomposition [107] has gained significant attention. Applications include, e.g., single cell RNA-Seq clustering based on Random Projection [129] or large-scale gene regulatory network inference using randomized Singular Value Decomposition [130]. Here, we want to present some of these major areas in randomized algorithms, i.e.: (i) Markov Chain Monte Carlo based sampling (Section 4.1); (ii) random forest regression (Section 4.2); (iii) random walks (Section 4.3); and (iv) randomized matrix decomposition (Section 4.4), alongside some of their applications in computational biology in general, and gene regulatory network inference in particular.

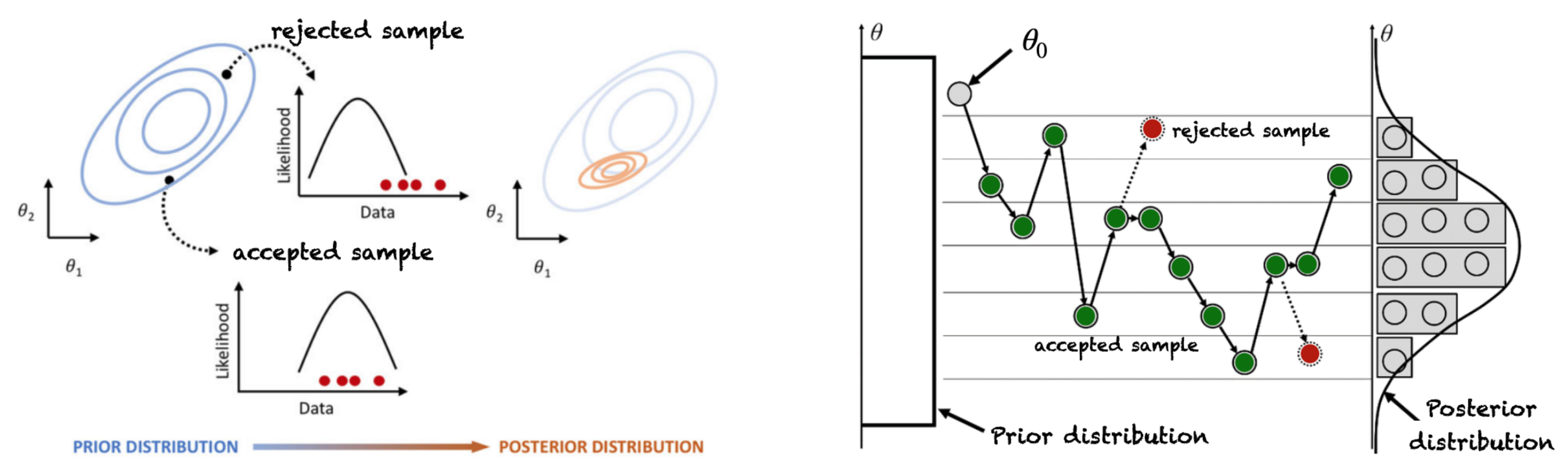
4.1. Markov Chain Monte Carlo Based Sampling for Gene Regulatory Network Structure Selection

Given a set of competing hypotheses regarding different models, one needs to find the one best explaining the observed data. In a Bayesian framework, models are compared via Bayes factors, i.e., the ratio of evidences, with the model’s evidence being the likelihood of the model given the data. Of equal interest is the inference of parameters that define a model. Bayesian modeling may be seen as a coherent system for such a probability-based belief updating. One may already possess some prior knowledge about a model, collect additional data and subsequently integrate the data with the priors to derive some posterior beliefs, that is what to believe about the model, i.e., model parameters, after having observed new data. Given such model parameters to be a hidden quantity, Bayesian inference describes the lack of certainty with regards to their specific value via probability distributions. As a consequence, any implementation centers on the estimation of the marginal likelihood of the data, given the model. This quantity is essential to compute the posterior probability of the model parameters, given the data as well as the model. It, however, requires a multidimensional integral over all parameters associated with the statistical model, making any direct computation typically intractable. It is a challenge analogous to estimating partition functions in statistical mechanics and techniques inspired by statistical mechanics, such as Markov Chain Monte Carlo (MCMC)-based sampling approaches [15,108,116], have been utilized to overcome this obstacle in Bayesian computation, and this is where randomness comes into play. In brief, MCMC simulations [131] generate sequences of random numbers, i.e., Markov chains, in order for their long-term statistical properties to converge towards the posterior distribution.

For instance, the target density $\pi$ may happen to be expressed in terms of multiple integrals that cannot be solved analytically. A Markov Chain Monte Carlo algorithm allows for an alternative resolution of this computational challenge by simulating a Markov chain that explores the space of interest without requiring any apriori knowledge on $\pi$, besides the ability to compute $\pi \left({\theta }_0\right)$ for a given parameter value ${\theta }_0$. Here, a Markov chain describes a stochastic process, in which the next state is solely dependent upon the current state based on some probability. More formally, a sequence of random variables $\{X_1,X_2,...,X_t\}$ on a discrete state space is called a (first order) Markov chain if $p(X_t=x_t|X_{t-1}=x_{t-1},...,X_1=x_1)=p(X_t=x_t|X_{t-1}=x_{t-1})$. The validation of this approach comes from the Markov chain being ergodic, i.e., it converges to a distribution with density $\pi$, no matter where the Markov chain begins at time $t_0$. The Metropolis–Hastings algorithm [132,133] implements this principle by choosing a proposal, that is, a conditional density $K\left({\theta }^{\prime }\right|\theta )$, also denoted as Markov kernel, and deriving a Markov chain by successive simulations of the transition:

$${\theta }_{t+1}=\left\{\begin{array}{cc}{\theta }^{\prime }\sim K\left({\theta }^{\prime }\right|\theta )\hfill & \mathrm{if}r<\alpha :=min\left(1,\frac{\pi \left({\theta }^{\prime }\right)K\left({\theta }_t\right|{\theta }^{\prime })}{\pi \left({\theta }_t\right)K\left({\theta }^{\prime }\right|{\theta }_t)}\right)\hfill \\ {\theta }_t\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

Here, r denotes a random sample drawn from a uniform distribution, and $\alpha$ is the acceptance probability of the new proposal ${\theta }^{\prime }$ (see Figure 2). This acceptance-rejection feature of the algorithm allows for targeting the density $\pi$ as its stationary distribution if the resulting Markov chain is irreducible, i.e., it has a greater than zero probability of visiting any region of the support of density $\pi$ in a finite number of iterations. Given the primary goal of simulating samples from a target distribution $\pi$, the performances of MCMC methods, including Metropolis–Hastings, vary, depending on the correspondence between the proposal K and the target $\pi$. For instance, if $K\left({\theta }^{\prime }\right|\theta )=\pi \left(\theta \right)$, the Metropolis–Hastings algorithm reduces to i.i.d. sampling from $\pi$, which proves impossible to implement. It should be noted once again that the application of MCMC based sampling is not constrained to a Bayesian modeling of a posterior distribution, but may be used in any situation where a probability distribution is defined up to its normalization factor.

A variety of modern MCMC variants now exist such as generalized Hamiltonian Monte Carlo methods [134], which exploit geometric information to increase the sampling efficiency. However, the computational requirements of MCMC methods can be prohibitive in applications that involve large, high-dimensional data sets or complex models [134]. An alternative is to abandon the theoretical guarantees of MCMC methods and to construct analytically tractable approximations to the true posterior distribution, which is the underlying motivation of variational methods [135].

As one relevant and representative example of using MCMC in a Bayesian inference context, we want to discuss the approach by Werhli and Husmeier [117] to identify the most plausible gene regulatory network architectures, given the data as well as additional prior biological knowledge. Werhli and Husmeier [117] utilize MCMC for sampling networks as well as parameters simultaneously from a posterior distribution. Given the network’s cyclic structure, the joint probability of all random variables factorizes into a product of less complex conditional probabilities according to conditional independence relationships defined by an individual, potential network structure m. In turn, given certain regularity conditions [117], the parameters associated with such conditional probabilities can be analytically integrated out, allowing for the estimation of the marginal likelihood or evidence $p\left(d\right|m)$, which captures how well the network structure m explains the data d. Since the objective is to learn causal relationships between interacting nodes in a network, one wants to find the network structure m that maximizes $p\left(m\right|d)$, i.e., the posterior. Unfortunately, the number of putative network architectures increases super-exponentially with the number of nodes. In addition, the amount of information from the data and the prior usually does not suffice to render the posterior distribution $p\left(m\right|d)$ sharply peaked into a single network structure and typically rather spreads over a large set of possible network architectures. As a consequence, one should refrain from explaining such a distribution by a single network and, instead, aim to sample a series network architectures from the posterior distribution $p\left(m\right|d)$ so as to obtain a reasonable collection of plausible networks as well as to capture inherent inference uncertainty.

Since direct sampling from this distribution is typically infeasible, Werhli and Husmeier [117] resort to Markov Chain Monte Carlo-based sampling. The posterior can be defined as $p\left(m\right|d)\propto p(d\left|m\right)p\left(m\right)$ where $p\left(d\right|m)$ is the evidence, and $p\left(m\right)$ denotes the prior distribution, i.e., prior knowledge, over network structures m. Given a network m, a new structure proposal $m^{\prime }$ is proposed from a proposal distribution $K\left(m^{\prime }\right|m)$, which is then rejected or accepted according to the standard Metropolis–Hastings scheme with acceptance probability $\alpha$ defined as:

$$\alpha :=min\left(1,\frac{p\left(d\right|m^{\prime })p\left(m^{\prime }\right)K\left(m\right|m^{\prime })}{p\left(d\right|m)p\left(m\right)K\left(m^{\prime }\right|m)}\right)$$

The functional form of the proposal distribution $K\left(m^{\prime }\right|m)$ depends on what kind of proposal moves are chosen. Werhli and Husmeier [117] select three edge-based proposal operations, i.e., edge creation, deletion and inversion.

Integration of Prior Knowledge on Network Structures

To incorporate biological prior knowledge, i.e., before any evaluation of the data d, about interactions between nodes, Werhli and Husmeier [117] define a matrix B, where $B_{ij}=0.5$ indicates no prior knowledge about an edge between nodes i and j, while $B_{ij}<0.5$ and $B_{ij}>0.5$ denote prior evidence of absence and, respectively, presence of an edge. To integrate such prior knowledge into the inference of gene regulatory networks, they define distance functions to evaluate the agreement between a proposed network structure m, represented as a binary adjacency matrix, and the biological prior knowledge, i.e., $E_k\left(m\right)={\sum }_{i,j}|B_{ij}-m_{ij}|$ with $k\in \{0,1\}$ where $E_0$ represents all edge prior beliefs $B_{ij}<0.5$ and $E_1$ all $B_{ij}>0.5$ and $i,j$ represent individual nodes. Hence, $E_0$, is associated with the absence of edges, while $E_1$, is associated with the presence of edges. The prior distribution over network structures m is then defined to form a Gibbs distribution as:

$$p\left(m\right|{\beta }_0,{\beta }_1)=\frac{e^{-({\beta }_0{E}_0\left(m\right)+{\beta }_1{E}_1\left(m\right))}}{Z({\beta }_0,{\beta }_1)}$$

Here, ${\beta }_0$ and ${\beta }_1$ are parameters denoting the weight of the respective source of prior knowledge with respect to the data, and the partition function may consequently be defined as $Z({\beta }_0,{\beta }_1)={\sum }_m{e}^{-({\beta }_0{E}_0\left(m\right)+{\beta }_1{E}_1\left(m\right))}$. Z sums over the set of all possible network structures and, as the number of putative architectures increases super-exponentially with the number of nodes, computation becomes intractable for large networks. Hence, given such a definition of the prior probability distribution over network structures as well as the distributions on the parameters ${\beta }_0$ and ${\beta }_1$, i.e., $p\left({\beta }_0\right)$ and $p\left({\beta }_1\right)$, the Metropolis–Hastings updating scheme may be augmented in order to simultaneously sample both the network structure and parameters from the posterior distribution $p(m,{\beta }_0,{\beta }_1|d)$. Then, a new network structure $m^{\prime }$ is sampled from the proposal distribution $K\left(m^{\prime }\right|m)$ as well as a set of new parameters from specific proposal distributions $K\left({\beta }_0^{\prime }\right|{\beta }_0)$ and $K\left({\beta }_1^{\prime }\right|{\beta }_1)$, given their acceptance probability $\alpha$ defined as:

$$\begin{array}{cc}\hfill \alpha & :=min\left(1,\frac{p(m^{\prime },{\beta }_0^{\prime },{\beta }_1^{\prime }|d)K\left(m\right|m^{\prime })K\left({\beta }_0\right|{\beta }_0^{\prime })K\left({\beta }_1\right|{\beta }_1^{\prime })}{p(m,{\beta }_0,{\beta }_1|d)K\left(m^{\prime }\right|m)K\left({\beta }_0^{\prime }\right|{\beta }_0)K\left({\beta }_1^{\prime }\right|{\beta }_1)}\right)\hfill \\ \hfill & =min\left(1,\frac{p\left(d\right|m^{\prime })p\left(m^{\prime }\right|{\beta }_0^{\prime },{\beta }_1^{\prime })p\left({\beta }_0^{\prime }\right)p\left({\beta }_1^{\prime }\right)K\left(m\right|m^{\prime })K\left({\beta }_0\right|{\beta }_0^{\prime })K\left({\beta }_1\right|{\beta }_1^{\prime })}{p\left(d\right|m)p\left(m\right|{\beta }_0,{\beta }_1)p\left({\beta }_0\right)p\left({\beta }_1\right)K\left(m^{\prime }\right|m)K\left({\beta }_0^{\prime }\right|{\beta }_0)K\left({\beta }_1^{\prime }\right|{\beta }_1)}\right)\hfill \end{array}$$

The acceptance probability and, as a consequence, the convergence of the Markov chain may be enhanced by dividing the proposal move into three sub-moves: (i) sampling a new network structure $m^{\prime }$ from the proposal distribution $K\left(m^{\prime }\right|m)$ for fixed set of parameters ${\beta }_0$ and ${\beta }_1$; (ii) sampling a new parameter ${\beta }_0^{\prime }$ from the proposal distribution $K\left({\beta }_0^{\prime }\right|{\beta }_0)$ for a fixed parameter ${\beta }_1$ as well as a fixed network structure m; and (iii) sampling a new parameter ${\beta }_1^{\prime }$ analogously to ${\beta }_0^{\prime }$. These three sub-moves may then be iterated until convergence.

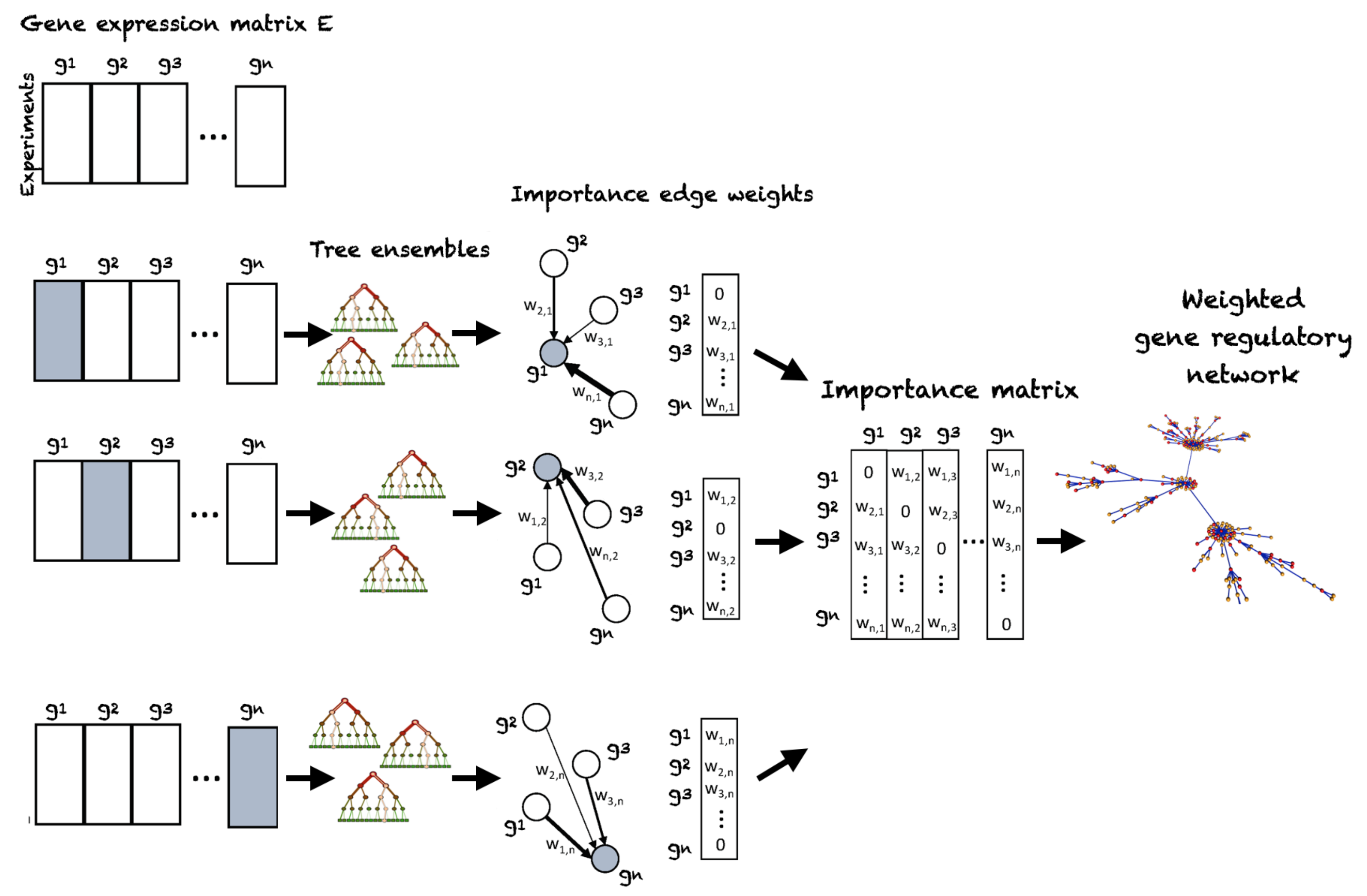
4.2. Random Forest Regression Based Gene Regulatory Network Inference from Transcriptomic Data

Regression-based approaches to gene regulatory network inference from transcriptomic data are based on the assumption that the expression profiles of the transcription factors that directly regulate a target gene are the most informative, among all transcription factors, to predict the expression profile of the target gene. In this regard, gene regulatory network inference is reformulated as a feature selection problem [119] that seeks to find the most predictive subset of transcription factors for each target gene. In order to infer the global gene regulatory network, a regression model is formulated to predict a set of putative direct regulators among all transcription factors $r_1,...r_M$ for each target gene g as ${\sum }_{i=1}^N{(e_i^g-f\left(e_i^{r_1,...,r_M}\right))}^2$. Here, $f(.)$ denotes a mapping function to combine the expression profiles $E_{r_1,...,r_M}$ (based on N individual expression samples) of M transcription factors to approximate the expression profile $E_g$ of a target gene, e.g., by minimizing the square error loss. Several alternative approaches have been proposed for implementing $f(.)$, resulting in feature selection strategies such as stepwise selection [136], ridge regression [137], least angle regression [138], or least absolute shrinkage and selection operator (LASSO) [139]. Among all these methods, LASSO has emerged as the most popular in gene network reconstruction [8]. Unlike ridge regression, which aims to shrink insignificant coefficients close to zero, Lasso exploits $L_1$ regularization [139] to shrink insignificant coefficients to be exactly zero. This leads to a much sparser linear model, i.e., only a few predicted regulators per target gene.

Several tree-based ensemble regression methods have been proposed [17,140,141,142,143,144]. In contrast to linear regression models, tree-based approaches do not make any assumptions about the nature of gene regulation. They can, therefore, handle combinatorial and non-linear interactions, as well as highly correlated input variables and provide an inherent measure of variable importance. Random forest regression has emerged as one of the most prominent examples of a tree based approach [105]. The methodology describes an ensemble of individual decision trees, each constructed based on random sampling a subset of the original data, to form a Random Forest, hence the name. Each decision tree describes several, binary if–else condition-based junctions, starting at the top with the initial starting node. Each node splits into a left and right node until the final, so called leaf nodes. The value in each leaf does not usually denote the average of observations occurring within that specific region. The results per tree are averaged across all trees. Randomness is, therefore, inherent to the model building process and is introduced in two ways, i.e., (i) each tree is created from a different sample of the data; and (ii) a different subspace of features is selected for splitting at each node within a tree. In this way, the inherent random selection process of this ensemble learning approach eradicates the limitations of the decision tree algorithm, reducing overfitting by achieving high diversity among the individual trees, as well as increasing robustness and precision. The method is also flexible in that it allows a variety of sampling strategies [106,145]. As already mentioned in the beginning of this section, tree-based methods rank among the best performing ensemble-based machine learning approaches for classification or regression tasks [119] and have been among the top performers in the DREAM5 network inference challenge [8], and on benchmarks on network inference from single-cell transcriptomic data [121]. Since its initial implementation, extensions have been proposed to handle time-series data [141,142,146] or integrate prior knowledge [143].

The generalized version of random forest regression based gene regulatory network inference is illustrated in Figure 3. The main rationale is that for each gene g, a number of decision trees are grown over different bootstrapped samples of the complete gene expression dataset. Within each decision tree, the method recursively splits the data sample. It applies binary tests per node in the tree based on a random subset of either only dedicated transcription factor genes, or, as in the generalized version, all remaining genes as putative regulators, trying to reduce the variance of the target gene expression profile. The logic, similar to linear regression approaches, is to select the set of putative regulator genes that best explains the expression profile of the target gene. More formally, let E represent a gene expression dataset with the input variables $N_r$ being all putative regulator genes r (e.g., transcription factors or all remaining genes). $N_s$ denotes the set of gene expression values (e.g., RNA samples from different experiments). For each gene g, a number $N_{tree}$ of decision trees is grown over different subsets of $N_s$. The decrease of Gini impurity ($DGI$) is typically used as a criterion for splitting a tree node [105] and selecting the splitting predictor, i.e., a putative regulator gene $r_i$. Within each tree, the Gini information gain ($IG$) of $r_i$ at node n, $IG(r_i,n)$, denotes the difference between the impurity at node n and the weighted average of impurities at each child node of n, i.e., $IG(r_i,n)=DGI(r_i,n)-w_{L}IG(r_i,n_L)-w_{R}IG(r_i,n_R)$, with $n_L$ and $n_R$ being the left and right child nodes of n. $w_L$ and $w_R$ are the ratios of the number of instances at the left and right child nodes to the number of instances at node n. At each node, a random subset $k_r$ of putative regulators is evaluated for node splitting based on $IG(r,n)$. Each tree-based model yields a separate ranking of the genes as potential regulators r of a target gene g. Averaging these individual predictions over several trees leads to a final prediction of regulators for each target gene. Note that, as depicted in Figure 3, gene regulatory networks are typically uni-directional, i.e., a regulator is controlling a target gene, however the opposite is generally not the case. Of course, the fact that, as stated in [17], a random forest regression model predicts asymmetric networks does not ensure that the prediction of these asymmetric links is really informative. Asymmetric predictions might correspond to spurious predictions, in particular when derived from steady state gene expression data. However, Huynh-thu et al. [17] were able to show that their random forest based algorithm tends to correctly assign the highest weight to the true directionality of a gene regulatory interaction.

A second type of tree-based models for gene regulatory network inference worth mentioning would be Gradient Boosting [147,148,149,150,151], an ensemble learning algorithm that uses boosting [152] as a strategy to combine weak learners, like shallow trees, into a strong predictor. In contrast, random forest regression uses bagging, also called bootstrap aggregation, for model averaging to improve regression accuracy.

Extension to Prior Knowledge Integration

Main rationale of the prior knowledge integrative approach to random forest regression as presented in [143] is to introduce a weighted sampling scheme within the random forest framework in order to incorporate information from additional data sources. As in [17], the model considers the expression of each gene as a function of the expression of other genes. However, for each node in the tree ensemble, instead of randomly sampling a subset of genes from the entire gene set, as done in [17], the approach samples genes, i.e., the potential regulators, according to the information provided by other data such as protein–protein interactions or expression data from perturbation experiments, so that genes supported by additional data will be favorably sampled as potential regulators. Hence, information embedded in these additional sources of data is integrated in the network being constructed, while the effective search space of potential regulators is at the same time significantly reduced.

4.3. Random Walks for Gene Module Detection in Biological Networks

Many methods have been proposed in order to reduce the complexity of large gene or protein networks into relevant subnetworks or modules, such as identifying relevant transcriptional modules from gene regulatory networks [153,154]. A recent community challenge performed a comprehensive assessment of module identification methods across diverse protein–protein interaction, signaling, gene co-expression, homology and cancer-gene networks [124]. Among the top performers of the challenge was a random walk based approach [125], an extension of the Markov Clustering (MCL) algorithm, originally proposed on protein–protein interaction networks [126]. In computational biology, MCL has become very popular specifically to cluster protein sequences as well as genes from co-expression data [155].

The main assumption of the Markov Clustering algorithm is that in a given graph, there will be more links within a cluster than between clusters. As a consequence, beginning at a particular node, and performing a random walk [156], i.e., randomly traveling between connected nodes, one is more likely to stay within a cluster than to travel between them. A random walk on a graph is generally calculated as a stochastic process called a Markov chain, as introduced in Section 4.1, in which the next state is solely dependent upon the current state based on some probability. More formally, given some network structure defined as a graph $G=(V,E)$ with nodes V and edges E, the graph G may be represented as an adjacency matrix A. One then simulates some imaginary particle starting a random walk at some initial node $v_0\in V$ and iteratively moving to a randomly selected neighboring node. Considering the time $t\in \mathbb{N}$, to be discrete, then after t time steps the particle would be at node $v_t$. It then walks from $v_t$ to $v_{t+1}$, some randomly chosen adjacent node of $v_t$ following the transition matrix M, i.e., the column normalization of A. Column normalization of A is achieved as $M=A{D}^{-1}$ with D being the diagonal degree matrix of graph G. Therefore, we can write $\forall x,y\in V,\forall t\in \mathbb{N}$:

$$p(v_{t+1}=y|v_t=x)=\left\{\begin{array}{cc}\frac{1}{d\left(x\right)}\hfill & \mathrm{if}(x,y)\in E,\hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

with $d\left(x\right)$ denoting the degree of x in the graph G. Defining $p_t\left(v\right)$ as the probability for the random walk to be at node v at time t, we can describe the evolution of its probability distribution $p_t={\left(p_t\left(v\right)\right)}_{v\in V}$ as: $p_{t+1}=M{p}_t$. If existing, the stationary distribution, i.e., the solution to the equation $p_{*}=M{p}_{*}$, describes the probability for the particle to remain at a given node for an infinite amount of time. When discussing random walks in the context of their application within the Markov Clustering algorithm in [126], one needs to consider two alternating operations to the transition matrix known as Inflation and Expansion, which are pivotal to the design of the MCL algorithm. Under Inflation, for each node the transition values are changed so that strong neighbor values are strengthened and large neighbor values are demoted, i.e., inflation changes the transition probabilities by favoring more probable walks over less probable ones. This is achieved by raising the values of each column to non-negative power and then re-normalizing it. Expansion on the other hand helps in making the farther nodes or neighbors reachable, i.e., it allows the random walk to take longer paths. This is achieved by taking n-th power of the transition matrix. See Algorithm 1 for a definition of the entire procedure.

Algorithm 1 Markov Clustering

Input: Graph adjacency matrix A, Expansion parameter e, inflation parameter i Output: Transition matrix M $A\leftarrow A+I$ // add self-loops to graph adjacency matrix A $M\leftarrow A{D}^{-1}$ // initialize canonical transition matrix M while M has not converged do     $M\leftarrow M^e$ // Expansion     for each $x\in V$ do         for each $y\in V$ do            $M_{xy}\leftarrow \frac{M_{xy}^i}{{\sum }_{y\in V}{M}_{xy}^i}$ // Inflation         end for     end for end while

The expansion operator is responsible for connecting different regions of the graph, and the combination of expansion and inflation boosts the probabilities of walks inside each cluster. Moreover, it will reduce walks between the clusters. The subsequent iteration of these two operations leads to the separation of the graph into individual, connected components, i.e., reaching convergence. Therefore, unlike many clustering algorithms that need the user to specify the expected number of clusters beforehand, Markov Clustering provides a clustering that naturally arises from the graph topology itself. An example of applying Markov Clustering in order to identify context-specific gene regulatory networks is given in [157].

Regularized Markov Clustering and Random Walks with Restart

The variant of the Markov Clustering algorithm that ranked among the top performers [125] in the aforementioned challenge is known as regularized Markov Clustering (r-MCL) [158]. It has been invented to address some of the limitations of the original MCL algorithms, such as fragmentations, i.e., too many clusters, or imbalanced outputs, i.e., large variation in cluster sizes. r-MCL modifies the expansion step by introducing a canonical flow matrix, ensuring the original topology of the graph to still influence the graph clustering process beyond the initial iteration. A limitation of MCL and its variants, e.g., regularized MCL, is that they typically only support hard clustering. This, however, can create an implausible constraint, given significant overlaps of genes or proteins across functional modules can regularly be observed. Hence, a soft clustering variation of r-MCL has been proposed based on the idea of iteratively (re-)executing r-MCL while ensuring that multiple executions do not always converge to the same clustering result and, as a consequence, allowing for overlapping clusters. The resulting algorithm, denoted soft regularized Markov Clustering, is shown to outperform a range of state-of-the-art approaches with respect to accuracy of identifying functional modules on protein–protein interaction networks [159].

Random walk with restart (RWR) [160,161] is another improvement of random walk based clustering approaches, that allows for the identification of multivariate relationships between nodes, while exploring the global topology of provided networks [160]. It contains a control parameter $\alpha$ that defines a restart probability, while $1-\alpha$ represents the probability of the aforementioned imaginary particle to continue moving from one node to an adjacent one. For a given graph, it can be defined by assigning transition probabilities to graph’s edges. In this way, the random walk performing particle may jump from one node to another. The mechanism prevents the walk to become trapped, and, in addition, assures the existence of a stationary distribution. Furthermore, restart positions of the particle may be restricted to specific nodes, called seeds. Hence, the particle will explore the graph focusing on the neighborhood of these seeds, and the stationary distribution can be considered as a measure of the proximity between the seeds and all other nodes in the graph. Formally, one may redefine the evolution of the transition probability as: $p_{t+1}=(1-\alpha )M{p}_t+\alpha p_0$, with M denoting the transition probability matrix and $p_0$ representing the vector of initial probability distributions [160]. Therefore, in $p_0$, only the seeds have values different from zero. After a series of iterations, a stationary probability distribution is reached, with the difference between the vectors $p_{t+1}$ and $p_t$ becoming negligible.

Random walk with restart based approaches have been used to identify putative drug-target interactions from heterogeneous biological data [162], or to determine associations between diseases and miRNAs [163].

4.4. Randomized Matrix Factorizations and Low Rank Approximations with Applications to High-Dimensional Gene Clustering and Gene Regulatory Network Inference

Matrix factorization describes the decomposition of a given matrix into a set of smaller matrices, in order to reduce the matrix to a lower rank while keeping as much information as possible, e.g., for dimensionality reduction or data compression purposes, or to reveal and exploit some underlying, latent factors or low-rank features exhibited by the original, high-dimensional, data matrix. Some of the early applications in computational biology, in particular gene expression analysis, include techniques such as Singular Value Decomposition [164] and Principal Component Analysis [165], Non-negative Matrix Factorization [166,167,168] or Network Component Analysis [169,170]. More recent applications include the inference of gene regulatory networks [130,171,172,173,174,175] or drug discovery [56,176]. For more in-depth surveys on factorization techniques for the analysis of omics datasets, we refer the interested reader to [177,178].

The emergence of ever increasing large-scale, high dimensional datasets, however, poses a computational challenge for traditional algorithms, placing significant constraints on both memory and processing power. Recently, the concept of randomness has been introduced as a strategy to ease the computational load, and, in particular, randomized algorithms have been established to efficiently compute matrix approximations [107,179,180], forming the field of randomized numerical linear algebra [127,128]. In their seminal work, Halko et al. [107] introduced a modular framework for randomized matrix factorization, as illustrated in Figure 4. Main rationale is to utilize randomness in order to derive a smaller matrix from a high-dimensional one, which captures all essential information. Thus, none of the randomness should obscure any dominant information—in a spectral sense—within the data as long as the original matrix features some low-rank structure. Then, deterministic matrix factorization methods may be applied to this smaller matrix to compute a near-optimal low-rank approximation. Here, following the notation and line of reasoning of Halko et al. [107], we discuss three of the most frequently used randomized matrix decomposition methodologies, accompanied and exemplified by biological applications.

4.4.1. Randomized Singular Value Decomposition

Singular Value Decomposition (SVD) provides an intuitive approach to matrix decomposition that can be used to obtain low-rank approximations, to find the least-squares and minimum norm solution of a linear model, or to compute the pseudo-inverse of a non-square matrix [164]. Further, SVD is the core algorithm behind a variety of machine learning concepts, for instance, matrix completion, dictionary learning, sparse coding, or Principle Component Analysis. It is particular intuitive as it explicitly tries to learn the original data’s underlying factors, denoted as singular values, as well as how the data and the features relate to these latent factors. Represented in mathematical form, for any given data matrix $X\in {\mathbb{R}}^{n\times m}$, the SVD of X takes the form $X=U\mathsf{\Sigma }{V}^T$ where the matrix $U\in {\mathbb{R}}^{n\times n}$ and matrix $V\in {\mathbb{R}}^{m\times m}$ consist of left and right singular vectors, respectively. The left singular vectors in U provide a basis for the range (column space), and the right singular vectors in V provide a basis for the domain (row space) of X. Both U and V are orthonormal so that $U^{T}U=I$ and $V^{T}V=I$, while the diagonal entries of the matrix $\mathsf{\Sigma }\in {\mathbb{R}}^{n\times m}$ denote the singular values ordered from the highest to lowest, i.e., ${\sigma }_1\left(X\right)\ge ...\ge {\sigma }_m\left(X\right)\ge 0$.

SVD plays a pivotal role because truncating it after k terms, i.e., keeping only the top k singular vectors and singular values, provides a best rank k approximation to X, denoted as as $X_k=U_k{\mathsf{\Sigma }}_k{V}_k^T$, with respect to the spectral and Frobenius norms [181]. Further, the Eckart–Young theorem [182] states that the best rank k approximation to X is provided in the least-square sense.

Since computing the SVD of a large matrix may be computationally infeasible, there are various alternative algorithms that compute near-best rank k matrix approximations from matrix-vector products [183]. Halko et al. [107] propose a two-stage computation: (i) compute an approximate basis for the range of X, i.e., a matrix Q with k orthonormal columns, with $k\le m$, that captures the action of X so that $X\approx Q{Q}^{T}X$; (ii) use Q to form a smaller matrix $X^{\prime }=Q^{T}X$, i.e., restrict the high-dimensional X to a lower dimensional space spanned by a near-optimal basis Q, and use $X^{\prime }$ to compute the matrix factorization. Note that we here ignore the use of oversampling Erichson2019 with respect to the number of orthonormal columns as originally proposed by Halko et al. [107] for simplification purposes. If Q is given, the matrix factorization based on randomized SVD may be computed by following algorithmic recipe 2.

The efficiency of this algorithm comes from $X^{\prime }$ being small compared to X. Since $X\approx Q{Q}^{T}X=Q{X}^{\prime }=Q\widehat{U}\mathsf{\Sigma }{V}^T=U\mathsf{\Sigma }{V}^T$, setting $U=Q\widehat{U}$ does produce a low-rank approximation $X\approx U\mathsf{\Sigma }{V}^T$ [181]. Note that randomness only occurs in forming an approximate basis Q while the application of the SVD is deterministic given Q. Hence, the challenge is to efficiently compute Q using a randomized approach. To this end Halko et al. present a series of algorithms, denoted as randomized range finders [107], based on the concept of Random Projection [184]. Main goal is to produce an orthonormal matrix Q that approximates the column space, i.e., range, of matrix X, thereby having as few columns as possible.

An example of applying randomized SVD to the inference of large-scale gene regulatory networks is given in [130]. Starting from an initial time course gene expression matrix $X\in {\mathbb{R}}^{n\times m}$ with n genes and m time points, Fan et al. [130] adopt a common ordinary differential equation (ODE) based model to represent the gene regulatory network as a dynamical system. In this model each gene $g_i$ at a specific point in time $t_k$ may be described as $\dot{x_i}\left(t_k\right)={\sum }_{j=1}^n{a}_{ij}\left(t_k\right)x_j\left(t_k\right)$, with $\dot{x_i}\left(t_k\right)\approx x_i\left(t_k\right)-x_i\left(t_{k-1}\right)$ and $a_{ij}\left(t_k\right)$ denoting the interaction strength from gene $g_j$ to gene $g_i$ at time point $t_k$, while $x_j\left(t_k\right)$ represents the expression level of gene j, also at time point $t_k$. In matrix notation this can be rewritten as $\dot{X}=AX$ with $\dot{X}\in {\mathbb{R}}^{n\times m}$ denoting the matrix of first derivatives of X, and $A\in {\mathbb{R}}^{n\times n}$ representing the (unknown) gene connectivity matrix, consisting of the interaction weights. In order to infer the unknown coefficients in A, the gene regulatory network inference problem is transformed into a least-squares problem, i.e., $\underset{A}{min}\left\{\right||AX-\dot{X}{\left|\right|}^2\}$, and the objective is to optimize the interaction strength weight values $a_{ij}$ of A. However, solving this minimization problem directly is possible only if $n>m$, which often is not the case, as there are generally fewer experimental time points than the number of measured genes. Hence, one typically resorts to the application of SVD to $X^T$ so that $A=\dot{X}{X}^T=\dot{X}U\mathsf{\Sigma }{V}^T$. If X is too large the direct application of SVD may, however, this also does not work due to memory limitations, as well as numerical instabilities of the smaller singular values. Therefore, Fan et al. [130] adopt the two step procedure by Halko et al. [107], that is X is first projected onto a smaller matrix using Gaussian Random Projection to form the orthonormal basis Q, and subsequently, SVD is applied as illustrated in Algorithm 2.

Algorithm 2 Randomized Singular Value Decomposition.

Input: Data matrix $X\in {\mathbb{R}}^{n\times m}$, target rank k Output: Left and right singular vector matrices U and $V^T$, singular value matrix $\mathsf{\Sigma }$   $Q=rp(X,k)$ // compute approximate basis $Q\in {\mathbb{R}}^{n\times k}$, e.g., via Algorithm 3   $X^{\prime }=Q^{T}X$ // project to low-dimensional space   $X^{\prime }=\widehat{U}\mathsf{\Sigma }{V}^T$ // compute SVD of $X^{\prime }$   $U=Q\widehat{U}$ // recover left singular values   $X\approx U\mathsf{\Sigma }{V}^T$ // compute SVD of X

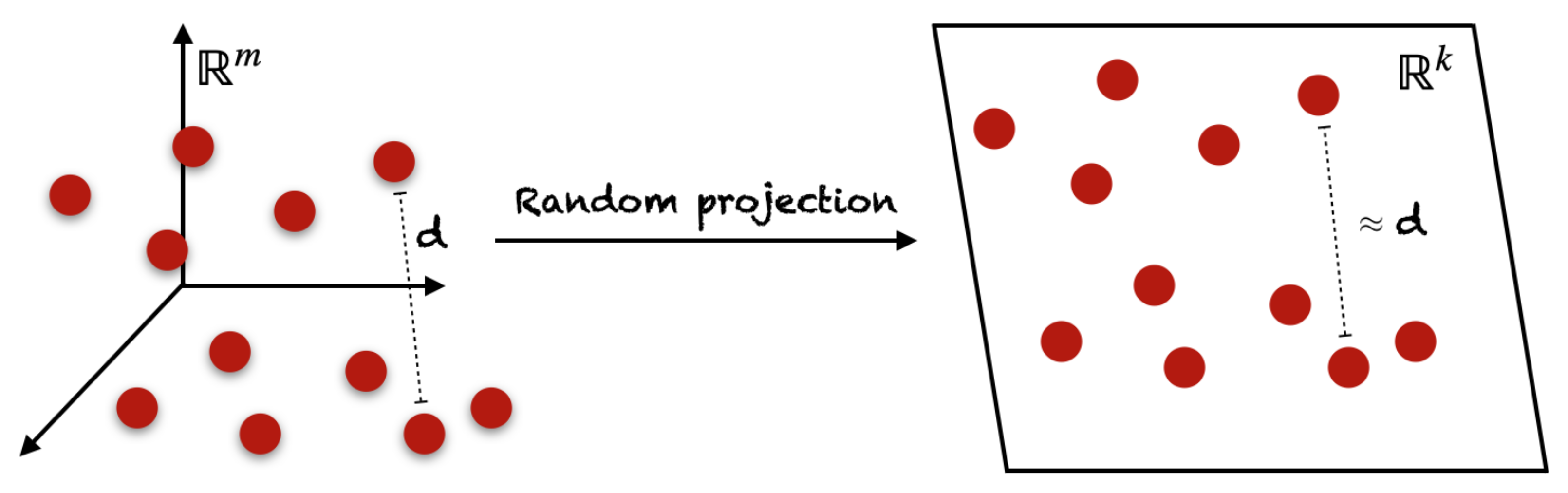
4.4.2. Random Projection

Halko et al.’s solution for finding an approximate basis for the range of the data matrix X, i.e., a matrix Q, based on the concept of Random Projection is motivated by Johnson and Lindenstrauss’s theorem [185] that states that pairwise distances d among a set of points within a Euclidean space will be approximately maintained when projected into a lower-dimensional Euclidean space, as illustrated in Figure 5. In general, it may be stated that Random Projection [184] projects a data matrix $X\in {\mathbb{R}}^{n\times m}$ onto a k-dimensional subspace, with $k<<m$ using a random matrix $W\in {\mathbb{R}}^{m\times k}$, whose columns have unit lengths, denoted as $X_{RP}=XW$, where $X_{RP}\in {\mathbb{R}}^{n\times k}$ is the projected matrix.

Random Projection depends upon the way the random projection matrix W is initialized. Main rationale by Halko et al. [107] is to generate an orthonormal Gaussian random matrix $\Omega \in {\mathbb{R}}^{m\times k}$ as the projection matrix, and then generate a sketch of X as $Y=X\Omega$. Y is used to construct the matrix Q. Intuitively, one randomly samples the range of X and subsequently finds an orthonormal basis for these vectors to obtain Q. The whole procedure is depicted in Algorithm 3. Note that, given its simplicity and effectiveness, Random Projection by itself has found applications, including gene expression-based cancer classification [186] or the clustering of large-scale high-dimensional single-cell RNA-seq data avoiding excessive distortion of cell-to-cell distances [129].

Algorithm 3 Orthonormal basis estimation via Gaussian Random Projection.

Input: Data matrix $X\in {\mathbb{R}}^{n\times m}$, target rank k Output: Approximate basis $Q\in {\mathbb{R}}^{n\times k}$   $\Omega =rnorm(m,k)$ // generate Gaussian random matrix   $Y=X\Omega$ // generate sketch   $Q=qr\left(Y\right)$ // form orthonormal basis Q, e.g., using QR factorization

4.4.3. Randomized Principal Component Analysis

Principal components analysis (PCA) [187] attempts to find a low-dimensional linear transformation of the data that maximizes the projected variance or, equivalently, minimizes the reconstruction error. Technically speaking, PCA tries to find a new set of basis vectors, denoted principal axes, so that these vectors sequentially, i.e., in descending magnitude, capture the variation in data, which is assumed to represent the data’s relevant information. Projections of the data on these principal axes are called principal components. More formally, given some data matrix $X\in {\mathbb{R}}^{n\times m}$, PCA relies on finding the eigenvectors of the covariance matrix $C=\frac{1}{n-1}{X}^{T}X\in {\mathbb{R}}^{m\times m}$. The decomposition is performed using either the SVD of the data matrix X or the eigen-decomposition of the covariance matrix C itself. In the eigen-decomposition approach, the covariance matrix C is first explicitly computed, then the decomposition is performed such that $C=V\Lambda V^T$ with $diag\left(\Lambda \right)={\lambda }_1,...,{\lambda }_m$ being the eigenvalues and V being the matrix of eigenvectors. The principal components P of the data are given by the projection of X onto the eigenvectors, i.e., $P=XV$ where the matrix P is usually truncated, i.e., $P_k=X{V}_k$, to have as many k columns as required for any downstream analysis. In the SVD approach C may be written as $C=\frac{1}{n-1}{X}^{T}X=\frac{1}{n-1}V{\mathsf{\Sigma }}^T{U}^{T}U\mathsf{\Sigma }{V}^T=\frac{1}{n-1}V{\mathsf{\Sigma }}^T\mathsf{\Sigma }{V}^T=V\frac{{\mathsf{\Sigma }}^2}{n-1}{V}^T$. After estimating the SVD for X, the eigenvalues may than be recovered as $\Lambda ={\mathsf{\Sigma }}^2/(n-1)$ and the principal components P as $P=XV=U\mathsf{\Sigma }{V}^{T}V=U\mathsf{\Sigma }$.

When n, the number of samples, does not exceed a few thousands, all eigenvectors can be computed by appropriate dense linear algebra routines, which, however, becomes impractical as n increases. Hence, randomized approaches to principal component analysis typically, similar to randomized SVD, rely on first constructing a relatively small matrix that captures, with high probability, the top eigenvalues and eigenvectors of the original data, thereby projecting the original eigenvalue problem onto a low-dimensional subspace, which includes an invariant subspace associated with the relevant eigenvectors. Next, standard SVD or eigen-decomposition are performed on the reduced matrix. The entire procedure for the case of using SVD is depicted in Algorithm 4.

In general, low-dimensional subspaces can be constructed in a variety of ways, e.g., by means of subspace iteration or Krylov projection schemes [188]. On the other hand, recent advances in the design and analysis of Randomized Numerical Linear Algebra [128] algorithms have yielded novel insights as well as fast and efficient alternatives to approximate the leading principal components of large matrices [107].

An example for a typical application of principal component analysis in computational biology would be genome-wide association studies (GWAS) as in [189]. In this context, PCA is typically used to account for population-specific variations in alleles distribution on the single nucleotide polymorphisms being analyzed [189]. Further examples of applying randomized PCA for genome-wide association studies are given in [190,191].As a side note, another randomized algorithm has recently been proposed as an alternative to traditional PCA, i.e., t-distributed stochastic neighbor embedding (t-SNE) [192], which is frequently used in computational biology, e.g., in single-cell transcriptomics [193].

Algorithm 4 Randomized Principal Component Analysis (via SVD).

Input: Data matrix $X\in {\mathbb{R}}^{n\times m}$ (centered, scaled), target rank $k<min(m,n)$ Output: Eigenvector matrix $V^T$, eigenvalue matrix $\Lambda$, k principal component matrix $P_k$   $U,\mathsf{\Sigma },V^T=rsvd\left(X\right)$ // compute randomized SVD of X (Algorithm 2)   $\Lambda ={\mathsf{\Sigma }}^2/(n-1)$ // recover eigenvalues   $P_k=U_k{\mathsf{\Sigma }}_k$ // compute k principal components

5. A Note on Deep Learning Based Methods for Computational Biology

We have recently seen a huge body of work in the area of deep learning and its application to the field of computational biology, including regulatory genomics [194,195,196,197,198,199], gene expression analysis [200], single-cell RNA-seq data analysis [150,201], and heterogeneous data integration [202], just to give a few examples. Although typically not considered randomized approaches, one may still highlight some of the principles from randomness that also contribute to the success of deep neural architectures, including: (i) randomness in the initialization of network architectures, such as weights [203]; (ii) randomness within individual layers, such as word embedding [204]; (iii) randomness in model regularization, such as dropout [205]; and (iv) randomness in optimization routines, such as stochastic gradient descent [206,207]. For more in depth surveys on deep learning and its application in computational biology, we refer the reader to [208,209,210].

6. Conclusions

Many of the fundamental concepts of transcriptional regulation were established in bacterial systems half a century ago. Such pioneering work highlighted transcription factors to bind specific genomic regions thereby recruiting the transcription apparatus. Although some of the basic principles are shared in eukaryotic systems, the regulatory networks are very complex, involving fine-regulated co-ordination of specific transcription factors, their co-factors, and various chromatin regulators. Especially since the advent of targeted genome editing technologies, better models of the transcriptional regulatory circuitry that integrate data on regulatory sequences, their occupancy by transcription factors, co-factors, chromatin regulators as well as genetic or epigenetic variations that affect regulatory sites have enormous potential to improve many key aspects of our life, ranging from genetic disease prevention and personalized medicine, to healthy and more efficient crop production.

The development of these models should thus be among the top priorities of biomedical research. Thus, to advance our understanding of these mechanisms, we need scalable approaches that can deal with the increasing number of large-scale, heterogeneous, high-resolution, biological datasets. Given the complexity and interdisciplinary nature of the gene regulatory network inference problem, the decision about what biological questions can be addressed by which methods requires a compendium of biological data comprehensively analyzed by both biological and computational scientists. It will therefore become increasingly important for these diverse groups of scientists to engage in a dialogue to solve this problem most efficiently together.

We hope this survey not only highlights the potential that randomized algorithms provide as alternatives to deterministic methods, but may also provide a platform to start such a dialogue about concepts and caveats of these approaches. We believe this to be a critical step to advance our understanding of the intricate web of highly dynamic, regulatory events underlying gene regulation and to eventually prevent misregulation through therapies that treat or cure diseases.