XGRN: Reconstruction of Biological Networks Based on Boosted Trees Regression
Abstract
1. Introduction
2. Materials and Methods
2.1. Extreme Gradient Boosting (XGBoost)
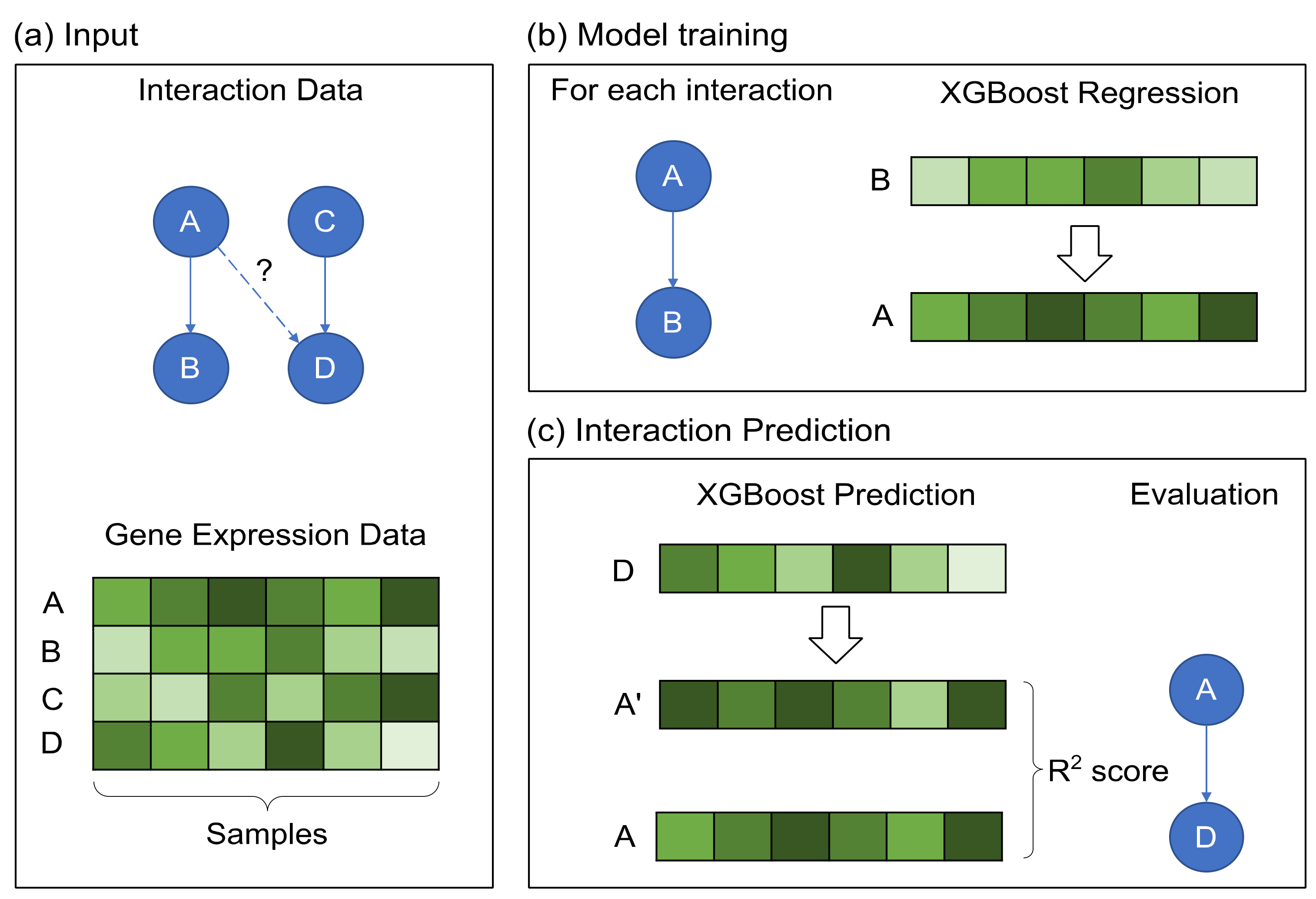
2.2. GRN Reconstruction
2.3. Data
2.4. Evaluation
3. Results
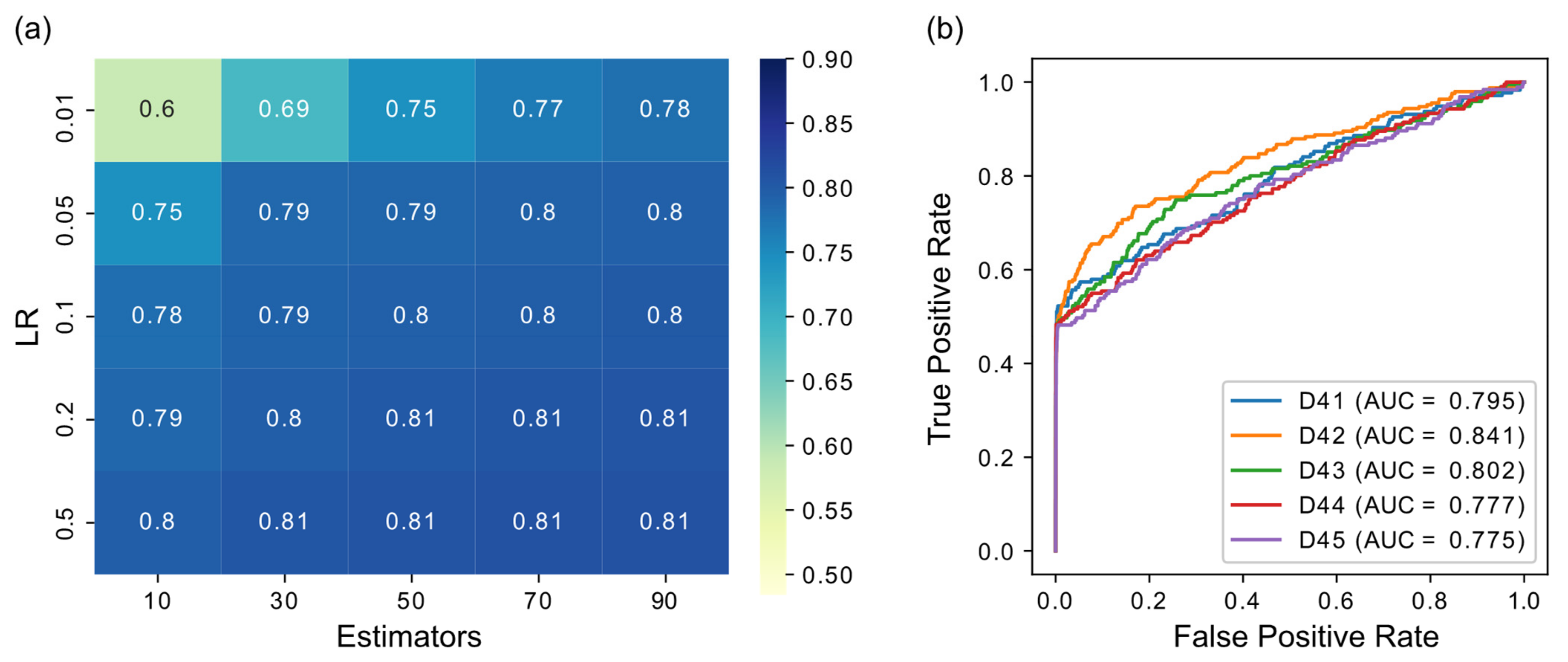
3.1. Parameter Selection
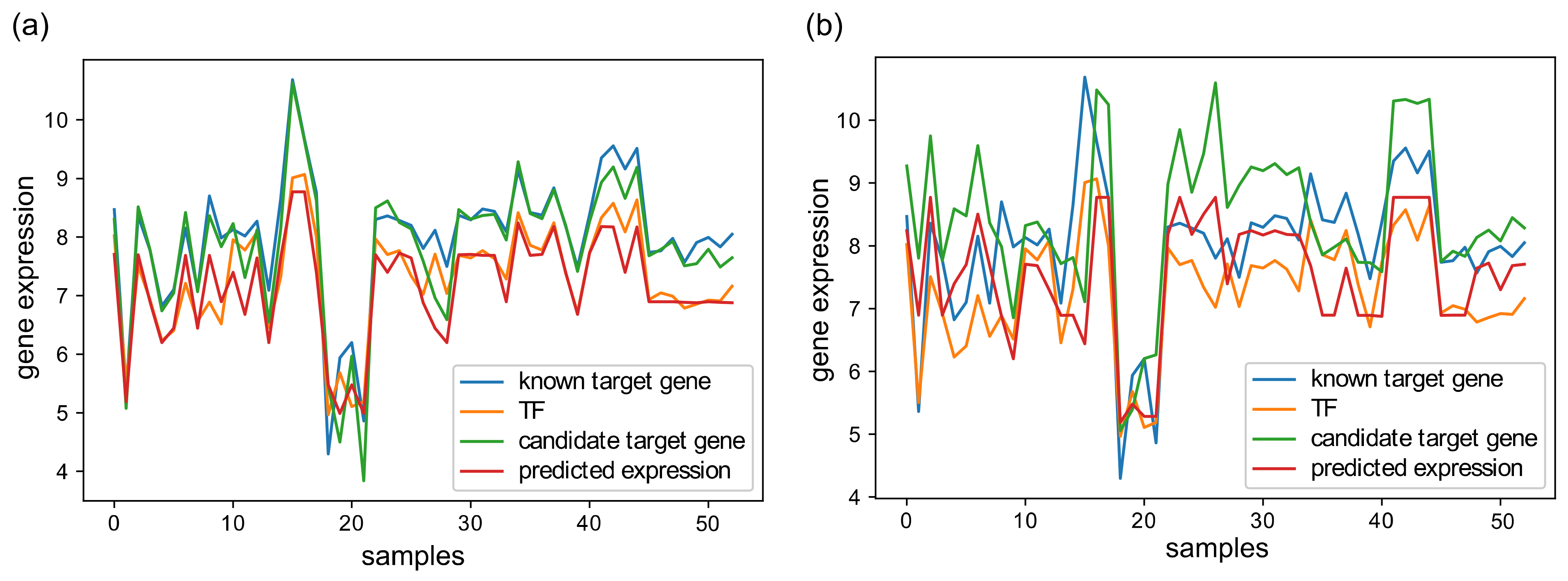
3.2. GRN Inference Performance
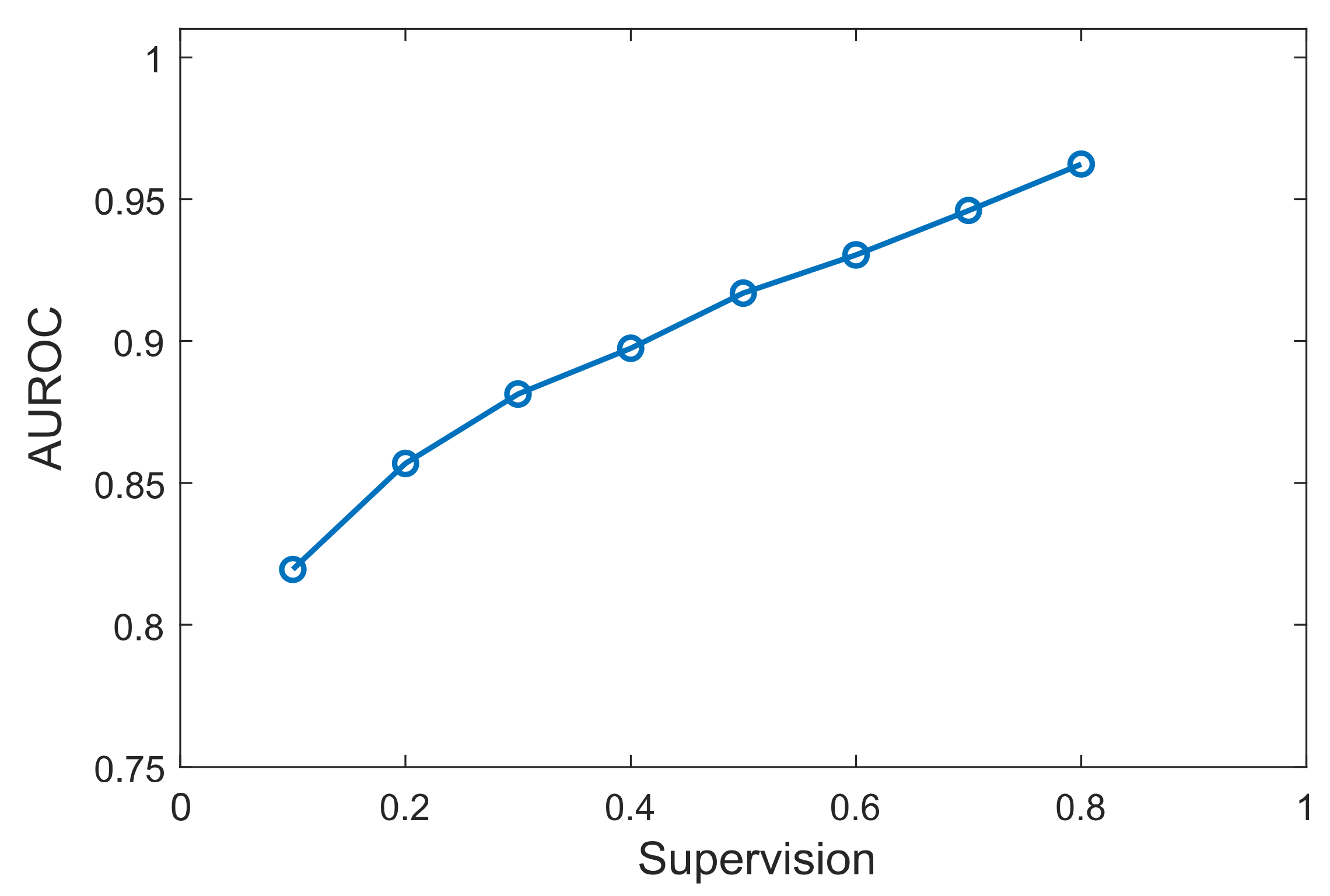
3.3. Effect of Prior Knowledge Percentage
4. Discussion
Funding
Data Availability Statement
Conflicts of Interest
References
- Ideker, T.; Krogan, N.J. Differential network biology. Mol. Syst. Biol. 2012, 8. [Google Scholar] [CrossRef] [PubMed]
- Vidal, M.; Cusick, M.E.; Barabási, A.L. Interactome networks and human disease. Cell 2011, 144, 986–998. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.S.; Park, J.; Kay, K.A.; Christakis, N.A.; Oltvai, Z.N.; Barabasi, A.-L. The implications of human metabolic network topology for disease comorbidity. Proc. Natl. Acad. Sci. USA 2008, 105, 9880–9885. [Google Scholar] [CrossRef] [PubMed]
- Csermely, P.; Korcsmáros, T.; Kiss, H.J.M.; London, G.; Nussinov, R. Structure and dynamics of molecular networks: A novel paradigm of drug discovery: A comprehensive review. Pharmacol. Ther. 2013, 138, 333–408. [Google Scholar] [CrossRef]
- Liu, Q.; Muglia, L.J.; Huang, L.F. Network as a biomarker: A novel network-based sparse bayesian machine for pathway-driven drug response prediction. Genes (Basel) 2019, 10, 602. [Google Scholar] [CrossRef]
- Network Medicine; Loscalzo, J., Barabási, A.-L., Silverman, E.K., Eds.; Harvard University Press: London, UK, 2017; ISBN 9780674545533. [Google Scholar] [CrossRef]
- Dimitrakopoulou, K.; Dimitrakopoulos, G.N.; Sgarbas, K.N.; Bezerianos, A. Tamoxifen integromics and personalized medicine: Dynamic modular transformations underpinning response to tamoxifen in breast cancer treatment. OMICS 2014, 18, 15–33. [Google Scholar] [CrossRef]
- Dimitrakopoulou, K.; Dimitrakopoulos, G.N.; Wilk, E.; Tsimpouris, C.; Sgarbas, K.N.; Schughart, K.; Bezerianos, A. Influenza a immunomics and public health omics: The dynamic pathway interplay in host response to H1N1 infection. Omi. A J. Integr. Biol. 2014, 18, 167–183. [Google Scholar] [CrossRef]
- Langfelder, P.; Horvath, S. WGCNA: An R package for weighted correlation network analysis. BMC Bioinform. 2008, 9, 559. [Google Scholar] [CrossRef]
- Margolin, A.A.; Nemenman, I.; Basso, K.; Wiggins, C.; Stolovitzky, G.; Favera, R.D.; Califano, A. ARACNE: An algorithm for the reconstruction of gene regulatory networks in a mammalian cellular context. BMC Bioinform. 2006, 7, S7. [Google Scholar] [CrossRef]
- Faith, J.J.; Hayete, B.; Thaden, J.T.; Mogno, I.; Wierzbowski, J.; Cottarel, G.; Kasif, S.; Collins, J.J.; Gardner, T.S. Large-scale mapping and validation of Escherichia coli transcriptional regulation from a compendium of expression profiles. PLoS Biol. 2007, 5, e8. [Google Scholar] [CrossRef]
- Serra, A.; Coretto, P.; Fratello, M.; Tagliaferri, R. Robust and sparse correlation matrix estimation for the analysis of high-dimensional genomics data. Bioinformatics 2018, 34, 625–634. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, J.; Hao, J.-K.; Zhao, X.-M.; Chen, L. Conditional mutual inclusive information enables accurate quantification of associations in gene regulatory networks. Nucleic Acids Res. 2015, 43, e31. [Google Scholar] [CrossRef]
- Zhao, J.; Zhou, Y.; Zhang, X.; Chen, L. Part mutual information for quantifying direct associations in networks. Proc. Natl. Acad. Sci. USA 2016, 113, 5130–5135. [Google Scholar] [CrossRef]
- Chan, T.E.; Stumpf, M.P.H.; Babtie, A.C. Gene Regulatory Network Inference from Single-Cell Data Using Multivariate Information Measures. Cell Syst. 2017, 5, 251–267. [Google Scholar] [CrossRef]
- Matsumoto, H.; Kiryu, H.; Furusawa, C.; Ko, M.S.H.; Ko, S.B.H.; Gouda, N.; Hayashi, T.; Nikaido, I. SCODE: An efficient regulatory network inference algorithm from single-cell RNA-Seq during differentiation. Bioinformatics 2017, 33, 2314–2321. [Google Scholar] [CrossRef]
- Frankowski, P.C.A.; Vert, J.P. Gene regulation inference from single-cell RNA-seq data with linear differential equations and velocity inference. Bioinformatics 2020, 36, 4774–4780. [Google Scholar] [CrossRef]
- Ma, B.; Fang, M.; Jiao, X. Inference of gene regulatory networks based on nonlinear ordinary differential equations. Bioinformatics 2020, 36, 4885–4893. [Google Scholar] [CrossRef]
- Herrera-Delgado, E.; Perez-Carrasco, R.; Briscoe, J.; Sollich, P. Memory functions reveal structural properties of gene regulatory networks. PLoS Comput. Biol. 2018, 14, e1006003. [Google Scholar] [CrossRef]
- Tian, T.; Burrage, K. Stochastic models for regulatory networks of the genetic toggle switch. Proc. Natl. Acad. Sci. USA 2006, 103, 8372–8377. [Google Scholar] [CrossRef]
- Barman, S.; Kwon, Y.-K. A Boolean network inference from time-series gene expression data using a genetic algorithm. Bioinformatics 2018, 34, i927–i933. [Google Scholar] [CrossRef]
- Zhang, R.; Ren, Z.; Chen, W. SILGGM: An extensive R package for efficient statistical inference in large-scale gene networks. PLoS Comput. Biol. 2018, 14, e1006369. [Google Scholar] [CrossRef] [PubMed]
- Friedman, N. Inferring Cellular Networks Using Probabilistic Graphical Models. Science 2004, 303, 799–805. [Google Scholar] [CrossRef] [PubMed]
- Dimitrakopoulou, K.; Tsimpouris, C.; Papadopoulos, G.; Pommerenke, C.; Wilk, E.; Sgarbas, K.N.; Schughart, K.; Bezerianos, A. Dynamic gene network reconstruction from gene expression data in mice after influenza A (H1N1) infection. J. Clin. Bioinforma. 2011, 1, 27. [Google Scholar] [CrossRef] [PubMed]
- Xing, L.; Guo, M.; Liu, X.; Wang, C.; Zhang, L. Gene Regulatory Networks Reconstruction Using the Flooding-Pruning Hill-Climbing Algorithm. Genes 2018, 9, 342. [Google Scholar] [CrossRef]
- Staunton, P.M.; Miranda-Casoluengo, A.A.; Loftus, B.J.; Gormley, I.C. BINDER: Computationally inferring a gene regulatory network for Mycobacterium abscessus. BMC Bioinform. 2019, 20, 466. [Google Scholar] [CrossRef]
- Magnusson, R.; Gustafsson, M. LiPLike: Towards gene regulatory network predictions of high certainty. Bioinformatics 2020, 36, 2522–2529. [Google Scholar] [CrossRef]
- Omranian, N.; Eloundou-Mbebi, J.M.O.; Mueller-Roeber, B.; Nikoloski, Z. Gene regulatory network inference using fused LASSO on multiple data sets. Sci. Rep. 2016, 6, 20533. [Google Scholar] [CrossRef]
- Ghosh Roy, G.; Geard, N.; Verspoor, K.; He, S. PoLoBag: Polynomial Lasso Bagging for signed gene regulatory network inference from expression data. Bioinformatics 2021, 36, 5187–5193. [Google Scholar] [CrossRef]
- Haury, A.C.; Mordelet, F.; Vera-Licona, P.; Vert, J.P. TIGRESS: Trustful Inference of Gene REgulation using Stability Selection. BMC Syst. Biol. 2012, 6, 145. [Google Scholar] [CrossRef]
- Mordelet, F.; Vert, J.P. SIRENE: Supervised inference of regulatory networks. Bioinformatics 2008, 24. [Google Scholar] [CrossRef]
- Huynh-Thu, V.A.; Irrthum, A.; Wehenkel, L.; Geurts, P. Inferring regulatory networks from expression data using tree-based methods. PLoS ONE 2010, 5, e12776. [Google Scholar] [CrossRef]
- Huynh-Thu, V.A.; Sanguinetti, G. Combining tree-based and dynamical systems for the inference of gene regulatory networks. Bioinformatics 2015, 31, 1614–1622. [Google Scholar] [CrossRef]
- Moerman, T.; Aibar Santos, S.; Bravo González-Blas, C.; Simm, J.; Moreau, Y.; Aerts, J.; Aerts, S. GRNBoost2 and Arboreto: Efficient and scalable inference of gene regulatory networks. Bioinformatics 2019, 35, 2159–2161. [Google Scholar] [CrossRef]
- Zheng, R.; Li, M.; Chen, X.; Wu, F.X.; Pan, Y.; Wang, J. BiXGBoost: A scalable, flexible boosting-based method for reconstructing gene regulatory networks. Bioinformatics 2019, 35, 1893–1900. [Google Scholar] [CrossRef]
- Maraziotis, I.A.; Dragomir, A.; Thanos, D. Gene regulatory networks modelling using a dynamic evolutionary hybrid. BMC Bioinformatics 2010, 11, 140. [Google Scholar] [CrossRef]
- Yang, Y.; Fang, Q.; Shen, H. Bin Predicting gene regulatory interactions based on spatial gene expression data and deep learning. PLoS Comput. Biol. 2019, 15, e1007324. [Google Scholar] [CrossRef]
- Penfold, C.A.; Millar, J.B.A.; Wild, D.L. Inferring orthologous gene regulatory networks using interspecies data fusion. Bioinformatics 2015, 31, i97–i105. [Google Scholar] [CrossRef][Green Version]
- Noor, A.; Serpedin, E.; Nounou, M.; Nounou, H.; Mohamed, N.; Chouchane, L. An overview of the statistical methods used for inferring gene regulatory networks and protein-protein interaction networks. Adv. Bioinform. 2013, 2013, 953814. [Google Scholar] [CrossRef]
- Lecca, P.; Priami, C. Biological network inference for drug discovery. Drug Discov. Today 2013, 18, 256–264. [Google Scholar] [CrossRef]
- Emmert-Streib, F.; Dehmer, M.; Haibe-Kains, B. Gene regulatory networks and their applications: Understanding biological and medical problems in terms of networks. Front. Cell Dev. Biol. 2014, 2, 38. [Google Scholar] [CrossRef]
- Muldoon, J.J.; Yu, J.S.; Fassia, M.K.; Bagheri, N. Network inference performance complexity: A consequence of topological, experimental and algorithmic determinants. Bioinformatics 2019, 35, 3421–3432. [Google Scholar] [CrossRef] [PubMed]
- Maetschke, S.R.; Madhamshettiwar, P.B.; Davis, M.J.; Ragan, M.A. Supervised, semi-supervised and unsupervised inference of gene regulatory networks. Brief. Bioinform. 2014, 15, 195–211. [Google Scholar] [CrossRef] [PubMed]
- Studham, M.E.; Tjärnberg, A.; Nordling, T.E.M.; Nelander, S.; Sonnhammer, E.L.L. Functional association networks as priors for gene regulatory network inference. Bioinformatics 2014, 30, i130–i138. [Google Scholar] [CrossRef] [PubMed]
- Siahpirani, A.F.; Roy, S. A prior-based integrative framework for functional transcriptional regulatory network inference. Nucleic Acids Res. 2017, 45, e21. [Google Scholar] [CrossRef]
- Wang, Y.; Goh, W.; Wong, L.; Montana, G. Random forests on Hadoop for genome-wide association studies of multivariate neuroimaging phenotypes. BMC Bioinform. 2013, 14 (Suppl. 1), S6. [Google Scholar] [CrossRef]
- Wuchty, S.; Arjona, D.; Li, A.; Kotliarov, Y.; Walling, J.; Ahn, S.; Zhang, A.; Maric, D.; Anolik, R.; Zenklusen, J.C.; et al. Prediction of associations between microRNAs and gene expression in glioma biology. PLoS ONE 2011, 6, e14681. [Google Scholar] [CrossRef]
- Dimitrakopoulos, G.N.; Balomenos, P.; Vrahatis, A.G.; Sgarbas, K.; Bezerianos, A. Identifying disease network perturbations through regression on gene expression and pathway topology analysis. In Proceedings of the 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016; pp. 5969–5972. [Google Scholar] [CrossRef]
- Dimitrakopoulos, G.N.; Vrahatis, A.G.; Plagianakos, V.; Sgarbas, K. Pathway analysis using XGBoost classification in Biomedical Data. In Proceedings of the 10th Hellenic Conference on Artificial Intelligence (SETN ’18), Patras, Greece, 9–12 July 2018; ACM: New York, NY, USA, 2018; p. 46. [Google Scholar] [CrossRef]
- Dimitrakopoulos, G.N.; Dimitrakopoulou, K.; Maraziotis, I.A.; Sgarbas, K.; Bezerianos, A. Supervised method for construction of microRNA-mRNA networks: Application in cardiac tissue aging dataset. In Proceedings of the 2014 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Chicago, IL, USA, 26–30 August 2014; pp. 318–321. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; ACM: New York, NY, USA, 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Marbach, D.; Prill, R.J.; Schaffter, T.; Mattiussi, C.; Floreano, D.; Stolovitzky, G. Revealing strengths and weaknesses of methods for gene network inference. Proc. Natl. Acad. Sci. USA 2010, 107, 6286–6291. [Google Scholar] [CrossRef]
- Marbach, D.; Costello, J.C.; Küffner, R.; Vega, N.M.; Prill, R.J.; Camacho, D.M.; Allison, K.R.; Kellis, M.; Collins, J.J.; Aderhold, A.; et al. Wisdom of crowds for robust gene network inference. Nat. Methods 2012, 9, 796–804. [Google Scholar] [CrossRef]
- Lawlor, N.; George, J.; Bolisetty, M.; Kursawe, R.; Sun, L.; Sivakamasundari, V.; Kycia, I.; Robson, P.; Stitzel, M.L. Single-cell transcriptomes identify human islet cell signatures and reveal cell-type-specific expression changes in type 2 diabetes. Genome Res. 2017, 2, 208–222. [Google Scholar] [CrossRef]
- Madhamshettiwar, P.B.; Maetschke, S.R.; Davis, M.J.; Reverter, A.; Ragan, M.A. Gene regulatory network inference: Evaluation and application to ovarian cancer allows the prioritization of drug targets. Genome Med. 2012, 4, 41. [Google Scholar] [CrossRef]
- Espinosa-Soto, C. On the role of sparseness in the evolution of modularity in gene regulatory networks. PLoS Comput. Biol. 2018, 14, e1006172. [Google Scholar] [CrossRef]
- Ouma, W.Z.; Pogacar, K.; Grotewold, E. Topological and statistical analyses of gene regulatory networks reveal unifying yet quantitatively different emergent properties. PLoS Comput. Biol. 2018, 14, e1006098. [Google Scholar] [CrossRef]
- Chen, S.; Mar, J.C. Evaluating methods of inferring gene regulatory networks highlights their lack of performance for single cell gene expression data. BMC Bioinform. 2018, 19, 232. [Google Scholar] [CrossRef]
- Raser, J.M.; O’Shea, E.K. Noise in gene expression: Origins, consequences, and control. Science 2005, 309, 2010–2013. [Google Scholar] [CrossRef]
- Tarca, A.L.; Draghici, S.; Khatri, P.; Hassan, S.S.; Mittal, P.; Kim, J.S.; Kim, C.J.; Kusanovic, J.P.; Romero, R. A novel signaling pathway impact analysis. Bioinformatics 2009, 24, 75–82. [Google Scholar] [CrossRef]
- Vrahatis, A.G.; Balomenos, P.; Tsakalidis, A.K.; Bezerianos, A. DEsubs: An R package for flexible identification of differentially expressed subpathways using RNA-seq experiments. Bioinformatics 2016, 32, 3844–3846. [Google Scholar] [CrossRef]
- Judeh, T.; Johnson, C.; Kumar, A.; Zhu, D. TEAK: Topology Enrichment Analysis frameworK for detecting activated biological subpathways. Nucleic Acids Res. 2013, 41, 1425–1437. [Google Scholar] [CrossRef]
- Vrahatis, A.G.; Dimitrakopoulos, G.N.; Tsakalidis, A.K.; Bezerianos, A. Identifying miRNA-mediated signaling subpathways by integrating paired miRNA/mRNA expression data with pathway topology. In Proceedings of the 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25–29 August 2015; pp. 3997–4000. [Google Scholar] [CrossRef]

| Dataset | Samples | Genes | TFs | Interactions 1 | Organism |
|---|---|---|---|---|---|
| DREAM 4.1 (D41) | 100 | 100 | 100 | 176 | Synthetic |
| DREAM 4.2 (D42) | 100 | 100 | 100 | 249 | Synthetic |
| DREAM 4.3 (D43) | 100 | 100 | 100 | 195 | Synthetic |
| DREAM 4.4 (D44) | 100 | 100 | 100 | 211 | Synthetic |
| DREAM 4.5 (D45) | 100 | 100 | 100 | 193 | Synthetic |
| DREAM 5.1 (D51) | 487 | 1643 | 178 | 4012 | Synthetic |
| DREAM 5.2 (D52) | 53 | 2810 | 38 | 515 | S. aureus |
| DREAM 5.3 (D53) | 487 | 4511 | 141 | 2066 | E. coli |
| DREAM 5.4 (D54) | 321 | 5950 | 114 | 3940 | S. cerevisiae |
| GSE86469 | 638 | 2287 | 280 | 6289 | Human |
| Dataset | R2 | MSE | MAE |
|---|---|---|---|
| D41 | 0.7949 | 0.8107 | 0.8098 |
| D42 | 0.8406 | 0.8125 | 0.8191 |
| D43 | 0.8023 | 0.7890 | 0.7979 |
| D44 | 0.7767 | 0.7704 | 0.7692 |
| D45 | 0.7747 | 0.7563 | 0.7562 |
| Average | 0.7978 | 0.7878 | 0.7905 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dimitrakopoulos, G.N. XGRN: Reconstruction of Biological Networks Based on Boosted Trees Regression. Computation 2021, 9, 48. https://doi.org/10.3390/computation9040048
Dimitrakopoulos GN. XGRN: Reconstruction of Biological Networks Based on Boosted Trees Regression. Computation. 2021; 9(4):48. https://doi.org/10.3390/computation9040048
Chicago/Turabian StyleDimitrakopoulos, Georgios N. 2021. "XGRN: Reconstruction of Biological Networks Based on Boosted Trees Regression" Computation 9, no. 4: 48. https://doi.org/10.3390/computation9040048
APA StyleDimitrakopoulos, G. N. (2021). XGRN: Reconstruction of Biological Networks Based on Boosted Trees Regression. Computation, 9(4), 48. https://doi.org/10.3390/computation9040048






