Abstract
In the present case study, a moisture diffusion model is developed to simulate the drying kinetics of Lavandula x allardii leaves for non-stationary convective drying regimes. Increasing temperature profiles are applied over the drying duration and the influence of temperature advancing rates on the moisture removal and the drying rate is investigated. The model assumes a one-dimensional moisture transfer under transient conditions, which occurs from the leaf center to the surface by liquid diffusion due to the concentration gradient developed by the surface water evaporation caused by the difference of water vapor partial pressure between the drying medium and the leaf surface. A numerical solution of Fick’s 2nd law is obtained by an in-house code using the finite volume method, including shrinkage and a variable temperature-dependent effective moisture diffusion coefficient. The numerical results have been validated against experimental data for selected cases using statistical indices and the predicted dehydration curves presented a good agreement for the higher temperature advancing rates. The examined modeling approach was found stable and can output, in a computationally efficient way, the temporal changes of moisture and drying rate. Thus, the present model could be used for engineering applications involving the design, optimization and development of drying equipment and drying schedules for the examined type of non-stationary drying patterns.
1. Introduction
Lavender is an important aromatic plant for essential oil production used by a series of industries for different applications. Lavandula x allardii is a hybrid of the lavender Lamiaceae family and is commonly found around the Mediterranean area. Fresh raw plant material is vulnerable to spoilage due to the growth of mold, yeast and bacteria leading to unwanted chemical reactions; thus, drying is required to remove the water and reduce the water activity for storing safely the products until further processing. Good knowledge and a proper design are required for drying processes, since drying temperature, airflow velocity, relative humidity and product positioning among rest parameters have a significant impact on product quality, cost and energy consumption.
Convective drying is a drying method applied widely on most agricultural products due to the cost-effectiveness and the scalability to different applications. Hot air gets in contact with the product surface where the existing surface water is evaporated and transferred to the airstream. In the vast majority of cases, convective drying is performed under constant operating drying conditions providing a better control over the drying process duration with a simpler implementation. However, non-stationary drying schemes involving drying parameter alterations over time or different kinds of intermittency may lead to improved output in terms of product quality and energy saving [1]. Such drying regimes are reported for medical and aromatic plants of peppermint (Mentha piperita L.) by Metin Ozguven et al. [2] and lemon balm (Melissa officinalis L.) by Cuervo-Andrade et al. [3] and Tarhan and Ertugrul [4].
Accurate modeling of drying processes is required for designing and optimizing the drying facilities as well as the drying regimes applied on each product. Most drying models found in literature can be classified as empirical or semi-empirical approaches that correlate moisture changes with time and are valid for a limited operation range, since different model coefficients are needed for each combination of drying conditions. In contrast, diffusion-based models derived from fundamental laws, are able to explain the physical phenomena occurring during drying [5,6]. The complexity of the previous models may vary based on the assumptions made regarding the mechanisms of simultaneous mass and heat transport in the product’s interior and the external conditions applied on the domain boundaries of product and drying air. These models are reported to be successfully implemented on various herbs such as tea, yerba mate and tobacco leaves [7,8,9].
The moisture transport inside the product during the drying process can be modeled by liquid diffusion, assuming it is the predominant transfer mechanism [10]. In this case the Fick’s second law for mass transfer can be applied and use numerical techniques such as the finite difference method (FDM), the finite volume method (FVM) or the finite element method (FEM) to approximate the solution of the governing partial differential equations (PDE) over the product domain. FVM discretization is preferred for moisture transport and liquid diffusion problems [11] and is used to obtain a set of algebraic equations. Depending on the product geometry, simplifications can be made on dimensions preferring the most simplifying approach that outputs satisfactory results compared with the actual experimental data, when examining rectangular, cylindrical or spherical pieces, slabs or slices of foods or fruits, using each time the most appropriate coordinate system. Success and accuracy of previous methods are reported to be obtained by models involving variable transport and thermophysical material properties, including domain shrinkage effects that should not be neglected [12,13,14,15].
The present study aims to develop a diffusion-based model to examine the moisture content and the rates of moisture removal of Lavandula x allardii, subjected to non-stationary drying regimes that involve a linear advancing pattern of drying temperature with different rates of temperature increment. For this purpose, a one-dimensional transient model is formulated, assuming that moisture travels from the leaf center to the surfaces by liquid diffusion symmetrically since airstream is parallel to the leaves that are arranged as a thin layer. The finite volume method is used to solve Fick’s second law PDE assuming a variable temperature-dependent moisture diffusion coefficient and a linear reduction of leaf thickness during drying duration.
2. Materials and Methods
2.1. Materials, Drying Experiments and Equipment
The leaf samples of Lavandula x allardii hybrid were harvested from the University of West Attica (37°58.73544′, 023°40.42014′), located in Athens, Greece. Inflorescences and stems were removed, and healthy leaves were spread on a tray as a thin layer, placed parallel with the flow. The initial moisture content of samples in wet basis was 61.0% and it was determined by the oven method [16]. The drying regimes were investigated, regarding the application of a linear increase of drying temperature starting from 40 °C and eventually reaching 60 °C after a different duration that is defined by the temperature advancing rate (TAR), expressed as °C/h. Temperature profiles were shaped using the VK 981(RH) TWIN Smart Curing control by regulating a heat resistance for the discontinuous heat provision to the airstream. Experiments were performed for temperature advancing rates of 2–4 °C/h at a 2 m/s airflow velocity, using a laboratory-scale convective dryer (Figure 1) of Vencon Varsos S.A (model MNLB118). The Reynolds number per unit length was ranged from 5.3 × 104 to 1.8 × 105. Approximately 100 g of lavender leaves were placed to the dryer’s perforated tray, having their surface parallel with the airflow. The fresh leaves were arranged as a thin-layer with a thickness equal to the leaves’ average thickness (L = 0.477 ± 0.044 mm) and were held by a plastic-fiber net, allowing both sides to be in contact with the hot air. Experimental moisture content was used to validate the diffusion model’s output and was computed by Equation (1), using the weight measurements obtained by the Kern PLS 1200-3A electronic balance.
where X is the moisture content in dry basis (kgwater/kgdry product), wt is the leaves’ mass at any time (kg) and wd is the dry matter weight of leaves (kg).

Figure 1.
Laboratory-scale convective dyer and three-perforated tray drying chamber.
2.2. Formulation of One-Dimensional Diffusion Model
Lavender leaves were considered as thin slabs where water transport occurs from the leaves’ center to the upper and the lower surface due to the potential gradient caused by the different moisture concentrations. The water is evaporated on the leaf surfaces and the moisture is transferred to the airstream. The governing equation describing moisture movement is given by the Fick’s second law for mass conservation, which is presented in one-dimensional, transient form:
where z ∈ [0, L/2] is the spatial coordinate, L is the leaf thickness, t is the drying time, ρs is the density of solid product (kg/m3) and Deff is the effective moisture diffusivity (m2/s).
The initial and boundary conditions of the present model, describe the domain to be initialized with uniform moisture (Xin) before drying process starts and set the mass transfer at leaf surfaces considering a Robin boundary condition. The current problem is treated as symmetrical since moisture travels from leaf central layers towards the two leaf surfaces, thus an additional boundary condition is added. The previous can be summarized in the following equations:
where hm is the mass transfer coefficient (m/s), C is the water vapor concentration (kg/m3), aw is the water activity, pvs is the saturated water vapor pressure, TL/2 is the temperature at leaf’s center and Rv = 461.52 J/kg/K is the specific gas constant of water vapor.
The previous PDE can be solved numerically by FVM as described by Patankar [17] and Versteeg and Malalasekera [11] in MATLAB. The one-dimensional domain of a single lavender leaf is illustrated in Figure 2. For a random P node and the nearby east (E) and west (W) nodes, the following discretization equation can be applied, using a fully implicit scheme and piecewise linear profile space discretization:
where Su and Sp are the constant and coefficient parts of the source term, respectively.
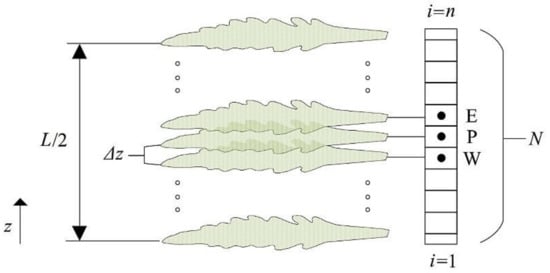
Figure 2.
One-dimensional computational domain of a single lavender leaf.
The system of the algebraic equations derived by each node can be solved with the Thomas algorithm, which is a computationally inexpensive direct method that can be applied to tridiagonal matrices. For the space and time discretization, a preliminary sensitivity analysis was performed using different node number (N) and timestep combinations, concluding that a spatial discretization of 500 nodes and timesteps lesser than 10 s were not significantly improving the accuracy of the numerical results.
Transport and thermophysical properties of air and lavender leaves, implemented in model, were either found in literature, or were experimentally obtained. The saturated water vapor pressure as a function of temperature [18] is given by:
where , , , , and .
The mass transfer coefficient (hm), Equation (11), was derived by the Chilton and Colburn analogy [19,20]. The convective heat transfer coefficient (h), Equation (12), was obtained by the Nusselt–Reynolds–Prandtl correlation that applies for turbulent flow over flat plates [21].
hm = h(Dva Le1/3/kair)
h = Nu kair/x; Pr = Cp,air μ x/kair; Le = aair/Dva; Re = ρairU∞x/μ
Water activity (aw) of lavender leaves was related with the experimentally determined equilibrium moisture content of samples that were placed in closed containers using salt solutions of KOH, NaCl, NaBr, Mg(NO3)2 and KCl with water activities ranging from 7.4% to 83.6% at 30 °C. The adsorption data was fit to the Chen model [22] (Equation (14)) by non-linear regression, using SPSS Statistics software [23]. The model coefficients were estimated to be k1 = 441.63, k2 = 444.78, k3 = 5.18·10−3 with R2 = 0.796.
where M is the moisture content in wet basis (kgwater/kgproduct).
The moisture diffusivity was calculated using the experimental moisture ratio data and the slope method, as described in Tzempelikos et al. [24], treating the leaf as a flat plate on which the one-dimensional mass-diffusion equation was applied [25]. An Arrhenius type equation is used to express the effective diffusion coefficient dependence with temperature, using the following expression:
where D0 is the pre-exponential factor of the Arrhenius equation (m2/s), Ea is the activation energy (kJ/mol), T is the absolute temperature (K) and R is the gas constant (kJ/mol/K).
Leaf temperature in this case was considered to be equal with the drying air temperature at any time due to the low leaf mass (<1 g) and thickness (L = 0.477 mm) that leads to a limited ability to store heat, resulting in a rapid increase or decrease of temperature. The activation energy and the pre-exponential factor of the Arrhenius equation of lavender leaves were calculated to 63.28 kJ/mol and 7.22·10−2 m2/s, respectively.
Leaf thickness shrinkage was also accounted for by an empirical relation that was derived by measurements of multiple leaves before and after the drying process. A linear relationship was found as most appropriate and linear regression was used to correlate the thickness shrinking ratio (L/L0) and the moisture ratio (MR), with R2 = 0.815. The leaf thickness was updated for each timestep, according to Equation (16).
where L is the leaf thickness at any time, Lin is the initial leaf thickness, Xt is the moisture content in dry basis at any drying time and Xin is the initial moisture content in dry basis of lavender leaves.
The goodness of fit between the measured and the computed moisture ratio was evaluated by three statistical indices, including the coefficient of determination (R2) (Equation (18)), the root mean square error (RMSE) (Equation (19)) and the sum of squared errors (SSE) (Equation (20)).
where N is the number of measured data, MRc,i is the model-computed moisture ratio, MRm,i is the experimentally measured moisture ratio and MRm,av is the average value of the measured moisture ratio.
3. Results and Discussion
Modeling the temporal evolution of moisture for different drying conditions is vital for the drying process control, production management and product safety, since early stopping of drying may lead to microbial growth and spoilage, whereas overdrying could deteriorate the product quality. Accurate models and predictions of the duration needed for each product to reach a safe moisture content is required to avoid extra costs related with increased energy consumption and product waste. For this reason, the model is validated against experimental measurements and the drying kinetic curves along with the drying rates are evaluated below.
The drying characteristics of lavender leaves were experimentally assessed in a laboratory-scale dryer, for TAR = 2–4 °C/h in the temperature range of 40–60 °C and 2 m/s airflow velocity. The experimental and the numerical output for the temporal evolution of moisture ratio for the investigated situations is shown in Figure 3a; the influence of various temperature advancing rates on the moisture ratio versus time is shown in Figure 3b.
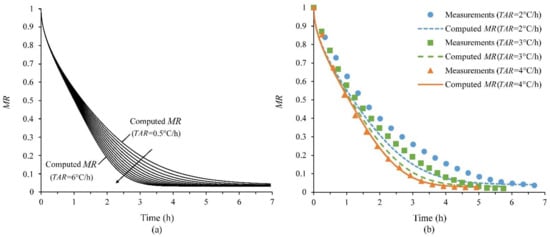
Figure 3.
(a) Measured and computed moisture ratio (MR) of lavender, (b) Computed MR for TAR = 0.5–6 °C/h with a 0.5 °C/h step at 2 m/s.
The moisture content is decreasing exponentially under a different rate for the investigated cases. Higher temperature advancing rates are noticed to result in increased moisture removal at respective drying times. Higher drying temperatures levels are applied in a shorter period of time for the greater temperature increasing rates; thus, a reduced overall drying time is associated with higher temperature advancing rates. This observation is explained by the increased moisture diffusivity coefficient values that are associated with the increased product temperature, as indicated by Equation (15), which depends on the drying temperature applied by each drying regime. Increasing the temperature advancing rate from 2 to 4 °C/h, a decrease of the total drying time is estimated to be 24%. The moisture removal is continued until an equilibrium is achieved between the surface of lavender leaves and the air’s vapor partial pressure. Drying duration was approximately 6.7 h for TAR = 2 °C/h, 5.7 h for TAR = 3 °C/h and 4.9 h for TAR = 4 °C/h.
The presented model is capable of predicting with reasonable accuracy the moisture ratio. The results of the statistical analysis are shown in Table 1. A good fit is noticed for the 4 °C/h temperature advancing rate case during the entire drying duration, in contrast with the rest experimentally examined cases where a slight divergence can be observed for MR < 0.4 as shown in Figure 3a. Thus, the examined modeling approach could be used to approximate the moisture evolution of the non-stationary drying using linearly advancing temperature schemes, and estimate the overall drying duration required for the process design.

Table 1.
Statistical analysis results of the moisture diffusion model.
The drying rate of lavender leaves for the investigated type of non-stationary drying schemes is presented in Figure 4. There is no constant drying rate period as the experimentally determined drying rate shows that the drying process occurs within the falling rate period, thus, the liquid diffusion is the dominant mechanism governing the water migration in the interior of leaves for the whole drying duration [26,27]. The difference in the concentration of vapor partial pressure between the air and the lavender leaves is the driving force for the moisture transfer via liquid diffusion, which is governed by internal resistance [28]. This potential difference diminishes with time, as the vapor pressure inside leaves and air approach to an equilibrium, resulting in a decrease of the drying rate. Higher temperature advancing rates have a larger impact on drying rate at the initial and the final drying stages, leading to a decrease of the drying time as shown in Figure 4a.
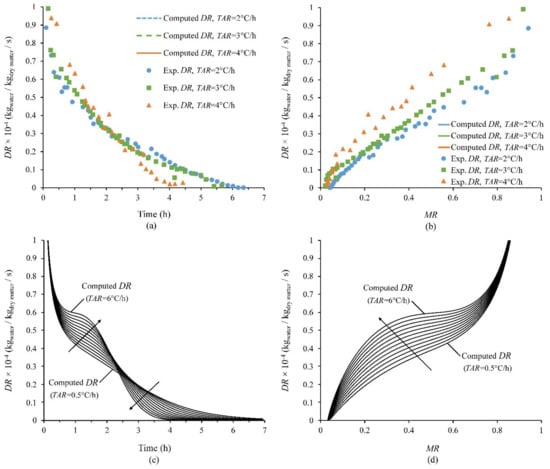
Figure 4.
Measured and computed drying rate (DR) of lavender versus time (a,c) and moisture ratio (MR) (b,d) at 2 m/s.
The influence of temperature advancing rates on the drying rates, as determined numerically is presented in Figure 4c,d. Lower temperature advancing rates exhibit a smooth drying rate curve, similar to the conventional convective drying at a constant temperature. For increased values of temperature advancing rates a different pattern is observed, including a sharp drop of the drying rate at initial stages, followed by a less steep change of moisture removal rate and then a second reducing drying rate period is obtained that remains until the end of the drying process. This drying rate behavior is visible by the drying curves of Figure 4a, explaining the different slope of each drying curve in the approximate range of 0.66–2 h and 3–4 h and the range of the corresponding moisture ratios, caused by the different temperature level applied by each drying regime for the same drying duration. In general, increased temperature advancing rates are responsible for inducing enhanced heat transfer to leaves, resulting in increased drying rates and shorter drying duration. Similar results are presented by drying kinetic studies and reviews [10,29,30,31,32], noting the lack of constant-rate intervals and a comparable trend between the applied drying temperature levels and the calculated drying rates.
4. Conclusions
A moisture diffusion model was developed to analyze the drying kinetics of Lavandula x allardii leaves subjected to non-stationary drying regimes of temperature increasing profiles. The moisture transport was modelled by liquid diffusion, using an effective moisture diffusion coefficient derived by experimental data, accounting its dependence on temperature. A mixed boundary condition was applied at leaf surfaces, including the effects of leaf thickness shrinkage on a one-dimensional domain for the solution of Fick’s second law, using the finite volume method. The drying rate and the moisture ratio were successfully predicted by a custom code developed and the numerical output was compared with experimental case studies. The presented modeling approach was stable and computationally efficient, estimating the drying kinetics of the examined non-stationary drying patterns more accurately for the higher temperature advancing rates. Thus, the present model can be further exploited for the improvement of the design and the development of drying equipment and drying schedules.
Author Contributions
Investigation, V.C. and D.T.; Methodology, V.C. and D.T.; Project administration, A.F.; Software, V.C.; Supervision, D.T. and A.F.; Validation, V.C. and D.T.; Visualization, V.C.; Writing—original draft, V.C.; Writing—review and editing, D.T. and A.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors would like to thank George Varsos from Vencon Varsos S.A. for his technical support and the provision of the laboratory-scale convective dryer.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Defraeye, T. Towards more efficient intermittent drying of fruit: Insights from combined hygrothermal-quality modelling. Innov. Food Sci. Emerg. Technol. 2016, 38, 262–271. [Google Scholar] [CrossRef] [Green Version]
- Metin Ozguven, M.; Tarhan, S.; Polatci, H.; Telci, I. A New Way to Improve the Drying Kinetics and Final Quality of Peppermint. J. Essent. Oil Bear. Plants 2016, 19, 1368–1379. [Google Scholar] [CrossRef]
- Cuervo-Andrade, S.P.; Hensel, O. Stepwise drying of medicinal plants as alternative to reduce time and energy processing. IOP Conf. Ser. Mater. Sci. Eng. 2016, 138, 012014. [Google Scholar] [CrossRef]
- Tarhan, S.; Ertugrul, M. The Change of Drying Time and Quality Parameters of Lemon Balm (Melissa officinalis L.) with Different Temperature Profiles of Drying Air. J. New Results Eng. Nat. Sci. 2019, 9, 1–10. [Google Scholar]
- Erbay, Z.; Icier, F. A Review of Thin Layer Drying of Foods: Theory, Modeling, and Experimental Results. Crit. Rev. Food Sci. Nutr. 2010, 50, 441–464. [Google Scholar] [CrossRef]
- Onwude, D.I.; Hashim, N.; Janius, R.B.; Nawi, N.M.; Abdan, K. Modeling the Thin-Layer Drying of Fruits and Vegetables: A Review. Compr. Rev. Food Sci. Food Saf. 2016, 15, 599–618. [Google Scholar] [CrossRef] [PubMed]
- Botheju, W.S.; Amarathunge, K.S.P.; Abeysinghe, I.S.B. Modeling Trough Withering System to Predict the Moisture Content of Tea Leaves at Real Time using One Dimensional Heat and Mass Transfer Finite Difference Model. Trop. Agric. Res. 2011, 22, 282–295. [Google Scholar] [CrossRef] [Green Version]
- Pilatti, D.; Johann, G.; Palú, F.; da Silva, E.A. Evaluation of a concentrated parameters mathematical model applied to drying of yerba mate leaves with variable mass transfer coefficient. Appl. Therm. Eng. 2016, 105, 483–489. [Google Scholar] [CrossRef]
- Kiranoudis, C.; Maroulis, Z.; Marinos-Kouris, D. Mass Transfer Modeling for Virginia Tobacco Curing. Dry. Technol. 1990, 8, 351–366. [Google Scholar] [CrossRef]
- Babu, A.; Kumaresan, G.; Raj, V.A.A.; Velraj, R. Review of leaf drying: Mechanism and influencing parameters, drying methods, nutrient preservation, and mathematical models. Renew. Sustain. Energy Rev. 2018, 90, 536–556. [Google Scholar] [CrossRef]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method; Pearson Education: New York, NY, USA, 2007. [Google Scholar]
- Ramallo, L.; Mascheroni, R. Effect of Shrinkage on Prediction Accuracy of the Water Diffusion Model for Pineapple Drying. J. Food Process. Eng. 2013, 36, 66–76. [Google Scholar] [CrossRef]
- Hassini, L.; Azzouz, S.; Peczalski, R.; Belghith, A. Estimation of potato moisture diffusivity from convective drying kinetics with correction for shrinkage. J. Food Eng. 2007, 79, 47–56. [Google Scholar] [CrossRef]
- Katekawa, M.E.; Silva, M.A. A Review of Drying Models Including Shrinkage Effects. Dry. Technol. 2006, 24, 5–20. [Google Scholar] [CrossRef]
- Tzempelikos, D.A.; Mitrakos, D.; Vouros, A.P.; Bardakas, A.V.; Filios, A.E.; Margaris, D.P. Numerical modeling of heat and mass transfer during convective drying of cylindrical quince slices. J. Food Eng. 2015, 156, 10–21. [Google Scholar] [CrossRef]
- AOAC. Official Methods of Analysis, 15th ed.; Association of Official Analytical Chemists: Arlington, VA, USA, 1990. [Google Scholar]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow; Hemisphere Publishing Corp: New York, NY, USA, 1980. [Google Scholar]
- Owen, M.S. ASHRAE Handbook: Fundamentals; American Society of Heating, Refrigerating and Air-Conditioning Engineers: Atlanta, GA, USA, 2009. [Google Scholar]
- Bergman, T.L.; Lavine, A.S.; Incropera, F.P.; DeWitt, D.P. Principles of Heat and Mass Transfer, 7th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Chilton, T.H.; Colburn, A.P. Mass Transfer (Absorption) Coefficients Prediction from Data on Heat Transfer and Fluid Friction. Ind. Eng. Chem. 1934, 26, 1183–1187. [Google Scholar] [CrossRef]
- Defraeye, T.; Verboven, P.; Ho, Q.T.; Nicolai, B. Convective heat and mass exchange predictions at leaf surfaces: Applications, methods and perspectives. Comput. Electron. Agric. 2013, 96, 180–201. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.S. Equilibrium Moisture Curves for Biological Materials. Trans. ASAE 1971, 14, 924–926. [Google Scholar] [CrossRef]
- IBM Corp. IBM SPSS Statistics for Windows; IBM: Armonk, NY, USA, 2020. [Google Scholar]
- Tzempelikos, D.A.; Vouros, A.P.; Bardakas, A.V.; Filios, A.E.; Margaris, D.P. Case studies on the effect of the air drying conditions on the convective drying of quinces. Case Stud. Therm. Eng. 2014, 3, 79–85. [Google Scholar] [CrossRef] [Green Version]
- Crank, J. The Mathematics of Diffusion; Oxford University Press: Oxford, UK, 1979. [Google Scholar]
- Kaya, A.; Aydın, O.; Dincer, I. Experimental and numerical investigation of heat and mass transfer during drying of Hayward kiwi fruits (Actinidia Deliciosa Planch). J. Food Eng. 2008, 88, 323–330. [Google Scholar] [CrossRef]
- Beigi, M. Numerical simulation of potato slices drying using a two-dimensional finite element model. Chem. Ind. Chem. Eng. Q. 2017, 23, 431–440. [Google Scholar] [CrossRef]
- Castro, A.; Mayorga, E.; Moreno, F. Mathematical modelling of convective drying of feijoa (Acca sellowiana Berg) slices. J. Food Eng. 2019, 252, 44–52. [Google Scholar] [CrossRef]
- Nadi, F. Estimation of the mass transfer parameters of Horseradish (Armoracia rusticana L.) under convective drying. In Proceedings of the 2nd Iranian Conference on Heat and Mass Transfer (ICHMT), Semnan, Iran, 19–20 November 2014; pp. 2–5. [Google Scholar]
- Calín-Sánchez, Á.; Figiel, A.; Lech, K.; Szumny, A.; Carbonell-Barrachina, Á.A. Effects of Drying Methods on the Composition of Thyme (Thymus vulgaris L.) Essential Oil. Dry. Technol. 2013, 31, 224–235. [Google Scholar] [CrossRef]
- Chua, L.Y.W.; Chua, B.L.; Figiel, A.; Chong, C.H.; Wojdyło, A.; Szumny, A.; Łyczko, J. Drying of Phyla nodiflora Leaves: Antioxidant Activity, Volatile and Phytosterol Content, Energy Consumption, and Quality Studies. Processes 2019, 7, 210. [Google Scholar] [CrossRef] [Green Version]
- Turan, O.Y.; Firatligil, F.E. Modelling and characteristics of thin layer convective air-drying of thyme (Thymus vulgaris) leaves. Czech J. Food Sci. 2019, 37, 128–134. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).