Abstract
Monte Carlo methods rely on sequences of random numbers to obtain solutions to many problems in science and engineering. In this work, we evaluate the performance of different pseudo-random number generators (PRNGs) of the Curand library on a number of modern Nvidia GPU cards. As a numerical test, we generate pseudo-random number (PRN) sequences and obtain non-uniform distributions using the acceptance-rejection method. We consider GPU, CPU, and hybrid CPU/GPU implementations. For the GPU, we additionally consider two different implementations using the host and device application programming interfaces (API). We study how the performance depends on implementation parameters, including the number of threads per block and the number of blocks per streaming multiprocessor. To achieve the fastest performance, one has to minimize the time consumed by PRNG seed setup and state update. The duration of seed setup time increases with the number of threads, while PRNG state update decreases. Hence, the fastest performance is achieved by the optimal balance of these opposing effects.
1. Introduction
The rapid development of GPU cards in recent decades led to widespread adoption in many areas of scientific computing [1,2,3,4,5,6]. If efficiently utilized, the many-core architecture of the GPUs enables high-performance parallel computations. A class of widely used methods that can benefit from parallelization is the Monte Carlo (MC) method. This method relies on sequences of pseudo-random numbers (PRNs) to perform computations [7,8,9]. Examples of MC applications range from the evaluation of integrals to particle transport simulations [10,11,12,13,14,15]. One of the main components of MC calculations is the generation of PRN sequences with a given probability distribution. The most common PRNGs produce sequences with uniform distributions. Non-uniform distributions can be obtained using algorithms such as acceptance-rejection (AR), inverse-transform, and other methods [7].
There have been many studies of parallel PRN generation on multi-core CPUs [16,17,18,19,20,21], and GPUs [22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52]. The idea is to have different instances of PRNGs on different threads, each of which produce unique sequences of random numbers. This can be achieved in two fundamentally different ways: splitting and parameterization [21,22,32]. The splitting method divides the entire sequence of PRNs that a serial process would produce into sub-sequences and assigns them to different processors/threads. In the parameterization method, different processors/threads can run the same (or the same type of) PRNG with distinct algorithm parameters so that they produce different samples. To maximize performance, the PRNG size should be small enough to fit into local memory. Reference [44] studied a GPU implementation of the Park-Miller PRNG using the CUDA platform, finding a speed-up by a factor of at least 44× compared to the CPU implementation. Ref. [48] implemented PRNG on GPU for an MC particles transport code and observed up to 8.1× speed-up compared to implementation on CPU with 4 to 6 cores. Furthermore, [53] studied the speed and quality of the proposed xorgenGP PRNG, finding a similar speed to the MTGP32 generator. Reference [54] proposed a GPU-based parallel PRNG on CUDA Fortran implemented using the global and shared memory modes. These are used to store a pre-generated table of seeds. Each thread runs PRNGs with unique seeds and generates independent parallel sequences of PRNs. They find a speedup of 150× and 470× over the single CPU core implementation for global and shared memory modes, respectively. However, compared to the Curand XORWOW generator, the proposed PRNG in shared memory mode was slower by . In [55], authors present optimization of SHR3 generator to solve differential equations, which outperformed the Curand XORWOW generator by 79% and 38% for uniform and normal distributions, respectively. Reference [56] compared the performance of PRNGs from the VecRNG package (VecRNG is a part of VecMath, a collection of vectorized algorithms for high-energy physics applications based on the VecCore library [56,57].) with the Curand library PRNGs to generate double precision PRNs. They find that the Curand library implementation of the PHILOX4_32_10 generator is five times faster than the VecRNG implementation, while the MRG32k3a generators in both libraries show a similar performance.
The main aim of this work is to assess the feasibility of using GPU computing for MC calculations. We focus on the most fundamental component of the MC methods: generation of sequences of PRNs with uniform and non-uniform distributions, which often represents a significant fraction of the overall computational cost of the method. We extend the previous works by considering a wider range of performance measures, including the data transfer time between CPU and GPU as well as execution of API function calls (e.g., memory allocation, device synchronization, etc.), all of which consume resources and affect the overall performance [58]. We use a selection of modern Nvidia cards and consider five different PRNGs from the Curand library: XORWOW, PHILOX4_32_10, MTGP32, MT19937, and MRG32k3a. These generators produce PRNs with uniform distribution. Using the AR method, we produce three different non-uniform distributions: the Rayleigh, Beta, and Gamma distributions [59,60,61]. These numerical experiments serve as idealized test calculations that model the most fundamental component of MC methods.
We study how the performance depends on implementation parameters. To that end, we consider implementations on GPU and CPU as well as a hybrid GPU/CPU implementation, in which the uniform PRNs are generated on the GPU and transformed into non-uniform distribution on a CPU core using the AR method. For the GPU implementation, we additionally consider two different implementations using the host and device application programming interfaces (API). We analyze the dependence of performance on the number of threads per block and the number of blocks per streaming multiprocessor. Finally, we provide a comparison of implementations on different GPUs.
2. Methodology
2.1. GPU Architecture
Nvidia GPU architecture consists of a set of streaming multiprocessors (SMs), which contain different computing units such as CUDA cores, special function units, loading/storing units, and schedulers. Additionally, modern high-end GPU cards contain tensor and ray tracing cores designed for the acceleration of matrix multiplications and for graphical rendering of shadows and light respectively.
Nvidia GPU cards can be programmed by using the CUDA computing platform [62,63]. GPUs can execute instructions on multiple threads in parallel. The parallel part is executed as kernels. Each SM can accommodate a fixed maximum amount of threads (e.g., 1536 for RTX3090) grouped in thread blocks. Thread blocks are allocated by GPU schedulers to SMs once a kernel is started. SM divides blocks into warps. A warp is a basic processing unit that consists of 32 threads. SM issues instructions to be executed by threads in a warp simultaneously. Multiple warps can be processed in an SM at the same time.
To efficiently utilize a parallel structure of GPU, a complex memory hierarchy located on different access levels is available. The global memory is the main and largest memory of GPU cards, reaching 32 GB on modern GPUs. It is accessible by all threads, but it has a high access latency of up to several hundred clock cycles. The shared memory is smaller and has lower latency and higher bandwidth when compared to the global memory. It is accessed by threads within the same block. The size can be managed by software and can reach 96 KB on modern GPU cards. The registers are the fastest type of memory. In modern GPU cards, each SM has 256 KB of register memory. This memory is allocated among threads, so each thread has private registers. In addition, there are constant and texture memory spaces that are read-only and are declared from the host before running the GPU kernel. Constant memory can be used to keep constants and input values, while texture memory can be used to cache 2D and 3D data located in global memory. Constant memory size is limited to 64 KB, whereas texture memory is defined by array dimensions. Both of them can be accessed by all threads. More detailed information about memory structure can be found in, e.g., [63,64].
2.2. PRNG Parameters
The main parameters of the five different PRNGs that we consider in our work are summarized in Table 1. The MTGP32 generator uses the parameterization method, while XORWOW, MT19937, and MRG32k3a use the splitting method. PHILOX4_32_10 in the host API implementation uses the parameterization method, whereas in the device API implementation, it uses the splitting method [65]. The period of a PRNG tells us how many PRNs we can generate until it repeats itself. The length of the sub-sequence shows us how many PRNs can generate each thread/stream without overlapping with other threads/streams. More information about these PRNGs can be found in [65].

Table 1.
Summary of the key parameters of the five Curand PRNGs considered in this work.
2.3. Experimental Setting
We perform calculations on a single AMD Ryzen Threadripper 3990X CPU core as well as on Nvidia GTX1080, GTX1080Ti, RTX3080, and RTX3090 GPU cards (see specifications of GPU cards in Table 2). We compare the Curand library PRNGs [65] using the same application, identical parameter sets (seed, ordering, etc.), and with a similar configuration of blocks and threads. Additionally, using different combinations of threads per block on various GPU cards, we find the range of threads per block that allows us to achieve the highest performance. We use programming language C/C++ and CUDA computing platform version 11.4 and Nvidia driver version 470.57.02. To measure the execution time of computations, we use metric functions such as clock_t, cudaEvent_t, nvprof, and nsys profiling tools. All calculations are made in single-precision floating point format.

Table 2.
Specifications of the Nvidia GPU cards considered in this work.
To study the performance of PRNGs on GPUs, we consider four different implementations: (1) The GPU implementation (G_imp), where the uniform PRNs are generated and then transformed into non-uniform distribution (i.e., Rayleigh, Beta, and Gamma distributions [59,60,61]) using the AR method on the GPU only. (2) The CPU implementation (C_imp), where all calculations take place on a single core of the CPU. (3) The hybrid implementation (H_imp), in which GPU generates uniform PRNs, then transfers them to the RAM, where the AR method is applied to obtain non-uniform distribution on a single core of the CPU, sequentially. (4) The GPU implementation with memory copy from the device to the host (G_imp_mcpy), to account for the time spent on transferring data from the GPU to the CPU at the end of the calculation.
We consider two different ways to call the PRNG functions in the G_imp implementation: using the host API and device API. For the former, the library functions are called on the CPU, but the computations are performed on the GPU. The PRNs can then be stored on the device’s global memory or can be copied to the CPU for subsequent use. The device API allows us to call the device functions to set up PRNG parameters, such as seed, state, sequence, etc., inside a GPU kernel. The generated PRNs can be used immediately in the GPU kernel without storing them in global memory. To minimize the data movement within the GPU memory, we implement all PRNG steps (such as seed setup, state update, etc.) in the device API using a single kernel. In Section 3.3, we present a detailed comparison of these two API implementations.
To obtain a sequence of PRNs with a probability distribution with the AR method, one generates two equal-length sequences of PRNs x and y with uniform distributions and then selects (accepts) the values of x that satisfy the condition [7]. The Beta, Gamma, and Rayleigh distribution functions that we consider in this work have acceptance rates of , , and , respectively. Figure 1 shows these functions for using normalization .
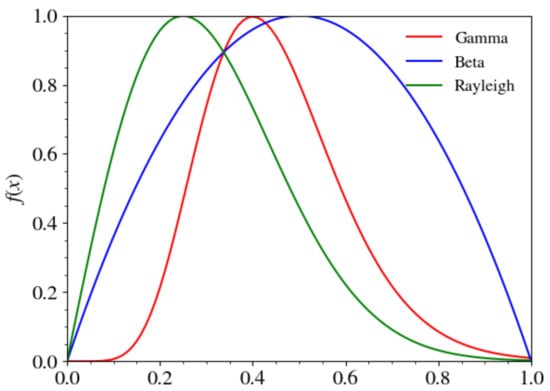
Figure 1.
The probability density functions of the Beta, Gamma, and Rayleigh distributions (normalized to ). The areas under the curves of Beta, Gamma, and Rayleigh distributions are 0.67, 0.36, and 0.41, respectively.
As a main measure of performance, we measure the time it takes to execute the computations. All the provided measurements are based on average over 100 iterations. In our default fiducial setup, we use the MRG32k3a PRNG, Beta distribution, Curand device API implementation on an RTX3090 GPU card, as summarized in Table 3. In the following section, we vary each of these parameters to investigate the dependence on them. We point out that our default parameters are not meant to represent the best or the optimal parameters. Instead, it serves as a baseline parameter set, with respect to which we compare the performance measure for other values of these parameters.

Table 3.
Default fiducial parameters of our experimental setup. The values of each of these parameters are varied to study the dependence of performance on these parameters.
3. Results
3.1. Comparison of GPU and CPU Implementations
Figure 2a shows the execution time as a function of the number of generated random candidate points (N) for different implementations. For small N in the range of , the CPU implementation C_imp is faster G_imp and H_imp by up to two orders of magnitude. This difference in speed is caused by low occupancy of the GPU of (The GPU occupancy is defined as the number of active warps to the maximum number of warps that can run on the GPU). For small N, in contrast to the CPU cores, the GPU cores are not fully utilized. Since a single GPU core is slower than a single CPU core, partially-utilized GPU leads to slower execution compared to a single CPU. The H_imp implementation, in which the PRNs are generated on the GPU, but AR-selected in the CPU, performs similarly to the G_imp implementation. This is again caused by the low occupancy of the GPU, which becomes a bottleneck for this implementation.
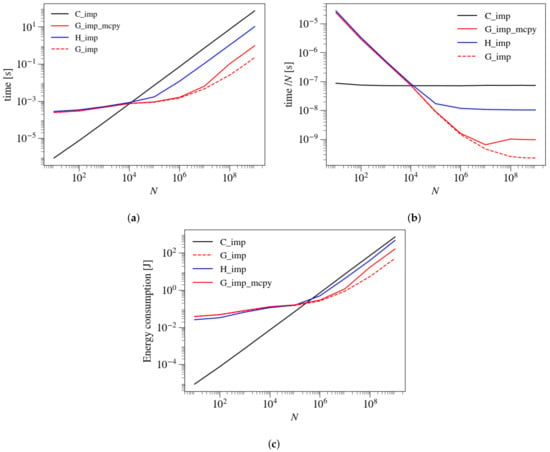
Figure 2.
Execution time of computation (a), execution time per candidate point (b), and (c) an approximate energy consumption by different implementations as a function of (N) for Beta distribution. The solid black line represents the CPU implementation (C_imp); the dashed red line is for GPU implementation (G_imp), while the solid red line is for G_imp_mcpy implementation; the blue solid line is for hybrid implementation (H_imp).
The utilization of the GPU increases with N and the GPU becomes faster than the CPU at . At , the GPU-based implementation is times faster than the CPU one. The H_imp implementation performs faster than C_imp by a factor of seven, roughly, but performs slower than the G_imp implementation by a factor of .
The execution times of the G_imp_mcpy and the G_imp are similar to each other at , but the two diverge at larger N. This happens because the transfer of data from GPU to CPU becomes the bottleneck for the G_imp_mcpy implementation for , whereas at lower loads the time spent on data transfer is negligible compared to the other components of the computation (e.g., seed setup, PRNG state update, and API function calls).
These findings are reflected in the behavior of the execution time per candidate point as a function of N, shown in Figure 2b. The execution time per candidate point in the C_imp implementation is constant and independent of N, which shows that the CPU core is fully utilized for any N (according to htop utility). In the G_imp implementation, due to the availability of many cores, the lowest execution time is reached at much larger N of . For G_imp_mcpy, the execution time per candidate point reaches its minimum at due to the overhead caused by the GPU-to-CPU data transfer. For H_imp, this execution time decreases with N until . At , it becomes independent of N. Since for this implementation the AR algorithm is performed on the CPU, and since the saturation is reached at much higher N for the GPU implementation G_imp, the independence of N suggests that the CPU becomes the bottleneck of the computation for for the H_imp implementation.
Figure 2c shows a rough estimate of energy usage by different implementations as a function of N. Power usage of the GPU card was monitored through the utility program nvidia-smi. For the CPU, since it is fully loaded for any value of N according to the data from htop utility, we use the maximum wattage of 10 W for a single AMD Threadripper 3990X core. The produce of power and the execution time yields the energy usage for various N. From Figure 2, we can conclude that for the G_imp is preferable in terms of speed and energy efficiency, while for smaller N, the GPU does not offer an advantage neither in terms of energy usage nor execution time.
3.2. Operation-Wise Load Analysis
The total cost of the generation of non-uniform PRNs consists of several components: the seed setup, PRNG state update, the AR algorithm, and API function calls. Figure 3a shows the execution time of these components for the G_imp implementation, and Figure 3b shows the corresponding percentile fraction with respect to the total computation time.
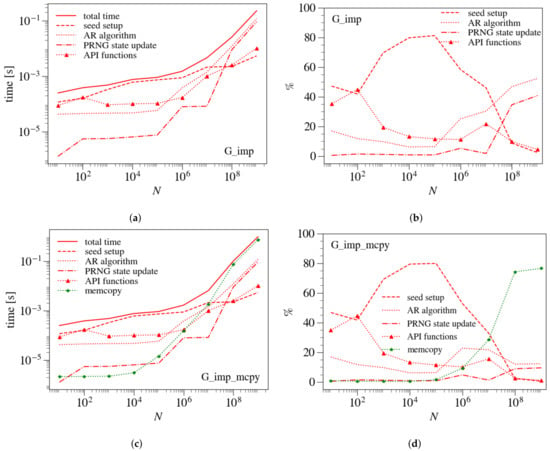
Figure 3.
Execution time and percentage ratio of different computational parts as a function of N for the G_imp (a,b) and G_imp_mcpy (c,d) implementations. The solid line represents the total computation time, the dashed line is PRNG seed setup time, the dotted line is AR algorithm time; the dashed-dotted line is the PRNG state update, and the dotted line with triangle marker is for the API functions. The green dotted line with star marker shows the memory copy time from device to host.
For , the seed time consumes more than of the overall time, reaching at . The PRNG state update takes less than for . The fraction of the PRNG state update grows to for . The AR algorithm takes less than for but then grows with N gradually and reaches for . The rest of the execution time goes to API function calls, the fraction of which is for , but drops below for . However, as we will see below, these findings depend on the PRNG parameters, including the seed setup and the state size. The G_imp_mcpy implementation, shown in Figure 3c,d, exhibits qualitatively similar breakdown of the total cost for . However, the contribution of data transfer to the GPU becomes dominant for (e.g., at , it reaches ). Hence, the relative contributions of the rest of the computations, including the AR algorithm, become smaller compared to those in the G_imp implementation.
3.3. Device API and Host API Implementations
As mentioned above, we consider two different ways to call the PRNG functions in the G_imp implementation: using the host API and device API. Figure 4a shows the execution time for the Beta distribution in the host and device API implementations for the MRG32k3a PRNG. The device API is faster than the host API implementation by about an order of magnitude for . This is attributed to the PRNG seed setup time (shown in dashed blue line), which is a bottleneck for host API implementation for . The host API implementation of the MRG32k3a generator by default initializes threads for any number of generated PRNs. Since each thread has its own state, the host API implementation has the same seed setup time of ms for any N. It is possible to speed up the PRNG seed setup time by varying the ordering parameter, i.e., the parameter that determines how the PRNs are ordered in device memory [65]. For example, using CURAND_ORDERING_PSEUDO_LEGACY option for MRG32k3a can speed up the seed setup by a factor of compared to the default parameter option. This is possible because fewer (4096) threads are initialized for this option. In the device API, for any N, we can choose a suitable number of initialized threads. As a result, the PRNG seed setup time in the device API implementation does not stay the same for any N. Instead, it increases with N from ms at to ms at (red dashed line in Figure 4a). Acceleration of the seed setup by changing the ordering option has also been discussed in [15,62].
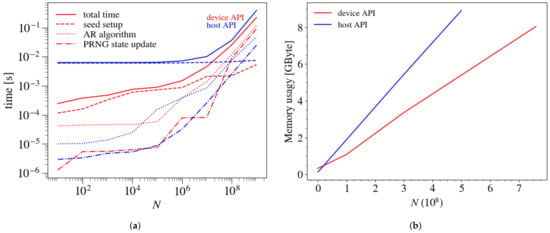
Figure 4.
The execution time (a) and the GPU global memory usage (b) as a function of N using host and device API implementations. In (a) the solid lines represent the total execution time, the dashed lines show seed setup time, and the dashed-dotted lines show the PRNG state update time; the dotted lines display time spent to apply the AR algorithm.
The execution time of the PRNG state update and AR algorithm (shown with dash-dotted and dotted lines, respectively) increases with N for both implementations. Due to this reason, the relative importance of the seed setup decreases with increasing N. As a result, the difference in the execution time between the device API and host API implementations decreases to eventually becoming a factor of at .
Figure 4b shows the global memory usage for the host API and device API implementations. Since the host API implementation requires storing the generated PRNs in global memory, it uses more memory than the device API implementation during the course of computation. The device API implementation allows us to use generated PRNs immediately without storing them in global memory. Thus, if PRNs need to be reused several times or copied to the CPU, then the host API implementation is a better choice. Otherwise, device API should be used in order to save memory space and to avoid extra loading and storing operations to global memory.
3.4. Comparison of Different PRNGs
Figure 5 shows the execution time for different PRNGs as a function of N for the host (Figure 5a) and device (Figure 5b) API implementations. Since in this section we compare different PRNGs, we consider only uniform distribution sequences in order to exclude the impact of the AR calculations. Note that since the MT19937 implementation does not support device API [65], it is omitted from Figure 5b. As discussed above for the MRG32k3a PRNG (cf. Section 3.3), the longer seed setup time in the host API implementation leads to longer execution times, especially at lower N. We find a similar difference between the two implementations for the rest of the PRNGs considered here.
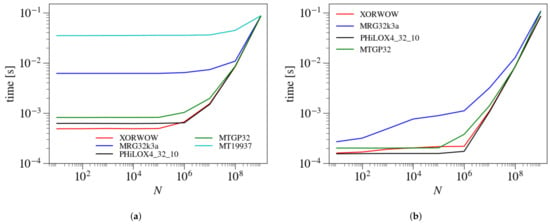
Figure 5.
Execution time for different PRNGs as a function of N using host API (a) and device API (b). Note that since the MT19937 implementation does not support device API [65], it is omitted from (b).
In both implementations, the XORWOW and PHILOX4_32_10 are the fastest generators followed by MTGP32. The XORWOW generator uses the XOR and shift bitwise operations which require one clock cycle for execution [71], while PHILOX4_32_10 is a non-state PRNG (i.e., it uses thread ID as its state) based on counter to generate PRNs, which enables faster speeds [69]. The slowest generators are MT19937 for the host API implementation (as mentioned earlier, this PRNG is not supported in the device API implementation), while the MRG32k3a generator is the slowest in the device API implementation. The big state size of MT19937 of 2.5 kB leads to low occupancy of SM cores because of the limited size of local memory per SM. The modulus operator of MRG32k3a generator has a latency of 22–29 clock cycles [63,71], which leads to longer execution times.
The difference in speed between different PRNGs is particularly strong at , but becomes small for . This is because the API functions become the dominant contributor to the execution time of the fastest three PRNGs (XORWOW, PHILOX4_32_10, and MTGP32) (cf. Figure 6), which brings them closer in speed to the slowest two PRNGs (MT19937 and MRG32k3a). For MT19937, the seed setup is the most expensive component of the overall computation for . For PHILOX4_32_10, almost 100% of computational time is consumed by the API function calls in the device API implementation.
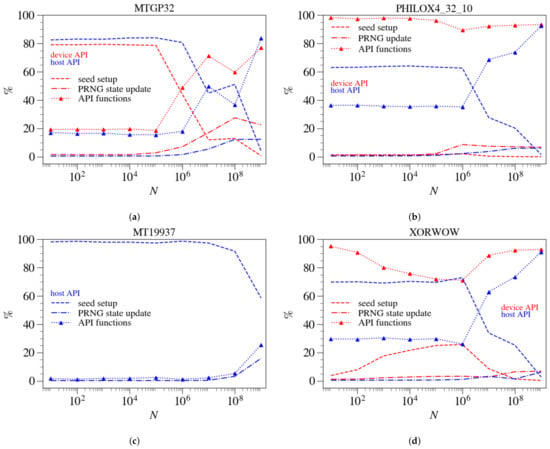
Figure 6.
Percentage ratio of different computational parts as a function of N for various PRNGs. (a) MTGP32 (b) PHILOX4_32_10 (c) MT19937 (only supported by host API) (d) XORWOW. The dashed lines represent the PRNG seed setup time; the dashed-dot lines are PRNG state update time, and the dotted lines with triangle markers are for API functions.
Figure 7 shows the normalized time as a function of GPU occupancy for the four PRNGs (note that since the MT19937 implementation does not support device API [65], it is omitted from this analysis). The time is normalized to its lowest value that can be reached for this PRNG and GPU for a given N. The PHiLOX4_32_10 generator reaches the fastest performance when the GPU occupancy is . This is due to a combination of two reasons. First, this PRNG has a small state (cf. Table 1), so we can fit more threads into the GPU memory. Second, this PRNG has a small seed setup time (cf. Figure 6), so increasing thread number, which leads to a longer seed setup, will not negatively affect the overall performance. Instead, more threads lead to faster PRNG state update and AR calculations due to enhanced parallelism. For XORWOW PRNG, the fastest performance is reached at occupancy of for and , while for , the execution is not sensitive to occupancy.
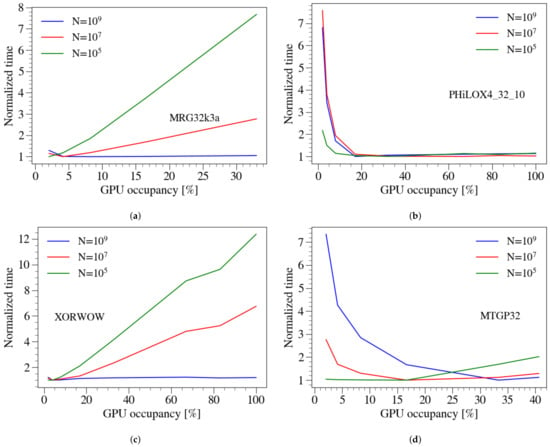
Figure 7.
Normalized execution time versus the GPU occupancy for different PRNGs using device API implementation. (a) MRG32k3a; (b) PHILOX4_32_10; (c) XORWOW; (d) MTGP32. The time is normalized with respect to the fastest time that can be achieved for a given N for RTX3090 card and device API implementation. The various lines correspond to different numbers of generated PRN with the uniform distribution. The GPU occupancy is the ratio of active warps on a streaming multiprocessor to the maximum possible warps that can be run simultaneously.
The situation is dramatically different for the other two PRNGs. For example, the MTGP32 generator never reaches occupancy above because of the limited number of blocks and threads that can be used to generate PRNs according to the implementation of this PRNG on GPU [65]. The MRG32k3a stays below occupancy. This is caused by memory intensive modulus operator that is used for seed setup and state update for this generator [63,68]. The occupancy does not increase with increasing N beyond , as demonstrated in Figure 8.
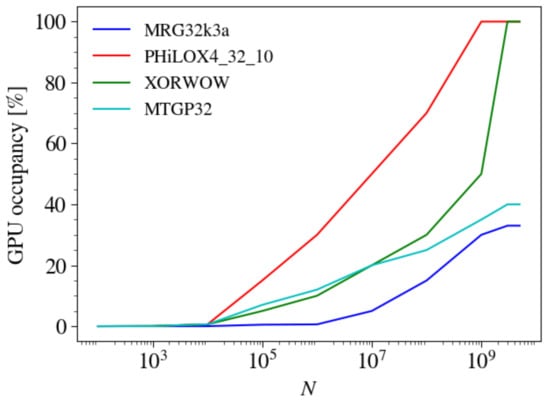
Figure 8.
GPU occupancy for different PRNGs to generate various numbers N of PRNs implemented in device API.
3.5. Comparison of Different GPU Cards
Figure 9 shows the execution time as a function of N for the default fiducial parameters for different GPU cards. Since GPU cards are under-utilized for small , different cards yield similar results. As the occupancy of the card grows with increasing N, different cards yield varying execution times. The fastest card is RTX3090, followed by RXT3080, GTX1080Ti, and GTX1080. This correlates with the number of cores available in these cards. Moreover, the RTX cards support the newer Ampere architecture compared to the Pascal architecture of the latter two.
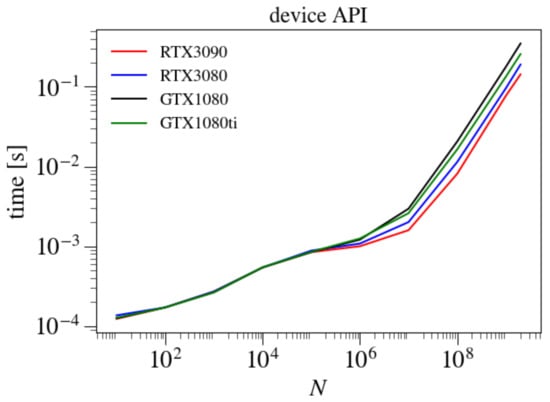
Figure 9.
Execution time to generate PRNs as a function of N for the Beta distribution and MRG32k3a generator for different GPU cards.
3.6. Dependence on Distributions
Figure 10 shows the execution time for uniform and non-uniform distributions for the G_imp implementation as a function of the number of “accepted” PRNs (). Since the uniform distribution does not require the application of the AR algorithm, it is the fastest to compute. For example, for , it is faster than the Gamma, Rayleigh, and Beta distributions by a factor of 2.78, 1.90, and 1.60, respectively. The different execution times of the non-uniform distributions are the direct result of the different acceptance rates of each distribution to construct non-uniform distributions (cf. Section 2.3). The execution times of different distributions diverge further with growing N. The reason for this behavior is that at smaller , the contribution of state setup and API function calls to the overall execution time dominates over the contributions of the AR algorithm and the PRN state update algorithm. At large , the contributions of the latter two become more pronounced, leading to stronger differences. For example, at , the uniform distribution is faster than the Gamma, Rayleigh, and Beta distributions by factors of , , and , respectively.
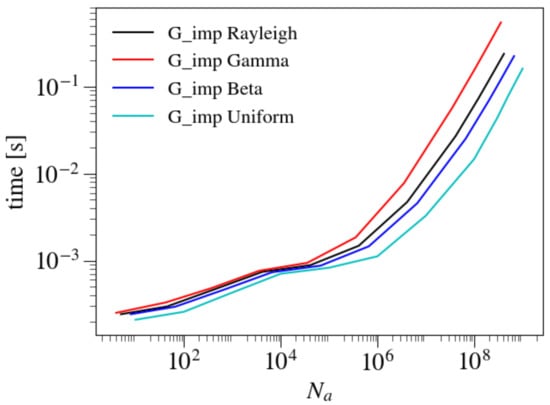
Figure 10.
Execution time to obtain PRNs with different distributions using the device API implementation and the MRG32k3a generator.
4. Conclusions
In this work, we evaluated the performance of different parallel pseudo-random number generators (PRNGs) on Nvidia GPU cards GTX1080, GTX1080Ti, RTX3080, and RTX3090. We consider five different PRNGs from the Curand library (XORWOW, PHILOX4_32_10, MTGP32, MT19937, and MRG32k3a). We generate sequences of random numbers with uniform distribution and transform them into non-uniform distributions using the acceptance-rejection (AR) method. We consider different implementations of the PRNGs: single-core CPU implementation (using AMD Ryzen Threadripper 3990X CPU), GPU implementation with and without data transfer from the GPU to the CPU host, and a hybrid CPU/GPU implementation, where PRNG are produced on a GPU and transformed to non-uniform sequence on a CPU using the AR method. For the GPU implementation, we additionally consider implementations via the host and device APIs. We consider different configurations of these parameters and study how the performance is affected with respect to our default configuration (cf. Table 3).
We find that when the length of the pseudo-random number (PRN) sequence is less than , a single CPU core is faster than the GPU. In this regime, unlike the CPU core, the GPU cores are not fully loaded. Since the single CPU core is much faster than the GPU core, sparsely loaded GPU yields a slower result than a fully-loaded CPU. For PRNs more than , the GPU cores are loaded more evenly, leading to faster performance. For PRNs, the GPU is faster than the CPU by two orders of magnitude.
To achieve the fastest performance on a GPU, one has to minimize the duration of the PRNG seed setup and state update. The former increases with the number of parallel threads, while the latter decreases. The fastest performance is achieved by the balance of these opposing effects. The right number of parallel threads depends on the number of PRNs that need to be generated. If the latter far exceeds the number of cores on a GPU (e.g., ), it is desirable to have the largest possible number of threads that can fit GPU. For such configuration, the relative importance of seed setup is minor compared to the overall execution time. For a smaller sequence of PRN, the number of parallel threads that yield the fastest performance is a compromise between the seed setup and state update durations and it is different for different PRNGs considered in this work. The findings will help us to choose the optimal performance parameters for our future scientific computing applications, including Monte Carlo radiative transfer simulations that we plan to perform in our future work.
Author Contributions
Writing—original draft preparation, T.A.; writing—review and editing, B.S., M.L. and E.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the Ministry of Education and Science of the Republic of Kazakhstan.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
This research has been funded by the Science Committee of the Ministry of Education and Science of the Republic of Kazakhstan (AP08856149, BR10965141).
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Xanthis, C.; Venetis, I.; Chalkias, A.; Aletras, A. MRISIMUL: A GPU-based parallel approach to MRI simulations. IEEE Trans. Med. Imaging 2014, 33, 607–617. [Google Scholar] [CrossRef] [PubMed]
- Yudanov, D.; Shaaban, M.; Melton, R.; Reznik, L. GPU-based simulation of spiking neural networks with real-time performance & high accuracy. In Proceedings of the International Joint Conference on Neural Networks, Barcelona, Spain, 18–23 July 2010; pp. 1–8. [Google Scholar] [CrossRef]
- Dolan, R.; DeSouza, G. GPU-based simulation of cellular neural networks for image processing. In Proceedings of the International Joint Conference on Neural Networks, Atlanta, GA, USA, 14–19 June 2009; pp. 730–735. [Google Scholar] [CrossRef] [Green Version]
- Heimlich, A.; Mol, A.; Pereira, C. GPU-based Monte Carlo simulation in neutron transport and finite differences heat equation evaluation. Prog. Nucl. Energy 2011, 53, 229–239. [Google Scholar] [CrossRef]
- Liang, Y.; Xing, X.; Li, Y. A GPU-based large-scale Monte Carlo simulation method for systems with long-range interactions. J. Comput. Phys. 2017, 338, 252–268. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Spurzem, R.; Aarseth, S.; Giersz, M.; Askar, A.; Berczik, P.; Naab, T.; Schadow, R.; Kouwenhoven, M. The DRAGON simulations: Globular cluster evolution with a million stars. Mon. Not. R. Astron. Soc. 2016, 458, 1450–1465. [Google Scholar] [CrossRef] [Green Version]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes 3rd Edition: The Art of Scientific Computing, 3rd ed.; Cambridge University Press: Cambridge, MA, USA, 2007. [Google Scholar]
- Hastings, W. Monte carlo sampling methods using Markov chains and their applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Kroese, D.; Brereton, T.; Taimre, T.; Botev, Z. Why the Monte Carlo method is so important today. Wiley Interdiscip. Rev. Comput. Stat. 2014, 6, 386–392. [Google Scholar] [CrossRef]
- Abdikamalov, E.; Burrows, A.; Ott, C.; Löffler, F.; O’Connor, E.; Dolence, J.; Schnetter, E. A new monte carlo method for time-dependent neutrino radiation transport. Astrophys. J. 2012, 755, 111. [Google Scholar] [CrossRef] [Green Version]
- Richers, S.; Kasen, D.; O’Connor, E.; Fernández, R.; Ott, C. Monte Carlo Neutrino Transport Through Remnant Disks from Neutron Star Mergers. Astrophys. J. 2015, 813, 38. [Google Scholar] [CrossRef] [Green Version]
- Murchikova, E.; Abdikamalov, E.; Urbatsch, T. Analytic closures for M1 neutrino transport. Mon. Not. R. Astron. Soc. 2017, 469, 1725–1737. [Google Scholar] [CrossRef] [Green Version]
- Foucart, F.; Duez, M.; Hebert, F.; Kidder, L.; Pfeiffer, H.; Scheel, M. Monte-Carlo Neutrino Transport in Neutron Star Merger Simulations. Astrophys. J. Lett. 2020, 902, L27. [Google Scholar] [CrossRef]
- Richers, S. Rank-3 moment closures in general relativistic neutrino transport. Phys. Rev. D 2020, 102, 083017. [Google Scholar] [CrossRef]
- Fatica, M.; Phillips, E. Pricing American options with least squares Monte Carlo on GPUs. In Proceedings of the WHPCF 2013: 6th Workshop on High Performance Computational Finance—Held in Conjunction with SC 2013: The International Conference for High Performance Computing, Networking, Storage and Analysis, Denver, CO, USA, 17–22 November 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Karl, A.T.; Eubank, R.; Milovanovic, J.; Reiser, M.; Young, D. Using RngStreams for parallel random number generation in C++ and R. Comput. Stat. 2014, 29, 1301–1320. [Google Scholar] [CrossRef] [Green Version]
- Entacher, K.; Uhl, A.; Wegenkittl, S. Parallel random number generation: Long-range correlations among multiple processors. In International Conference of the Austrian Center for Parallel Computation; Springer: Berlin/Heidelberg, Germany, 1999; pp. 107–116. [Google Scholar]
- Entacher, K. On the CRAY-system random number generator. Simulation 1999, 72, 163–169. [Google Scholar] [CrossRef]
- Coddington, P.D. Random number generators for parallel computers. Northeast. Parallel Archit. Cent. 1997, 2. Available online: https://surface.syr.edu/cgi/viewcontent.cgi?article=1012&context=npac (accessed on 3 November 2021).
- De Matteis, A.; Pagnutti, S. Parallelization of random number generators and long-range correlations. Numer. Math. 1988, 53, 595–608. [Google Scholar] [CrossRef]
- l’Ecuyer, P. Random number generation with multiple streams for sequential and parallel computing. In Proceedings of the 2015 Winter Simulation Conference (WSC), Huntington Beach, CA, USA, 6–9 December 2015; pp. 31–44. [Google Scholar]
- Manssen, M.; Weigel, M.; Hartmann, A.K. Random number generators for massively parallel simulations on GPU. Eur. Phys. J. Spec. Top. 2012, 210, 53–71. [Google Scholar] [CrossRef] [Green Version]
- Kirk, D.; Wen-Mei, W.H. Programming Massively Parallel Processors: A Hands-On Approach; Morgan Kaufmann: Burlington, MA, USA, 2016. [Google Scholar]
- L’Ecuyer, P.; Oreshkin, B.; Simard, R. Random Numbers for Parallel Computers: Requirements and Methods. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.434.9223&rep=rep1&type=pdf (accessed on 3 November 2021).
- Wadden, J.; Brunelle, N.; Wang, K.; El-Hadedy, M.; Robins, G.; Stan, M.; Skadron, K. Generating efficient and high-quality pseudo-random behavior on Automata Processors. In Proceedings of the 2016 IEEE 34th International Conference on Computer Design (ICCD), Scottsdale, AZ, USA, 2–5 October 2016; pp. 622–629. [Google Scholar]
- Ciglarič, T.; Češnovar, R.; Štrumbelj, E. An OpenCL library for parallel random number generators. J. Supercomput. 2019, 75, 3866–3881. [Google Scholar] [CrossRef]
- Demchik, V. Pseudorandom numbers generation for Monte Carlo simulations on GPUs: OpenCL approach. In Numerical Computations with GPUs; Springer: Berlin/Heidelberg, Germany, 2014; pp. 245–271. [Google Scholar]
- Kim, Y.; Hwang, G. Efficient Parallel CUDA Random Number Generator on NVIDIA GPUs. J. KIISE 2015, 42, 1467–1473. [Google Scholar] [CrossRef]
- Mohanty, S.; Mohanty, A.; Carminati, F. Efficient pseudo-random number generation for monte-carlo simulations using graphic processors. J. Phys. 2012, 368, 012024. [Google Scholar] [CrossRef] [Green Version]
- Barash, L.Y.; Shchur, L.N. PRAND: GPU accelerated parallel random number generation library: Using most reliable algorithms and applying parallelism of modern GPUs and CPUs. Comput. Phys. Commun. 2014, 185, 1343–1353. [Google Scholar] [CrossRef] [Green Version]
- Bradley, T.; du Toit, J.; Tong, R.; Giles, M.; Woodhams, P. Parallelization techniques for random number generators. In GPU Computing Gems Emerald Edition; Elsevier: Amsterdam, The Netherlands, 2011; pp. 231–246. [Google Scholar]
- Sussman, M.; Crutchfield, W.; Papakipos, M. Pseudorandom number generation on the GPU. In Proceedings of the SIGGRAPH/Eurographics Workshop on Graphics Hardware, Vienna, Austria, 3–4 September 2006; pp. 87–94. [Google Scholar] [CrossRef]
- Abeywardana, N. Efficient Random Number Generation for Fermi Class GPUs. Available online: https://www.proquest.com/openview/e4cd0bc00b2dd0572824fe304b5851e4/1?pq-origsite=gscholar&cbl=18750 (accessed on 3 November 2021).
- Howes, L.; Thomas, D. Efficient random number generation and application using CUDA. GPU Gems 2007, 3, 805–830. [Google Scholar]
- Preis, T.; Virnau, P.; Paul, W.; Schneider, J. GPU accelerated Monte Carlo simulation of the 2D and 3D Ising model. J. Comput. Phys. 2009, 228, 4468–4477. [Google Scholar] [CrossRef]
- Thomas, D.B.; Howes, L.; Luk, W. A comparison of CPUs, GPUs, FPGAs, and massively parallel processor arrays for random number generation. In Proceedings of the ACM/SIGDA International Symposium on Field Programmable Gate Arrays, Monterey, CA, USA, 22–24 February 2009; pp. 63–72. [Google Scholar]
- Anker, M. Pseudo Random Number Generators on Graphics Processing Units, with Applications in Finance. Mémoire de maîtrise à l’Université d’Edinburgh. 2013. Available online: https://static.epcc.ed.ac.uk/dissertations/hpc-msc/2012-2013/Pseudo (accessed on 3 November 2021).
- Jia, X.; Gu, X.; Sempau, J.; Choi, D.; Majumdar, A.; Jiang, S. Development of a GPU-based Monte Carlo dose calculation code for coupled electron-photon transport. Phys. Med. Biol. 2010, 55, 3077–3086. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alerstam, E.; Svensson, T.; Andersson-Engels, S. Parallel computing with graphics processing units for high-speed Monte Carlo simulation of photon migration. J. Biomed. Opt. 2008, 13, 060504. [Google Scholar] [CrossRef] [Green Version]
- Bert, J.; Perez-Ponce, H.; Bitar, Z.; Jan, S.; Boursier, Y.; Vintache, D.; Bonissent, A.; Morel, C.; Brasse, D.; Visvikis, D. Geant4-based Monte Carlo simulations on GPU for medical applications. Phys. Med. Biol. 2013, 58, 5593–5611. [Google Scholar] [CrossRef] [PubMed]
- Okada, S.; Murakami, K.; Incerti, S.; Amako, K.; Sasaki, T. MPEXS-DNA, a new GPU-based Monte Carlo simulator for track structures and radiation chemistry at subcellular scale. Med. Phys. 2019, 46, 1483–1500. [Google Scholar] [CrossRef] [Green Version]
- Spiechowicz, J.; Kostur, M.; Machura, L. GPU accelerated Monte Carlo simulation of Brownian motors dynamics with CUDA. Comput. Phys. Commun. 2015, 191, 140–149. [Google Scholar] [CrossRef] [Green Version]
- Ayubian, S.; Alawneh, S.; Thijssen, J. GPU-based monte-carlo simulation for a sea ice load application. In Proceedings of the Summer Computer Simulation Conference, Montreal, QC, Canada, 24–27 July 2016; pp. 1–8. [Google Scholar]
- Langdon, W.B. PRNG Random Numbers on GPU; Technical Report; University of Essex: Colchester, UK, 2007. [Google Scholar]
- Passerat-Palmbach, J.; Mazel, C.; Hill, D.R. Pseudo-random number generation on GP-GPU. In Proceedings of the 2011 IEEE Workshop on Principles of Advanced and Distributed Simulation, Nice, France, 14–17 June 2011; pp. 1–8. [Google Scholar]
- Fog, A. Pseudo-random number generators for vector processors and multicore processors. J. Mod. Appl. Stat. Methods 2015, 14, 23. [Google Scholar] [CrossRef] [Green Version]
- Beliakov, G.; Johnstone, M.; Creighton, D.; Wilkin, T. An efficient implementation of Bailey and Borwein’s algorithm for parallel random number generation on graphics processing units. Computing 2013, 95, 309–326. [Google Scholar] [CrossRef]
- Gong, C.; Liu, J.; Chi, L.; Hu, Q.; Deng, L.; Gong, Z. Accelerating Pseudo-Random Number Generator for MCNP on GPU. AIP Conf. Proc. 2010, 1281, 1335–1337. [Google Scholar]
- Gao, S.; Peterson, G.D. GASPRNG: GPU accelerated scalable parallel random number generator library. Comput. Phys. Commun. 2013, 184, 1241–1249. [Google Scholar] [CrossRef] [Green Version]
- Monfared, S.K.; Hajihassani, O.; Kiarostami, M.S.; Zanjani, S.M.; Rahmati, D.; Gorgin, S. BSRNG: A High Throughput Parallel BitSliced Approach for Random Number Generators. In Proceedings of the 49th International Conference on Parallel Processing-ICPP, Workshops, Edmonton, AB, Canada, 17–20 August 2020; pp. 1–10. [Google Scholar]
- Pang, W.M.; Wong, T.T.; Heng, P.A. Generating massive high-quality random numbers using GPU. In Proceedings of the 2008 IEEE Congress on Evolutionary Computation (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–6 June 2008; pp. 841–847. [Google Scholar]
- Yang, B.; Hu, Q.; Liu, J.; Gong, C. GPU optimized Pseudo Random Number Generator for MCNP. In Proceedings of the IEEE Conference Anthology, Shanghai, China, 1–8 January 2013; pp. 1–6. [Google Scholar]
- Nandapalan, N.; Brent, R.P.; Murray, L.M.; Rendell, A.P. High-performance pseudo-random number generation on graphics processing units. In International Conference on Parallel Processing and Applied Mathematics; Springer: Berlin/Heidelberg, Germany, 2011; pp. 609–618. [Google Scholar]
- Kargaran, H.; Minuchehr, A.; Zolfaghari, A. The development of GPU-based parallel PRNG for Monte Carlo applications in CUDA Fortran. AIP Adv. 2016, 6, 045101. [Google Scholar] [CrossRef] [Green Version]
- Riesinger, C.; Neckel, T.; Rupp, F.; Hinojosa, A.P.; Bungartz, H.J. Gpu optimization of pseudo random number generators for random ordinary differential equations. Procedia Comput. Sci. 2014, 29, 172–183. [Google Scholar] [CrossRef] [Green Version]
- Jun, S.; Canal, P.; Apostolakis, J.; Gheata, A.; Moneta, L. Vectorization of random number generation and reproducibility of concurrent particle transport simulation. J. Phys. 2020, 1525, 012054. [Google Scholar] [CrossRef]
- Amadio, G.; Canal, P.; Piparo, D.; Wenzel, S. Speeding up software with VecCore. J. Phys. Conf. Ser. 2018, 1085, 032034. [Google Scholar] [CrossRef]
- Gregg, C.; Hazelwood, K. Where is the data? Why you cannot debate CPU vs. GPU performance without the answer. In Proceedings of the (IEEE ISPASS) IEEE International Symposium on Performance Analysis of Systems and Software, Austin, TX, USA, 10–12 April 2011; pp. 134–144. [Google Scholar]
- Hoffman, D.; Karst, O.J. The theory of the Rayleigh distribution and some of its applications. J. Ship Res. 1975, 19, 172–191. [Google Scholar] [CrossRef]
- Theodoridis, S. Chapter 2—Probability and Stochastic Processes. In Machine Learning, 2nd ed.; Theodoridis, S., Ed.; Academic Press: Cambridge, MA, USA, 2020; pp. 19–65. [Google Scholar] [CrossRef]
- Papoulis, A. Probability, Random Variables and Stochastic Processes. IEEE Trans. Acoust. Speech Signal Process. 1985, 33, 1637. [Google Scholar] [CrossRef]
- Fatica, M.; Ruetsch, G. CUDA Fortran for Scientists and Engineers: Best Practices for Efficient CUDA Fortran Programming; Elsevier Inc.: Amsterdam, The Netherlands, 2013; pp. 1–323. [Google Scholar] [CrossRef]
- Nvidia, C. CUDA C Programming Guide, Version 11.2; NVIDIA Corp.: 2020. Available online: https://docs.nvidia.com/cuda/pdf/CUDA_C_Programming_Guide.pdf (accessed on 3 November 2021).
- Nvidia, C. CUDA C Best Practices Guide; NVIDIA Corp.: 2020. Available online: https://www.clear.rice.edu/comp422/resources/cuda/pdf/CUDA_C_Best_Practices_Guide.pdf (accessed on 3 November 2021).
- Nvidia, C. Toolkit 11.0 CURAND Guide. 2020. Available online: https://docs.nvidia.com/cuda/cuda-toolkit-release-notes/index.html (accessed on 3 November 2021).
- Marsaglia, G. Xorshift RNGs. J. Stat. Softw. 2003, 8, 1–6. [Google Scholar] [CrossRef]
- Saito, M.; Matsumoto, M. Variants of Mersenne twister suitable for graphic processors. ACM Trans. Math. Softw. 2013, 39, 1–20. [Google Scholar] [CrossRef] [Green Version]
- L’ecuyer, P. Good parameters and implementations for combined multiple recursive random number generators. Oper. Res. 1999, 47, 159–164. [Google Scholar] [CrossRef] [Green Version]
- Salmon, J.K.; Moraes, M.A.; Dror, R.O.; Shaw, D.E. Parallel random numbers: As easy as 1, 2, 3. In Proceedings of the 2011 International Conference for High Performance Computing, Networking, Storage and Analysis, Seattle, WA, USA, 12–18 November 2011; pp. 1–12. [Google Scholar]
- Matsumoto, M.; Nishimura, T. Mersenne twister: A 623-dimensionally equidistributed uniform pseudo-random number generator. ACM Trans. Model. Comput. Simul. (TOMACS) 1998, 8, 3–30. [Google Scholar] [CrossRef] [Green Version]
- Fog, A. Instruction Tables: Lists of Instruction Latencies, Throughputs and Micro-Operation Breakdowns for Intel, AMD and VIA CPUs; Technical Report; Copenhagen University College of Engineering: Ballerup, Denmark, 2021. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).