Generalized Multiscale Finite Element Method for Elastic Wave Propagation in the Frequency Domain
Abstract
1. Introduction
2. Problem Formulation
3. Fine Grid Approximation
4. Multiscale Method on the Coarse Grid
- 1.
- construction of the coarse grid and local domains;
- 2.
- construction of the multiscale basis functions by the solution of the local eigenvalue problem in each local domains;
- 3.
- construction of the projection matrix R (from fine grid to coarse grid) using computed multiscale basis functions;
- 4.
- construction of the fine grid system and projection to the coarse grid using matrix R;
- 5.
- solution of the reduced order model and reconstruction of the fine grid solution.
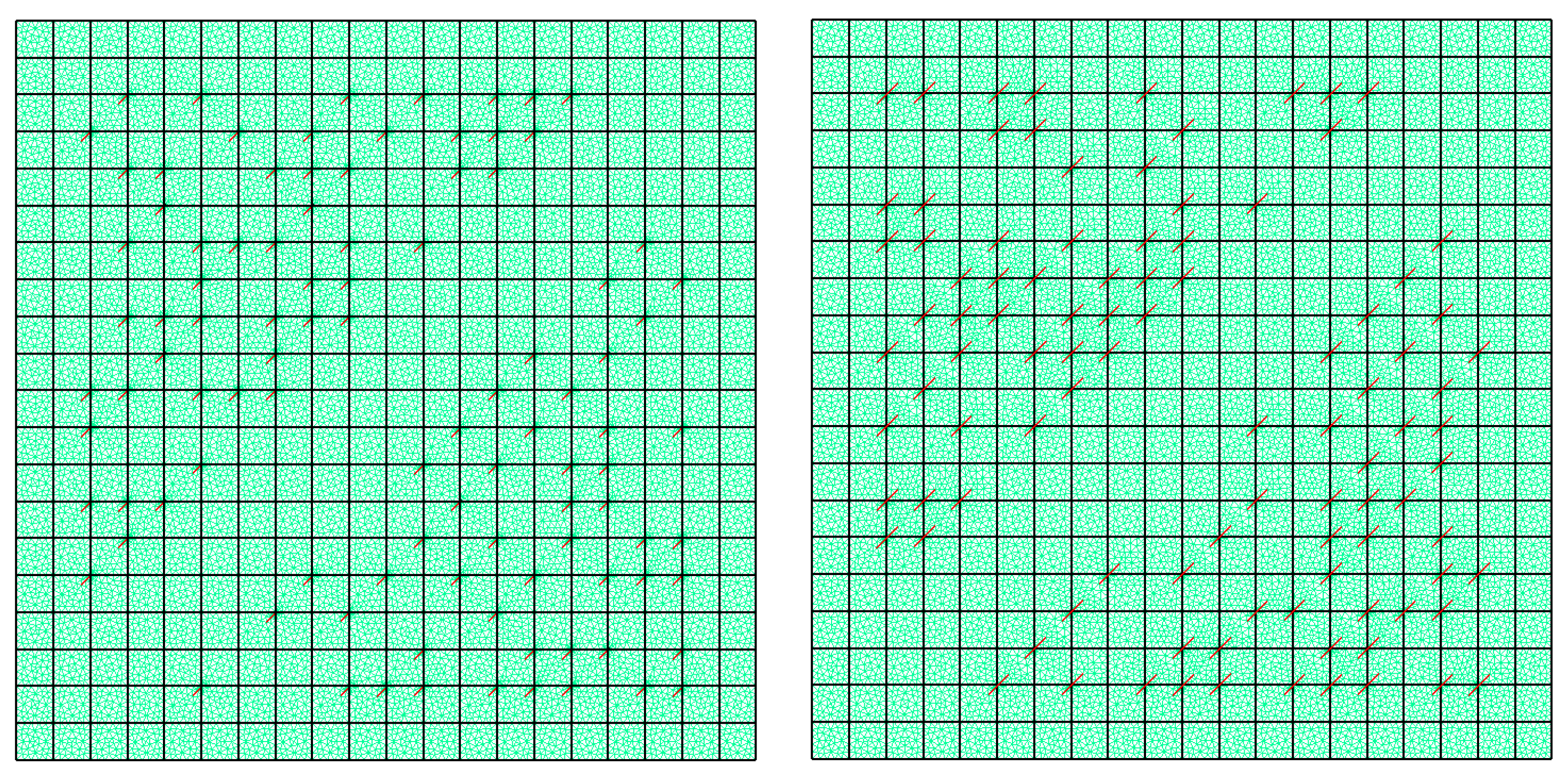
- for CG-GMsFEM, the local domain are defined as a coarse neighborhood that contains four coarse grid quadrilateral cells around coarse grid node, where and is the number of the coarse grid nodes (see Figure 2 for illustration);
- for DG-GMsFEM, the local domain is the coarse grid cell , where and is the number of the coarse grid cells.
4.1. Multiscale Basis Functions for CG-GMsFEM
4.2. Multiscale Basis Functions for DG-GMsFEM
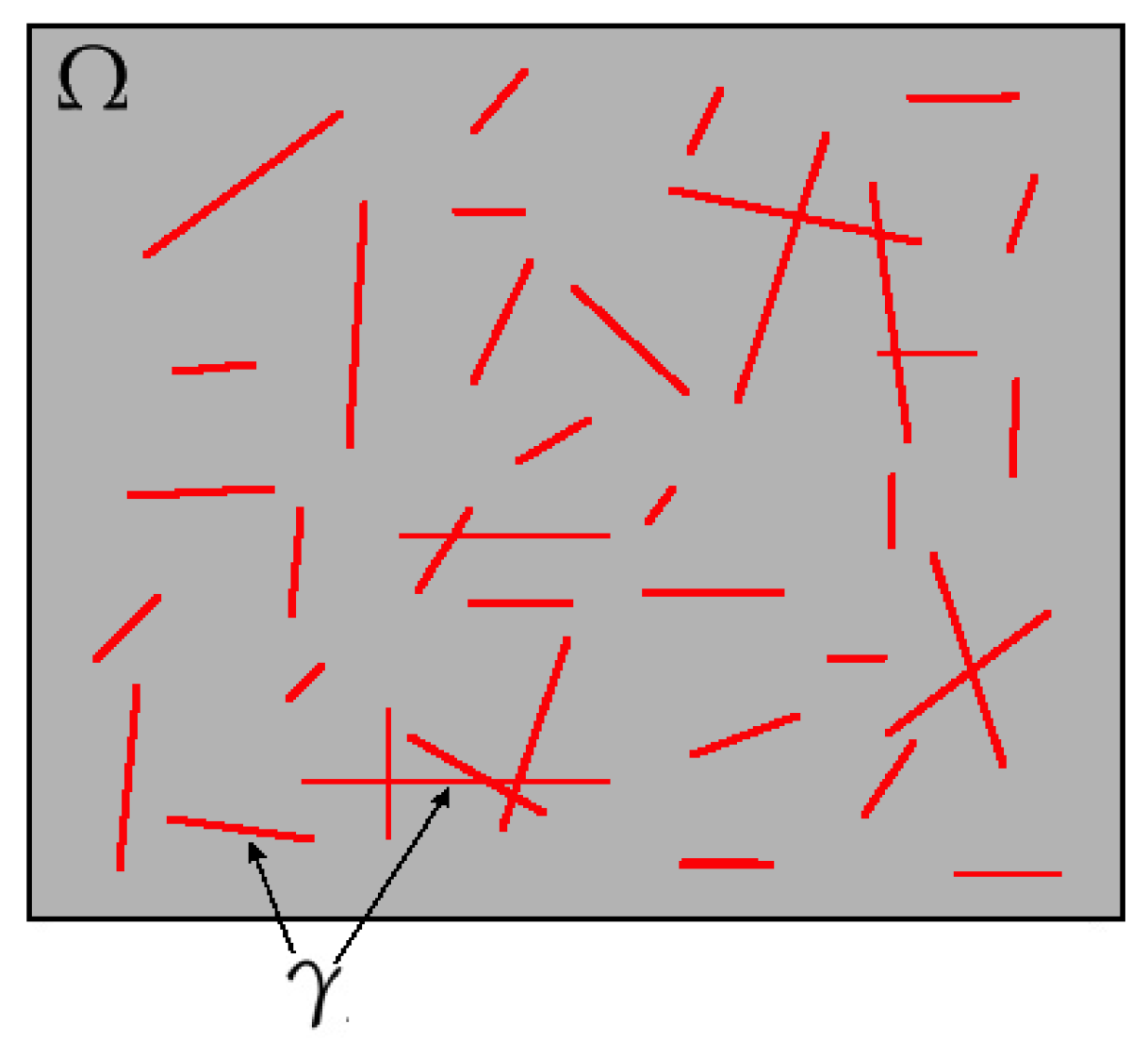
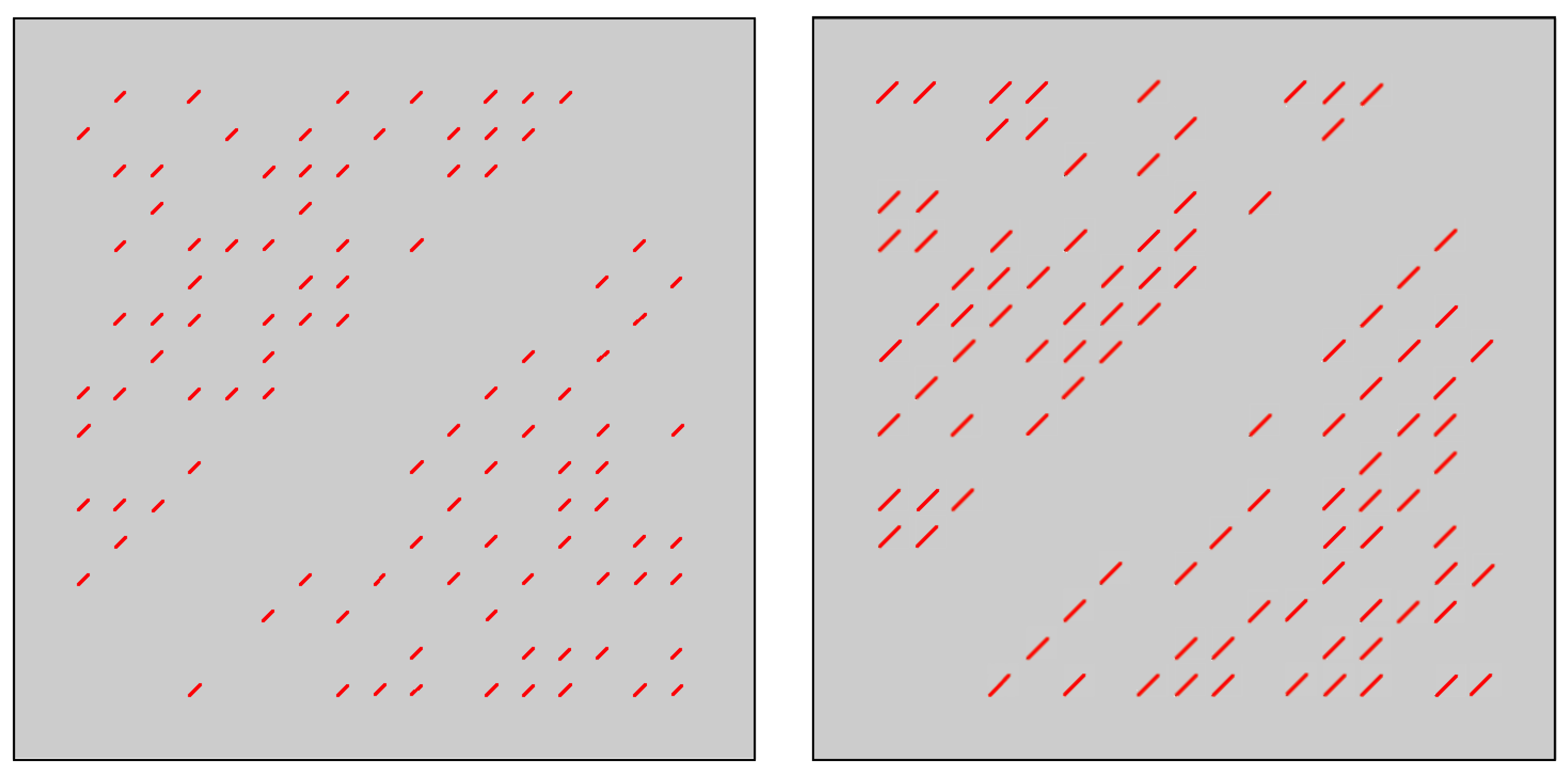
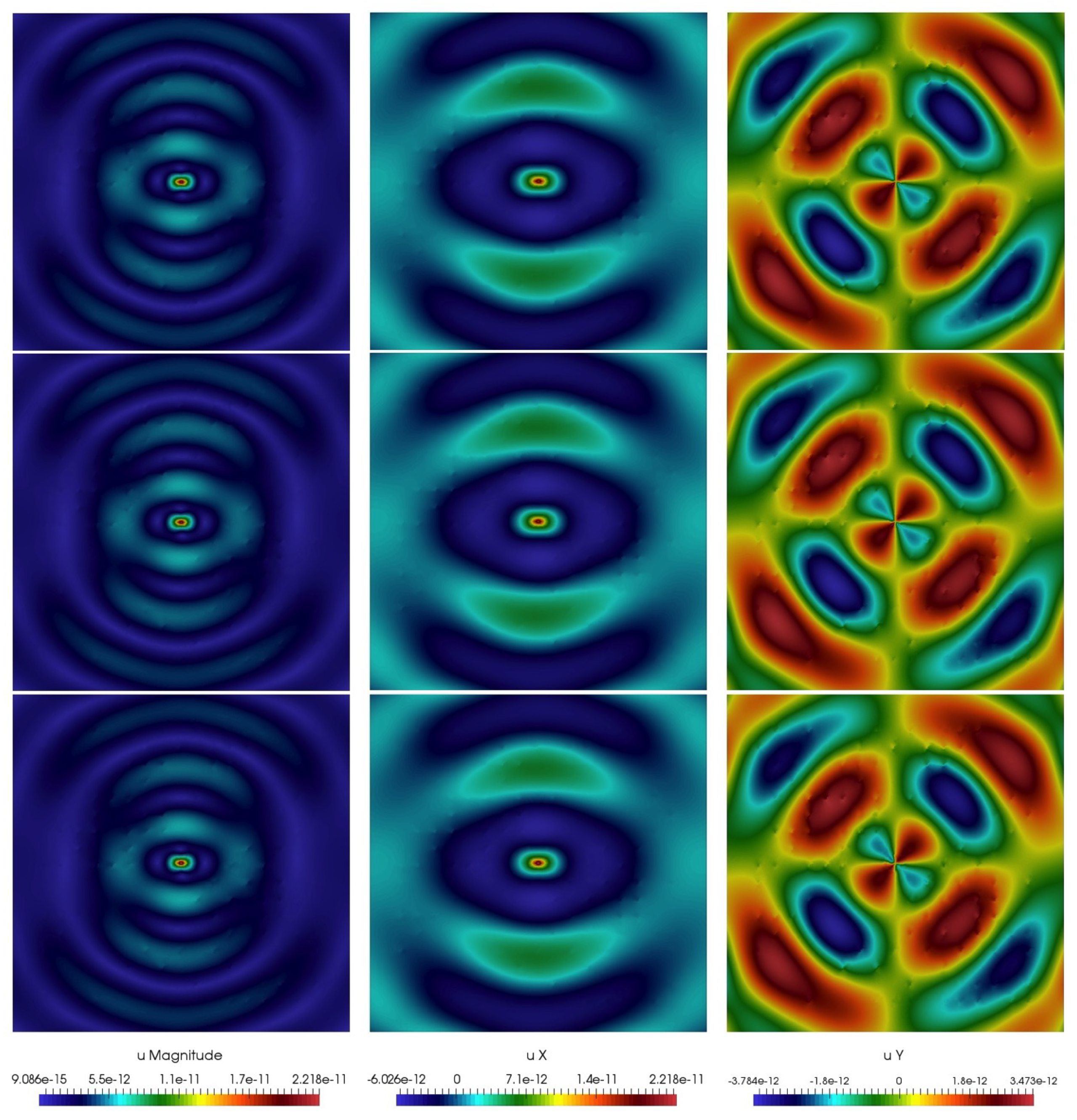
5. Numerical Results
- Geometry 1: Fine grid contains 16,077 vertices and 31,752 triangle elements.
- Geometry 2: Fine grid contains 16,509 vertices and 32,616 triangle elements.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Santos, J.E.; Gauzellino, P.M. Numerical Simulation in Applied Geophysics; Lecture Notes in Geosystems Mathematics and Computing; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Shekhar, R.; Gibson, R.L., Jr. Correlated fracture network modeling using simulated annealing. In SEG Technical Program Expanded Abstracts 2008; Society of Exploration Geophysicists: Tulsa, OK, USA, 2008; pp. 1541–1545. [Google Scholar]
- Cui, X.; Lines, L.R.; Krebes, E.S. Seismic modelling for geological fractures. Geophys. Prospect. 2017, 66, 157–168. [Google Scholar] [CrossRef]
- Bosma, S.; Hajibeygi, H.; Tene, M.; Tchelepi, H.A. Multiscale finite volume method for discrete fracture modeling on unstructured grids (MS-DFM). J. Comput. Phys. 2017, 351, 145–164. [Google Scholar] [CrossRef]
- Ruzhanskaya, A.; Khokhlov, N. Modelling of Fractures Using the Chimera Grid Approach. In Proceedings of the 2nd Conference on Geophysics for Mineral Exploration and Mining, Porto, Portugal, 9–12 September 2018; European Association of Geoscientists & Engineers, 2018; Volume 2018, pp. 1–5. [Google Scholar]
- Khokhlov, N.; Stognii, P. Novel Approach to Modeling the Seismic Waves in the Areas with Complex Fractured Geological Structures. Minerals 2020, 10, 122. [Google Scholar] [CrossRef]
- Vamaraju, J.; Sen, M.K.; De Basabe, J.; Wheeler, M. Enriched Galerkin finite element approximation for elastic wave propagation in fractured media. J. Comput. Phys. 2018, 372, 726–747. [Google Scholar] [CrossRef]
- Grechka, V.; Kachanov, M. Effective elasticity of fractured rocks: A snapshot of the work in progress. Geophysics 2006, 71, W45–W58. [Google Scholar] [CrossRef]
- Efendiev, Y.; Hou, T. Multiscale Finite Element Methods: Theory and Applications; Vol. 4, Surveys and Tutorials in the Applied Mathematical Sciences; Springer: New York, NY, USA, 2009. [Google Scholar]
- Efendiev, Y.; Galvis, J.; Hou, T.Y. Generalized multiscale finite element methods (GMsFEM). J. Comput. Phys. 2013, 251, 116–135. [Google Scholar] [CrossRef]
- Gao, K.; Chung, E.T.; Gibson, R.L., Jr.; Fu, S.; Efendiev, Y. A numerical homogenization method for heterogeneous, anisotropic elastic media based on multiscale theory. Geophysics 2015, 80, D385–D401. [Google Scholar] [CrossRef]
- Gao, K.; Fu, S.; Chung, E.T. A high-order multiscale finite-element method for time-domain acoustic-wave modeling. J. Comput. Phys. 2018, 360, 120–136. [Google Scholar] [CrossRef]
- Chung, E.T.; Leung, W.T. Mixed GMsFEM for the simulation of waves in highly heterogeneous media. J. Comput. Appl. Math. 2016, 306, 69–86. [Google Scholar] [CrossRef]
- Chung, E.; Pun, S.M. Computational multiscale methods for first-order wave equation using mixed CEM-GMsFEM. J. Comput. Phys. 2020, 109359. [Google Scholar] [CrossRef]
- Chung, E.T.; Efendiev, Y.; Gibson, R.L.; Lyeva, M. A generalized multiscale finite element method for elastic wave propagation in fractured media. GEM-Int. J. Geomath. 2016, 7, 163–182. [Google Scholar] [CrossRef]
- Chung, E.; Efendiev, Y.; Leung, W.T. An adaptive generalized multiscale discontinuous Galerkin method (GMsDGM) for high-contrast flow problems. arXiv 2014, arXiv:1409.3474. [Google Scholar]
- Chung, E.T.; Efendiev, Y.; Fu, S. Generalized multiscale finite element method for elasticity equations. GEM-Int. J. Geomath. 2014, 5, 225–254. [Google Scholar] [CrossRef]
- Efendiev, Y.; Galvis, J.; Li, G.; Presho, M. Generalized multiscale finite element methods: Oversampling strategies. Int. J. Multiscale Comput. Eng. 2014, 12, 465–484. [Google Scholar] [CrossRef]
- Calo, V.M.; Efendiev, Y.; Galvis, J.; Li, G. Randomized Oversampling for Generalized Multiscale Finite Element Methods. Multiscale Model. Simul. 2016, 14, 482–501. [Google Scholar] [CrossRef]
- Vasilyeva, M.; De Basabe, J.; Efendiev, Y.; Gibson, R., Jr. Multiscale model reduction of the wave propagation problem in viscoelastic fractured media. Geophys. J. Int. 2019, 217, 558–571. [Google Scholar] [CrossRef]
- Kellogg, O.D. Foundations of Potential Theory; Springer: Berlin/Heidelberg, Germany, 2012; Volume 31. [Google Scholar]
- Arfken, G.B.; Weber, H.J. Mathematical methods for physicists. Am. J. Phys. 1999, 67, 165. [Google Scholar] [CrossRef]
- Zhang, J. Elastic wave modeling in fractured media with an explicit approach. Geophysics 2005, 70, T75–T85. [Google Scholar] [CrossRef]
- Schoenberg, M. Elastic wave behavior across linear slip interfaces. J. Acoust. Soc. Am. 1980, 68, 1516–1521. [Google Scholar] [CrossRef]
- Engquist, B.; Majda, A. Absorbing boundary conditions for numerical simulation of waves. Proc. Natl. Acad. Sci. USA 1977, 74, 1765–1766. [Google Scholar] [CrossRef]
- Grote, M.J.; Schneebeli, A.; Schötzau, D. Discontinuous Galerkin finite element method for the wave equation. SIAM J. Numer. Anal. 2006, 44, 2408–2431. [Google Scholar] [CrossRef]
- Arnold, D.N. An interior penalty finite element method with discontinuous elements. SIAM J. Numer. Anal. 1982, 19, 742–760. [Google Scholar] [CrossRef]
- Lähivaara, T. Discontinuous Galerkin Method for Time-Domain Wave Problems; University of Eastern Finland Joensuu: Joensuu, Finland, 2010. [Google Scholar]
- Chung, E.T.; Efendiev, Y.; Leung, W.T. An Online Generalized Multiscale Discontinuous Galerkin Method (GMsDGM) for Flows in Heterogeneous Media. Commun. Comput. Phys. 2017, 21, 401–422. [Google Scholar] [CrossRef]
- Chung, E.T.; Efendiev, Y.; Leung, W.T. Generalized multiscale finite element methods for wave propagation in heterogeneous media. Multiscale Model. Simul. 2014, 12, 1691–1721. [Google Scholar] [CrossRef]
- Gao, K.; Fu, S.; Gibson, R.L.; Chung, E.T.; Efendiev, Y. Generalized Multiscale Finite-Element Method (GMsFEM) for elastic wave propagation in heterogeneous, anisotropic media. J. Comput. Phys. 2015, 295, 161–188. [Google Scholar] [CrossRef]


| Geometry 1 | Geometry 2 | ||||||
|---|---|---|---|---|---|---|---|
| (%) | (%) | (%) | (%) | ||||
| 5 | 2205 | 5.683 | 44.617 | 5 | 2205 | 22.032 | 49.143 |
| 10 | 4410 | 3.750 | 37.737 | 10 | 4410 | 3.174 | 37.845 |
| 15 | 6615 | 2.570 | 34.923 | 15 | 6615 | 2.944 | 35.137 |
| 20 | 8820 | 1.921 | 32.049 | 20 | 8820 | 3.540 | 32.216 |
| 25 | 11,025 | 1.591 | 30.422 | 25 | 11,025 | 3.559 | 30.903 |
| 50 | 22,050 | 1.187 | 25.187 | 50 | 22,050 | 2.676 | 25.583 |
| 5 | 2205 | 8.717 | 41.269 | 5 | 2205 | 25.635 | 47.053 |
| 10 | 4410 | 5.383 | 34.477 | 10 | 4410 | 3.9745 | 35.073 |
| 15 | 6615 | 3.495 | 31.825 | 15 | 6615 | 3.7782 | 32.420 |
| 20 | 8820 | 2.567 | 29.241 | 20 | 8820 | 3.8773 | 29.772 |
| 25 | 11,025 | 2.184 | 27.861 | 25 | 11,025 | 3.6346 | 28.403 |
| 50 | 22,050 | 1.343 | 23.025 | 50 | 22,050 | 2.4719 | 23.345 |
| 5 | 2205 | 19.997 | 42.195 | 5 | 2205 | 49.906 | 57.898 |
| 10 | 4410 | 8.927 | 32.913 | 10 | 4410 | 8.128 | 33.930 |
| 15 | 6615 | 5.217 | 30.303 | 15 | 6615 | 6.779 | 31.575 |
| 20 | 8820 | 2.970 | 27.818 | 20 | 8820 | 6.506 | 29.065 |
| 25 | 11,025 | 2.669 | 26.493 | 25 | 11,025 | 6.577 | 27.819 |
| 50 | 22,050 | 1.924 | 21.754 | 50 | 22,050 | 4.945 | 22.936 |
| Geometry 1 | Geometry 2 | ||||||
|---|---|---|---|---|---|---|---|
| (%) | (%) | (%) | (%) | ||||
| 5 | 4000 | 86.368 | 99.956 | 5 | 4000 | 86.412 | 99.969 |
| 10 | 8000 | 64.157 | 78.074 | 10 | 8000 | 70.890 | 81.704 |
| 15 | 12,000 | 34.960 | 53.810 | 15 | 12,000 | 35.100 | 54.556 |
| 20 | 16,000 | 13.730 | 41.178 | 20 | 16,000 | 21.538 | 44.009 |
| 25 | 20,000 | 7.556 | 33.535 | 25 | 20,000 | 10.007 | 34.752 |
| 50 | 40,000 | 2.236 | 16.672 | 50 | 40,000 | 3.516 | 17.245 |
| 5 | 4000 | 98.804 | 99.992 | 5 | 4000 | 99.136 | 100.004 |
| 10 | 8000 | 77.995 | 80.921 | 10 | 8000 | 87.598 | 86.050 |
| 15 | 12,000 | 28.137 | 49.248 | 15 | 12,000 | 31.581 | 50.711 |
| 20 | 16,000 | 12.443 | 37.775 | 20 | 16,000 | 19.672 | 40.105 |
| 25 | 20,000 | 7.534 | 30.598 | 25 | 20,000 | 9.890 | 31.458 |
| 50 | 40,000 | 2.069 | 15.541 | 50 | 40,000 | 3.295 | 16.074 |
| 5 | 4000 | 99.264 | 99.986 | 5 | 4000 | 99.446 | 99.994 |
| 10 | 8000 | 92.430 | 86.462 | 10 | 8000 | 98.481 | 90.507 |
| 15 | 12,000 | 42.383 | 52.390 | 15 | 12,000 | 45.749 | 54.527 |
| 20 | 16,000 | 20.054 | 38.037 | 20 | 16,000 | 26.519 | 41.610 |
| 25 | 20,000 | 11.739 | 30.303 | 25 | 20,000 | 13.800 | 32.069 |
| 50 | 40,000 | 3.4803 | 15.492 | 50 | 40,000 | 6.327 | 17.354 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gavrilieva, U.; Vasilyeva, M.; Chung, E.T. Generalized Multiscale Finite Element Method for Elastic Wave Propagation in the Frequency Domain. Computation 2020, 8, 63. https://doi.org/10.3390/computation8030063
Gavrilieva U, Vasilyeva M, Chung ET. Generalized Multiscale Finite Element Method for Elastic Wave Propagation in the Frequency Domain. Computation. 2020; 8(3):63. https://doi.org/10.3390/computation8030063
Chicago/Turabian StyleGavrilieva, Uygulana, Maria Vasilyeva, and Eric T. Chung. 2020. "Generalized Multiscale Finite Element Method for Elastic Wave Propagation in the Frequency Domain" Computation 8, no. 3: 63. https://doi.org/10.3390/computation8030063
APA StyleGavrilieva, U., Vasilyeva, M., & Chung, E. T. (2020). Generalized Multiscale Finite Element Method for Elastic Wave Propagation in the Frequency Domain. Computation, 8(3), 63. https://doi.org/10.3390/computation8030063





