Pythagorean Triples before and after Pythagoras

Abstract

Following the corrected chronology of ancient Hindu scientists/mathematicians, in this article, a sincere effort is made to report the origin of Pythagorean triples. We shall account for the development of these triples from the period of their origin and list some known astonishing directions. Although for researchers in this field, there is not much that is new in this article, we genuinely hope students and teachers of mathematics will enjoy this article and search for new directions/patterns.

1. Introduction

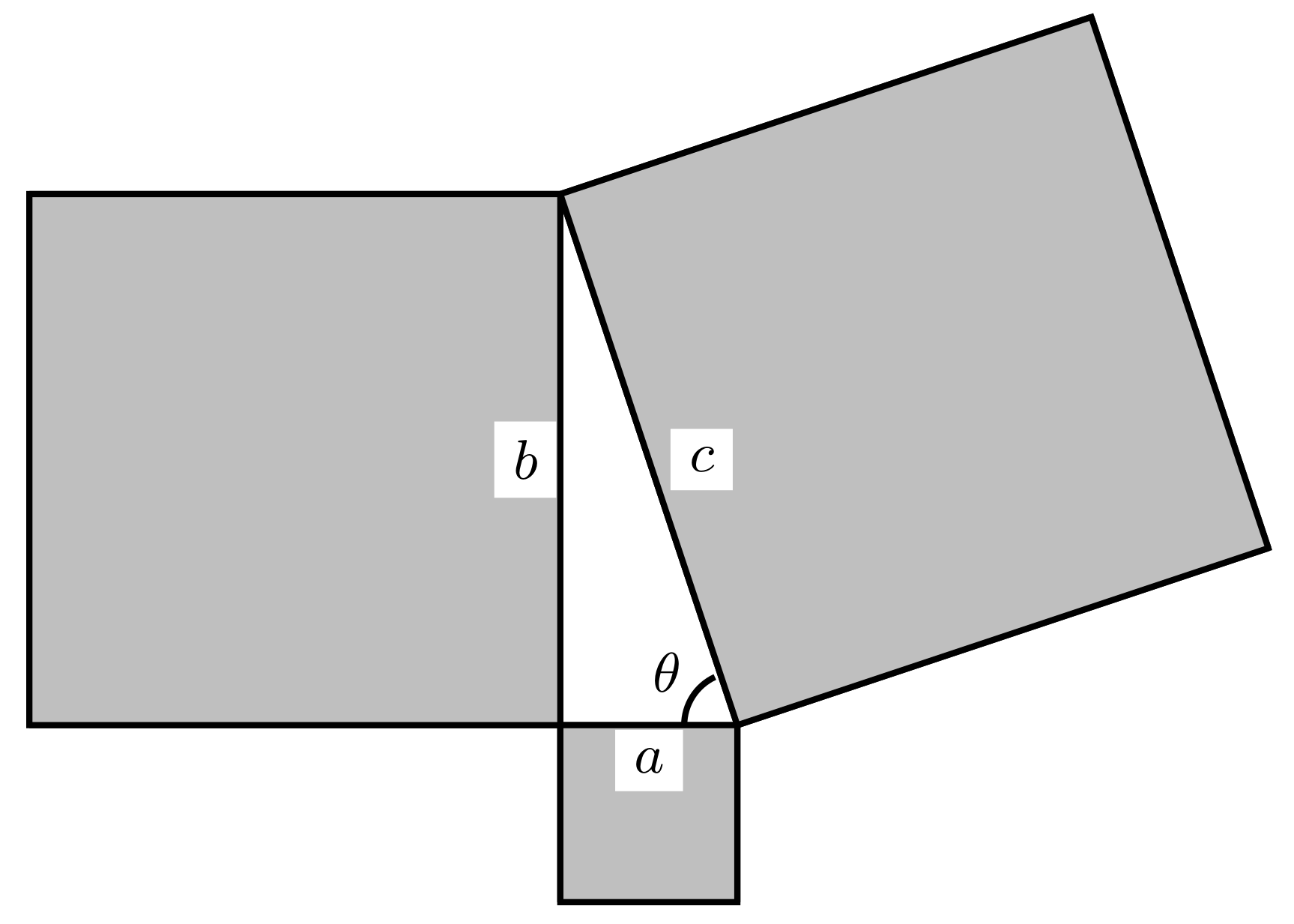
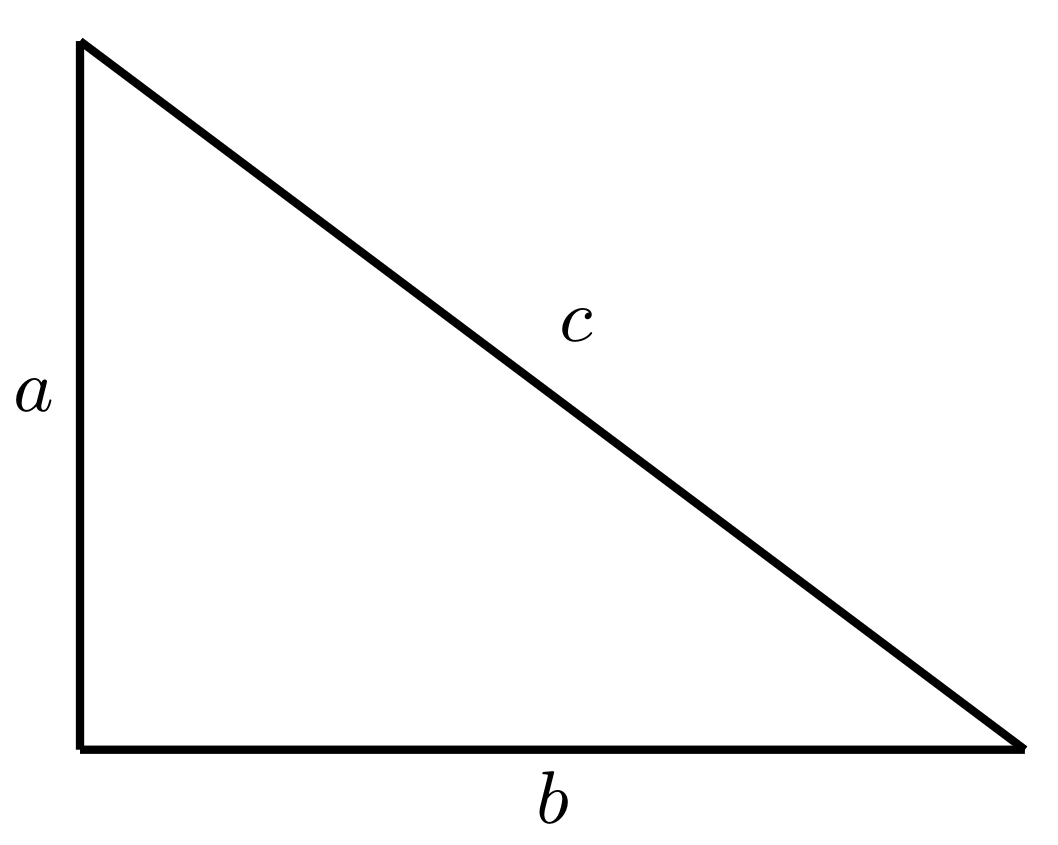
The Pythagorean theorem (after Pythagoras, around 582–481 BC) states that: If a and b are the lengths of the two legs of a right triangle and c is the length of the hypotenuse (see Figure 1), then the sum of the areas of the two squares on the legs equals the area of the square on the hypotenuse, i.e.,

$$a^2+b^2=c^2.$$

(1)

For the origin of this theorem, its far reaching extensions, and applications, see Agarwal [1]. A set of three positive integers $a,b,$ and c, which satisfies Pythagorean Relation (1), is called a Pythagorean triple (or triad) and written as ordered triple $(a,b,c).$ For convenience, it is always assumed that $0<a<b<c.$ A triangle whose sides (line segments whose lengths are denoted by integers) form a Pythagorean triple is called a Pythagorean triangle; it is clearly a right triangle. Pythagorean triangles tell us which pairs of points with whole-number coordinates on the horizontal and vertical direction are also a whole-number distance apart. Thus, there is a one-to-one correspondence between Pythagorean triangles and Pythagorean triples. Therefore, we can use Pythagorean triangle and Pythagorean triple interchangeably. A Pythagorean triangle $(a,b,c)$ is said to be primitive (sometimes reduced) if $a,b,c$ have no common divisor other than one. Thus, each primitive Pythagorean triple has a unique representation $(a,b,c).$ It is obvious that every primitive Pythagorean triangle can lead to infinitely many non-primitive triangles, for, if $(a,b,c)$ is a primitive Pythagorean triangle, then $(ka,kb,kc)$ is a non-primitive Pythagorean triangle, where $k>1$ is an integer. Conversely, every non-primitive Pythagorean triangle gives rise to a primitive Pythagorean triangle. Therefore, it suffices to study only primitive Pythagorean triangles. In recent years, primitive Pythagorean triples have been used in cryptography as random sequences and for the generation of keys; see Kak and Prabhu [2].

Pythagorean triples $(3,4,5),(12,16,20),(15,20,25),(5,12,13),(8,15,17),$ and $(12,$$35,37)$ first appeared in Apastamba (one of seven available Sulbasutras, first about 3200 BC, named after the sages; see by Lakshmikantham et al. [3] and Agarwal et al. [4]). These triples were used for the precise construction of altars. In 1943, Plimpton 322 (written between 1790 and 1750 BC, during the time of the Babylonian king Hammurabi (around 1811–1750 BC) in old Babylonian script) was classified as a “commercial account”. However, two years later, two prominent historians of mathematics Otto Neugebauer (1899–1990) and Abraham Sachs (1915–1983) made a startling discovery that the content of Plimpton 322 was a list of Pythagorean triples.

Table 1. Numbers in the brackets are wrong.

${(\mathit{c}/\mathit{b})}^2$	a	c
(1,)59,00,15	1,59	2,49	1
(1,)56,56,58,14,50,06,15	56,07	(3,12,01)1,20,25	2
(1,)55,07,41,15,33,45	1,16,41	1,50,49	3
(1,)53,10,29,32,52,16	3,31,49	5,09,01	4
(1,)48,54,01,40	1,05	1,37	5
(1,)47,06,41,40	5,19	8,01	6
(1,)43,11,56,28,26,40	38,11	59,01	7
(1,)41,33,59,03,45	13,19	20,49	8
(1,)38,33,36,36	(9,01)8,01	12,49	9
(1,)35,10,02,28,27,24,26,40	1,22,41	2,16,01	10
(1,)33,45	45	1,15	11
(1,)29,21,54,02,15	27,59	48,49	12
(1,)27,00,03,45	(7,12,01)2,41	4,49	13
(1,)25,48,51,35,06,40	29,31	53,49	14
(1,)23,13,46,40	56	(53)1,46	15

reproduces the text in modern notation with base $60.$ There are four columns, of which the rightmost, headed by the words “its name” in the original text, merely gives the sequential number of the lines 1 to 15. The second column and third columns (counting from the right to left) are headed “solving number of the diagonal” and “solving number of the width,” respectively; that is, they give the length of the diagonal and of the short side of a rectangular, or equivalently, the length of the hypotenuse and the short leg of a right triangle. We will label these columns with letters c and $a,$ respectively. The leftmost column is the most curious of all. Its heading again mentions the word “diagonal,” but the exact meaning of the remaining text is not entirely clear. However, when one examines its entries, an unexpected fact emerges: this column gives ${(c/b)}^2,$ that is the value of ${csc}^2\theta ,$ where $\theta$ is the angle opposite side of b and csc is the cosecant function (see Figure 1). As an example, in the third line, we read $a=1,16,41=1\times {60}^2+16\times 60+41=4601,$ and $c=1,50,49=1\times {60}^2+50\times 60+49=6649,$ and hence $b=\sqrt{{6649}^2-{4601}^2}=\sqrt{23040000}=4800,$ giving us the triple $(4601,4800,6649).$ Unfortunately, the table contains some obvious errors. In Line 2, we have $a=56,07=56\times 60+7=3367$ and $c=3,12,01=3\times {60}^2+12\times 60+1=11,521$, and these do not form a Pythagorean triple (the third number b not being an integer). However, if we replace $3,12,01$ by $1,20,25=1\times {60}^2+20\times 60+25=4825,$ we get an integer value of $b=\sqrt{{4825}^2-{3367}^2}=\sqrt{11943936}=3456,$ which leads to the Pythagorean triple $(3367,3456,4825).$ In Line 9, we find $a=9,1=9\times 60+1=541$ and $c=12,49=12\times 60+49=769,$ and these do not form a Pythagorean triple. However, if we replace $9,1$ by $8,1=481,$ we do indeed get an integer value of $b;b=\sqrt{{769}^2-{481}^2}=\sqrt{360000}=600,$ resulting in the triple $(481,600,769).$ Again in Line 13, we have $a=7,12,1=7\times {60}^2+12\times 60+1=25921$ and $c=4,49=4\times 60+49=289,$ and these do not form a Pythagorean triple; however, we may notice that 25921 is the square of 161, and the numbers 161 and 289 do form the triple $(161,240,289).$ In Row 15, we find $c=53,$ whereas the correct entry should be twice that number, that is $106=1,46$, producing the triple $(56,90,106).$ This, however, is not a primitive triple, since its members have the common factor of two; it can be reduced to the simple triple $(28,45,53).$ Similarly, Row 11 is not a primitive triple $(45,60,75),$ since its members have the common factor of $15;$ it can be reduced to $(3,4,5),$ which is the smallest and best known Pythagorean triple.

Table 2. Numbers in the brackets are wrong.

${(\mathit{c}/\mathit{b})}^2$	b	a	c
1.9834027	120	119	169	1
1.9491585	3456	3367	(11521) 4825	2
1.9188021	4800	4601	6649	3
1.8862478	13500	12709	18541	4
1.8150076	72	65	97	5
1.7851928	360	319	481	6
1.7199836	2700	2291	3541	7
1.6927093	960	799	1249	8
1.6426694	600	(541)481	769	9
1.5861225	6480	4961	8161	10
1.5625000	60	45	75	11
1.4894168	2400	1679	2929	12
1.4500173	240	(25921)161	289	13
1.4302388	2700	1771	3229	14
1.3871604	90	56	(53)106	15

produces the text in the decimal system. In this table, we find that the values of ${(c/b)}^2$ continuously decrease from $1.9834027$ to $1.3871604.$ This implies that the values of $c/b=csc\theta$ continuously decrease, and this in turn shows that $\theta$ increases steadily from approximately 45${}^{\circ }$ to 58${}^{\circ }$. The question that baffles the mind even today is how did the Babylonians find these particular triples, including such enormously large ones as (13500, 12709, 18541). There seems to be only the following plausible explanation: they were not only familiar with the Pythagorean theorem, but knew an algorithm to compute Pythagorean triples and had enormous computational skills; see Siu [5].

Finding Pythagorean triples is one of the earliest problems in the theory of numbers, and certainly, Pythagorean triples are some of the oldest known solutions of the nonlinear Diophantus (about 250) Equation (1). In Apastamba, it was recorded that the triplets:

$$\left(m,\frac{m^2-1}{2},\frac{m^2+1}{2}\right),$$

(2)

where m is an odd number, and:

$$\left(m,\frac{1}{4}{m}^2-1,\frac{1}{4}{m}^2+1\right),$$

(3)

where m is an even number, are Pythagorean triples. The Chinese mathematician Liu Hui (around 220–280) in his commentary on the Jiuzhang Suanshu (Nine Chapters on the Mathematical Art), which is believed to have been written around 1000 BC, included Pythagorean triples and mentioned right triangles. It is a tradition to assume that Pythagoras himself gave the following partial solution of Equation (1),

$$a=2n+1,b=2n^2+2n,c=2n^2+2n+1,n\ge 1.$$

(4)

He presumably arrived at (4) from the relation:

$$(2k-1)+{(k-1)}^2=k^2$$

(5)

and then searching for those k for which $2k-1$ is a perfect square, i.e., $2k-1=m^2$ (since $m^2$ is odd, m must be odd). This gives:

$$k=\frac{m^2+1}{2}\mathrm{and}k-1=\frac{m^2-1}{2}.$$

Thus, the relation (5) can be written as:

$$m^2+{\left(\frac{m^2-1}{2}\right)}^2={\left(\frac{m^2+1}{2}\right)}^2$$

from which it is clear that (1) is satisfied with:

$$a=m,b=\frac{m^2-1}{2},c=\frac{m^2+1}{2},$$

(6)

Finally, in (6) letting $m=2n+1,n\ge 1,$ we obtain (4). Notice that in (4), the sum of the long side and hypotenuse is $4n^2+4n+1={(2n+1)}^2,$ which is the square of the small side. We also remark that (6) is the same as (2).

We can directly verify that (4) is a solution of (1). Indeed, we have:

$$c^2={(2n^2+2n+1)}^2={(2n^2+2n)}^2+2(2n^2+2n)+1={(2n^2+2n)}^2+{(2n+1)}^2=a^2+b^2.$$

Since $c-b=1,$ it follows that b and c are relatively prime, i.e., a positive integer that divides both of them is one, and consequently, Pythagorean triples $(a,b,c)$ generated from (4) must be primitive. Some of the Pythagorean triples that can be obtained from (4) are given in the following table.

$$\begin{array}{cccc}n& a& b& c\\ 1& 3& 4& 5\\ 2& 5& 12& 13\\ 3& 7& 24& 25\\ 4& 9& 40& 41\\ 5& 11& 60& 61\\ 6& 13& 84& 85\\ 7& 15& 112& 113\\ 8& 17& 144& 145\end{array}$$

It is interesting to note that between the series of larger legs $4,12,24,40,60,84,$$112,144,\cdots$ and of hypotenuses $5,13,25,41,61,85,113,145,\cdots$, there is a fascinating pattern (see Boardman [6]):

$$\begin{array}{ccc}\hfill 3^2+4^2& =\hfill & 5^2\hfill \\ \hfill {10}^2+{11}^2+{12}^2& =\hfill & {13}^2+{14}^2\hfill \\ \hfill {21}^2+{22}^2+{23}^2+{24}^2& =\hfill & {25}^2+{26}^2+{27}^2\hfill \\ \hfill {36}^2+{37}^2+{38}^2+{39}^2+{40}^2& =\hfill & {41}^2+{42}^2+{43}^2+{44}^2\hfill \\ \hfill \cdots & =\hfill & \cdots \hfill \end{array}$$

The following table gives Pythagorean triples obtained from (4) by letting $n=10,{10}^2,\cdots ,{10}^5.$

$$\begin{array}{cccc}n& a& b& c\\ 10& 21& 220& 221\\ {10}^2& 201& 20200& 20201\\ {10}^3& 2001& 2002000& 2002001\\ {10}^4& 20001& 200020000& 200020001\\ {10}^5& 200001& 20000200000& 20000200001\end{array}$$

The above table gives an obvious pattern, so that if we know one row, then we can continue this table indefinitely. From (4), it follows that there are countably infinitely many primitive Pythagorean triples.

Clearly, Pythagoras’s solution has the special feature of producing right triangles having the characteristic that the hypotenuse exceeds the larger leg by one. According to Proclus Diadochus (410–485 AD), Plato of Athens (around 427–347 BC) gave a method for finding Pythagorean triples that combined algebra and geometry. His solution of Equation (1) is:

$$a=2n,b=n^2-1,c=n^2+1,n\ge 2.$$

(7)

For this, it suffices to note that:

$$c^2={(n^2+1)}^2={(n^2-1+2)}^2={(n^2-1)}^2+4(n^2-1)+4={(n^2-1)}^2+{\left(2n\right)}^2=b^2+a^2.$$

It is interesting to note that for $m=2n,$ (3) is the same as (7). Some of the Pythagorean triples that can be obtained from (7) are given in the following table.

$$\begin{array}{ccccc}n& a& b& c& (a,b,c)\\ 2& 4& 3& 5& (3,4,5)\\ 3& 6& 8& 10& (6,8,10)\\ 4& 8& 15& 17& (8,15,17)\\ 5& 10& 24& 26& (10,24,26)\\ 6& 12& 35& 37& (12,35,37)\\ 7& 14& 48& 50& (14,48,50)\\ 8& 16& 63& 65& (16,63,65)\\ 9& 18& 80& 82& (18,80,82)\\ 10& 20& 99& 101& (20,99,101)\end{array}$$

(For $n=2$, the Pythagorean triple is written as $(3,4,5).$) From (7) it follows that the hypotenuse exceeds one of the legs by two. Further, for $n=4$, we have the Pythagorean triple $(8,15,17),$ which cannot be obtained from Pythagoras’s formula (4). Moreover, for $n=2k+1,k\ge 1,$ (7) becomes:

$$a=2(2k+1),b=4k^2+4k,c=4k^2+4k+2,k\ge 1$$

(8)

i.e., for odd $n,$ (7) does not give primitive triples, and upon dividing (8) by two, we find:

$$a=2k+1,b=2k^2+2k,c=2k^2+2k+1,k\ge 1.$$

However, this is the same as (4). Thus, in conclusion, the primitive triples obtained from (7) include those given by (4).

The following interesting table gives Pythagorean triples obtained from (7) by letting $n=2\times 10$, $2\times {10}^2$, $2\times {10}^3$, $2\times {10}^4$.

$$\begin{array}{ccc}a& b& c\\ 40& 399& 401\\ 400& 39999& 40001\\ 4000& 3999999& 4000001\\ 40000& 399999999& 400000001\end{array}$$

We note that (7) for $n=k+1,k\ge 1$ becomes $a=2(k+1),b=k(k+2),c=k^2+2k+2.$ Thus, if $k\ge 1,$

$$\frac{1}{k}+\frac{1}{k+2}=\frac{a}{b},$$

where a and b are reduced, will yield a primitive Pythagorean triple with $c=\sqrt{a^2+b^2}.$ As an example, for $k=2,$ we have $(1/2)+(1/4)=(3/4).$ Thus, $a=3,b=4,$ and $c=\sqrt{3^2+4^2}=5.$

2. Characterization

Unfortunately, even (7) does not provide all Pythagorean triples, and it was not until Euclid of Alexandria (around 325–265 BC) in his Elements (Book X, Lemma I; also see Lemma II after Proposition 28) formalized the following statement (fabricated in geometric language): Let u and v be any two positive integers, with $u>v,$ then the three numbers:

$$a=u^2-v^2,b=2uv,c=u^2+v^2$$

(9)

form a Pythagorean triple. This seems to be the first regressively proven complete integer solution of in indeterminate equation. If in (9), $a>b$, we interchange a and b (if in addition, u and v are of opposite parity—one even and the other odd—and they are coprime, i.e., they do not have any common factor other than one, then $(a,b,c)$ is a primitive Pythagorean triple).

It is easy to verify that the numbers $a,b,$ and c as given by Equation (9) satisfy the equation $a^2+b^2=c^2$:

$$\begin{array}{cc}{a}^2+b^2\hfill & = {(u^2-v^2)}^2+{\left(2uv\right)}^2\hfill \\ \hfill \\ & = u^4-2u^2{v}^2+v^4+4u^2{v}^2\hfill \\ \hfill \\ & = u^4+2u^2{v}^2+v^4\hfill \\ \hfill \\ & = {(u^2+v^2)}^2=c^2.\hfill \end{array}$$

The integers u and $v,$ or simply $(u,v)$ in the formula (9), are called the generating numbers or generators of the triple $(a,b,c).$ Neugebauer claims that this sufficiency part was known to the Babylonians.

From (9), the following relations are immediate:

$$u=\sqrt{\frac{c+a}{2}},v=\sqrt{\frac{c-a}{2}},\frac{u}{v}=\frac{c+a}{b},$$

$$c-b={(u-v)}^2,\frac{1}{2}(c-a)=u^2.$$

Diophantus in his Arithmetica (Claude Gaspard Bachet de Méziriac (1581–1638) made it fully available in Greek and Latin in 1621) also arrived at the solution (9) of (1) by using the following reasoning. In (1), let $b=ka-c,$ where k is any rational number. Then, it follows that:

$$c^2-a^2=b^2={(ka-c)}^2=k^2{a}^2-2kac+c^2,$$

which leads to:

$$-a^2=k^2{a}^2-2kac,$$

or

$$-a=k^{2}a-2kc.$$

Thus, we have:

$$a=\frac{2k}{k^2+1}c,$$

which gives:

$$b=ka-c=\frac{k^2-1}{k^2+1}c.$$

Let $k=u/v,$ with u and v integers (we can assume that $u>v$), so that:

$$a=\frac{2uv}{u^2+v^2}c,b=\frac{u^2-v^2}{u^2+v^2}c.$$

Now, we set $c=u^2+v^2,$ to obtain $a=2uv,b=u^2-v^2,c=u^2+v^2.$

Bhaskara II or Bhaskaracharya (working 486) also gave a tentative partial solution of (1), which in number theory is considered an exciting result.

The converse, i.e., showing that any Pythagorean triple is necessarily of the form (9), is more difficult. The earliest record for some special cases of the proof of the converse can be found in the solutions of Problems 8 and 9 of Book II of the Arithmetica of Diophantus. Next, the converse was discussed in the works of Arab mathematicians around the Tenth Century. The details of the Arab’s work was available to the well-traveled Fibonacci (Leonardo of Pisa, around 1170–1250). It seems the first explicit, rigorous proof of the converse was given in 1738, by C.A.Koerbero (Dickson [7], Vol. 2). In 1901, Leopold Kronecker (1823–1891) gave the first proof that all positive integer solutions of $a^2+b^2=c^2$ are given without duplication by $a=2uvk,b=(u^2-v^2)k,c=(u^2+v^2)k,$ where $u,v$, and k are positive integers such that $u>v,u$ and v are not both odd, and u and v are relatively prime. In what follows, we shall discuss a simplified and extended version of a known proof (see, e.g., Burton [8]) of Euclid’s Proposition and its converse.

Step 1.

If $(a,b,c)$ is a primitive Pythagorean triple, then $gcd(a,b)=1.$ Here, $gcd(a,b)$ denotes the greatest common divisor of a and $b.$ For, if $gcd(a,b)=d$, then $d|c$ (d divides c), so that d is a common divisor of $a,b,$ and $c,$ and consequently, $(a,b,c)$ is not a primitive Pythagorean triple.

Step 2.

If $(a,b,c)$ is a Pythagorean triple, then $gcd(a,b)=1$ implies $gcd(b,c)=1$ and $gcd(a,c)=1.$ For, if b and c have a common divisor, say $d\ne 1,$ then d is also a divisor of a, and consequently, d is a common divisor of a and $b,$ which is not possible. Hence, $gcd(b,c)=1.$ The proof for $gcd(a,c)=1$ is similar.

Step 3.

If $(a,b,c)$ is a primitive solution of (1), then exactly one of a and b must be even, and c must be odd. For, if a and b are both even, then c must also be even; and consequently, $a,b,c$ will have a common divisor other than one. If a and b are both odd, say, $a=2m+1,b=2n+1,$ then $a^2+b^2=2[2(m^2+n^2+m+n)+1]=2(2t+1)$, which is impossible since no perfect square can be of the form $2(2t+1).$ Thus, exactly one of a and b must be odd, and the other must be even. Furthermore, then, $a^2+b^2$ must be odd, and so, c must be odd (By virtue of this step, there exists no primitive Pythagorean triple all of whose numbers $a,b,c$ are prime. There are primitive Pythagorean triples in which c and one of a or b is prime, for example, $(3,4,5),(5,12,13),(11,60,61).$ It is not known if there exist infinitely many such triples.).

Step 4.

If $p,q,r$ are integers such that $p^2=qr,$ and $gcd(q,r)=1,$ then q and r must be perfect squares. In fact, writing out the prime factorizations of q and $r,$ we have:

$$q=q_1^{a_1}{q}_2^{a_2}\cdots {q_s}^{a_s},r=r_1^{b_1}{r}_2^{b_2}\cdots {r_t}^{b_t}.$$

Since $gcd(q,r)=1,$ therefore no prime can occur in either decomposition. Since $p^2=qr$ and since prime factorization is unique, therefore,

$$p^2=q_1^{a_1}{q}_2^{a_2}\cdots {q_s}^{a_s}{r}_1^{b_1}{r}_2^{b_2}\cdots {r_t}^{b_t},$$

where $q_1,q_2,\cdots ,q_s,r_1,r_2,\cdots ,r_t$ are distinct primes. Since $p^2$ is a perfect square, it is necessary that $a_1,a_2,\cdots ,a_s,b_1,b_2,\cdots ,b_t$ must be all even, and consequently, q and r must be perfect squares. Similarly, it follows that if $p^n=qr$ and $gcd(q,r)=1,$ then q and r must be of the $n^{\mathrm{th}}$ power. We note that Step 4 can also be proven by induction on $p.$ For $p=1$ and $p=2$, it is trivially true (Professor Cuthbert Calculus (French: Professeur Tryphon Tournesol) meaning “Professor Tryphon Sunflower”, is a fictional character in The Adventures of Tintin. He discovered an amusing proof of Step 4 while he was in jail for having failed the president’s son. The prisoners were put in a long row of cells. At first, all the doors were unlocked, but then, the jailor walked by and locked every second door. He walked again and stopped at every third door, locking it if it was unlocked, but unlocking if it was locked. On the next round, he stopped at every fourth door, locking it if it was unlocked, unlocking if it was locked, and so on. Professor Tournesol soon realized that the $q^{\mathrm{th}}$ cell would be unlocked in the end just in case q had an odd number of divisors. Now, if d divides q, then so does $q|d$, and it would seem that the divisors of q come in pairs. Unless …“what if $d=q|d?,$” thought the professor, “then the divisor d does not pair off with another, and $d=q|d$ just in case q is a square.”).

Step 5.

If $(a,b,c)$ is a primitive solution of (1) and a is odd (similar arguments hold if a is even), then there must exist positive integers u and v such that $u>v$ with $gcd(u,v)=1,$ and exactly one of u and v being odd, such that $a=u^2-v^2,b=2uv,c=u^2+v^2.$ Since a is odd, by Step 3, b must be even. Let $b=2p,$ for some $p.$ From $b^2=c^2-a^2,$ we have:

$$4p^2=(c+a)(c-a).$$

(10)

Now, $(c+a)$ and $(c-a)$ are both even (for by Step 3, a and c are both odd). Let us put $c+a=2q,c-a=2r,$ i.e., $c=q+r,a=q-r.$ Then, from (10), we have $p^2=qr.$ Next, we shall show that q and r are relatively prime. For, if d is a common divisor of q and $r,$ then d must also be a common divisor of c and $a,$ and therefore also a divisor of $b.$ Thus, $a,b,c$ will have a common divisor $d.$ Since the solution $(a,b,c)$ is a primitive solution, we must have $d=\pm 1,$ i.e., q and r must be relatively prime. Thus, by Step 4 (from Professor Tournesol’s discovery), q and r must be perfect squares. Let $q=u^2,r=v^2$ for some integers u and v, which are taken to be positive. Then, $c=u^2+v^2,a=u^2-v^2,b^2=c^2-a^2=4u^2{v}^2,$ so that $b=2uv.$ It is clear that $gcd(u,v)=1,$ for if $gcd(u,v)=d,$ then d will be a divisor of $a,b$, and $c.$ Furthermore, u and v cannot be both odd or both even, for in either case, c will be even, and this will contradict the result in Step 3.

Step 6.

If $a=u^2-v^2,b=2uv,c=u^2+v^2$ where u and v are positive integers such that $u>v,$$gcd(u,v)=1$ and exactly one of u and v is odd, then $(a,b,c)$ is a primitive solution of (1). By actual substitution, we find that:

$$a^2+b^2={(u^2-v^2)}^2+4u^2{v}^2={(u^2+v^2)}^2=c^2,$$

so that $(a,b,c)$ is a solution. To show that $(a,b,c)$ is a primitive solution, assume to the contrary that p is an odd prime that divides both a and $c.$ This implies $p|c+a$ and $p|c-a,$ i.e., p divides both $2u^2$ and $2v^2.$ Since p is odd, it follows that p divides both $u^2$ and $v^2.$ Since p is a prime, it must divide both u and $v.$ However, $gcd(u,v)=1$ implies that this is impossible. Thus, the only possible common divisor that a and c may have must be a power of two. However, this is also not possible because a must be odd. Thus, $gcd(a,c)=1$, and $(a,b,c)$ is a primitive solution.

Summing the above steps, we find that (9) generates all primitive Pythagorean triples.

The following proof (see Beauregard and Suryanarayan [9] and Joyce [10]) of the converse of Euclid’s statement is short and elementary.

If $(a,b,c)$ is a primitive Pythagorean triple, then by Step 1, $gcd(a,b)=1,$ so we can always choose a to be odd. Now, from (1), it follows that:

$$1=\left(\frac{c}{b}+\frac{a}{b}\right)\left(\frac{c}{b}-\frac{a}{b}\right).$$

Thus, the two terms on the right are rational and reciprocals of each other. Let the first one be $u/v$ in lowest terms, then the second is $v/u,$ i.e.,

$$\frac{c}{b}+\frac{a}{b}=\frac{u}{v}\mathrm{and}\frac{c}{b}-\frac{a}{b}=\frac{v}{u}.$$

Solving these equations, we get:

$$\frac{c}{b}=\frac{u^2+v^2}{2uv}\mathrm{and}\frac{a}{b}=\frac{u^2-v^2}{2uv}.$$

(11)

Since $gcd(u,v)=1,$ both u and v cannot be even. If they both are odd, then $u^2-v^2$ will have four as the minimum possible factor, whereas $2uv$ will have two as the maximum possible factor, and this will imply that a is even, which contradicts our assumption that a is odd. Thus, one of u and v must be odd, and the other should be even. Hence, $u^2\pm v^2$ both must be odd, and obviously, $u>v.$ In conclusion, both fractions in (11) are fully reduced and hence lead to Euclid’s formula $a=u^2-v^2,b=2uv,c=u^2+v^2.$

The Pythagorean triple $(13500,12709,18541)$ in Row 4, Table 2, can be obtained by letting $u=125,v=54$ in (9). It is interesting to note that the corresponding u and v for each row in Table 2 have no prime factors other than $2,3$, and 5 (the prime divisors of the Babylonian scale 60), and $v<60.$ For $u=n+1,v=n,n\ge 1$, Formula (9) reduces to (4). Indeed, then we have $u^2-v^2=2n+1,2uv=2n^2+2n,u^2+v^2=2n^2+2n+1.$ For $u=n,v=1,n\ge 2$, Formula (9) reduces to (7). Indeed, then we have $2uv=2n,u^2-v^2=n^2-1,u^2+v^2=n^2+1.$ In general, (9) gives infinitely many primitive Pythagorean triples in which the hypotenuse exceeds one of the legs by $2v^2.$

Table 3. Pythagorean triples.

($3,4,5$)	($5,12,13$)	($8,15,17$)	($7,24,25$)
($20,21,29$)	($12,35,37$)	($9,40,41$)	($28,45,53$)
($11,60,61$)	($16,63,65$)	($33,56,65$)	($48,55,73$)
($13,84,85$)	($36,77,85$)	($39,80,89$)	($65,72,97$)
($20,99,101$)	($60,91,109$)	($15,112,113$)	($44,117,125$)
($88,105,137$)	($17,144,145$)	($24,143,145$)	($51,140,149$)
($85,132,157$)	($119,120,169$)	($52,165,173$)	($19,180,181$)
($57,176,185$)	($104,153,185$)	($95,168,193$)	($28,195,197$)
($84,187,205$)	($133,156,205$)	($21,220,221$)	($140,171,221$)
($60,221,229$)	($105,208,233$)	($120,209,241$)	($32,255,257$)
($23,264,265$)	($96,247,265$)	($69,260,269$)	($115,252,277$)
($160,231,281$)	($161,240,289$)	($68,285,293$)	($136,273,305$)
($207,224,305$)	($25,312,313$)	($75,308,317$)	($36,323,325$)
($204,253,325$)	($175,288,337$)	($180,299,349$)	($225,272,353$)
($27,364,365$)	($76,357,365$)	($252,275,373$)	($135,352,377$)
($152,345,377$)	($189,340,389$)	($228,325,397$)	($40,399,401$)
($120,391,409$)	($29,420,421$)	($87,416,425$)	($297,304,425$)
($145,408,433$)	($84,437,445$)	($203,396,445$)	($280,351,449$)
($168,425,457$)	($261,380,461$)	($31,480,481$)	($319,360,481$)
($44,483,485$)	($93,476,485$)	($132,475,493$)	($155,468,493$)
($217,456,505$)	($336,377,505$)	($220,459,509$)	($279,440,521$)
($92,525,533$)	($308,435,533$)	($341,420,541$)	($33,544,545$)
($184,513,545$)	($165,532,557$)	($276,493,565$)	($396,403,565$)
($231,520,569$)	($48,575,577$)	($368,465,593$)	($240,551,601$)
($35,612,613$)	($105,608,617$)	($336,527,625$)	($100,621,629$)
($429,460,629$)	($200,609,641$)	($315,572,653$)	($300,589,661$)
($385,552,673$)	($52,675,677$)	($37,684,685$)	($156,667,685$)
($111,680,689$)	($400,561,689$)	($185,672,697$)	($455,528,697$)
($260,651,701$)	($259,660,709$)	($333,644,725$)	($364,627,725$)
($108,725,733$)	($216,713,745$)	($407,624,745$)	($468,595,757$)
($39,760,761$)	($481,600,769$)	($195,748,773$)	($56,783,785$)
($273,736,785$)	($168,775,793$)	($432,665,793$)	($555,572,797$)
($280,759,809$)	($429,700,821$)	($540,629,829$)	($41,840,841$)
($116,837,845$)	($123,836,845$)	($205,828,853$)	($232,825,857$)
($287,816,865$)	($504,703,865$)	($348,805,877$)	($369,800,881$)
($60,899,901$)	($451,780,901$)	($464,777,905$)	($616,663,905$)
($43,924,925$)	($533,756,925$)	($129,920,929$)	($215,912,937$)
($580,741,941$)	($301,900,949$)	($420,851,949$)	($615,728,953$)
($124,957,965$)	($387,884,965$)	($248,945,977$)	($473,864,985$)
($696,697,985$)	($372,925,997$)

gives primitive Pythagorean triples with $c\le 1000,$ sorted by increasing $c.$

3. Properties, Patterns, Extensions, and Problems

After the publication of Euclid’s Elements (Book X, Proposition 29), hundreds of professional, as well as non-professional mathematicians have tried to find the properties/patterns of Pythagorean triples, alternatives to Euclid’s formula (9), different forms of the generators $(u,v),$ and Pythagorean triples with specified properties. This has led to many interesting number-theoretical results, as well as several innocent looking problems, which are still waiting for their solutions. Dickson [7], in his three-volume history of number theory, gave a twenty-five-page account of what was achieved in the field of Pythagorean triangles during more than two millennia and up to Leonhard Euler (1707–1783) and modern times. The inspiration of this modern development was provided by the father of modern number theory Pierre de Fermat (1601–1665), who in his marginal notes stated without proof many theorems involving these integers. Later, these theorems were proven and intensified by great mathematicians such as Euler, Joseph Louis Lagrange (1736–1813), Karl Friedrich Gauss (1777–1855), and Joseph Liouville (1809–1882). In the following, we present some elementary results to this introductory branch of number theory.

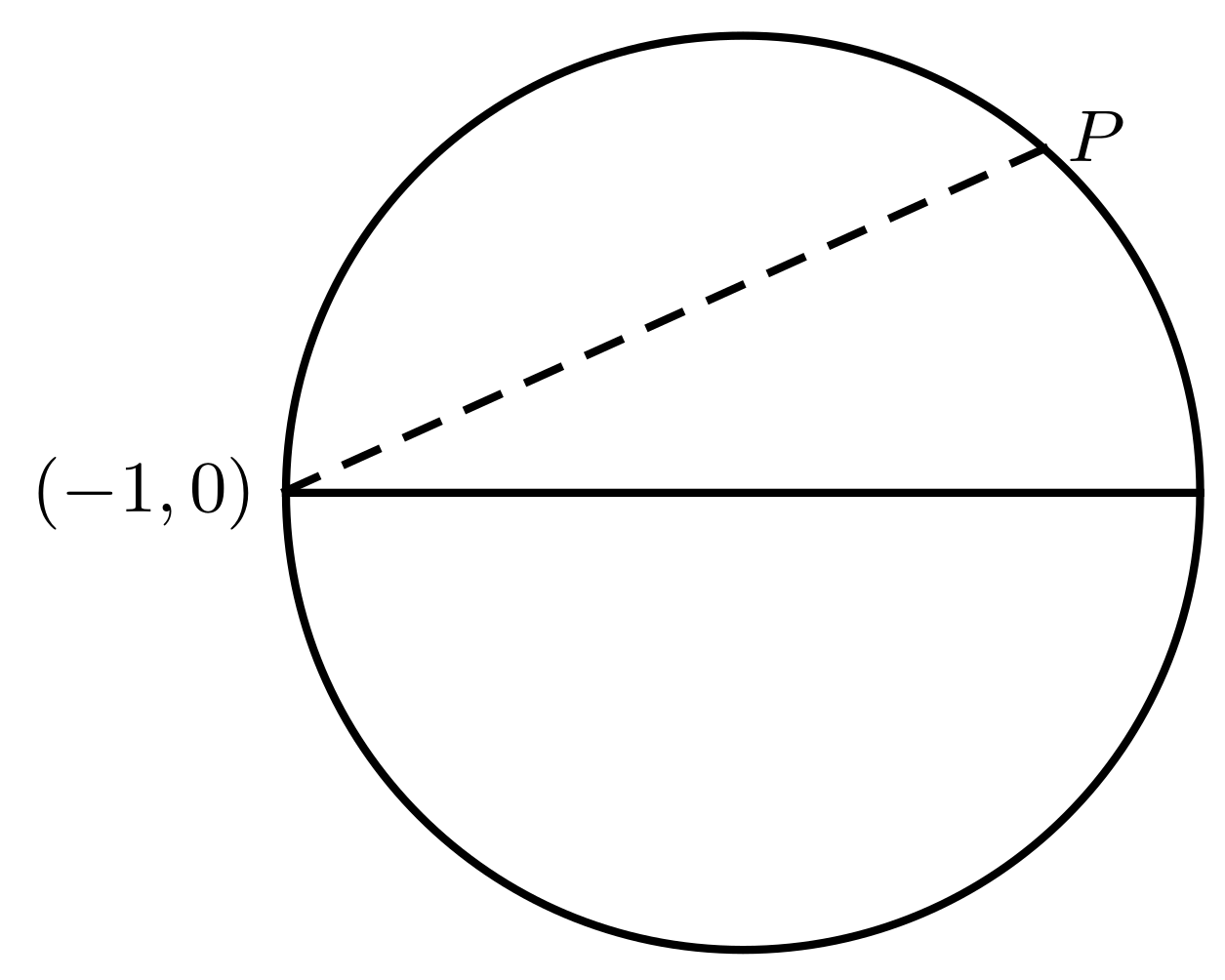
P1. 

From (9), it follows that in a Pythagorean triangle (see Figure 1):

$$sin\theta =\frac{2uv}{u^2+v^2}=y\left(\mathrm{say}\right),cos\theta =\frac{u^2-v^2}{u^2+v^2}=x\left(\mathrm{say}\right),tan\theta =\frac{2uv}{u^2-v^2}.$$

Further, from the half-angle formula $tan\theta /2=sin\theta /(1+cos\theta ),$ we have $tan(\theta /2)=v/u.$ We also note that $y=(v/u)(x+1).$ Thus, if we draw a unit circle in the $xy$-plane with the origin at $(0,0)$ and a straight line from the point $(-1,0)$ with slop $v/u,$ then $P=((u^2-v^2)/(u^2+v^2),2uv/(u^2+v^2))$ is the other point of intersection of the line and the circle; see Figure 2.

P2. 

From (9) it follows that $(c-a)(c-b)/2=u^2{(u-v)}^2,$ i.e., $(c-a)(c-b)/2$ is always a perfect square. This is only a necessary condition, but not a sufficient one (see Posamentier [11], p. 156). For example, consider the triple $(4,8,12)$ for which $(c-a)(c-b)/2=4^2,$ but it is not a Pythagorean triple. We also note from this simple observation that $(3,4,7)$ cannot be a Pythagorean triple.

P3. 

If P is the perimeter of a primitive Pythagorean triangle $(a,b,c),$ then P is even and $P|ab.$ Indeed, we have $P=a+b+c=u^2-v^2+2uv+u^2+v^2=2u(u+v)$ and $ab=(u^2-v^2)\left(2uv\right)=2u(u+v)v(u-v)=P\left[v(u-v)\right].$ Thus, in particular, the perimeter P divides $2A,$ where $A=(1/2)ab$ is the area of the triangle. Fermat proved that A can never be a square number (see P37); later, it was shown that it cannot be twice the square number (see Carmichael [12,13]).

P4. 

In a primitive Pythagorean triple $(a,b,c),$ either a or b is divisible by three. For this, first we note that any number m can be written either as $3k,3k+1,$ or $3k+2.$ However, since ${(3k+2)}^2=9k^2+12k+4=3(3k^2+4k+1)+1$ is of the form $3h+1,$ no integer $m^2$ can be written in the form $3k+2;$ hence, all integers squared are of the form $3k$ or $3k+1.$ Thus, if in (9) either $u^2$ or $v^2$ happens to be of the form $3k$ (that is to say, if either $3|u^2$ or $3|v^2$), then $3|u$ or $3|v,$ in which case $3|2uv.$ Now, assume that both $u^2$ and $v^2$ take the form $3k+1;$ to be specific, let $u^2=3k+1$ and $v^2=3h+1.$ Then, we have $u^2-v^2=(3k+1)-(3h+1)=3(k-h).$ Hence, $3|u^2-v^2.$ In conclusion, in a primitive Pythagorean triple $(a,b,c)$, exactly one of the integers is divisible by three. As an example, see any triple in Table 3.

P5. 

In a primitive Pythagorean triple $(a,b,c),$ either a or b is divisible by four. In (9), u and v are of opposite parity-one even and the other odd, and hence $4|2uv.$ In conclusion, in a primitive Pythagorean triple $(a,b,c)$ exactly one of the integers is divisible by four. As an example, see any triple in Table 3.

P6. 

In a primitive Pythagorean triple $(a,b,c),$ one side is divisible by five. For this, first we note that any number m can be written either as $5k,5k+1,5k+2,5k+3,$ or $5k+4.$ However, $m^2$ can be written only as $5k,5k+1,$ or $5k+4.$ Thus, if in (9), either $u^2$ or $v^2$ happens to be of the form $5k$ (that is to say, if either $5|u^2$ or $5|v^2$), then $5|u$ or $5|v,$ in which case $5|2uv.$ Now, assume that both $u^2$ and $v^2$ take the form $5k+1;$ to be specific, let $u^2=5k+1$ and $v^2=5h+1.$ Then, we have $u^2-v^2=(3k+1)-(3h+1)=5(k-h).$ Hence, $5|u^2-v^2.$ Similarly, if $u^2=5k+4$ and $v^2=5h+4,$ then $5|u^2-v^2.$ Finally, if $u^2=5k+4$ and $v^2=5h+1,$ then $u^2+v^2=5(k+h+1),$ and this implies that $5\left|\right(u^2+v^2).$ In conclusion, in a primitive Pythagorean triple $(a,b,c)$ exactly one of the integers is divisible by five. As an example, see any triple in Table 3.

From P4–P6, it follows that in every primitive Pythagorean triple $(a,b,c),$ the product $ab$ is divisible by $12,$ and the product $abc$ is divisible by $60.$ The smallest and best known Pythagorean triple $(3,4,5)$ shows that this observation is the best possible; see MacHale and van den Bosch [14]. Further, out of three divisors $3,4,5$, one of the numbers $a,b,c$ may have any two of these divisors, e.g., $(8,15,17),(7,24,25),(20,21,29),$ or even all three as in $(11,60,61).$ It is not known if there are two distinct Pythagorean triples having the same product. The existence of two such triples corresponds to a nonzero solution of a Diophantine equation.

P7. 

In a primitive Pythagorean triple $(a,b,c)$, none of the sides can be of the form $4n+2,n\ge 1.$ Since u and v are of different parity, $a=u^2-v^2$ is of the form $4k\pm 1,k\ge 1,$$b=2uv$ is of the form $4k,k\ge 1,$ and $c=u^2+v^2$ is of the form $4k\pm 1,k\ge 1.$

P8. 

From P3, it follows that $P=A,$ i.e., the perimeter of a Pythagorean triangle and its area are the same if and only if $2u(u+v)=u(u+v)v(u-v),$ which is the same as $v(u-v)=2.$ Thus, either (i) $v=2,u-v=1,$ or (ii) $v=1,u-v=2.$ The case (i) gives $u=3,v=2$ and leads to the Pythagorean triple $(5,12,13),$ whereas the case (ii) implies $u=3,v=1$ and gives the Pythagorean triple $(6,8,10).$ Thus, there is only one primitive Pythagorean triangle $(5,12,13)$ for which $P=A.$

P9. 

There exist primitive Pythagorean triangles having the same perimeter $P=2u(u+v).$ The first two primitive Pythagorean triangles with the same perimeter 1716 are $(364,627,725)$ and $(195,748,773).$ Next, two primitive Pythagorean triangles $(340,1131,1181)$ and $(51,1300,1301)$ correspond to the same perimeter $2652.$ Other parameters that have more than one primitive Pythagorean triangle are $3876,3960,4290,5244,5700,5720,6900,6930,8004,8700,9300,9690,10010,10788,11088,12180,12876,$ 12920, $13020,13764,14280,15252,15470,15540,15960,16380,17220,17480,18018,18060,18088,18204,$ 19092,19320, $20592,20868,\cdots .$ The first three primitive Pythagorean triangles with the same perimeter 14280 are $(3255,5032,5993),(168,7055,7057)$, and $(119,7080,7081).$ The next perimeter is 72930 with three primitive Pythagorean triangles $(18480,$$24089,30361),(7905,32032,32993),$ and $(2992,34905,35033).$ Four primitive Pythagorean triangles having a common perimeter also exist. For a perimeter less than ${10}^6,$ there exist only seven quads. The smallest value of the perimeter, for which a quad is possible, is $317460.$

P10. 

Fermat gave a simple method to find pairs of Pythagorean triangles with equal areas. If $(a,b,c)$ is a primitive Pythagorean triple, then the legs of the Pythagorean triangle having $u=c^2,v=2ab$ as generators will be $u^2-v^2=c^4-4a^2{b}^2={(b^2-a^2)}^2,2uv=4ab{c}^2,$ and hypotenuse $u^2+v^2=c^4+4a^2{b}^2.$ The area of this triangle is $2ab{c}^2{(b^2-a^2)}^2.$ Furthermore, the area of the Pythagorean triangle having legs $2ca(b^2-a^2),2cb(b^2-a^2),$ and hypotenuse $2c^2(b^2-a^2),$ i.e., $pa,pb,pc$ where $p=2c(b^2-a^2)$ is $2c^{2}ab{(b^2-a^2)}^2.$ Taking $a=3,b=4,c=5$, we find that the Pythagorean triangles $(49,1200,1201)$ and $(210,280,350)$ have the same area, namely $29400.$ Notice that the triple $(210,280,350)$ is not primitive. The smallest two primitive Pythagorean triples having the same common area 210 are $(20,21,29)$ and $(12,35,37).$ Some other primitive Pythagorean triples having the same area are $(60,91,109),(28,195,197)$ with common area $2730;$$(95,168,193),(40,399,401)$ with common area $7980;$ and $(341,420,541),(132,1085,$$1093)$ with common area $71610.$

Three Pythagorean triangles having the same area can also be found. It is easy to see that if $p,q,r,s$ are four numbers in arithmetic progression, then the Pythagorean triangles corresponding to generators (i) $u=rs,v=pq,$ (ii) $u=r(r+q),v=p(r-q),$ (iii) $u=q(r+q),v=s(r-q)$ will all have the same area $(r^2{s}^2-p^2{q}^2)pqrs.$ For example, let us take $p=1,q=2,r=3,s=4.$ Then, respectively, we have:

(A)

$u=rs=12,v=pq=2,a=u^2-v^2=140,b=2uv=48,c=u^2+v^2=148;$

(B)

$u=r(r+q)=15,v=p(r-q)=1,a=u^2-v^2=224,b=2uv=30,c=u^2+v^2=226;$

(C)

$u=q(r+q)=10,v=s(r-q)=4,a=u^2-v^2=84,b=2uv=80,c=u^2+v^2=116.$

Three Pythagorean triangles obtained from (A), (B), (C) are $(48,140,148),$$(30,224,226),(80,84,$$116).$ They all have a common area $3360.$ Notice that none of these triples is primitive. Another construction for three Pythagorean triangles having the same area was suggested by Beiler [15]: Take three sets of generators as $(u_1=u^2+uv+v^2,v_1=u^2-v^2),$$(u_2=u^2+uv+v^2,v_2=2uv+v^2),$ and $(u_3=u^2+2uv,v_3=u^2+uv+v^2).$ Then, the right triangle generated by each triple $(u_i^2-v_i^2,2u_i{v}_i,u_i^2+v_i^2)$ has common area $A=uv(2u+v)(u+2v)(u+v)(u-v)(u^2+uv+v^2).$ In particular, for $u=2,v=1$, the three Pythagorean triangles are $(40,42,58),(24,70,74),$ and $(15,112,113)$, and the common area is $840.$ Three primitive Pythagorean triples that have the same area are $(4485,5852,7373),(3059,8580,$$9109),(1380,19019,19069)$ with the area $13123110.$ This was discovered by Shedd [16] in 1945. Sets of four Pythagorean triangles with equal area are also known; the one having the smallest area is $(111,6160,6161),(231,2960,2969),(518,1320,1418)$, $(280,2442,2458)$ with area 341880 (see Beiler [15], p. 127, and Guy [17], pp. 188–190). In general, Fermat proved that for each natural number $n,$ there exist n Pythagorean triangles with different hypotenuses and the same area.

P11. 

Pythagorean triangles whose areas consists of a single digit include $(3,4,5)$ (area of six) and $(693,1924,2045)$ (area of $666666)$ (see Wells [18], p. 89).

P12. 

For $u=149,v=58$, we get a Pythagorean triple $(17284,18837,25565),$ the area of the triangle corresponding to which is $162789354,$ a number using all nine digits $1,2,\cdots ,9.$ Many such triples are known. Another such triple is $(26767,68544,73585)$ obtained by letting $u=224$ and $v=153,$ the corresponding area being $917358624.$

P13. 

There are Pythagorean triples for which the area of the corresponding triangle is represented by a number using all ten digits. One such triple is $(6660,443531,443581)$ obtained by letting $u=666$ and $v=5.$ The corresponding area is $1476958230.$ Another such triple is $(86995,226548,242677)$ obtained by putting $u=406$ and $v=279,$ the corresponding area being $9854271630.$

P14. 

In 1643, Fermat wrote a letter to Pére Marin Mersenne (1588–1648) in which he posed the problem of finding a Pythagorean triangle $(a,b,c)$ whose hypotenuse and sum of the legs were squares of integers, i.e., find integers p and q such that $c=p^2$ and $a+b=q^2.$ By using Fermat’s method of infinite descent (The earliest uses of the method of infinite descent appear in Euclid’s Elements, Book VII, Proposition 31. In this method, one assumes the existence of a solution, which is related to one or more integers, and shows the existence of another solution, which is related to smaller one or more integers, and this process infinitely continues. This leads to a contradiction.), it is found that the values $u=2150905,v=246792$ give a desired solution. In fact, we find:

$$a=u^2-v^2=4565486027761,b=2uv=1061652293520$$

and

$$c=u^2+v^2=4687298610289={2165017}^2,x+y=5627138321281={2372159}^2.$$

There exist infinitely many such Pythagorean triples, but the above values are the smallest possible.

P15. 

Two triples are called siblings if they have a common hypotenuse, e.g., (16, 63, 65), (33, 56, 65) and (13, 84, 85), (36, 77, 85) in Table 3. If we search among larger hypotenuses, we may find larger sets of siblings, e.g., there are four primitive triples with hypotenuses 1105: (47, 1104, 1105), (264, 1073, 1105), (576, 943, 1105), (744, 817, 1105). The hypotenuse 32045 has eight primitive triples: (716, 32037, 32045), (2277, 31964, 32045), (6764, 31323, 32045), (8283, 30956, 32045), (15916, 27813, 32045), (17253, 27004, 32045), (21093, 24124, 32045), (22244, 23067, 32045). A twin Pythagorean triple is a Pythagorean triple $(a,b,c)$ for which two values are consecutive integers. In the following table (see http://oeis.org/A101903), we present the number of twin Pythagorean triples, denoted as $a\left(n\right)$ with hypotenuse less than ${10}^n,n\le 24.$

$$\begin{array}{cccccccc}n& a\left(n\right)& n& a\left(n\right)& n& a\left(n\right)& n& a\left(n\right)\\ 1& 1& 2& 7& 3& 24& 4& 74\\ 5& 228& 6& 712& 7& 2243& 8& 7079\\ 9& 22370& 10& 70722& 11& 223619& 12& 707120\\ 13& 2236083& 14& 7071084& 15& 22360697& 16& 70710696\\ 17& 223606818& 18& 707106802& 19& 2236067999& 20& 7071067836\\ 21& 22360679800& 22& 70710678145& 23& 223606797778& 24& 707106781216\end{array}$$

P16. 

Let $N_h\left(n\right)$ and $N_p\left(n\right)$ denote the number of primitive Pythagorean triangles whose hypotenuses and perimeters do not exceed $n,$ respectively. In 1900, Derrick Norman Lehmer (1867–1938) proved that:

$$\underset{n\to \infty }{lim}\frac{N_h\left(n\right)}{n}=\frac{1}{2\pi }\mathrm{and}\underset{n\to \infty }{lim}\frac{N_p\left(n\right)}{n}=\frac{ln\left(2\right)}{{\pi }^2}.$$

From (9), hypotenuse $=c=u^2+v^2<n$ implies that u and v must lie in the positive quarter of the circle with radius $\sqrt{n}.$ Further, since $u>v,$$u,v$ must lie below the line $u=v;$ see Figure 2. The area of this segment is $n\pi /8.$ Ernesto Cesaro (1859–1906) in 1880 showed that the probability of $gcd(u,v)=1$ is equal to $6/{\pi }^2.$ Further, the probability of both u and v not being odd conditioned to the coprime is $2/3.$ Thus, we have:

$$N_h\left(n\right)\simeq \frac{n\pi }{8}\times \frac{6}{{\pi }^2}\times \frac{2}{3}=\frac{n}{2\pi }.$$

Similarly, we can show that $N_p\left(n\right)\simeq (nln2)/{\pi }^2.$ From these approximations, it follows that $N_h\left(1000\right)\simeq 159.15$ and $N_p\left(1000\right)\simeq 70.23.$ From Table 3, actual computation gives $N_h\left(1000\right)=158$ and $N_p\left(1000\right)=71.$ In 2002, Benito and Varona [19] proved that the number $N_{a,b}\left(n\right)$ of primitive Pythagorean triangles $(a,b,c)$ such that both the legs a and b do not exceed n is:

$$N_{a,b}\left(n\right)=\frac{4ln(1+\sqrt{2})}{{\pi }^2}n+O\left(\sqrt{n}\right).$$

On counting, we find that the exact value of $N_{a,b}\left(1000\right)=358,$ whereas the above formula gives $N_{a,b}\left(1000\right)\simeq 357.$

P17. 

Since ${(u+vi)}^2=(u^2-v^2)+i\left(2uv\right),$ it follows from (9) that the square of any complex number $u+vi$ (where $u,v$ are coprime positive integers with $u>v$) yields the legs of a primitive Pythagorean triangle. Thus, for example, ${(4+3i)}^2=7+24i$ gives $a=7$ and $b=24,$ and from (1), we have $7^2+{24}^2={25}^2,$ i.e., $(7,24,25)$ is a Pythagorean triple.

P18. 

There are Pythagorean triples (not necessarily primitive) each side of which is a Pythagorean triangular number $t_n=n(n+1)/2,$ for example $(t_{132},t_{143},t_{164})=(8778,10296,13530).$ It is not known whether infinitely many such triples exist.

P19. 

Consider any two integers u and v such that $u>v>0.$ Then, from the four integers $\{u-v,v,u,u+v\}$ known as the Pythagorean triangle generator, we can always calculate a Pythagorean triangle. For this, we take the product of the outer two integers, i.e., $(u-v)(u+v)=u^2-v^2,$ which gives one leg, then we take twice the product of the middle two integers, i.e., $2uv$, which gives the another leg, and then take the the sum of squares of the inner two integers, i.e., $u^2+v^2,$ which gives the hypotenuse of the triangle. For example, for $u=2,v=1,$ we have $\{1,1,2,3\}$, and from this, we can easily calculate the primitive Pythagorean triple $(3,4,5).$ If we take $u=3,v=1,$ then we have $\{2,1,3,4\}$, and we get the triple $(6,8,10)$, which is not primitive. Now, recall that Fibonacci numbers (first introduced by Pingala around 500 BC) are generated from the recurrence relation (due to Albert Girard 1595–1632) $F_{k+2}=F_{k+1}+F_k,F_1=1,F_2=1.$ The first few Fibonacci numbers are $1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,2584,4181,6765,10946,17711,28657.$ Now, we choose two consecutive Fibonacci numbers $v=F_{k+1}$ and $u=F_{k+2}$ and, from the recurrence relation, note that $u-v=F_{k+2}-F_{k+1}=F_k$ and $u+v=F_{k+2}+F_{k+1}=F_{k+3},$ and hence, $\{F_k,F_{k+1},F_{k+2},F_{k+3}\}$ forms a Pythagorean triangle generator. This leads to the relation (see Dujella, [20]):

$${\left(F_k{F}_{k+3}\right)}^2+{\left(2F_{k+1}{F}_{k+2}\right)}^2={(F_{k+1}^2+F_{k+2}^2)}^2,k\ge 1.$$

(12)

Now, from a well known identity $F_{k+1}^2+F_{k+2}^2=F_{2k+3}$ (see Burton [8]), (12) can be better written as:

$${\left(F_k{F}_{k+3}\right)}^2+{\left(2F_{k+1}{F}_{k+2}\right)}^2=F_{2k+3}^2,k\ge 1.$$

(13)

As an illustration, for $\{F_6=8,F_7=13,F_8=21,F_9=34\}$, Relation (12) gives:

$${(8\times 34)}^2+{(2\times 13\times 21)}^2={({13}^2+{21}^2)}^2,$$

which is the same as:

$${272}^2+{546}^2={(169+441)}^2={610}^2=F_{15}^2.$$

It does not give a primitive Pythagorean triple $(272,546,610).$ However, for $\{5,8,13,21\}$, Relation (12) leads to:

$${\left(105\right)}^2+{\left(208\right)}^2={233}^2,$$

which gives a primitive Pythagorean triple $(105,208,233).$

In conclusion, (12), or equivalently (13), furnishes primitive, as well as non-primitive Pythagorean triples. Further, it does not provide all primitive Pythagorean triples.

P20. 

To find Pythagorean triangles with all three sides’ consecutive integers, let p be a positive integer. From (9), we have either (i) $2uv=p,u^2-v^2=p+1,u^2+v^2=p+2$ or (ii) $u^2-v^2=p,2uv=p+1,u^2+v^2=p+2.$ Clearly, (i) implies that $(u^2-v^2)+(u^2+v^2)=2u^2=2p+3,$ which is impossible. Next, (ii) implies that $2u^2=2p+2,$ i.e., $u^2=p+1.$ Furthermore, we have $2uv=p+1,$ and hence, $u^2=2uv,$ i.e., $u=2v.$ Now, since u and v are relatively prime, we must have $u=2,v=1,$ and hence, $a=u^2-v^2=3,b=2uv=4,c=u^2+v^2=5.$ In conclusion, $(3,4,5)$ is the only primitive Pythagorean triple with the three sides’ consecutive integers. This fact can also be seen as follows: If $(a,a+1,a+2)$ is a Pythagorean triple, then $a^2+{(a+1)}^2={(a+2)}^2,$ which is the same as $a^2-2a-3=(a-3)(a+1)=0,$ and hence, $a=3.$ Similarly, it follows that the only Pythagorean triangles with sides in arithmetic progression are those with sides $3n,4n,5n,n=1,2,3,\cdots .$

P21. 

To find Pythagorean triangles in which the hypotenuse exceeds the larger leg by one, we shall show that Formula (4) generates all such Pythagorean triangles. Since (9) generates all primitive Pythagorean triangles, either (i) $u^2+v^2=u^2-v^2+1$ or (ii) $u^2+v^2=2uv+1.$ However, (i) leads to $2v^2=1,$ which is impossible. Now, (ii) is the same as ${(u-v)}^2=1,$ which implies that $u=v+1.$ Letting $v=n,$ then $u=n+1.$ Putting this u and v in (9), we obtain (4). Thus, there are infinite such Pythagorean triangles.

In Dudley’s book [21], page 127, the following problem was given: Prove that if the sum of two consecutive integers is a square, then the smaller is the leg and the larger the hypotenuse of a Pythagorean triangle. His obvious solution was $k+(k+1)=m^2$ implying that $k^2+m^2={(k+1)}^2.$ However, the question is for what integers k and $m,k+(k+1)=m^2.$ From P21, we notice that the only choice is $k=2n^2+2n$ and $m=(2n+1).$

P22. 

To find Pythagorean triangles with consecutive legs, from (9), it is necessary that either (i) $u^2-v^2=2uv+1$ or (ii) $2uv=u^2-v^2+1.$ In Case (i), it follows that ${(u-v)}^2=2v^2+1,$ which is the same as ${(u-v)}^2-2v^2=1.$ Similarly, Case (ii) leads to the equation ${(u-v)}^2-2v^2=-1.$ Thus, in Case (i), we need to find integer solutions of the equation $x^2-2y^2=1,$ whereas in Case (ii) of the equation, $x^2-2y^2=-1.$ In the literature, these equations are mistakenly known as Pell’s equation. In fact, the English mathematician John Pell (1611–1685) has nothing to do with these equations. Euler mistakenly attributed to Pell a solution method that had in fact been found by another English mathematician, William Brouncker (1620–1684), in response to a challenge by Fermat. In reality, second order indeterminate equations, of the form $N{x}^2+1=y^2$ where N is an integer, were first discussed by Brahmagupta (born 30 BC). For their solution, he employed his “Bhavana” method and showed that they have infinitely many solutions. Unfortunately, it has been recorded that Fermat was the first to assert that it has infinitely many solutions. His celebrated work Br$\overline{a}$hmasphutasiddh$\overline{a}$nta was translated into English by Henry Thomas Colebrooke (1765–1837). We shall use the inductive method to show that all solutions of these equations can be generated by the recurrence equations:

$$\begin{array}{ccc}{x}_{n+1}\hfill & =\hfill & 3x_n+4y_n\hfill \\ y_{n+1}\hfill & =\hfill & 2x_n+3y_n,n\ge 1.\hfill \end{array}$$

(14)

For this, we assume the existence of the minimal solution (known as the fundamental solution) $(x_1,y_1)$ of the concerned equation and assume that $(x_n,y_n)$ is also a solution, then it follows that:

$$x_{n+1}^2-2y_{n+1}^2={(3x_n+4y_n)}^2-2{(2x_n+3y_n)}^2=x_n^2-2y_n^2,$$

and this shows that $(x_{n+1},y_{n+1})$ is also a solution of the equation. For the equation $x^2-2y^2=1$, the minimal solution (by inspection) is (3,2), and the next three solutions obtained from (14) are (17,12), (99,70), and (577,408). Similarly, for the equation $x^2-2y^2=-1$, the minimal solution of (1,1) and the next three solutions generated from (14) are (7,5), (41,29), and (239,169). In the following table, we use these eight values to record $u(=x+y),v(=y),u^2-v^2,2uv,u^2+v^2$ and the corresponding Pythagorean triples. From the table, it is clear that the numbers are increasing very rapidly, but still, such triples are infinite.

$$\begin{array}{cccccc}u& v& u^2-v^2& 2uv& u^2+v^2& (a,b,c)\\ 2& 1& 3& 4& 5& (3,4,5)\\ 5& 2& 21& 20& 29& (20,21,29)\\ 12& 5& 119& 120& 169& (119,120,169)\\ 29& 12& 697& 696& 985& (696,697,985)\\ 70& 29& 4059& 4060& 5741& (4059,4060,5741)\\ 169& 70& 23661& 23660& 33461& (23660,23661,33461)\\ 408& 169& 137903& 137904& 195025& (137903,137904,195025)\\ 985& 408& 803761& 803760& 1136689& (803760,803761,1136689)\end{array}$$

Upon scanning the data in Table 3, we notice that triples satisfying $c-b=1$ are more dense than those satisfying $b-a=1.$ The fact that there are infinitely many Pythagorean triples of this type can also be shown rather easily: If $(a,a+1,c)$ happens to be a Pythagorean triple, so is $(3a+2c+1,3a+2c+2,4a+3c+2).$ Indeed, we have:

$$\begin{array}{cc}{(3a+2c+1)}^2+{(3a+2c+2)}^2\hfill & = 18a^2+8c^2+5+24ac+18a+12c\hfill \\ & = 9(a^2+{(a+1)}^2)+8c^2+24ac+12c-4\hfill \\ & = 17c^2+24ac+12c-4={(4a+3c+2)}^2.\hfill \end{array}$$

Diophantus set the problem of finding a number p such that both $10p+9$ and $5p+4$ are squares. Letting $10p+9=x^2$ and $5p+4=y^2,$ we get the same equation $x^2-2y^2=1,$ for which the minimal solution (which gives the nonzero solution) is $(17,12).$ Solving the equations $10p+9={17}^2$ and $5p+4={12}^2,$ we find $x=28.$

P23. 

Diophantus as a problem asked to find a Pythagorean triangle in which the hypotenuse minus each of the legs is a cube. His answer was $(40,96,104),$ which leads to the required primitive Pythagorean triple $(5,12,13).$ From (9), we note that we need to find the solutions of the equations $c-a=p^3,c-b=q^3,$ where p and q are some positive integers. However, since $c-a=2v^2$ and $c-b={(u-v)}^2$ from the equation $c-a=2v^2=p^3$, we must have $v=2,$ and now from the equation $c-b={(u-v)}^2={(u-2)}^2=q^3,$ it follows that $u-2=k^3$ or $u=k^3+2,$ where k is any positive integer. Thus, the required members of all Pythagorean triples are $a={(k^3+2)}^2-2^2,b=2^2(k^3+2),c={(k^3+2)}^2+2^2,k\ge 1$ with $c-a=2^3$ and $c-b={\left(k^2\right)}^3.$ For $k=1,2,3$, we get the triples $(5,12,13),(40,96,104),$ and $(116,837,845),$ i.e., we get primitive, as well as non-primitive Pythagorean triples.

P24. 

To find primitive Pythagorean triangles, one of whose legs is a perfect square, we need to solve the equation ${\left(x^2\right)}^2+b^2=c^2,$ which is the same as $x^4=(c+b)(c-b).$ We recall that $(c,b)=1$ and c is always odd, so there are two possible cases to consider: (i) b is even; and (ii) b is odd. In Case (i), equation $x^4=(c+b)(c-b)$ holds provided there exist odd integers p and q such that $p>q$ and $c+b=p^4,c-b=q^4$ (see Step 4 above), and hence:

$$c=\frac{p^4+q^4}{2},b=\frac{p^4-q^4}{2},a=x^2=p^2{q}^2.$$

We present some desired triples in the following table.

$$\begin{array}{ccccc}p& q& a& b& c\\ 3& 1& 9=3^2& 40& 41\\ 5& 1& 25=5^2& 312& 313\\ 5& 3& 225={15}^2& 272& 353\\ 7& 1& 49=7^2& 1200& 1201\end{array}$$

Clearly, there exist infinitely many Pythagorean triples whose odd member is a perfect square.

In Case (ii), we can choose $c+b=2^3{s}^4,c-b=2t^4,$ where t is odd. These relations give:

$$c=2^2{s}^4+t^4,b=2^2{s}^4-t^4,a=x^2=2^2{s}^2{t}^2.$$

Using these relations, we compute some Pythagorean triples in the following table.

$$\begin{array}{cccccc}s& t& a& b& c& (a,b,c)\\ 1& 1& 4=2^2& 3& 5& (3,4,5)\\ 2& 1& 16=4^2& 63& 65& (16,63,65)\\ 3& 1& 36=6^2& 323& 325& (36,323,325)\\ 4& 1& 64=8^2& 1023& 1025& (64,1023,1025)\\ 4& 3& 576={24}^2& 943& 1105& (576,943,1105)\end{array}$$

Clearly, there exist infinitely many Pythagorean triples whose even member is a perfect square.

P25. 

To find primitive Pythagorean triangles whose hypotenuse is a perfect square, we need to deal with the equation $a^2+b^2={\left(z^2\right)}^2,$ which is the same as $(a+ib)(a-ib)=z^4.$ Now, since $gcd(a,b)=1,$ there exist integers p and q such that $(p,q)=1$ and $a+ib={(p+iq)}^4$ also $a-ib={(p-iq)}^4.$ Next, comparing the real and imaginary parts, we find:

$$a=|p^4+q^4-6p^2{q}^2|\mathrm{and}b=4pq|p^2-q^2|;$$

here, the modulus sign is taken without loss of generality (we need $a^2$ and $b^2$). Then, we also have:

$$c={(p+iq)}^2{(p-iq)}^2={(p^2+q^2)}^2.$$

We present some required triples in the following table.

$$\begin{array}{cccccc}p& q& a& b& c& (a,b,c)\\ 2& 1& 7& 24& 25=5^2& (7,24,25)\\ 3& 2& 119& 120& 169={13}^2& (119,120,169)\\ 4& 1& 161& 240& 289={17}^2& (161,240,289)\\ 4& 3& 527& 336& 625={25}^2& (336,527,625)\\ 5& 1& 476& 480& 676={26}^2& (119,120,169)\\ 5& 2& 41& 840& 841={29}^2& (41,840,841)\\ 5& 3& 644& 960& 1156={34}^2& (161,240,289)\\ 5& 4& 1519& 720& 1681={41}^2& (1519,720,1681)\end{array}$$

Note that in the above table, $p=3,q=2$ and $p=5,q=1$ give the same primitive Pythagorean triple. The same holds for $p=4,q=1$ and $p=5,q=3.$

P26. 

To find primitive Pythagorean triangles $L_p\left(n\right)$ whose one leg $n>0$ is given, there are two cases to consider: (i) n is odd, then $u^2-v^2=n;$ or (ii) n is even, then $2uv=n.$ The number of integer solutions of these equations depends on the prime factorization of $n.$ Let $n=2^s{p}_1^{s_1}\cdots p_k^{s_k},$ where $p_1,p_2,\cdots ,p_k$ are distinct primes. If $s=0,n$ is odd and $u>v,$ then n can be factored as a product of two relatively prime factors in $2^{k-1}$ ways. Corresponding to each such way, $u^2-v^2=n$ has exactly one solution in positive integers, and hence, there will be $2^{k-1}$ solutions. If $s=1,$ then n is an odd multiple of two, and the equation $2uv=n$ does not have any solution in integers because $2uv$ is a multiple of four. If $s\ge 2$ and $u>v$, then the number of ways in which n can be factored into a pair of relatively prime factors is $2^{(k+1)-1},$ i.e., $2^k,$ and therefore, there are $2^k$ solutions of $2uv=n$ with $u>v.$ Summarizing these arguments, we have the following result: If n is of the form $4p+2,$ then $L_p\left(n\right)=0$ (see P7). If n is not of this form, then $L_p\left(n\right)=2^{q-1},$ where q is the number of distinct primes occurring in the prime factorization of $n.$ As examples, consider the cases $n=60,65,75,86.$ Since $60=2^2\times 3\times 5,$ the number of primes occurring in the factorization is $q=3$, and so, there are $2^{3-1},$ i.e., four primitive Pythagorean triangles having 60 as a leg. From Table 3, these triples are $(11,60,61),(60,91,109),(60,221,229),$ and $(60,899,901).$ Since $65=5\times 13,q=2$, and so, there are $2^{2-1}=2$ primitive triangles having 65 as a leg. These triples are $(65,72,97)$ and $(65,2112,2113).$ Since $75=3\times 5^2,q=2$, and so, there are $2^{2-1}=2$ primitive Pythagorean triangles having 75 as a leg. These triples are $(75,308,317)$ and $(75,2812,2813).$ Since $86=4\left(21\right)+2$, there are no primitive Pythagorean triangles having 86 as a leg.

In a similar way (see Beiler [15]), we can find the number of primitive Pythagorean triangles $H_p\left(n\right)$ having n as a hypotenuse. We factorize n as:

$$n=2^{a_0}\left(p_1^{a_1}\cdots p_s^{a_s}\right)\left(q_1^{b_1}\cdots q_t^{b_t}\right),$$

where $p^{\prime }s$ are of the form $4r-1$ and $q^{\prime }s$ are of the form $4r+1.$ Then,

$$H_p\left(n\right)=\left\{\begin{array}{cc}{2}^{t-1}\hfill & \mathrm{if}s=0\mathrm{and}{a}_0=0\hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

As an example, we consider $65,75,325,$ and $389.$ Since $65=(4+1)(4\times 3+1),s=0,a_0=0$, and $t=2$, so $H_p\left(65\right)=2^{2-1}=2.$ From Table 3, these triples are $(16,63,65)$ and $(33,56,65).$ Since $75=(4-1){(4+1)}^2$, $s=1,a_0=0$, so $H_p\left(75\right)=0.$ Since $325={(4+1)}^2(4\times 3+1),s=0,a_0=0$ and $t=2$, so $H_p\left(325\right)=2.$ From Table 3, these triples are $(36,323,325)$ and $(204,253,325).$ Since $389=(4\times 97+1),s=0,a_0=0$ and $t=1$, so $H_p\left(389\right)=1.$ From Table 3, this triple is $(189,340,389).$

Combining the above results, we can find the total number of ways in which a given n may be either a leg or hypotenuse of a primitive Pythagorean triangle as $T_p\left(n\right)=L_p\left(n\right)+H_p\left(n\right).$ As an example, we consider $325.$ Since $325=5^2\times 13={(4+1)}^2(4\times 3+1)$, it follows that $L_p\left(325\right)=2$ and $H_p\left(325\right)=2,$ and hence, $T_p\left(325\right)=2+2=4.$ Indeed, the triples are $(228,325,397),(325,52812,52813),$$(36,323,325),$ and $(204,253,325).$

If $n=2^m,m\ge 2$, then $L_p\left(2^m\right)=1$ and $H_p\left(2^m\right)=0.$ To find the unique primitive Pythagorean triangle whose one leg is $2^m,$ from (9), it follows that $b=2uv=2^m$ or $uv=2^{m-1}.$ Thus, from Step 4 and the fact that $u>v,$ we have $u=2^{m-1}$ and $v=1.$ Hence, the members of the required triple are $2^{2(m-1)}-1,2^m,2^{2(m-1)}+1,$ which for $p=2$ and $p=3,$ respectively, give the primitive Pythagorean triples as $(3,2^2,5)$ and $(2^3,15,17).$ Now, we shall show that there are exactly $m-2,m\ge 3$ non-primitive triangles whose one leg is $2^m.$ Clearly, for a non-primitive triple, the members are:

$$a=d(u^2-v^2),b=d\left(2uv\right),c=d(u^2+v^2),d\ge 2.$$

If $2^m=d(u^2-v^2),$ then from the fact that $u>v,$ and u and v are of different parity $(u^2-v^2)\ge 3$ and odd. Thus, it is necessary that $d=2^{m}D,D\ge 1.$ However, then $2^m=2^{m}D(u^2-v^2),$ which means $1=D(u^2-v^2).$ However, this is impossible. Similarly, we can show that $2^m\ne d(u^2+v^2).$ Thus, the only possibility left is $2^m=d\left(2uv\right)$ or $2^{m-1}=d\left(uv\right),$ which implies that there exists some $2^k=d,0\le k\le m-1.$ However, the cases $k=0$ and $k=m-1$ can be ruled out. Indeed, for $k=0,$ it gives $d=1,$ but we have $d\ge 2;$ and the fact that $uv$ is even assures that k cannot be $m-1.$ In conclusion, we have $uv=2^{m-k-1},1\le k\le m-2,$ which implies that $u=2^{m-k-1},v=1.$ This leads to the following members of the non-primitive triples:

$$2^m,2^k(2^{2(m-k-1)}-1),2^k(2^{2(m-k-1)}-1),k=1,2,\cdots ,m-2.$$

For $m=4$, two non-primitive triples are $(2^4,30,34),(12,2^4,20)$, and for $m=5$, three non-primitive triples are $(2^5,126,130),(2^5,60,68),(24,2^5,40).$ This corrects a minor error in the work of Zelator [22] (also see [23]) and supplements the conclusion of Problem 5 on page 240 in the book of Burton [8].

P27. 

In a triangle, we can draw a circle touching all three sides, and this circle is called in-circle with the radius as in-radius denoted as r and the center as the in-center. The in-radius of a Pythagorean triangle $(a,b,c)$ satisfies (see Burton [8], page 239) the relation $r(a+b+c)=2\Delta =ab$ (two formulae for r in terms of the sides $a,b,c$ were known to Liu Hui; see Nine Chapters on the Mathematical Arts). In this relation, substituting $a=k(u^2-v^2),b=k\left(2uv\right),c=k(u^2+v^2)$ (here, $k>0$ is an integer), we get $r=k(u-v)v,$ which shows that the in-radius of a Pythagorean triangle is an integer. The number of distinct primitive Pythagorean triangles having a common in-radius r depends on the number of distinct prime divisors of $r.$ If the prime factorization of r contains n distinct odd primes, then there exist $2^n$ distinct primitive Pythagorean triangles having a common in-radius r (see Robbins [24] and Omland [25]). For example, we consider $u=985,v=408,k=1$, so that $r=577\times 408$, whose prime factors are $2^3\times 3\times 17\times 577,$ and hence, there exist exactly $8(=2^3)$ distinct primitive Pythagorean triangles having in-radius $577\times 408.$ One of such triples is $(803760,803761,1136689).$

In addition, the total number $N\left(r\right)$ of distinct Pythagorean triangles (not necessarily primitive) having a given in-radius r can be determined by writing down the prime factorization of $r.$ It is also known that if $r=2^s{p}_1^{s_1}{p}_2^{s_2}\cdots ,p_n^{s_n},$ where $p_1,p_2,\cdots ,p_n$ are distinct odd primes, then:

$$N\left(r\right)=(s+1)(2s_1+1)\cdots (2s_n+1).$$

For $r=577\times 408=2^3\times 3\times 17\times 577,N\left(r\right)=(3+1)(2+1)(2+1)(2+1)=108.$

P28. 

It is possible to construct Pythagorean triples (not necessarily primitive) by factoring c into smaller factors, each of which is itself a sum of two squares. For this, we need the following well known result from elementary number theory (see Burton [8] and Grosswald [26]): A positive integer c is representable as the sum of two squares if and only if each of its prime factors of the form $4k+3$ occurs to an even power (this theorem supplements Fermat’s theorem: an odd prime p is uniquely expressible as a sum of two squares if and only if p is of the form $4k+1$). For example, $5=1^2+2^2,10=3^2+1^2,17=4^2+1^2$, $18=3^2+3^2$; however, the numbers $3,6,7,11,19$ cannot be written as the sum of two squares. We further note that 50 is the smallest number that can be written as a sum of two squares in two ways, namely $50=7^2+1^2=5^2+5^2;$ the next such integer is $65=1^2+8^2=4^2+7^2.$

For the given $a,b,c,$ and d real numbers, we shall also need the following Diophantus identities (these identities are also known in the literature as Brahmagupta–Fibonacci identities):

$$(a^2+b^2)(c^2+d^2)={(ac+bd)}^2+{(ad-bc)}^2$$

(15)

$$(a^2+b^2)(c^2+d^2)={(ac-bd)}^2+{(ad+bc)}^2.$$

(16)

These equalities can be proven directly by squaring the right sides or using the fact:

$${|a\mp bi|}^2{|c+di|}^2={|(ac\pm bd)+i(ad\mp bc)|}^2.$$

Now, we consider the number:

$$493=17\times 29=(1^2+4^2)(2^2+5^2)$$

(17)

for which Equalities (15) and (16) give:

$$493={(1\times 2+4\times 5)}^2+(1\times 5-4\times 2)={22}^2+3^2$$

(18)

and:

$$493={(1\times 2-4\times 5)}^2+(1\times 5+4\times 2)={18}^2+{13}^2.$$

(19)

Equalities (18) and (19), in view of (15) and (16), respectively, give:

$${493}^2=(3^2+{22}^2){({13}^2+18)}^2={(3\times 13+22\times 18)}^2+{(3\times 18-22\times 13)}^2={435}^2+{232}^2$$

and:

$${493}^2=(3^2+{22}^2){({13}^2+18)}^2={(3\times 13-22\times 18)}^2+{(3\times 18+22\times 13)}^2={357}^2+{340}^2.$$

This gives the Pythagorean triples $(232,435,493)$ and $(340,357,493),$ which are not primitive. In fact, dividing these triples, respectively, by 29 and $17,$ we get the primitive Pythagorean triples $(8,15,17)$ and $(20,21,29).$

Notice that we also have:

$$\begin{array}{cc}{493}^2\hfill & = {17}^2\times {29}^2=(8^2+{15}^2)\times ({20}^2+{21}^2)\hfill \\ \hfill \\ & = {(8\times 20+15\times 21)}^2+{(8\times 21-15\times 20)}^2={475}^2+{132}^2,\hfill \end{array}$$

and:

$${493}^2={(8\times 20-15\times 21)}^2+{(8\times 21+15\times 20)}^2={155}^2+{468}^2.$$

This gives the primitive Pythagorean triples $(132,475,493)$ and $(155,468,493)$ (see Table 3).

P29. 

In 1934, Berggren [27] introduced three matrices with the same values in each position, but differing in sign $A_i,i=1,2,3,$ where:

$$A_1=\left(\begin{array}{ccc}\hfill 1& \hfill 2& \hfill 2\\ \hfill -2& \hfill -1& \hfill -2\\ \hfill 2& \hfill 2& \hfill 3\end{array}\right),A_2=\left(\begin{array}{ccc}\hfill 1& \hfill 2& \hfill 2\\ \hfill 2& \hfill 1& \hfill 2\\ \hfill 2& \hfill 2& \hfill 3\end{array}\right),A_3=\left(\begin{array}{ccc}\hfill -1& \hfill -2& \hfill -2\\ \hfill 2& \hfill 1& \hfill 2\\ \hfill 2& \hfill 2& \hfill 3\end{array}\right)$$

and showed that from a given primitive Pythagorean triple $(a_0,b_0,c_0)$, three new primitive Pythagorean triples $(a_i,b_i,c_i),i=1,2,3$ can be generated by:

$$(a_i,b_i,c_i)=(a_0,b_0,c_0)A_i,i=1,2,3.$$

(20)

He also showed that by using these three matrices, all primitive Pythagorean triples can be generated from the triple $(a_0,b_0,c_0)=(3,4,5).$ A simple calculation shows that with this triple $(a_0,b_0,c_0),$ (20) gives $(5,12,13),$$(21,20,29)$, which we have agreed to write as $(20,21,29),$ and $(15,8,17)$, which we have agreed to write as $(8,15,17).$ Now, if we take $(a_0,b_0,c_0)=(5,12,13),$ then (20) generates $(7,24,25),$$(48,55,73),(28,45,53).$ Thus, $(7,24,25)=(3,4,5)A_1{A}_1.$ In fact, Hall [28] and Roberts [29] proved that $(a,b,c)$ is a primitive Pythagorean triple if and only if $(a,b,c)=(3,4,5)U,$ where U is a finite product of the matrices $A_1,A_2,A_3.$ In other words, the triple $(3,4,5)$ is the parent of all primitive Pythagorean triples.

P30. 

In 2008, Price [30] found three new matrices:

$$A_1^{\prime }=\left(\begin{array}{ccc}\hfill 2& \hfill -2& \hfill -2\\ \hfill 1& \hfill 2& \hfill 1\\ \hfill -1& \hfill 2& \hfill 3\end{array}\right),A_2^{\prime }=\left(\begin{array}{ccc}\hfill 2& \hfill 2& \hfill 2\\ \hfill 1& \hfill -2& \hfill -1\\ \hfill 1& \hfill 2& \hfill 3\end{array}\right),A_3^{\prime }=\left(\begin{array}{ccc}\hfill 2& \hfill 2& \hfill 2\\ \hfill -1& \hfill 2& \hfill 1\\ \hfill 1& \hfill 2& \hfill 3\end{array}\right)$$

and showed that like (20):

$$(a_i,b_i,c_i)=(a_0,b_0,c_0)A_i^{\prime },i=1,2,3.$$

(21)

also produce all primitive Pythagorean triples. However, the three new triples obtained from $\left(21\right)$ may not be the same as calculated from (20). As an example, we find that from $(a_0,b_0,c_0)=(3,4,5),\left(21\right)$ produces the new triples $(5,12,13),(8,15,17),$ and $(7,24,25).$ Further, with $(a_0,b_0,c_0)=(5,12,13),\left(21\right)$ gives $(9,40,41),(12,35,37),$ and $(11,60,61).$

P31. 

In 1994, Saunders and Randall [31] established the following three new matrices:

$$B_1=\left(\begin{array}{cc}\hfill 2& \hfill 1\\ \hfill -1& \hfill 0\end{array}\right),B_2=\left(\begin{array}{cc}\hfill 2& \hfill 1\\ \hfill 1& \hfill 0\end{array}\right),B_3=\left(\begin{array}{cc}\hfill 1& \hfill 0\\ \hfill 2& \hfill 1\end{array}\right)$$

and showed that from a given generator $(u,v)$ of the Pythagorean triple, three new generators that preserve coprimeness and opposite parity can be obtained by:

$$(U_i,V_i)=(u,v)B_i,i=1,2,3.$$

For this, it suffices to show that each $(U_1,V_1)=(2u-v,u),(U_2,V_2)=(2u+v,u),(U_3,V_3)=(u+2v,v)$ generates the Pythagorean triple, i.e., $(a_i=U_i^2-V_i^2,b_i=2U_i{V}_i,c_i=U_i^2+V_i^2),i=1,2,3$ are Pythagorean triples. In particular, for $u=2,v=1$, we have $(U_1,V_1)=(3,2),(U_2,V_2)=(5,2),(U_3,V_3)=(4,1)$, and these respectively generate Pythagorean triples $(5,12,13),(20,21,29),(8,15,17).$

P32. 

Consider the famous tournament problem, which was posed to Fibonacci by Master John of Palermo, a member of the entourage of the Holy Roman Emperor Frederick II: Find a number x such that both $x^2+5$ and $x^2-5$ are squares of rational numbers, i.e.,

$$x^2+5=a^2\mathrm{and}{x}^2-5=b^2.$$

(22)

We will see that the solution requires Pythagorean triples. We express $x,a,$ and b as fractions with a common denominator:

$$x=\frac{x_1}{d},a=\frac{a_1}{d},b=\frac{b_1}{d}.$$

Substituting these values in Equation (22) and multiplying throughout by $d^2,$ we get the equations:

$$x_1^2+5d^2=a_1^2,x_1^2-5d^2=b_1^2.$$

(23)

Subtracting the second equation from the first, we obtain:

$$10d^2=a_1^2-b_1^2=(a_1+b_1)(a_1-b_1).$$

Since the left-hand side is even, both $a_1$ and $b_1$ must be even or odd. In either case, $a_1-b_1$ is an even integer, say $a_1-b_1=2k,$ from this, it follows that $a_1+b_1=5d^2/k.$ Now, solving the last two equations, we find:

$$a_1=\frac{5d^2}{2k}+k,b_1=\frac{5d^2}{2k}-k.$$

Substituting these expressions in (23), we get:

$$x_1^2+5d^2={\left(\frac{5d^2}{2k}+k\right)}^2={\left(\frac{5d^2}{2k}\right)}^2+5d^2+k^2,$$

$$x_1^2-5d^2={\left(\frac{5d^2}{2k}-k\right)}^2={\left(\frac{5d^2}{2k}\right)}^2-5d^2+k^2,$$

which on addition yields the single condition:

$${\left(\frac{5d^2}{2k}\right)}^2+k^2=x_1^2.$$

Thus, the three numbers $5d^2/2k,k$, and $x_1$ form a primitive Pythagorean triple and hence can be written as:

$$\frac{5d^2}{2k}=u^2-v^2,k=2uv,x_1=u^2+v^2,$$

where the positive integers u and v are such that $u>v,u$ and v are of opposite parity, and they are coprime. Now, to eliminate $k,$ we take the product of the first two of these equations, to obtain:

$$5d^2=4uv(u^2-v^2).$$

Clearly, we need integers u and v, which will make the right-hand side of this equation five times a perfect square. For this, we set $u=5,$ so that the condition reduces to:

$$d^2=4v(5^2-v^2).$$

Evidently, the right-hand side becomes a square when $v=4:$

$$d^2=4·4(5^2-4^2)=16·9={12}^2.$$

These values for u and v lead to:

$$x_1=u^2+v^2=5^2+4^2=41.$$

Putting these pieces together, we get:

$$x=\frac{x_1}{d}=\frac{41}{12}$$

as a solution to Fibonacci’s tournament problem.

P33. 

For the construction of right-angled triangles whose sides are rational numbers or rational cyclic quadrilaterals (all vertices lie on a single circle), Brahmagupta gave the solution (9), where u and v are unequal rational numbers. In particular, for a given rational side $a,$ Brahmagupta’s solution is:

$$\frac{1}{2}\left(\frac{a^2}{n}-n\right),a,\frac{1}{2}\left(\frac{a^2}{n}+n\right),$$

(24)

where n is a rational number different from zero. Bh$\overline{a}$skaraand Mah$\overline{a}$v$\overline{i}$ra (817–875) gave the solution:

$$\frac{2ma}{m^2-1},a,\frac{m^2+1}{m^2-1}a,$$

(25)

where m is any rational number other than $\pm 1.$

The eighth problem in the second book of the Arithmetica of Diophantus is to express 16 as a sum of two rational squares. For this, in the identity:

$${\left[a(m^2+1)\right]}^2={\left(2am\right)}^2+{\left[a(m^2-1)\right]}^2,$$

which follows from (25), he used $a=16/5$ and $m=1/2$ and obtained $16={(16/5)}^2+{(12/5)}^2.$

According to Bibhtibhushan Datta (1888–1958) (see [32]) and Puttaswamy [33], Karavindaswami’s (nothing seems to be known about him except a summary of his mathematical work) solution is:

$$\frac{m^2+2m}{2m+2}a,a,\frac{m^2+2m+2}{2m+2}a,$$

(26)

where m is any rational number other than $-1.$ It is interesting to note that these solutions can easily be deduced from (24). Indeed, for $n=\frac{m-1}{m+1}a,$ (24) becomes (25), whereas for $n=\frac{a}{m+1}$, it reduces to (26).

For the given rational hypotenuse $c,$ Mah$\overline{a}$v$\overline{i}$ra constructed a rational right-angled triangle. His solution is:

$$\frac{2mnc}{m^2+n^2},\frac{m^2-n^2}{m^2+n^2}c,c,$$

whereas Bh$\overline{a}$skara gives the solution as:

$$\frac{2qc}{q^2+1},\frac{q^2-1}{q^2+1}c,c,$$

which readily follows from Mah$\overline{a}$v$\overline{i}$ra’s solution by putting $q=m/n.$ These solutions were later attributed to Fibonacci and Francois Viéte (1540–1603), respectively.

P34. 

For each $n\ge 1$, equation $c^n=a^2+b^2$ has an infinite number of solutions. Case $n=1$ has been discussed in P28, whereas for $n=2$, it is Pythagorean Relation (1). For $n\ge 3,$ we begin with an arbitrary c, which can be written as the sum of two squares, i.e.,

$$c=p^2+q^2={|p+iq|}^2,$$

and note that:

$$\begin{array}{ccc}{c}^n={\left|{(p+iq)}^n\right|}^2\hfill & = \hfill & {\displaystyle {\left|\sum _{k=0}^n\left(\genfrac{}{}{0pt}{}{n}{k}\right)p^{n-k}{\left(iq\right)}^k\right|}^2}\hfill \\ \hfill \\ & = \hfill & {\displaystyle {\left|Re\left(\sum _{k=0}^n\left(\genfrac{}{}{0pt}{}{n}{k}\right)p^{n-k}{\left(iq\right)}^k\right)\right|}^2+{\left|\mathrm{Im}\left(\sum _{k=0}^n\left(\genfrac{}{}{0pt}{}{n}{k}\right)p^{n-k}{\left(iq\right)}^k\right)\right|}^2.}\hfill \end{array}$$

In particular, we have:

$$c^3={(p^3-3p{q}^2)}^2+{(3p^{2}q-q^3)}^2$$

and:

$$c^4={(p^4-6p^2{q}^2+q^4)}^2+{(4p^{3}q-4p{q}^3)}^2.$$

For $c=5=2^2+1^2,$ the above relations, respectively, give $5^3=2^2+{11}^2$ and $5^4=7^2+{24}^2.$

Now, we shall show that for each $n\ge 1$, equation $c^2=a^n+b^2$ has an infinite number of solutions. We assume that c and b are relatively prime and rewrite the equation as $a^n=c^2-b^2=(c-b)(c+b).$ Then, there exist integers u and v such that $c-b=u^n$ and $c+b=v^n.$ Hence, $c=(u^n+v^n)/2$ and $b=(v^n-u^n)/2.$ In particular, if a is odd, we can choose $v=a$ and $u=1.$ As a simple example, we consider Pythagorean consecutive triangular numbers $t_n=n(n+1)/2,t_{n-1}=(n-1)n/2.$ Since $t_n^2-t_{n-1}^2=n^3,$ the equation $c^2=a^3+b^2$ has an infinite number of solutions. Similarly, we can show that for each $n\ge 1$, equation $c^2=a^2+b^n$ has an infinite number of solutions.

P35. 

In the literature, Fermat’s claim (intellectual curiosity) of 1637, found by his son Samuel, that the equation:

$$a^n+b^n=c^n$$

(27)

has no positive integer solutions for $a,b,$ and c if $n>2$ is known as Fermat’s last theorem (“last” because it took longer than any other conjecture by Fermat to be proven, finally by Andrew Wiles (born 1953) in 1994). Thus, a cube cannot be written as the sum of two smaller cubes; a fourth power cannot be written as the sum of two fourth powers, and so on. In his personal copy of Diophantus’s Arithmetica (translated by Claude Bachet, 1581–1638), Fermat just commented that he had discovered a “truly marvelous” proof of this fact, but the margin of the book was too narrow for him to jot it down! It is believed that Fermat himself had a proof for $n=4,$ and Euler in 1753 (published in 1770) succeeded in the more difficult case of $n=3$ (this case can also be settled by using the method of infinite descent, e.g., see Carmichael [12,13]). In the 1820s, Marie-Sophie Germain (1776–1831) showed that (27) has no solution when $abc$ is not divisible by n for n any odd prime less than $100;$ however, her method did not help to prove the theorem in the case when one of $a,b,c$ is divisible by $n.$ In 1825, Legendre and Peter Gustav Lejeune Dirichlet (1805–1859) independently succeeded in proving the theorem for $n=5.$ In 1832, Dirichlet settled the theorem for $n=14,$ and in 1839, Gabriel Lamé (1795–1870) resolved the problem for $n=7.$ For each of these cases, several alternative proofs were developed later by many prominent mathematicians including Gauss for $n=3,$ but none of these proofs worked for the general case. A significant contribution toward a proof of Fermat’s last theorem was made during 1850–1861 by the German mathematician Ernst Eduard Kummer (1810–1893). Inspired by Gauss’s proof for the case $n=3$ using algebraic integers, Kummer invented the concept of ideal numbers (different from the ideal number 5040 due to Plato), which is destined to play a key role in the development of modern algebra and number theory. Using this, Kummer proved that Fermat’s last theorem holds when n is a prime number of a certain type, known as regular primes. The power of Kummer’s result is indicated by the fact that the smallest prime that is not regular is $37.$ Thus, the cases $n=3,5,7,11,13,17,19,23,29,$ and 31 (and many others) are disposed of all at once. In fact, the only primes less than 100 that are not regular are $37,59$ and $67.$ Unfortunately, there are still infinitely many primes that are not regular. In 1908, a sensational announcement was made that a prize of 100,000 marks would be awarded for the complete solution of Fermat’s problem. The funds for this prize, which was the largest ever offered in mathematics, were bequeathed by a German mathematician Paul Friedrich Wolfskehl (1856–1906) to the “Konigliche Gesellschaft der Wissenschaften in Göttingen” for this purpose. This announcement drew so much attention that during a brief span of three years (1908–1911), over a thousand papers containing supposed solutions reached the Committee. Unfortunately, all were wrong. Since then, the number of papers submitted for this prize became so large that they would fill a library. The Committee then very wisely included as one of the conditions that the article be printed, otherwise the number would have been still larger. In 1983, Gerd Faltings (born 1954) proved a very decisive result: for $n>2$, Equation (27) can have at most a finite number of integer solutions. In 1988, the world thought that the Japanese mathematician Yoichi Miyaoka (born 1949), working at the Max Plank Institute in Bonn, Germany, might have discovered the proof of the theorem. However, his announcement turned out to be premature, as a few weeks later, holes were found in his argument that could not be repaired. Episodes like this had indeed occurred many times in the three-and-a-half century history of this famous problem. It is said that the famous number theorist Edmund Georg Hermann Landau (1877–1938) had printed post cards that read, “Dear Sir/Madam: Your attempted proof of Fermat’s Theorem has been received and is herewith returned. The mistake is on page —–, line —–.” Landau would give them to his students to fill in the missing numbers. From 1977 to 1992, with the help of computers, Fermat’s last theorem was verified up to $n=4,000,000.$

A momentous occasion occurred on 23 June 1993, when Andrew Wiles, a Cambridge trained mathematician working at Princeton University, announced the proof of the theorem. In developing his solution scheme, Andrew Wiles employed theories from many branches of mathematics: crystalline cohomology, Galois representation, L-functions, modular forms, deformation theory, Gorenstein rings, etc., and relied on research findings from colleagues in France, Germany, Italy, Japan, Australia, Columbia, Brazil, Russia, the United States, etc. However, soon after Wiles’s Cambridge announcement, gaps in his 200-page-long proof surfaced. Fortunately, this time, with the help from his colleagues, most notably his ex-student Richard Taylor (born 1962), Wiles finally filled these gaps after another year hard work. In 1994, Fermat’s last theorem was finally resolved. In 1997, Andrew Wiles was awarded the long time unclaimed award whose worth then was $40,000. However, now the world awaits a simpler proof. Fermat’s last theorem may not seem to be a deeply earth-shattering result. Its importance lies in the fact that it has captured the imagination of some of the most brilliant minds over 350 years, and their attempts at solving this conundrum, no matter how incomplete or futile, have led to the development of some of the most important branches of modern mathematics. It is to be noted that Brahmagupta and Bhaskara II had addressed themselves to some of Fermat’s problems long before they were thought of in the west and had solved them thoroughly. They have not held a proper place in mathematical history, nor received credit for their problems and methods of solution. Andre Weil (1906–1998) wrote in 1984, “What would have been Fermat’s astonishment, if some missionary, just back from India, had told him that his problem had been successfully tackled by native mathematicians almost six centuries earlier”.

Proving Fermat’s last theorem for a given exponent $n>2$ also settles it for any multiple of $n.$ For example, knowing that $a^5+b^5=c^5$ is impossible in positive integers also covers the case $n=10,$ since if we had $x^{10}+y^{10}=z^{10},$ then $a=x^2,b=y^2,c=z^2$ would satisfy the first equation. Similarly, if we had $x^{15}+y^{15}=z^{15},$ then $a=x^3,b=y^3,c=z^3$ will lead to the first equation. Thus, to prove Fermat’s last theorem in general, it suffices to prove that (27) has no positive integer solutions for $n=4$ and for any value of n that is an odd prime. The case $n=4$ is the only one for which a short proof is known. For this, first we shall use Fermat’s method of infinite descent to show that there are no positive integers $a,b$ and c such that $a^4+b^4=c^2.$ To obtain a contradiction, suppose there are such integers. Let us take such a triple with the product $ab$ minimized. Then, $gcd(a,b)=1.$ Since $a^2,b^2$ and c are the sides of a primitive Pythagorean triangle, exactly one of a and b is even. Without loss of generality, let us assume that a is even. By (9), there are positive integers u and $v,$ not both odd, with $gcd(u,v)=1,$ such that $a^2=2uv$ and $b^2=u^2-v^2.$ Since $v^2+b^2=u^2$ and b is odd, v must be even. Since $(2v,u)=1$ and $2uv=a^2,$ it follows that $2v$ and u are squares. Thus, $u=p^2$ for some positive integer $p.$ Again by (9), there are positive integers s and $t,$ not both odd, with $gcd(s,t)=1,$ such that $v=2st$ and $u=s^2+t^2.$ Since $2v$ is a square, so is $2v/4=v/2=st.$ Thus, there are positive integers x and y such that $s=x^2$ and $t=y^2.$ The fact that $u=s^2+t^2$ implies that $x^4+y^4=p^2.$ Moreover, ${\left(xy\right)}^2=st=v/2<2uv=a^2\le {\left(ab\right)}^2$, so that $xy<ab.$ However, this contradicts the minimality of $ab.$ From this, it immediately follows that $a^4+b^4=c^4$ has no solution in positive integers. Indeed, if $a_0,b_0,c_0$ is a solution of $a^4+b^4=c^4,$ then $a_0,b_0,c_0^2$ is a solution of $a^4+b^4=c^2.$

An immediate consequence of this result is that there is no primitive Pythagorean triple all the sides of which are squares. However, there exist Pythagorean triples (not necessarily primitive) whose sides if increased by one are squares. For example, $(99,168,195)=({10}^2-1,{13}^2-1,{14}^2-1).$ It is not known whether infinitely many such triples exist. We can also deduce that the equations $(a^4/p^4)+(b^4/q^4)=c^2$ and $(1/a^4)+(1/b^4)=c^2$ do not have solutions in positive integers.

Fermat’s last theorem is a very special case of a central problem in diophantine analysis. It is required to devise criteria to decide in a finite number of non-tentative steps whether or not a given diophantine equation is solvable.

P36. 

Fermat’s method of infinite descent also applies to show that there are no positive integers $a,b,$ and c such that $a^4-b^4=c^2$ (see Burton [8]).

From P35 and P36, it follows that in a Pythagorean triple $(a,b,c)$, at most one of the members can be a perfect square. This is clear from the fact that none of the equations $x^4+y^4=z^4,x^4+y^4=z^2,x^4=y^4+z^2$ has a solution.

P37. 

In P3, we mentioned that the area $A=(1/2)ab$ of a primitive Pythagorean triangle $(a,b,c)$ can never be a square number. To show this, assume that $(1/2)ab=u^2,$ which is the same as $2ab=4u^2.$ Adding and subtracting this relation from $a^2+b^2=c^2$ give:

$${(a+b)}^2=c^2+4u^2\mathrm{and}{(a-b)}^2=c^2-4u^2.$$

Multiplying these relations, we find:

$${(a^2-b^2)}^2=c^4-16u^4=c^4-{\left(2u\right)}^4,$$

which in view of P36 is impossible.

P38. 

Consider the reciprocal Pythagorean relation, i.e.,

$$\frac{1}{a^2}+\frac{1}{b^2}=\frac{1}{c^2},$$

where $(a,b,c)$ is primitive (Eli Maor [34] calls this relation the little Pythagorean relation). The only positive integer solutions of this equation are given by:

$$a=2uv(u^2+v^2),b=(u^4-v^4),c=2uv(u^2-v^2),$$

where u and v are relatively prime positive integers, one of which is even, and $u>v.$ In particular, for $u=2,v=1$, we have $1/{20}^2+1/{15}^2=1/{12}^2.$

P39. 

Jordanus De Nemore (around 1225–1237) found integers $x,y,$ and z so that $z^2-y^2=y^2-x^2,$ i.e., $z^2+x^2=2y^2,$ which can be written as:

$${\left(\frac{z+x}{2}\right)}^2+{\left(\frac{z-x}{2}\right)}^2=y^2.$$

Since $x^2+z^2$ is even, x and z must be of the same parity. This shows that $(z+x)/2$ and $(z-x)/2$ are integers, but then, this is the same as the Pythagorean triple problem and has an infinite number of integer solutions, namely from (9), $(z-x)/2=u^2-v^2,(z+x)=2uv,y=u^2+v^2.$ Thus, it follows that:

$$x=v^2-u^2+2uv,y=u^2+v^2,z=u^2-v^2+2uv,$$

where $u>v$ and are of different parity. As an example, for $u=6,v=5$, we have $x=49,y=61,z=71,$ and hence, ${71}^2-{61}^2={61}^2-{49}^2.$ We also note that $(z-x)/2=11,(z+x)/2=60$, and we get the Pythagorean triple $(11,60,61);$ see Table 3. If we begin with the Pythagorean triple $\left(\right(z-x)/2,(z+x)/2,y)=(3,4,5),$ then $x=1,y=5,z=7,$ and the equality $7^2-5^2=5^2-1^1$ holds. Similarly, for the Pythagorean triple $\left(\right(z-x)/2,(z+x)/2,y)=(8,15,17),$ we have $x=7,y=17,z=23$, and the relation ${23}^2-{17}^2={17}^2-7^2$ holds. In conclusion, there is a one-to-one correspondence between Pythagorean triples and the solutions of $z^2-y^2=y^2-x^2.$

We can also find integer solutions of the equation $x^2+2y^2=z^2,$ where $gcd(x,y,z)=1.$ Since $2y^2=z^2-x^2=(z+x)(z-x),$ we must have $z+x=2u^2$, $z-x=v^2$, which gives $x=(2u^2-v^2)/2$, $y=uv$, $z=(2u^2+v^2)/2$, which is better written as:

$$x=(2u^2-v^2),y=2uv,z=(2u^2+v^2).$$

If we let $u=7,v=5,$ then $x=73,y=70,z=123,$ and this gives ${73}^2+2\times {70}^2={123}^2.$ If we take $u=6,v=4,$ then $x=56,y=48,z=88,$ which upon dividing by eight gives $x=7,y=6,z=11,$ and we have the identity $7^2+2\times 6^2={11}^2.$ Finally, if we take $u=11,v=6,$ then after dividing by two, we obtain $x=103,y=66,z=139,$ and the equality ${103}^2+2\times {66}^2={139}^2.$

P40. 

The origin of De Nemore’s problem comes from Diophantus’ Problem II-19, which states: Find three squares such that the difference between the greatest and the middle has a given ratio $p:1$ to the difference between the middle and the least. If we let nonzero real numbers $x,y,z$ such that $x^2<y^2<z^2,$ then we need to find the solution of the equation:

$$z^2-y^2=p(y^2-x^2),$$

(28)

where $p>0.$ It is clear that if $x,y,z$ is a solution of (28), then $dx,dy,dz,d\ne 0$ is also a solution. Thus, it suffices to consider only integer solutions of (28). The case $p=1$ has been discussed in P39, so we will mainly take up the case when $p\ne 1.$ We rewrite (28) as:

$$\frac{z+y}{y+x}=p\frac{y-x}{z-y}=k\left(\mathrm{some}\mathrm{nonzero}\mathrm{real}\mathrm{number}\right),$$

which leads to the equations:

$$z+(1-k)y-kx=0\mathrm{and}z-\left(1+\frac{p}{k}\right)y+\frac{p}{k}x=0.$$

Solving these equations, we get:

$$x=(2k+p-k^2)r,y=(p+k^2)r,z=(2pk+k^2-p)r,$$

(29)

where r is an arbitrary positive real number, and it will be chosen so that $x,y,$ and z are integers with $gcd(x,y,z)=1.$ Using (29) on both sides of (28), we find:

$$z^2-y^2=p(y^2-x^2)=4p(k-1)k(k+p)r^2.$$

(30)

Thus, $x^2<y^2<z^2$ holds provided $k>1.$ If $k=1$ or $k=0,$ we have $x=y=z,$ which is an empty case. If $0<k<1,$ then we have $x^2>y^2>z^2,$ and in such a case, we rewrite (28) as:

$$x^2-y^2=\frac{1}{p}(y^2-z^2).$$

(31)

If $-p<k<0,$ then once again, we have $x^2<y^2<z^2,$ and hence, (28) holds. If $k=-p,$ then we have $x=y=z,$ which is again an empty case. Finally, if $k<-p,$ then we find $x^2>y^2>z^2,$ and therefore, (31) holds.

If $p=1,r=1,$ and $k=n\ge 2$ is a natural number, then from (29), we find:

$$u=2n,v=n^2-1,y=n^2+1,$$

which gives Plato’s characterization of the Pythagorean triples (7). For $k=3/2,p=1/4,$ from (29), we get $x=(4/4)r,y=(10/4)r,z=(11/4)r,$ so we choose $r=4,$ to obtain $x=4,y=10,z=11$, and from (28), we have the equality $({11}^2-{10}^2)=(1/4)({10}^2-4^2).$ For $k=1/2,p=2,$ from (29), we get $x=(23/9)r,y=(19/9)r,z=-(5/9)r,$ and we choose $r=9$ so that $x=23,y=19,z=-5;$ and from (31), we get the equality $({23}^2-{19}^2)=(1/2)({19}^2-{(-5)}^2).$ For $k=-1,$ (29) reduces to $x=(p-3)r,y=(p+1)r,z=(-3p+1)r.$ Thus, in particular, for $p=11/2$ and $r=2,$ we have $x=5,y=13,z=-31,$ and from (28) follows the equality $({(-31)}^2-{13}^2)=(11/2)({13}^2-5^2).$ For $k=-(17/3),p=4,$ and $r=9/5,$ (29) gives $x=-71,y=65,z=31,$ and from (31), we have the equality $({(-71)}^2-{65}^2)=(1/4)({65}^2-{31}^2).$

Diophantus gives only one solution for $p=3,$ that is $x^2=25/4,y^2=49/4,z^2=121/4$ (the common factor $1/4$ can be removed). Unfortunately, this solution cannot be obtained from (29). Thus, (29) does not generate all solutions of (28). Extending Diophantus’ method, we assume that $y=x+a,z=x+b,b>a>0$ and $x>0,$ then the Equation (28) gives:

$$x=\frac{b^2-(p+1)a^2}{2\left[a\right(p+1)-b]},y=x+a=\frac{{(b-a)}^2+p{a}^2}{2\left[a\right(p+1)-b]},z=x+b=\frac{a(p+1)(2b-a)-b^2}{2\left[a\right(p+1)-b]},$$

(32)

where $(b/a)<(p+1)<{(b/a)}^2,$ so that $x>0.$ It follows that:

$${(x+b)}^2-{(x+a)}^2=p({(x+a)}^2-x^2)=\frac{pab(b-a)}{a(p+1)-b}>0.$$

For $p=3,a=2,b=6,$ from (32), we get $x=5,y=7,z=11,$ i.e., $x^2=25,y^2=49,z^2=121,$ which is the same as Diophantus’ solution. Similarly, for $p=5,a=3,b=8,$ we get $x^2=1/4,y^2=49/4,z=289/4.$

P41. 

A Heronian triangle $(a,b,c)$ (see Carlson [35]) has integer sides whose area is also an integer. Since in a Pythagorean triple at least one of the legs $a,b$ must be even and the area $A=ab/2$ is an integer, every Pythagorean triple is a Heronian triple; however, the converse is not true: the Heronian triple $(4,13,15)$ has the area $24,$ but it is not a Pythagorean triple. These triangles are named because such triangles are related to Heron’s (Bhaskara I, born before 123 BC) formula $A=\sqrt{s(s-a)(s-b)(s-c)},$ where $s=(a+b+c)/2.$ Finding a Heronian triangle is therefore equivalent to solving the Diophantine equation $A^2=s(s-a)(s-b)(s-c).$ As for Pythagorean triples, if $(a,b,c)$ is a Heronian triple, so is $(na,nb,nc),n>1.$ The Heronian triple $(a,b,c)$ is called primitive provided $a,b,c$ are pairwise relatively prime. There are infinitely many primitive Heronian triples. Brahmagupta acquired the parametric solution such that every Heronian triangle has sides proportional to:

$$a=v(u^2+k^2),b=u(v^2+k^2),c=(u+v)(uv-k^2)$$

$$s=uv(u+v),A=kuv(u+v)(uv-k^2),$$

where $gcd(u,v,k)=1,uv>k^2\ge 1,$ and $u\ge v\ge 1.$ The proportionality factor is generally a rational $p/q$ where $q=gcd(a,b,c)$ reduces the generated Heronian triangle to its primitive and p scales up this primitive to the required size. For example, taking $u=4,v=2$ and $k=1$ produces a triangle with $a=34,b=20$ and $c=42,$ which is similar to the $(10,17,21)$ primitive Heronian triangle with the proportionality factors $p=1$ and $q=2.$ It is known that the perimeter of a Heronian triangle is always an even number, and every primitive Heronian triangle has exactly one even side. The area of a Heronian triangle is always divisible by six. Further, by Heron’s formula, it follows that a triple $(a,b,c)$ with $0<a<b<c$ is Heronian if ${(a^2+b^2+c^2)}^2-2(a^4+b^4+c^4)$ is a nonzero perfect square divisible by $16.$

A few primitive Heronian triangles that are not Pythagorean triples, sorted by increasing areas, are:

$$\begin{array}{cc}(4,13,15)\mathrm{with}\mathrm{area}24,\hfill & (3,25,26)\mathrm{with}\mathrm{area}36\hfill \\ (9,10,17)\mathrm{with}\mathrm{area}36,\hfill & (7,15,20)\mathrm{with}\mathrm{area}42\hfill \\ (6,25,29)\mathrm{with}\mathrm{area}60,\hfill & (11,13,20)\mathrm{with}\mathrm{area}66\hfill \\ (13,14,15)\mathrm{with}\mathrm{area}84,\hfill & (10,17,21)\mathrm{with}\mathrm{area}84\hfill \end{array}$$

P42. 

A congruent number n is a positive integer that is equal to the area of a rational right triangle, i.e., it is a rational solution of Equation (1), which in addition satisfies the equation $(1/2)ab=A=n.$ Clearly, every Pythagorean triple (primitive, as well as non-primitive) gives a congruent number, but in view of P37, A and hence n cannot be a perfect square. Thus, $2^2,3^2,4^2,\cdots$ cannot be congruent numbers. If n is a congruent number, i.e., $A=(1/2)ab=n,$ then $m^{2}n$ is also a congruent number for any positive integer $m;$ indeed, it follows from the facts that:

$${\left(\frac{a}{m}\right)}^2+{\left(\frac{b}{m}\right)}^2={\left(\frac{c}{m}\right)}^2\mathrm{and}\frac{1}{2}\left(\frac{a}{m}\right)\left(\frac{b}{m}\right)=B$$

imply $B=m^{2}n.$ Thus, the main interest is in square-free congruent numbers. Fermat in 1640 proved that there is no right triangle with rational sides and area one; he also showed that two and three are not congruent numbers. From an Arab manuscript of the 10th Century, it is known that five and six are congruent numbers. In fact, we have:

$${\left(\frac{20}{3}\right)}^2+{\left(\frac{3}{2}\right)}^2={\left(\frac{41}{6}\right)}^2\mathrm{and}\frac{1}{2}\left(\frac{20}{3}\right)\left(\frac{3}{2}\right)=5,$$

and the first Pythagorean triple $(3,4,5)$ gives the number six. We also have:

$${\left(\frac{7}{10}\right)}^2+{\left(\frac{120}{7}\right)}^2={\left(\frac{1201}{70}\right)}^2\mathrm{and}\frac{1}{2}\left(\frac{7}{10}\right)\left(\frac{120}{7}\right)=6,$$

and (see Conrad [36]),

$${\left(\frac{1437599}{168140}\right)}^2+{\left(\frac{2017680}{1437599}\right)}^2={\left(\frac{2094350404801}{241717895860}\right)}^2\mathrm{and}\frac{1}{2}\left(\frac{1437599}{168140}\right)\left(\frac{2017680}{1437599}\right)=6,$$

i.e., the same congruent number can have several (may be infinite) rational right triangles. Don Bernard Zagier (born 29 June 1951) computed the simplest rational right triangle (see Figure 3) for the congruent number 157 (the same has also appeared in several places, e.g., Peng [37], Veljan [38], and Wiles [39])

where:

$$a=\frac{6803298487826435051217540}{411340519227716149383203},b=\frac{411340519227716149383203}{21666555693714761309610}$$

and

$$c=\frac{224403517704336969924557513090674863160948472041}{8912332268928859588025535178967163570016480830}.$$

While in 1986, Kramarz [40] listed all congruent numbers up to less than 2000, to find if a given positive integer n is congruent remains an open number-theoretic problem. The relation of this problem to elliptic curves has been studied extensively; see Koblitz [41]. Furthermore, its beautiful equivalent form: n is a congruent number, if and only if,

$$\begin{array}{ccc}{x}^2+n{t}^2\hfill & =\hfill & y^2\hfill \\ x^2-n{t}^2\hfill & =\hfill & z^2\hfill \end{array}$$

has solutions; further, if $(x,y,z,t)$ is a solution, then:

$$a=\frac{y-z}{t},b=\frac{y+z}{t},c=\frac{2x}{t}$$

is only of theoretical interset.

P43. 

A Pythagorean quadruple is a tuple of four integers $a,b,c,$ and $d,$ such that $a^2+b^2+c^2=d^2.$ A Pythagorean quadruple $(a,b,c,d)$ is called primitive if the greatest common divisor of its numbers is one. The set of primitive Pythagorean quadruples for which a is odd can be generated by (see Carmichael [12,13] and Spira [42]):

$$a=u^2+v^2-p^2-q^2,b=2(uq+vp),c=2(vq-up),d=u^2+v^2+p^2+q^2,$$

where $u,v,p,q$ are non-negative integers with the greatest common divisor one such that $u+v+p+q$ is odd. Thus, all primitive Pythagorean quadruples are characterized by Henri Léon Lebesgue’s (1875-1941) identity:

$${(u^2+v^2-p^2-q^2)}^2+{(2uq+2vp)}^2+{(2vq-2up)}^2={(u^2+v^2+p^2+q^2)}^2.$$

As an example, for $u=1,v=3,p=2,q=1,$ we have $a=5,b=14,c=2,d=15$, and hence, $(2,5,14,15)$ is a primitive Pythagorean quadruple. Indeed, we have the identity:

$$2^2+5^2+{14}^2={15}^2.$$

Besides $(2,5,14,15)$, there are 30 more primitive Pythagorean quadruples in which all entries are less than 30 (see https://en.wikipedia.org/wiki/Pythagorean_quadruple):

$$\begin{array}{c}(1,2,2,3),(2,10,11,15),(4,13,16,21),(2,10,25,27),(2,3,6,7)\hfill \\ (1,12,12,17),(8,11,16,21),(2,14,23,27),(1,4,8,9),(8,9,12,17)\hfill \\ (3,6,22,23),(7,14,22,27),(4,4,7,9),(1,6,18,19),(3,14,18,23)\hfill \\ (10,10,23,27),(2,6,9,11),(6,6,17,19),(6,13,18,23),(3,16,24,29)\hfill \\ (6,6,7,11),(6,10,15,19),(9,12,20,25),(11,12,24,29),(3,4,12,13)\hfill \\ (4,5,20,21),(12,15,16,25),(12,16,21,29),(4,8,19,21),(2,7,26,27)\hfill \end{array}$$

Quadruple $(a,b,c,d)$ can also be obtained by the simple identity:

$${(a^2-b^2-c^2)}^2+{\left(2ab\right)}^2+{\left(2ac\right)}^2={(a^2+b^2+c^2)}^2.$$

(33)

For example, for $a=3,b=2,c=2$, this identity reduces to $1^2+{12}^2+{12}^2={17}^2.$ Thus, we get back the quadruple $(1,12,12,17).$

P44. 

We note that the Euler–Aida Ammei (1747–1817) identity:

$${(x_0^2-x_1^2-\cdots -x_n^2)}^2+{\left(2x_0{x}_1\right)}^2+\cdots +{\left(2x_0{x}_n\right)}^2={(x_0^2+x_1^2+\cdots +x_n^2)}^2$$

(34)

implies that the sum of $n+1$ squares is the square of the sum of $n+1$ squares. Identity (34) for $n=1$, $x_0=u$, $x_1=v$ gives (9); for $n=2,x_0=a,x_1=b,x_2=c$, it reduces to (33); and for $n=3,x_0=a,x_1=b,x_2=c$, $x_3=d$, it gives quintuples:

$${(a^2-b^2-c^2-d^2)}^2+{\left(2ab\right)}^2+{\left(2ac\right)}^2+{\left(2ad\right)}^2={(a^2+b^2+c^2+d^2)}^2.$$

(35)

For example, for $a=4,b=3,c=2,d=1$, this identity reduces to $2^2+{24}^2+{16}^2+8^2={30}^2.$ Thus, dividing this relation by $2^2,$ we get the quintuple $(1,4,8,12,15).$

P45. 

Euler in 1748 gave the following Brahmagupta–Diophantus–Fibonacci (15), (16), type four-square identity:

$$\begin{array}{c}{(a_1{b}_1-a_2{b}_2-a_3{b}_3-a_4{b}_4)}^2+{(a_1{b}_2+a_2{b}_1+a_3{b}_4-a_4{b}_3)}^2+{(a_1{b}_3-a_2{b}_4+a_3{b}_1+a_4{b}_2)}^2\hfill \\ +{(a_1{b}_4+a_2{b}_3-a_3{b}_2+a_4{b}_1)}^2=(a_1^2+a_2^2+a_3^2+a_4^2)(b_1^2+b_2^2+b_3^2+b_4^2).\hfill \end{array}$$

(36)

Clearly, as in P28, Equality (36) can be used to find new four-square identities. We also note that for $a_i=b_i,i=1,2,3,4,$ Equality (36) is the same as (35).

P46. 

Carl Ferdinand Degen (1766–1825) around 1818 discovered the eight-square identity:

$$\begin{array}{c}{(a_1{b}_1-a_2{b}_2-a_3{b}_3-a_4{b}_4-a_5{b}_5-a_6{b}_6-a_7{b}_7-a_8{b}_8)}^2\hfill \\ +{(a_1{b}_2+a_2{b}_1+a_3{b}_4-a_4{b}_3+a_5{b}_6-a_6{b}_5-a_7{b}_8+a_8{b}_7)}^2\hfill \\ +{(a_1{b}_3-a_2{b}_4+a_3{b}_1+a_4{b}_2+a_5{b}_7+a_6{b}_8-a_7{b}_5-a_8{b}_6)}^2\hfill \\ +{(a_1{b}_4+a_2{b}_3-a_3{b}_2+a_4{b}_1+a_5{b}_8-a_6{b}_7+a_7{b}_6-a_8{b}_5)}^2\hfill \\ +{(a_1{b}_5-a_2{b}_6-a_3{b}_7-a_4{b}_8+a_5{b}_1+a_6{b}_2+a_7{b}_3+a_8{b}_4)}^2\hfill \\ +{(a_1{b}_6+a_2{b}_5-a_3{b}_8+a_4{b}_7-a_5{b}_2+a_6{b}_1-a_7{b}_4+a_8{b}_3)}^2\hfill \\ +{(a_1{b}_7+a_2{b}_8+a_3{b}_5-a_4{b}_6-a_5{b}_3+a_6{b}_4+a_7{b}_1-a_8{b}_2)}^2\hfill \\ +{(a_1{b}_8-a_2{b}_7+a_3{b}_6+a_4{b}_5-a_5{b}_4-a_6{b}_3+a_7{b}_2+a_8{b}_1)}^2\hfill \\ =(a_1^2+a_2^2+a_3^2+a_4^2+a_5^2+a_6^2+a_7^2+a_8^2)(b_1^2+b_2^2+b_3^2+b_4^2+b_5^2+b_6^2+b_7^2+b_8^2).\hfill \end{array}$$

(37)

Clearly, for $a_i=b_i,i=1,\cdots ,8,$ Equality (37) is the same as (34) with $n=7.$ The equality (37) was independently rediscovered by John Thomas Graves (1806–1870) in 1843 and Arthur Cayley (1821–1895) in 1845. In 1898, Adolf Hurwitz (1859–1919) proved that there is no similar identity for 16 squares or any other number of squares except for 1,2,4, and 8.

P47. 

Srinivasa Ramanujan’s (1887–1920) identity:

$${(3a^2+5ab-5b^2)}^3+{(4a^2-4ab+6b^2)}^3+{(5a^2-5ab-3b^2)}^3={(6a^2-4ab+4b^2)}^3$$

(38)

parameterizes the sum of three cubes into a cube, i.e., $x_1^3+x_2^3+x_3^3=c^3$ (known as Fermat’s cubic) whose general solution was found by Euler and Viéte. Identity (38) for $a=1,b=0$ reduces to Euler’s equality $3^3+4^3+5^3=6^3=216$ (this smallest number is known as Plato’s number), whereas for $a=2,b=1$, it gives ${17}^3+{14}^3+7^3={20}^3.$ The sum of three cubes into a cube can also be parameterized as (see Hardy and Wright [43]):

$$b^3{(a^3+b^3)}^3+a^3{(a^3-2b^3)}^3+b^3{(2a^3-b^3)}^3=a^3{(a^3+b^3)}^3,$$

(39)

or as:

$$a^3{(a^3-b^3)}^3+b^3{(a^3-b^3)}^3+b^3{(2a^3+b^3)}^3=a^3{(a^3+2b^3)}^3.$$

(40)

For $a=2,b=1$, Identities (39) and (40), respectively, reduce to $9^3+{12}^3+{15}^3={18}^3$ (which is the same as $3^3+4^3+5^3=6^3$) and ${14}^3+7^3+{17}^3={20}^3$ (which is the same as given by (38)).

P48. 

In 1769, Euler made the conjecture that:

$$x_1^k+x_2^k+\cdots +x_n^k=c^k$$

(41)

implies $n\ge k.$ This conjecture makes an effort to generalize Fermat’s last theorem, which in fact is a special case; indeed, if $x_1^k+x_2^k=c^k$, then $2\ge k.$ In view of Fermat’s last theorem and P48, Euler’s conjecture holds for $k=3;$ however, it has been disproven for $k=4$ and $k=5,$ and for $k\ge 6$, the answer is unknown. For the cases $k=4$ and 5, the known counterexamples are:

Noam David Elkies [44] in 1986,

$${2682440}^4+{15365639}^4+{18796760}^4={20615673}^4$$

Roger Frye [45] in 1988,

$${95800}^4+{217519}^4+{414560}^4={422481}^4$$

Leon Lander and Thomas Parkin [46] in 1966,

$${27}^5+{84}^5+{110}^5+{133}^5={144}^5$$

Roger Frye in 2004,

$${55}^5+{3183}^5+{28969}^5+{85282}^5={85359}^5$$

The following identities support Euler’s conjecture:

R. Norrie in 1911,

$${30}^4+{120}^4+{272}^4+{315}^4={353}^4$$

Leon Lander, Thomas Parkin, and John Selfridge (LPS) [47] in 1967,

$${19}^5+{43}^5+{46}^5+{47}^5+{67}^5={72}^5$$

S. Sastry [48] in 1934,

$$7^5+{43}^5+{57}^5+{80}^5+{100}^5={107}^5$$

LPS in 1967,

$${74}^6+{234}^6+{402}^6+{474}^6+{702}^6+{894}^6+{1077}^6={1141}^6$$

LPS in 1967,

$$8^6+{12}^6+{30}^6+{78}^6+{102}^6+{138}^6+{165}^6+{246}^6={251}^6$$

M. Dodrill in 1999,

$${127}^7+{258}^7+{266}^7+{413}^7+{430}^7+{439}^7+{525}^7={568}^7$$

S. Chase in 2000,

$${90}^8+{223}^8+{478}^8+{524}^8+{748}^8+{1088}^8+{1190}^8+{1324}^8={1409}^8$$

For sixth power summations, several more identities are available at https://mathworld.wolfram.com/DiophantineEquation6thPowers.html.

P49. 

Euler gave a parametric solution of the equation:

$$x_1^3+x_2^3=x_3^3+x_4^3$$

(42)

namely,

$$x_1=1-(a-3b)(a^2+3b^2),x_2=(a+3b)(a^2+3b^2)-1$$

$$x_3=(a+3b)-{(a^2+3b^2)}^2,x_4={(a^2+3b^2)}^2-(a-3b),$$

where a and b are any integers. Equation (42) has the following 10 solutions with sum $<{10}^5$ (see Guy [17]):

$$\begin{array}{ccccc}1729\hfill & =\hfill & 1^3+{12}^3\hfill & =\hfill & 9^3+{10}^3\hfill \\ 4104\hfill & =\hfill & 2^3+{16}^3\hfill & =\hfill & 9^3+{15}^3\hfill \\ 13832\hfill & =\hfill & 2^3+{24}^3\hfill & =\hfill & {18}^3+{20}^3\hfill \\ 20683\hfill & =\hfill & {10}^3+{27}^3\hfill & =\hfill & {19}^3+{24}^3\hfill \\ 32832\hfill & =\hfill & 4^3+{32}^3\hfill & =\hfill & {18}^3+{30}^3\hfill \\ 39312\hfill & =\hfill & 2^3+{34}^3\hfill & =\hfill & {15}^3+{33}^3\hfill \\ 40033\hfill & =\hfill & 9^3+{34}^3\hfill & =\hfill & {16}^3+{33}^3\hfill \\ 46683\hfill & =\hfill & 3^3+{36}^3\hfill & =\hfill & {27}^3+{30}^3\hfill \\ 64232\hfill & =\hfill & {17}^3+{39}^3\hfill & =\hfill & {26}^3+{36}^3\hfill \\ 65728\hfill & =\hfill & {12}^3+{40}^3\hfill & =\hfill & {31}^3+{33}^3\hfill \end{array}$$

From Euler’s parametric solution of (42), we cannot find a and b to obtain the relation $1729=1^3+{12}^3=9^3+{10}^3.$ However, one of Ramanujan’s parametrizations:

$${(a^2+7ab-9b^2)}^3+{(2a^2-4ab+12b^2)}^3={(2a^2+10b^2)}^3+{(a^2-9ab-b^2)}^3$$

with $a=b=1$ does give this relation. In the literature, the number 1729 is known as the taxicab or Hardy–Ramanujan number. For this, the story is as follows: Once, Hardy went to see Ramanujan when he was in a nursing home and remarked that he had traveled in a taxi with a rather dull number, 1729, at which Ramanujan exclaimed, “No, Hardy, 1729 is a very interesting number. It is the smallest number that can be expressed as the sum of two cubes ($1729=1^3+{12}^3=9^3+{10}^3$), and the next such number is very large”. We are told Ramanujan was endowed with an astounding memory and remembered the idiosyncrasies of the first 10,000 integers to such an extent that each number became like a personal friend to him. Hardy and Wright [43] proved that there are numbers that are expressible as the sum of two cubes in n ways for any $n.$ For example, the numbers representable in three ways as the sum of two cubes are:

$$\begin{array}{ccccccc}87539319\hfill & =\hfill & {167}^3+{436}^3\hfill & =\hfill & {228}^3+{423}^3\hfill & =\hfill & {255}^3+{414}^3\hfill \\ 119824488\hfill & =\hfill & {11}^3+{493}^3\hfill & =\hfill & {90}^3+{492}^3\hfill & =\hfill & {346}^3+{428}^3\hfill \\ 143604279\hfill & =\hfill & {111}^3+{522}^3\hfill & =\hfill & {359}^3+{460}^3\hfill & =\hfill & {408}^3+{423}^3\hfill \\ 175959000\hfill & =\hfill & {70}^3+{560}^3\hfill & =\hfill & {198}^3+{552}^3\hfill & =\hfill & {315}^3+{525}^3\hfill \\ 327763000\hfill & =\hfill & {300}^3+{670}^3\hfill & =\hfill & {339}^3+{661}^3\hfill & =\hfill & {510}^3+{580}^3\hfill \end{array}$$

Euler also proved that there exist infinitely many solutions of the equation $x_1^4+x_2^4=x_3^4+x_4^4,$ and its smallest solution is (see Dunham [49]):

$${59}^4+{158}^4={133}^4+{134}^4=635318657.$$

The following equalities are provided by Guy [17].

$$\begin{array}{ccc}\hfill 3^6+{19}^6+{22}^6& \hfill =& {10}^6+{15}^6+{23}^6\left(\mathrm{K}.\mathrm{Subba}\mathrm{Rao}\mathrm{in}1934\right)\hfill \\ \hfill {36}^6+{37}^6+{67}^6& \hfill =& {15}^6+{52}^6+{65}^6\hfill \\ \hfill {33}^6+{47}^6+{74}^6& \hfill =& {23}^6+{54}^6+{73}^6\hfill \\ \hfill {32}^6+{43}^6+{81}^6& \hfill =& 3^6+{55}^6+{80}^6\hfill \\ \hfill {37}^6+{50}^6+{81}^6& \hfill =& {11}^6+{65}^6+{78}^6\hfill \\ \hfill {25}^6+{62}^6+{138}^6& \hfill =& {82}^6+{92}^6+{135}^6\hfill \\ \hfill {51}^6+{113}^6+{136}^6& \hfill =& {40}^6+{125}^6+{129}^6\hfill \\ \hfill {71}^6+{92}^6+{147}^6& \hfill =& 1^6+{132}^6+{133}^6\hfill \\ \hfill {111}^6+{121}^6+{230}^6& \hfill =& {26}^6+{169}^6+{225}^6\hfill \\ \hfill {75}^6+{142}^6+{245}^6& \hfill =& {14}^6+{163}^6+{243}^6\hfill \end{array}$$

In P48 and P49, the amount of effort necessary to find examples/counterexamples—even when the effort came from computers—was then astonishing. In view of some of these equalities in 1967, LPS made the following conjecture: If:

$$\sum _{i=1}^n{x}_i^k=\sum _{j=1}^m{y}_j^k,$$

(43)

where $x_i\ne y_j$ are positive integers for all $1\le i\le n$ and $1\le j\le m,$ then $m+n\ge k.$ Clearly, for $m=1,$ (43) is the same as Relation (41), but then, $n+1\ge k.$

P50. 

In 1844, Eugéne Charles Catalan (1814–1894) made the conjecture that eight and nine are the only numbers that differ by one and are both exact powers $8=2^3,9=3^2.$ This conjecture was proven by Preda Mihăilescu (Born 1955) after one hundred and fifty-eight years and published two years later in [50]. Thus, the only solution in natural numbers of the Diophantine equation $x^a-y^b=1$ for $a,b>1,x,y>0$ is $x=3$, $a=2,y=2,b=3$. In 1931, Subbayya Sivasankaranarayana Pillai (1901–1950) conjectured that for fixed positive integers $A,B,C$, the Diophantine equation $A{x}^n-B{y}^m=C$ has only finitely many solutions $(x,y,m,n)$ with $(m,n)\ne (2,2).$

4. Conclusions

In this article, we systematically and exhaustively discussed one of the most basic problems in the field of number theory, namely Pythagorean triples. The quote of Francois Marie Arouet Voltaire (1694–1778, one of the greatest French writers and philosophers), which has also been cited by Thomas Stearns Eliot (1888–1965, American-British poet, Nobel Prize winner in 1948) “I am convinced that everything has come down to us from the banks of Ganga–Astronomy, Astrology, and Spiritualism. Pythagoras went from Samos to Ganga 2600 years ago to learn Geometry. He would not have undertaken this journey had the reputation of the Indian science had not been established before” suggests Pythagoras learned about his theorem and triples probably in India. We provided necessary and sufficient conditions with detailed proofs for the construction of Pythagorean triples. This was followed by a list of 50 properties and patterns, extensions, and some problems. It is our hope that students and teachers of mathematics will appreciate this article and explore new directions/relations.