Method of the Analysis of the Connectivity of Road and Street Network in Terms of Division of the City Area

Abstract

The transport system of a Smart City consists of many subsystems; therefore, the modeling of the transportation network, which maps its structure, requires consideration of both the connections between individual subsystems and the relationships within each of them. The road and street network is one of the most important subsystems, whose main task is to ensure access to places generating travel demand in the city. Thus, its effectiveness should be at an appropriate level of quality. Connectivity is one of the most important characteristics of a road and street network. It describes how elements of that network are connected, which translates to travel times and costs. The analysis of the connectivity of the road and street network in urban areas is often conducted with the application of topological measures. In the case of a large area of the city, such analysis requires its division into smaller parts, which may affect the computational results of these measures; therefore, the main goal of the study was to present a method of performing analysis based on the computation of numerical values of selected measures of connectivity of road and street network, for a city area divided into fields of regular shape. To achieve that goal, the analyzed area was split into a regular grid. Subsequently, numerical values of the chosen measures of connectivity were calculated for each basic field, and the results allowed us to determine whether they are influenced by the method of division of the area. Obtained results showed that the size of the basic field influences the numerical values of measures of connectivity; however that influence is different for each of the selected measures.

1. Introduction

One of the most important features of the transport system in Smart Cities is ensuring an adequate level of accessibility of this system both for all residents and for other people using its infrastructure [1,2]. It largely depends on the structure of the transportation network, which should be characterized by an adequate level of redundancy, causing little vulnerability to disturbance [3,4,5,6,7,8]. The connectivity of the road and street network is a feature that may significantly contribute to maintaining the proper level of the quality of the transport system in cities. It is particularly important in cases of network disturbances caused by congestion or traffic incidents, when it is necessary to determine detour routes. It is also a significant aspect in emergencies in which users should be evacuated. The issue is an essential question in the planning and optimization of the transportation network elements both on a local and on a global scale.

Methods for modeling transport supply are among the most important aspects of the transport activity of Smart Cities [9]; therefore, the main goal of the paper was to present a method of performing analysis based on the computation of numerical values of selected measures of connectivity of road and street networks, for a city area divided into fields of regular shapes. The proposed method may support the selection of the measures of connectivity basing on its sensitivity to the division method of the city area. The provided mathematical modeling allows implementing presented formulas into software to facilitate the computation. The presented method may be applied to other types of transportation networks.

The area of analysis covering urban space requires accurate delimitation of its borders and impact zone; however, more detailed research is conducted when dividing the city into smaller territorial units. There are many ways to divide the geographical space, including both the division into areas of regular shape and the division into so-called traffic analysis zones (TAZs) corresponding with the administrative borders or with the various types of natural or spatial barriers. This creates areas of analysis consisting of the so-called basic fields. Proper division of the area is a necessary step to identify its homogeneous aspects and conduct further analysis in smaller but more homogeneous territorial units. The results of the literature review on this issue are elaborated on in Section 2.

Analysis of the structure of the transportation network is a very complex issue. There are a lot of measures that characterize the network configuration in different ways, depending on the purpose of the research [10,11,12,13,14,15,16,17,18]. This article focuses on presenting results of the analyzes related to the connectivity of the road and street network. Section 2 shows the literature review in terms of various approaches to measuring the broadly understood connectivity of the transport network.

When dividing geographical space into fields of regular shapes, the size of a single basic field is very important. According to the authors, it can significantly affect the values of measures of connectivity of the road and street network structure; however, to the best of the authors’ knowledge, there are no articles in the literature that directly provide unequivocal research results in this area. Therefore, by filling the research gap, a comparative analysis was carried out for selected measures of connectivity, when dividing the analyzed area into regular shaped basic fields of various sizes. In this article, we present the methodology of research and the results for an example area in a real urban network. An attempt to determine the relationship between the values of selected measures of connectivity of road and street network and the size of the basic field has been also made.

This article also contains the case study covering the results of the analyses that were carried out to determine the effect of the division of the area on the assessment of the road and street network in terms of its connectivity.

2. Literature Review

The city area should be treated as a geographical space, i.e., a real heterogeneous space, taking into account both the diversity of the natural environment and the human environment; therefore, there may be distinguished in it [19,20]:

• Ecological space, in which the laws of nature prevail.
• Economic space, in which business activity is conducted.

The performance of the city area is connected with the realization of transport needs, which have a source in activities of inhabitants and visitors as well as trading, manufacturing, and commercial activity of economic entities in the city and its surroundings; therefore, in the geographical space of the city, it is possible to distinguish transportation space, which contains transport systems with determined traffic organization and organization of transport services. Transportation space is created, above all, by technical infrastructure (point and linear) with a network structure, in which pedestrians and vehicles, which create flows of goods, vehicles, and passengers, move. The interrelation of transport needs and land use, which represent the spatial allocation of these needs, i.e., spatial allocation of places of social and commercial activity or places of activity of inhabitants and visitors, creates transportation space. The shaping of transportation space is connected with solving of the problems of congestion [21] or disruptions of traffic flows [22,23] by implementing certain actions associated with mobility management and intelligent transport systems [24,25], which form a dedicated functional and operational configuration for sustainable development of transport systems [26]. On the other hand, shaping transportation space influences changes in land use and geographical space by creating transport accessibility for new or planned places of social and commercial activity in physical urban space. These mutual impacts between transportation urban space and physical urban space create feedback of a positive character—associated with an increase of transport accessibility of the city area but also of negative characteristics associated with the effects of transport congestion and sustainable exploitation of transport systems.

Cities are very complex systems composed of many human factors interacting in physical urban space. The shape of the current urban form depends on the socio-economic conditions developed over previous historical events and political dependencies. The most frequently cited features of urban space are [26,27,28,29,30]: continuity, finiteness, resilience, fulfillment, diversification, structure, accessibility, quality, dynamics (variability), and functionality (potential, planned, and present).

Due to the significant structural complexity and size associated with the scale problem, for the conducted analyses, the city area used to be divided into smaller territorial units [31,32,33]; however, all divisions and classifications of geographical space should be preceded by the delimitation of its borders, i.e., by the determining the extent of its occurrence. In this context, it is therefore important to determine the criteria for the division that should specify the features and principles underlying further classification.

In general, two models of division of geographic space may be distinguished [34,35,36,37,38]:

• Vector spatial data models, in which the analysis area is divided into irregularly shaped territorial units.
• Raster spatial data models, in which the analysis area is divided into regularly shaped territorial units.

The basic feature of a vector spatial data model is its unambiguous assignment to a spatial unit. The object is identified by providing its identifier. Each element of the urban space is classified into the appropriate geometric type [34]:

• Points, coded as single coordinate pairs.
• Lines, coded as series of ordered coordinate pairs or curves described by mathematical functions.
• Polygons, coded as one or more segments of closed planes.

The coordinates determine the geometric shape of the object, i.e., the location of the point in two- or multi-dimensional space.

In the case of the division of geographical space into territorial units of irregular shape for transport analyses, it is usually assumed that the areas have a certain level of homogeneity due to the analyzed feature (e.g., structure of land use, demographic and social features, traffic intensity, or level of urbanization). The method and scope of the division of the analysis area strictly depend on the purpose of the research. For example, the division of geographical space for the construction of a transport model includes spatial and demographic analyzes as well as socio-economic analyzes that should allow the identification of specific transport zones (called traffic analysis zones, TAZs), that form the areas of irregular shape, with an interpretation of the basic structure of territorial units in which the demand for travel is generated and absorbed. When dividing the area into smaller parts, the following criteria of determining borders should be taken into account [26,39]:

• Administrative criteria of delimitation at the national, regional, voivodship, subregional, metropolitan, agglomeration, local level, etc.
• Structural criteria related to the studied area, taking into account, among others:

  −

  Spatial distribution of density of inhabitants in households.

  −

  Spatial distribution of density of workplaces.

  −

  Trip generation objects with homogeneous activities or motivations.

  −

  Natural and artificial barriers for traffic flows (rivers and other infrastructural water facilities. roads of the highest classes and categories, railways, undeveloped areas).

  −

  Other detailed criteria for creating borders of transport zones.

• Technical and functional criteria related to the implemented project, taking into account the specifics of the studied area and the purpose of the analyzes (e.g., schedule and specific condition of passenger information systems or public transport management system).

In the raster spatial data model, the urban space is divided into basic fields, which should be understood as an elementary spatial unit, to which a given value of the analyzed feature or set of attributes is assigned. In the raster description, the values of the attributes cover the entire studied geographical space. It requires the imposition of a regular grid (i.e., square, hexagonal, triangular, etc.) on the image or the map. The position of the basic field is described by the number of rows and columns of the array of the interpretation of the raster or chorochromatic map. The division of urban space into raster fields is also called regular tessellation [40]. This approach has been applied, among others, in the analyses of the urban sprawl phenomenon, using cellular automata (CA) and multi-agent models, for Chicago and Calgary [41,42,43].

When dividing the area into the fields of equal size, the size of the basic field should be properly determined, depending to a large extent on the possibility of obtaining data at the appropriate level of detail [44]. The size of the basic field is also important in assessing the structure of the road and street network, which in urban areas usually consists of a small number of large arterial roads, a medium number of midsized collector streets, and a large number of capillary local streets [45].

The transport network is a set of selected, physically existing objects in the studied area, which together form a specific spatial structure resulting from connections created between settlement units as a result of social, economic, and natural factors [46,47,48,49]. In urban areas, the road and street network is one of the most important elements of the system, and its structure often determines the efficiency of the entire transportation network. There are different types of the structure of road networks, including grids, trees, hubs and spokes, or lines. In practice, mixed structures are often a combination of basic ones. Each type of network structure may differ in complexity [50].

Various types of measures are used to estimate the structure of the transportation network [51,52,53]. The connectivity of the urban network is, next to density and resilience, one of the most important measures describing the complexity of the network [45,54,55,56,57]. Connectivity represents the fewest number of nodes or edges that will disconnect the network if they are removed [58,59]. A graph is connected if there is at least one path between each pair of vertices in the graph. Because it assesses the degree of connection between vertices in the transportation network, it also gains special signification when comparing different network structures and when analyzing network development over time. The development of transport connections between nodes is directly related to the increase in transport demand; therefore, connectivity is a measure that also proves the complexity of socio-economic connections of the city area. In addition, transportation networks with low average connectivity are characterized by a high level of vulnerability. Traffic jams and disturbances can arise when the urban form generates traffic through critical points with low capacity; thus, the connectivity of a graph is an important measure of its resilience as a network.

The simplest measures of connectivity use the topological properties of the graph and assess the shape and physical configuration of a system [53]. The most commonly used connectivity measures for planar graphs are presented in

Table 1. Description of selected measures characterizing the connectivity of the planar graph.

Measure	Definition	Examples of Applications
degree of network connectivity	the ratio of the maximum number of possible edges in the graph to the number of observed edges	Prihar (1956), Garrison (1960), Kansky (1963), Vetter (1970)
cyclomatic number	the number of circuits in the graph	Berge (1962), Kansky (1963), Vetter (1970), Alao (1973)
alfa index	number of cycles in a graph in comparison with the maximum number of cycles	Kansky (1963), Vetter (1970), Alao (1973), Leusmann (1974)
beta index	ratio of the number of edges to the number of vertices	Kansky (1963), Vetter (1970), Alao (1973), Taylor (1975)
gamma index	ratio of the number of observed edges to the number of possible edges	Kansky (1963), Vetter (1970), Alao (1973), Hay (1973), Leusmann (1974)
eta index	average edge length	Kansky (1963), Hay (1973)
theta index	average length (traffic flow, volume of freight) per vertex	Kansky (1963)
iota index	average distance per ton/ average freight carried per mile	Kansky (1963)
graph development degree	number of edges missing to form a complete graph per one vertex	Zagożdżon (1970), Łoboda (1973), Szmytkie (2017)
average shortest path length	the average number of stops needed to reach two distant nodes in the graph	Rodrigue et al. (2006)
assortative coefficient	the Pearson correlation between the order (degree) of nodes at both ends of each link (edge) in the network	Rodrigue et al. (2006)
intersection count	number of intersections in the network	Boeing (2018)
dead-and count	number of dead-end nodes in the network	Boeing (2018)
dead-end proportion	proportion of nodes that are dead-ends	Boeing (2018)
three-way intersection count	number of three-way intersections in the network	Boeing (2018)
three-way intersection proportion	proportion of nodes that are three-way intersections	Boeing (2018)
four-way intersection count	number of four-way intersections in the network	Boeing (2018)
four-way intersection proportion	proportion of nodes that are four-way intersections	Boeing (2018)
average node degree	mean number of inbound and outbound edges incident to the nodes	Boeing (2018)

Source: own study based on [45,51,60,61,62,63,64].

.

According to Table 1, there are many different measures of connectivity, which differ from each other in terms of i.e., complexity. Measures, such as “four-way intersection count” or “intersection count” are expressed simply as numbers of particular objects. Other measures, such as beta, gamma, or eta, introduced by Kansky [61], are ratios. Some measures, i.e., “assortative coefficient”, require more complicated calculations.

3. Methodology

3.1. General Overview of the Proposed Approach

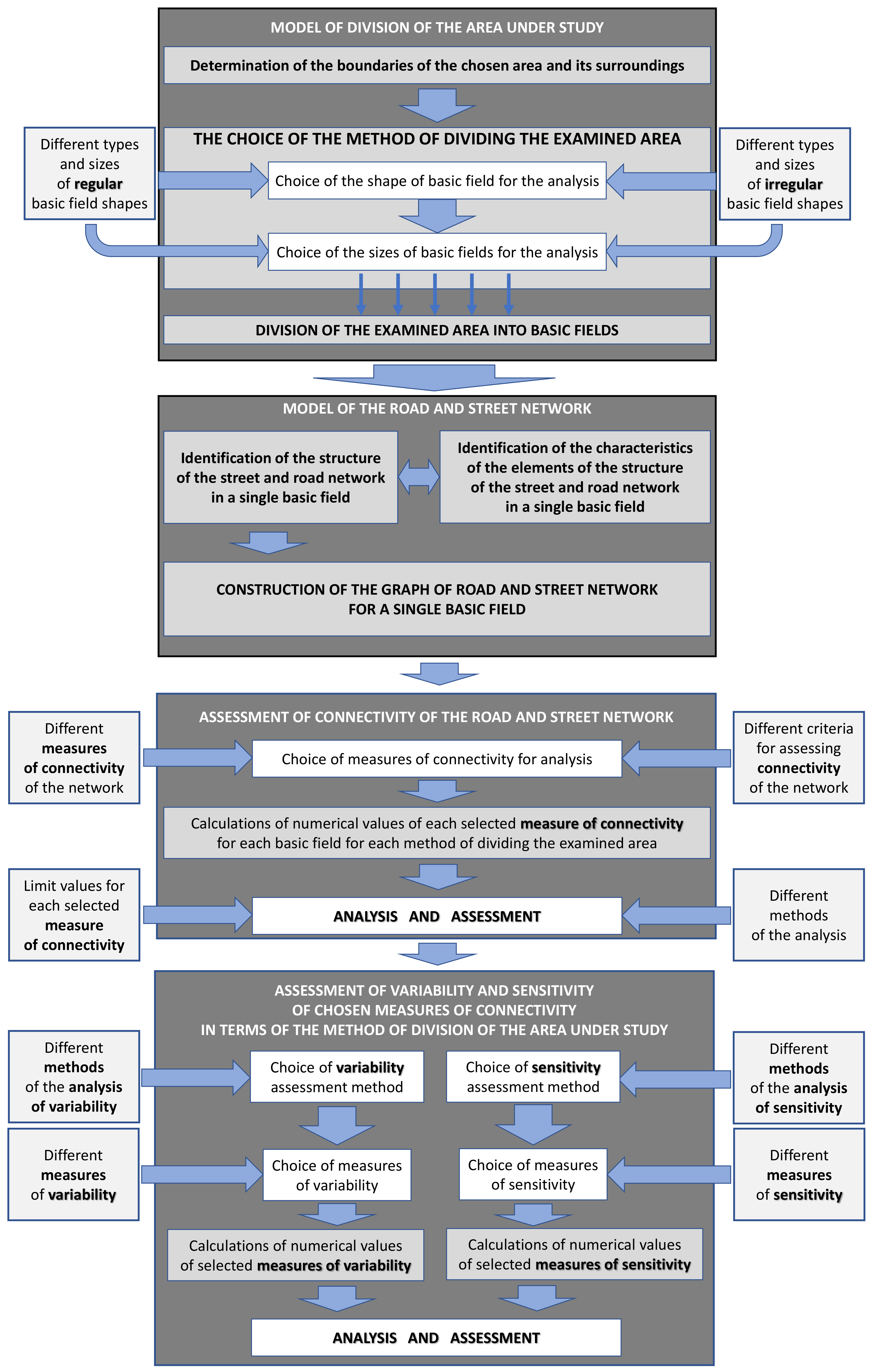
Before proceeding with the analysis of the connectivity of the road and street network in the aspect of the method of division of the studied area, a general research scheme should be prepared, appropriate assumptions should be adopted, and the order of calculation procedures should be determined. This approach also allows for showing the relationships between the various stages of research, organize the computational process, and assist in making various types of decisions and choices at individual stages of the analysis. Figure 1 shows the general scheme of the proposed approach.

The proposed method consists of four main stages. In the first stage, the model of the division of the area is created. It requires determination of the boundaries of the area and a choice of the method of division. The area may be divided into basic fields of regular or irregular shape. Subsequently, the choice of the size of basic fields is determined. In the second stage, the road and street network is modeled. Such a process requires identification of the structure of the network in a single basic field, as well as identification of characteristics of the elements of the structure of road and street network. On that basis, the graph of the network is constructed. The third stage is the assessment of the connectivity of road and street networks for each basic field and the average value for the entire area is estimated. It requires the choice of measures of connectivity and calculations of their numerical values. The last stage is the analysis of the variability and sensitivity to the method of division of the area for each measure. This stage also requires the choice of appropriate measures. Each stage of the method may be adjusted to be more suitable for different, specific problems.

The systemic approach to the examined issue makes it possible to present the proposed method in a general way as an ordered vector:

$$MACRSNDCA=\langle MDCA,MRSN,FC,\mathit{F}\mathit{V}\mathit{S}\rangle$$

(1)

where:

$MACRSNDCA$—Method of the Analysis of the Connectivity of Road and Street Network in terms of Division of the City Area.

$MDCA$−model of division of the city area under study.

$MRSN$—model of the road and street network.

$FC$—matrix containing the values of the measures of the connectivity of the road and street network selected during the analysis.

$\mathit{F}\mathit{V}\mathit{S}$—set of the values of the measures of the variability and sensitivity of the connectivity measures, selected during the analysis.

3.2. Model of the Division of the City Area under Study

The proposed approach assumed that the studied area was divided into a regular grid with basic fields of equal sizes [49,50,65,66,67]. To identify the impact of the size of the basic field on the values of the measures of the assessment of the connectivity of the road and street network, several ways of dividing the analyzed area were introduced. This division is closely related to the size of the basic field. The set of the ways of dividing the analyzed city area (geographical space) into basic fields has been determined as:

$$\mathit{K}=\left\{1, \dots , k, \dots , \overline{K}\right\}$$

(2)

where:

$k$—number of the individual way of dividing the area.

$\overline{K}$—number of all analyzed ways of dividing the area (the size of the set $\mathit{K}$).

Each way of dividing a city area has specific features. In the proposed approach, these values are used at the last stage when analyzing the sensitivity of selected measures of the connectivity of the road and street network. A set of characteristics of the division of the city area was determined in form matrix as:

$$FK=\left[f{k}_{nk}\left(k\right):\hspace{1em}k\in \mathit{K},nk=\overline{1,Nk}\right],$$

(3)

where $f{k}_{nk}\left(k\right)$ has an interpretation of the value (for a quantitative feature) or verbal description (for a quality feature) of the $nk$-th type of attribute of the $k$-th way of dividing the area.

The geographical space, divided in this way, consists of ordered basic fields whose location may be described using the matrix description. This means that each basic field is identified by the row and column number for the $k$-th way of dividing the area of analysis. Appropriate sets of numbers both for rows and for columns were introduced as:

$${\mathit{I}}^k=\left\{1, \dots ,i, \dots , \overline{I^k}\right\},\hspace{1em}k\in \mathit{K},$$

(4)

$${\mathit{J}}^k=\left\{1, \dots ,j, \dots , \overline{J^k}\right\},\hspace{1em}k\in \mathit{K},$$

(5)

where:

$i$—number of the individual row of the matrix describing the divided area.

$\overline{I^k}$—number of all rows in the matrix describing the area divided according to $k$-th way of division (the size of the set ${\mathit{I}}^k$).

$j$—number of the individual column of the matrix describing the divided area.

$\overline{J^k}$—number of all columns in the matrix describing the area divided according to $k$-th way of division (the size of the set ${\mathit{J}}^k$).

The analysis of the assessment of the road and street network connectivity only applies to those basic fields in which elements of the linear transport infrastructure have been identified; therefore, the $inf{r}^k\left(i,j\right)$ coefficient, described on the Cartesian product ${\mathit{I}}^k\times {\mathit{J}}^k$, has been introduced. It takes the value 1, if there is an element of linear transport infrastructure in the basic field located in the $i$-th row and $j$-th column for the $k$-th way of division of the analyzed area; otherwise, the $inf{r}^k\left(i,j\right)$ coefficient equals 0.

The studied area, divided by $k$-th way of division, was determined as a set of the basic fields, as follows:

$${\mathit{R}}^k=\left\{r^k\left(i,j\right):\hspace{1em}inf{r}^k\left(i,j\right)=1, i\in {\mathit{I}}^k,j\in {\mathit{J}}^k\right\},\hspace{1em}k\in \mathit{K},$$

(6)

where $r^k\left(i,j\right)$ has an interpretation of the basic field located at $i$-th row and $j$-th column of the matrix describing the area divided according to $k$-th way of division.

The set containing the models of the city area, divided by selected ways of division was described as:

$$\mathit{R}=\left\{{\mathit{R}}^k:\hspace{1em}k\in \mathit{K}\right\}.$$

(7)

Thus, the model of division of the city area under study $MDCA$ was determined as:

$$MDCA=\langle \mathit{K},FK, \mathit{R}\rangle ,$$

(8)

where:

$\mathit{K}$—set of the ways of dividing the analyzed city area into basic fields.

$FK$—matrix containing the characteristics of the way of dividing the city area.

$\mathit{R}$—set of the models of the city area, divided by selected ways of division.

3.3. Model of the Road and Street Network for the Assessment of Its Connectivity

To assess the structure of the road and street network, it is necessary to build its model, which is a simplified representation of reality [48,49,68]. By introducing simplifications, it is possible to reproduce only this part of the object or its attributes, whose mapping is necessary according to the purpose of the research [23,25,69]. Most often, the transportation network model is presented using graph theory [46,48,70]. In the case of topological assessment, in which the analysis pertains to the assessment of the degree of connections between vertices in a spatial system, the network can be mapped in the form of an undirected, weighted graph [14,50,60,61,63].

The proposed approach assumes that for each basic field, in which elements of transport infrastructure has been identified, an individual graph, containing edges and vertices representing real infrastructure elements (i.e., transport vertices), and intersection points of linear infrastructure elements with the border of the basic field (i.e., border vertices), may be determined.

The graph describing the structure of the road and street network for the basic field has been written as:

$$\mathit{G}\left(r^k\left(i,j\right)\right)=\left(\mathit{W}\left(r^k\left(i,j\right)\right), \mathit{V}\left(r^k\left(i,j\right)\right),\mathit{E}\left(r^k\left(i,j\right)\right)\right),\hspace{1em}{r}^k\left(i,j\right)\in {\mathit{R}}^k,\hspace{1em}k\in \mathit{K},$$

(9)

where:

$\mathit{W}\left(r^k\left(i,j\right)\right)$—set of transport vertices of the graph $\mathit{G}\left(r^k\left(i,j\right)\right)$.

$\mathit{V}\left(r^k\left(i,j\right)\right)$—set of border vertices of the graph $\mathit{G}\left(r^k\left(i,j\right)\right)$.

$\mathit{E}\left(r^k\left(i,j\right)\right)$—set of edges of the graph $\mathit{G}\left(r^k\left(i,j\right)\right)$.

The method of construction of such a graph for an exemplary urban area is shown in Figure 2.

All vertices and edges in each of the basic fields of the graph $\mathit{G}\left(r^k\left(i,j\right)\right)$ are appropriately numbered; therefore, the set of transport vertices of the graph $\mathit{G}\left(r^k\left(i,j\right)\right)$ was determined as:

$$\mathit{W}\left(r^k\left(i,j\right)\right)=\left\{1,\dots ,w,\dots ,\overline{W\left(r^k\left(i,j\right)\right)}\right\},\hspace{1em}{r}^k\left(i,j\right)\in {\mathit{R}}^k,\hspace{1em}k\in \mathit{K},$$

(10)

where:

$w$—number of the individual transport vertex.

$\overline{W\left(r^k\left(i,j\right)\right)}$—number of all transport vertices of the graph $\mathit{G}\left(r^k\left(i,j\right)\right)$.

(the size of the set $\mathit{W}\left(r^k\left(i,j\right)\right)$).

The set of border vertices of the graph $\mathit{G}\left(r^k\left(i,j\right)\right)$ is written as:

$$\begin{gathered} \mathit{V}\left(r^k\left(i,j\right)\right)=\left\{\overline{W\left(r^k\left(i,j\right)\right)}+1,\dots ,v,\dots ,\overline{W\left(r^k\left(i,j\right)\right)}+\overline{V\left(r^k\left(i,j\right)\right)}\right\}, \\ {r}^k\left(i,j\right)\in {\mathit{R}}^k,\hspace{1em}k\in \mathit{K}, \end{gathered}$$

(11)

where:

$v$—number of the individual border vertex of the graph $\mathit{G}\left(r^k\left(i,j\right)\right),$

$\overline{V\left(r^k\left(i,j\right)\right)}$—number of all border vertices of the graph $\mathit{G}\left(r^k\left(i,j\right)\right)$, (the size of the set $\mathit{V}\left(r^k\left(i,j\right)\right)$).

In turn, the set of the edges of the graph $\mathit{G}\left(r^k\left(i,j\right)\right)$ is determined as:

$$\mathit{E}\left(r^k\left(i,j\right)\right)=\left\{1,\dots ,e,\dots ,\overline{E\left(r^k\left(i,j\right)\right)}\right\},\hspace{1em}{r}^k\left(i,j\right)\in {\mathit{R}}^k,\hspace{1em}k\in \mathit{K},$$

(12)

where:

$e$—number of the individual edge of the graph $\mathit{G}\left(r^k\left(i,j\right)\right)$.

$\overline{E\left(r^k\left(i,j\right)\right)}$—number of all edges of the graph $\mathit{G}\left(r^k\left(i,j\right)\right)$ (the size of the set $\mathit{E}\left(r^k\left(i,j\right)\right)$).

Therefore, the structure of the road-street network of the entire, studied area of the city can be presented as a set of graphs of the structure for all basic fields into which this city area was divided, i.e.,

$$\mathit{G}=\left\{\mathit{G}\left(r^k\left(i,j\right)\right):\hspace{1em}{r}^k\left(i,j\right)\in {\mathit{R}}^k, k\in \mathit{K}\right\},$$

(13)

Many different measures are used to assess network connectivity. Some of them are calculated using the characteristics of the elements of the road and street network structure. They can be assigned both to the transport vertices and to the edges. These characteristics are determined for each primary field. Formally, the matrices containing the values of these functions for each single basic field $\left(r^k\left(i,j\right)\right)$ were determined as:

$$FW\left(r^k\left(i,j\right)\right)=\left[f{w}_{nw}\left(w\right):\hspace{1em}w\in \mathit{W}\left(r^k\left(i,j\right)\right),nw=\overline{1,Nw}\right],\hspace{1em}{r}^k\left(i,j\right)\in {\mathit{R}}^k, k\in \mathit{K}$$

(14)

where $f{w}_{nw}\left(w\right)$ has an interpretation of the value of the $nw$-th type of function for the $w$-th transport vertex, and

$$FE\left(r^k\left(i,j\right)\right)=\left[f{e}_{ne}\left(e\right):\hspace{1em}e\in \mathit{E}\left(r^k\left(i,j\right)\right),ne=\overline{1,Ne}\right],\hspace{1em}{r}^k\left(i,j\right)\in {\mathit{R}}^k, k\in \mathit{K}$$

(15)

where $f{e}_{ne}\left(w\right)$ has an interpretation of the value of the $ne$-th type of function for the $e$-th edge.

The matrices containing the values of the characteristics of the elements of the road and street network for all basic fields can be written, respectively, as:

$$FW=\left[FW\left(r^k\left(i,j\right)\right):\hspace{1em}{r}^k\left(i,j\right)\in {\mathit{R}}^k, k\in \mathit{K}\right],$$

(16)

and

$$FE=\left[FE\left(r^k\left(i,j\right)\right):\hspace{1em}{r}^k\left(i,j\right)\in {\mathit{R}}^k, k\in \mathit{K}\right].$$

(17)

The characteristics of the elements of the road and street network structure are not determined for the border vertices.

Thus, the model of road and street network for the assessment of its connectivity, $MRSN$ is determined as:

$$MRSN=\langle \mathit{G},FW, FE\rangle ,$$

(18)

where:

$\mathit{G}$—set of graphs of the structure of all basic fields into which the city area has been divided.

$FW$—matrix containing the values of the characteristics of the transport vertices for all basic fields.

$FE$—matrix containing the values of the characteristics of the edges for all basic fields.

3.4. The Measures of Assessment of Connectivity Road and Street Network

To compare two or several transportation networks, measures describing the degree of the connectivity are used, basing on the topological properties of graphs. In the proposed approach, such measures can also be applied when conducting comparative analyses of the connectivity of road and street networks built for different ways of divisions of the city area under study. The choice of these measures depends primarily on the objectives of the research and the resulting selection criteria.

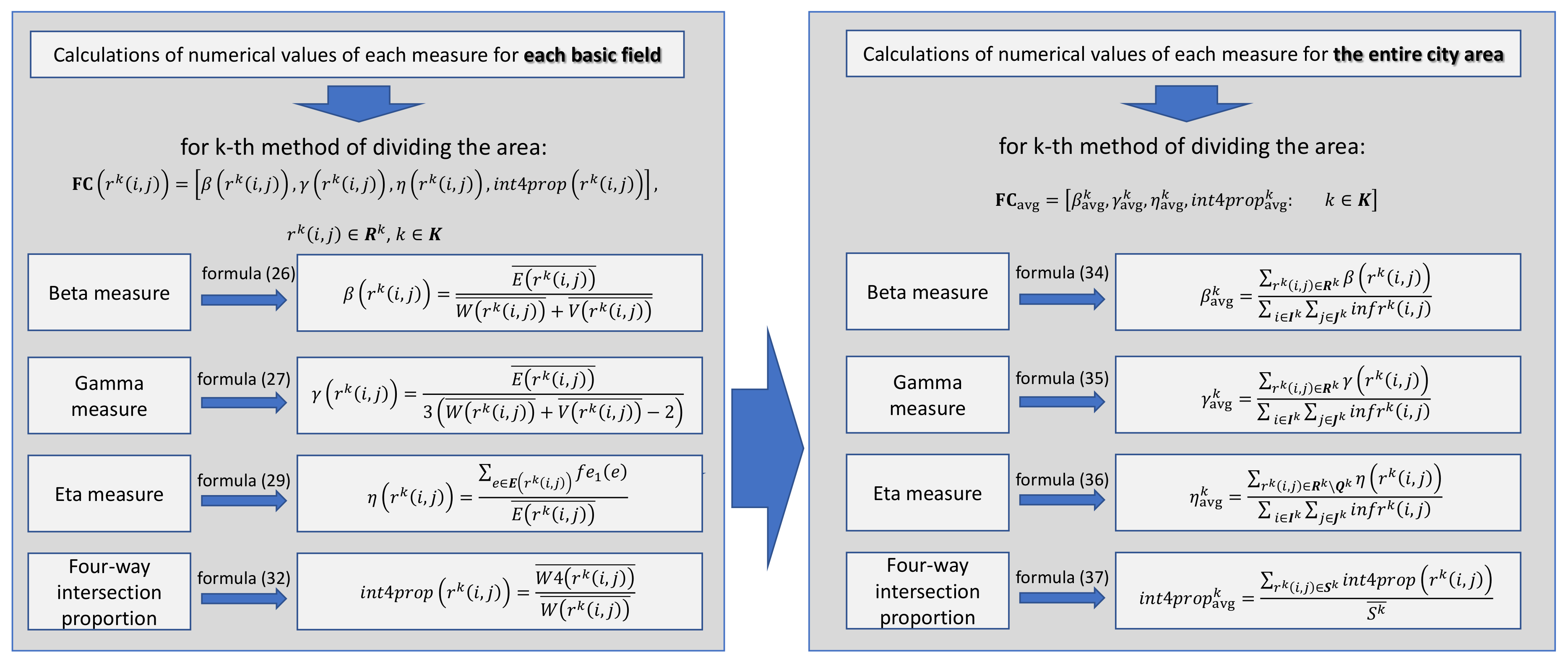
Measures of the connectivity of the road and street network are calculated for every single basic field; therefore, their values for all basic fields can be formally written in the form of the matrix as follows:

$$FC=\left[f{c}_{nc}\left(r^k\left(i,j\right)\right):\hspace{1em}{r}^k\left(i,j\right)\in {\mathit{R}}^k, k\in \mathit{K}, nc=\overline{1,Nc}\right],$$

(19)

where $f{c}_{nc}\left(r^k\left(i,j\right)\right)$ has an interpretation of the value of the $nc$-th type of measure of the connectivity of the road and street network for the basic field $\left(r^k\left(i,j\right)\right)$.

In the proposed approach, the range of values for each of the measures was divided into levels to which limit values were assigned. This allows us to color the basic fields and conduct graphical comparative analyses, which greatly facilitates the formulation of conclusions.

In addition, the average values for each of the measures of connectivity were calculated, which can be written as:

$$f{c}_{nc,\mathrm{avg}}^k=\frac{{{\displaystyle \sum }}_{r^k\left(i,j\right)\in {\mathit{R}}^k}f{c}_{nc}\left(r^k\left(i,j\right)\right)}{{{\displaystyle \sum }}_{ i\in {\mathit{I}}^k}{{\displaystyle \sum }}_{j\in {\mathit{J}}^k}inf{r}^k\left(i,j\right)},\hspace{1em}k\in \mathit{K}, nc=\overline{1,Nc}$$

(20)

For each of the $nc$-th measure of connectivity, the matrix containing the average values for different ways of dividing the city area can be determined as:

$$F{C}_{nc,\mathrm{avg}}=\left[f{c}_{nc,\mathrm{avg}}^k:\hspace{1em}k\in \mathit{K}\right],\hspace{1em}nc=\overline{1,Nc},$$

(21)

In turn, the matrix containing the average values for all selected measures of the connectivity of the road and street network can be written as:

$$F{C}_{\mathrm{avg}}=\left[f{c}_{nc,\mathrm{avg}}^k:\hspace{1em}k\in \mathit{K}, nc=\overline{1,Nc}\right],$$

(22)

This approach makes it possible to compare the values of measures of connectivity for different ways of dividing a city area.

3.5. Assessment of the Variability and Sensitivity of the Measures of the Connectivity to the Method of the Division of the Area

The assessment of the variability and sensitivity of selected measures of the connectivity of the road and street network is an important part of the proposed method. These are two separate methods, but because both are based on statistical techniques, here they are treated together.

The measures used in assessing variability show the average variation between the possible levels of the variable describing the results of the research and its expected value. The starting point for determining the measures of variation is the expected value of the results.

In the proposed method, the variability assessment relates to the measures of the connectivity of the road and street network. The variability measures have been calculated based on the average values of these measures, i.e., $f{c}_{nc,\mathrm{avg}}^k$, for different ways of dividing the studied area of the city.

The matrix containing the values of the measures of the variability of the connectivity measures selected during the analysis is determined as:

$$FV=\left[f{v}_{nv}\left(F{C}_{nc,\mathrm{avg}}\right):\hspace{1em}nc=\overline{1,Nc},nv=\overline{1,Nv}\right],$$

(23)

where $f{v}_{nv}\left(F{C}_{nc,\mathrm{avg}}\right)$ has an interpretation of the value of the $nv$-th type of the measures of the variability of the average values of the $nc$-th measure of connectivity collected in the matrix $F{C}_{nc,\mathrm{avg}}$ for different ways of dividing the city area.

In turn, the sensitivity analysis is based on the assessment of the degree of changes in the output characteristic (dependent variable) caused by changes in the input data (independent variable). This type of analysis supports the prediction of the results using variables that affect these results. There are many techniques used in sensitivity analyzes, among which the most common and simplest are based on regression models [71,72,73,74,75].

In the proposed method, the sensitivity assessment relates both to the measures of the connectivity of the road and street network and to the feature distinguishing different ways of dividing the studied area of the city. Therefore, the matrix containing the values of the measures of the sensitivity of the connectivity measures selected during the analysis is determined as:

$$FS=\left[f{s}_{ns}\left(FK,F{C}_{nc,\mathrm{avg}}\right):\hspace{1em}nc=\overline{1,Nc},ns=\overline{1,Ns}\right],$$

(24)

where $f{s}_{ns}\left(FK,F{C}_{nc,\mathrm{avg}}\right)$ has an interpretation of the value of the $ns$-th type of the measures of the sensitivity of the average values of the $nc$-th measure of connectivity collected in the matrix $F{C}_{nc,\mathrm{avg}}$ for different ways of dividing the city area with respect to the attribute of the method of this division collected in the matrix $FK$.

Thus, the set containing both values of variability measures and sensitivity measures of connectivity of the road and street network is determined as follows:

$$\mathit{F}\mathit{V}\mathit{S}=\left\{FV, FS\right\}\mathbf{.}$$

(25)

3.6. Example of the Computation Procedure for Assessment of the Connectivity of the Road and Street Network with Selected Measures

The Method of the Analysis of the Connectivity of Road and Street Network in terms of Division of the City Area ($MACRSNDCA$) presented in a general manner in the previous sections can be adapted to individual calculation needs, taking into account selected measures. In the presented example, it was assumed that the city area is divided into basic fields of the same square shape; therefore, the way of dividing the area refers only to the size of these fields.

To give an example of the application of the proposed method, the following measures were selected for assessing the connectivity of the road and street network:

• Beta measure.
• Gamma measure.
• Eta measure.
• Four-way intersection proportion.

Because an additional goal of the study was to facilitate the choice of measures, suitable for different sizes of basic fields selected measures needed to be diversified. Hence, authors decided to choose the eta measure, as a measure about the characteristics of the edges of the graph and four-way intersection proportion, and as a measure calculated basing on the characteristics of transport vertices. The set of measures was complemented with beta and gamma measures, both about a ratio of edges and vertices of a graph. Nevertheless, beta and gamma measures are among the most employed measures of connectivity of transport networks [62]. Therefore, based on their significance, the authors decided that these measures must not be omitted.

3.6.1. Beta Measure

The beta measure describes the relationship between the number of edges and the number of vertices in a transportation network. For planar graphs, its value ranges from 0.0 to 3.0. The more complex the network structure is, the higher the numerical values the beta measure adopts. The values lower than one characterize different types of disconnected networks and trees, zero can be obtained for networks without edges, and a value of one means that there is only one circuit in the network. When the disconnected network changes its structure and its connectivity increases with a constant number of edges, a decreasing number of vertices is observed (as in the case of overlapping endpoints into higher-order intersections). The increase in the numerical values of the beta measure is associated with a decrease in the number of graph vertices.

The beta measure for the individual basic field $r^k\left(i,j\right)$ was evaluated as:

$$\beta \left(r^k\left(i,j\right)\right)=f{c}_1\left(r^k\left(i,j\right)\right)=\frac{\overline{E\left(r^k\left(i,j\right)\right)}}{\overline{W\left(r^k\left(i,j\right)\right)}+\overline{V\left(r^k\left(i,j\right)\right)}},\hspace{1em}{r}^k\left(i,j\right)\in {\mathit{R}}^k,\hspace{1em}k\in \mathit{K},$$

(26)

3.6.2. Gamma Measure

The gamma index is the ratio of the observed number of edges to their maximum number. The numerical value close to one is assigned to completely connected networks. On the other hand, values approaching zero distinguish different types of disconnected networks and trees. The gamma measure informs about the size of additions in the network structure necessary to build a completely connected network. This measure does not depend on the number of vertices of the transportation network.

The gamma measure for the individual basic field $r^k\left(i,j\right)$ was evaluated as:

$$\gamma \left(r^k\left(i,j\right)\right)=f{c}_2\left(r^k\left(i,j\right)\right)=\frac{\overline{E\left(r^k\left(i,j\right)\right)}}{3\left(\overline{W\left(r^k\left(i,j\right)\right)}+\overline{V\left(r^k\left(i,j\right)\right)}-2\right)},\hspace{1em}{r}^k\left(i,j\right)\in {\mathit{R}}^k,\hspace{1em}k\in \mathit{K},$$

(27)

3.6.3. Eta Measure

The eta measure expresses the relationship between the transportation network as a whole and its routes as an individual element of the network. The totality of a given transportation network may be determined in various ways, e.g., by the sum of the length of the edges or the size of the traffic flow (the quantity of cargo unit, number of people, etc.). Thus, the eta measure may be calculated as a ratio of the total mileage of the network and the observed number of edges, and expresses the average edge length. The growth in the complexity of the road and street network by introducing additional vertices increases the number of edges (by dividing them) without increasing the total length of the edges. This reduces the numerical value of the eta measure.

The eta measure cannot be evaluated when there is only one edge in the basic field (i.e., when the sum of all vertices (transport vertices and border ones) in this field is equal 2); therefore, the set of the basic fields, in which this case occurs was determined as follows:

$${\mathit{Q}}^k=\left\{r^k\left(i,j\right):\hspace{1em}\overline{E\left(r^k\left(i,j\right)\right)}=1,r^k\left(i,j\right)\in {\mathit{R}}^k\right\},\hspace{1em}k\in \mathit{K},$$

(28)

In addition, information on the length of each edge of the graph for the basic field is necessary to determine this measure. Denoting as $f{e}_1\left(e\right)$ the length of a single edge (with the number $e$) in the graph, the eta measure for the individual basic field $r^k\left(i,j\right)$ was evaluated as:

$$\eta \left(r^k\left(i,j\right)\right)=f{c}_3\left(r^k\left(i,j\right)\right)=\frac{{{\displaystyle \sum }}_{e\in \mathit{E}\left(r^k\left(i,j\right)\right)}f{e}_1\left(e\right)}{\overline{E\left(r^k\left(i,j\right)\right)}},\hspace{1em}{r}^k\left(i,j\right)\in {\mathit{R}}^k\backslash {\mathit{Q}}^k,\hspace{1em}k\in \mathit{K},$$

(29)

3.6.4. Four-Way Intersection Proportion

The degree of an individual vertex of the transportation network is related to the level of its connectivity. It is obvious that the higher the number of four-way intersections is, the more paths may be led between any two places in the network; therefore, the four-way intersection proportion may be treated as a measure of connectivity of road and street network and higher numerical values of this measure (close to one) correspond to the greater connectivity of this network.

This measure can be determined only for basic fields with at least one transport vertex. Therefore, the set of such basic fields was denoted as:

$${\mathit{S}}^k=\left\{r^k\left(i,j\right):\hspace{1em}\mathit{W}\left(r^k\left(i,j\right)\right)\ne \varnothing ,r^k\left(i,j\right)\in {\mathit{R}}^k\right\},\hspace{1em}k\in \mathit{K},$$

(30)

Transport vertices representing the nodes in the real road and street network, i.e., intersections, have a different number of approaches. The methodology assumes that the greater the number of approaches occurs at the intersection, the greater the connectivity of the transport network in the city exists; therefore, vertices representing four-approach intersections have been separated from the set of transport vertices. By determining the number of approaches of single intersection as $f{w}_1\left(w\right)$, the set of four-approach intersections for a basic field may be written as

$$\mathit{W}\mathbf{4}\left(r^k\left(i,j\right)\right)=\left\{w:\hspace{1em}f{w}_1\left(w\right)=4,w\in \mathit{W}\left(r^k\left(i,j\right)\right)\right\},\hspace{1em}{r}^k\left(i,j\right)\in {\mathit{S}}^k,k\in \mathit{K},$$

(31)

Then four-way intersection proportion for the individual basic field $r^k\left(i,j\right)$ may be written as:

$$int4prop\left(r^k\left(i,j\right)\right)=f{c}_4\left(r^k\left(i,j\right)\right)=\frac{\overline{W4\left(r^k\left(i,j\right)\right)}}{\overline{W\left(r^k\left(i,j\right)\right)}},\hspace{1em}{r}^k\left(i,j\right)\in {\mathit{S}}^k, k\in \mathit{K},$$

(32)

where $\overline{W4\left(r^k\left(i,j\right)\right)}$ denotes the number of all four-approach intersections in the single basic field $r^k\left(i,j\right)$, i.e., the size of the set $\mathit{W}\mathbf{4}\left(r^k\left(i,j\right)\right)$.

The set of the measures of the connectivity of the road and street network for the individual basic field $r^k\left(i,j\right)$ was determined as:

$$FC\left(r^k\left(i,j\right)\right)=\left[\beta \left(r^k\left(i,j\right)\right),\gamma \left(r^k\left(i,j\right)\right),\eta \left(r^k\left(i,j\right)\right),int4prop\left(r^k\left(i,j\right)\right)\right],\hspace{1em}{r}^k\left(i,j\right)\in {\mathit{R}}^k, k\in \mathit{K}$$

(33)

The general scheme for assessing the connectivity of the road and street network using the selected four measures is shown in Figure 3.

The average values of all selected measures of the connectivity of the road and street network for the entire area divided by the $k$-th method of division were evaluated as:

$${\beta }_{\mathrm{avg}}^k\equiv f{c}_{1,\mathrm{avg}}^k=\frac{{{\displaystyle \sum }}_{r^k\left(i,j\right)\in {\mathit{R}}^k}\beta \left(r^k\left(i,j\right)\right)}{{{\displaystyle \sum }}_{ i\in {\mathit{I}}^k}{{\displaystyle \sum }}_{j\in {\mathit{J}}^k}inf{r}^k\left(i,j\right)},\hspace{1em}k\in \mathit{K},$$

(34)

$${\gamma }_{\mathrm{avg}}^k\equiv f{c}_{2,\mathrm{avg}}^k=\frac{{{\displaystyle \sum }}_{r^k\left(i,j\right)\in {\mathit{R}}^k}\gamma \left(r^k\left(i,j\right)\right)}{{{\displaystyle \sum }}_{ i\in {\mathit{I}}^k}{{\displaystyle \sum }}_{j\in {\mathit{J}}^k}inf{r}^k\left(i,j\right)},\hspace{1em}k\in \mathit{K},$$

(35)

$${\eta }_{\mathrm{avg}}^k\equiv f{c}_{3,\mathrm{avg}}^k=\frac{{{\displaystyle \sum }}_{r^k\left(i,j\right)\in {\mathit{R}}^k\backslash {\mathit{Q}}^k}\eta \left(r^k\left(i,j\right)\right)}{{{\displaystyle \sum }}_{ i\in {\mathit{I}}^k}{{\displaystyle \sum }}_{j\in {\mathit{J}}^k}inf{r}^k\left(i,j\right)},\hspace{1em}k\in \mathit{K},$$

(36)

$$int4pro{p}_{\mathrm{avg}}^k\equiv f{c}_{4,\mathrm{avg}}^k=\frac{{{\displaystyle \sum }}_{r^k\left(i,j\right)\in {\mathit{S}}^k}int4prop\left(r^k\left(i,j\right)\right)}{\overline{{\mathit{S}}^k}},\hspace{1em}k\in \mathit{K},$$

(37)

where $\overline{S^k}$ denotes the size of the set ${\mathit{S}}^k$.

The matrices containing the average values for each of these measure of connectivity for different ways of dividing the city area can be determined respectively as:

$$F{C}_{1,\mathrm{avg}}=\left[{\beta }_{\mathrm{avg}}^k:\hspace{1em}k\in \mathit{K}\right],$$

(38)

$$F{C}_{2,\mathrm{avg}}=\left[{\gamma }_{\mathrm{avg}}^k:\hspace{1em}k\in \mathit{K}\right],$$

(39)

$$F{C}_{3,\mathrm{avg}}=\left[{\eta }_{\mathrm{avg}}^k:\hspace{1em}k\in \mathit{K}\right],$$

(40)

$$F{C}_{4,\mathrm{avg}}=\left[int4pro{p}_{\mathrm{avg}}^k:\hspace{1em}k\in \mathit{K}\right],$$

(41)

Therefore, the set of the average values of the measures of the connectivity of the road and street network values calculated according to the Equations (34)–(37) was also determined as the matrix:

$$F{C}_{\mathrm{avg}}=\left[{\beta }_{\mathrm{avg}}^k,{\gamma }_{\mathrm{avg}}^k,{\eta }_{\mathrm{avg}}^k,int4pro{p}_{\mathrm{avg}}^k:\hspace{1em}k\in \mathit{K}\right]$$

(42)

The process of calculation of the numerical values of these measures is presented in Figure 4.

3.6.5. Measures of Variability

To assess the variability of the measures of the connectivity to the method of the division of the area selected measures were exploited. In the example, from the numerous set of variability measures, which can generally be divided into classic and positional, as well as into absolute and relative measures, the two most commonly used measures were selected: standard deviation and coefficient of variation. Each of them refers to the average values of the measures of the connectivity, i.e., the values collected in the matrices $F{C}_{1,\mathrm{avg}}$-$F{C}_{4,\mathrm{avg}}$ according to Equations (38)–(41).

The standard deviation was calculated for each of the average values of the measures of the connectivity collected in the matrix $F{C}_{nc,\mathrm{avg}}$ based on the following general equation as:

$$sd\left(F{C}_{nc,\mathrm{avg}}\right)\equiv f{v}_1\left(F{C}_{nc,\mathrm{avg}}\right)=\sqrt{\frac{{{\displaystyle \sum }}_{k=1}^{\overline{K}}{\left(f{c}_{nc,\mathrm{avg}}^k-\overline{f{c}_{nc,\mathrm{avg}}^k}\right)}^2}{\overline{K}}},\hspace{1em}nc=\overline{1,Nc}$$

(43)

where $\overline{f{c}_{nc,\mathrm{avg}}^k}$ means the average value calculated as:

$$\overline{f{c}_{nc,\mathrm{avg}}^k}=\frac{{{\displaystyle \sum }}_{k=1}^{\overline{K}}f{c}_{nc,\mathrm{avg}}^k}{\overline{K}},\hspace{1em}nc=\overline{1,Nc}$$

(44)

The standard deviation is the measure that informs about the average important absolute deviations of the possible outcomes from the expected result. In this case, the higher the value of this deviation, the greater the impact of the way the city area is divided on the values of the connectivity measures of the road and street network.

The second measure selected for the assessment of the connectivity measures concerning the way of division of the area under study is the coefficient of variation, which shows the relationship between the variability of the result and its expected value. This coefficient was calculated for each of the measures of the connectivity collected in the matrix $F{C}_{nc,\mathrm{avg}}$ as a ratio of the standard deviation and the absolute value of the average $\overline{f{c}_{nc,\mathrm{avg}}^k}$, i.e.,

$$cv\left(F{C}_{nc,\mathrm{avg}}\right)\equiv f{v}_2\left(F{C}_{nc,\mathrm{avg}}\right)=\frac{sd\left(F{C}_{nc,\mathrm{avg}}\right)}{\left|\overline{f{c}_{nc,\mathrm{avg}}^k}\right|},\hspace{1em}nc=\overline{1,Nc}$$

(45)

The coefficient of variation shows the amount of deviation of the outcome per unit of the expected result. Higher values of the measure suggest higher dispersion of the average value among different cases of the size of basic fields. It shows whether the values of a given measure in each basic fields are highly diversified in a given method of the division of the area.

Therefore, the matrix containing the values of the measures of the variability of the connectivity measures selected during the analysis was determined as:

$$FV=\left[sd\left(F{C}_{nc,\mathrm{avg}}\right),cv\left(F{C}_{nc,\mathrm{avg}}\right):\hspace{1em}nc=\overline{1,Nc}\right],$$

(46)

3.6.6. Measures of Sensitivity

Sensitivity analysis is a method of checking how systematic changes in model variables affect the effects of these changes. Sensitivity measures used in practice depend mainly on the possibility of formalizing the issue into a mathematical model [71,72,73,74,75]. The simplest solution assumes a linear regression model.

In the example, based on a graphic analysis, a linear relationship between the average value of the connectivity measure and the attribute associated with the size of the basic field being was assumed. The length of the side of a regular square-shaped basic field denoted as $f{k}_1\left(k\right)$ was selected as the attribute depending on the way the area was divided. Therefore, the set of characteristics of the division of the city may be written as:

$$FK=\left[f{k}_1\left(k\right):\hspace{1em}k\in \mathit{K}\right],$$

(47)

Therefore, the linear regression model for each selected measure of connectivity is presented in the following form:

$${\widehat{fc}}_{nc,\mathrm{avg}}^k= {\beta }_{1,nc}·f{k}_1\left(k\right)+{\beta }_{0,nc},\hspace{1em}nc=\overline{1,Nc}$$

(48)

where ${\beta }_{0,nc}$ and ${\beta }_{1,nc}$ are the linear regression coefficients of the model built for $nc$-th measure of connectivity.

In the example, presented in the paper, one measure has been chosen to assess the sensitivity of the models. It is the partial derivative of the regression function relative to the independent variable and it may be written as:

$$f{s}_1\left(FK,F{C}_{nc,\mathrm{avg}}\right)=\frac{\delta \left({\widehat{fc}}_{nc,\mathrm{avg}}^k\right)}{\delta \left(f{k}_1\left(k\right)\right)},\hspace{1em}nc=\overline{1,Nc}$$

(49)

In the case of a simple linear regression, it is equal to the coefficient ${\beta }_{1,nc}$ that expresses the slope of the regression line to the abscissa.

Therefore, the matrix containing the values of the measures of the sensitivity of the connectivity measures selected during the analysis was determined as:

$$FS=\left[f{s}_1\left(FK,F{C}_{nc,\mathrm{avg}}\right):\hspace{1em}nc=\overline{1,Nc}\right],$$

(50)

4. Case Study

To present a practical application of the proposed method and to study the influence of the method of division of the area on the assessment of the connectivity of road and street network a case study was performed. It consisted of several steps, as presented in Figure 3.

The analysis was conducted for road and street network in the city center of Katowice. It was assumed that basic fields would have the regular shape of a square, rather than irregular shape. Hence, a square with a side of 2000 m was overlaid on a chosen part of the city center of Katowice, creating the area of analysis. Subsequently, that area was split into smaller squares (basic fields) to create a regular grid. Four cases of the size of basic fields were analyzed, each one constitutes a separate case of analysis; therefore, for purposes of this analysis, it was assumed that there were four ways of dividing the area $\left(k=1,\dots ,4\right)$, differing in the size of the basic field, not its shape:

• $k=1$-basic fields with a 100 [m] side.
• $k=2$-basic fields with a 200 [m] side.
• $k=3$-basic fields with a 400 [m] side.
• $k=4$-basic fields with a 500 [m] side.

The method of splitting the area into a regular grid has been presented in Figure 5:

Four measures were chosen for further calculations:

• Beta measure-($\beta \left(r^k\left(i,j\right)\right)$).

• Gamma measure-($\gamma \left(r^k\left(i,j\right)\right)$).

• Eta measure-($\eta \left(r^k\left(i,j\right)\right)$).

• Four-way intersection proportion-($int4prop\left(r^k\left(i,j\right)\right))$.

The equations necessary to calculate each measure are presented in Section 3.6. Results of calculations for each basic field in each case of analysis have been presented in graphic form in Figure 6, Figure 7, Figure 8 and Figure 9. In

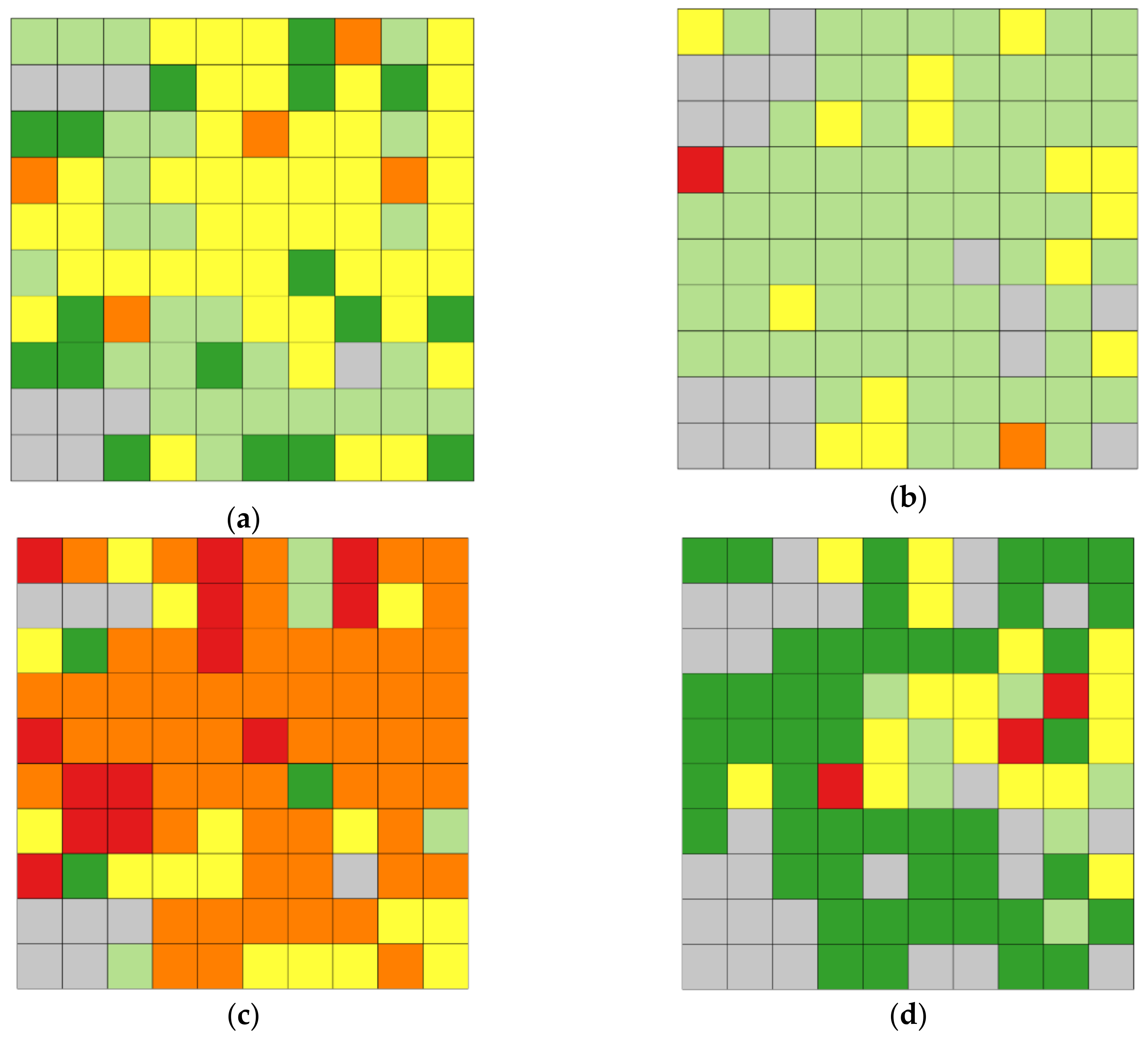
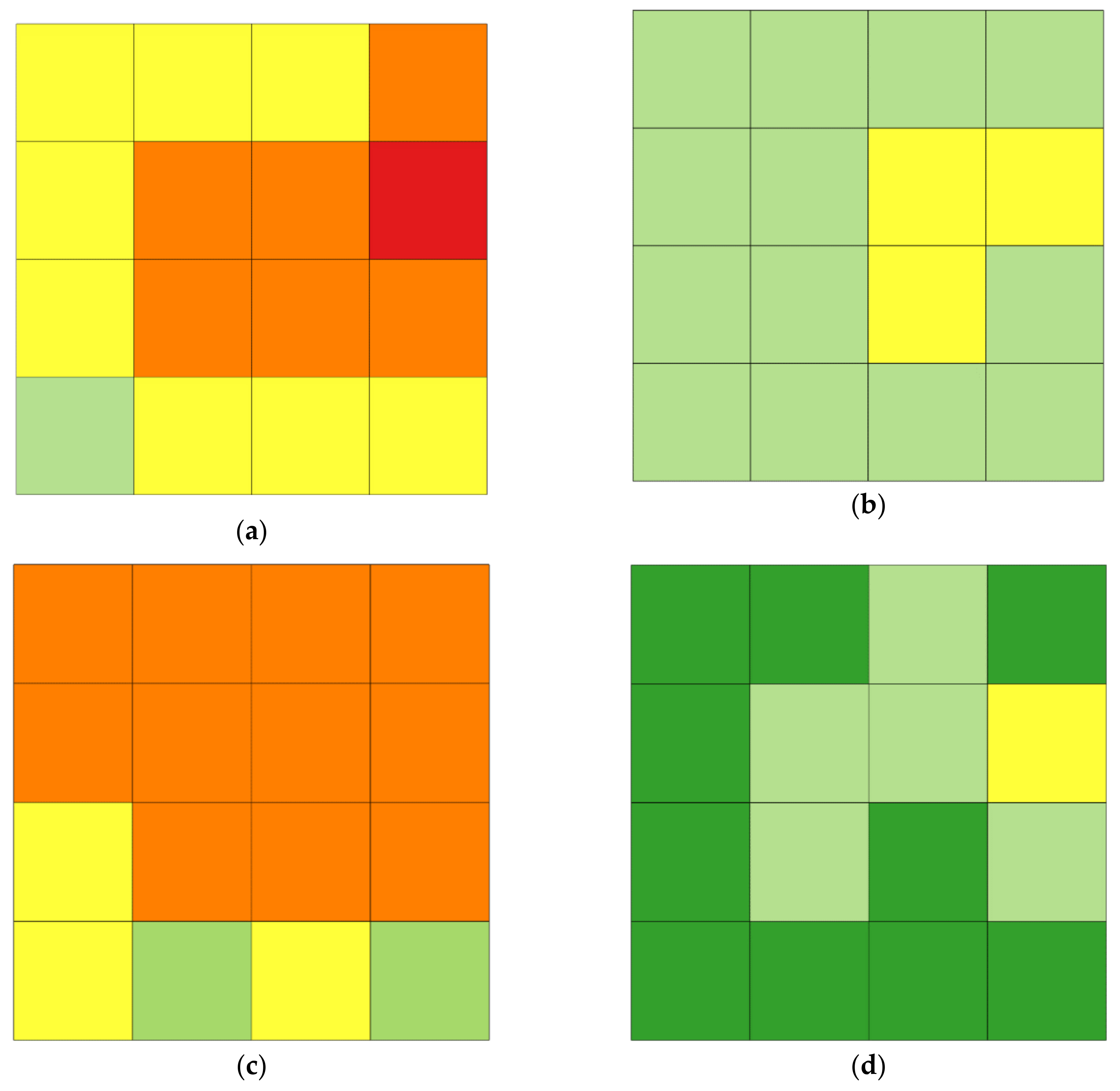
Table 2. Levels of connectivity for each measure.

Level	Color	Numerical Values of:
		$\mathit{\beta }\left({\mathit{r}}^{\mathit{k}}\left(\mathit{i},\mathit{j}\right)\right)$ [-]	$\mathit{\gamma }\left({\mathit{r}}^{\mathit{k}}\left(\mathit{i},\mathit{j}\right)\right)$ [-]	$\mathit{\eta }\left({\mathit{r}}^{\mathit{k}}\left(\mathit{i},\mathit{j}\right)\right)$ [m]	$\mathit{i}\mathit{n}\mathit{t}4\mathit{p}\mathit{r}\mathit{o}\mathit{p}\left({\mathit{r}}^{\mathit{k}}\left(\mathit{i},\mathit{j}\right)\right)$ [-]
Level 1 (very low)		(0.25–0.50>	<0–0.20)	<200–250>	<0–0.20)
Level 2 (low)		(0.50–0.75>	<0.20–0.40)	<150–200)	<0.20–0.40)
Level 3 (average)		(0.75–1.00>	<0.40–0.60)	<100–150)	<0.40–0.60)
Level 4 (high)		(1.00–1.25>	<0.60–0.80)	<50–100)	<0.60–0.80)
Level 5 (very high)		(1.25–1.50>	<0.80–1.00>	<0–50)	<0.80–1.00>
no value

, levels of connectivity for each measure with the corresponding color are presented. The bigger the number of levels, the higher the connectivity of the road and street network in a given basic field.

Results of calculations for the first case of analysis ($k=1$-basic fields with a side of 100 m) are presented in Figure 6.

As can be seen in Figure 6, in the first case of analysis, the numerical values of the beta measure were usually very low or low (level 1 and 2) or low (level 2) and average (level 3) for gamma measure. In the case of only one basic field, the gamma measure exceeded 0.60. On the other hand, values of eta measure were usually high or very high. In the case of four-way intersection proportion, one can observe a high diversification, both very low and very high values were obtained; however, in the case of that measure, there is also the biggest number of basic fields with no value. Results of calculations for the second case of analysis ($k=2$-basic fields with a side of 200 m) have been presented in Figure 7.

According to Figure 7, there are significant differences between levels of connectivity of road and street network in the case of different measures. The eta measure provides higher levels than other measures—like in the case of 100 m basic fields. It seems that the level of connectivity in the case of gamma measure was relatively low (second level) and similar in most of the area. The level of connectivity assessed using beta measure was usually average. Lowest levels of connectivity were obtained while using the four-way intersection proportion measure. In the case of this measure, there was also the biggest number of basic fields with no calculated values (as there were no intersections in said basic fields, it was impossible to calculate the numerical value).

Results of calculations for the third case of analysis ($k=3$-basic fields with a side of 400 m) are presented in Figure 8.

In the case of analysis (basic fields with a twice bigger side than in the second case of analysis), there was a significantly smaller number of basic fields with no calculated value—only one for each measure. It is also worth noting that there are differences in results of the assessment of connectivity of road and street network in the case of each measure. The level of connectivity in the same basic field may be assessed as very low, low, average, or high. In the case of beta measure, for most basic fields, the level of connectivity was assessed as average or high. Similar results were obtained for the eta measure, however with a prevalence of the high level. Lower values were calculated in the case of the gamma measure and the lowest for four-way intersection proportion. It is also important to notice that 19 out of 25 basic fields in the case of gamma measure were assigned to the same level of connectivity.

Results of calculations for the fourth case of analysis ($k=4$-basic fields with a side of 500 m) are presented in Figure 9.

The last case of analysis pertained to the analysis of basic fields with a side of 500 m. It can be observed that the highest levels of connectivity were calculated for the beta and eta measures. Results for the gamma measure seem to be similar to these for the third case of analysis; however, only 3 out of 16 basic fields were not assigned to the second level of connectivity. Again, in the case of the four-way intersection proportion, the lowest levels of connectivity were obtained. When using 500 m side of a basic field, it was possible to calculate the numerical values of each measure for each basic field.

The number of basic fields in each case of analysis for which it was possible to calculate the value of each measure is presented in

Table 3. Number and share of basic fields with the calculated value of each measure in each case of analysis.

Case of Analysis	$\mathit{\beta }\left({\mathit{r}}^{\mathit{k}}\left(\mathit{i},\mathit{j}\right)\right)$		$\mathit{\gamma }\left({\mathit{r}}^{\mathit{k}}\left(\mathit{i},\mathit{j}\right)\right)$		$\mathit{\eta }\left({\mathit{r}}^{\mathit{k}}\left(\mathit{i},\mathit{j}\right)\right)$		$\mathit{i}\mathit{n}\mathit{t}4\mathit{p}\mathit{r}\mathit{o}\mathit{p}\left({\mathit{r}}^{\mathit{k}}\left(\mathit{i},\mathit{j}\right)\right)$
	[-]	[%]	[-]	[%]	[-]	[%]	[-]	[%]
100 [m] basic fields	306	80.00	227	56.75	306	76.50	178	44.50
200 [m] basic fields	91	91.00	83	83.00	91	91.00	73	73.00
400 [m] basic fields	24	96.00	24	96.00	24	96.00	24	96.00
500 [m] basic fields	16	100.00	16	100.00	16	100.00	16	100.00

.

According to Table 3, there are differences among the number of basic fields for which it was possible to calculate the numerical values of each measure in each case of analysis. These differences occur for gamma measure and four-way intersection proportion. The latter is a measure with the smallest number of basic fields with the numerical value, for the first and second case of analysis. In the case of the gamma measure, the number of basic fields with numerical value was bigger, although smaller than for the beta measure and eta measure.

In each case of analysis, the mean value for each measure was calculated. The results are presented in

Table 4. Mean values for each measure of the connectivity of the road and street network-$F{C}_{\mathrm{avg}.}$

Case of Analysis	${\mathit{\beta }}_{\mathbf{a}\mathbf{v}\mathbf{g}}^{\mathit{k}}$ [-]	${\mathit{\gamma }}_{\mathbf{a}\mathbf{v}\mathbf{g}}^{\mathit{k}}$ [-]	${\mathit{\eta }}_{\mathbf{a}\mathbf{v}\mathbf{g}}^{\mathit{k}}$ [m]	$\mathit{i}\mathit{n}\mathit{t}4\mathit{p}\mathit{r}\mathit{o}{\mathit{p}}_{\mathbf{a}\mathbf{v}\mathbf{g}}^{\mathit{k}}$ [-]
100 [m] basic fields	0.65	0.39	58.08	0.23
200 [m] basic fields	0.78	0.36	84.12	0.18
400 [m] basic fields	0.98	0.36	94.44	0.17
500 [m] basic fields	0.99	0.35	95.06	0.15

.

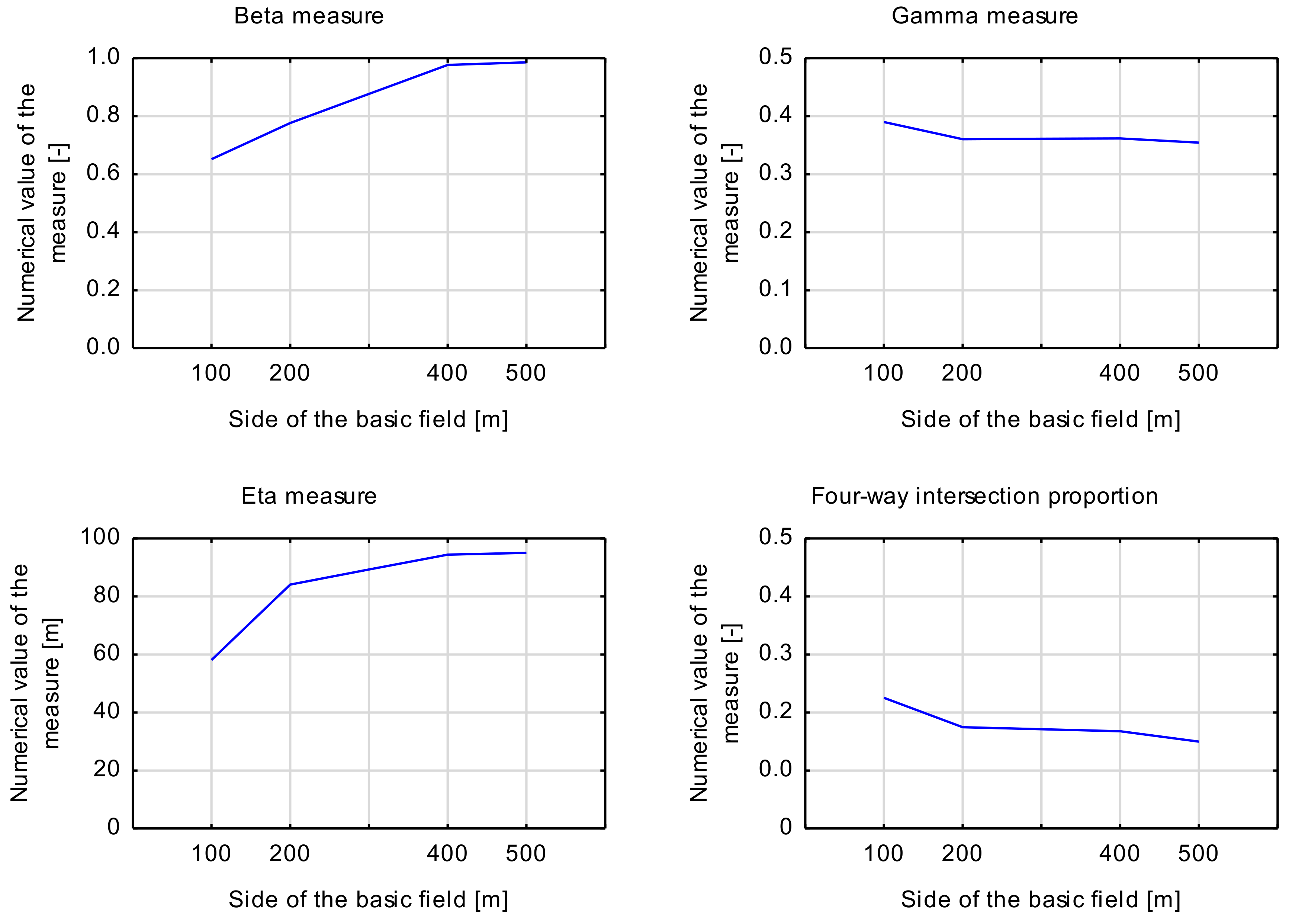
It is also important to analyze the direction of the tendency of variation of the mean value of each measure for each case of the division of the area. Said tendency may be unidirectional or non-unidirectional. To examine it, the variation of the mean value of each measure is presented in a diagram in Figure 10.

According to Table 4 and Figure 10, in the case of two measures: the beta measure and the eta measure, the level of connectivity increases as the size of the basic field increases; however, in the case of the four-way intersection proportion measure and gamma measure the average level was lower in bigger basic fields. This leads to the conclusion that the influence of the size of the basic field on the assessment of the level of density is complex and not similar among examined measures. What also varies is the strength of the impact of the size of the basic field. In the case of beta measure, the difference between average values in each case of analysis was much higher than in the case of the gamma measure. This can lead to the conclusion that beta measure is much more sensitive to the change in the size of the basic field. On the other hand, the gamma measure seems to display the lowest sensitivity to such change.

To study the variability of each measure to the size of the basic field, a standard deviation, as well as a coefficient of variation, were calculated for each measure. The coefficient of variation is a measure calculated by dividing the standard deviation by a mean value of a variable. Hence, the higher the value of the coefficient of variation, the bigger the dispersion of the mean value, and the bigger the variance of the measure in different cases of the size of the basic field. The results of the calculations are presented in

Table 5. Measures of the variability.

Measure of the Variability	${\mathit{\beta }}_{\mathbf{a}\mathbf{v}\mathbf{g}}^{\mathit{k}}$ [-]	${\mathit{\gamma }}_{\mathbf{a}\mathbf{v}\mathbf{g}}^{\mathit{k}}$ [-]	${\mathit{\eta }}_{\mathbf{a}\mathbf{v}\mathbf{g}}^{\mathit{k}}$ [m]	$\mathit{i}\mathit{n}\mathit{t}4\mathit{p}\mathit{r}\mathit{o}{\mathit{p}}_{\mathbf{a}\mathbf{v}\mathbf{g}}^{\mathit{k}}$ [-]
mean value-$\overline{f{c}_{nc,\mathrm{avg}}^k}$	0.85	0.37	82.93	0.18
standard deviation-$sd\left(F{C}_{nc,\mathrm{avg}}\right)$	0.14	0.02	14.99	0.03
coefficient of variation-$cv\left(F{C}_{nc,\mathrm{avg}}\right)$	0.17	0.04	0.18	0.16

.

According to Table 5, the measure with the lowest coefficient of variation is a gamma measure, which indicates that its mean value is the most stable in all cases of the size of the basic field.

Subsequently, the sensitivity of each measure to the change of the size of the basic field was calculated. Results are presented in

Table 6. Measure of the sensitivity.

Measure of the Sensitivity	${\mathit{\beta }}_{\mathbf{a}\mathbf{v}\mathbf{g}}^{\mathit{k}}$ [-]	${\mathit{\gamma }}_{\mathbf{a}\mathbf{v}\mathbf{g}}^{\mathit{k}}$ [-]	${\mathit{\eta }}_{\mathbf{a}\mathbf{v}\mathbf{g}}^{\mathit{k}}$ [m]	$\mathit{i}\mathit{n}\mathit{t}4\mathit{p}\mathit{r}\mathit{o}{\mathit{p}}_{\mathbf{a}\mathbf{v}\mathbf{g}}^{\mathit{k}}$ [-]
$f{s}_1\left(FK,F{C}_{nc,\mathrm{avg}}\right)$	0.0009	−0.00008	0.0843	−0.0002

.

According to results presented in Table 6, the measure of the connectivity that exhibits the lowest sensitivity to the change of the size of the basic field is the gamma measure. In the case of this measure, the line of regression is almost parallel to the abscissa (the slope is relatively small and equals −0.00008). Other measures are more sensitive to the change in the size of the basic field.

5. Discussion

Obtained results of the analysis of the variability and the sensitivity of selected measures of connectivity show a significant diversification among them.

In the case of the beta measure, it can be observed that the level of connectivity was increasing with the increase of the side of the basic field. In the first case of analysis, the level of connectivity was assessed as low or even very low, for the second case of analysis, the level of connectivity was assessed mostly as average, and for third and fourth, generally as either average or high.

For the gamma measure, it was observed that the average level of connectivity assessed using this measure was decreasing. It is also worth noticing that the gamma measure can give a false sense of equality of the level of connectivity in case of bigger basic fields. Only in the case of 100 m was there a diversification of assessed levels among analyzed fields. For this measure, it was not possible to calculate the numerical value in case of more basic fields than for beta measure.

Using the eta measure led to a much higher assessment of the level of connectivity than in case of other measures and the case of the first and second cases of analysis. In the third and fourth cases, results obtained using this measure were similar to beta measure.

On the other hand, using of four-way intersection proportion led to the lowest assessment of the level of connectivity. It is also worth noticing that for the first case of analysis there were significantly more basic fields with no value than for other measures.

These results suggest that the scope of application of each measure is not similar. Numerical values of beta and gamma measures, calculated for smaller basic fields seem to be too low, as in case of the basic field with a side of 100 and 200 m, it is much more possible that the graph of road and street network will be disconnected and that it will consist of several short edges. In the case of bigger basic fields, edges are divided by the border of basic fields less often, and values of beta and eta measures seem to be stable. Hence, it seems that the values of beta and eta measure should be computed only if the road and street network is divided into regular fields with a side of at least 400 m. The values of gamma measure and four-way intersection proportions seem to be more stable. That conclusion is confirmed by the analysis of variability and sensitivity—the gamma measure has the lowest values of both exploited measures of variability and the measure of sensitivity as well. It implies that the gamma measure may not depict the differences among graphs of different sizes (the bigger the basic field the bigger the graphs that represent the road and street network). This conclusion seems to be in accordance with other research, i.e., [60]. The values of the measures of variability and sensitivity for the four-way intersection proportion are also relatively small; however, they are much closer to the values calculated for the beta measure.

6. Conclusions

Findings on measures of connectivity of road and street network, presented in this paper, combined with the mathematical description of the method of computation in the case of an area divided into fields of regular size may be applied in a variety of research associated with the modeling of transport supply in Smart Cities. The results of the analysis of the variability and the sensitivity of selected measures of connectivity to the size of basic fields may facilitate decisions on which measures should be used for a given size of a territorial unit. Mathematical description and presented formulas may be implemented into a dedicated software for computation.

Future research should be focused on increasing the number of analyzed cities and their networks and the application of other measures of connectivity. Another possible area of research is the analysis of different measures of the structure of road and street networks, i.e., density, to provide a comprehensive view on the variety of aspects of transport supply in Smart Cities.