Symbolic Computation to Solving an Irrational Equation on Based Symmetric Polynomials Method
Abstract
1. Introduction
2. The Method of Symmetric Polynomials for Solving Irrational Equations Using Computer Mathematical Packages
2.1. The Core of the Problem of the Extraneous Solutions
2.2. Methods of Elimination of the False Solutions
2.2.1. Validation by the Numerical Solution
2.2.2. Determining the Domain of the Admissible Solutions through Symmetric Polynomials
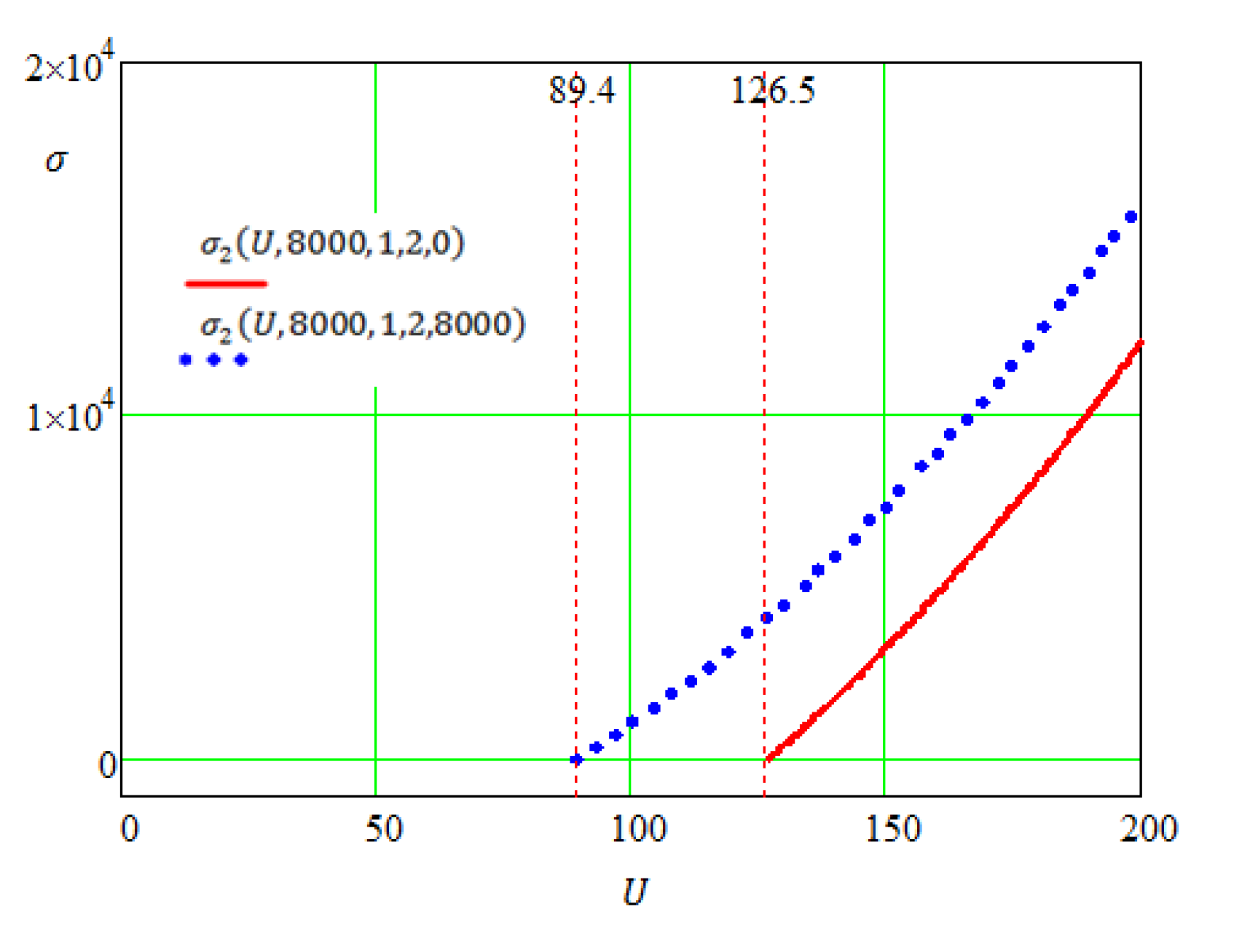
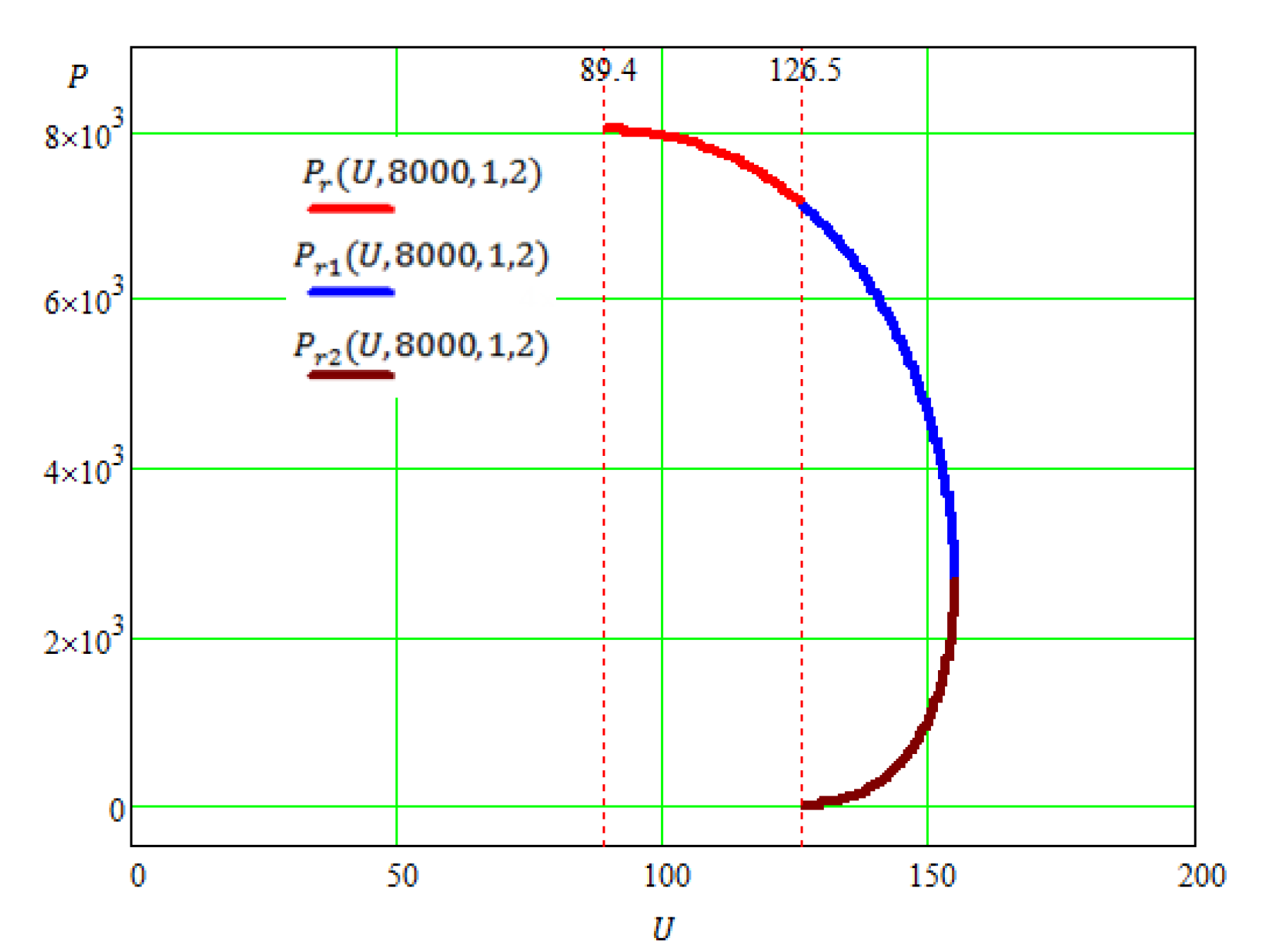
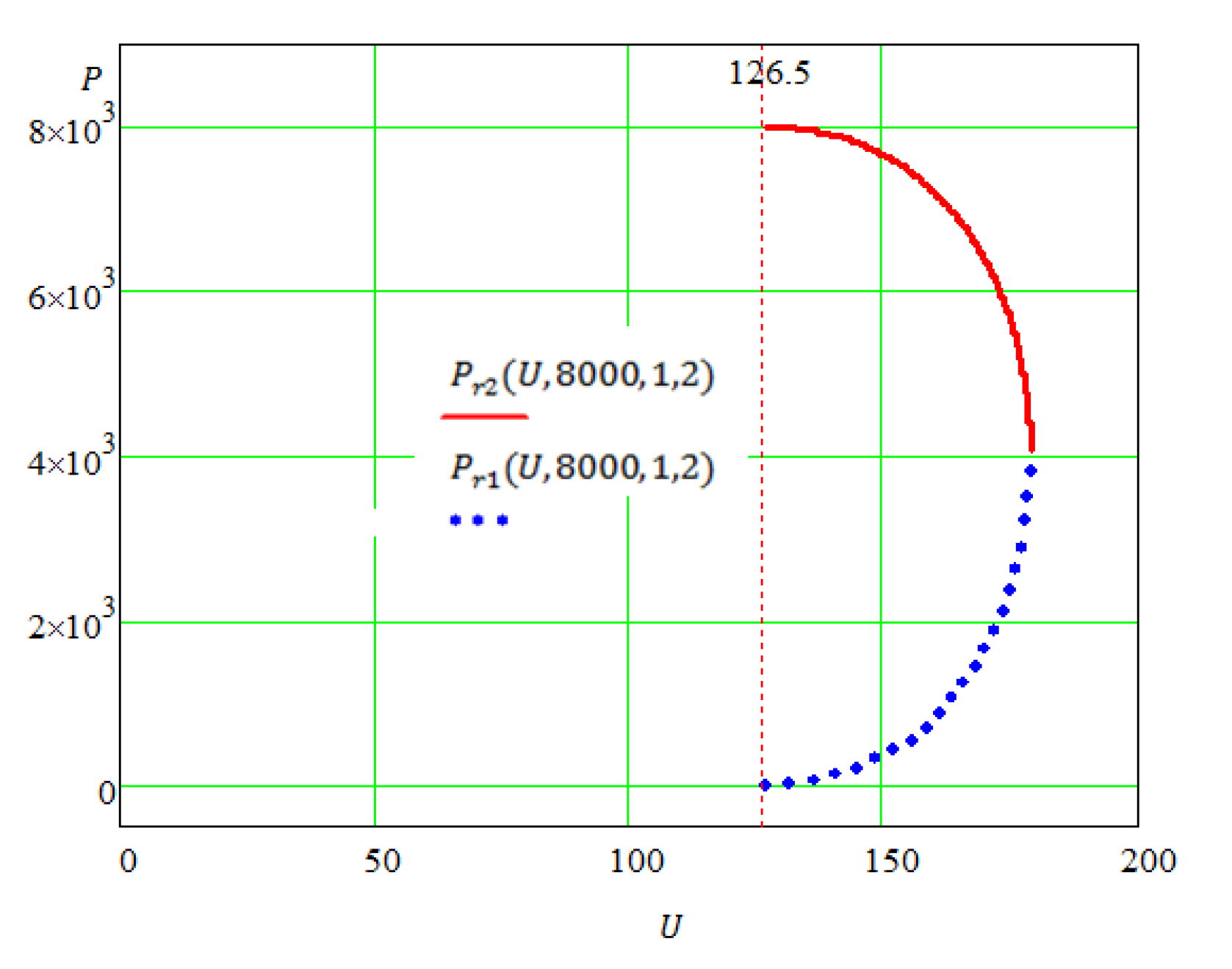
2.3. Application of the Proposed Method for Solving an Electrical Problem
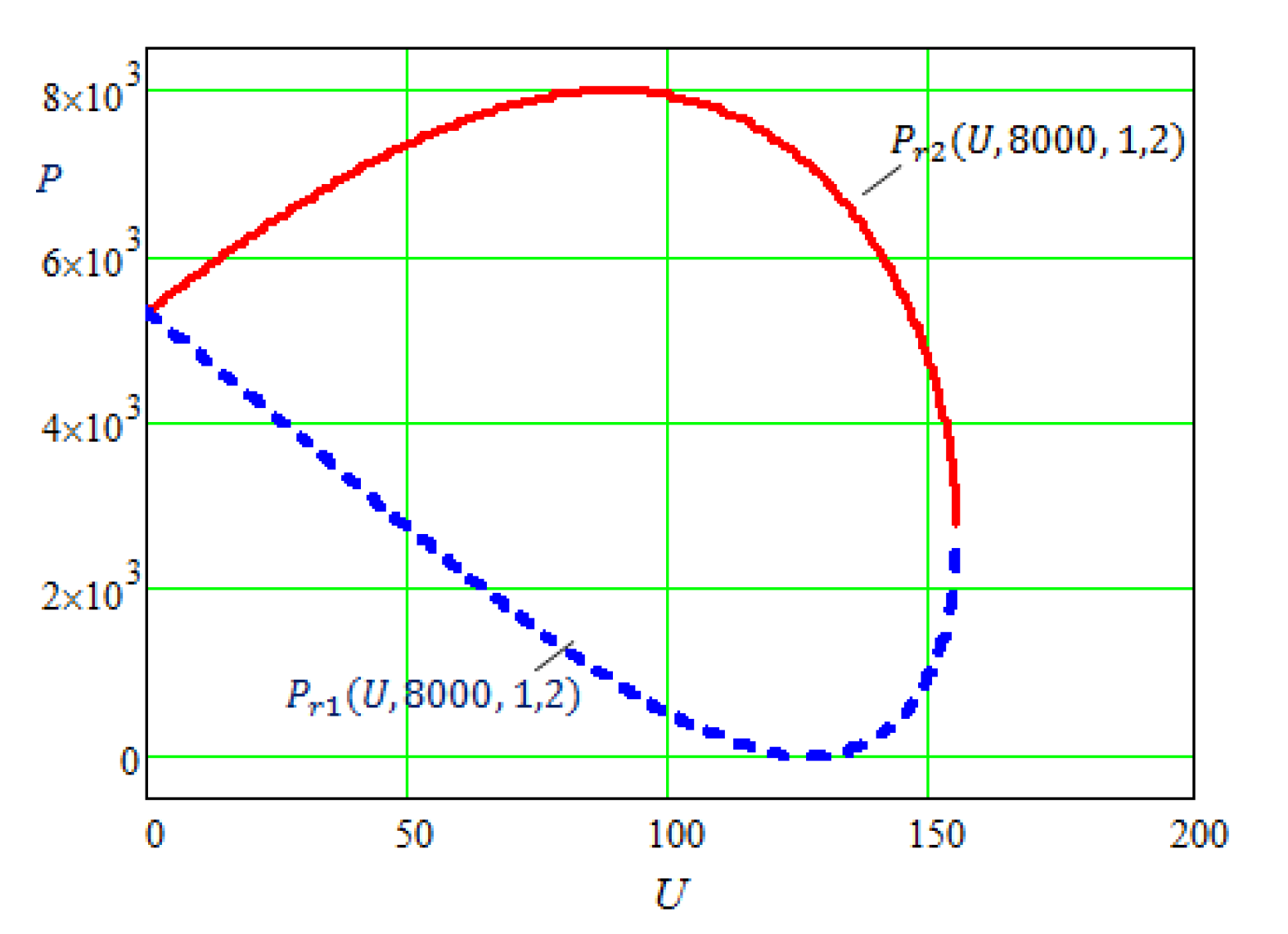
- For U < 89.4 both solutions Pr1 (U, 8000, 1, 2) and Pr2 (U, 8000, 1, 2) are false;
- For 89.4 ≤ U < 126.5 solution Pr1 (U, 8000, 1, 2) is false, while Pr2 (U, 8000, 1, 2) is true;
- For U ≥ 126.5 both solutions Pr1 (U, 8000, 1, 2) and Pr2 (U, 8000, 1, 2) are true.
2.3.1. Implementation of the Proposed Method
2.3.2. A Special Case
3. Application of Additional Methods of Analysis for Solving Irrational Equations Using Computer Mathematical Packages
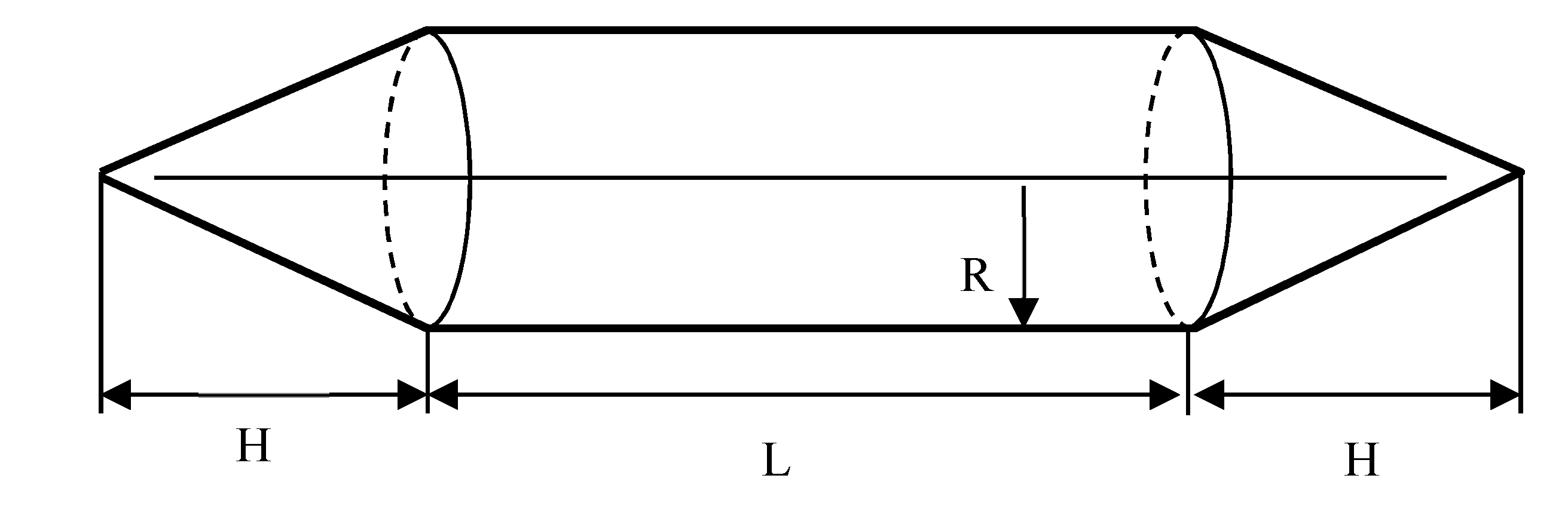
3.1. Initial Formulation of the Problem
3.2. Solution of the Problem in the Initial Formulation
3.2.1. Analytical Solution
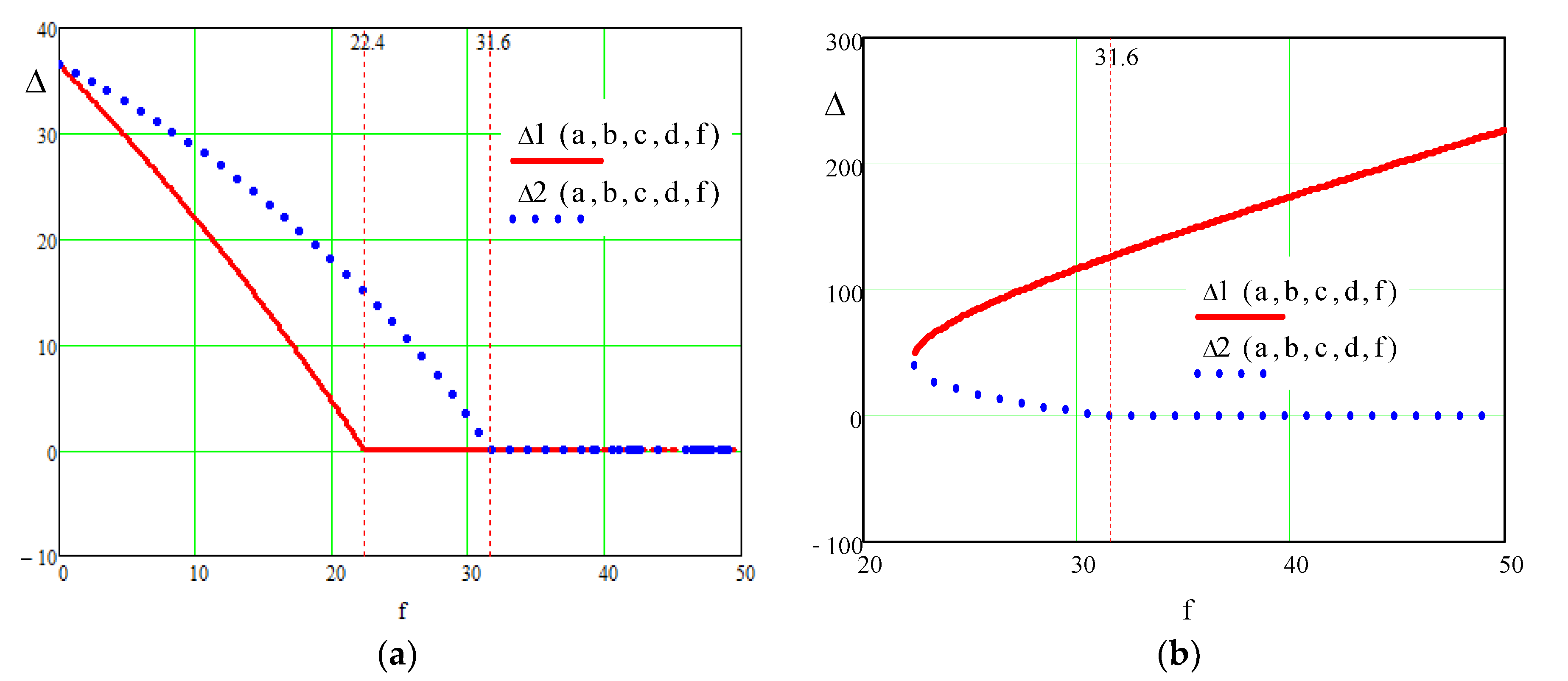
3.2.2. Analysis of the Solution of the Problem in the Initial Formulation
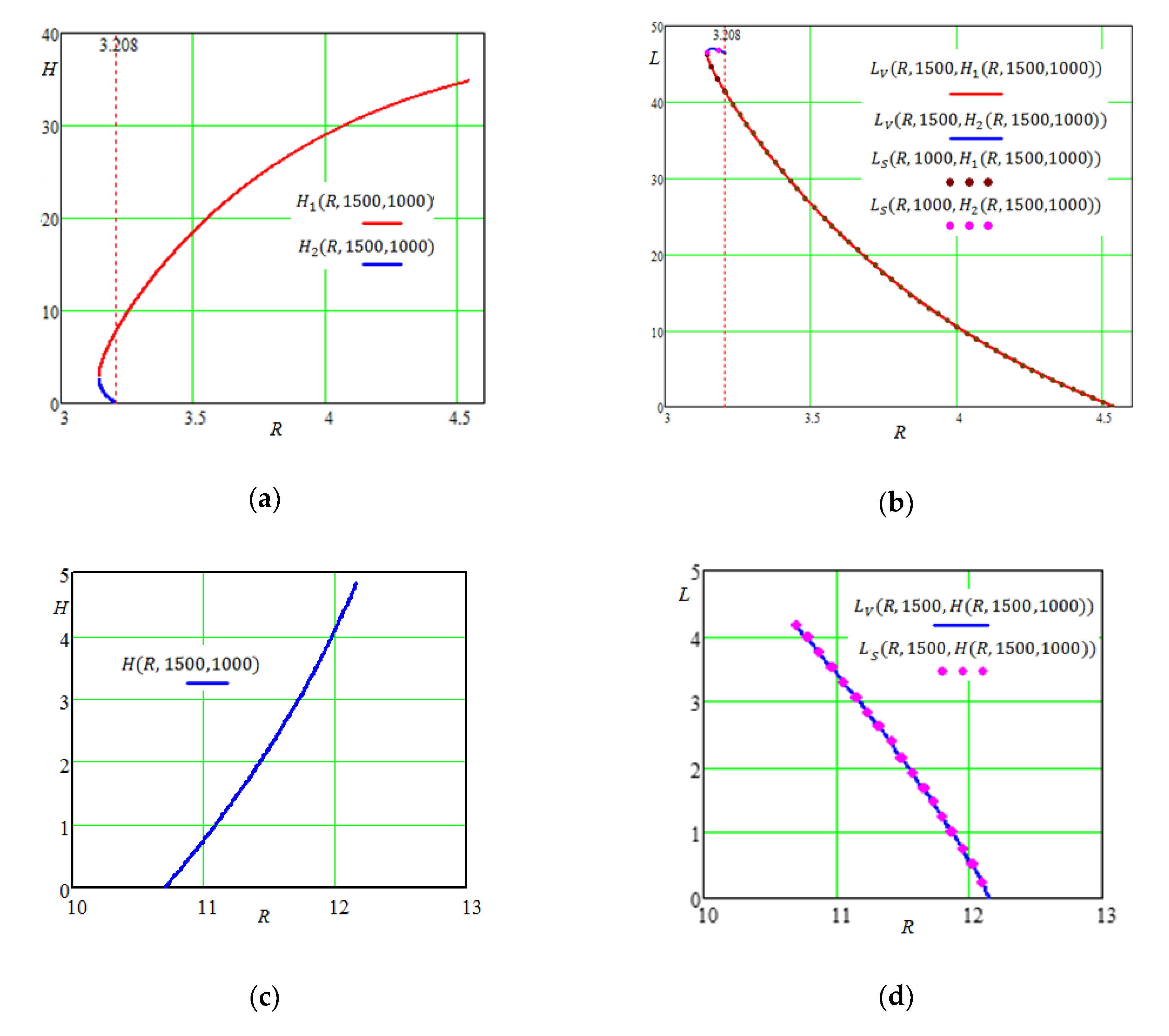
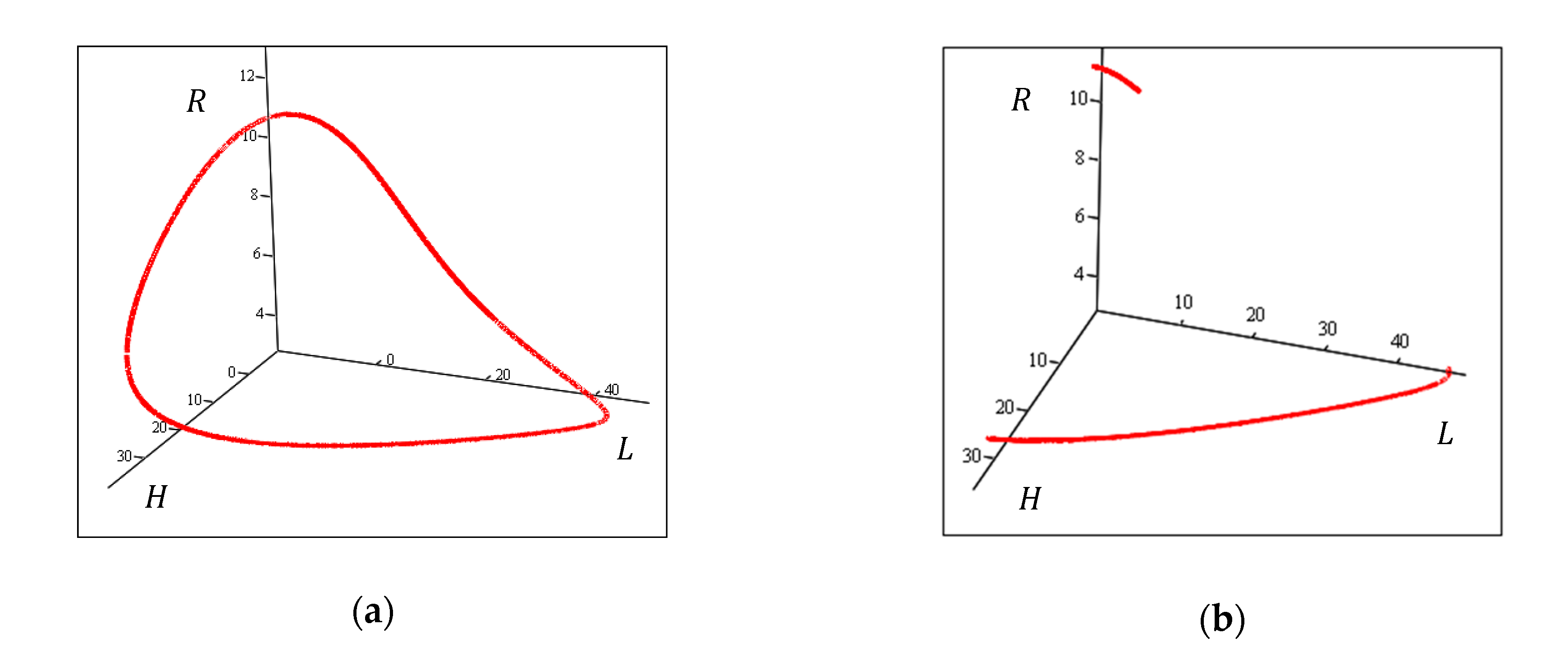
3.3. Problem Solution Based on Symmetric Polynomials
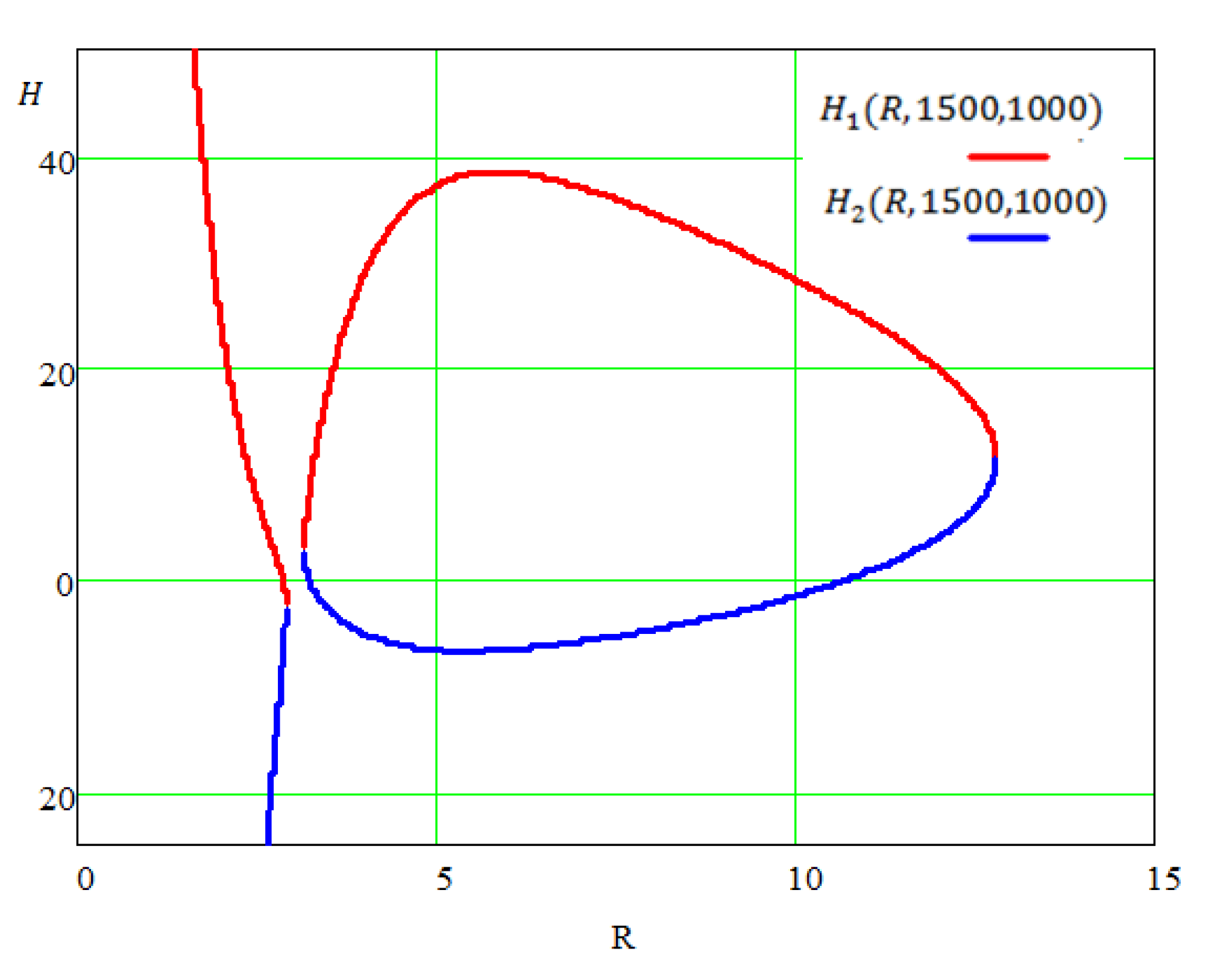
3.3.1. Determining the Range of Admissible Solutions
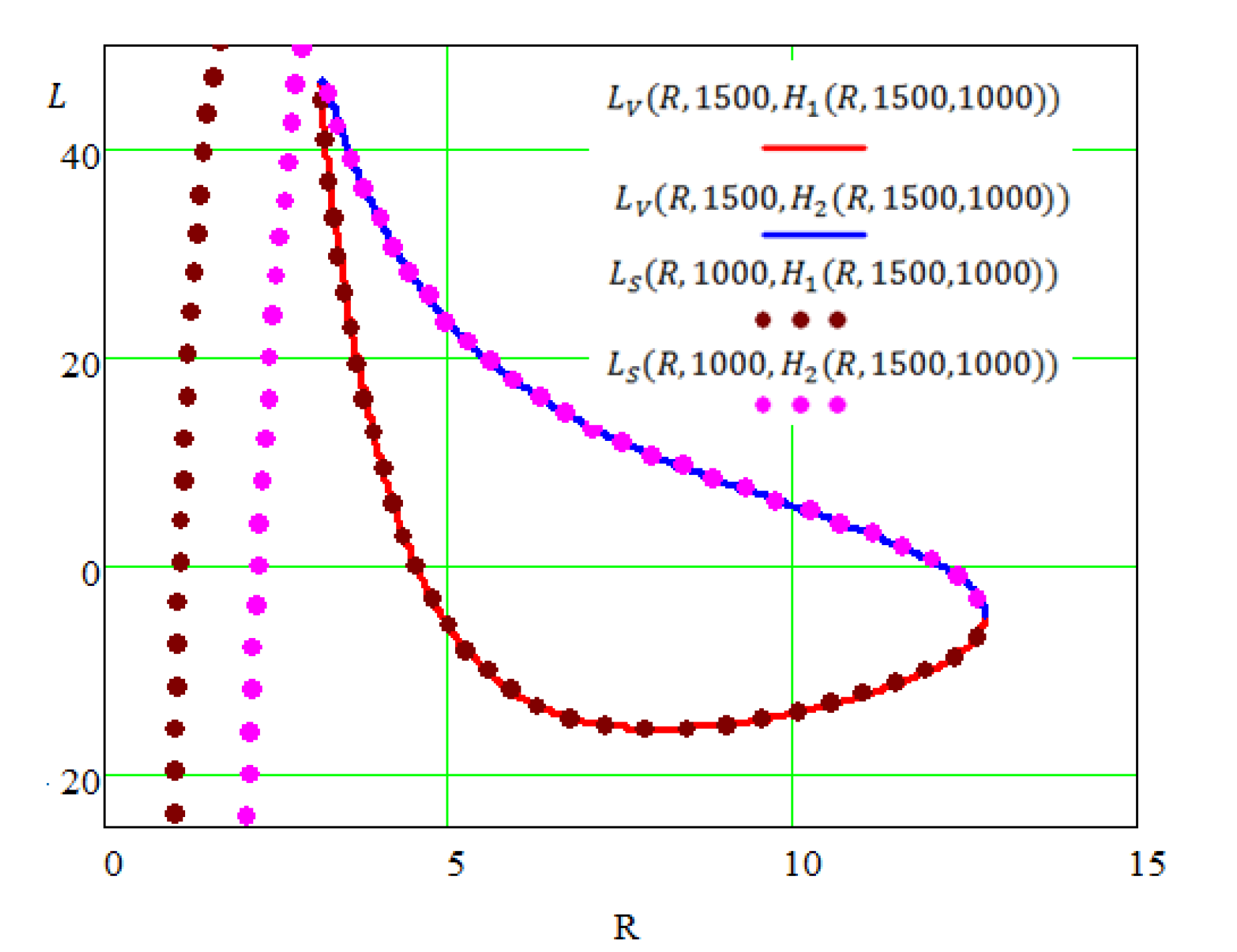
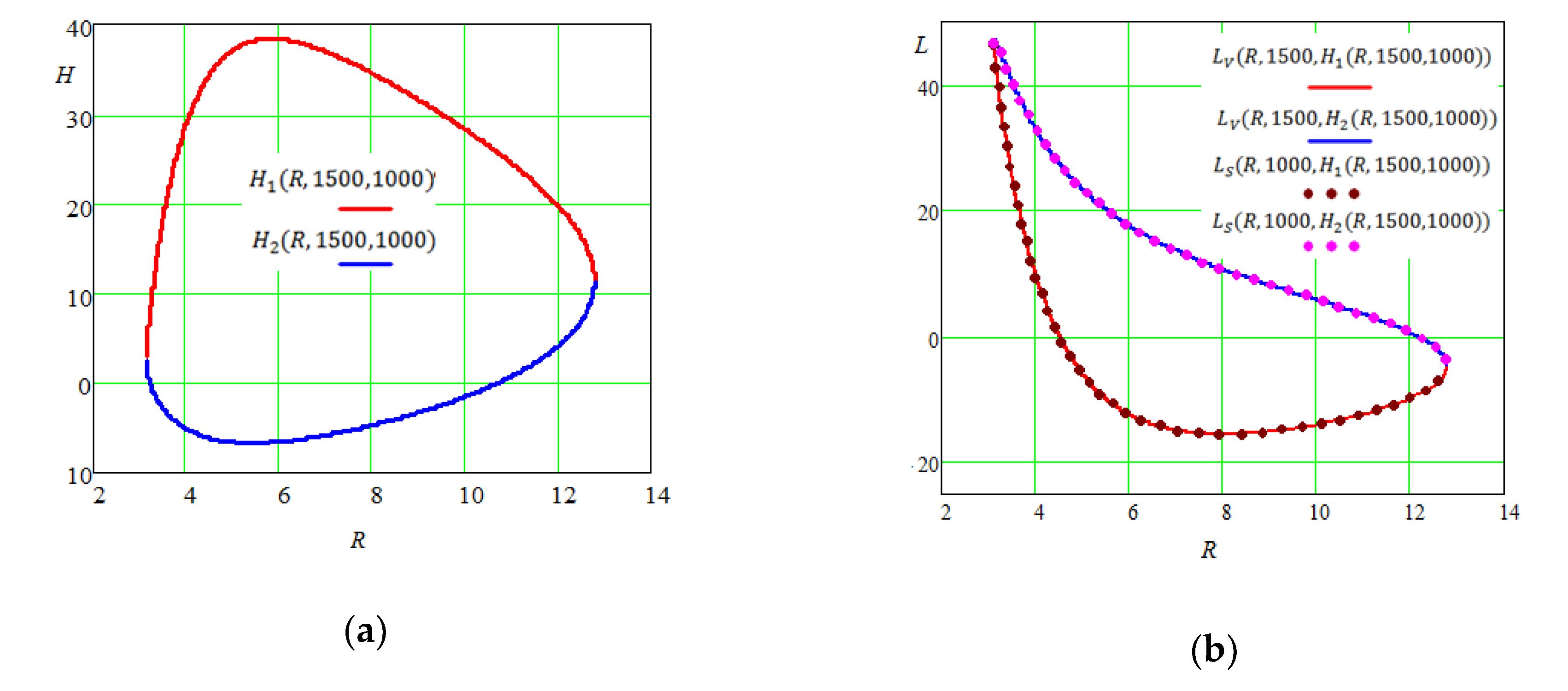
3.3.2. Eliminating Solutions without Physical Meaning
4. Discussions of the Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Fre, P.G.; Fedotov, A. Groups and Manifolds: Lectures for Physicists with Examples in Mathematica; Walter de Gruyter: Berlin, Germany, 2018; 475p. [Google Scholar]
- Brenner, A.; Shacham, M.; Cutlip, B. Applications of mathematical software packages for modeling and simulations in environmental engineering education. Environ. Model. Softw. 2005, 20, 1307–1313. [Google Scholar] [CrossRef]
- Steeb, W.-H.; Tanski, I.; Hardy, Y. Problems and Solutions for Groups, Lie Groups, Lie Algebras with Applications; World Scientific Publishing Company: Singapore, 2012. [Google Scholar] [CrossRef]
- Meier, J.; Smith, D. Algebra and symmetry. In Exploring Mathematics: An Engaging Introduction to Proof (Cambridge Mathematical Textbooks); Cambridge University Press: Cambridge, MA, USA, 2017; pp. 229–249. [Google Scholar] [CrossRef]
- Goodman, F.M. Algebra: Abstract and Concrete; SemiSimple Press: Iowa City, IA, USA, 2015. [Google Scholar]
- Kuang, Y.; Zheng, Y.; Åström, K. Partial Symmetry in Polynomial Systems and Its Applications in Computer Vision. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 438–445. [Google Scholar] [CrossRef]
- Larsson, V.; Åström, K. Uncovering Symmetries in Polynomial Systems. In Proceedings of the 14th European Conference Computer Vision—ECCV 2016, Amsterdam, The Netherlands, 11–14 October 2016; Part III. pp. 252–267. [Google Scholar] [CrossRef]
- Maxfield, B. Essential Mathcad for Engineering, Science, and Math ISE, 2nd ed.; Academic Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Maxfield, B. Essential PTC Mathcad Prime 3.0. A Guide for New and Current Users; Academic Press: Cambridge, MA, USA, 2013; 584p. [Google Scholar] [CrossRef]
- Dugopolski, M. Elementary and Intermediate Algebra, 4th ed.; McGraw-Hill: New York, NY, USA, 2012; 1104p. [Google Scholar]
- Aufmann, R.N.; Barker, V.N.; Lockwood, J. Algebra: Introductory and Intermediate, 4th ed.; Houghton Mifflin: Boston, MA, USA, 2007. [Google Scholar]
- Bird, J. Electrical Circuit Theory and Technology, 6th ed.; Routledge: London, UK, 2017. [Google Scholar]
- Napolitano, J.A. Mathematica Primer for Physicists; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Gilat, A. Matlab: An Introduction with Applications, 6th ed.; Wiley: Hoboken, NJ, USA, 2017. [Google Scholar]
- Michalowski, T. Applications of Matlab in Science and Engineering; InTech: London, UK, 2011. [Google Scholar] [CrossRef]
- Swokowski, E.; Cole, J.A. Algebra and Trigonometry with Analytic Geometry, 12th ed.; Brooks Cole: Belmont, CA, USA, 2010. [Google Scholar]
- Bodrova, E.V.; Golovanova, N.B. Modernization of the higher technical school: Historical experience and prospects. Russ. Technol. J. 2017, 5, 73–97. (In Russian) [Google Scholar] [CrossRef]
- Ochkov, V. 25 Problems for STEM Education; Chapman and Hall/CRC: Boca Raton, FL, USA, 2020. [Google Scholar]
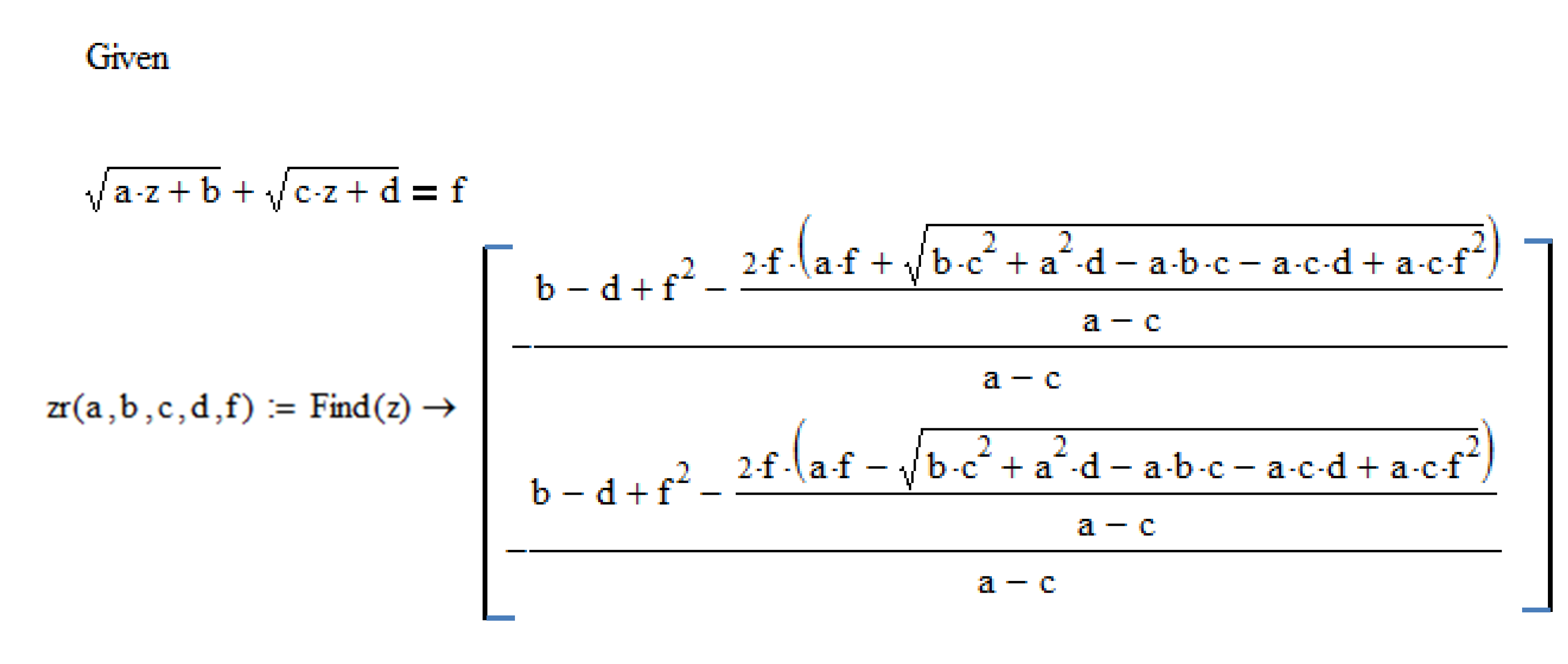
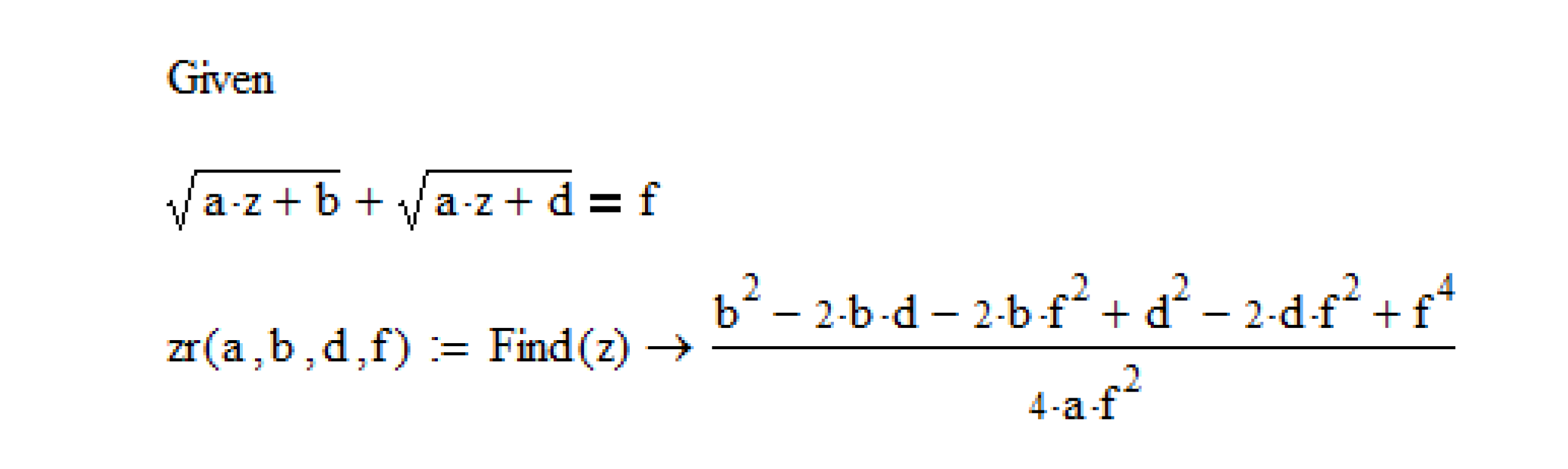






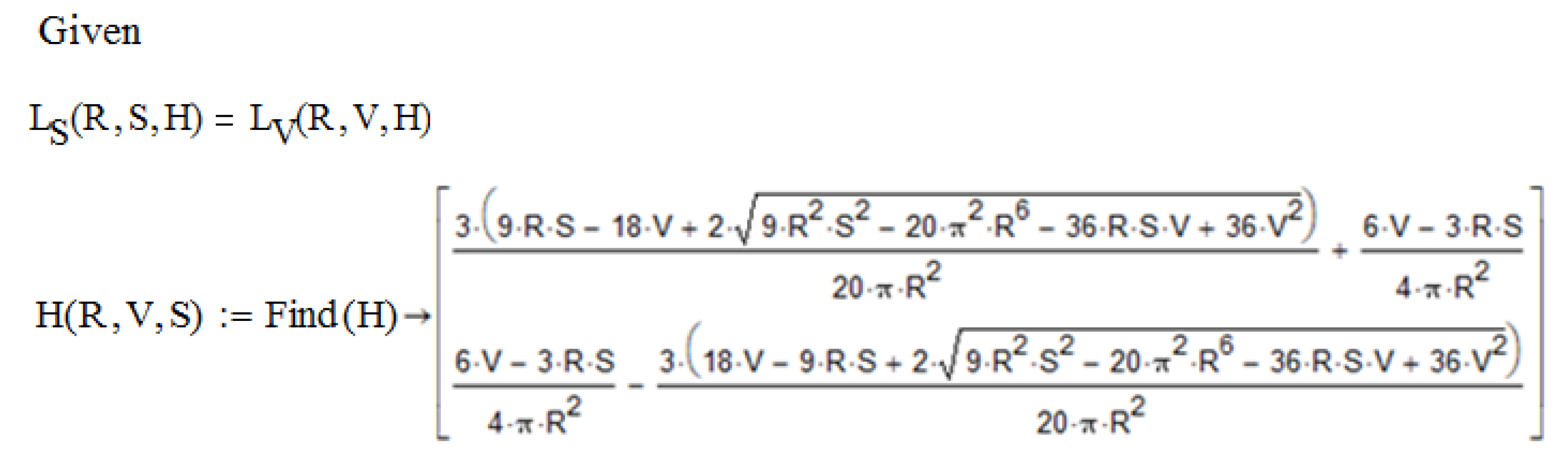
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ochkov, V.; Vasileva, I.; Nori, M.; Orlov, K.; Nikulchev, E. Symbolic Computation to Solving an Irrational Equation on Based Symmetric Polynomials Method. Computation 2020, 8, 40. https://doi.org/10.3390/computation8020040
Ochkov V, Vasileva I, Nori M, Orlov K, Nikulchev E. Symbolic Computation to Solving an Irrational Equation on Based Symmetric Polynomials Method. Computation. 2020; 8(2):40. https://doi.org/10.3390/computation8020040
Chicago/Turabian StyleOchkov, Valery, Inna Vasileva, Massimiliano Nori, Konstantin Orlov, and Evgeny Nikulchev. 2020. "Symbolic Computation to Solving an Irrational Equation on Based Symmetric Polynomials Method" Computation 8, no. 2: 40. https://doi.org/10.3390/computation8020040
APA StyleOchkov, V., Vasileva, I., Nori, M., Orlov, K., & Nikulchev, E. (2020). Symbolic Computation to Solving an Irrational Equation on Based Symmetric Polynomials Method. Computation, 8(2), 40. https://doi.org/10.3390/computation8020040





