Abstract
In scientific computing, the acceleration of atomistic computer simulations by means of custom hardware is finding ever-growing application. A major limitation, however, is that the high efficiency in terms of performance and low power consumption entails the massive usage of low precision computing units. Here, based on the approximate computing paradigm, we present an algorithmic method to compensate for numerical inaccuracies due to low accuracy arithmetic operations rigorously, yet still obtaining exact expectation values using a properly modified Langevin-type equation.
1. Introduction
Molecular dynamics (MD) is a very powerful and widely used technique to study thermodynamic equilibrium properties, as well as the real-time dynamics of complex systems made up of interacting atoms [1]. This is done by numerically solving Newton’s equations of motion in a time-discretized fashion via computing the nuclear forces of all atoms at every time step [2]. Computing these forces by analytically differentiating the interatomic potential with respect to the nuclear coordinates is computationally rather expensive, which is particularly true for electronic structure-based ab-initio MD simulations [3,4,5,6].
For a long time, newly developed microchips have become faster and more efficient due to new manufacturing processes and shrinking transistor sizes. However, this development is slowly coming to an end as scaling down the structures of silicon-based chips becomes more and more difficult. The focus therefore shifts towards making efficient use of the available technology. Hence, besides algorithmic developments [7,8,9,10,11,12,13,14], there have been numerous custom computing efforts in this area to increase the efficiency of MD simulations by means of hardware acceleration, which we take up in this work. Examples of the latter are MD implementations on graphics processing units (GPUs) [15,16,17,18,19,20,21], field-programmable gate arrays (FPGAs) [22,23], and application-specific integrated circuits (ASICs) [24,25]. While the use of GPUs for scientific applications is relatively widespread [26,27,28], the use of ASICs [29,30,31,32] and FPGAs is less common [33,34,35,36,37,38], but has gained attention over the last few years. In general, to maximize the computational power for a given silicon area, or equivalently minimize the power-consumption per arithmetic operation, more and more computing units are replaced with lower precision units. This trend is mostly driven by the market considerations of the gaming and artificial intelligence industries, which are the target customers of hardware accelerators and naturally do not absolutely rely on full computing accuracy.
In the approach presented in this paper, we mimic in software how it is possible to make effective use of low accuracy special-purpose hardware for general-purpose scientific computing by leveraging the approximate computing (AC) paradigm [39,40]. The general research goal of AC is to devise and explore ingenious techniques to relax the exactness of a calculation to facilitate the design of more powerful and/or more efficient computer systems. However, in scientific computing, where the exactness of all computed results is of paramount importance, attenuating accuracy requirements is not an option. Yet, assuming that the inaccuracies within the nuclear forces due to the usage of low precision arithmetic operations can be approximately considered as white noise, we will demonstrate that it is nevertheless possible to compensate for such numerical errors rigorously and still obtain exact expectation values, as obtained by ensemble averages of a properly modified Langevin equation.
The remainder of the paper is organized as follows. In Section 2, we revisit the basic principles of AC before introducing our modified Langevin equation in Section 3. Thereafter, in Section 4, we describe the computational details of our computational experiments. Our results are presented and discussed in Section 5 before concluding the paper in Section 6.
2. Approximate Computing
A basic method of approximation and a key requirement for efficient use of processing hardware is the use of adequate data widths in computationally intensive kernels. While in many scientific applications, the use of the double-precision floating-point is most common, this precision is not always required. For example, iterative methods can exhibit resilience against low precision arithmetic, as has been shown for the computation of inverse matrix roots [41] and for solving systems of linear equations [39,42,43,44]. Mainly driven by the growing popularity of artificial neural networks [45], we can observe growing support of low precision data types in hardware accelerators. In fact, recent GPUs targeting the data center have started supporting half-precision as well, nearly doubling the peak performance compared to single-precision and quadrupling it compared to double-precision arithmetics [46]. However, due to the low number of exponent bits, half-precision only provides a very limited dynamic range. In contrast, bfloat16 provides the same dynamic range as single-precision and just reduces precision. It is currently supported by Google’s Tensor Processing Units (TPU) [47], and support has been announced for future Intel Xeon processors [48] and Intel AgileX FPGAs. A list of commonly used data types, together with the corresponding number of bits used to store the exponent and the mantissa, are shown in Table 1 beside the double-precision de facto standard.

Table 1.
Bitwidth of common floating-point formats.
Yet, programmable hardware such as FPGAs, as a platform for custom-built accelerator designs [49,50,51], can make effective use of all of these, but also entirely custom number formats. Developers can specify the number of exponent and mantissa bits and trade-off precision against the amount of memory blocks required to store values and the number of logic elements required to perform arithmetic operations on them.
In addition to floating-point formats, also fixed-point representations can be used. Here, all numbers are stored as integers of a fixed size with a predefined scaling factor. Calculations are thereby performed using integer arithmetic. On CPUs and GPUs, only certain models can perform integer operations with a peak performance similar to that of floating-point arithmetic, depending on the capabilities of the vector units/stream processors. Nevertheless, FPGAs typically can perform integer operations with performance similar to or even higher than that of the floating-point. Due to the high flexibility of FPGAs with respect to different data formats and the possible use of entirely custom data types, we see them as the main target technology for our work. For this reason, we consider both floating-point and fixed-point arithmetic in the following.
3. Methodology
The error introduced by low precision floating-point or fixed-point computations can in general be modeled as white noise if unbiased rounding techniques are used in all arithmetic operations. A widely employed rounding technique is round half to even, which does not introduce a systematic bias and is used by default in IEEE 754 floating-point arithmetic [52]. In the following, we assume the usage of such a rounding technique also for fixed-point arithmetic, leading to only an unbiased error within the computed interatomic forces.
To demonstrate the concept of approximate computing, we introduce white noise to the interatomic forces that are computed while running the MD simulation. In this section, we describe in detail how we introduce the noise to mimic in software the behavior that would be observed when running the MD on the actual FPGA or GPU hardware with reduced numerical precision. We classify the computational errors into two types: fixed-point errors and floating-point errors. Assuming that are the exact and the noisy forces from an MD simulation with low precision on an FPGA for instance, fixed-point errors can by modeled by:
whereas floating-point errors are described by:
Therein, , , and are random values chosen in the range [−0.5, 0.5], whereas , , and are the individual force components of , respectively. The floating-point scaling factor is denoted as and the magnitude of the applied noise by .
To correct the errors introduced by numerical noise rigorously, we employ a modified Langevin equation. In particular, we model the force as obtained by a low precision computation on a GPU or FPGA-based accelerator as:
where is an additive white noise for which:
holds. Throughout, denotes Boltzmann-weighted ensemble averages as obtained by the partition function , where E is the potential energy, the so-called Boltzmann constant, and T the temperature. Given that is unbiased, which in our case is true by its very definition, it is nevertheless possible to sample the Boltzmann distribution accurately by means of a Langevin-type equation [53,54,55], which in its general form reads as:
where are the nuclear coordinates (the dot denotes the time derivative), are the nuclear masses, and is a damping coefficient, which is chosen to compensate for . The latter, in order to guarantee an accurate canonical sampling, has to obey the fluctuation-dissipation theorem:
Substituting Equation (3) into Equation (5) results in the desired modified Langevin equation:
which will be used throughout the remainder of this paper. This is to say that the noise, as originating from a low precision computation, can be thought of as the additive white noise of a damping coefficient , which satisfies the fluctuation-dissipation theorem of Equation (6). The specific value of is determined in such a way so as to generate the correct average temperature, as measured by the equipartition theorem:
4. Computational Details
To demonstrate our approach, we implemented it in the CP2K suite of programs [56,57]. More precisely, we conducted MD simulations of liquid silicon (Si) at 3000 K using the environment-dependent interatomic potential of Bazant et al. [58,59]. All simulations consisted of 1000 Si atoms in a 3D-periodic cubic box of length 27.155 Å. Using the algorithm of Ricci and Ciccotti [60], Equation (5) was integrated with a discretized time step of 1.0 fs with fs.
Whereas the latter settings were used to compute our reference data, in total, six different cases of fixed-point and floating-point errors were investigated by varying the exponent between zero (huge noise) and three (tiny noise) that is, ranging from of the physical force up to the same magnitude as the force. As already alluded to above, the additive white noise is compensated via Equation (7) by continuously adjusting the friction coefficient using the adaptive Langevin technique of Leimkuhler and coworkers so as to satisfy the equipartition theorem of Equation (8) [61,62,63]. In this method, is reinterpreted as a dynamical variable, defined by a negative feedback loop control law as in the Nosé–Hoover scheme [64,65]. The corresponding dynamical equation for reads as:
where K is the kinetic energy, n is the number of degrees of freedom, and is the Nosé–Hoover fictitious mass with time constant . Alternatively, can be estimated by integrating the autocorrelation function of the additive white noise [66]. In Table 2, the resulting values of for fixed-point and for floating-point errors are reported as a function of .

Table 2.
Values for and as a function of .
5. Results and Discussion
As can be directly deduced from Table 2, the smaller values of for a given immediately suggested a higher noise resilience when using floating-point as compared to fixed-point numbers.
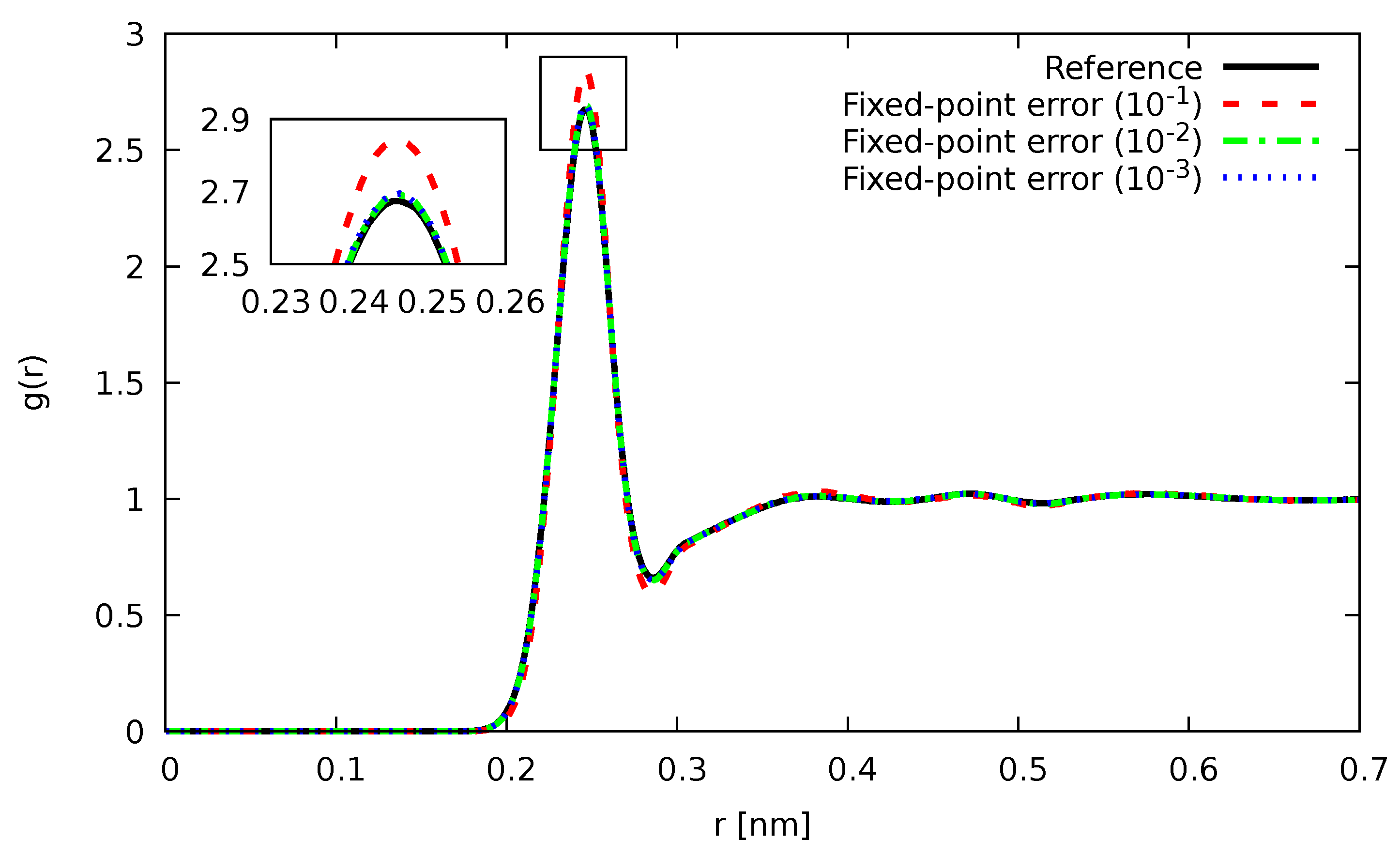
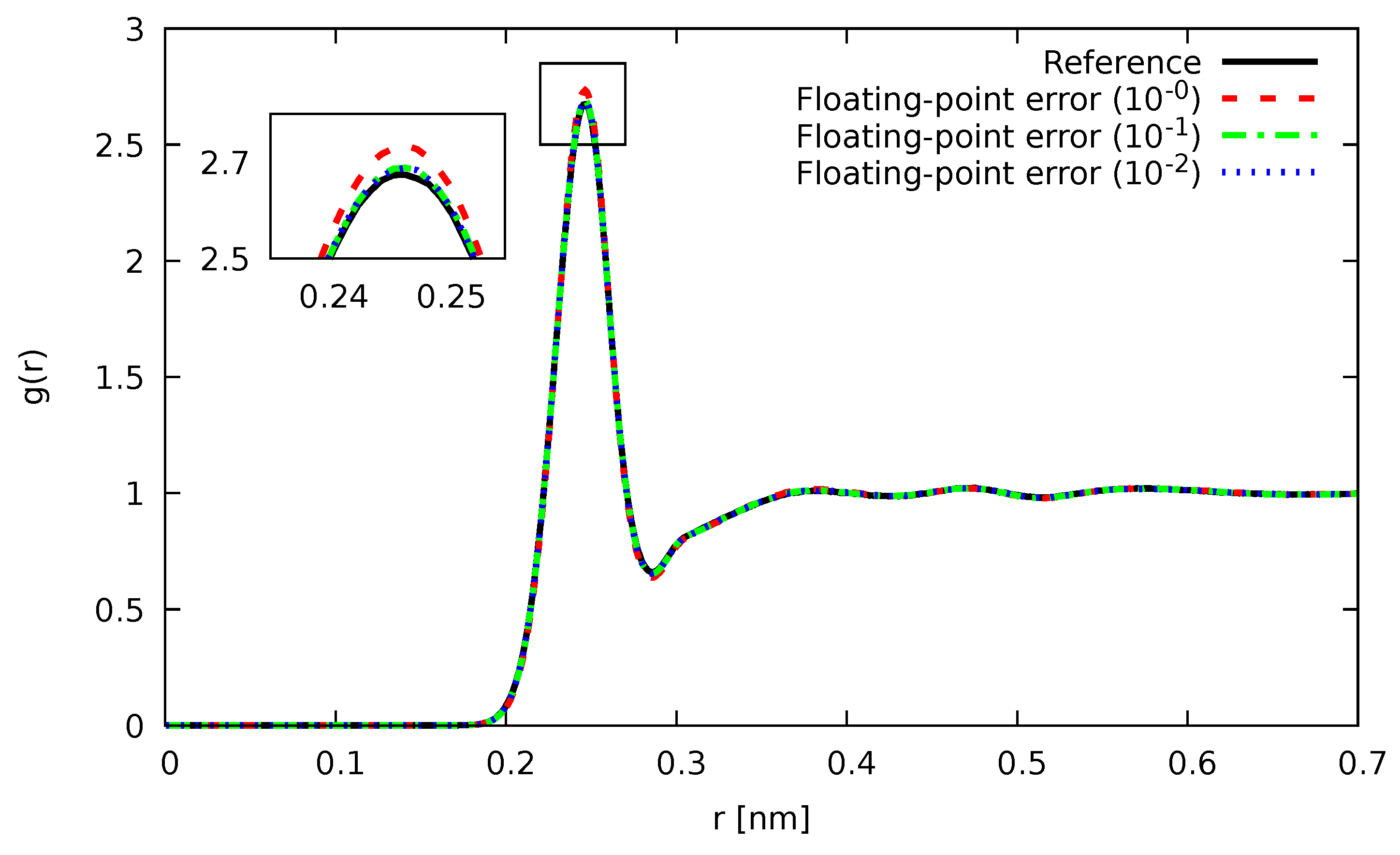
In Figure 1 and Figure 2, the Si-Si partial pair-correlation function , which describes how the particle-density varies as a function of distance from a reference particle (atoms, molecules, colloids, etc.), as computed using an optimal scheme for orthorhombic systems [67], is shown for different values of . As can be seen, for both fixed-point and floating-point errors, the agreement with our reference calculation was nearly perfect up to the highest noise we investigated. As already anticipated earlier, the usage of floating-point errors was not only able to tolerate higher noise levels, but was also more accurate throughout.
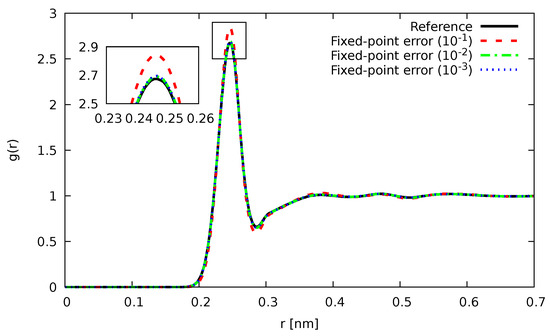
Figure 1.
Partial pair correlation function for liquid Si at 3000 K with noisy forces introduced by fixed-point errors of magnitude (blue), (green), and (red). For comparison, the results, as obtained by our reference calculations without noise, are shown in black.
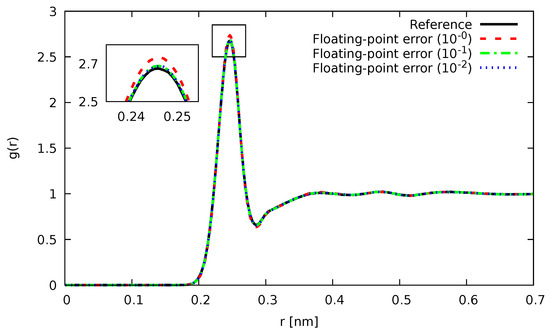
Figure 2.
Partial pair correlation function for liquid Si at 3000 K with noisy forces introduced by floating-point errors of magnitude (blue), (green), and (red). For comparison, the results, as obtained by our reference calculations without noise, are shown in black.
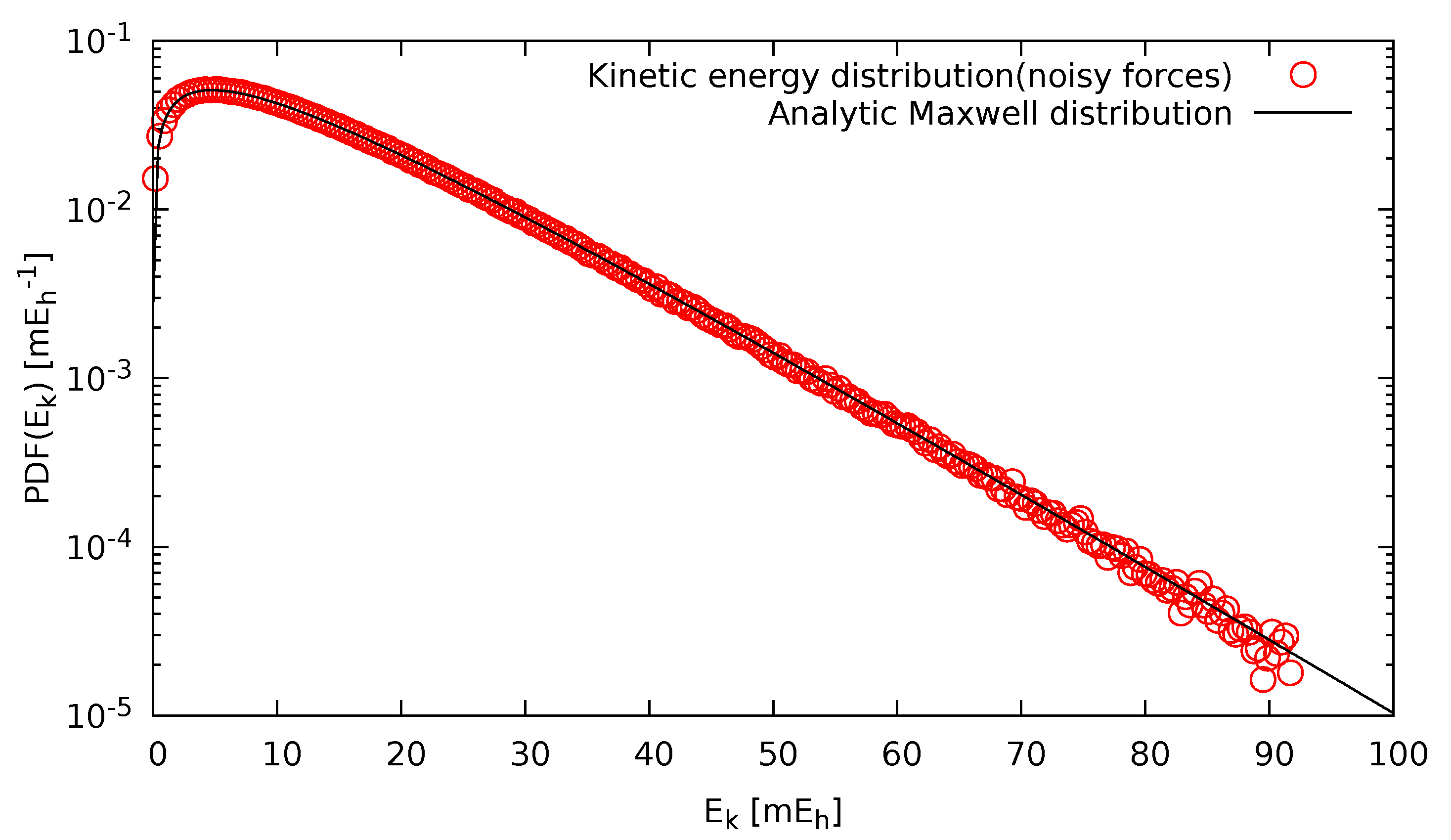
To verify that the sampling was indeed canonical, in Figure 3, the actual kinetic energy distribution as obtained by our simulations using noisy forces is depicted and compared to the analytic Maxwell distribution. It was evident that if sampled long enough, not only the mean value, but also the distribution tails were in excellent agreement with the exact Maxwellian kinetic energy distribution, which demonstrated that we were indeed performing a canonical sampling.
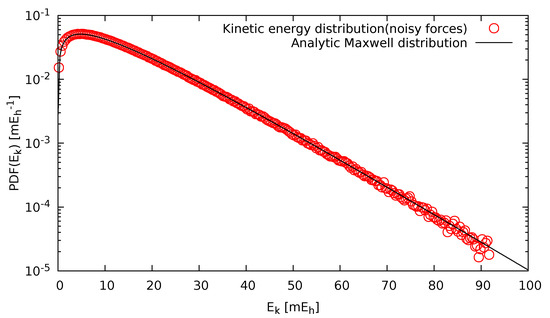
Figure 3.
Kinetic energy distribution of liquid Si at 3000 K, as obtained by our simulations using noisy forces (circles). For comparison, the analytic Maxwell distribution is also shown (line).
To further assess the accuracy of the present method, we expanded the autocorrelation of the noisy forces, i.e.,
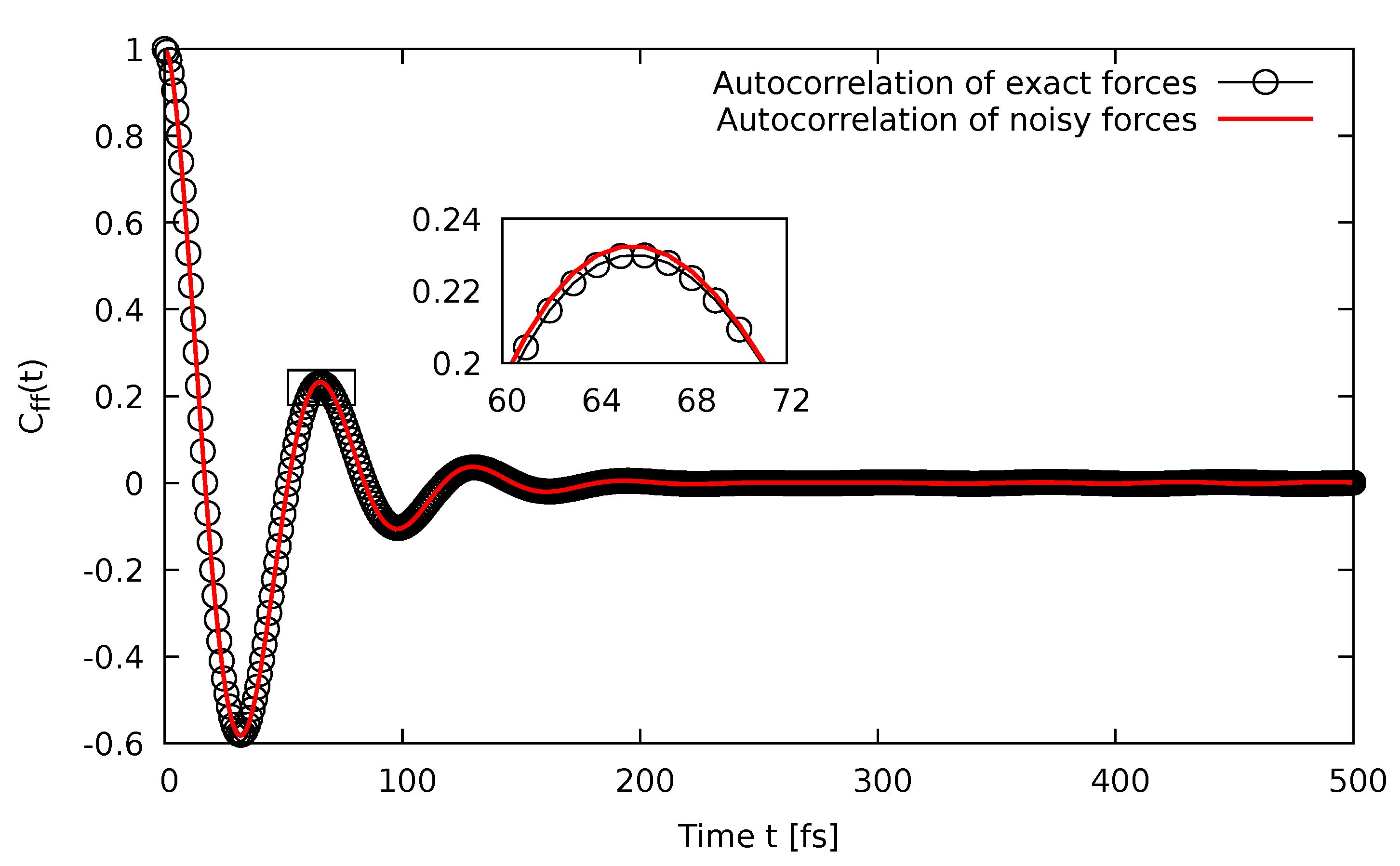
Since the cross-correlation terms between the exact force and the additive white noise were vanishing due to Equation (4), comparing the autocorrelation of the noisy forces with the autocorrelation of the exact forces permitted assessing the localization of the last term of Equation (10c). The fact that was essentially identical to , as can be seen in Figure 4, implied that was very close to a -function as required by the fluctuation-dissipation theorem in order to ensure an accurate canonical sampling of the Boltzmann distribution. In other words, from this, it followed that our initial assumption underlying Equation (7), to model the noise due to a low precision calculation as an additive white noise channel, was justified.
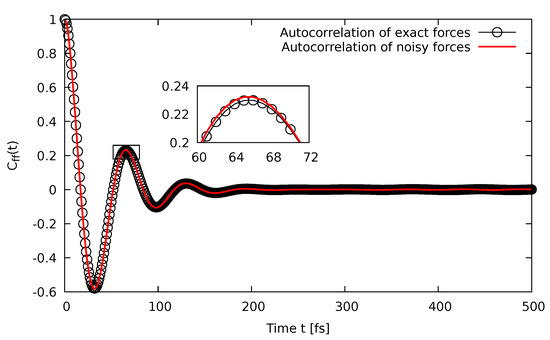
Figure 4.
The autocorrelation of the noisy forces (line), which are compared to the autocorrelation of the exact forces (circles).
6. Conclusions
We conclude by noting that the presented method was recently implemented in the universal force engine i-PI [68], which can be generally applied to all sorts of forces affected by stochastic noise such as those computed by GPUs or other hardware accelerators [15,16,17,18,19,20,21], and potentially even quantum computing devices [69,70,71,72]. The possibility to apply similar ideas to N-body simulations [73,74] and to combine them with further algorithmic approximations [75] is to be underlined and will be presented elsewhere.
Author Contributions
V.R. wrote the code and conducted the calculations, V.R. and M.L. analyzed the data, M.L., C.P. and T.D.K. interpreted the results, M.L., V.R. and T.D.K. wrote the paper, C.P. and T.D.K. conceived the study and directed the project. All authors have read and agreed to the published version of the manuscript.
Funding
The authors would like to thank the Paderborn Center for Parallel Computing (PC) for computing time on OCULUS and FPGA-based supercomputer NOCTUA. Funding from Paderborn University’s research award for “Green IT” is kindly acknowledged. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (Grant Agreement No. 716142) and from the German Research Foundation (DFG) under the project PerficienCC (grant agreement No PL 595/2-1).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Alder, B.J.; Wainwright, T.E. Phase Transition for a Hard Sphere System. J. Chem. Phys. 1957, 27, 1208–1209. [Google Scholar] [CrossRef]
- Rahman, A. Correlations in the Motion of Atoms in Liquid Argon. Phys. Rev. 1964, 136, A405–A411. [Google Scholar] [CrossRef]
- Car, R.; Parrinello, M. Unified approach for molecular dynamics and density-functional theory. Phys. Rev. Lett. 1985, 55, 2471–2474. [Google Scholar] [CrossRef] [PubMed]
- Kühne, T.D.; Krack, M.; Mohamed, F.R.; Parrinello, M. Efficient and accurate Car-Parrinello-like approach to Born-Oppenheimer molecular dynamics. Phys. Rev. Lett. 2007, 98, 066401. [Google Scholar] [CrossRef]
- Payne, M.C.; Teter, M.P.; Allan, D.C.; Arias, T.A.; Joannopoulos, J.D. Iterative minimization techniques for ab initio total-energy calculations: Molecular dynamics and conjugate gradients. Rev. Mod. Phys. 1992, 64, 1045–1097. [Google Scholar] [CrossRef]
- Kühne, T.D. Second generation Car–Parrinello molecular dynamics. WIREs Comput. Mol. Sci. 2014, 4, 391–406. [Google Scholar] [CrossRef]
- Tuckerman, M.E.; Berne, B.J.; Martyna, G.J. Reversible multiple time scale molecular dynamics. J. Chem. Phys. 1992, 97, 1990–2001. [Google Scholar] [CrossRef]
- Snir, M. A note on N-body computations with cutoffs. Theor. Comput. Syst. 2004, 37, 295–318. [Google Scholar] [CrossRef]
- Shan, Y.; Klepeis, J.L.; Eastwood, M.P.; Dror, R.O.; Shaw, D.E. Gaussian split Ewald: A fast Ewald mesh method for molecular simulation. J. Chem. Phys. 2005, 122, 054101. [Google Scholar] [CrossRef]
- Shaw, D.E. A fast, scalable method for the parallel evaluation of distance-limited pairwise particle interactions. J. Comput. Chem. 2005, 26, 1318–1328. [Google Scholar] [CrossRef]
- Gonnet, P. Pairwise Verlet Lists: Combining Cell Lists and Verlet Lists to Improve Memory Locality and Parallelism. J. Comput. Chem. 2012, 33, 76–81. [Google Scholar] [CrossRef] [PubMed]
- Gonnet, P. A quadratically convergent SHAKE in O(n(2)). J. Comput. Phys. 2007, 220, 740–750. [Google Scholar] [CrossRef]
- John, C.; Spura, T.; Habershon, S.; Kühne, T.D. Quantum ring-polymer contraction method: Including nuclear quantum effects at no additional computational cost in comparison to ab initio molecular dynamics. Phys. Rev. E 2016, 93, 043305. [Google Scholar] [CrossRef] [PubMed]
- Kühne, T.D.; Prodan, E. Disordered Crystals from First Principles I: Quantifying the Configuration Space. Ann. Phys. 2018, 391, 120–149. [Google Scholar] [CrossRef]
- Anderson, J.A.; Lorenz, C.D.; Travesset, A. General purpose molecular dynamics simulations fully implemented on graphics processing units. J. Comput. Phys. 2008, 227, 5342–5359. [Google Scholar] [CrossRef]
- Stone, J.E.; Hardy, D.J.; Ufimtsev, I.S.; Schulten, K. GPU-accelerated molecular modeling coming of age. J. Mol. Graph. Model. 2010, 29, 116–125. [Google Scholar] [CrossRef]
- Eastman, P.; Pande, V.S. OpenMM: A Hardware-Independent Framework for Molecular Simulations. Comput. Sci. Eng. 2010, 12, 34–39. [Google Scholar] [CrossRef]
- Colberg, P.H.; Höfling, F. Highly accelerated simulations of glassy dynamics using GPUs: Caveats on limited floating-point precision. Comput. Phys. Commun. 2011, 182, 1120–1129. [Google Scholar] [CrossRef]
- Brown, W.M.; Kohlmeyer, A.; Plimpton, S.J.; Tharrington, A.N. Implementing molecular dynamics on hybrid high performance computers – Particle–particle particle-mesh. Comput. Phys. Commun. 2012, 183, 449–459. [Google Scholar] [CrossRef]
- Le Grand, S.; Götz, A.W.; Walker, R.C. SPFP: Speed without compromise—A mixed precision model for GPU accelerated molecular dynamics simulations. Comput. Phys. Commun. 2013, 184, 374–380. [Google Scholar] [CrossRef]
- Abraham, A.J.; Murtola, T.; Schulz, R.; Pall, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef]
- Herbordt, M.C.; Gu, Y.; VanCourt, T.; Model, J.; Sukhwani, B.; Chiu, M. Computing Models for FPGA-Based Accelerators. Comput. Sci. Eng. 2008, 10, 35–45. [Google Scholar] [CrossRef] [PubMed]
- Herbordt, M.C.; Gu, Y.; VanCourt, T.; Model, J.; Sukhwani, B.; Chiu, M. Explicit design of FPGA-based coprocessors for short-range force computations in molecular dynamics simulations. Parallel Comput. 2008, 34, 261–277. [Google Scholar] [CrossRef]
- Shaw, D.E.; Deneroff, M.M.; Dror, R.O.; Kuskin, J.S.; Larson, R.H.; Salmon, J.K.; Young, C.; Batson, B.; Bowers, K.J.; Chao, J.C.; et al. Anton, a Special-purpose Machine for Molecular Dynamics Simulation. In Proceedings of the 34th Annual International Symposium on Computer Architecture, San Diego, CA, USA, 9–13 June 2007; ACM: New York, NY, USA, 2007; pp. 1–12. [Google Scholar] [CrossRef]
- Shaw, D.E.; Grossman, J.P.; Bank, J.A.; Batson, B.; Butts, J.A.; Chao, J.C.; Deneroff, M.M.; Dror, R.O.; Even, A.; Fenton, C.H.; et al. Anton 2: Raising the Bar for Performance and Programmability in a Special-purpose Molecular Dynamics Supercomputer. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, New Orleans, LA, USA, 16–21 November 2014; IEEE Press: Piscataway, NJ, USA, 2014; pp. 41–53. [Google Scholar] [CrossRef]
- Owens, J.D.; Houston, M.; Luebke, D.; Green, S.; Stone, J.E.; Phillips, J.C. GPU Computing. Proc. IEEE 2008, 96, 879–899. [Google Scholar] [CrossRef]
- Preis, T.; Virnau, P.; Paul, W.; Schneider, J.J. GPU accelerated Monte Carlo simulation of the 2D and 3D Ising model. J. Comput. Phys. 2009, 228, 4468–4477. [Google Scholar] [CrossRef]
- Weigel, M. Performance potential for simulating spin models on GPU. J. Comput. Phys. 2012, 231, 3064–3082. [Google Scholar] [CrossRef]
- Brown, F.R.; Christ, N.H. Parallel Supercomputers for Lattice Gauge Theory. Science 1988, 239, 1393–1400. [Google Scholar] [CrossRef]
- Boyle, P.A.; Chen, D.; Christ, N.H.; Clark, M.A.; Cohen, S.D.; Cristian, C.; Dong, Z.; Gara, A.; Joo, B.; Jung, C.; et al. Overview of the QCDSP and QCDOC computers. IBM J. Res. Dev. 2005, 49, 351–365. [Google Scholar] [CrossRef]
- Hut, P.; Makino, J. Astrophysics on the GRAPE Family of Special-Purpose Computers. Science 1999, 283, 501–505. [Google Scholar] [CrossRef]
- Fukushige, T.; Hut, P.; Makino, J. High-performance special-purpose computers in science. Comput. Sci. Eng. 1999, 1, 12–13. [Google Scholar] [CrossRef][Green Version]
- Belletti, F.; Cotallo, M.; Cruz, A.; Fernandez, L.A.; Gordillo-Guerrero, A.; Guidetti, M.; Maiorano, A.; Mantovani, F.; Marinari, E.; Martin-Mayor, V.; et al. Janus: An FPGA-Based System for High-Performance Scientific Computing. Comput. Sci. Eng. 2009, 11, 48. [Google Scholar] [CrossRef]
- Baity-Jesi, M.; Banos, R.A.; Cruz, A.; Fernandez, L.A.; Gil-Narvion, J.M.; Gordillo-Guerrero, A.; Iniguez, D.; Maiorano, A.; Mantovani, F.; Marinari, E.; et al. Janus II: A new generation application-driven computer for spin-system simulations. Comput. Phys. Commun. 2014, 185, 550–559. [Google Scholar] [CrossRef]
- Meyer, B.; Schumacher, J.; Plessl, C.; Forstner, J. Convey vector personalities—FPGA acceleration with an openmp-like programming effort? In Proceedings of the 22nd International Conference on Field Programmable Logic and Applications (FPL), Oslo, Norway, 29–31 August 2012; pp. 189–196. [Google Scholar] [CrossRef]
- Giefers, H.; Plessl, C.; Förstner, J. Accelerating Finite Difference Time Domain Simulations with Reconfigurable Dataflow Computers. SIGARCH Comput. Archit. News 2014, 41, 65–70. [Google Scholar] [CrossRef]
- Kenter, T.; Förstner, J.; Plessl, C. Flexible FPGA design for FDTD using OpenCL. In Proceedings of the 2017 27th International Conference on Field Programmable Logic and Applications (FPL), Ghent, Belgium, 4–8 September 2017. [Google Scholar] [CrossRef]
- Kenter, T.; Mahale, G.; Alhaddad, S.; Grynko, Y.; Schmitt, C.; Afzal, A.; Hannig, F.; Förstner, J.; Plessl, C. OpenCL-based FPGA Design to Accelerate the Nodal Discontinuous Galerkin Method for Unstructured Meshes. In Proceedings of the 2018 IEEE 26th Annual International Symposium on Field-Programmable Custom Computing Machines (FCCM), Boulder, CO, USA, 29 April–1 May 2018; Volume 1, pp. 189–196. [Google Scholar] [CrossRef]
- Klavík, P.; Malossi, A.C.I.; Bekas, C.; Curioni, A. Changing Computing Paradigms Towards Power Efficiency. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2014, 372. [Google Scholar] [CrossRef]
- Plessl, C.; Platzner, M.; Schreier, P.J. Approximate Computing. Inform. Spektrum 2015, 38, 396–399. [Google Scholar] [CrossRef]
- Lass, M.; Kühne, T.D.; Plessl, C. Using Approximate Computing for the Calculation of Inverse Matrix p-th Roots. IEEE Embed. Syst. Lett. 2018, 10, 33–36. [Google Scholar] [CrossRef]
- Angerer, C.M.; Polig, R.; Zegarac, D.; Giefers, H.; Hagleitner, C.; Bekas, C.; Curioni, A. A fast, hybrid, power-efficient high-precision solver for large linear systems based on low precision hardware. Sustain. Comput. Inform. Syst. 2016, 12, 72–82. [Google Scholar] [CrossRef]
- Haidar, A.; Wu, P.; Tomov, S.; Dongarra, J. Investigating half precision arithmetic to accelerate dense linear system solvers. In Proceedings of the 8th Workshop on Latest Advances in Scalable Algorithms for Large-Scale Systems, Denver, CO, USA, 13 November 2017. [Google Scholar] [CrossRef]
- Haidar, A.; Tomov, S.; Dongarra, J.; Higham, N.J. Harnessing GPU tensor cores for fast FP16 arithmetic to speed up mixed-precision iterative refinement solvers. In Proceedings of the International Conference for High Performance Computing, Networking, Storage, and Analysis, Dallas, TX, USA, 11–16 November 2018. [Google Scholar] [CrossRef]
- Gupta, S.; Agrawal, A.; Gopalakrishnan, K.; Narayanan, P. Deep learning with limited numerical precision. In Proceedings of the 32nd International Conference on International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 1737–1746. [Google Scholar]
- NVIDIA Corporation. Tesla P100 Data Sheet; NVIDIA: Santa Clara, CA, USA, 2016. [Google Scholar]
- The Next Platform. Tearing Apart Google’s TPU 3.0 AI Coprocessor. Available online: https://www.nextplatform.com/2018/05/10/tearing-apart-googles-tpu-3-0-ai-coprocessor/ (accessed on 27 April 2020).
- Top 500. Intel Lays Out New Roadmap for AI Portfolio. Available online: https://www.top500.org/news/intel-lays-out-new-roadmap-for-ai-portfolio/ (accessed on 27 April 2020).
- Strzodka, R.; Goddeke, D. Pipelined Mixed Precision Algorithms on FPGAs for Fast and Accurate PDE Solvers from Low Precision Components. In Proceedings of the 14th Annual IEEE Symposium on Field-Programmable Custom Computing Machines, Napa, CA, USA, 24–26 April 2006. [Google Scholar] [CrossRef]
- Kenter, T.; Vaz, G.; Plessl, C. Partitioning and Vectorizing Binary Applications. In Lecture Notes in Computer Science, Proceedings of the International Conference on Reconfigurable Computing: Architectures, Tools and Applications (ARC), Vilamoura, Portugal, 14–16 April 2014; Springer: Berlin/Heidelberg, Germany, 2014; Volume 8405, pp. 144–155. [Google Scholar] [CrossRef]
- Kenter, T.; Schmitz, H.; Plessl, C. Pragma based parallelization—Trading hardware efficiency for ease of use? In Proceedings of the 2012 International Conference on Reconfigurable Computing and FPGAs, Cancun, Mexico, 5–7 December 2012. [CrossRef]
- Microprocessor Standards Committee of the IEEE Computer Society. IEEE Std. 754-2019—IEEE Standard for Floating-Point Arithmetic; IEEE: Toulouse, France, 2019. [Google Scholar]
- Krajewski, F.R.; Parrinello, M. Linear scaling electronic structure calculations and accurate statistical mechanics sampling with noisy forces. Phys. Rev. B 2006, 73, 041105. [Google Scholar] [CrossRef]
- Richters, D.; Kühne, T.D. Self-consistent field theory based molecular dynamics with linear system-size scaling. J. Chem. Phys. 2014, 140, 134109. [Google Scholar] [CrossRef]
- Karhan, K.; Khaliullin, R.Z.; Kühne, T.D. On the role of interfacial hydrogen bonds in “on-water” catalysis. J. Chem. Phys. 2014, 141, 22D528. [Google Scholar] [CrossRef]
- Hutter, J.; Iannuzzi, M.; Schiffmann, F.; VandeVondele, J. CP2K: Atomistic simulations of condensed matter systems. WIREs Comput. Mol. Sci. 2014, 4, 15–25. [Google Scholar] [CrossRef]
- Kühne, T.; Iannuzzi, M.; Del Ben, M.; Rybkin, V.; Seewald, P.; Stein, F.; Laino, T.; Khaliullin, R.; Schütt, O.; Schiffmann, F.; et al. CP2K: An Electronic Structure and Molecular Dynamics Software Package—Quickstep: Efficient and Accurate Electronic Structure Calculations. arXiv 2020, arXiv:physics.chem-ph/2003.03868. [Google Scholar]
- Bazant, M.Z.; Kaxiras, E. Modeling of Covalent Bonding in Solids by Inversion of Cohesive Energy Curves. Phys. Rev. Lett. 1996, 77, 4370–4373. [Google Scholar] [CrossRef] [PubMed]
- Bazant, M.Z.; Kaxiras, E.; Justo, J.F. Environment-dependent interatomic potential for bulk silicon. Phys. Rev. B 1997, 56, 8542–8552. [Google Scholar] [CrossRef]
- Ricci, A.; Ciccotti, G. Algorithms for Brownian dynamics. Mol. Phys. 2003, 101, 1927–1931. [Google Scholar] [CrossRef]
- Jones, A.; Leimkuhler, B. Adaptive stochastic methods for sampling driven molecular systems. J. Chem. Phys. 2011, 135, 084125. [Google Scholar] [CrossRef]
- Mones, L.; Jones, A.; Goötz, A.W.; Laino, T.; Walker, R.C.; Leimkuhler, B.; Csanyi, G.; Bernstein, N. The Adaptive Buffered Force QM/MM Method in the CP2K and AMBER Software Packages. J. Comput. Chem. 2015, 36, 633–648. [Google Scholar] [CrossRef]
- Leimkuhler, B.; Sachs, M.; Stoltz, G. Hypocoercivity Properties Of Adaptive Langevin Dynamics. arXiv 2019, arXiv:math.PR/1908.09363. [Google Scholar]
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef]
- Scheiber, H.; Shi, Y.; Khaliullin, R.Z. Communication: Compact orbitals enable low cost linear-scaling ab initio molecular dynamics for weakly-interacting systems. J. Chem. Phys. 2018, 148, 231103. [Google Scholar] [CrossRef] [PubMed]
- Röhrig, K.A.F.; Kühne, T.D. Optimal calculation of the pair correlation function for an orthorhombic system. Phys. Rev. E 2013, 87, 045301. [Google Scholar] [CrossRef] [PubMed]
- Kapil, V.; Rossi, M.; Marsalek, O.; Petraglia, R.; Litman, Y.; Spura, T.; Cheng, B.; Cuzzocrea, A.; Meißner, R.H.; Wilkins, D.M.; et al. i-PI 2.0: A universal force engine for advanced molecular simulations. Comput. Phys. Commun. 2019, 236, 214–223. [Google Scholar] [CrossRef]
- Steane, A.M. Efficient fault-tolerant quantum computing. Nature 1999, 399, 124–126. [Google Scholar] [CrossRef]
- Knill, E. Quantum computing with realistically noisy devices. Nature 2005, 434, 39–44. [Google Scholar] [CrossRef]
- Benhelm, J.; Kirchmair, G.; Roos, C.F.; Blatt, R. Towards fault-tolerant quantum computing with trapped ions. Nat. Phys. 2008, 4, 463–466. [Google Scholar] [CrossRef]
- Chow, J.M.; Gambetta, J.M.; Magesan, E.; Abraham, D.W.; Cross, A.W.; Johnson, B.R.; Masluk, N.A.; Ryan, C.A.; Smolin, J.A.; Srinivasan, S.J.; et al. Implementing a strand of a scalable fault-tolerant quantum computing fabric. Nat. Commun. 2014, 5, 4015. [Google Scholar] [CrossRef]
- Efstathiou, G.; Davis, M.; Frenk, C.S.; White, S.D.M. Numerical techniques for large cosmological N-body simulations. Astrophys. J. 1985, 57, 241–260. [Google Scholar] [CrossRef]
- Hernquist, L.; Hut, P.; Makino, J. Discreteness Noise versus Force Errors in N-Body Simulations. Astrophys. J. 1993, 402, L85. [Google Scholar] [CrossRef]
- Lass, M.; Mohr, S.; Wiebeler, H.; Kühne, T.D.; Plessl, C. A Massively Parallel Algorithm for the Approximate Calculation of Inverse P-th Roots of Large Sparse Matrices. In Proceedings of the Platform for Advanced Scientific Computing Conference, Basel, Switzerland, 2–4 July 2018; ACM: New York, NY, USA, 2018; pp. 7:1–7:11. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).