Enzyme Immobilization on Polymer Membranes: A Quantum and Molecular Mechanics Study
Abstract
1. Introduction
2. Computational Approach
2.1. Quantum Calculations
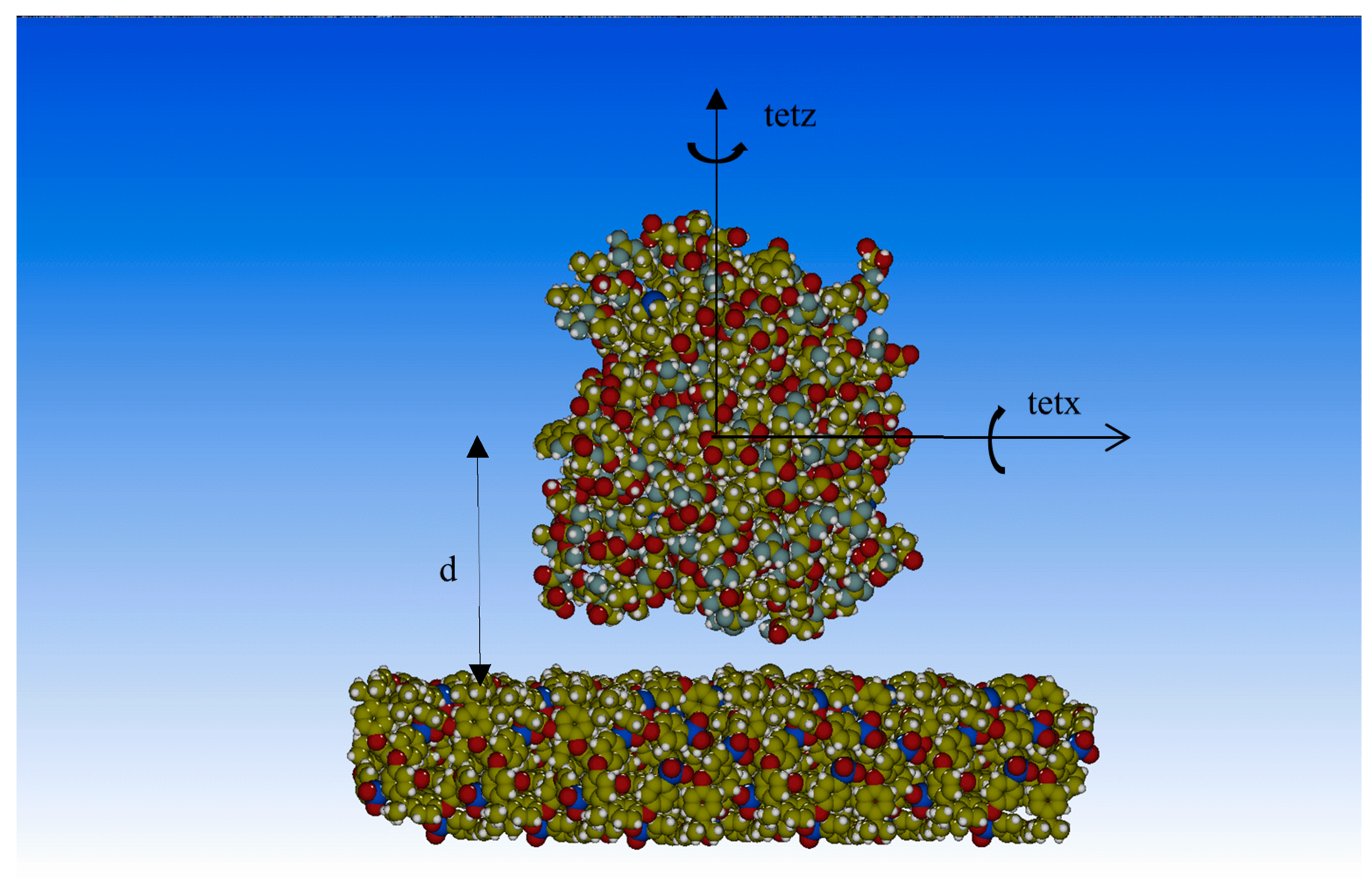
2.2. Molecular Mechanics Optimizations
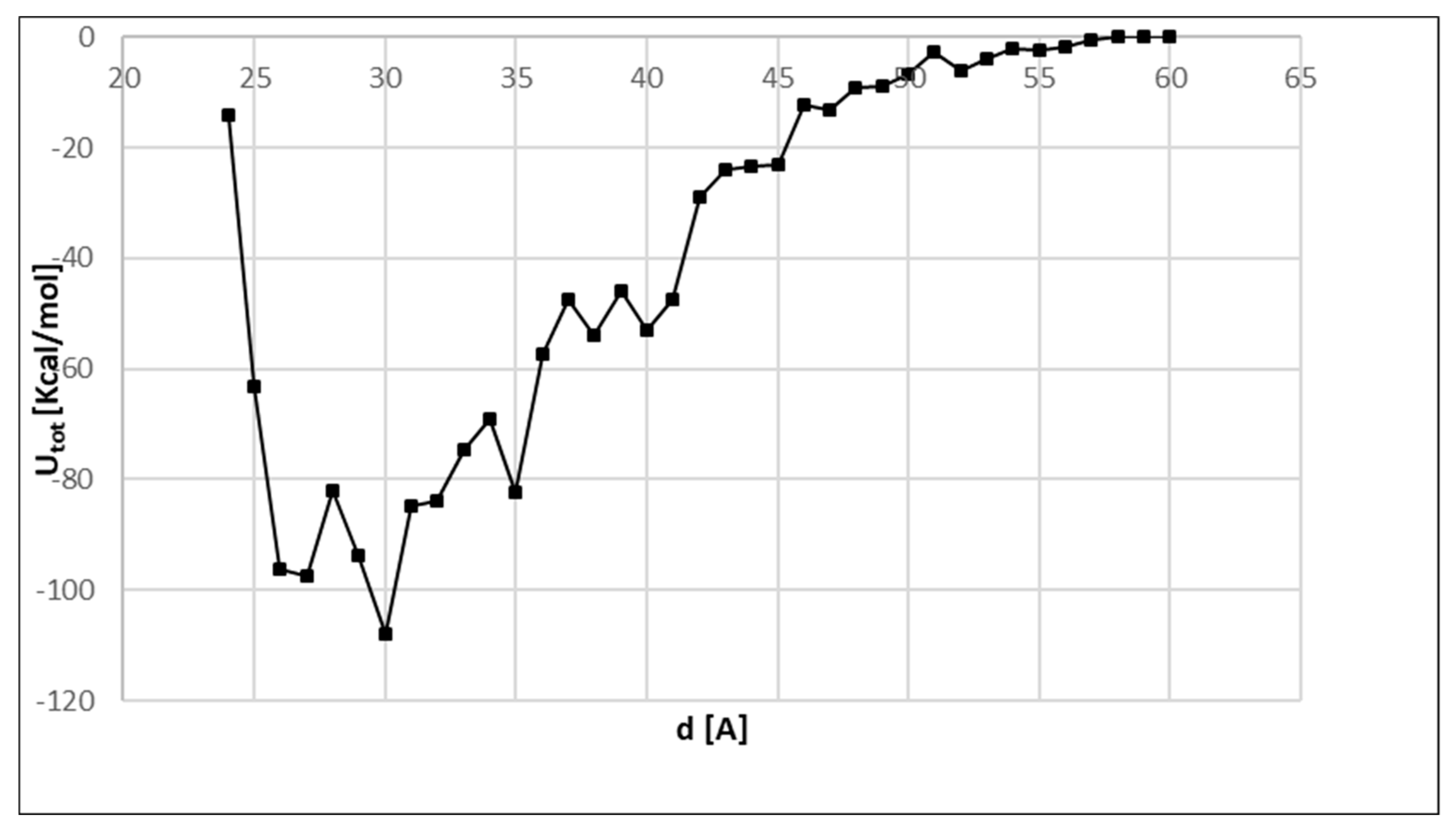
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Weinan, E.; Li, X.; Vanden-Eijnden, E. Some Recent Progress in Multiscale Modeling; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Horstemeyer, M. Multiscale Modeling: A review. In Practical Aspects of Computational Chemistry; Springer: New York, NY, USA, 2009; pp. 87–135. [Google Scholar]
- Parekh, S.; Vinci, V.A.; Strobel, R.J. Improvement of microbial strains and fermentation processes. Appl. Microbiol. Biotechnol. 2000, 54, 287–301. [Google Scholar] [CrossRef] [PubMed]
- Gurung, N.; Ray, S.; Bose, S.; Rai, V. A broader view: Microbial enzymes and their relevance in industries, medicine, and beyond. BioMed Res. Int. 2013, 2013, 329121. [Google Scholar] [CrossRef] [PubMed]
- Underkofler, L.A.; Barton, R.R.; Rennert, S.S. Production of microbial enzymes and their applications. Appl. Microbiol. 1958, 6, 212–221. [Google Scholar] [PubMed]
- Raushel, F.M.; Holden, H.M. Phosphotriesterase: An enzyme in search of its natural substrate. Adv. Enzymol. Relat. Areas Mol. Biol. 2000, 74, 51–93. [Google Scholar] [PubMed]
- Nguyen, H.; Kim, M. An overview of techniques in enzyme immobilization. Appl. Sci. Converg. Technol. 2017, 26, 157–163. [Google Scholar]
- DiCosimo, R.; McAuliffe, J.; Poulose, A.J.; Bohlmann, G. Industrial use of immobilized enzymes. Chem. Soc. Rev. 2013, 42, 6437–6474. [Google Scholar] [CrossRef]
- Datta, S.; Christena, L.R.; Rajaram, Y.R.S. Enzyme immobilization: An overview on techniques and support materials. 3 Biotech 2013, 3, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Kazemi, P.; Renka, R.J. A Levenberg–Marquardt method based on Sobolev gradients. Nonlinear Anal. 2012, 16, 6170–6179. [Google Scholar] [CrossRef]
- Han, L.; Neumann, M. Effect of dimensionality on the Nelder–Mead simplex method. Optim. Methods Softw. 2006, 21, 1–16. [Google Scholar] [CrossRef]
- Curcio, S.; Petrosino, F.; Morrone, M.; De Luca, G. Interactions between proteins and the membrane surface in multiscale modeling of organic fouling. J. Chem. Inf. Model. 2018, 58, 1815–1827. [Google Scholar] [CrossRef]
- De Luca, G.; Bisignano, F.; Paone, F.; Curcio, S. Multi-scale modeling of protein fouling in ultrafiltration process. J. Membr. Sci. 2014, 452, 400–414. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, H.; Liu, X.; Zhou, W.; Rao, Z. The crystal structure of the phosphotriesterase from M.tuberculosis, another member of phosphotriesterase-like lactonase family. Biochem. Biophys. Res. Commun. 2019, 510, 224–229. [Google Scholar] [CrossRef] [PubMed]
- Valiev, M.; Bylaska, E.J.; Govind, N.; Kowalski, K.; Straatsma, T.P.; Van Dam, H.J.J.; Wang, D.; Nieplocha, J.; Apra, E.; Windus, T.L.; et al. NWChem: A comprehensive and scalable open-source solution for large scale molecular simulations. Comput. Phys. Commun. 2010, 181, 1477–1489. [Google Scholar] [CrossRef]
- Malki, Z.E.; Bouzzine, S.M.; Bejjit, L.; Haddad, M.; Hamidi, M.; Bouachrine, M. Density functional theory [B3LYP/6-311G(d,p)] study of a new copolymer based on carbazole and (3,4-Ethylenedioxythiophene) in their aromatic and polaronic states. J. Appl. Polym. Sci. 2011, 122, 3351–3360. [Google Scholar] [CrossRef]
- Klamt, A.; Schüürmann, G. COSMO: A new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient. J. Chem. Soc. Perkin Trans. 2 1993, 2, 799–805. [Google Scholar] [CrossRef]
- Lund, M.; Jönsson, B. A mesoscopic model for Protein-Protein interactions in solution. Biophys. J. 2003, 85, 2940–2947. [Google Scholar] [CrossRef]
- Zhou, A.Q.; O’Hern, C.S.; Regan, L. The power of hard-sphere models: Explaining side-chain dihedral angle distributions of thr and val. Biophys. J. 2012, 102, 2345–2352. [Google Scholar] [CrossRef]
- Morris, G.M.; Goodsell, D.S.; Huey, R.; Olson, A.J. Distributed automated docking of flexible ligands to proteins: Parallel applications of AutoDock 2.4. J. Comput.Aided Mol. Des. 1996, 10, 293–304. [Google Scholar] [CrossRef]
- Van der Waals Potential Energy. Available online: http://www.csb.yale.edu/userguides/datamanip/autodock/html/Using_AutoDock_305.a.html (accessed on 17 July 2019).
- Attaway, S. Matlab: A Practical Introduction to Programming and Problem Solving; Butterworth-Heinemann: Oxford, UK, 2009; ISBN 978-0-08-094325-1. [Google Scholar]
- Lu, D.R.; Lee, S.J.; Park, K. Calculation of solvation interaction energies for protein adsorption on polymer surfaces. J. Biomater. Sci. Polym. Ed. 1992, 3, 127–147. [Google Scholar] [CrossRef]
- Jeyachandran, Y.L.; Mielczarski, E.; Rai, B.; Mielczarski, J.A. Quantitative and qualitative evaluation of adsorption/desorption of bovine serum albumin on hydrophilic and hydrophobic surfaces. Langmuir 2009, 25, 11614–11620. [Google Scholar] [CrossRef]
- Salgın, S.; Takaç, S.; Özdamar, T.H. Adsorption of bovine serum albumin on polyether sulfone ultrafiltration membranes: Determination of interfacial interaction energy and effective diffusion coefficient. J. Membr. Sci. 2006, 278, 251–260. [Google Scholar] [CrossRef]
- May, S.; Harries, D.; Ben-Shaul, A. Lipid Demixing and Protein-Protein interactions in the adsorption of charged proteins on mixed membranes. Biophys. J. 2000, 79, 1747–1760. [Google Scholar] [CrossRef]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Petrosino, F.; Curcio, S.; Chakraborty, S.; De Luca, G. Enzyme Immobilization on Polymer Membranes: A Quantum and Molecular Mechanics Study. Computation 2019, 7, 56. https://doi.org/10.3390/computation7040056
Petrosino F, Curcio S, Chakraborty S, De Luca G. Enzyme Immobilization on Polymer Membranes: A Quantum and Molecular Mechanics Study. Computation. 2019; 7(4):56. https://doi.org/10.3390/computation7040056
Chicago/Turabian StylePetrosino, Francesco, Stefano Curcio, Sudip Chakraborty, and Giorgio De Luca. 2019. "Enzyme Immobilization on Polymer Membranes: A Quantum and Molecular Mechanics Study" Computation 7, no. 4: 56. https://doi.org/10.3390/computation7040056
APA StylePetrosino, F., Curcio, S., Chakraborty, S., & De Luca, G. (2019). Enzyme Immobilization on Polymer Membranes: A Quantum and Molecular Mechanics Study. Computation, 7(4), 56. https://doi.org/10.3390/computation7040056






