Machine-Learning Methods for Computational Science and Engineering
Abstract
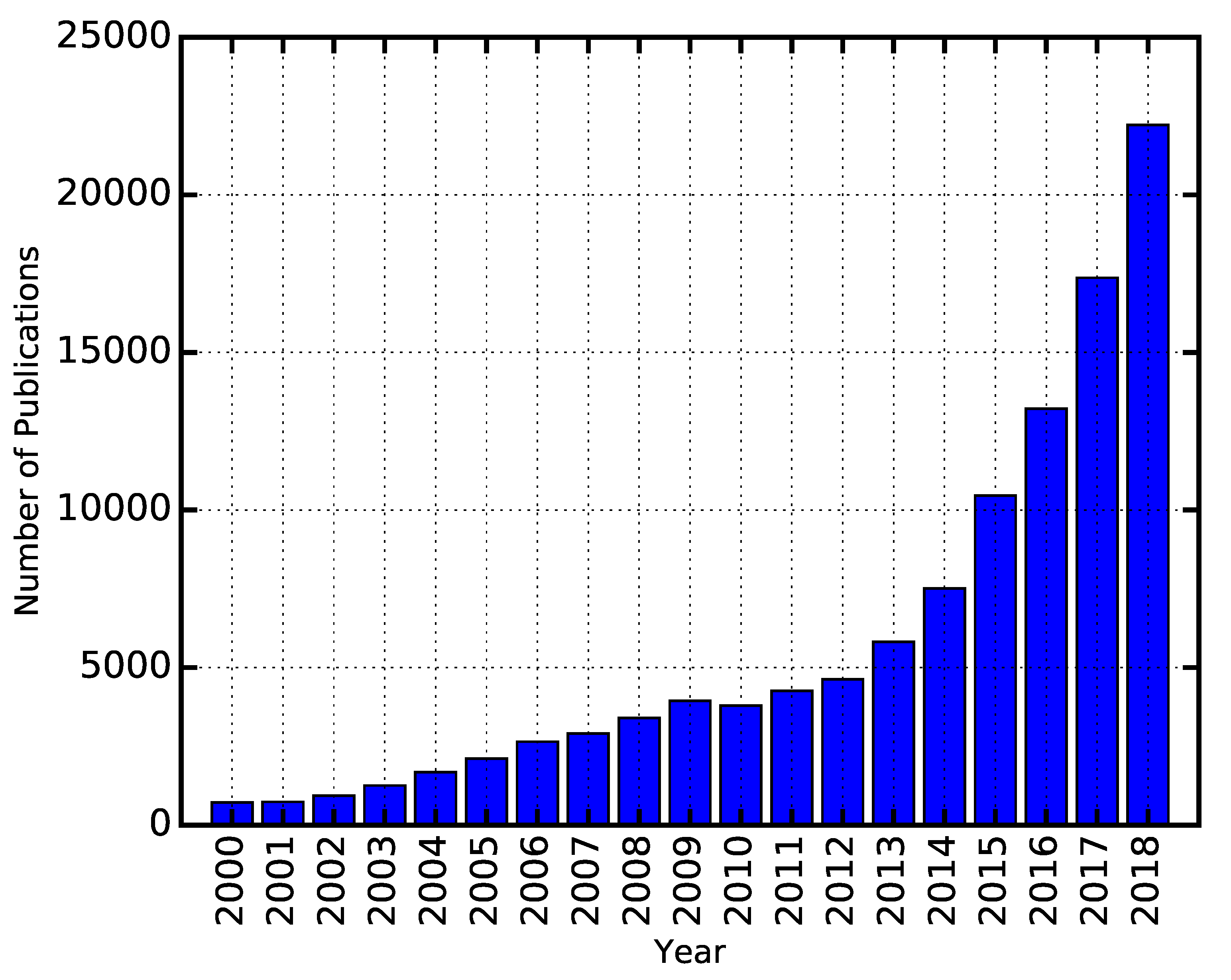
1. Introduction
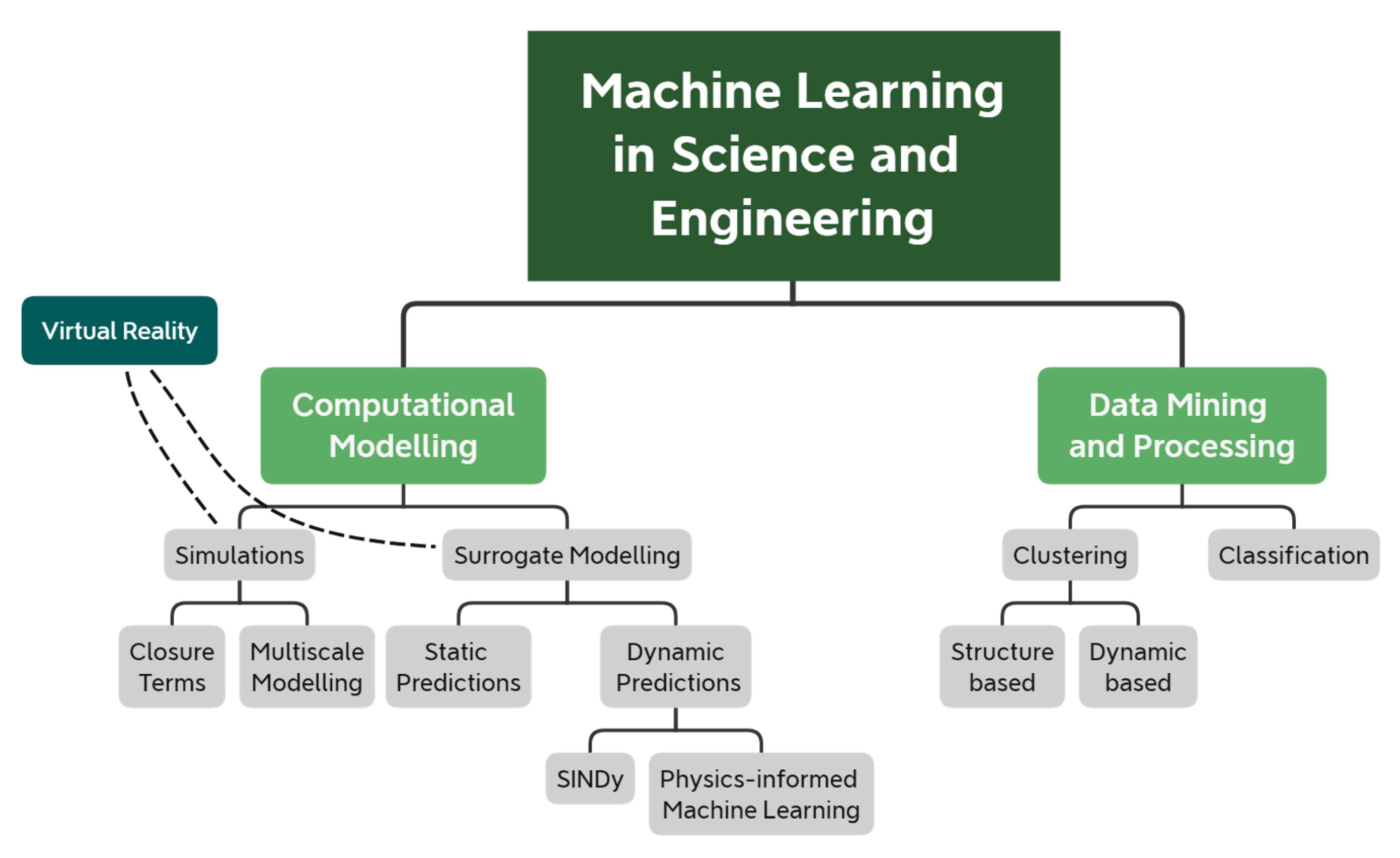
- Section 2 reviews recent ML-based methods that speed up or improve the accuracy of computational models. We further break down computational modelling into computer simulations and surrogate models. Here, simulations refer to the computational models that explicitly solve a set of differential equations that govern some physical processes. Instead, surrogate models refer to (semi-) empirical models that replace and substantially simplify the governing equations, thus providing predictive capabilities at a fraction of the time.
- Section 3 reviews ML-based methods that have been used in science and engineering to process large and complex datasets and extract meaningful quantities.
- Section 5 summarizes the current efforts for ML in engineering and discusses future perspective endeavors.
2. Machine Learning for Computational Modelling
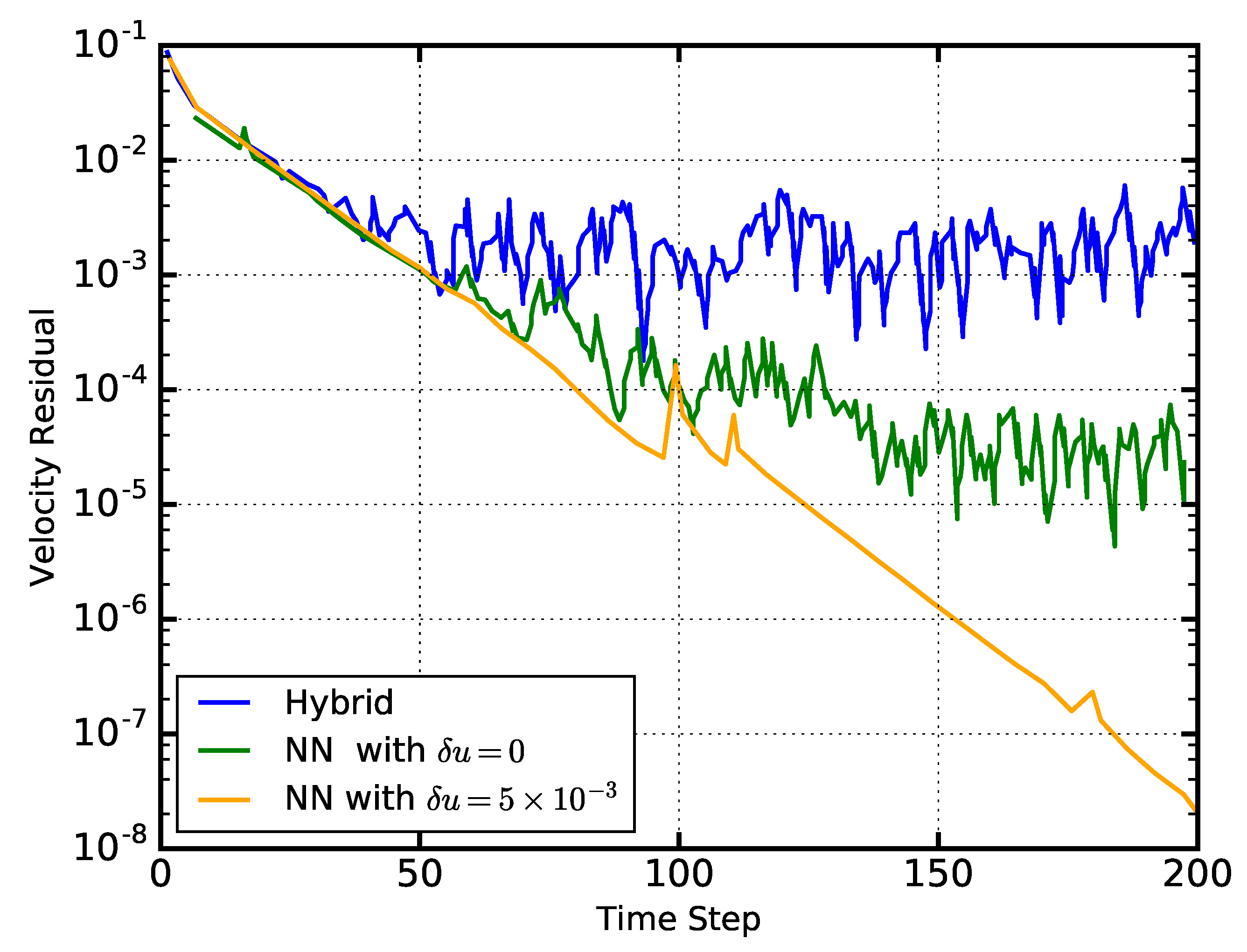
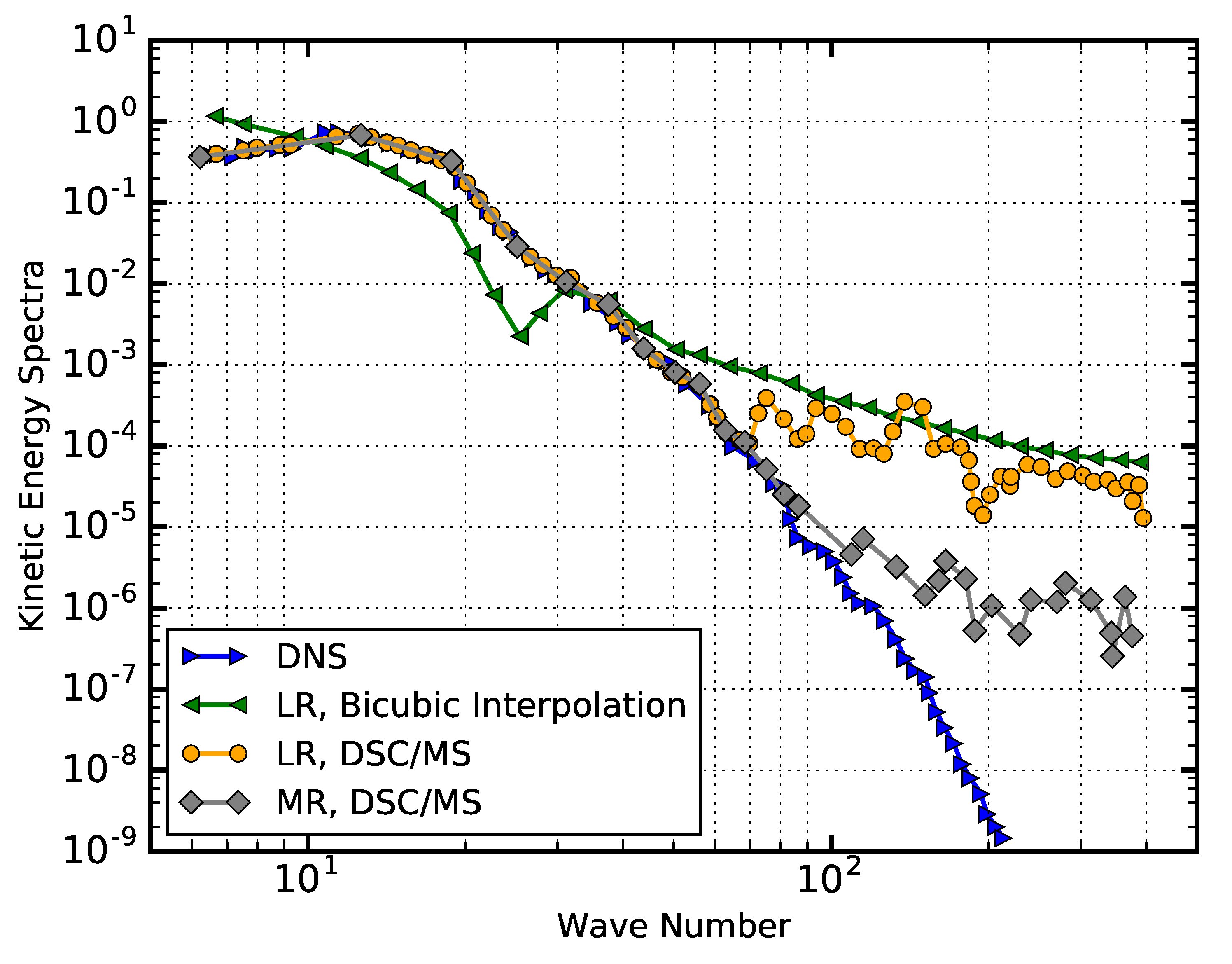
2.1. Simulations
2.2. Surrogate Modelling
3. Machine Learning in Data-Mining and Processing
4. Machine Learning and Virtual Environments
5. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AD | Alzheimer’s Disease |
| ANN | Artificial Neural Networks |
| AR | Augmented Reality |
| BNN | Bayesian Neural Networks |
| BS | Base Stations |
| CFD | Computational Fluid Dynamics |
| CNN | Convolutional Neural Networks |
| CT | Computerized Tomography |
| DBM | Deep Boltzmann Machine |
| DFT | Density Functional Theory |
| DL | Deep Learning |
| DNN | Deep Neural Networks |
| DNS | Direct Numerical Simulation |
| DSC/MS | Downsampled Skip-Connection/Multi-Scale |
| ESN | Echo State Networks |
| FPMD | First Principal Molecular Dynamics |
| GP | Gaussian Process |
| HMI | Human-Machine Interfaces |
| HPC | High-Performance Computing |
| ITS | Intelligent Tutoring System |
| KNN | K-Nearest Neighbors |
| KRR | Kernel Ridge Regression |
| LES | Large Eddy Simulation |
| LSM | Liquid State Machine |
| LSTM | Long Short-Term Memory |
| MD | Molecular Dynamics |
| MCI | Mild Cognitive Impairment |
| ML | Machine Learning |
| MRI | Magnetic Resonance Imaging |
| NPCs | Non-Player Characters |
| PCA | Principal Component Analysis |
| PCCA | Perron Cluster Cluster Analysis |
| PES | Potential Energy Surface |
| PET | Positron Emission Tomography |
| QM | Quantum Mechanics |
| QoS | Quality-of-Service |
| RANS | Reynolds Averaged Navier–Stokes |
| RBM | Restricted Boltzmann Machine |
| RNN | Recurrent Neural Networks |
| SA | Spallart–Allmaras |
| SINDy | Sparse Identification of Non-linear Dynamics |
| SCN | Small Cell Networks (SCN) |
| SVM | Support Vector Machine |
| VANETs | Vehicular Ad-Hoc Networks systems |
| UAV | Unmanned Aerial Vehicles |
| VR | Virtual Reality |
References
- Patrignani, C.; Weinberg, D.; Woody, C.; Chivukula, R.; Buchmueller, O.; Kuyanov, Y.V.; Blucher, E.; Willocq, S.; Höcker, A.; Lippmann, C.; et al. Review of particle physics. Chin. Phys. 2016, 40, 100001. [Google Scholar]
- Tanabashi, M.; Hagiwara, K.; Hikasa, K.; Nakamura, K.; Sumino, Y.; Takahashi, F.; Tanaka, J.; Agashe, K.; Aielli, G.; Amsler, C.; et al. Review of particle physics. Phys. Rev. D 2018, 98, 030001. [Google Scholar] [CrossRef]
- Calixto, G.; Bernegossi, J.; de Freitas, L.; Fontana, C.; Chorilli, M. Nanotechnology-based drug delivery systems for photodynamic therapy of cancer: A review. Molecules 2016, 21, 342. [Google Scholar] [CrossRef] [PubMed]
- Jahangirian, H.; Lemraski, E.G.; Webster, T.J.; Rafiee-Moghaddam, R.; Abdollahi, Y. A review of drug delivery systems based on nanotechnology and green chemistry: Green nanomedicine. Int. J. Nanomed. 2017, 12, 2957. [Google Scholar] [CrossRef] [PubMed]
- Contreras, J.; Rodriguez, E.; Taha-Tijerina, J. Nanotechnology applications for electrical transformers—A review. Electr. Power Syst. Res. 2017, 143, 573–584. [Google Scholar] [CrossRef]
- Scheunert, G.; Heinonen, O.; Hardeman, R.; Lapicki, A.; Gubbins, M.; Bowman, R. A review of high magnetic moment thin films for microscale and nanotechnology applications. Appl. Phys. Rev. 2016, 3, 011301. [Google Scholar] [CrossRef]
- Lu, J.; Chen, Z.; Ma, Z.; Pan, F.; Curtiss, L.A.; Amine, K. The role of nanotechnology in the development of battery materials for electric vehicles. Nat. Nanotechnol. 2016, 11, 1031. [Google Scholar] [CrossRef]
- Olafusi, O.S.; Sadiku, E.R.; Snyman, J.; Ndambuki, J.M.; Kupolati, W.K. Application of nanotechnology in concrete and supplementary cementitious materials: A review for sustainable construction. SN Appl. Sci. 2019, 1, 580. [Google Scholar] [CrossRef]
- Giustino, F. Materials Modelling Using Density Functional Theory: Properties and Predictions; Oxford University Press: Oxford, UK, 2014. [Google Scholar]
- Conlisk, A.T. Essentials oF Micro-and Nanofluidics: With Applications to the Biological and Chemical Sciences; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Hubbe, M.A.; Tayeb, P.; Joyce, M.; Tyagi, P.; Kehoe, M.; Dimic-Misic, K.; Pal, L. Rheology of nanocellulose-rich aqueous suspensions: A review. BioResources 2017, 12, 9556–9661. [Google Scholar]
- Shah, D.A.; Murdande, S.B.; Dave, R.H. A review: Pharmaceutical and pharmacokinetic aspect of nanocrystalline suspensions. J. Pharm. Sci. 2016, 105, 10–24. [Google Scholar] [CrossRef]
- Van Duin, A.C.; Dasgupta, S.; Lorant, F.; Goddard, W.A. ReaxFF: A reactive force field for hydrocarbons. J. Phys. Chem. A 2001, 105, 9396–9409. [Google Scholar] [CrossRef]
- Drikakis, D.; Frank, M. Advances and challenges in computational research of micro-and nanoflows. Microfluidics Nanofluidics 2015, 19, 1019–1033. [Google Scholar] [CrossRef][Green Version]
- Drikakis, D.; Frank, M.; Tabor, G. Multiscale computational fluid dynamics. Energies 2019, 12, 3272. [Google Scholar] [CrossRef]
- Rider, W.; Kamm, J.; Weirs, V. Verification, validation, and uncertainty quantification for coarse grained simulation. Coarse Grained Simul. Turbul. Mix. 2016, 168–189. [Google Scholar]
- Drikakis, D.; Kwak, D.; Kiris, C. Computational Aerodynamics: Advances and Challenges. Aeronaut. J. 2016, 120, 13–36. [Google Scholar] [CrossRef]
- Norton, T.; Sun, D.W. Computational fluid dynamics (CFD) ‚Äì an effective and efficient design and analysis tool for the food industry: A review. Trends Food Sci. Technol. 2006, 17, 600–620. [Google Scholar] [CrossRef]
- Kobayashi, T.; Tsubokura, M. CFD Application in Automotive Industry. In Notes on Numerical Fluid Mechanics and Multidisciplinary Design; Hirschel, E.H., Krause, E., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 100. [Google Scholar]
- Mitchell, T.M. Machine Learning; McGraw Hill: Burr Ridge, IL, USA, 1997; Volume 45, pp. 870–877. [Google Scholar]
- Vega, C.; Abascal, J.L. Simulating water with rigid non-polarizable models: A general perspective. Phys. Chem. Chem. Phys. 2011, 13, 19663–19688. [Google Scholar] [CrossRef]
- Blank, T.B.; Brown, S.D.; Calhoun, A.W.; Doren, D.J. Neural network models of potential energy surfaces. J. Chem. Phys. 1995, 103, 4129–4137. [Google Scholar] [CrossRef]
- Brown, D.F.; Gibbs, M.N.; Clary, D.C. Combining ab initio computations, neural networks, and diffusion Monte Carlo: An efficient method to treat weakly bound molecules. J. Chem. Phys. 1996, 105, 7597–7604. [Google Scholar] [CrossRef]
- Lorenz, S.; Groß, A.; Scheffler, M. Representing high-dimensional potential-energy surfaces for reactions at surfaces by neural networks. Chem. Phys. Lett. 2004, 395, 210–215. [Google Scholar] [CrossRef]
- Behler, J.; Parrinello, M. Generalized Neural-Network Representation of High-Dimensional Potential-Energy Surfaces. Phys. Rev. Lett. 2007, 98, 146401. [Google Scholar] [CrossRef] [PubMed]
- Bartók, A.P.; Payne, M.C.; Kondor, R.; Csányi, G. Gaussian approximation potentials: The accuracy of quantum mechanics, without the electrons. Phys. Rev. Lett. 2010, 104, 136403. [Google Scholar] [CrossRef] [PubMed]
- Chmiela, S.; Tkatchenko, A.; Sauceda, H.E.; Poltavsky, I.; Schütt, K.T.; Müller, K.R. Machine learning of accurate energy-conserving molecular force fields. Sci. Adv. 2017, 3, e1603015. [Google Scholar] [CrossRef] [PubMed]
- Smith, J.S.; Nebgen, B.T.; Zubatyuk, R.; Lubbers, N.; Devereux, C.; Barros, K.; Tretiak, S.; Isayev, O.; Roitberg, A.E. Approaching coupled cluster accuracy with a general-purpose neural network potential through transfer learning. Nat. Commun. 2019, 10, 2903. [Google Scholar] [CrossRef] [PubMed]
- Csányi, G.; Albaret, T.; Payne, M.C.; De Vita, A. “Learn on the Fly”: A Hybrid Classical and Quantum-Mechanical Molecular Dynamics Simulation. Phys. Rev. Lett. 2004, 93, 175503. [Google Scholar] [CrossRef]
- Li, Z.; Kermode, J.R.; De Vita, A. Molecular dynamics with on-the-fly machine learning of quantum-mechanical forces. Phys. Rev. Lett. 2015, 114, 096405. [Google Scholar] [CrossRef]
- Botu, V.; Ramprasad, R. Adaptive machine learning framework to accelerate ab initio molecular dynamics. Int. J. Quantum Chem. 2015, 115, 1074–1083. [Google Scholar] [CrossRef]
- Sosso, G.C.; Miceli, G.; Caravati, S.; Behler, J.; Bernasconi, M. Neural network interatomic potential for the phase change material GeTe. Phys. Rev. B 2012, 85, 174103. [Google Scholar] [CrossRef]
- Sosso, G.C.; Miceli, G.; Caravati, S.; Giberti, F.; Behler, J.; Bernasconi, M. Fast crystallization of the phase change compound GeTe by large-scale molecular dynamics simulations. J. Phys. Chem. Lett. 2013, 4, 4241–4246. [Google Scholar] [CrossRef]
- Gabardi, S.; Baldi, E.; Bosoni, E.; Campi, D.; Caravati, S.; Sosso, G.; Behler, J.; Bernasconi, M. Atomistic simulations of the crystallization and aging of GeTe nanowires. J. Phys. Chem. C 2017, 121, 23827–23838. [Google Scholar] [CrossRef]
- Bartók, A.P.; De, S.; Poelking, C.; Bernstein, N.; Kermode, J.R.; Csányi, G.; Ceriotti, M. Machine learning unifies the modeling of materials and molecules. Sci. Adv. 2017, 3, e1701816. [Google Scholar] [CrossRef] [PubMed]
- Behler, J.; Martoňák, R.; Donadio, D.; Parrinello, M. Metadynamics simulations of the high-pressure phases of silicon employing a high-dimensional neural network potential. Phys. Rev. Lett. 2008, 100, 185501. [Google Scholar] [CrossRef] [PubMed]
- Deringer, V.L.; Bernstein, N.; Bartók, A.P.; Cliffe, M.J.; Kerber, R.N.; Marbella, L.E.; Grey, C.P.; Elliott, S.R.; Csányi, G. Realistic atomistic structure of amorphous silicon from machine-learning-driven molecular dynamics. J. Phys. Chem. Lett. 2018, 9, 2879–2885. [Google Scholar] [CrossRef] [PubMed]
- Gastegger, M.; Behler, J.; Marquetand, P. Machine learning molecular dynamics for the simulation of infrared spectra. Chem. Sci. 2017, 8, 6924–6935. [Google Scholar] [CrossRef]
- Pérez, S.; Imberty, A.; Engelsen, S.B.; Gruza, J.; Mazeau, K.; Jimenez-Barbero, J.; Poveda, A.; Espinosa, J.F.; van Eyck, B.P.; Johnson, G.; et al. A comparison and chemometric analysis of several molecular mechanics force fields and parameter sets applied to carbohydrates. Carbohydr. Res. 1998, 314, 141–155. [Google Scholar] [CrossRef]
- Raval, A.; Piana, S.; Eastwood, M.P.; Dror, R.O.; Shaw, D.E. Refinement of protein structure homology models via long, all-atom molecular dynamics simulations. Proteins Struct. Funct. Bioinform. 2012, 80, 2071–2079. [Google Scholar] [CrossRef]
- Frank, M.; Drikakis, D. Solid-like heat transfer in confined liquids. Microfluidics Nanofluidics 2017, 21, 148. [Google Scholar] [CrossRef]
- Frank, M.; Drikakis, D. Thermodynamics at Solid–Liquid Interfaces. Entropy 2018, 20, 362. [Google Scholar] [CrossRef]
- Papanikolaou, M.; Frank, M.; Drikakis, D. Nanoflow over a fractal surface. Phys. Fluids 2016, 28, 082001. [Google Scholar] [CrossRef]
- Papanikolaou, M.; Frank, M.; Drikakis, D. Effects of surface roughness on shear viscosity. Phys. Rev. E 2017, 95, 033108. [Google Scholar] [CrossRef]
- Frank, M.; Papanikolaou, M.; Drikakis, D.; Salonitis, K. Heat transfer across a fractal surface. J. Chem. Phys. 2019, 151, 134705. [Google Scholar] [CrossRef] [PubMed]
- Asproulis, N.; Drikakis, D. Nanoscale materials modelling using neural networks. J. Comput. Theor. Nanosci. 2009, 6, 514–518. [Google Scholar] [CrossRef]
- Asproulis, N.; Drikakis, D. An artificial neural network-based multiscale method for hybrid atomistic-continuum simulations. Microfluidics Nanofluidics 2013, 15, 559–574. [Google Scholar] [CrossRef]
- Thornber, B.; Mosedale, A.; Drikakis, D. On the implicit large eddy simulations of homogeneous decaying turbulence. J. Comput. Phys. 2007, 226, 1902–1929. [Google Scholar] [CrossRef]
- Jiménez, J. Near-wall turbulence. Phys. Fluids 2013, 25, 1–28. [Google Scholar] [CrossRef]
- Drikakis, D. Advances in turbulent flow computations using high-resolution methods. Prog. Aerosp. Sci. 2003, 39, 405–424. [Google Scholar] [CrossRef]
- Kobayashi, H.; Matsumoto, E.; Fukushima, N.; Tanahashi, M.; Miyauchi, T. Statistical properties of the local structure of homogeneous isotropic turbulence and turbulent channel flows. J. Turbul. 2011, 12. [Google Scholar] [CrossRef]
- Giralt, F.; Arenas, A.; Ferre-Gine, J.; Rallo, R.; Kopp, G. The simulation and interpretation of free turbulence with a cognitive neural system. Phys. Fluids 2000, 12, 1826–1835. [Google Scholar] [CrossRef]
- Milano, M.; Koumoutsakos, P. Neural network modeling for near wall turbulent flow. J. Comput. Phys. 2002, 182, 1–26. [Google Scholar] [CrossRef]
- Chang, F.J.; Yang, H.C.; Lu, J.Y.; Hong, J.H. Neural network modelling for mean velocity and turbulence intensities of steep channel flows. Hydrol. Process. Int. J. 2008, 22, 265–274. [Google Scholar] [CrossRef]
- Duraisamy, K.; Iaccarino, G.; Xiao, H. Turbulence modeling in the age of data. Annu. Rev. Fluid Mech. 2019, 51, 357–377. [Google Scholar] [CrossRef]
- Xiao, H.; Wu, J.L.; Wang, J.X.; Sun, R.; Roy, C. Quantifying and reducing model-form uncertainties in Reynolds-averaged Navier–Stokes simulations: A data-driven, physics-informed Bayesian approach. J. Comput. Phys. 2016, 324, 115–136. [Google Scholar] [CrossRef]
- Tracey, B.D.; Duraisamy, K.; Alonso, J.J. A machine learning strategy to assist turbulence model development. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015; p. 1287. [Google Scholar]
- Zhu, L.; Zhang, W.; Kou, J.; Liu, Y. Machine learning methods for turbulence modeling in subsonic flows around airfoils. Phys. Fluids 2019, 31, 15105. [Google Scholar] [CrossRef]
- Ling, J.; Kurzawski, A.; Templeton, J. Reynolds averaged turbulence modelling using deep neural networks with embedded invariance. J. Fluid Mech. 2016, 807, 155–166. [Google Scholar] [CrossRef]
- Kutz, J.N. Deep learning in fluid dynamics. J. Fluid Mech. 2017, 814, 1–4. [Google Scholar] [CrossRef]
- Cheung, S.H.; Oliver, T.A.; Prudencio, E.E.; Prudhomme, S.; Moser, R.D. Bayesian uncertainty analysis with applications to turbulence modeling. Reliab. Eng. Syst. Saf. 2011, 96, 1137–1149. [Google Scholar] [CrossRef]
- Edeling, W.; Cinnella, P.; Dwight, R.P.; Bijl, H. Bayesian estimates of parameter variability in the k–ε turbulence model. J. Comput. Phys. 2014, 258, 73–94. [Google Scholar] [CrossRef]
- Zhang, Z.J.; Duraisamy, K. Machine learning methods for data-driven turbulence modeling. In Proceedings of the 22nd AIAA Computational Fluid Dynamics Conference, Dallas, TX, USA, 22–26 June 2015; p. 2460. [Google Scholar]
- Duraisamy, K.; Zhang, Z.J.; Singh, A.P. New approaches in turbulence and transition modeling using data-driven techniques. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015; p. 1284. [Google Scholar]
- Parish, E.J.; Duraisamy, K. A paradigm for data-driven predictive modeling using field inversion and machine learning. J. Comput. Phys. 2016, 305, 758–774. [Google Scholar] [CrossRef]
- Geneva, N.; Zabaras, N. Quantifying model form uncertainty in Reynolds-averaged turbulence models with Bayesian deep neural networks. J. Comput. Phys. 2019, 383, 125–147. [Google Scholar] [CrossRef]
- Wang, J.X.; Wu, J.L.; Xiao, H. Physics-informed machine learning approach for reconstructing Reynolds stress modeling discrepancies based on DNS data. Phys. Rev. Fluids 2017, 2, 034603. [Google Scholar] [CrossRef]
- Wu, J.L.; Xiao, H.; Paterson, E. Physics-informed machine learning approach for augmenting turbulence models: A comprehensive framework. Phys. Rev. Fluids 2018, 3, 074602. [Google Scholar] [CrossRef]
- Sarghini, F.; De Felice, G.; Santini, S. Neural networks based subgrid scale modeling in large eddy simulations. Comput. Fluids 2003, 32, 97–108. [Google Scholar] [CrossRef]
- Moreau, A.; Teytaud, O.; Bertoglio, J.P. Optimal estimation for large-eddy simulation of turbulence and application to the analysis of subgrid models. Phys. Fluids 2006, 18, 105101. [Google Scholar] [CrossRef]
- Beck, A.D.; Flad, D.G.; Munz, C.D. Deep neural networks for data-driven turbulence models. arXiv 2018, arXiv:1806.04482. [Google Scholar]
- Maulik, R.; San, O.; Rasheed, A.; Vedula, P. Subgrid modelling for two-dimensional turbulence using neural networks. J. Fluid Mech. 2019, 858, 122–144. [Google Scholar] [CrossRef]
- Fukami, K.; Fukagata, K.; Taira, K. Super-resolution reconstruction of turbulent flows with machine learning. J. Fluid Mech. 2019, 870, 106–120. [Google Scholar] [CrossRef]
- Lu, C. Artificial Neural Network for Behavior Learning From Meso-Scale Simulations, Application to Multi-Scale Multimaterial Flows; University of Lowa: Lowa City, IA, USA, 2010. [Google Scholar]
- Gibou, F.; Hyde, D.; Fedkiw, R. Sharp interface approaches and deep learning techniques for multiphase flows. J. Comput. Phys. 2019, 380, 442–463. [Google Scholar] [CrossRef]
- Ma, M.; Lu, J.; Tryggvason, G. Using statistical learning to close two-fluid multiphase flow equations for a simple bubbly system. Phys. Fluids 2015, 27, 092101. [Google Scholar] [CrossRef]
- Qi, Y.; Lu, J.; Scardovelli, R.; Zaleski, S.; Tryggvason, G. Computing curvature for volume of fluid methods using machine learning. J. Comput. Phys. 2019, 377, 155–161. [Google Scholar] [CrossRef]
- Chang, C.W.; Dinh, N.T. Classification of machine learning frameworks for data-driven thermal fluid models. Int. J. Therm. Sci. 2019, 135, 559–579. [Google Scholar] [CrossRef]
- Ling, J.; Templeton, J. Evaluation of machine learning algorithms for prediction of regions of high Reynolds averaged Navier Stokes uncertainty. Phys. Fluids 2015, 27, 085103. [Google Scholar] [CrossRef]
- Wu, J.L.; Wang, J.X.; Xiao, H.; Ling, J. A priori assessment of prediction confidence for data-driven turbulence modeling. Flow Turbul. Combust. 2017, 99, 25–46. [Google Scholar] [CrossRef]
- Yang, C.; Yang, X.; Xiao, X. Data-driven projection method in fluid simulation. Comput. Animat. Virtual Worlds 2016, 27, 415–424. [Google Scholar] [CrossRef]
- Tompson, J.; Schlachter, K.; Sprechmann, P.; Perlin, K. Accelerating eulerian fluid simulation with convolutional networks. In Proceedings of the 34th International Conference on Machine Learning-Volume 70. JMLR. org, Sydney, Australia, 6–11 August 2017; pp. 3424–3433. [Google Scholar]
- Unger, J.F.; Könke, C. Coupling of scales in a multiscale simulation using neural networks. Comput. Struct. 2008, 86, 1994–2003. [Google Scholar] [CrossRef]
- Unger, J.F.; Könke, C. Neural networks as material models within a multiscale approach. Comput. Struct. 2009, 87, 1177–1186. [Google Scholar] [CrossRef]
- Hambli, R. Numerical procedure for multiscale bone adaptation prediction based on neural networks and finite element simulation. Finite Elem. Anal. Des. 2011, 47, 835–842. [Google Scholar] [CrossRef]
- Hambli, R. Apparent damage accumulation in cancellous bone using neural networks. J. Mech. Behav. Biomed. Mater. 2011, 4, 868–878. [Google Scholar] [CrossRef]
- Sha, W.; Edwards, K. The use of artificial neural networks in materials science based research. Mater. Des. 2007, 28, 1747–1752. [Google Scholar] [CrossRef]
- Trott, A.; Moorhead, R.; McGinley, J. Wavelets applied to lossless compression and progressive transmission of floating point data in 3-D curvilinear grids. Proceedings of Seventh Annual IEEE Visualization’96, San Francisco, CA, USA, 27 October–1 November 1996; pp. 385–388. [Google Scholar]
- Kang, H.; Lee, D.; Lee, D. A study on CFD data compression using hybrid supercompact wavelets. KSME Int. J. 2003, 17, 1784–1792. [Google Scholar] [CrossRef]
- Sakai, R.; Sasaki, D.; Nakahashi, K. Parallel implementation of large-scale CFD data compression toward aeroacoustic analysis. Comput. Fluids 2013, 80, 116–127. [Google Scholar] [CrossRef]
- Carlberg, K.T.; Jameson, A.; Kochenderfer, M.J.; Morton, J.; Peng, L.; Witherden, F.D. Recovering missing CFD data for high-order discretizations using deep neural networks and dynamics learning. J. Comput. Phys. 2019, 395, 105–124. [Google Scholar] [CrossRef]
- Rupp, M. Machine learning for quantum mechanics in a nutshell. Int. J. Quantum Chem. 2015, 115, 1058–1073. [Google Scholar] [CrossRef]
- Rupp, M.; Tkatchenko, A.; Müller, K.R.; Von Lilienfeld, O.A. Fast and accurate modeling of molecular atomization energies with machine learning. Phys. Rev. Lett. 2012, 108, 058301. [Google Scholar] [CrossRef] [PubMed]
- Hansen, K.; Montavon, G.; Biegler, F.; Fazli, S.; Rupp, M.; Scheffler, M.; Von Lilienfeld, O.A.; Tkatchenko, A.; Müller, K.R. Assessment and validation of machine learning methods for predicting molecular atomization energies. J. Chem. Theory Comput. 2013, 9, 3404–3419. [Google Scholar] [CrossRef] [PubMed]
- Carleo, G.; Troyer, M. Solving the quantum many-body problem with artificial neural networks. Science 2017, 355, 602–606. [Google Scholar] [CrossRef] [PubMed]
- Handley, C.M.; Popelier, P.L. Dynamically polarizable water potential based on multipole moments trained by machine learning. J. Chem. Theory Comput. 2009, 5, 1474–1489. [Google Scholar] [CrossRef]
- Hautier, G.; Fischer, C.C.; Jain, A.; Mueller, T.; Ceder, G. Finding nature’s missing ternary oxide compounds using machine learning and density functional theory. Chem. Mater. 2010, 22, 3762–3767. [Google Scholar] [CrossRef]
- Bishop, C.M.; James, G.D. Analysis of multiphase flows using dual-energy gamma densitometry and neural networks. Nucl. Instrum. Methods Phys. Res. Sect. A 1993, 327, 580–593. [Google Scholar] [CrossRef]
- Xie, T.; Ghiaasiaan, S.; Karrila, S. Artificial neural network approach for flow regime classification in gas–liquid–fiber flows based on frequency domain analysis of pressure signals. Chem. Eng. Sci. 2004, 59, 2241–2251. [Google Scholar] [CrossRef]
- Al-Rawahi, N.; Meribout, M.; Al-Naamany, A.; Al-Bimani, A.; Meribout, A. A neural network algorithm for density measurement of multiphase flow. Multiph. Sci. Technol. 2012, 24, 89–103. [Google Scholar] [CrossRef]
- Mi, Y.; Ishii, M.; Tsoukalas, L. Flow regime identification methodology with neural networks and two-phase flow models. Nucl. Eng. Des. 2001, 204, 87–100. [Google Scholar] [CrossRef]
- Hernandez, L.; Juliá, J.; Chiva, S.; Paranjape, S.; Ishii, M. Fast classification of two-phase flow regimes based on conductivity signals and artificial neural networks. Measur. Sci. Technol. 2006, 17, 1511. [Google Scholar] [CrossRef]
- Juliá, J.E.; Liu, Y.; Paranjape, S.; Ishii, M. Upward vertical two-phase flow local flow regime identification using neural network techniques. Nuclear Eng. Des. 2008, 238, 156–169. [Google Scholar] [CrossRef]
- Rey-Fabret, I.; Sankar, R.; Duret, E.; Heintze, E.; Henriot, V. Neural networks tools for improving tacite hydrodynamic simulation of multiphase flow behavior in pipelines. Oil Gas Sci. Technol. 2001, 56, 471–478. [Google Scholar] [CrossRef]
- Lee, C.; Kim, J.; Babcock, D.; Goodman, R. Application of neural networks to turbulence control for drag reduction. Phys. Fluids 1997, 9, 1740–1747. [Google Scholar] [CrossRef]
- Rabault, J.; Kuchta, M.; Jensen, A.; Réglade, U.; Cerardi, N. Artificial neural networks trained through deep reinforcement learning discover control strategies for active flow control. J. Fluid Mech. 2019, 865, 281–302. [Google Scholar] [CrossRef]
- Ghaboussi, J.; Garrett, J.; Wu, X. Material modeling with neural networks. In Proceedings of the International Conference on Numerical Methods In Engineering: Theory and Applications, Swansea, UK, 7–11 January 1990; pp. 701–717. [Google Scholar]
- Ghaboussi, J.; Garrett, J., Jr.; Wu, X. Knowledge-based modeling of material behavior with neural networks. J. Eng. Mech. 1991, 117, 132–153. [Google Scholar] [CrossRef]
- Yeh, I.C. Modeling of strength of high-performance concrete using artificial neural networks. Cem. Concr. Res. 1998, 28, 1797–1808. [Google Scholar] [CrossRef]
- Waszczyszyn, Z.; Ziemiański, L. Neural networks in mechanics of structures and materials–new results and prospects of applications. Comput. Struct. 2001, 79, 2261–2276. [Google Scholar] [CrossRef]
- Zimmerman, D.C.; Hasselman, T.; Anderson, M. Approximation and calibration of nonlinear structural dynamics. Nonlinear Dyn. 2005, 39, 113–128. [Google Scholar] [CrossRef]
- Kerschen, G.; Worden, K.; Vakakis, A.F.; Golinval, J.C. Past, present and future of nonlinear system identification in structural dynamics. Mech. Syst. Signal Process. 2006, 20, 505–592. [Google Scholar] [CrossRef]
- Xuan, Y.; Li, Q. Heat transfer enhancement of nanofluids. Int. J. Heat Fluid Flow 2000, 21, 58–64. [Google Scholar] [CrossRef]
- Eastman, J.A.; Choi, S.; Li, S.; Yu, W.; Thompson, L. Anomalously increased effective thermal conductivities of ethylene glycol-based nanofluids containing copper nanoparticles. Appl. Phys. Lett. 2001, 78, 718–720. [Google Scholar] [CrossRef]
- Choi, S.; Zhang, Z.; Yu, W.; Lockwood, F.; Grulke, E. Anomalous thermal conductivity enhancement in nanotube suspensions. Appl. Phys. Lett. 2001, 79, 2252–2254. [Google Scholar] [CrossRef]
- Keblinski, P.; Phillpot, S.; Choi, S.; Eastman, J. Mechanisms of heat flow in suspensions of nano-sized particles (nanofluids). Int. J. Heat Mass Transf. 2002, 45, 855–863. [Google Scholar] [CrossRef]
- Evans, W.; Fish, J.; Keblinski, P. Role of Brownian motion hydrodynamics on nanofluid thermal conductivity. Appl. Phys. Lett. 2006, 88, 093116. [Google Scholar] [CrossRef]
- Sankar, N.; Mathew, N.; Sobhan, C. Molecular dynamics modeling of thermal conductivity enhancement in metal nanoparticle suspensions. Int. Commun. Heat Mass Transf. 2008, 35, 867–872. [Google Scholar] [CrossRef]
- Frank, M.; Drikakis, D.; Asproulis, N. Thermal conductivity of nanofluid in nanochannels. Microfluidics Nanofluidics 2015, 19, 1011–1017. [Google Scholar] [CrossRef]
- Deepak, K.; Frank, M.; Drikakis, D.; Asproulis, N. Thermal properties of a water-copper nanofluid in a graphene channel. J. Comput. Theor. Nanosci. 2016, 13, 79–83. [Google Scholar] [CrossRef]
- Papari, M.M.; Yousefi, F.; Moghadasi, J.; Karimi, H.; Campo, A. Modeling thermal conductivity augmentation of nanofluids using diffusion neural networks. Int. J. Therm. Sci. 2011, 50, 44–52. [Google Scholar] [CrossRef]
- Hojjat, M.; Etemad, S.G.; Bagheri, R.; Thibault, J. Thermal conductivity of non-Newtonian nanofluids: Experimental data and modeling using neural network. Int. J. Heat Mass Transf. 2011, 54, 1017–1023. [Google Scholar] [CrossRef]
- Longo, G.A.; Zilio, C.; Ceseracciu, E.; Reggiani, M. Application of artificial neural network (ANN) for the prediction of thermal conductivity of oxide–water nanofluids. Nano Energy 2012, 1, 290–296. [Google Scholar] [CrossRef]
- Esfe, M.H.; Afrand, M.; Yan, W.M.; Akbari, M. Applicability of artificial neural network and nonlinear regression to predict thermal conductivity modeling of Al2O3–water nanofluids using experimental data. Int. Commun. Heat Mass Transf. 2015, 66, 246–249. [Google Scholar] [CrossRef]
- Ariana, M.; Vaferi, B.; Karimi, G. Prediction of thermal conductivity of alumina water-based nanofluids by artificial neural networks. Powder Technol. 2015, 278, 1–10. [Google Scholar] [CrossRef]
- Esfe, M.H.; Afrand, M.; Wongwises, S.; Naderi, A.; Asadi, A.; Rostami, S.; Akbari, M. Applications of feedforward multilayer perceptron artificial neural networks and empirical correlation for prediction of thermal conductivity of Mg (OH) 2–EG using experimental data. Int. Commun. Heat Mass Transf. 2015, 67, 46–50. [Google Scholar] [CrossRef]
- Esfe, M.H.; Rostamian, H.; Afrand, M.; Karimipour, A.; Hassani, M. Modeling and estimation of thermal conductivity of MgO–water/EG (60: 40) by artificial neural network and correlation. Int. Commun. Heat Mass Transf. 2015, 68, 98–103. [Google Scholar] [CrossRef]
- Esfe, M.H.; Naderi, A.; Akbari, M.; Afrand, M.; Karimipour, A. Evaluation of thermal conductivity of COOH-functionalized MWCNTs/water via temperature and solid volume fraction by using experimental data and ANN methods. J. Therm. Anal. Calorim. 2015, 121, 1273–1278. [Google Scholar] [CrossRef]
- Esfe, M.H.; Yan, W.M.; Afrand, M.; Sarraf, M.; Toghraie, D.; Dahari, M. Estimation of thermal conductivity of Al2O3/water (40%)–ethylene glycol (60%) by artificial neural network and correlation using experimental data. Int. Commun. Heat Mass Transf. 2016, 74, 125–128. [Google Scholar] [CrossRef]
- Esfe, M.H.; Motahari, K.; Sanatizadeh, E.; Afrand, M.; Rostamian, H.; Ahangar, M.R.H. Estimation of thermal conductivity of CNTs-water in low temperature by artificial neural network and correlation. Int. Commun. Heat Mass Transf. 2016, 76, 376–381. [Google Scholar] [CrossRef]
- Esfe, M.H.; Saedodin, S.; Sina, N.; Afrand, M.; Rostami, S. Designing an artificial neural network to predict thermal conductivity and dynamic viscosity of ferromagnetic nanofluid. Int. Commun. Heat Mass Transf. 2015, 68, 50–57. [Google Scholar] [CrossRef]
- Vafaei, M.; Afrand, M.; Sina, N.; Kalbasi, R.; Sourani, F.; Teimouri, H. Evaluation of thermal conductivity of MgO-MWCNTs/EG hybrid nanofluids based on experimental data by selecting optimal artificial neural networks. Phys. E 2017, 85, 90–96. [Google Scholar] [CrossRef]
- Srivastava, A.N.; Han, J. Machine Learning and Knowledge Discovery for Engineering Systems Health Management; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Napolitano, M.R.; Chen, C.I.; Naylor, S. Aircraft failure detection and identification using neural networks. J. Guid. Control Dyn. 1993, 16, 999–1009. [Google Scholar] [CrossRef]
- Napolitano, M.R.; Neppach, C.; Casdorph, V.; Naylor, S.; Innocenti, M.; Silvestri, G. Neural-network-based scheme for sensor failure detection, identification, and accommodation. J. Guid. Control Dyn. 1995, 18, 1280–1286. [Google Scholar] [CrossRef]
- Napolitano, M.R.; An, Y.; Seanor, B.A. A fault tolerant flight control system for sensor and actuator failures using neural networks. Aircr. Des. 2000, 3, 103–128. [Google Scholar] [CrossRef]
- Chen, Y.; Lee, M. Neural networks-based scheme for system failure detection and diagnosis. Math. Comput. Simul. 2002, 58, 101–109. [Google Scholar] [CrossRef]
- Nanduri, A.; Sherry, L. Anomaly detection in aircraft data using Recurrent Neural Networks (RNN). In Proceedings of the 2016 IEEE Integrated Communications Navigation and Surveillance (ICNS) 2016, Herndon, VA, USA, 19–21 April 2016. [Google Scholar]
- Poloni, C.; Giurgevich, A.; Onesti, L.; Pediroda, V. Hybridization of a multi-objective genetic algorithm, a neural network and a classical optimizer for a complex design problem in fluid dynamics. Comput. Methods Appl. Mech. Eng. 2000, 186, 403–420. [Google Scholar] [CrossRef]
- Esau, I. On application of artificial neural network methods in large-eddy simulations with unresolved urban surfaces. Mod. Appl. Sci. 2010, 4, 3. [Google Scholar] [CrossRef][Green Version]
- Paez, T.L.; Hunter, N. Dynamical System Modeling via Signal Reduction and Neural Network Simulation; Technical report; Sandia National Labs.: Albuquerque, NM, USA, 1997. [Google Scholar]
- Smaoui, N. A Model for the Unstable Manifold of the Bursting Behavior in the 2D Navier–Stokes Flow. SIAM J. Sci. Comput. 2001, 23, 824–839. [Google Scholar] [CrossRef]
- Smaoui, N.; Al-Enezi, S. Modelling the dynamics of nonlinear partial differential equations using neural networks. J. Comput. Appl. Math. 2004, 170, 27–58. [Google Scholar] [CrossRef]
- Nakajima, Y.; Kikuchi, R.; Kuramoto, K.; Tsutsumi, A.; Otawara, K. Nonlinear modeling of chaotic dynamics in a circulating fluidized bed by an artificial neural network. J. Chem. Eng. Jpn. 2001, 34, 107–113. [Google Scholar] [CrossRef]
- Otawara, K.; Fan, L.; Tsutsumi, A.; Yano, T.; Kuramoto, K.; Yoshida, K. An artificial neural network as a model for chaotic behavior of a three-phase fluidized bed. Chaos Solitons Fractals 2002, 13, 353–362. [Google Scholar] [CrossRef]
- Lin, H.; Chen, W.; Tsutsumi, A. Long-term prediction of nonlinear hydrodynamics in bubble columns by using artificial neural networks. Chem. Eng. Process. Process Intensif. 2003, 42, 611–620. [Google Scholar] [CrossRef]
- Bakker, R.; De Korte, R.; Schouten, J.; Van Den Bleek, C.; Takens, F. Neural networks for prediction and control of chaotic fluidized bed hydrodynamics: A first step. Fractals 1997, 5, 523–530. [Google Scholar] [CrossRef]
- Bakker, R.; Schouten, J.C.; Giles, C.L.; Takens, F.; Bleek, C.M.v.d. Learning chaotic attractors by neural networks. Neural Comput. 2000, 12, 2355–2383. [Google Scholar] [CrossRef] [PubMed]
- Jeong, S.; Solenthaler, B.; Pollefeys, M.; Gross, M. Data-driven fluid simulations using regression forests. ACM Trans. Graphics (TOG) 2015, 34, 199. [Google Scholar]
- Wang, Z.; Xiao, D.; Fang, F.; Govindan, R.; Pain, C.C.; Guo, Y. Model identification of reduced order fluid dynamics systems using deep learning. Int. J. Numer. Methods Fluids 2018, 86, 255–268. [Google Scholar] [CrossRef]
- Brunton, S.L.; Proctor, J.L.; Kutz, J.N. Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc. Natl. Acad. Sci. USA 2016, 113, 3932–3937. [Google Scholar] [CrossRef]
- Lui, H.F.; Wolf, W.R. Construction of reduced-order models for fluid flows using deep feedforward neural networks. J. Fluid Mech. 2019, 872, 963–994. [Google Scholar] [CrossRef]
- Pan, S.; Duraisamy, K. Long-time predictive modeling of nonlinear dynamical systems using neural networks. Complexity 2018, 2018. [Google Scholar] [CrossRef]
- Owhadi, H. Bayesian numerical homogenization. Multiscale Model. Simul. 2015, 13, 812–828. [Google Scholar] [CrossRef]
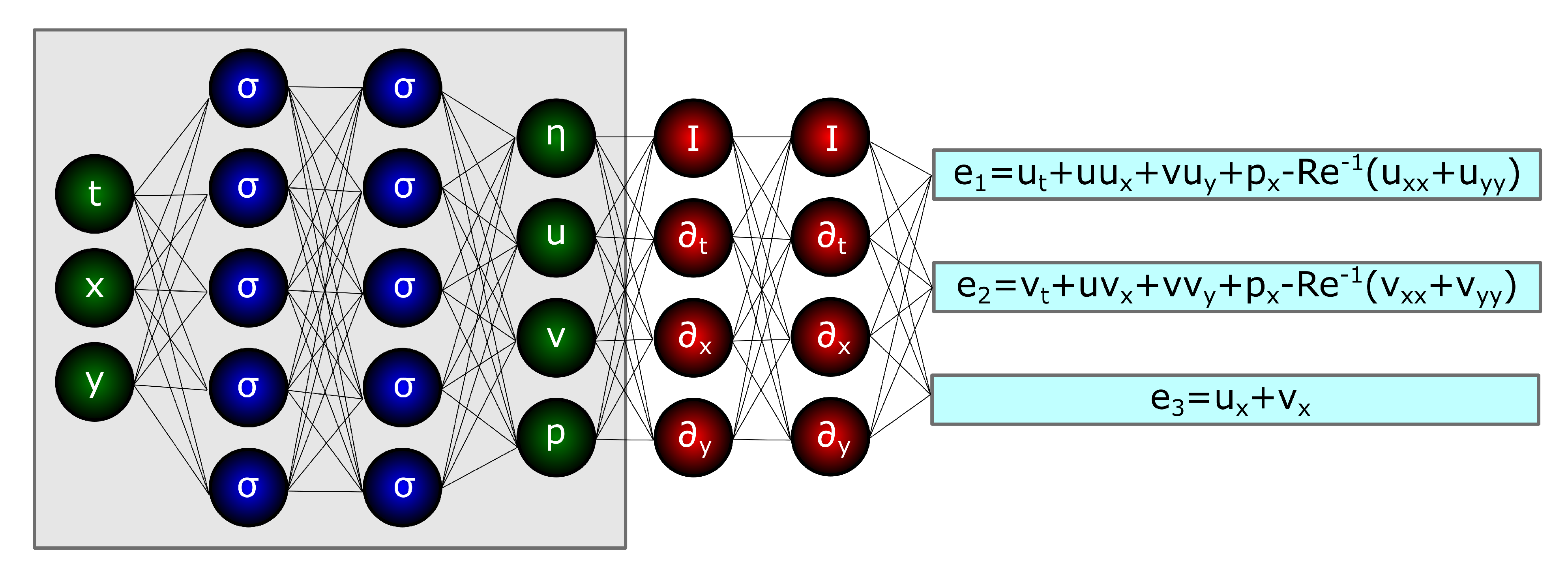
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Inferring solutions of differential equations using noisy multi-fidelity data. J. Comput. Phys. 2017, 335, 736–746. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Machine learning of linear differential equations using Gaussian processes. J. Comput. Phys. 2017, 348, 683–693. [Google Scholar] [CrossRef]
- Raissi, M.; Karniadakis, G.E. Hidden physics models: Machine learning of nonlinear partial differential equations. J. Comput. Phys. 2018, 357, 125–141. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Numerical Gaussian processes for time-dependent and nonlinear partial differential equations. SIAM J. Sci. Comput. 2018, 40, A172–A198. [Google Scholar] [CrossRef]
- Baydin, A.G.; Pearlmutter, B.A.; Radul, A.A.; Siskind, J.M. Automatic differentiation in machine learning: A survey. J. Mach. Learn. Res. 2018, 18, 5595–5637. [Google Scholar]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics informed deep learning (part i): Data-driven solutions of nonlinear partial differential equations. arXiv 2017, arXiv:1711.10561. [Google Scholar]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics informed deep learning (part ii): Data-driven discovery of nonlinear partial differential equations. arXiv 2017, arXiv:1711.10566. [Google Scholar]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Raissi, M.; Wang, Z.; Triantafyllou, M.S.; Karniadakis, G.E. Deep learning of vortex-induced vibrations. J. Fluid Mech. 2019, 861, 119–137. [Google Scholar] [CrossRef]
- Sirignano, J.; Spiliopoulos, K. DGM: A deep learning algorithm for solving partial differential equations. J. Comput. Phys. 2018, 375, 1339–1364. [Google Scholar] [CrossRef]
- Zhu, Y.; Zabaras, N.; Koutsourelakis, P.S.; Perdikaris, P. Physics-constrained deep learning for high-dimensional surrogate modeling and uncertainty quantification without labeled data. J. Comput. Phys. 2019, 394, 56–81. [Google Scholar] [CrossRef]
- Ramsundar, B.; Eastman, P.; Walters, P.; Pande, V. Deep Learning for the Life Sciences: Applying Deep Learning to Genomics, Microscopy, Drug Discovery, and More; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2019. [Google Scholar]
- Wolf, A.; Kirschner, K.N. Principal component and clustering analysis on molecular dynamics data of the ribosomal L11· 23S subdomain. J. Mol. Model. 2013, 19, 539–549. [Google Scholar] [CrossRef] [PubMed]
- Shin, J.; Berg, D.A.; Zhu, Y.; Shin, J.Y.; Song, J.; Bonaguidi, M.A.; Enikolopov, G.; Nauen, D.W.; Christian, K.M.; Ming, G.l.; et al. Single-cell RNA-seq with waterfall reveals molecular cascades underlying adult neurogenesis. Cell Stem Cell 2015, 17, 360–372. [Google Scholar] [CrossRef] [PubMed]
- Decherchi, S.; Berteotti, A.; Bottegoni, G.; Rocchia, W.; Cavalli, A. The ligand binding mechanism to purine nucleoside phosphorylase elucidated via molecular dynamics and machine learning. Nat. Commun. 2015, 6, 6155. [Google Scholar] [CrossRef]
- Schütte, C.; Fischer, A.; Huisinga, W.; Deuflhard, P. A direct approach to conformational dynamics based on hybrid Monte Carlo. J. Comput. Phys. 1999, 151, 146–168. [Google Scholar] [CrossRef]
- Huisinga, W.; Best, C.; Roitzsch, R.; Schütte, C.; Cordes, F. From simulation data to conformational ensembles: Structure and dynamics-based methods. J. Comput. Chem. 1999, 20, 1760–1774. [Google Scholar] [CrossRef]
- Noé, F.; Horenko, I.; Schütte, C.; Smith, J.C. Hierarchical analysis of conformational dynamics in biomolecules: Transition networks of metastable states. J. Chem. Phys. 2007, 126, 04B617. [Google Scholar] [CrossRef]
- Deuflhard, P.; Weber, M. Robust Perron cluster analysis in conformation dynamics. Linear Algebra Appl. 2005, 398, 161–184. [Google Scholar] [CrossRef]
- Weber, M.; Kube, S. Robust perron cluster analysis for various applications in computational life science. In Proceedings of the International Symposium on Computational Life Science, Konstanz, Germany, 25–27 September 2005; Springer: Berlin, Germany, 2005; pp. 57–66. [Google Scholar]
- Karpen, M.E.; Tobias, D.J.; Brooks, C.L., III. Statistical clustering techniques for the analysis of long molecular dynamics trajectories: Analysis of 2.2-ns trajectories of YPGDV. Biochemistry 1993, 32, 412–420. [Google Scholar] [CrossRef]
- Angermueller, C.; Pärnamaa, T.; Parts, L.; Stegle, O. Deep learning for computational biology. Mol. Syst. Biol. 2016, 12, 878. [Google Scholar] [CrossRef]
- Pérez, A.; Martínez-Rosell, G.; De Fabritiis, G. Simulations meet machine learning in structural biology. Curr. Opin. Struct. Biol. 2018, 49, 139–144. [Google Scholar] [CrossRef] [PubMed]
- Park, Y.; Kellis, M. Deep learning for regulatory genomics. Nat. Biotechnol. 2015, 33, 825. [Google Scholar] [CrossRef] [PubMed]
- Xiong, H.Y.; Alipanahi, B.; Lee, L.J.; Bretschneider, H.; Merico, D.; Yuen, R.K.; Hua, Y.; Gueroussov, S.; Najafabadi, H.S.; Hughes, T.R.; et al. The human splicing code reveals new insights into the genetic determinants of disease. Science 2015, 347, 1254806. [Google Scholar] [CrossRef] [PubMed]
- Alipanahi, B.; Delong, A.; Weirauch, M.T.; Frey, B.J. Predicting the sequence specificities of DNA-and RNA-binding proteins by deep learning. Nat. Biotechnol. 2015, 33, 831. [Google Scholar] [CrossRef]
- Zeng, H.; Edwards, M.D.; Liu, G.; Gifford, D.K. Convolutional neural network architectures for predicting DNA–protein binding. Bioinformatics 2016, 32, i121–i127. [Google Scholar] [CrossRef]
- Nguyen, N.G.; Tran, V.A.; Ngo, D.L.; Phan, D.; Lumbanraja, F.R.; Faisal, M.R.; Abapihi, B.; Kubo, M.; Satou, K. DNA sequence classification by convolutional neural network. J. Biomed. Sci. Eng. 2016, 9, 280. [Google Scholar] [CrossRef]
- Zhou, J.; Troyanskaya, O.G. Predicting effects of noncoding variants with deep learning–based sequence model. Nat. Methods 2015, 12, 931. [Google Scholar] [CrossRef]
- Krishnaiah, V.; Narsimha, D.G.; Chandra, D.N.S. Diagnosis of lung cancer prediction system using data mining classification techniques. Int. J. Comput. Sci. Inf. Technol. 2013, 4, 39–45. [Google Scholar]
- Kuruvilla, J.; Gunavathi, K. Lung cancer classification using neural networks for CT images. Comput. Methods Programs Biomed. 2014, 113, 202–209. [Google Scholar] [CrossRef]
- D’Cruz, J.; Jadhav, A.; Dighe, A.; Chavan, V.; Chaudhari, J. Detection of lung cancer using backpropagation neural networks and genetic algorithm. Comput. Technol. Appl. 2016, 6, 823–827. [Google Scholar]
- Kumar, D.; Wong, A.; Clausi, D.A. Lung nodule classification using deep features in CT images. In Proceedings of the 2015 IEEE 12th Conference on Computer and Robot Vision, Halifax, NS, Canada, 3–5 June 2015; pp. 133–138. [Google Scholar]
- Song, Q.; Zhao, L.; Luo, X.; Dou, X. Using deep learning for classification of lung nodules on computed tomography images. J. Healthc. Eng. 2017, 2017. [Google Scholar] [CrossRef] [PubMed]
- Teramoto, A.; Tsukamoto, T.; Kiriyama, Y.; Fujita, H. Automated classification of lung cancer types from cytological images using deep convolutional neural networks. BioMed Res. Int. 2017, 2017. [Google Scholar] [CrossRef] [PubMed]
- Chon, A.; Balachandar, N. Deep Convolutional Neural Networks for Lung Cancer Detection; Standford University: Stanford, CA, USA, 2017. [Google Scholar]
- Serj, M.F.; Lavi, B.; Hoff, G.; Valls, D.P. A deep convolutional neural network for lung cancer diagnostic. arXiv 2018, arXiv:1804.08170. [Google Scholar]
- Mendoza, J.; Pedrini, H. Detection and classification of lung nodules in chest X-ray images using deep convolutional neural networks. Comput. Intell. 2019. [Google Scholar] [CrossRef]
- Rehman, M.Z.; Nawi, N.M.; Tanveer, A.; Zafar, H.; Munir, H.; Hassan, S. Lungs Cancer Nodules Detection from CT Scan Images with Convolutional Neural Networks. In Proceedings of the International Conference on Soft Computing and Data Mining, Melaka, Malaysia, 22–23 January 2020; Springer: Berlin, Germany, 2020; pp. 382–391. [Google Scholar]
- Ren, Y.; Tsai, M.Y.; Chen, L.; Wang, J.; Li, S.; Liu, Y.; Jia, X.; Shen, C. A manifold learning regularization approach to enhance 3D CT image-based lung nodule classification. Int. J. Comput. Assisted Radiol. Surg. 2019, 15, 287–295. [Google Scholar] [CrossRef]
- Kharya, S.; Dubey, D.; Soni, S. Predictive machine learning techniques for breast cancer detection. Int. J. Comput. Sci. Inf. Technol. 2013, 4, 1023–1028. [Google Scholar]
- Osareh, A.; Shadgar, B. Machine learning techniques to diagnose breast cancer. In Proceedings of the 2010 5th International Symposium on Health Informatics and Bioinformatics, Antalya, Turkey, 20–22 April 2010; pp. 114–120. [Google Scholar]
- Asri, H.; Mousannif, H.; Al Moatassime, H.; Noel, T. Using machine learning algorithms for breast cancer risk prediction and diagnosis. Procedia Comput. Sci. 2016, 83, 1064–1069. [Google Scholar] [CrossRef]
- Joshi, N.; Billings, S.; Schwartz, E.; Harvey, S.; Burlina, P. Machine Learning Methods for 1D Ultrasound Breast Cancer Screening. In Proceedings of the 2017 16th IEEE International Conference on Machine Learning and Applications (ICMLA), Cancun, Mexico, 18–21 December 2017; pp. 711–715. [Google Scholar]
- Lötsch, J.; Sipilä, R.; Tasmuth, T.; Kringel, D.; Estlander, A.M.; Meretoja, T.; Kalso, E.; Ultsch, A. Machine-learning-derived classifier predicts absence of persistent pain after breast cancer surgery with high accuracy. Breast Cancer Res. Treat. 2018, 171, 399–411. [Google Scholar] [CrossRef]
- Zupan, B.; DemšAr, J.; Kattan, M.W.; Beck, J.R.; Bratko, I. Machine learning for survival analysis: A case study on recurrence of prostate cancer. Artif. Intell. Med. 2000, 20, 59–75. [Google Scholar] [CrossRef]
- Wang, J.; Wu, C.J.; Bao, M.L.; Zhang, J.; Wang, X.N.; Zhang, Y.D. Machine learning-based analysis of MR radiomics can help to improve the diagnostic performance of PI-RADS v2 in clinically relevant prostate cancer. Eur. Radiol. 2017, 27, 4082–4090. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Sridharan, S.; Macias, V.; Kajdacsy-Balla, A.; Melamed, J.; Do, M.N.; Popescu, G. Automatic Gleason grading of prostate cancer using quantitative phase imaging and machine learning. J. Biomed. Opt. 2017, 22, 036015. [Google Scholar] [CrossRef] [PubMed]
- Barlow, H.; Mao, S.; Khushi, M. Predicting high-risk prostate cancer using machine learning methods. Data 2019, 4, 129. [Google Scholar] [CrossRef]
- Li, S.; Shi, F.; Pu, F.; Li, X.; Jiang, T.; Xie, S.; Wang, Y. Hippocampal shape analysis of Alzheimer disease based on machine learning methods. Am. J. Neuroradiol. 2007, 28, 1339–1345. [Google Scholar] [CrossRef] [PubMed]
- Suk, H.I.; Lee, S.W.; Shen, D.; Alzheimer’s Disease Neuroimaging Initiative. Hierarchical feature representation and multimodal fusion with deep learning for AD/MCI diagnosis. NeuroImage 2014, 101, 569–582. [Google Scholar] [CrossRef]
- Mirzaei, G.; Adeli, A.; Adeli, H. Imaging and machine learning techniques for diagnosis of Alzheimer’s disease. Rev. Neurosci. 2016, 27, 857–870. [Google Scholar] [CrossRef]
- Khagi, B.; Kwon, G.R.; Lama, R. Comparative analysis of Alzheimer’s disease classification by CDR level using CNN, feature selection, and machine-learning techniques. Int. J. Imaging Syst. Technol. 2019, 29, 297–310. [Google Scholar] [CrossRef]
- Tahir, N.M.; Manap, H.H. Parkinson Disease Gait Classification based on Machine Learning Approach. J. Appl. Sci. Faisalabad (Faisalabad) 2012, 12, 180–185. [Google Scholar]
- Salvatore, C.; Cerasa, A.; Castiglioni, I.; Gallivanone, F.; Augimeri, A.; Lopez, M.; Arabia, G.; Morelli, M.; Gilardi, M.; Quattrone, A. Machine learning on brain MRI data for differential diagnosis of Parkinson’s disease and Progressive Supranuclear Palsy. J. Neurosci. Methods 2014, 222, 230–237. [Google Scholar] [CrossRef]
- Abós, A.; Baggio, H.C.; Segura, B.; García-Díaz, A.I.; Compta, Y.; Martí, M.J.; Valldeoriola, F.; Junqué, C. Discriminating cognitive status in Parkinson’s disease through functional connectomics and machine learning. Sci. Rep. 2017, 7, 45347. [Google Scholar] [CrossRef]
- Rastegari, E.; Azizian, S.; Ali, H. Machine Learning and Similarity Network Approaches to Support Automatic Classification of Parkinson’s Diseases Using Accelerometer-based Gait Analysis. In Proceedings of the 52nd Hawaii International Conference on System Sciences, Grand Wailea, Maui, HI, USA, 8–11 January 2019. [Google Scholar]
- Riordon, J.; Sovilj, D.; Sanner, S.; Sinton, D.; Young, E.W. Deep learning with microfluidics for biotechnology. Trends Biotechnol. 2018, 37, 310–324. [Google Scholar] [CrossRef]
- Schneider, G. Automating drug discovery. Nat. Rev. Drug Discov. 2018, 17, 97. [Google Scholar] [CrossRef] [PubMed]
- Berg, B.; Cortazar, B.; Tseng, D.; Ozkan, H.; Feng, S.; Wei, Q.; Chan, R.Y.L.; Burbano, J.; Farooqui, Q.; Lewinski, M.; et al. Cellphone-based hand-held microplate reader for point-of-care testing of enzyme-linked immunosorbent assays. ACS Nano 2015, 9, 7857–7866. [Google Scholar] [CrossRef] [PubMed]
- Bailey, M.; Oberheide, J.; Andersen, J.; Mao, Z.M.; Jahanian, F.; Nazario, J. Automated classification and analysis of internet malware. In Proceedings of the International Workshop on Recent Advances in Intrusion Detection, Gold Coast, Australia, 5–7 September 2007; Springer: Berlin, Germany, 2007; pp. 178–197. [Google Scholar]
- Bayer, U.; Comparetti, P.M.; Hlauschek, C.; Kruegel, C.; Kirda, E. Scalable, behavior-based malware clustering. NDSS Citeseer 2009, 9, 8–11. [Google Scholar]
- Rieck, K.; Laskov, P. Linear-time computation of similarity measures for sequential data. J. Mach. Learn. Res. 2008, 9, 23–48. [Google Scholar]
- Rieck, K.; Trinius, P.; Willems, C.; Holz, T. Automatic analysis of malware behavior using machine learning. J. Comput. Secur. 2011, 19, 639–668. [Google Scholar] [CrossRef]
- Nataraj, L.; Karthikeyan, S.; Jacob, G.; Manjunath, B. Malware images: Visualization and automatic classification. In Proceedings of the 8th International Symposium on Visualization for Cyber Security, Pittsburgh, PA, USA, 20 July 2011; ACM: New York, NY, USA, 2011; p. 4. [Google Scholar]
- Narayanan, B.N.; Djaneye-Boundjou, O.; Kebede, T.M. Performance analysis of machine learning and pattern recognition algorithms for malware classification. In Proceedings of the 2016 IEEE National Aerospace and Electronics Conference (NAECON) and Ohio Innovation Summit (OIS), Dayton, OH, USA, 25–29 July 2016; pp. 338–342. [Google Scholar]
- Ball, N.M.; Brunner, R.J. Data mining and machine learning in astronomy. Int. J. Mod. Phys. D 2010, 19, 1049–1106. [Google Scholar] [CrossRef]
- Way, M.J.; Scargle, J.D.; Ali, K.M.; Srivastava, A.N. Advances in Machine Learning and Data Mining for Astronomy; Chapman and Hall/CRC: Boca Raton, FL, USA, 2012. [Google Scholar]
- Ivezić, Ž.; Connolly, A.J.; VanderPlas, J.T.; Gray, A. Statistics, Data Mining, and Machine Learning in Astronomy: A Practical Python Guide for the Analysis of Survey Data; Princeton University Press: Princeton, NJ, USA, 2014; Volume 1. [Google Scholar]
- VanderPlas, J.; Connolly, A.J.; Ivezić, Ž.; Gray, A. Introduction to astroML: Machine learning for astrophysics. In Proceedings of the 2012 IEEE Conference on Intelligent Data Understanding, Boulder, CO, USA, 24–26 October 2012; pp. 47–54. [Google Scholar]
- Kremer, J.; Stensbo-Smidt, K.; Gieseke, F.; Pedersen, K.S.; Igel, C. Big universe, big data: Machine learning and image analysis for astronomy. IEEE Intell. Syst. 2017, 32, 16–22. [Google Scholar] [CrossRef]
- Andreon, S.; Gargiulo, G.; Longo, G.; Tagliaferri, R.; Capuano, N. Wide field imaging—I. Applications of neural networks to object detection and star/galaxy classification. Mon. Not. R. Astron. Soc. 2000, 319, 700–716. [Google Scholar] [CrossRef]
- Kim, E.J.; Brunner, R.J. Star-galaxy classification using deep convolutional neural networks. Mon. Not. R. Astron. Soc. 2016, 464, 4463–4475. [Google Scholar] [CrossRef]
- Walmsley, M.; Smith, L.; Lintott, C.; Gal, Y.; Bamford, S.; Dickinson, H.; Fortson, L.; Kruk, S.; Masters, K.; Scarlata, C.; et al. Galaxy Zoo: Probabilistic Morphology through Bayesian CNNs and Active Learning. arXiv 2019, arXiv:1905.07424. [Google Scholar] [CrossRef]
- Zhu, X.P.; Dai, J.M.; Bian, C.J.; Chen, Y.; Chen, S.; Hu, C. Galaxy morphology classification with deep convolutional neural networks. Astrophys. Space Sci. 2019, 364, 55. [Google Scholar] [CrossRef]
- Hoyle, B. Measuring photometric redshifts using galaxy images and Deep Neural Networks. Astron. Comput. 2016, 16, 34–40. [Google Scholar] [CrossRef]
- Pasquet, J.; Bertin, E.; Treyer, M.; Arnouts, S.; Fouchez, D. Photometric redshifts from SDSS images using a convolutional neural network. Astron. Astrophys. 2019, 621, A26. [Google Scholar] [CrossRef]
- Chan, M.C.; Stott, J.P. Deep-CEE I: Fishing for Galaxy Clusters with Deep Neural Nets. arXiv 2019, arXiv:1906.08784. [Google Scholar] [CrossRef]
- Hezaveh, Y.D.; Levasseur, L.P.; Marshall, P.J. Fast automated analysis of strong gravitational lenses with convolutional neural networks. Nature 2017, 548, 555. [Google Scholar] [CrossRef] [PubMed]
- Schaefer, C.; Geiger, M.; Kuntzer, T.; Kneib, J.P. Deep convolutional neural networks as strong gravitational lens detectors. Astron. Astrophys. 2018, 611, A2. [Google Scholar] [CrossRef]
- Pearson, J.; Pennock, C.; Robinson, T. Auto-detection of strong gravitational lenses using convolutional neural networks. Emergent Sci. 2018, 2, 1. [Google Scholar] [CrossRef]
- Ribli, D.; Pataki, B.Á.; Matilla, J.M.Z.; Hsu, D.; Haiman, Z.; Csabai, I. Weak lensing cosmology with convolutional neural networks on noisy data. arXiv 2019, arXiv:1902.03663. [Google Scholar] [CrossRef]
- Flamary, R. Astronomical image reconstruction with convolutional neural networks. In Proceedings of the 2017 25th European Signal Processing Conference (EUSIPCO), Kos Island, Greece, 28 August–2 September 2017; pp. 2468–2472. [Google Scholar]
- Karpathy, A.; Toderici, G.; Shetty, S.; Leung, T.; Sukthankar, R.; Fei-Fei, L. Large-scale video classification with convolutional neural networks. In Proceedings of the IEEE conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 1725–1732. [Google Scholar]
- Abu-El-Haija, S.; Kothari, N.; Lee, J.; Natsev, P.; Toderici, G.; Varadarajan, B.; Vijayanarasimhan, S. Youtube-8m: A large-scale video classification benchmark. arXiv 2016, arXiv:1609.08675. [Google Scholar]
- Miech, A.; Laptev, I.; Sivic, J. Learnable pooling with context gating for video classification. arXiv 2017, arXiv:1706.06905. [Google Scholar]
- Wang, H.D.; Zhang, T.; Wu, J. The monkeytyping solution to the youtube-8m video understanding challenge. arXiv 2017, arXiv:1706.05150. [Google Scholar]
- Li, F.; Gan, C.; Liu, X.; Bian, Y.; Long, X.; Li, Y.; Li, Z.; Zhou, J.; Wen, S. Temporal modeling approaches for large-scale youtube-8m video understanding. arXiv 2017, arXiv:1707.04555. [Google Scholar]
- Chen, S.; Wang, X.; Tang, Y.; Chen, X.; Wu, Z.; Jiang, Y.G. Aggregating frame-level features for large-scale video classification. arXiv 2017, arXiv:1707.00803. [Google Scholar]
- Skalic, M.; Pekalski, M.; Pan, X.E. Deep learning methods for efficient large scale video labeling. arXiv 2017, arXiv:1706.04572. [Google Scholar]
- Bhardwaj, S.; Srinivasan, M.; Khapra, M.M. Efficient Video Classification Using Fewer Frames. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 354–363. [Google Scholar]
- Alahi, A.; Goel, K.; Ramanathan, V.; Robicquet, A.; Fei-Fei, L.; Savarese, S. Social lstm: Human trajectory prediction in crowded spaces. In Proceedings of the IEEE conference on computer vision and pattern recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 961–971. [Google Scholar]
- Yi, S.; Li, H.; Wang, X. Pedestrian behavior understanding and prediction with deep neural networks. In European Conference on Computer Vision; Springer: Berlin, Germany, 2016; pp. 263–279. [Google Scholar]
- Gupta, A.; Johnson, J.; Fei-Fei, L.; Savarese, S.; Alahi, A. Social gan: Socially acceptable trajectories with generative adversarial networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 2255–2264. [Google Scholar]
- Xu, Y.; Piao, Z.; Gao, S. Encoding crowd interaction with deep neural network for pedestrian trajectory prediction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 5275–5284. [Google Scholar]
- Zou, H.; Su, H.; Song, S.; Zhu, J. Understanding human behaviors in crowds by imitating the decision-making process. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LO, USA, 2–7 February 2018. [Google Scholar]
- Kitani, K.M.; Ziebart, B.D.; Bagnell, J.A.; Hebert, M. Activity forecasting. In European Conference on Computer Vision; Springer: Berlin, Germany, 2012; pp. 201–214. [Google Scholar]
- Jaipuria, N.; Habibi, G.; How, J.P. A transferable pedestrian motion prediction model for intersections with different geometries. arXiv 2018, arXiv:1806.09444. [Google Scholar]
- Sadeghian, A.; Kosaraju, V.; Sadeghian, A.; Hirose, N.; Rezatofighi, H.; Savarese, S. Sophie: An attentive gan for predicting paths compliant to social and physical constraints. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 1349–1358. [Google Scholar]
- Yagi, T.; Mangalam, K.; Yonetani, R.; Sato, Y. Future person localization in first-person videos. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7593–7602. [Google Scholar]
- Liang, J.; Jiang, L.; Niebles, J.C.; Hauptmann, A.G.; Fei-Fei, L. Peeking into the future: Predicting future person activities and locations in videos. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 5725–5734. [Google Scholar]
- Laukkanen, S.; Karanta, I.; Kotovirta, V.; Markkanen, J.; Rönkkö, J. Adding intelligence to virtual reality. In Proceedings of the 16th European Conference in Artificial Intelligence, Valencia, Spain, 22–27 August 2004; pp. 1136–1144. [Google Scholar]
- Yang, H.W.; Pan, Z.G.; Xu, B.; Zhang, L.M. Machine learning-based intelligent recommendation in virtual mall. In Proceedings of the IEEE Third International Conference on Machine Learning and Cybernetics, Guangzhou, China, 18–21 August 2004; pp. 2634–2639. [Google Scholar]
- Altarteer, S.; Charissis, V. Technology acceptance model for 3D virtual reality system in luxury brands online stores. IEEE Access 2019, 54, 64053–64062. [Google Scholar] [CrossRef]
- Martínez, H.; Skournetou, D.; Hyppölä, J.; Laukkanen, S.; Heikkilä, A. Drivers and bottlenecks in the adoption of augmented reality applications. J. Multimed. Theory Appl. 2014, 1, 27–44. [Google Scholar] [CrossRef]
- Olshannikova, E.; Ometov, A.; Koucheryavy, Y.; Olsson, T. Visualizing Big Data with augmented and virtual reality: Challenges and research agenda. J. Big Data 2018, 2, 1–27. [Google Scholar] [CrossRef]
- Lagoo, R.; Charissis, V.; Harrison, D. Mitigating Driver’s Distraction with the use of Augmented Reality Head-Up Display and Gesture Recognition system. IEEE Consum. Electron. Mag. 2019, 8, 79–85. [Google Scholar] [CrossRef]
- Charissis, V.; Papanastasiou, S. Artificial Intelligence Rationale for Autonomous Vehicle Agents Behaviour in Driving Simulation Environment. Adv. Robot. Autom. Control 2008, 314–332. [Google Scholar]
- Ropelato, S.; Zünd, F.; Magnenat, S.; Menozzi, M.; Sumner, R.W. Adaptive Tutoring on a Virtual Reality Driving Simulator. In Proceedings of the International SERIES on Information Systems and Management in Creative eMedia (CreMedia), Bangkok, Thailand, 27–30 November 2017; pp. 12–17. [Google Scholar]
- Lin, C.T.; Chung, I.F.; Ko, L.W.; Chen, Y.C.; Liang, S.F.; Duann, J.R. EEG-Based assessment of driver cognitive responses in a dynamic virtual-reality driving environment. IEEE Trans. Biomed. Eng. 2007, 54, 1349–1352. [Google Scholar] [PubMed]
- Charissis, V.; Papanastasiou, S. Human-Machine Collaboration Through Vehicle Head-Up Display Interface. Int. J. Cogn. Technol. Work 2010, 12, 41–50. [Google Scholar] [CrossRef]
- Charissis, V.; Papanastasiou, S.; Chan, W.; Peytchev, E. Evolution of a full-windshield HUD designed for current VANET communication standards. In Proceedings of the 2013 IEEE Intelligent Transportation Systems International Conference, The Hague, Netherlands, 6–9 October 2013; pp. 1637–1643. [Google Scholar]
- Wang, S.; Charissis, V.; Lagoo, R.; Campbell, J.; Harrison, D. Reducing Driver Distraction by Utilising Augmented Reality Head-Up Display System for Rear Passengers. In Proceedings of the 2019 IEEE International Conference on Consumer Electronics (ICCE), Las Vegas, NV, USA, 11–13 January 2019; pp. 1–6. [Google Scholar]
- Feng, L.F.; Fei, J. Gesture recognition algorithm based on image information fusion in virtual reality. Pers. Ubiquitous Comput. 2019, 23, 487–497. [Google Scholar]
- Petrovic, V. Artificial Intelligence and Virtual Worlds—Toward Human-Level AI Agents. IEEE Access 2019, 1–6. [Google Scholar] [CrossRef]
- Lim, M.Y.; Dias, J.; Aylett, R.; Paiva, A. Creating adaptive affective autonomous NPCs. Auton. Agents Multi-Agent Syst. 2012, 24, 287–311. [Google Scholar] [CrossRef]
- Zhou, C.N.; Yu, X.L.; Sun, J.Y.; Yan, X.L. Affective computation based NPC behaviors modeling. In Proceedings of the International Conference on Web Intelligence and Intelligent Agent Technology, Madrid, Spain, 21–23 September 2006; pp. 1–4. [Google Scholar]
- Vazquez, D.; Meyer, L.A.; Marın, J.; Ponsa, D.; Geronimo, D. Virtual and Real World Adaptation for Pedestrian Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 797–809. [Google Scholar] [CrossRef]
- Vazquez, D.; Meyer, L.A.; Marın, J.; Ponsa, D.; Geronimo, D. Deep Learning Development Environment in Virtual Reality. CoRR 2019, 1–10. [Google Scholar]
- Harley, A.W. An interactive node-link visualization of convolutional neural networks. Adv. Visual Comput. 2015, 9474, 867–877. [Google Scholar]
- Harley, A.W.; Ufkes, A.; Derpanis, K.G. Evaluation of deep convolutional nets for document image classification and retrieval. In Proceedings of the 13th International Conference on Document Analysis and Recognition (ICDAR), Nancy, France, 23–26 August 2015; pp. 991–995. [Google Scholar]
- Qi, Q.; Tao, F. Digital Twin and Big Data towards smart manufacturing and industry 4.0: 360 degree comparison. IEEE Access 2018, 6, 3585–3593. [Google Scholar] [CrossRef]
- Qiao, Q.; Wang, J.; Ye, L.; Gao, R.X. Digital Twin for machining tool condition prediction. CIRP Conf. Manuf. Syst. 2019, 81, 1388–1393. [Google Scholar] [CrossRef]
- Madni, A.M.; Madni, C.C.; Lucero, S.D. Leveraging Digital Twin Technology in Model-Based Systems Engineering. Systems 2019, 7, 7. [Google Scholar] [CrossRef]
- Jaensch, F.; Csiszar, A.; Scheifele, C.; Verl, A. Digital Twins of Manufacturing Systems as a Base for Machine Learning. In Proceedings of the IEEE 25th International Conference on Mechatronics and Machine Vision in Practice (IEEE M2VIP), Stuttgart, Germany, 20–22 November 2018; pp. 1–13. [Google Scholar]
- Chen, M.; Saad, W.; Yin, C. Virtual Reality Over Wireless Networks: Quality-of-Service Model and Learning-Based Resource Management. IEEE Trans. Commun. 2018, 66, 5621–5635. [Google Scholar] [CrossRef]
- Chen, M.; Saad, W.; Yin, C.; Dbbah, M. Data Correlation-Aware Resource Management in Wireless Virtual Reality (VR): An Echo State Transfer Learning Approach. IEEE Trans. Commun. 2019, 67, 4267–4280. [Google Scholar] [CrossRef]
- Chen, M.; Saad, W.; Yin, C. Echo-Liquid State Deep Learning for 360° Content Transmission and Caching in Wireless VR Networks With Cellular Connected UAVs. IEEE Trans. Commun. 2019, 67, 6386–6400. [Google Scholar] [CrossRef]
- Alkhateeb, A.; Alex, S.; Varkey, P.; Li, Y.; Qu, Q.; Tujkovic, D. Deep Learning Coordinated Beamforming for Highly-Mobile Millimeter Wave Systems. IEEE Access 2019, 6, 37328–37348. [Google Scholar] [CrossRef]
- Strubell, E.; Ganesh, A.; McCallum, A. Energy and Policy Considerations for Deep Learning in NLP. arXiv 2019, arXiv:1906.02243. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frank, M.; Drikakis, D.; Charissis, V. Machine-Learning Methods for Computational Science and Engineering. Computation 2020, 8, 15. https://doi.org/10.3390/computation8010015
Frank M, Drikakis D, Charissis V. Machine-Learning Methods for Computational Science and Engineering. Computation. 2020; 8(1):15. https://doi.org/10.3390/computation8010015
Chicago/Turabian StyleFrank, Michael, Dimitris Drikakis, and Vassilis Charissis. 2020. "Machine-Learning Methods for Computational Science and Engineering" Computation 8, no. 1: 15. https://doi.org/10.3390/computation8010015
APA StyleFrank, M., Drikakis, D., & Charissis, V. (2020). Machine-Learning Methods for Computational Science and Engineering. Computation, 8(1), 15. https://doi.org/10.3390/computation8010015






