Range of Applying the Boundary Condition at Fluid/Porous Interface and Evaluation of Beavers and Joseph’s Slip Coefficient Using Finite Element Method
Abstract
1. Introduction
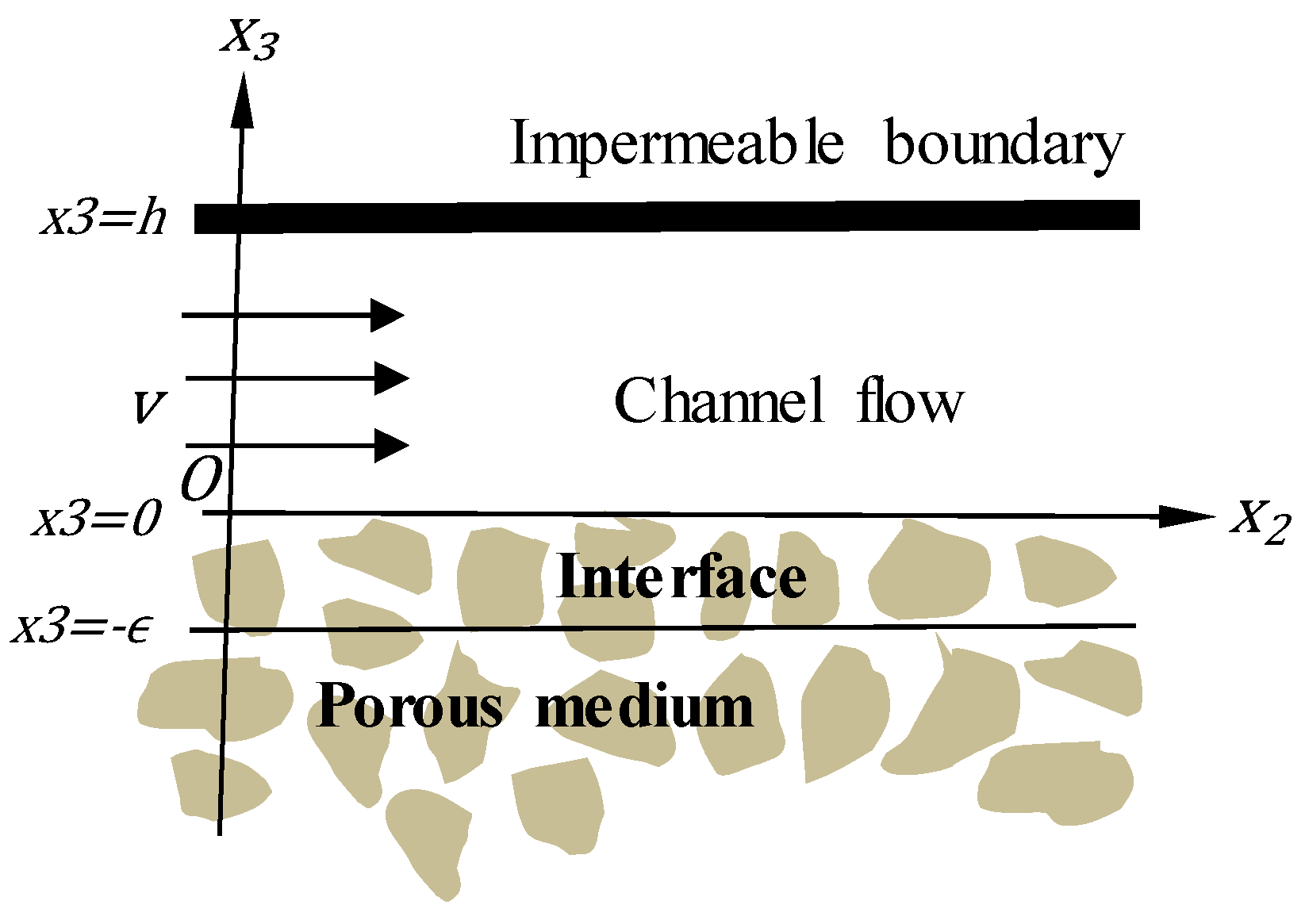
2. Description of the Problem
2.1. Channel Flow
2.2. Flow in the Strict Interior of the Porous Medium
2.3. Flow in the Interface
3. Finite Element Formulation
4. The Velocity in the Interface
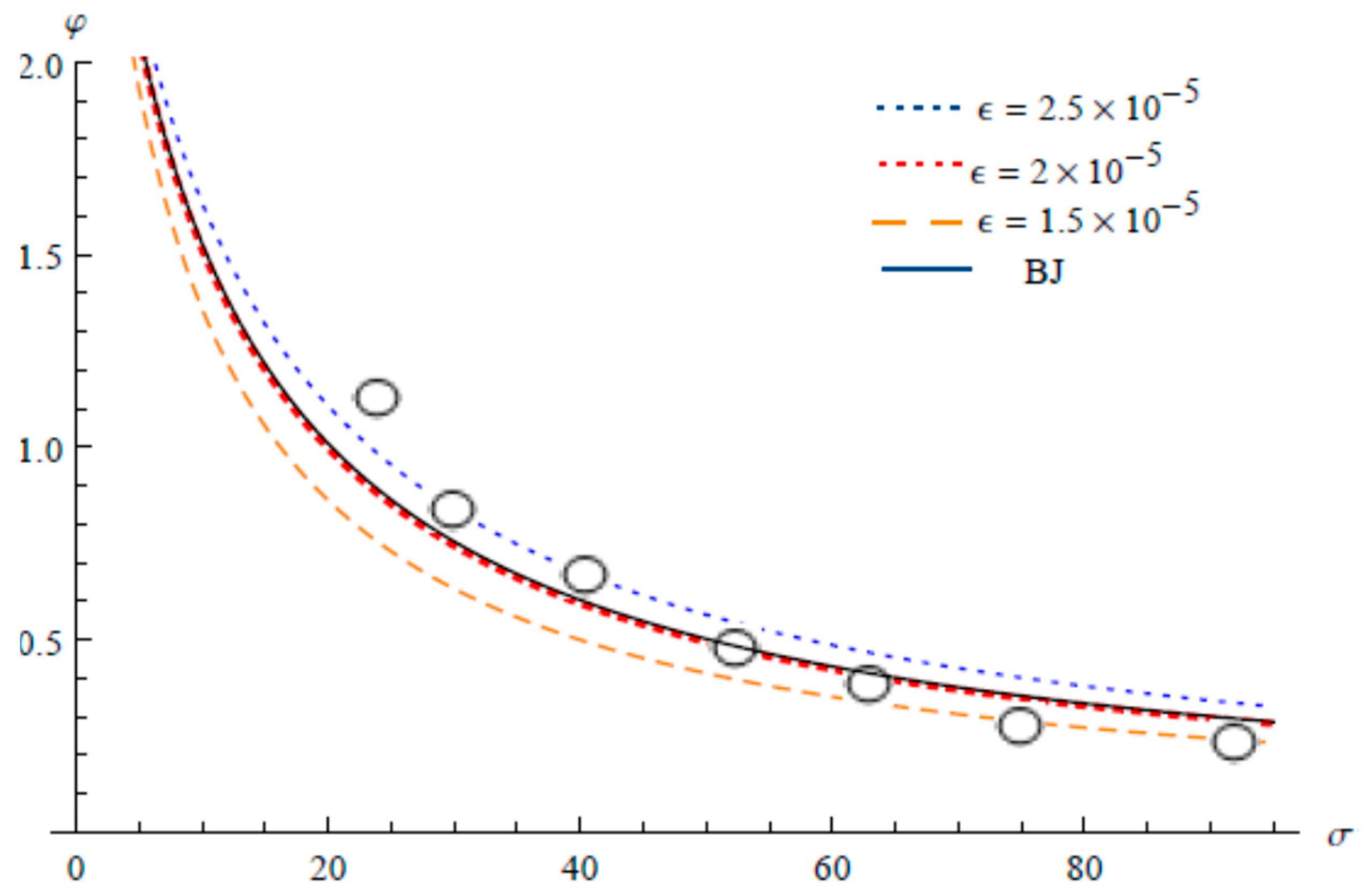
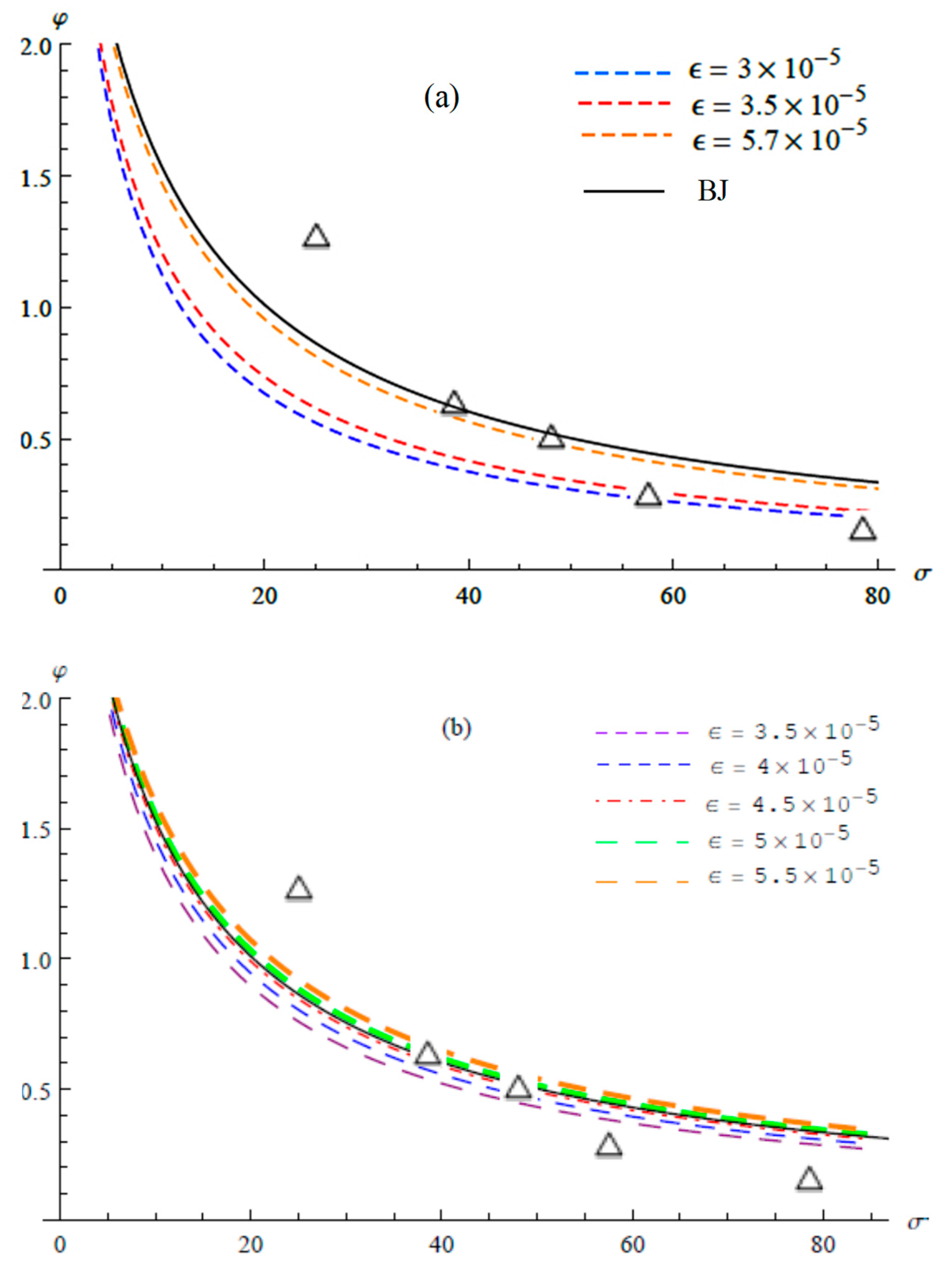
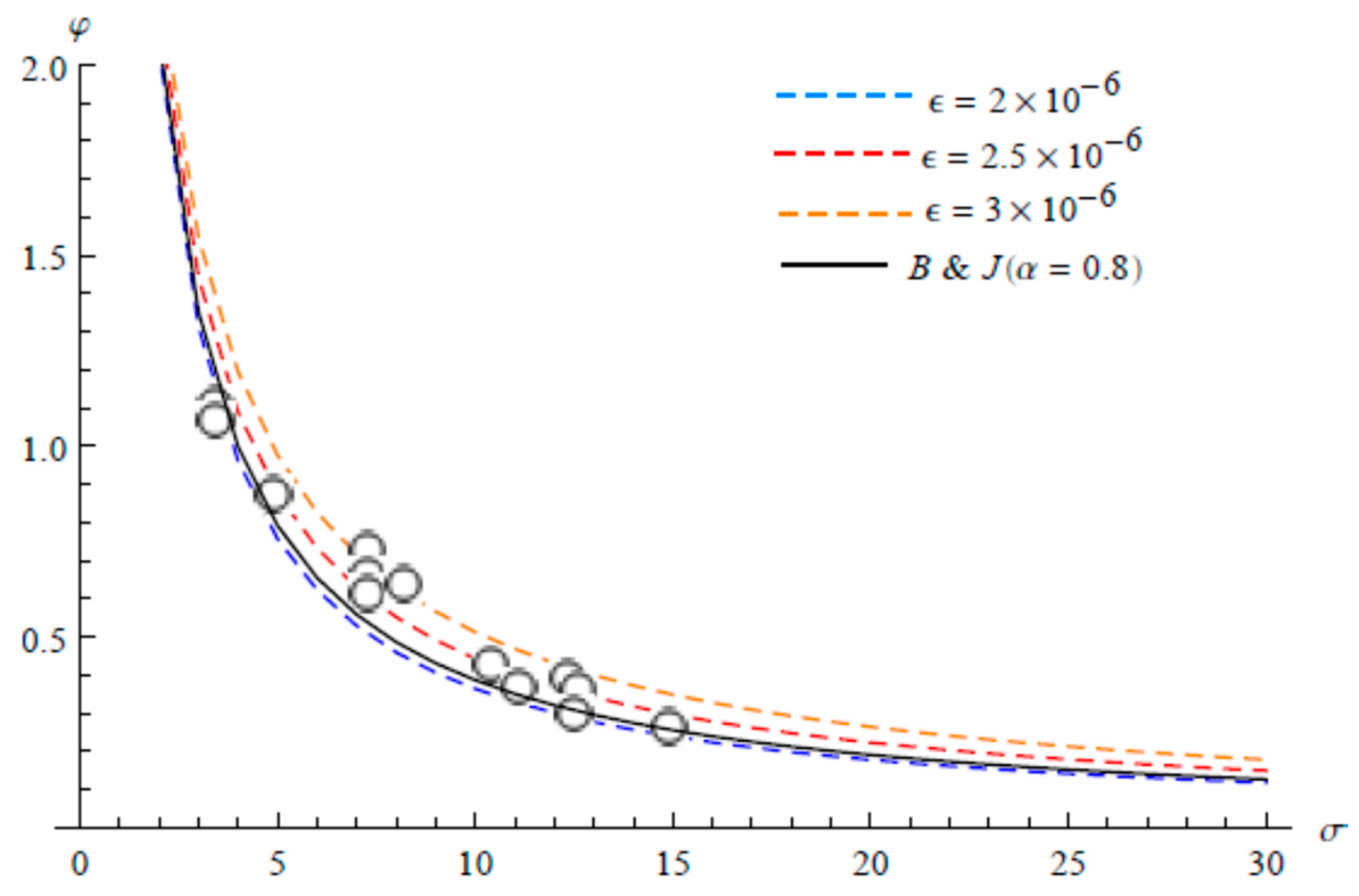
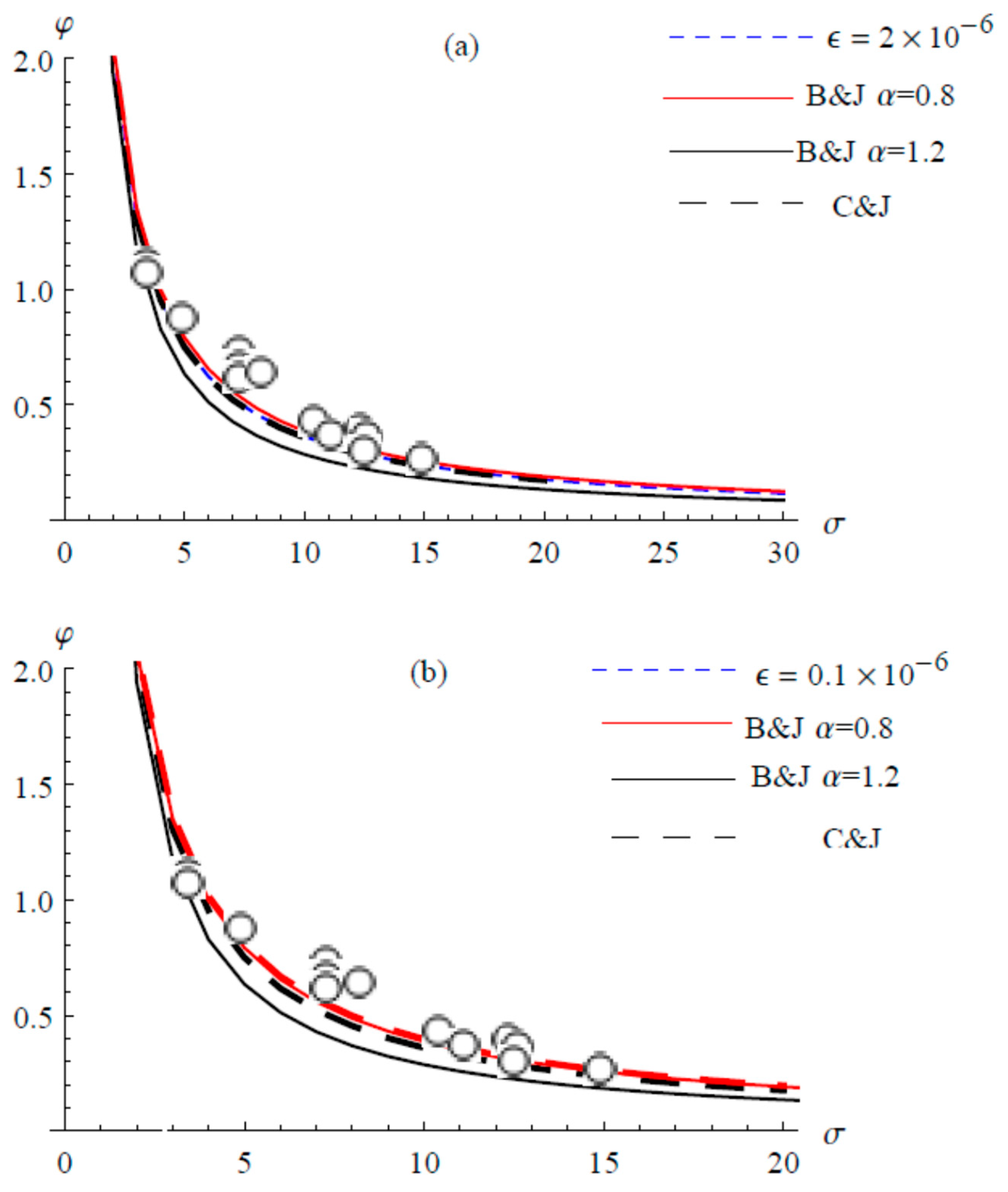
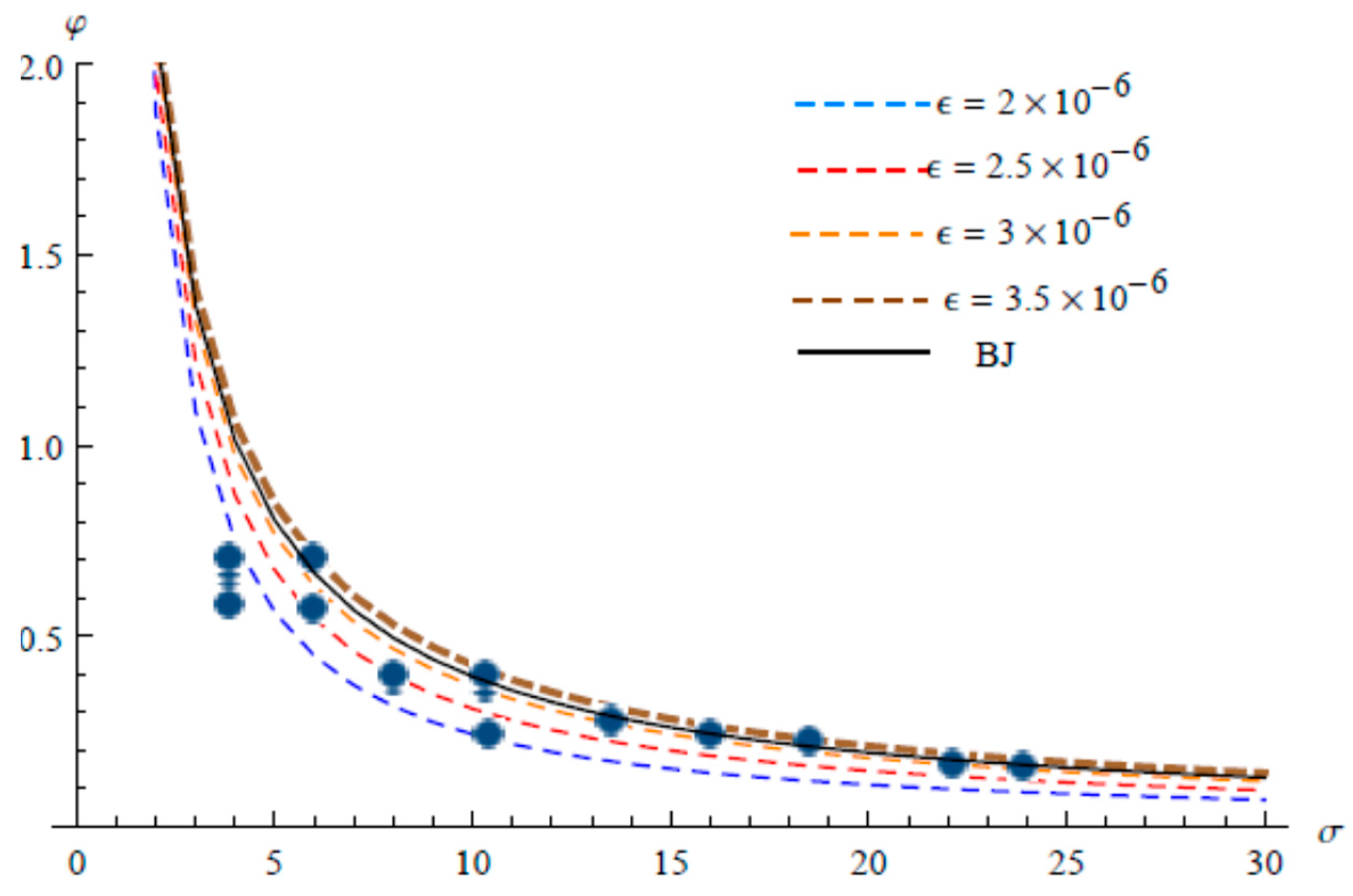
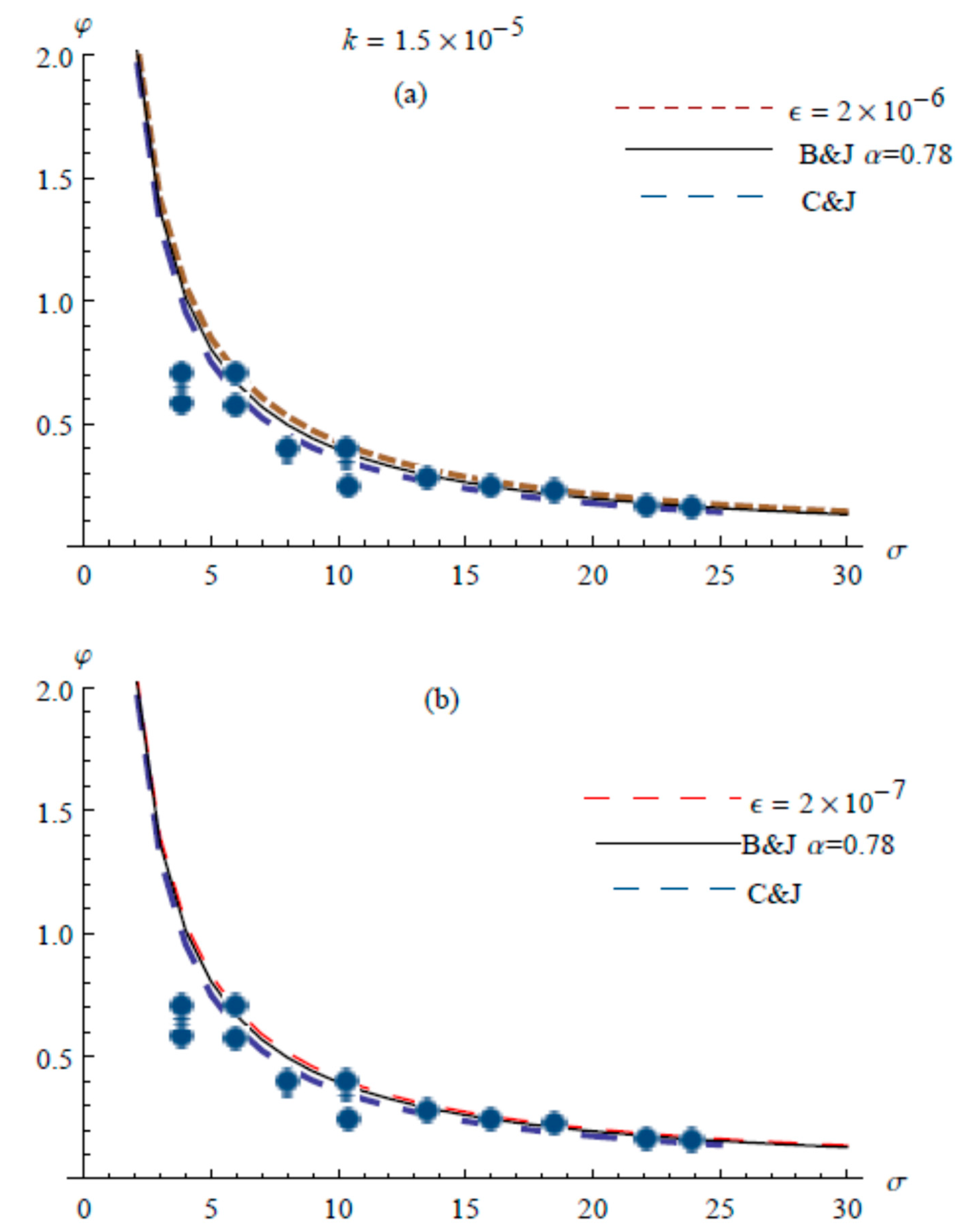
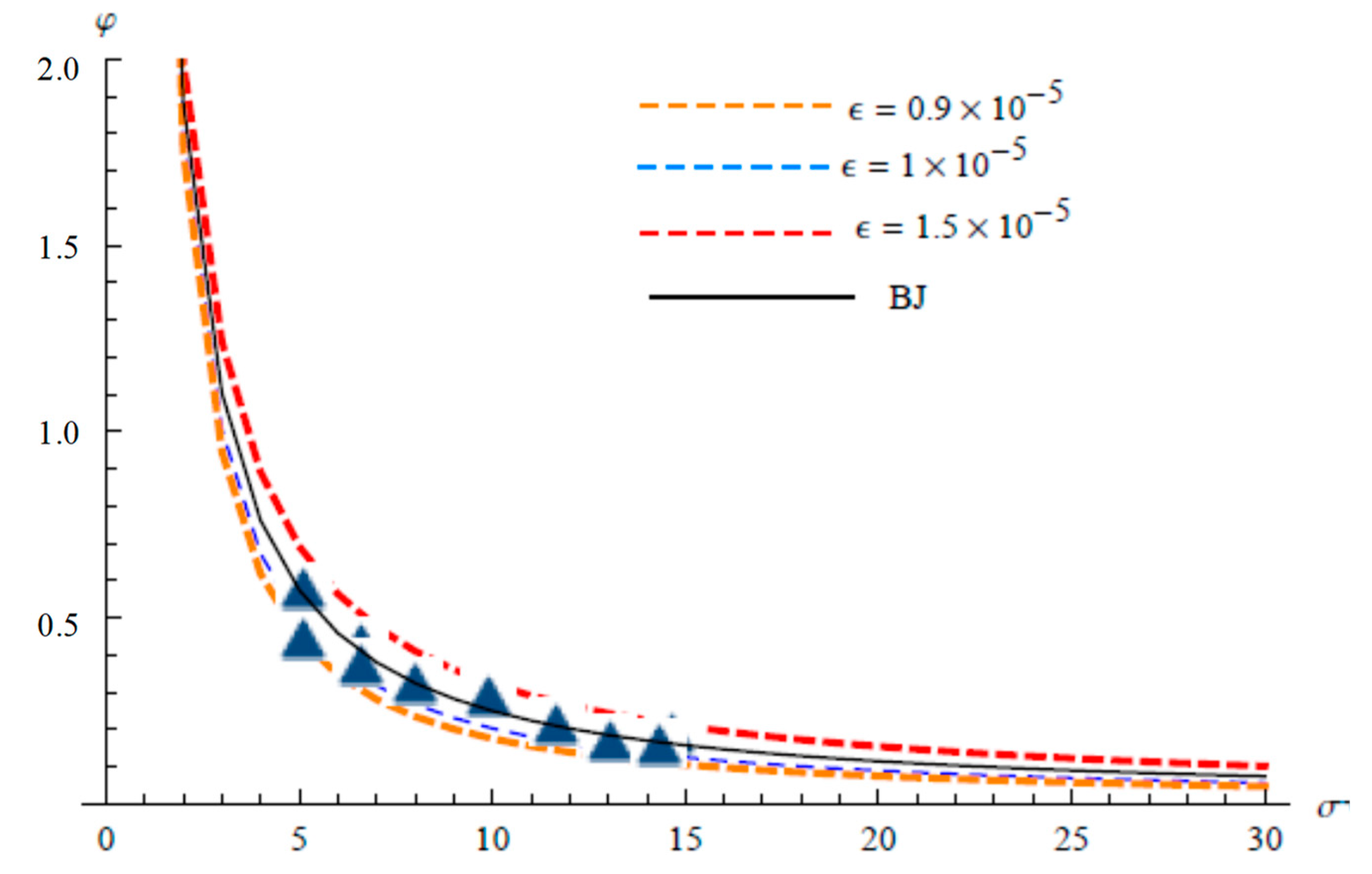
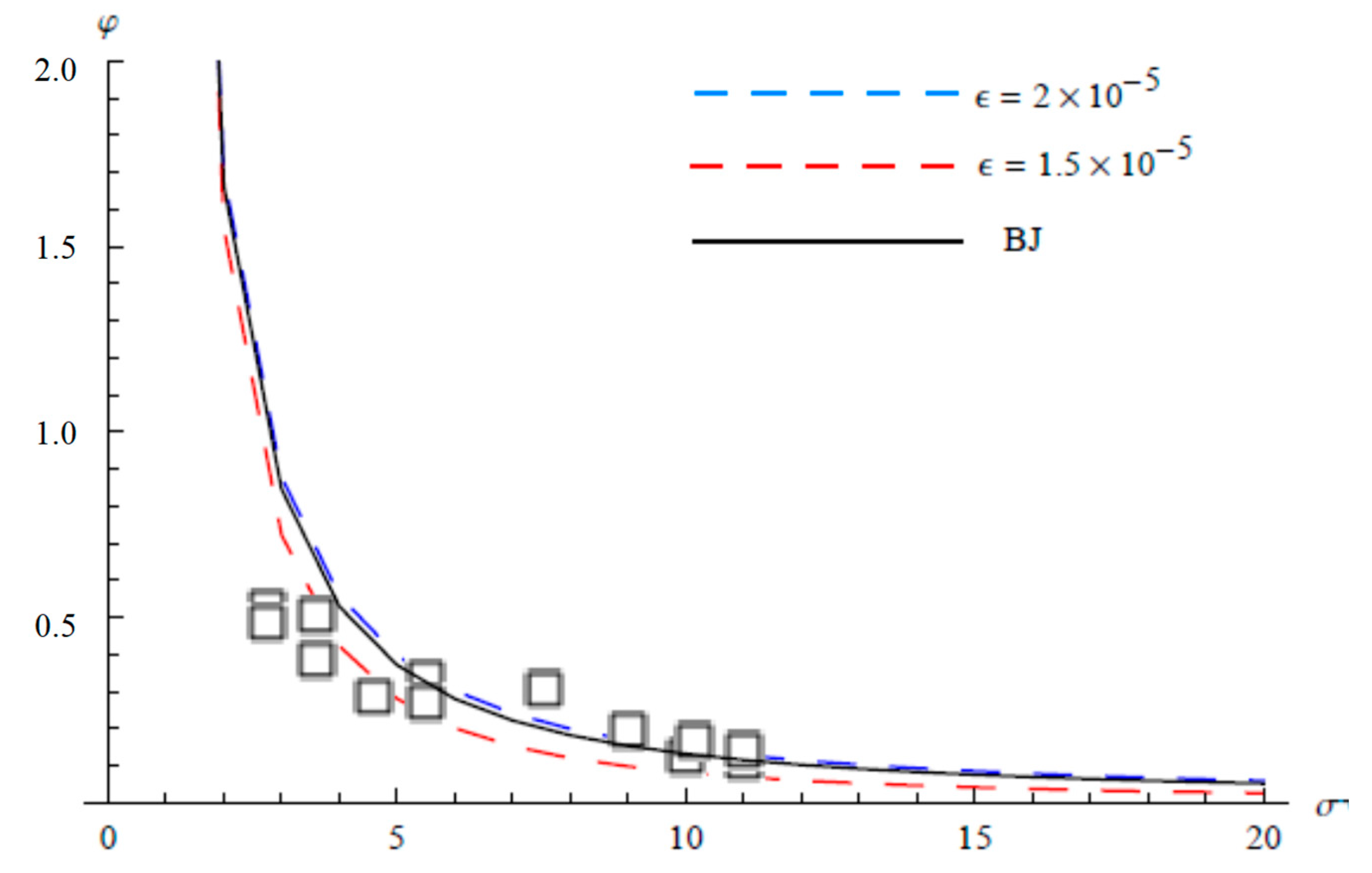
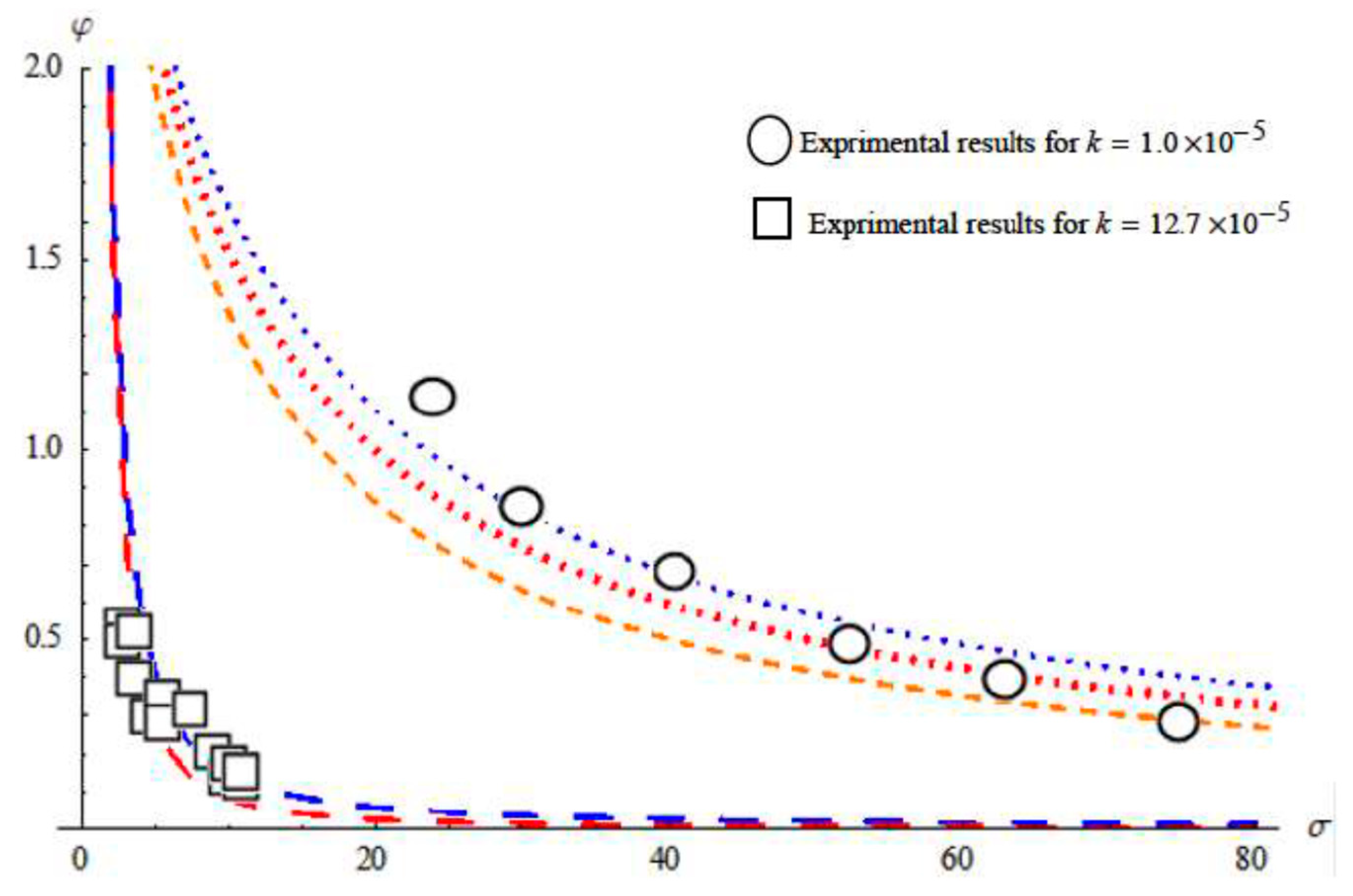
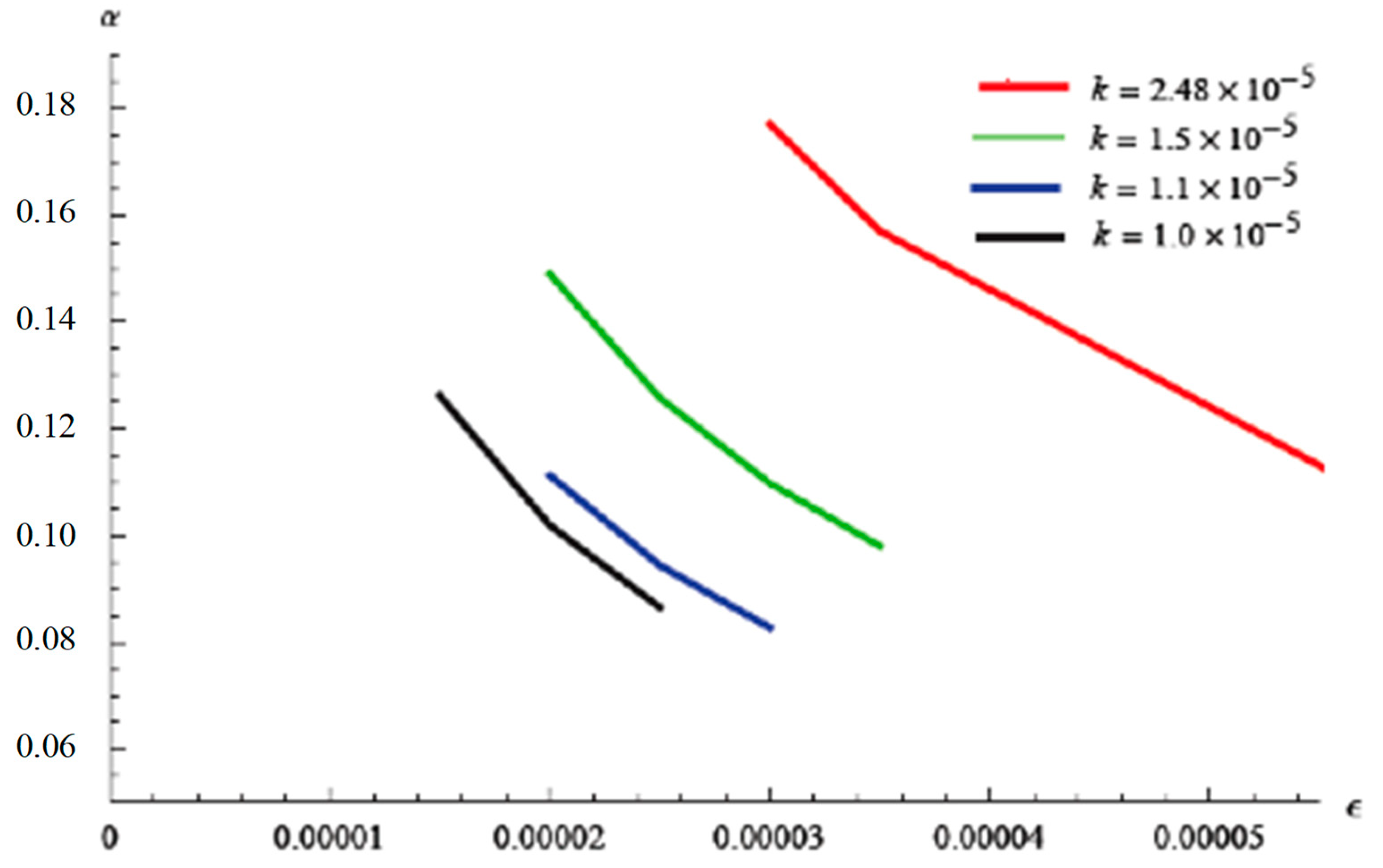
5. Comparisons with Experimental Data and Analytical Solution
6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Carraro, T.; Goll, C.; Marciniak-Czochra, A.; Mikelic, A. Effective interface conditions for the forced infiltration of a viscous fluid into a porous medium using homogenization. Comput. Methods Appl. Mech. Eng. 2015, 292, 195–220. [Google Scholar] [CrossRef]
- Beavers, G.S.; Joseph, D.D. Boundary conditions at a naturally permeable wall. J. Fluid Mech. 1967, 30, 197–207. [Google Scholar] [CrossRef]
- Saffman, P.G. On the boundary condition at the interface of a porous medium. Stud. Appl. Math. 1971, 1, 93–101. [Google Scholar] [CrossRef]
- Carraro, T.; Goll, C.; Marciniak-Czochra, A.; Mikelic, A. Pressure jump interface law for the Stokes—Darcy coupling: Confirmation by direct numerical simulations. J. Fluid Mech. 2013, 732, 510–536. [Google Scholar] [CrossRef]
- Kaviany, M. Principles of Heat Transfer in Porous Media, 2nd ed.; Springer: New York, NY, USA, 1995; pp. 71–78. [Google Scholar]
- Sahraoui, M.; Kaviany, M. Slip and no-slip velocity boundary conditions at interface of porous, plain media. Int. J. Heat Mass Transf. 1992, 35, 927–943. [Google Scholar] [CrossRef]
- Marciniak-Czochra, A.; Mikelic, A. Effective pressure interface law for transport phenomena between an unconfined fluid and a porous medium using homogenization. Multiscale Model. Simul. 2012, 10, 285–305. [Google Scholar] [CrossRef]
- Jäger, W.; Mikelic, A. On the interface boundary conditions by Beavers, Joseph and Saffman. J. Appl. Math. 2000, 60, 1111–1127. [Google Scholar]
- Jäger, W.; Mikelic, A.; Neuß, N. Asymptotic analysis of the laminar viscous flow over a porous bed. J. Sci. Stat. Comput. 2001, 22, 2006–2028. [Google Scholar] [CrossRef]
- Murdoch, A.I.; Soliman, A. On the slip-boundary condition for liquid flow over planar porous boundaries. Proc. R. Soc. Lond. A 1999, 455, 1315–1340. [Google Scholar] [CrossRef]
- Chandesris, M.; Jamet, D. Boundary conditions at a planar fluid-porous interface for a Poiseuille flow. Int. J. Heat Mass Transf. 2006, 49, 2137–2150. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Rezaeianjouybari, B.; Darzi, M.; Shafee, A.; Li, Z.; Nguyen, T.K. Application of nano-refrigerant for boiling heat transfer enhancement employing an experimental study. Int. J. Heat Mass Transf. 2019, 141, 974–980. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Haq, R.; Shafee, A.; Li, Z. Heat transfer behavior of nanoparticle enhanced PCM solidification through an enclosure with V shaped fins. Int. J. Heat Mass Transf. 2019, 130, 1322–1342. [Google Scholar] [CrossRef]
- Sheikholeslami, M. Simulation of nanofluid flow and natural convection in a porous media under the influence of electric field using CVFEM. Int. J. Heat Mass Transf. 2018, 120, 772–781. [Google Scholar] [CrossRef]
- Hutton, D. Fundamentals of Finite Element Analysis; Mc GRAW HILL: Boston, MA, USA, 2004; pp. 131–156. [Google Scholar]
- Fahmy, M.A. A time-stepping DRBEM for magneto-thermo-viscoelastic interactions in a rotating nonhomogeneous anisotropic solid. Int. J. Appl. Mech. 2011, 3, 711–734. [Google Scholar] [CrossRef]
- Fahmy, M.A. A time-stepping DRBEM for the transient magneto-thermo-visco-elastic stresses in a rotating non-homogeneous anisotropic solid. Eng. Anal. Bound. Elem. 2012, 36, 335–345. [Google Scholar] [CrossRef]
- Fahmy, M.A. Transient magneto-thermoviscoelastic plane waves in a non-homogeneous anisotropic thick strip subjected to a moving heat source. Appl. Math. Model. 2012, 36, 4565–4578. [Google Scholar] [CrossRef]
- Fahmy, M.A. Numerical modeling of transient magneto-thermo-viscoelastic waves in a rotating nonhomogeneous anisotropic solid under initial stress. Int. J. Model. Simul. Sci. Comput. 2012, 3, 1250002. [Google Scholar] [CrossRef]
- Fahmy, M.A. The effect of rotation and inhomogeneity on the transient magneto-thermoviscoelastic stresses in an anisotropic solid. ASME J. Appl. Mech. 2012, 79, 1015. [Google Scholar] [CrossRef]
- Fahmy, M.A. Transient magneto-thermo-viscoelastic stresses in a rotating nonhomogeneous anisotropic solid with and without a moving heat source. J. Eng. Phys. Thermophys. 2012, 85, 950–958. [Google Scholar] [CrossRef]
- Fahmy, M.A. Transient magneto-thermo-elastic stresses in an anisotropic viscoelastic solid with and without moving heat source. Numer. Heat Transf. Part A Appl. 2012, 61, 547–564. [Google Scholar] [CrossRef]
- Fahmy, M.A. Implicit-Explicit time integration DRBEM for generalized magneto-thermoelasticity problems of rotating anisotropic viscoelastic functionally graded solids. Eng. Anal. Bound. Elem. 2013, 37, 107–115. [Google Scholar] [CrossRef]
- Fahmy, M.A. Generalized magneto-thermo-viscoelastic problems of rotating functionally graded anisotropic plates by the dual reciprocity boundary element method. J. Therm. Stresses 2013, 36, 284–303. [Google Scholar] [CrossRef]
- Fahmy, M.A. A three-dimensional generalized magneto-thermo-viscoelastic problem of a rotating functionally graded anisotropic solids with and without energy dissipation. Numer. Heat Transf. Part A Appl. 2013, 63, 713–733. [Google Scholar] [CrossRef]
- Fahmy, M.A. A Computerized DRBEM model for generalized magneto-thermo-visco-elastic stress waves in functionally graded anisotropic thin film/substrate structures. Latin Am. J. Solids Structures 2014, 11, 386–409. [Google Scholar] [CrossRef]
- Fahmy, M.A. Shape design sensitivity and optimization for two-temperature generalized magneto-thermoelastic problems using time-domain DRBEM. J. Therm. Stresses 2018, 41, 119–138. [Google Scholar] [CrossRef]
- Fahmy, M.A. Shape design sensitivity and optimization of anisotropic functionally graded smart structures using bicubic B-splines DRBEM. Eng. Anal. Bound. Elem. 2018, 87, 27–35. [Google Scholar] [CrossRef]
- Fahmy, M.A. Modeling and Optimization of Anisotropic Viscoelastic Porous Structures Using CQBEM and Moving Asymptotes Algorithm. Arabian J. Sci. Eng. 2019, 44, 1671–1684. [Google Scholar] [CrossRef]
- Fahmy, M.A. A new LRBFCM-GBEM modeling algorithm for general solution of time fractional order dual phase lag bioheat transfer problems in functionally graded tissues. Numer. Heat Transf. Part A Appl. 2019, 75, 616–626. [Google Scholar] [CrossRef]
- Fahmy, M.A. Design Optimization for A Simulation of Rotating Anisotropic Viscoelastic Porous Structures Using Time-Domain OQBEM. Math. Comput. Simul. 2019, 66, 193–205. [Google Scholar] [CrossRef]
- Fahmy, M.A. A new convolution variational boundary element technique for design sensitivity analysis and topology optimization of anisotropic thermo-poroelastic structures. Arab J. Basic Appl. Sci. 2020, 27, 1–12. [Google Scholar] [CrossRef]
- Fahmy, M.A. A New Computerized Boundary Element Algorithm for Cancer Modeling of Cardiac Anisotropy on the ECG Simulation. Asian J. Res. Comput. Sci. 2018, 2, 1–10. [Google Scholar] [CrossRef][Green Version]
- Fahmy, M.A. Boundary Element Algorithm for Modeling and Simulation of Dual Phase Lag Bioheat Transfer and Biomechanics of Anisotropic Soft Tissues. Int. J. Appl. Mech. 2018, 10, 1850108. [Google Scholar] [CrossRef]
- Fahmy, M.A. Boundary Element Modeling and Simulation of Biothermomechanical Behavior in Anisotropic Laser-Induced Tissue Hyperthermia. Eng. Anal. Bound. Elem. 2019, 101, 156–164. [Google Scholar] [CrossRef]
| Porous Species | for Beavers and Joseph | |||
|---|---|---|---|---|
| Fometal | ||||
| Fometal A | ||||
| Fometal B | ||||
| Fometal C | ||||
| Aloxite A | ||||
| Aloxite B |
| Porous Species | for Beavers and Joseph | |||
|---|---|---|---|---|
| Fometal | ||||
| Fometal A | 0.815955 – 0.657912 | |||
| Aloxite B | 3.5–5.5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soliman, A.H.; Fahmy, M.A. Range of Applying the Boundary Condition at Fluid/Porous Interface and Evaluation of Beavers and Joseph’s Slip Coefficient Using Finite Element Method. Computation 2020, 8, 14. https://doi.org/10.3390/computation8010014
Soliman AH, Fahmy MA. Range of Applying the Boundary Condition at Fluid/Porous Interface and Evaluation of Beavers and Joseph’s Slip Coefficient Using Finite Element Method. Computation. 2020; 8(1):14. https://doi.org/10.3390/computation8010014
Chicago/Turabian StyleSoliman, Azza Hassan, and Mohamed Abdelsabour Fahmy. 2020. "Range of Applying the Boundary Condition at Fluid/Porous Interface and Evaluation of Beavers and Joseph’s Slip Coefficient Using Finite Element Method" Computation 8, no. 1: 14. https://doi.org/10.3390/computation8010014
APA StyleSoliman, A. H., & Fahmy, M. A. (2020). Range of Applying the Boundary Condition at Fluid/Porous Interface and Evaluation of Beavers and Joseph’s Slip Coefficient Using Finite Element Method. Computation, 8(1), 14. https://doi.org/10.3390/computation8010014






